1. Introduction
Of all environmental stresses, drought causes the greatest losses in global agricultural production [
1,
2,
3,
4]. In response to the severe effects of this abiotic stress on plant growth and development, breeding is an effective tool to reduce the vulnerability of crops [
5]. Breeders have developed studies to understand the morphological, physiological, and agronomic responses of water-stressed plants, as well as to select higher-yield genotypes of the major crops under water stress [
1,
2,
6,
7,
8] with a view to mitigating the effects of climate change, mainly perceptible in the poor temporal and spatial distribution of rainfall.
Abiotic stresses are deleterious environmental influences on the plant life cycle and affect crop growth and structure development, preventing the expression of the full genetic potential [
9]. In this sense, water stress causes physiological and biochemical disturbances in plants, which can result in reduced leaf expansion and metabolic cell activity, stomatal closure, photosynthesis inhibition, and changes in carbon partitioning, among others, thus reducing yields [
9,
10].
Understanding the genetic basis of agronomically and economically important traits is one of the initial phases of breeding programs for higher yields in water-stressed environments. In this sense, diallel crosses have been widely used for parent selection and the study of the genetic mode of action (additive or non-additive effects) under full irrigation and water stress conditions [
2,
11]. However, other basic information about the mechanism of gene action and trait inheritance is scarce, e.g., the number of genes involved and the mean degree of dominance and heritability. For specialty maize types, such as popcorn, studies addressing drought adaptation [
8] or analyses of the gene action in the control of the relevant crop traits are even rarer.
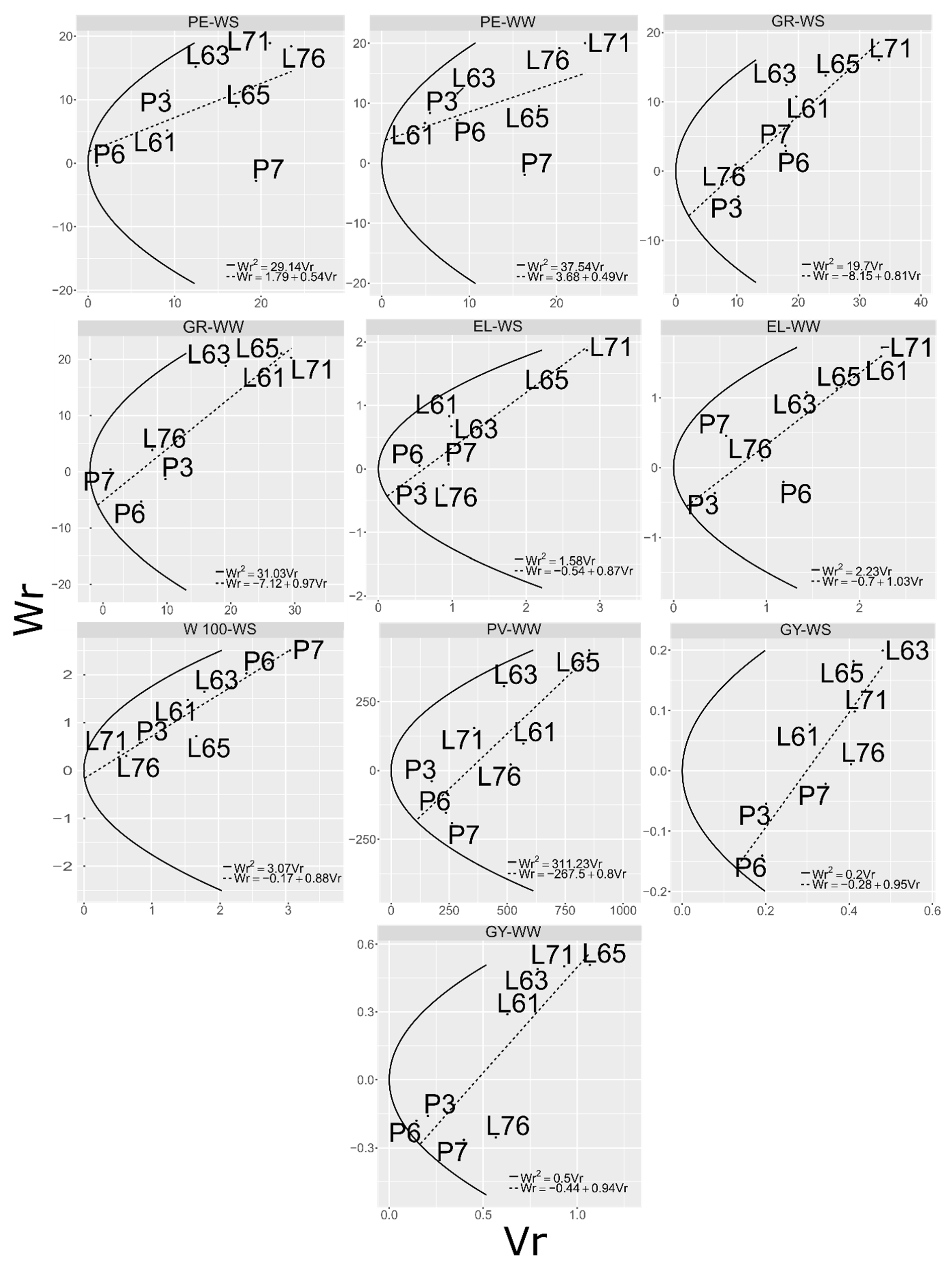
A robust option for the study of inheritance is the methodology of Hayman [
12]. This method is not based on previously established statistical models, but on knowledge about the environmental and genetic nature of statistics, such as means, variances, and covariances, listed in a diallel table. This is an interesting approach, in particular because it exempts the need to establish the F
2 generation, instead requiring only the parents and F
1. The application of the methodology requires some assumptions, as pointed out by Hayman [
12], namely: (a) Diploid segregation, (b) parental homozygosis, (c) no maternal effects, (d) no multiple allelism, (e) independent distribution of parents, and (f) no epistasis.
Studies on the genetic effects on trait inheritance of popcorn under full irrigation [
13,
14,
15,
16,
17] and under biotic stress [
18,
19], and among these, those using Hayman’s diallel analysis [
15,
20], showed that the gene action of popping expansion is additive while that of grain yield and related components is mostly non-additive. For popcorn in water-stressed environments, this information is not available. Thus, the following questions arise: What is the mode of gene action of traits of drought-stressed popcorn? Is the mode of gene action of the traits the same under full irrigation and drought? Can the same breeding methods be used for both cultivation conditions?
The objective of this study was to determine the inheritance patterns of economically important popcorn traits under different water availability conditions. An additional objective was to estimate the number of genes involved in drought stress tolerance as well as the mean degree of dominance, trait heritability, and other genetic parameters and components by Hayman’s methodology to establish a guideline for choosing the best-suited strategies for breeding programs for improved genotypes.
2. Materials and Methods
Twenty-eight simple popcorn hybrids and the eight parents were evaluated under contrasting water regimes, in a full diallel mating scheme without reciprocals. The parents were selected from a group of 20 lines of the UENF (Universidade Estadual do Norte Fluminense Darcy Ribeiro) genebank, 3 of which were high-yielding (P3, P6, and P7), 3 were low-yielding (L61, L63, and L65), and 2 were intermediate (L71 and L76) under drought stress [
8]. This set of parents were selected in this way to meet the assumptions of allelic symmetry for grain yield under drought stress, as defined by the methodology of Hayman [
12].
The use of a limited number of parents (
p < 10) and the fixed genetic model is suggested by Hayman [
12] to improve the effectiveness of its diallel methodology and to prevent estimates of genetic parameters from being compromised by assumption failures. For this reason, the analysis was performed with 8 parents. It was also decided not to use reciprocal hybrids because normally, there are no reciprocal effects for grain yield traits under well-irrigated [
17,
21] and water-stress conditions [
11,
22].
The experiments were initiated in a low rainfall period, i.e., from May to August (autumn/winter), at the "Antonio Sarlo" State College of Agriculture, Campos dos Goytacazes—RJ, in 2018. The phenotypic traits of plants grown at two levels of water availability were evaluated: The first level consisted of adequate irrigation—well-watered (WW) conditions, maintaining soil moisture at field capacity (−0.01 MPa) and the second level consisted of irrigation suspension between the phenological stages pre-flowering (10 days before flowering) and grain filling—water stress (WS). We tried to compare whether the genetic effects present under well-irrigated conditions were the same under water stress. Therefore, water stress was applied during the period considered critical for the crop (flowering and grain filling) [
23,
24].
To control the irrigation level, a drip system (flow rate 2.3 mm h
−1) with one katif dripper per plant was used under both water regimes. The soil water potential was monitored by Decagon MPS-6 tensiometers installed between plants, at a depth of 0.20 m. The well-watered environment was irrigated whenever necessary to maintain field capacity. The weekly applied irrigation levels are listed in
Table 1. In the WS treatment, irrigation was suspended 10 days before the date of male flowering (
Table 1). The soil water potential was monitored throughout the experiment (
Figure S1).
The WS environment was watered with 217.5 mm and the WW with 335.1 mm (
Table 1). Rainfall during the experiment was measured by an automatic weather station of the National Institute of Meteorology (INMET), installed at the experimental site (
Table 1). The mean temperature was 22 °C, relative air humidity was 77%, and the photosynthetic photon flow was 1208 μmol m
2 s
−1 (
Figure S2).
In the water-stressed environment, the soil reached the permanent wilting point (−1.5 MPa) twice (
Figure S1)—the first time during flowering (68 days after sowing) and the second during grain filling (90 days after sowing).
The experiment was arranged in a randomized complete block design with three replications. Each plot consisted of one 4.80-m row, with plants spaced 0.20 m and rows 0.80 m apart, with a total of 23 plants per row. Three seeds per planting hole were sown in the conventional planting system. Fertilization at sowing consisted of 30 kg N ha−1 (as urea), 60 kg P2O5·ha−1 (triple superphosphate), and 60 kg K2O ha−1 (potassium chloride). In the stage of two well-defined leaves, the stand was thinned to 5 plants m−1. About 30 days after sowing, 100 kg N ha −1 (as urea) was applied.
The following traits were assessed: Mean grain number per row (GR), by counting; ear diameter (ED), measured with a caliper (cm); ear length (EL), measured with a ruler (cm); 100-grain weight (W100), by weighing and averaging (g) two 100-grain samples per plot; grain yield (GY), weighed after threshing the ears of each plot and corrected to 13% moisture (kg.ha−1); popping expansion (PE), by measuring the volume of a 30 g grain sample irradiated in a special microwaveable paper bag at 1000 W for 2 min 10 s in a beaker and expressed as the ratio of popcorn volume by grain weight (in mL.g−1); and expanded popcorn volume per hectare (PV), by multiplying GY and PE (m3 ha−1).
The statistical design used for the experiment was based on a combined analysis between water conditions, i.e.,
, where
is the ith genotype in the jth water condition in the kth block;
is the general constant;
_i is the fixed effect of the ith genotype;
is the effect of the ith block within environment j;
is the fixed effect of the jth water condition, with NID(0, σ
2);
is the fixed effect of the interaction between the ith genotype with the jth water condition with NID (0, σ
2); and
is the random experimental error associated with the Y_ijk observation, with NID (0, σ
2). As it is not possible to perform a combined analysis by the Hayman diallel [
12], it was decided to present only the individual analysis for each water condition.
The data were subjected to individual variance analysis for each water regime (WS and WW), based on the statistical model: , where o is the observed value of the ith genotype in the jth block; μ is the general constant; is the fixed effect attributed to the ith genotype; is the effect of block j; and is the random error associated with observation , normally independently distributed (NID) (0, σ2).
Hayman’s diallel analysis [
12] is based on previously established statistical models, associated with knowledge of the environmental and genetic nature of statistics, such as means, variances, and covariance. This method imposes the following assumptions: Homozygous parents, diploid segregation, absence of maternal effect, absence of multiple allelism, genes independently distributed among parents, and absence of epistasis. The parameters are obtained from a diallel table involving p homozygous parents. These are supposed to differ by one locus (T/t), while there is still a proportion of u with favorable alleles and another with unfavorable alleles [
24]. It is also considered that the genes in question have an independent distribution among the parents, and the genotypic values related to the TT, Tt, and tt genotypes are, respectively, dt, ht, and −dt. It is assumed that, normally, between hybrids and their reciprocal, there are no differences. Thus, the diallel table uses symmetry, in which the hybrid combination is represented by (Y
ij + Y
ji)/2. Thus, considering only the environmental (residual) components, we have: E (Y
2ii) = ε; E (Y
2ij) = ½ ε, where ε and ε ’are the residual variances associated, respectively, with parents and hybrids.
Thereafter, the Hayman diallel analysis [
12] was performed. To validate the assumptions of Hayman (1954), the sufficiency of the model was evaluated. It was tested based on linear regression analysis of
(covariance between parent means and the mean of crosses between the parents) as a function of
(variance between the mean of the cross between parents). Thus, two tests were performed: The first tested whether the regression coefficient did not differ from 1 and the hypothesis was evaluated by the t-test, associated with p − 2 degrees of freedom; the second was based on the t-statistic, a test that weighted
(covariance between parent means and ith means and variance between means of the ith line, respectively) by a 45° rotation of the axes represented by
and
. Based on the new values of
and
, hypothesis H0 was tested: b’: 0 (b’ is the regression coefficient after rotation) by the t or F test, associated with 1 and p − 2 degrees of freedom.
Then, the genetic and environmental components were estimated:
is the environmental variance component, represented by the mean square error (experimental error);
is the variance component associated with additive effects; a
are the variance components associated with dominance deviations;
is the quadratic component determined by the difference between hybrid and parent means;
is the component associated with covariance between additive and non-additive effects; and
is the component expressing the difference between additive and dominant gene effects. In addition, the following genetic parameters were estimated:
is the mean degree of dominance;
is the distance between alleles (symmetry);
is the dominant/recessive ratio;
is the number of dominant genes;
is the determination coefficient in the narrow sense;
is the determination coefficient in the broad sense; correlations between the mean values of parents (
) and the sum of covariance between parent means and means of the
line (
) and the variance between means of the
line (
); expected coordinate values
; and
and the predicted value for the parent with the maximum number of dominant (
) and recessive (
) alleles. The terms’ components and parents were used as explained by Hayman [
12] and Cruz et al. [
25]. For the genetic statistical analysis, the genotype effect was considered fixed. The analyses were performed with software GENES [
26].