Quantitative Trait Loci (QTL) Identification in the Progeny of a Polycross
Abstract
:1. Introduction
2. Results
2.1. Paternity Identification
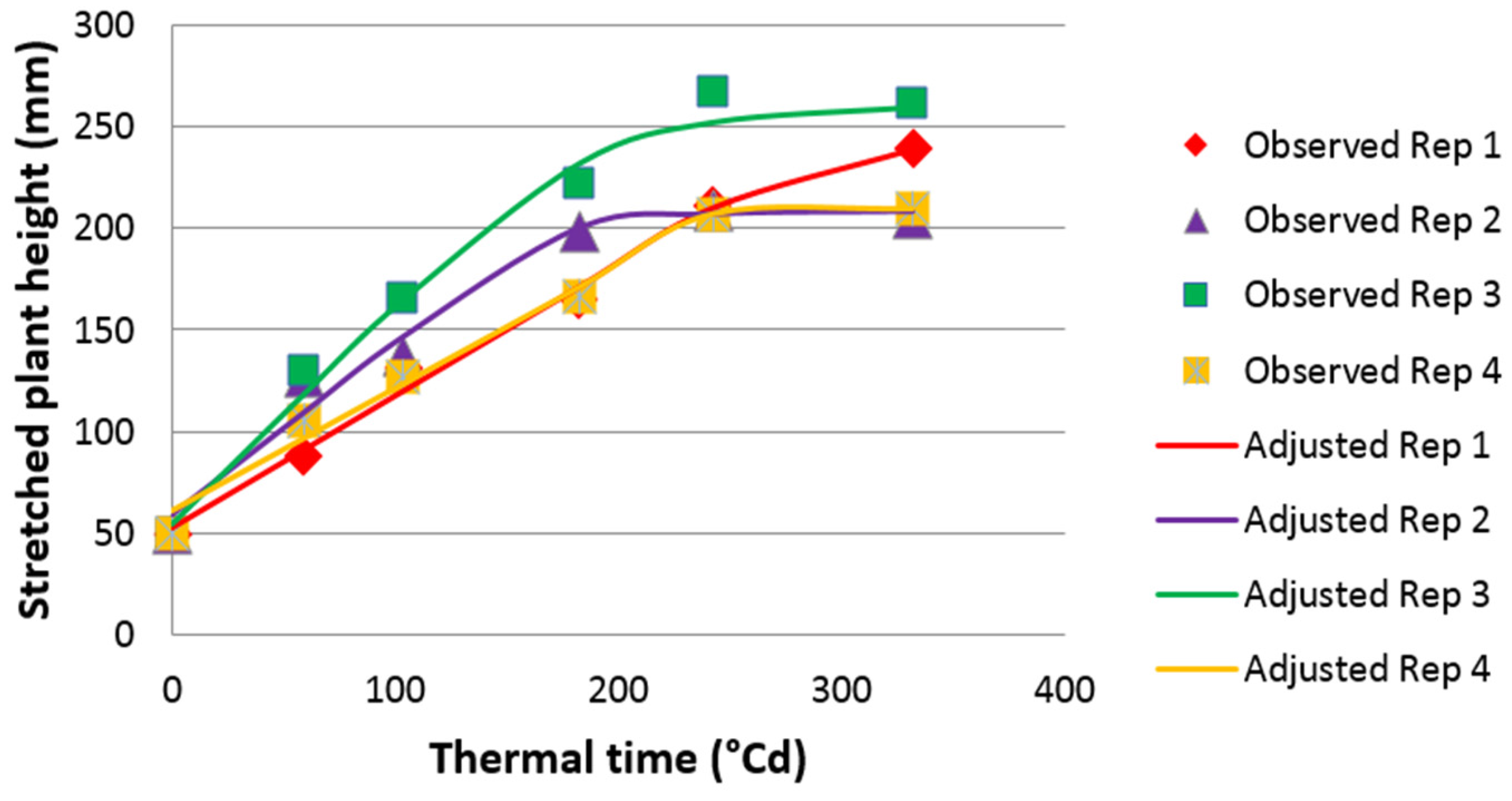
2.2. Phenotypic Analyses
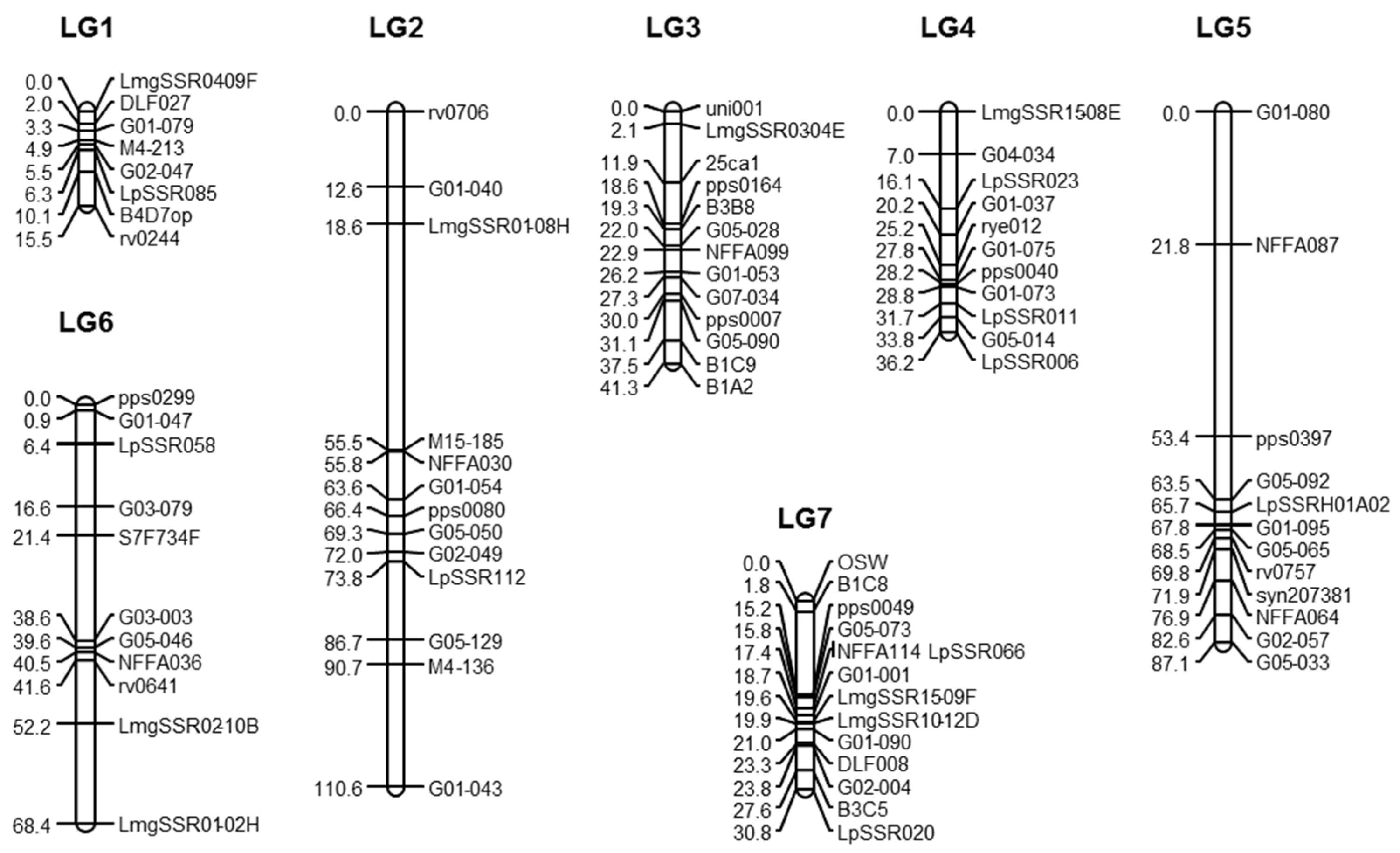
2.3. Genetic Map
2.4. QTL Identification
3. Discussion
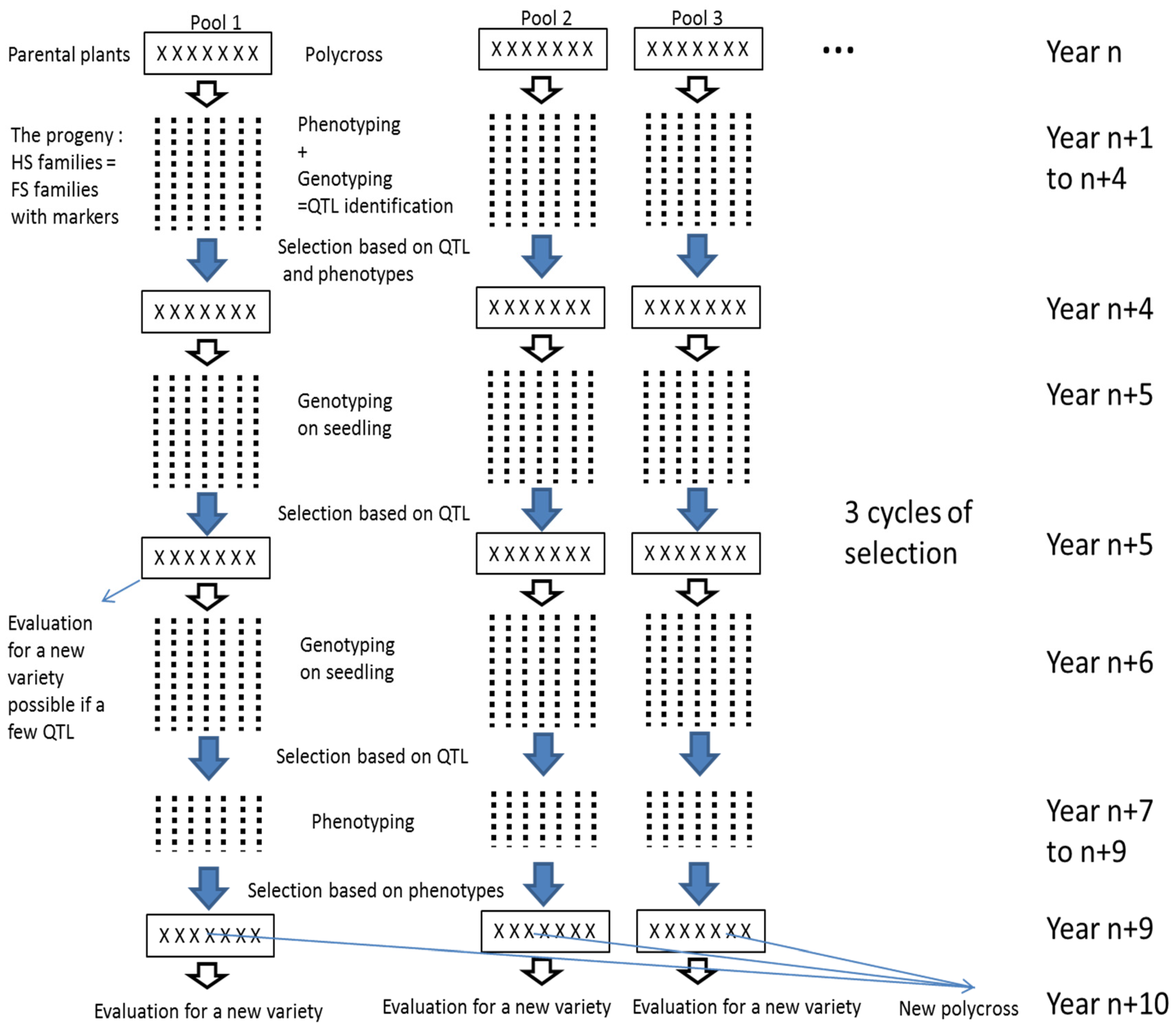
4. Materials and Methods
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hill, W.G. Quantitative genetics in the genomic era. Curr. Genom. 2012, 13, 196–206. [Google Scholar] [CrossRef] [PubMed]
- Pérez-de-Castro, A.M.; Vilanova, S.; Cañizares, J.; Pascual, L.; Blanca, J.M.; Diez, M.J.; Prohens, J.; Pico, B. Application of genomic tools in plant breeding. Curr. Genom. 2012, 13, 179–195. [Google Scholar] [CrossRef] [PubMed]
- Rafalski, A. Application of single nucleotide polymorphisms in crop genetics. Curr. Opin. Plant Biol. 2002, 54, 94–100. [Google Scholar] [CrossRef]
- Smith, S.E. Breeding synthetic cultivars. In Encyclopedia of Plant and Crop Science; Goodman, R.M., Ed.; Rutgers University: New Brunswick, NJ, USA, 2004; pp. 205–206. [Google Scholar]
- Gallais, A. Théorie De La Sélection en Amélioration Des Plantes; Masson: Paris, France; Milan, Italy; Barcelon, Spain; Mexico, NM, USA, 1990; pp. 12–26. [Google Scholar]
- Flint-Garcia, S.A.; Thornsberry, J.M.; Buckler, E.S. Structure of linkage disequilibrium in plants. Annu. Rev. Plant Biol. 2003, 54, 357–374. [Google Scholar] [CrossRef] [PubMed]
- Auzanneau, J.; Huyghe, C.; Escobar-Gutierrez, A.J.; Julier, B.; Gastal, F.; Barre, P. Association study between the gibberellic acid insensitive gene and leaf length in a Lolium perenne L. Synthetic variety. BMC Plant Biol. 2011, 11, 183–196. [Google Scholar] [CrossRef] [PubMed]
- Wilkins, P.; Humphreys, M. Progress in breeding perennial forage grasses for temperate agriculture. J. Agric. Sci. 2003, 140, 129–150. [Google Scholar] [CrossRef]
- Auzanneau, J.; Huyghe, C.; Julier, B.; Barre, P. Linkage disequilibrium in synthetic varieties of perennial ryegrass. Theor. Appl. Genet. 2007, 115, 837–847. [Google Scholar] [CrossRef] [PubMed]
- Brazauskas, G.; Lenk, I.; Pedersen, M.G.; Studer, B.; Lubberstedt, T. Genetic variation, population structure, and linkage disequilibrium in european elite germplasm of perennial ryegrass. Plant Sci. 2011, 181, 412–420. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, I. The relationship between productivity and some components of canopy structure in ryegrass (Lolium spp.). II. Yield, canopy structure and ligth interception. J. Agric. Sci. 1971, 77, 283–292. [Google Scholar] [CrossRef]
- Rhodes, I. The relationship between productivity and some components of canopy structure in ryegrass (Lolium spp.) III. Spaced plant characters, their heritabilities and relationship to sward yield. J. Agric. Sci. 1973, 80, 171–176. [Google Scholar] [CrossRef]
- Rhodes, I.; Mee, S. Changes in dry matter yield associated with selection for canopy characters in ryegrass. Grass Forage Sci. 1980, 35, 35–39. [Google Scholar] [CrossRef]
- Horst, G.L.; Nelson, C.J.; Asay, K.H. Relationship of leaf elongation to forage yield of tall fescue genotypes. Crop Sci. 1978, 18, 715–719. [Google Scholar] [CrossRef]
- Hazard, L.; Ghesquière, M. Productivity under contrasting cutting regimes of perennial ryegrass selected for short and long leaves. Euphytica 1997, 95, 295–299. [Google Scholar] [CrossRef]
- Barre, P.; Emile, J.C.; Betin, M.; Surault, F.; Ghesquière, M.; Hazard, L. Morphological characteristics of perennial ryegrass leaves that influence short-term intake in dairy cows. Agron. J. 2006, 98, 978–985. [Google Scholar] [CrossRef]
- Hazard, L.; Ghesquière, M. Evidence from the use of isozyme markers of competition in swards between short-leaved and long-leaved perennial ryegrass. Grass Forage Sci. 1995, 50, 241–248. [Google Scholar] [CrossRef]
- Parsons, A.J.; Robson, M.J. Seasonal changes in the physiology of s24 perennial ryegrass (Lolium perenne L.). I. Response of leaf extension to temperature during the transition from vegetative to reproductive growth. Ann. Bot. 1980, 46, 435–444. [Google Scholar]
- Jones, E.S.; Mahoney, N.L.; Hayward, M.D.; Armstead, I.P.; Jones, J.; Humphreys, M.O.; King, I.P.; Kishida, T.; Yamada, T.; Balfourier, F.; et al. An enhanced molecular marker based genetic map of perennial ryegrass (Lolium perenne) reveals comparative relationships with other poaceae genome. Genome 2002, 45, 282–295. [Google Scholar] [CrossRef] [PubMed]
- Riday, H. Paternity testing: A non-linkage based marker-assisted selection scheme for outbred forage species. Crop Sci. 2011, 51, 631–641. [Google Scholar] [CrossRef]
- Gillet, M. Un plan systématique de polycross pour les nombres de base pairs. Ann. Amélior. Plantes 1963, 13, 269–276. [Google Scholar]
- Barre, P.; Moreau, L.; Mi, F.; Turner, L.; Gastal, F.; Julier, B.; Ghesquiere, M. Quantitative trait loci for leaf length in perennial ryegrass (Lolium perenne L.). Grass Forage Sci. 2009, 64, 310–321. [Google Scholar] [CrossRef]
- Jensen, L.B.; Muylle, H.; Arens, P.; Andersen, C.H.; Holm, P.B.; Ghesquière, M.; Julier, B.; Lübberstedt, T.; Nielsen, K.K.; De Riek, J.; et al. Development and mapping of a public reference set of ssr markers in Lolium perenne L. Mol. Ecol. Notes 2005, 5, 951–957. [Google Scholar] [CrossRef]
- Pauly, L.; Flajoulot, S.; Garon, J.; Julier, B.; Beguier, V.; Barre, P. Detection of favorable alleles for plant height and crown rust tolerance in three connected populations of perennial ryegrass (Lolium perenne L.). Theor. Appl. Genet. 2012, 124, 1139–1153. [Google Scholar] [CrossRef] [PubMed]
- Faville, M.; Vecchies, A.; Schreiber, M.; Drayton, M.; Hughes, L.; Jones, E.; Guthridge, K.; Smith, K.; Sawbridge, T.; Spangenberg, G.; et al. Functionally associated molecular genetic marker map construction in perennial ryegrass (Lolium perenne L.). Theor. Appl. Genet. 2004, 110, 12–32. [Google Scholar] [CrossRef] [PubMed]
- Gill, G.; Wilcox, P.; Whittaker, D.; Winz, R.; Bickerstaff, P.; Echt, C.; Kent, J.; Humphreys, M.; Elborough, K.; Gardner, R. A framework linkage map of perennial ryegrass based on ssr markers. Genome 2006, 49, 354–364. [Google Scholar] [CrossRef] [PubMed]
- Studer, B.; Byrne, S.; Nielsen, R.O.; Panitz, F.; Bendixen, C.; Islam, M.S.; Pfeifer, M.; Lubberstedt, T.; Asp, T. A transcriptome map of perennial ryegrass (Lolium perenne L.). BMC Genom. 2012, 13, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Studer, B.; Kolliker, R.; Muylle, H.; Asp, T.; Frei, U.; Roldan-Ruiz, I.; Barre, P.; Tomaszewski, C.; Meally, H.; Barth, S.; et al. Est-derived ssr markers used as anchor loci for the construction of a consensus linkage map in ryegrass (Lolium spp.). BMC Plant Biol. 2010, 10, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Byrne, S.; Czaban, A.; Studer, B.; Panitz, F.; Bendixen, C.; Asp, T. Genome wide allele frequency fingerprints (gwaffs) of populations via genotyping by sequencing. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Elshire, R.J.; Glaubitz, J.C.; Sun, Q.; Poland, J.A.; Kawamoto, K.; Buckler, E.S.; Mitchell, S.E. A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, S.; Humphreys, M.O.; Tase, K.; Sanada, Y.; Yamada, T. Molecular marker dissection of ryegrass plant development and its response to growth environments and foliage cuts. Crop Sci. 2011, 51, 600–611. [Google Scholar] [CrossRef]
- Sartie, A.M.; Matthew, C.; Easton, H.S.; Faville, M.J. Phenotypic and qtl analyses of herbage production-related traits in perennial ryegrass (Lolium perenne L.). Euphytica 2011, 182, 295–315. [Google Scholar] [CrossRef]
- Yamada, T.; Jones, E.S.; Cogan, N.O.I.; Vecchies, A.C.; Nomura, T.; Hisano, H.; Shimamoto, Y.; Smith, K.F.; Hayward, M.D.; Forster, J.W. QTL analysis of morphological, developmental, and winter hardiness-associated traits in perennial ryegrass. Crop Sci. 2004, 44, 925–935. [Google Scholar] [CrossRef]
- Turner, L.; Cairns, A.; Armstead, I.; Thomas, H.; Humphreys, M.W.; Humphreys, M.O. Does fructan have a functional role in physiological traits? Investigation by quantitative trait locus mapping. New Phytol. 2008, 179, 765–777. [Google Scholar] [CrossRef] [PubMed]
- Studer, B.; Jensen, L.B.; Hentrup, S.; Brazauskas, G.; Kölliker, R.; Lübberstedt, T. Genetic characterisation of seed yield and fertility traits in perennial ryegrass (Lolium perenne L.). Theor. Appl. Genet. 2008, 117, 781–791. [Google Scholar] [CrossRef] [PubMed]
- Muranty, H. Power of tests for quantitative trait loci detection using full-sib families in different schemes. Heredity 1996, 76, 156–165. [Google Scholar] [CrossRef]
- Blanc, G.; Charcosset, A.; Mangin, B.; Gallais, A.; Moreau, L. Connected populations for detecting quantitative trait loci and testing for epistasis: An application in maize. Theor. Appl. Genet. 2006, 113, 206–224. [Google Scholar] [CrossRef] [PubMed]
- Billotte, N.; Jourjon, M.F.; Marseillac, N.; Berger, A.; Flori, A.; Asmady, H.; Adon, B.; Singh, R.; Nouy, B.; Potier, F.; et al. QTL detection by multi-parent linkage mapping in oil palm (Elaeis guineensis Jacq.). Theor. Appl. Genet. 2010, 120, 1673–1687. [Google Scholar] [CrossRef] [PubMed]
- Hirata, M.; Cai, H.W.; Inoue, M.; Yuyama, N.; Miura, Y.; Komatsu, T.; Takamizo, T.; Fujimori, M. Development of simple sequence repeat (SSR) markers and construction of an ssr-based linkage map in italian ryegrass (Lolium multiflorum Lam.). Theor. Appl. Genet. 2006, 113, 270–279. [Google Scholar] [CrossRef] [PubMed]
- Lauvergeat, V.; Barre, P.; Bonnet, M.; Ghesquière, M. Sixty simple sequence repeat markers for use in the festuca—Lolium complex of grasses. Mol. Ecol. Notes 2005, 5, 401–405. [Google Scholar] [CrossRef]
- Studer, B.; Asp, T.; Frei, U.; Hentrup, S.; Meally, H.; Guillard, A.; Barth, S.; Muylle, H.; Roldan-Ruiz, I.; Barre, P.; et al. Expressed sequence tag-derived microsatellite markers of perennial ryegrass (Lolium perenne L.). Mol. Breed. 2008, 21, 533–548. [Google Scholar] [CrossRef]
- Jones, E.S.; Dupal, M.P.; Kölliker, R.; Drayton, M.C.; Forster, J.W. Development and characterisation of simple sequence repeat (SSR) markers for perennial ryegrass (Lolium perenne L.). Theor. Appl. Genet. 2001, 102, 405–415. [Google Scholar] [CrossRef]
- Kubik, C.; Sawkins, M.; Meyer, W.A.; Gaut, B.S. Genetic diversity in seven perennial ryegrass (Lolium perenne L.) cultivars based on ssr markers. Crop Sci. 2001, 41, 1565–1572. [Google Scholar] [CrossRef]
- Saha, M.C.; Rouf Mian, M.A.; Eujayl, I.; Zwonitzer, J.C.; Wang, L.; May, G.D. Tall fescue est-ssr markers with transferability across several grass species. Theor. Appl. Genet. 2004, 109, 783–791. [Google Scholar] [CrossRef] [PubMed]
- Lem, P.; Lallemand, J. Grass consensus sts markers: An efficient approach for detecting polymorphism in Lolium. Theor. Appl. Genet. 2003, 107, 1113–1122. [Google Scholar] [CrossRef] [PubMed]
- SAS, Version 9.3; Sas Institute Inc.: Cary, NC, USA, 2000.
- StatSoft. Statistica Pour Windows. Available online: Http://www.Statsoft.Fr (accessed on 20 September 2016).
- Van Ooijen, J.W.; Voorrips, R.E. Joinmap 3.0 Software for the Calculation of Genetic Linkage Maps; Plant Research International: Wageningen, The Netherlands, 2001; pp. 1–51. [Google Scholar]
- Voorrips, R.E. Mapchart: Software for the graphical presentation of linkage maps and qtls. J. Hered. 2002, 93, 77–78. [Google Scholar] [CrossRef] [PubMed]
- Jourjon, M.F.; Jasson, S.; Marcel, J.; Ngom, B.; Mangin, B. Mcqtl: Multi-allelic qtl mapping in multi-cross design. Bioinformatics 2005, 21, 128–130. [Google Scholar] [CrossRef] [PubMed]

| Nemo A | Nemo B | Nemo C | Nemo D | Nemo G | Total Number of Genotypes per HS Family | Heading Dates 1 | |
|---|---|---|---|---|---|---|---|
| Nemo A | 84 | 157 | |||||
| Nemo B | 20 | 55 | 157 | ||||
| Nemo C | 5 | 3 | 48 | 153 | |||
| Nemo D | 27 | 5 | 10 | 67 | 156 | ||
| Nemo G | 23 | 22 | 2 | 16 | 70 | 157 | |
| Nemo H | 9 | 5 | 28 | 9 | 7 | 58 | 154 |
| Traits | σ2g | σ2e | H2 |
|---|---|---|---|
| PH0309 | 414 | 382 | 0.52 |
| PH0409_1 | 172 | 164 | 0.51 |
| PH0409_2 | 451 | 451 | 0.50 |
| PH0409_3 | 378 | 360 | 0.51 |
| PH0409_4 | 512 | 552 | 0.48 |
| PH0409_5 | 595 | 665 | 0.47 |
| PGR | 0.039 | 0.083 | 0.32 |
| PH0909 | 426 | 394 | 0.52 |
| Traits | Average | Minimum | Maximum | Standard Deviation |
|---|---|---|---|---|
| PH0309 | 129 | 71 | 190 | 22 |
| PH0409_1 | 114 | 66 | 147 | 15 |
| PH0409_2 | 134 | 53 | 185 | 24 |
| PH0409_3 | 137 | 96 | 237 | 22 |
| PH0409_4 | 198 | 114 | 266 | 25 |
| PH0409_5 | 205 | 123 | 282 | 28 |
| PGR | 0.95 | 0.48 | 1.66 | 0.25 |
| PH0909 | 203 | 116 | 271 | 24 |
| Traits | PH0309 | PH0409_1 | PH0409_2 | PH0409_3 | PH0409_4 | PH0409_5 | PGR |
|---|---|---|---|---|---|---|---|
| PH0409_1 | 0.83 *** | ||||||
| PH0409_2 | 0.89 *** | 0.90 *** | |||||
| PH0409_3 | 0.83 *** | 0.83 *** | 0.88 *** | ||||
| PH0409_4 | 0.81 *** | 0.83 *** | 0.87 *** | 0.88 *** | |||
| PH0409_5 | 0.77 *** | 0.82 *** | 0.83 *** | 0.87 *** | 0.88 *** | ||
| PGR | 0.81 *** | 0.86 *** | 0.90 *** | 0.78 *** | 0.73 *** | 0.68 *** | |
| PH0909 | 0.18 * | 0.11 ns | 0.15 * | 0.13 ns | 0.20 ** | 0.17 * | 0.13 ns |
| Additive Effects | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traits | LG | Markers | Map Location (cM) | Confidence Interval | r2 (%) | Global r2 (%) | Nemo A | Nemo B | Nemo C | Nemo D | Nemo G | Nemo H |
| PH0309 | 3 | pps0007 | 29.3 | 28.1–41.2 | 12.0 | 28.1 | −1.8 1 | 4.5 | 5.2 | 4.6 | −9.5 | 1.9 |
| 4 | LpSSR011 | 30.8 | 26.4–35.9 | 20.1 | −3.8 | 7.4 | 10.7 | −1.2 | 3.4 | 10.8 | ||
| PH0409_1 | 3 | pps0007 | 29.3 | 27.0–30.6 | 14.0 | 28.4 | −1.7 | 0.9 | 5.8 | 4.8 | −5.5 | 1.0 |
| 4 | G01-073 | 28.8 | 27.9–34.4 | 19.2 | −3.3 | 4.1 | 5.7 | 0.1 | 4.0 | 6.0 | ||
| PH0409_2 | 3 | pps0007 | 29.3 | 27.2–30.6 | 15.6 | 27.7 | −1.2 | 3.0 | 8.8 | 8.3 | −9.7 | 3.1 |
| 4 | G01-075 | 27.8 | 26.2–32.6 | 17.3 | −4.6 | 4.5 | 9.6 | 1.5 | 5.6 | 10.6 | ||
| PH0409_3 | 4 | pps0040 | 28.2 | 25.8–35.1 | 17.3 | −6.6 | 4.3 | 7.4 | 1.2 | 6.7 | 8.7 | |
| PH0409_4 | 4 | LpSSR011 | 31.7 | 26.2–35.0 | 16.1 | −5.3 | 11.8 | 7.8 | 0.8 | 4.0 | 9.1 | |
| PH0409_5 | 4 | LpSSR011 | 30.8 | 27.5–33.0 | 22.1 | −6.6 | 12.4 | 11.7 | −2.6 | 8.4 | 11.6 | |
| PGR | 4 | G05-014 | 33.8 | 19.2–36.2 | 12.3 | −0.05 | 0.08 | 0.11 | −0.04 | 0.02 | 0.06 | |
| Marker Names | Reference | LG | Marker Names | Reference | LG |
|---|---|---|---|---|---|
| 25ca1 | [26] | 3 | LmgSSR01-08H | [39] | 2 |
| B1A2 | [40] | 3 | LmgSSR02-10B | 6 | |
| B1C8 | 7 | LmgSSR03-04E | 3 | ||
| B1C9 | 3 | LmgSSR04-09F | 1 | ||
| B3B8 | 3 | LmgSSR10-12D | 7 | ||
| B3-C5 | 7 | LmgSSR15-08E | 4 | ||
| B4D7op | 1 | LmgSSR15-09F | 7 | ||
| DLF008 | [23] | 7 | LpSSR006 | [23] | 4 |
| DLF027 | 1 | LpSSR011 | 4 | ||
| G01-001 | [41] | 7 | LpSSR020 | 7 | |
| G01-037 | 4 | LpSSR023 | 4 | ||
| G01-040 | 2 | LpSSR058 | 6 | ||
| G01-043 | 2 | LpSSR066 | 7 | ||
| G01-047 | 6 | LpSSR085 | 1 | ||
| G01-053 | 3 | LpSSR112 | 2 | ||
| G01-054 | 2 | LpSSRH01A02 | [42] | 5 | |
| G01-073 | 4 | M15-185 | [43] | 2 | |
| G01-075 | 4 | M4-136 | 2 | ||
| G01-079 | 1 | M4-213 | 1 | ||
| G01-080 | 5 | NFFA030 | [44] | 2 | |
| G01-090 | 7 | NFFA036 | 6 | ||
| G01-095 | 5 | NFFA064 | 5 | ||
| G02-004 | 7 | NFFA087 | 5 | ||
| G02-047 | 1 | NFFA099 | 3 | ||
| G02-049 | 2 | NFFA114 | 7 | ||
| G02-057 | 5 | OSW | [45] | 7 | |
| G03-003 | 6 | pps0007 | [25] | 3 | |
| G03-079 | 6 | pps0040 | 4 | ||
| G04-034 | 4 | pps0049 | 7 | ||
| G05-014 | 4 | pps0080 | 2 | ||
| G05-028 | 3 | pps0164 | 3 | ||
| G05-033 | 5 | pps0299 | 6 | ||
| G05-046 | 6 | pps0397 | 5 | ||
| G05-050 | 2 | rv0244 | [26] | 1 | |
| G05-065 | 5 | rv0641 | 6 | ||
| G05-073 | 7 | rv0706 | 2 | ||
| G05-090 | 3 | rv0757 | 5 | ||
| G05-092 | 5 | rye012 | [23] | 4 | |
| G05-129 | 2 | S7F7-3-4F | [39] | 6 | |
| G07-034 | 3 | syn20738-1 | [22] | 5 | |
| LmgSSR01-02H | [39] | 6 | uni001 | [23] | 3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pauly, L.; Flajoulot, S.; Garon, J.; Julier, B.; Béguier, V.; Barre, P. Quantitative Trait Loci (QTL) Identification in the Progeny of a Polycross. Agronomy 2016, 6, 51. https://doi.org/10.3390/agronomy6040051
Pauly L, Flajoulot S, Garon J, Julier B, Béguier V, Barre P. Quantitative Trait Loci (QTL) Identification in the Progeny of a Polycross. Agronomy. 2016; 6(4):51. https://doi.org/10.3390/agronomy6040051
Chicago/Turabian StylePauly, Laurence, Sandrine Flajoulot, Jérôme Garon, Bernadette Julier, Vincent Béguier, and Philippe Barre. 2016. "Quantitative Trait Loci (QTL) Identification in the Progeny of a Polycross" Agronomy 6, no. 4: 51. https://doi.org/10.3390/agronomy6040051
APA StylePauly, L., Flajoulot, S., Garon, J., Julier, B., Béguier, V., & Barre, P. (2016). Quantitative Trait Loci (QTL) Identification in the Progeny of a Polycross. Agronomy, 6(4), 51. https://doi.org/10.3390/agronomy6040051





