Climate-Optimized Planting Windows for Cotton in the Lower Mississippi Delta Region
Abstract
:1. Introduction
2. Materials and Methods
2.1. RZWQM2 Model
2.2. Field Experiments
2.3. Model Application: Determining Optimum Planting Window
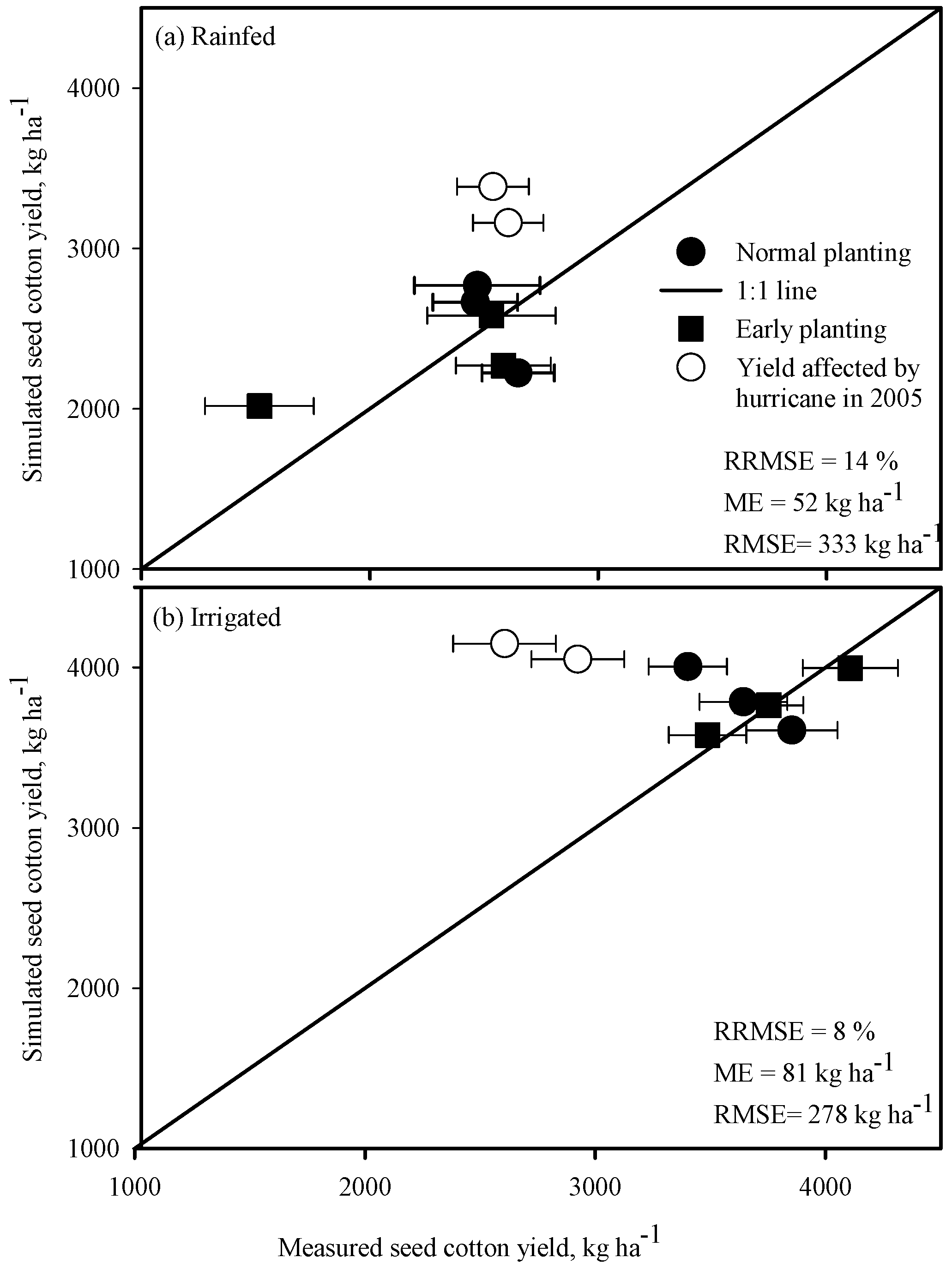
2.4. Statistics for Model Calibration and Evaluations
3. Results and Discussion
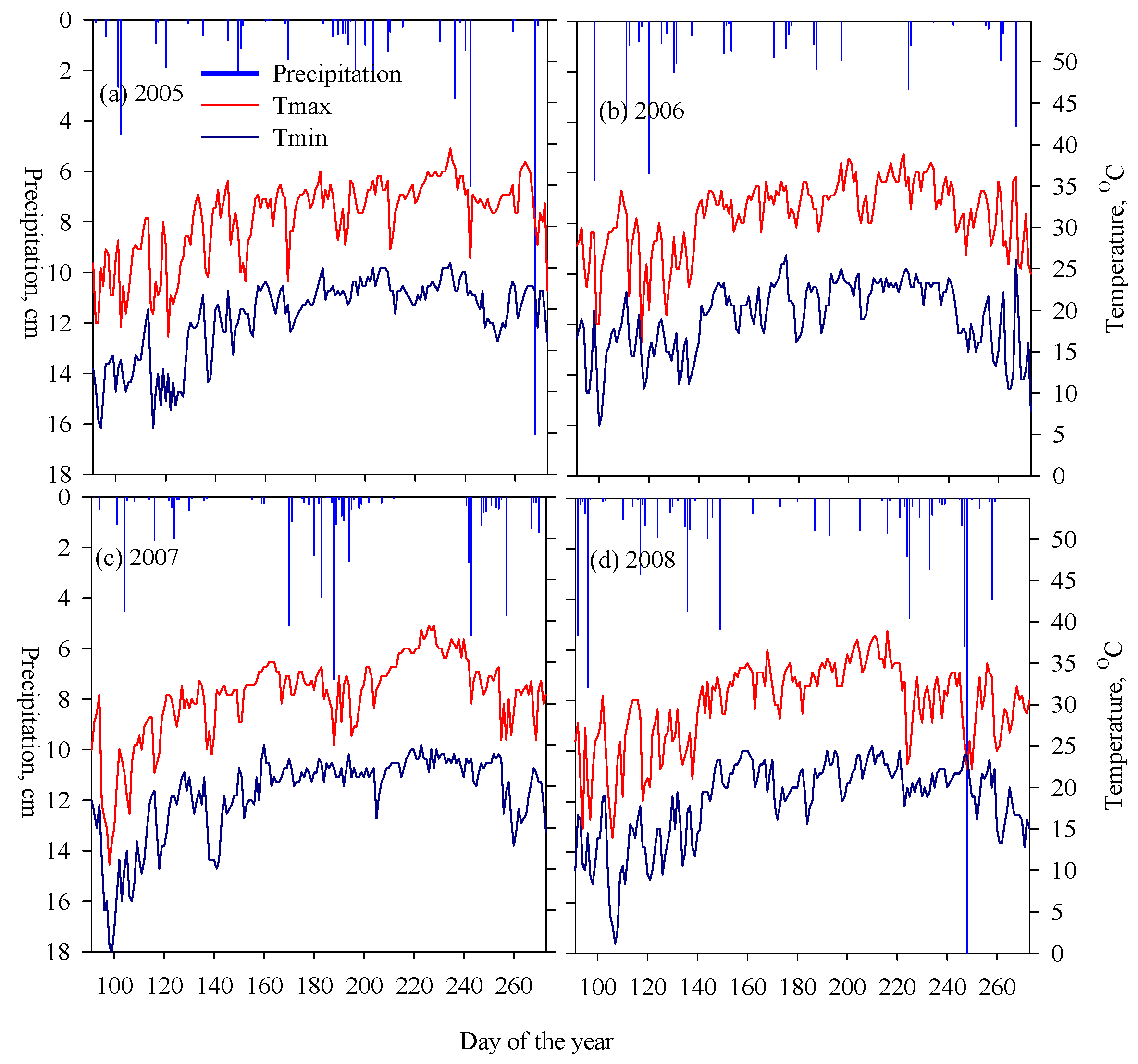
3.1. Climate of the Location
3.2. Calibration and Validation of the Model
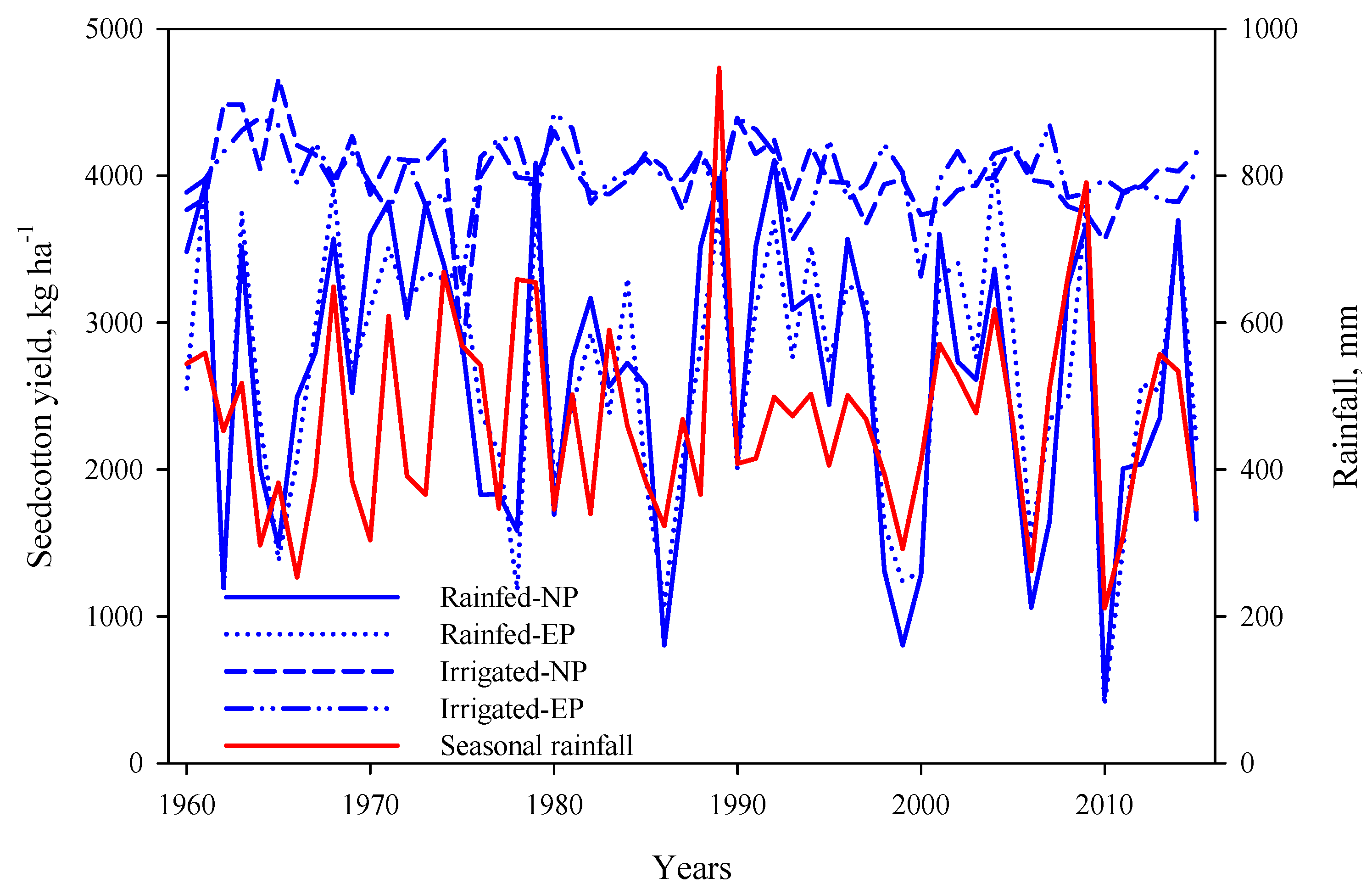
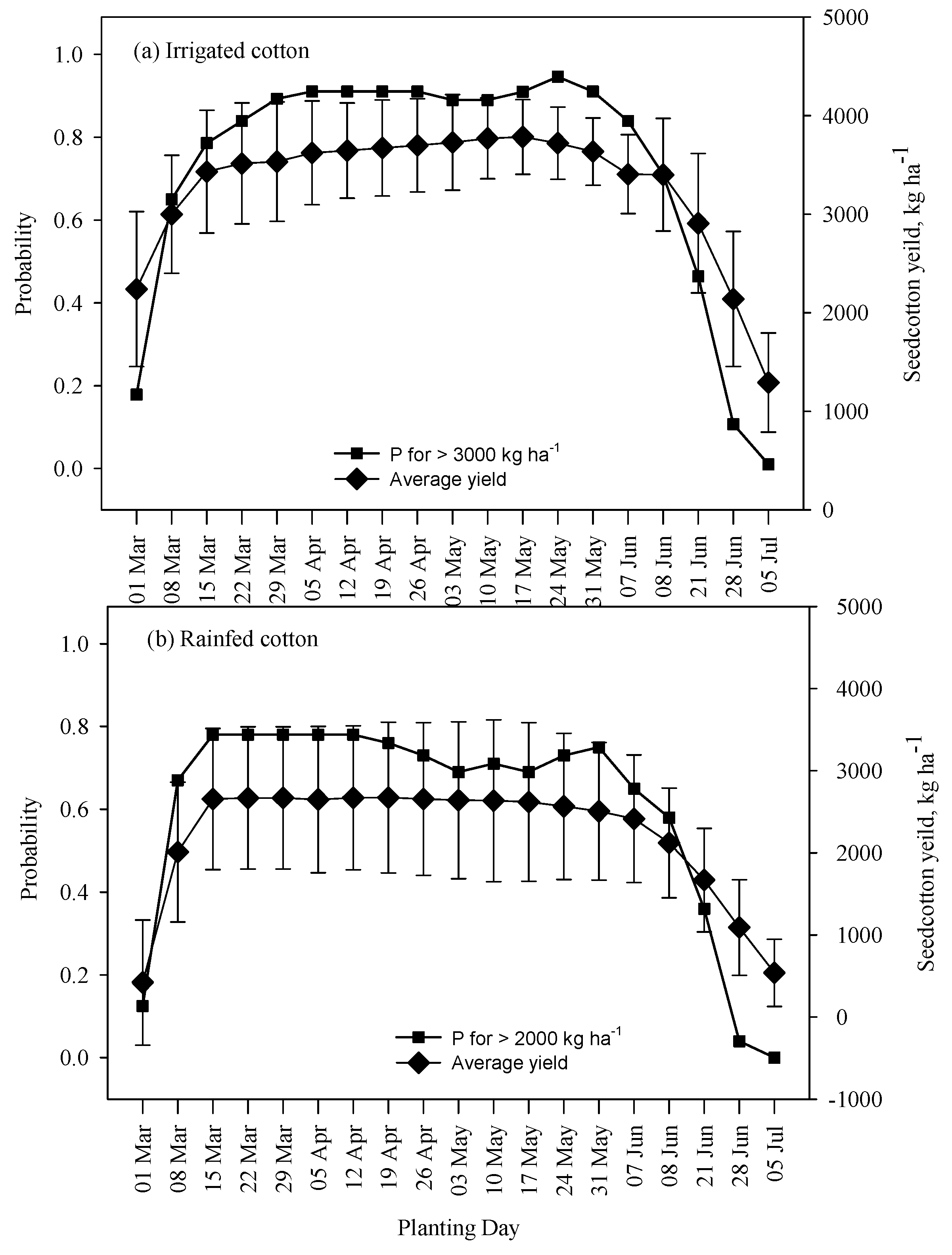
3.3. Planting Windows
3.4. Optimum Planting Windows (Climate-Optimized Planting Windows)
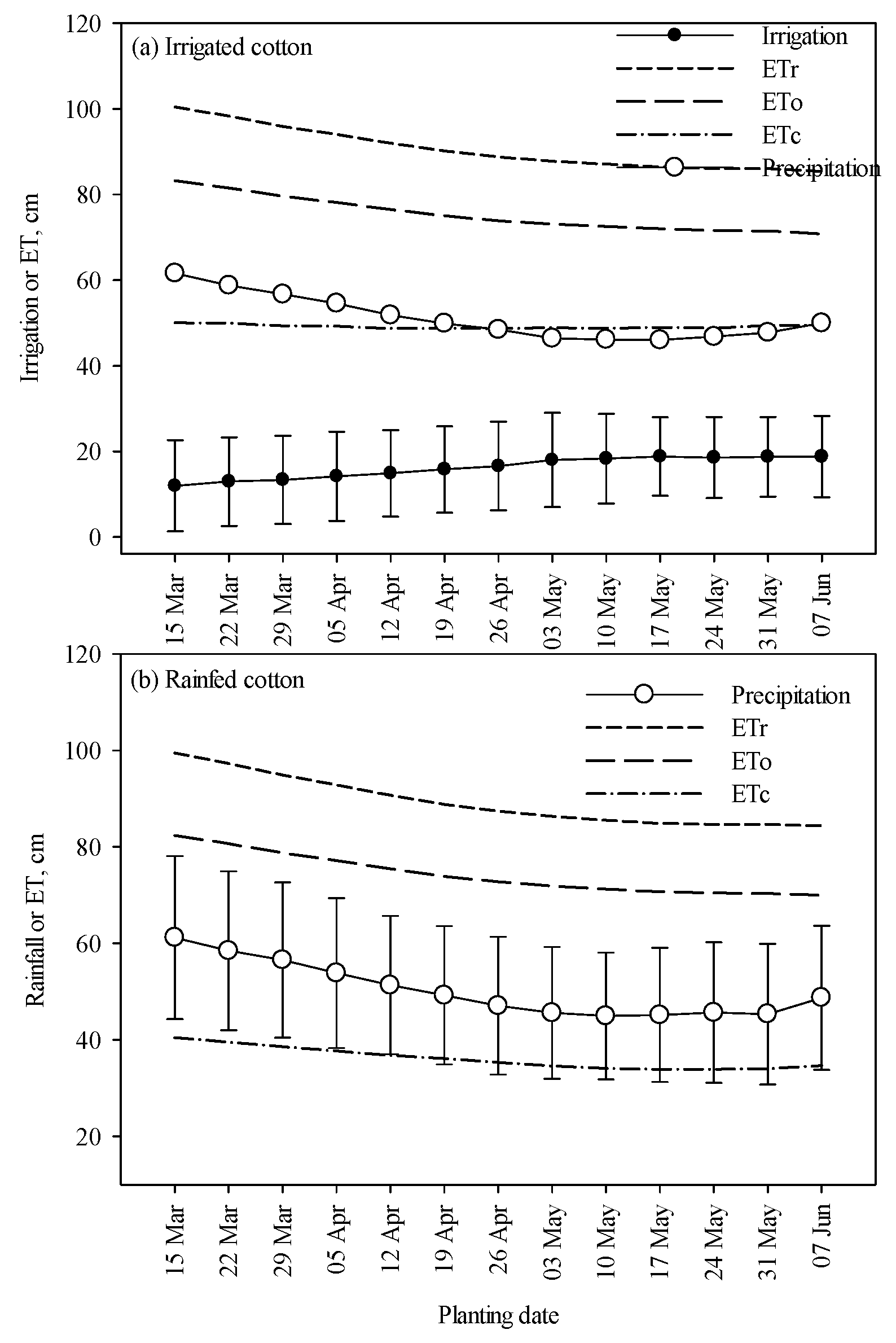
3.5. Irrigation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Riley, J.A. Soil Temperatures and Cotton Planting in the Mid-South; State College: Pennsylvania, PA, USA; Mississippi State University: Starkville, MS, USA; Agricultural Experiment Station: Fayetteville, AR, USA, 1964; p. 11. [Google Scholar]
- Delta Research and Extension Center. Available online: http://www.deltaweather.msstate.edu/ (accessed on 26 September 2016).
- Bridge, R.R.; Meredith, W.R.; Chism, J.F. Influence of cotton planting dates studied. Miss. Farm Res. 1971, 34, 4–6. [Google Scholar]
- Pettigrew, W.T.; Dowd, M.K. Varying planting dates or irrigation regimes alters cottonseed composition. Crop Sci. 2011, 51, 2155–2164. [Google Scholar] [CrossRef]
- Wrather, J.A.; Phipps, B.J.; Stevens, W.E.; Phillips, A.S.; Vories, E.D. Cotton planting date and plant population effects on yield and fiber quality in the Mississippi Delta. J. Cotton Sci. 2008, 12, 1–7. [Google Scholar]
- Adams, B.; Catchot, A.; Gore, J.; Cook, D.; Musser, F.; Dodds, D. Impact of planting date and varietal maturity on tarnished plant bug (Hemiptera: Miridae) in cotton. Cotton J. Econ. Entomol. 2013, 106, 2378–2383. [Google Scholar] [CrossRef] [PubMed]
- Pettigrew, W.T.; Molin, W.T.; Stetina, S.R. Impact of varying planting dates and tillage systems on cotton growth and lint yield production. Agron. J. 2009, 101, 1131–1138. [Google Scholar] [CrossRef]
- Pettigrew, W.T.; Meredith, W.R., Jr. Seed quality and planting date eff ects on cotton lint yield, yield components, and fiber quality. J. Cotton Sci. 2009, 13, 37–47. [Google Scholar]
- Berry, N.B.O.; Faircloth, J.C.; Edmisten, K.L.; Collins, G.D.; Stewart, A.M.; Abaye, A.O.; Herbert, D.A., Jr.; Haygood, R.A. Plant population and planting date effects on cotton (Gossypium hirsutum L.) Growth and Yield. J. Cotton Sci. 2008, 12, 178–187. [Google Scholar]
- Pettigrew, W.T. Improved yield potential with an early planting cotton production system. Agron. J. 2002, 94, 997–1003. [Google Scholar] [CrossRef]
- Pettigrew, W.T. Impact of varying planting dates and irrigation regimes on cotton growth and lint yield production. Agron. J. 2010, 102, 1379–1387. [Google Scholar] [CrossRef]
- Pettigrew, W.T.; Dowd, M.K. Interactions between irrigation regimes and varieties result in altered cottonseed composition. J. Cotton Sci. 2010, 201, 16–42. [Google Scholar]
- Hoogenboom, G.; Jones, J.W.; Boote, K.J. A decision support system for prediction of crop yield, evapotranspiration, and irrigation management. In Proceedings of the 1991 National Conference, Honolulu, HI, USA, 22–26 July 1991; pp. 198–204.
- Ahuja, L.R.; Rojas, K.W.; Hanson, J.D.; Shafer, M.J.; Ma, L. Root Zone Water Quality Model. Modeling Management Effects on Water Quality and Crop Production; Water Resources Publications, LLC: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Ahuja, L.R.; Ma, L.; Lascano, R.J.; Saseendran, S.A.; Fang, Q.X.; Nielsen, D.C.; Colaizzi, P.D. Practical Applications of Agricultural System Models to Optimize the Use of Limited Water. Available online: https://portal.sciencesocieties.org/resources/files/Downloads/pdf/B40818.pdf (accessed on 26 September 2016).
- Ahuja, L.R.; Ma, L.; Fang, Q.X.; Saseendran, S.A.; Islam, A.; Malone, R.W. Computer modeling: Applications to environment and food security. In Encyclopedia of Agriculture and Food Systems; van Alfen, N., Ed.; Elsevier Publishers: New York, NY, USA, 2014; pp. 337–358. [Google Scholar]
- Saseendran, S.A.; Ma, L.; Nielsen, D.C.; Vigil, M.F.; Ahuja, L.R. Simulating planting date effects on corn production using RZWQM and CERES-Maize. Agron. J. 2005, 97, 58–71. [Google Scholar] [CrossRef]
- Garcia y Garcia, A.; Persson, T.; Paz, J.O.; Fraisse, C.; Hoogenboom, G. ENSO-based climate variability affects water use efficiency of rainfed cotton grown in the southeastern USA. Agric. Ecosyst. Environ. 2010, 139, 629–635. [Google Scholar] [CrossRef]
- Paz, J.O.; Woli, P.; Garcia, A.G.; Hoogenboom, G. Cotton yields as influenced by ENSO at different planting dates and spatial aggregation levels. Agric. Syst. 2012, 111, 42–52. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. DSSAT Cropping System Model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Guerra, L.C.; Garcia y Garcia, A.; Hook, J.E.; Harrison, K.A.; Thomas, D.L.; Stooksbury, D.E.; Hoogenboom, G. Irrigation water use estimates based on crop simulation models and kriging. Agric. Water Manag. 2007, 89, 199–207. [Google Scholar] [CrossRef]
- Boote, K.J.; Pickering, N.B. Modeling photosynthesis of row crop canopies. Hort. Sci. 1994, 29, 1423–1434. [Google Scholar]
- Kebede, H.; Fisher, D.K.; Sui, R.; Reddy, K.N. Irrigation methods and scheduling in the delta region of Mississippi: Current status and strategies to improve irrigation efficiency. Am. J. Plant Sci. 2014, 5, 2917–2928. [Google Scholar] [CrossRef]
- Clark, B.R.; Hart, R.M.; Gurdak, J.J. Groundwater Availability of the Mississippi Embayment: U.S. Geological Survey Professional Paper; BiblioGov: Columbus, OH, USA, 2011. [Google Scholar]
- Ma, L.; Hoogenboom, G.; Saseendran, S.A.; Bartling, P.N.S.; Ahuja, L.R.; Green, T.R. Estimates of soil hydraulic properties and root growth factor on soil water balance and crop production. Agron. J. 2009, 101, 572–583. [Google Scholar] [CrossRef]
- Ma, L.; Nielsen, D.C.; Ahuja, L.R.; Malone, R.W.; Saseendran, S.A.; Rojas, K.W.; Hanson, J.D.; Benjamin, J.G. Evaluation of RZWQM under varying irrigation levels in eastern Colorado. Trans. ASAE 2003, 46, 39–49. [Google Scholar]
- Saseendran, S.A.; Ahuja, L.R.; Nielsen, D.C.; Trout, T.J.; Ma, L. Use of crop simulation models to evaluate limited irrigation management options for corn in a semiarid environment. Water Rescour. Res. 2008. [Google Scholar] [CrossRef]
- Saseendran, S.A.; Nielsen, D.C.; Lyon, D.J.; Ma, L.; Felter, D.G.; Baltensperger, D.D.; Hoogenboom, G.; Ahuja, L.R. Modeling responses of dryland spring triticale, proso millet and foxtail millet to initial soil water in the High Plains. Field Crops Res. 2009, 10, 48–63. [Google Scholar] [CrossRef]
- Saseendran, S.A.; Ahuja, L.R.; Ma, L.; Trout, T.J.; McMaster, G.S.; Andales, A.A.; Chavez, J.; Ham, J. Enhancing RZWQM2 for water stress responses of corn (Zea mays. L.). Agron. J. 2014, 106, 81–94. [Google Scholar] [CrossRef]
- Nimah, M.N.; Hanks, R.J. Model for estimating soil water, plant and atmospheric inter relations: I. description and sensitivity. Proc. Soil Sci. Soc. Am. 1973, 37, 522–527. [Google Scholar] [CrossRef]
- Ma, L.; Hoogenboom, G.; Ahuja, L.R.; Ascough, J.C., II; Saseendran, S.A. Evaluation of the RZWQM-CERES-Maize hybrid model for maize production. Agric. Syst. 2006, 87, 274–295. [Google Scholar] [CrossRef]
- Hoogenboom, G.; Jones, J.W.; Wilkens, P.W.; Porter, C.H.; Boote, K.J.; Hunt, L.A.; Singh, U.; Lizaso, J.L.; White, J.W.; Uryasev, O.; et al. Decision Support System for Agrotechnology Transfer (DSSAT) Version 4.5 [CD-ROM]; University of Hawaii: Honolulu, HI, USA, 2012. [Google Scholar]
- United States Department of Agriculture—Agricultural Research Service. Available online: http://arsagsoftware.ars.usda.gov/DownloadSoftware.aspx (accessed on 26 September 2016).
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics. 1. Flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Ma, L.; Ahuja, L.R.; Saseendran, S.A.; Malone, R.W.; Green, T.R.; Nolan, B.T.; Bartling, P.N.S.; Flerchinger, G.N.; Boote, K.J.; Hoogenboom, G. A Protocol for Parameterization and Calibration of RZWQM2 in Field Research. In Methods of Introducing System Models into Agricultural Research; Ahuja, L.R., Ma, L., Eds.; Advances in Agricultural Systems Modeling Series 2; American Society of Agronomy: Madison, WI, USA, 2011; pp. 1–64. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964; pp. 1–15. [Google Scholar]
- Boykin, D.L.; Carle, R.R.; Ranney, C.D.; Shanklin, R. Weather Data Summary for 1964–1993 at Stoneville, Mississippi; Mississippi Agriculture and Forestry Experiment Station: Pontotoc, MS, USA, 1995; pp. 1–28. [Google Scholar]
- Pettigrew, W.T. The effect of higher temperatures on cotton lint yield production and fiber quality. Crop Sci. 2008, 48, 278–285. [Google Scholar] [CrossRef]
- Scott, H.D.; Feguson, J.A.; Hanson, L.; Fugitt, T.; Smith, E. Agricultural Water Management in the Mississppi Region of Arkansas; Arkansas Agricultural Experiment Station: Fayetteville, AR, USA, 1998. [Google Scholar]
- Biggar, J.W.; Bloodworth, M.E.; Burleson, C.A. Effect of Precipitation Differentials and Plantings Date on the Growth, Yield, and Fiber Characteristics of Cotton in the Lower Rio Grande Valley; Texas Agriculture Experiment Station: Brazos, TX, USA, 1957. [Google Scholar]
- Bilbro, J.D.; Ray, L.L. Differential Effects of Planting Date on the Performance of Cotton Varieties on the High Plains of Texas, 1960–1965; Texas Agriculture Experiment Station: Brazos, TX, USA, 1969; pp. 1–7. [Google Scholar]
- Pettigrew, W.T.; Meredith, M.R., Jr. Leaf gas exchange parameters vary among cotton genotypes. Crop Sci. 1994, 34, 700–705. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirement; United Nations Food and Agriculture Organization, Irrigation and Drainage: Rome, Italy, 1998. [Google Scholar]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation. In Standardization of Reference Evapotranspiration Task Committee Final Report; Allen, R.G., Walter, I.A., Elliot, R.L., Howell, T.A., Itenfisu, D., Jensen, M.E., Snyder, R.L., Eds.; Environmental and Water Resources Institute: Reston, VA, USA; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–11. [Google Scholar]


| Parameters | Definitions | Values |
|---|---|---|
| CSDL | Critical Short Day Length below which reproductive development progresses with no day length effect (for short day plants) (hour) | 23.0 |
| PPSEN | Slope of the relative response of development to photoperiod with time (positive for short day plants) (1/hour) | 0.01 |
| EM-FL | Time between plant emergence and flower appearance (R1)(photothermal days) | 41.0 |
| FL-SH | Time between first flower and first pod (R3) (photothermal days) | 11.0 |
| FL-SD | Time between first flower and first seed (R5) (photothermal days) | 17.0 |
| SD-PM | Time between first seed (R5) and physiological maturity (R7) (photothermal days) | 40.0 |
| FL-LF | Time between first flower (R1) and end of leaf expansion (photothermal days) | 65.0 |
| LFMAX | Maximum leaf photosynthesis rate at 30 C, 350 vpm CO2, and high light(mg CO2/m2s) | 1.4 |
| SLAVR | Specific leaf area of cultivar under standard growth conditions (cm2/g) | 170.0 |
| SIZLF | Maximum size of full leaf (three leaflets) (cm2) | 200.0 |
| XFRT | Maximum fraction of daily growth that is partitioned to seed + shell | 0.50 |
| WTPSD | Maximum weight per seed (g) | 0.15 |
| SFDUR | Seed filling duration for pod cohort at standard growth conditions (photothermal days) | 35.0 |
| SDPDV | Average seed per pod under standard growing conditions (#/pod) | 20.0 |
| PODUR | Time required for cultivar to reach final pod load under optimal conditions (photothermal days) | 8.0 |
| Tmin (°C) | Tmax (°C) | Precipitation (cm) | |
|---|---|---|---|
| 2005 | |||
| April | 13.4 | 25.3 | 10.8 |
| May | 14.4 | 25.3 | 5.1 |
| June | 14.8 | 25.2 | 1.8 |
| July | 13.2 | 25.0 | 10.2 |
| August | 12.9 | 24.8 | 12.2 |
| September | 12.7 | 24.6 | 17.2 |
| 2006 | |||
| April | 13.8 | 25.6 | 18.0 |
| May | 13.7 | 25.6 | 7.0 |
| June | 13.6 | 25.5 | 3.2 |
| July | 13.3 | 25.2 | 4.3 |
| August | 13.0 | 24.9 | 3.8 |
| September | 12.6 | 24.4 | 6.6 |
| 2007 | |||
| April | 14.6 | 26.3 | 8.2 |
| May | 14.8 | 26.4 | 3.0 |
| June | 14.6 | 26.2 | 9.5 |
| July | 14.2 | 25.8 | 18.6 |
| August | 13.7 | 25.4 | 8.4 |
| September | 13.0 | 24.6 | 11.3 |
| 2008 | |||
| April | 14.3 | 29.1 | 14.0 |
| May | 16.3 | 31.5 | 16.8 |
| June | 17.6 | 32.7 | 1.0 |
| July | 14.5 | 28.9 | 4.0 |
| August | 13.5 | 26.1 | 14.6 |
| September | 13.1 | 24.0 | 28.6 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anapalli, S.S.; Pettigrew, W.T.; Reddy, K.N.; Ma, L.; Fisher, D.K.; Sui, R. Climate-Optimized Planting Windows for Cotton in the Lower Mississippi Delta Region. Agronomy 2016, 6, 46. https://doi.org/10.3390/agronomy6040046
Anapalli SS, Pettigrew WT, Reddy KN, Ma L, Fisher DK, Sui R. Climate-Optimized Planting Windows for Cotton in the Lower Mississippi Delta Region. Agronomy. 2016; 6(4):46. https://doi.org/10.3390/agronomy6040046
Chicago/Turabian StyleAnapalli, Saseendran S., William T. Pettigrew, Krishna N. Reddy, Liwang Ma, Daniel K. Fisher, and Ruixiu Sui. 2016. "Climate-Optimized Planting Windows for Cotton in the Lower Mississippi Delta Region" Agronomy 6, no. 4: 46. https://doi.org/10.3390/agronomy6040046
APA StyleAnapalli, S. S., Pettigrew, W. T., Reddy, K. N., Ma, L., Fisher, D. K., & Sui, R. (2016). Climate-Optimized Planting Windows for Cotton in the Lower Mississippi Delta Region. Agronomy, 6(4), 46. https://doi.org/10.3390/agronomy6040046







