Integrating Wheat Canopy Temperatures in Crop System Models
Abstract
:1. Introduction
- (I)
- developing empirical models to predict maximum, minimum and mean daily canopy temperatures based on meteorological data and environmental variables available from the output of a crop system model operated at a daily time step and
- (II)
- studying potential effects of using derived canopy temperatures as input temperature in crop system models.
2. Material and Methods
2.1. Research Sites and Experimental Set-Up
| Year | Irrigation | Site | n | Rep | Observation Period | Water Supply |
|---|---|---|---|---|---|---|
| 2010 | W0 | HS | W0: 78 | 1 | W0: 05/13–07/30 | 4 |
| W1 | W1: 78 | W1: 05/13–07/30 | 177 | |||
| W2 | W2: 78 | W2: 05/13–07/30 | 314 | |||
| 2011 | W0 | HS | W0: 56 | 1 | W0: 05/08–07/11 1 | 31 |
| W1 | W1: 82 | W1: 05/08–07/30 | 197 | |||
| W2 | W2: 74 | W2: 05/08–07/30 1 | 361 | |||
| 2013 | W0 | HS | W0: 57 | 2 | W0: 05/24–07/19 | 43 |
| W2 | W2: 57 | W2: 05/24–07/19 | 306 | |||
| 2014 | W0 W2 | HS, BS | W0: 17 (HS) W2: 43 (HS), W2: 65 (BS) | 1 | W0 (HS): 04/19–05/05 | 15 |
| W2 (HS, P1): 04/19–05/20 | 295 | |||||
| W2 (HS, P2): 04/19–04/30 | 295 | |||||
| W2 (BS): 05/16–07/19 | 383 |
2.2. Canopy Temperature Data
2.3. Crop System Modeling
2.4. Statistical Data Analysis and Model Formulation
2.5. Impact Study
- (I)
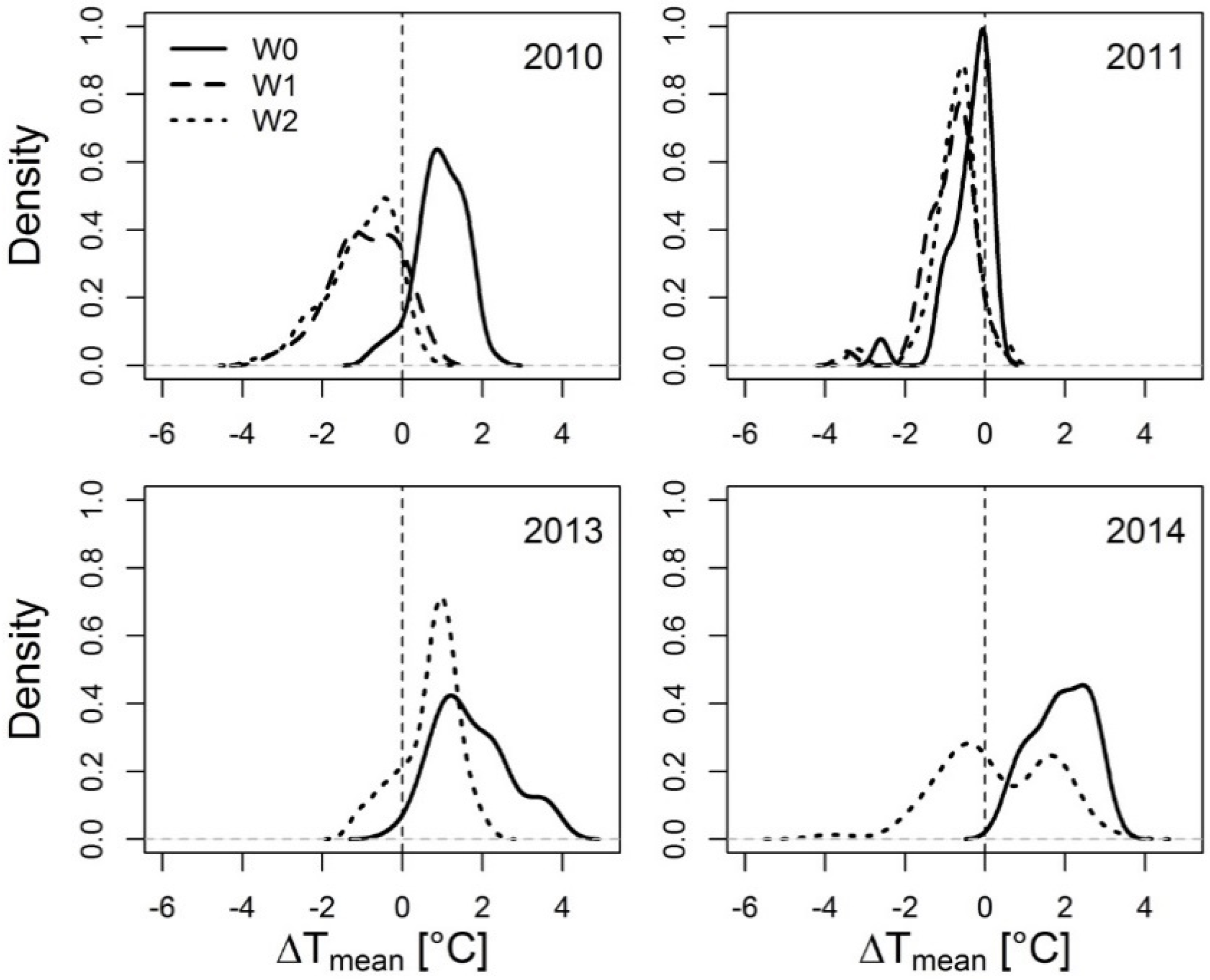
- calculate cumulative sum curves of the difference between modeled daily canopy temperature and the air temperature (∆T),
- (II)
- compute the number of days where modeled and measured canopy temperatures and air temperatures exceed temperature thresholds of 20 °C, 25 °C and 30 °C,
- (III)
- calculate extreme thermal unit (ETU) sums above the optimal temperature of 20 °C (according to [52]).
3. Results and Discussion
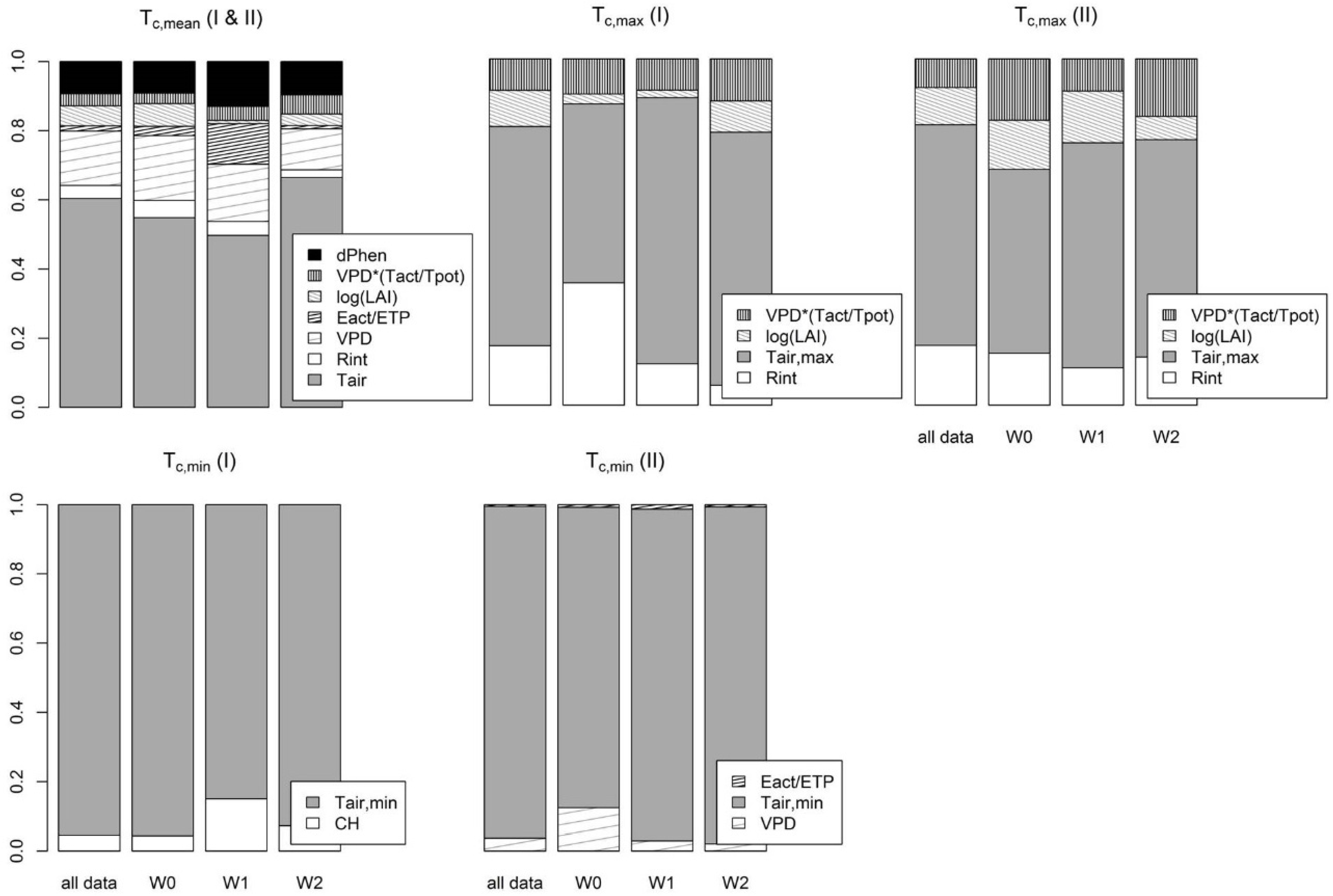
3.1. Empirical Models of Daily Canopy Temperatures
| Estimate | SE | p-Value | |
|---|---|---|---|
| I & II | I & II | I & II | |
| Intercept | 2.730 | 0.266 | <2e−16 |
| Tair,mean | 0.942 | 0.015 | <2e−16 |
| Rint | 0.005 | 0.001 | 1.27e−13 |
| LAIlog | −1.358 | 0.082 | <2e−16 |
| (1-Dphen)*Eact/ETP | −5.491 | 0.953 | 1.87e−08 |
| Dphen*VPD | −0.263 | 0.023 | <2e−16 |
| (1-Dphen)*(VPD*(Tact/Tpot)) | −0.299 | 0.033 | <2e−16 |
| Estimate | SE | p-Value | ||||
|---|---|---|---|---|---|---|
| I | II | I | II | I | II | |
| Intercept | 4.241 | 4.011 | 0.942 | 0.633 | 1.39e−05 | 1.58e−09 |
| Rint | 0.016 | 0.014 | 0.002 | 0.002 | 1.75e−09 | 1.15e−15 |
| Tair,max | 0.922 | 0.888 | 0.055 | 0.029 | <2e−16 | <2e−16 |
| LAIlog | −2.816 | −1.847 | 0.340 | 0.176 | 8.59e−14 | <2e−16 |
| VPD*(Tact/Tpot) | −0.447 | −0.623 | 0.113 | 0.063 | 0.000118 | <2e−16 |
| Estimate | SE | p-Value | ||||
|---|---|---|---|---|---|---|
| I | II | I | II | I | II | |
| Intercept | 1.116 | −0.202 | 0.410 | 0.276 | 0.00729 | 0.466 |
| CH | −4.147 | - | 0.546 | - | 3.64e−12 | - |
| VPD | - | −0.101 | - | 0.019 | - | 2.89e−07 |
| Tair,min | 1.088 | 1.013 | 0.031 | 0.024 | <2e−16 | <2e−16 |
| Eact/ETP | - | −3.158 | - | 0.715 | - | 1.65e−05 |
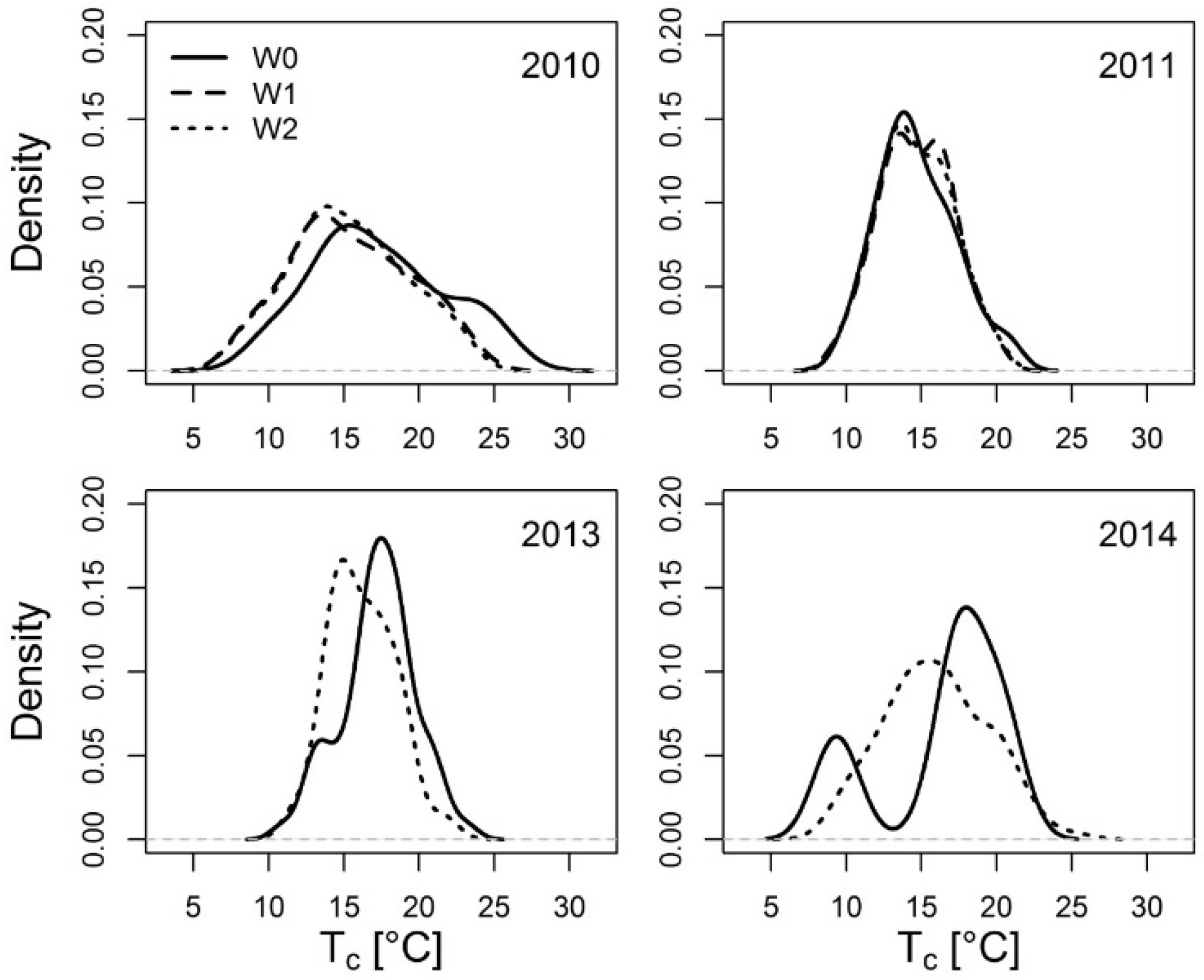
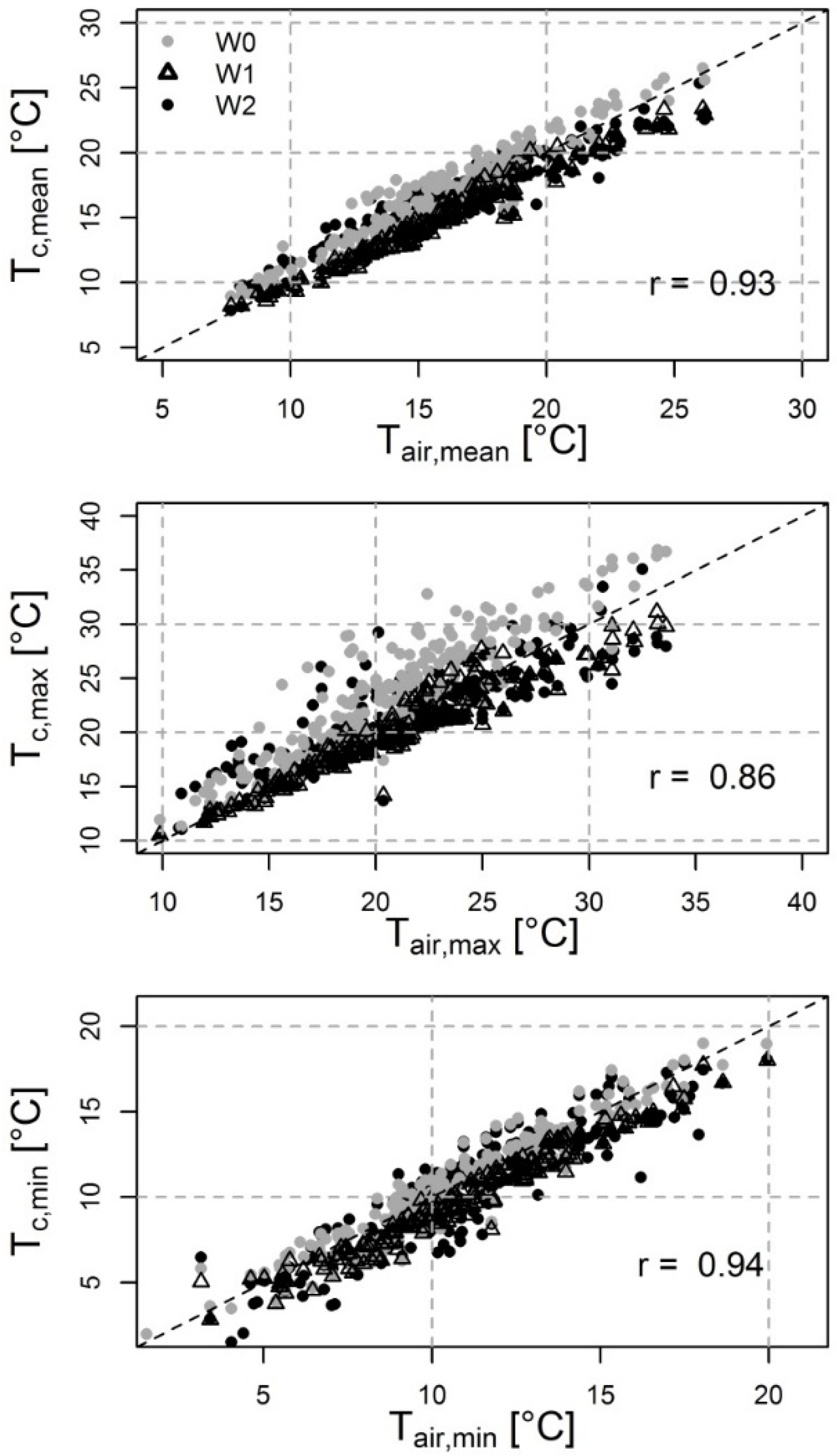
3.2. Variability of Canopy Surface Temperatures
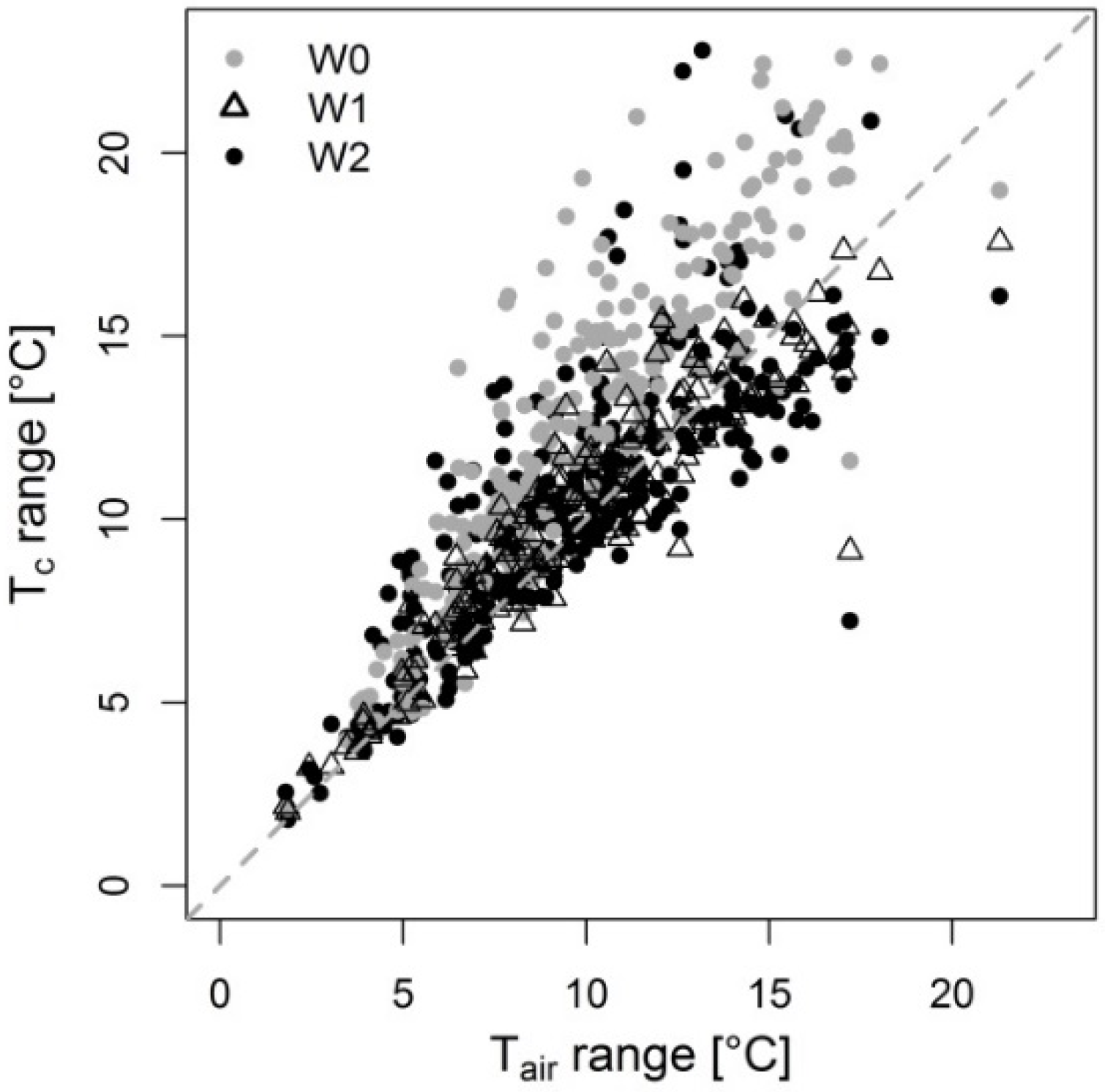
3.3. Predictive Ability of the Empirical Canopy Temperature Models
| Target Variable | Treatment | Phase | Training | Testing | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |||
| Tc,mean | All | I & II | 0.95 | 0.78 | 0.94 | 0.81 |
| W0 | I & II | 0.97 | 0.64 | 0.95 | 0.72 | |
| W1 | I & II | 0.99 | 0.36 | 0.99 | 0.39 | |
| W2 | I & II | 0.92 | 0.88 | 0.93 | 0.87 | |
| Tc,max | All | I | 0.79 | 2.08 | 0.83 | 1.84 |
| W0 | I | 0.89 | 1.62 | 0.91 | 1.60 | |
| W1 | I | 0.91 | 0.86 | 0.93 | 0.94 | |
| W2 | I | 0.74 | 2.29 | 0.72 | 1.90 | |
| Tc,max | All | II | 0.91 | 1.43 | 0.9 | 1.56 |
| W0 | II | 0.93 | 1.48 | 0.92 | 1.49 | |
| W1 | II | 0.95 | 0.97 | 0.96 | 0.77 | |
| W2 | II | 0.89 | 1.26 | 0.88 | 1.52 | |
| Tc,min | All | I | 0.9 | 1.04 | 0.86 | 1.19 |
| W0 | I | 0.9 | 1.02 | 0.89 | 1.04 | |
| W1 | I | 0.92 | 0.73 | 0.75 | 1.00 | |
| W2 | I | 0.9 | 1.11 | 0.88 | 1.29 | |
| Tc,min | All | II | 0.91 | 0.81 | 0.91 | 0.85 |
| W0 | II | 0.94 | 0.67 | 0.93 | 0.80 | |
| W1 | II | 0.97 | 0.45 | 0.96 | 0.54 | |
| W2 | II | 0.89 | 0.89 | 0.88 | 0.95 | |
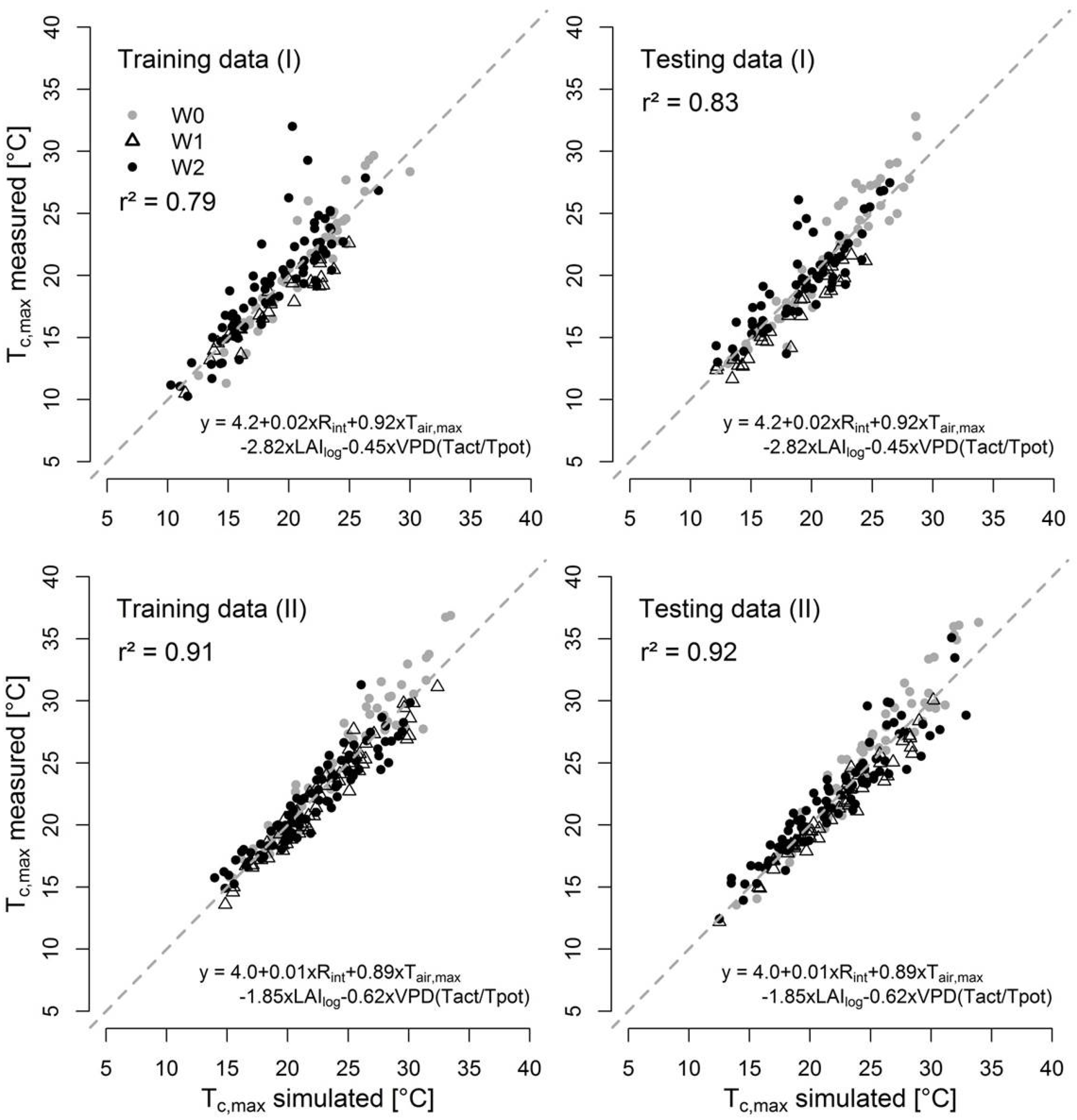
3.4. Case Study: Wheat Canopy versus Air Temperature

| Variable | Year | Days > 20 °C | Days > 25 °C | Days > 30 °C |
|---|---|---|---|---|
| Tc,max W0 | 2010 | 60 (61) | 30 (36) | 12 (17) |
| Tc,max W2 | 2010 | 55 (42) | 20 (14) | 2 (0) |
| Tair,max | 2010 | 53 (55) | 19 (20) | 10 (10) |
| Tc,max W0 | 2011 | 55 (26) | 12 (8) | 1 (0) |
| Tc,max W2 | 2011 | 44 (30) | 4(6) | 0 (0) |
| Tair,max | 2011 | 42 (34) | 7 (6) | 0 (0) |
| Tc,max W0 | 2013 | 55 (47) | 29 (33) | 3 (7) |
| Tc,max W2 | 2013 | 37 (34) | 6 (5) | 0 (0) |
| Tair,max | 2013 | 31 (29) | 9 (9) | 1 (1) |
| Tc,max W0 | 2014 | 77 (13) | 36 (5) | 12 (0) |
| Tc,max W2 | 2014 | 59 (68) | 15 (26) | 1 (3) |
| Tair,max | 2014 | 54 (53) | 13 (18) | 0 (3) |
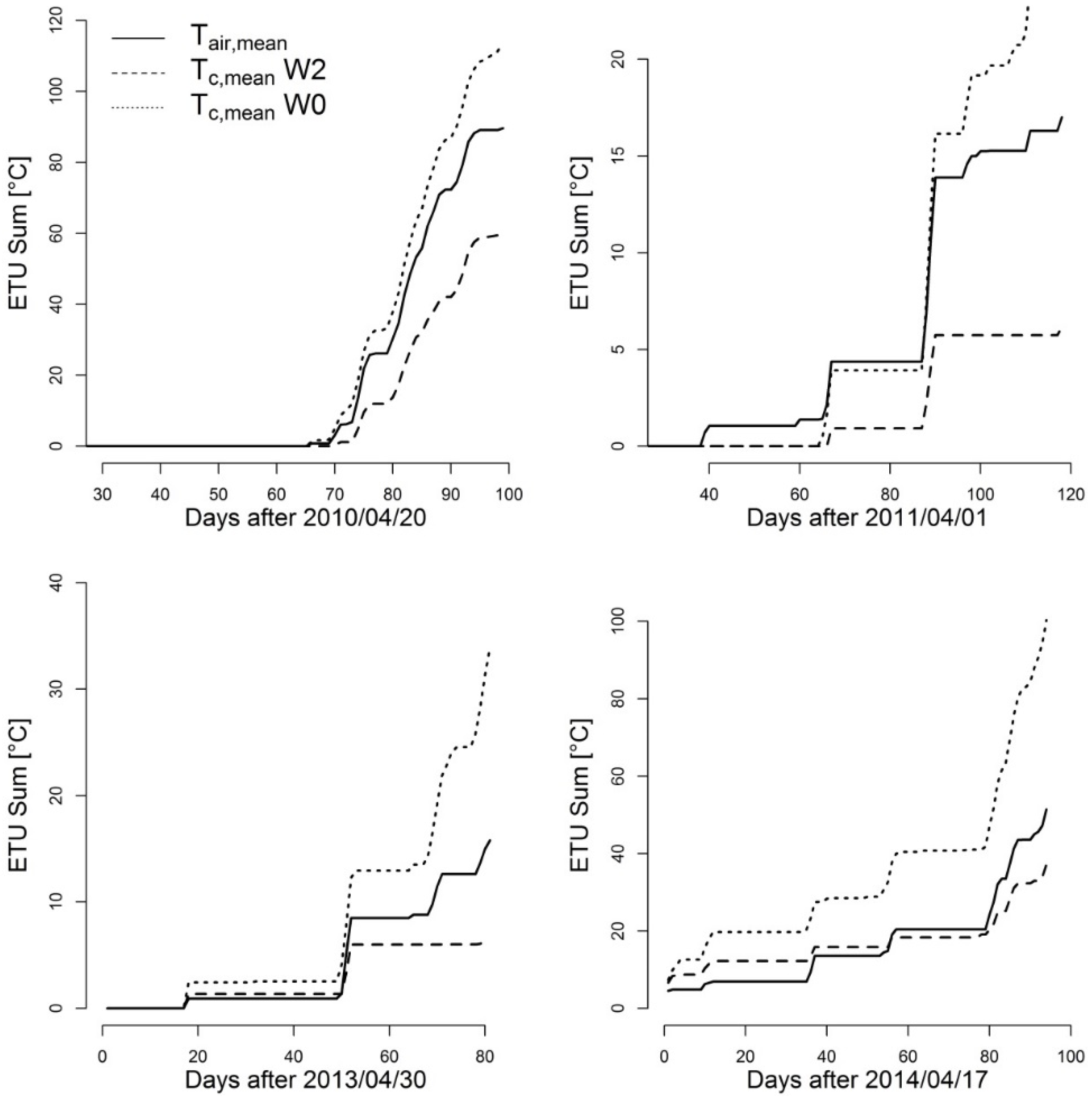
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hoogenboom, G. Contribution of agrometeorology to the simulation of crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Gates, D.M. Transpiration and Leaf Temperature. Ann. Rev. Plant Physiol. 1968, 19, 211–238. [Google Scholar] [CrossRef]
- Burke, J.J.; Upchurch, D.R. Leaf temperature and transpirational control in cotton. Environ. Exp. Bot. 1989, 29, 487–492. [Google Scholar] [CrossRef]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Rezaei, E.; Webber, H.; Gaiser, T.; Naab, J.; Ewert, F. Heat stress in cereals: Mechanisms and modelling. Eur. J. Agron. 2015, 64, 98–113. [Google Scholar] [CrossRef]
- Jarvis, P.P.G. Coupling of transpiration to the atmosphere in horticultural crops: The omega factor. Acta Hortic. 1985, 171, 187–206. [Google Scholar] [CrossRef]
- Tanny, J. Microclimate and evapotranspiration of crops covered by agricultural screens: A review. Biosyst. Eng. 2013, 114, 26–43. [Google Scholar] [CrossRef]
- Van Oort, P.A.J.; Saito, K.; Zwart, S.J.; Shrestha, S. A simple model for simulating heat induced sterility in rice as a function of flowering time and transpirational cooling. Field Crops Res. 2014, 156, 303–312. [Google Scholar] [CrossRef]
- Alderman, P.; Quilligan, E.; Asseng, S.; Ewert, F.; Reynolds, M. Proceedings of the Workshop on Modeling Wheat Response to High Temperature, Texcoco, Mexico, 19–21 June 2013; CIMMYT: El Batán, Mexico, 2013. [Google Scholar]
- Cho, J.; Oki, T. Application of temperature, water stress, CO2 in rice growth models. Rice 2012, 5. [Google Scholar] [CrossRef]
- Siebert, S.; Ewert, F.; Rezaei, E.E.; Kage, H.; Graß, R. Impact of heat stress on crop yield—On the importance of considering canopy temperature. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Webber, H.; Martre, P.; Asseng, S.; Kimball, B.; White, J.; Ottman, M.; Wall, G.W.; de Sanctis, G.; Doltra, J.; Grant, R.; et al. Canopy temperature for simulation of heat stress in irrigated wheat in a semi-arid environment: A multi-model comparison. Field Crops Res. 2015. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed]
- Lamsal, A.; Amgai, L.; Giri, A. Modeling the sensitivity of CERES-Rice model: An experience of Nepal. Agron. J. Nepal 2013, 3, 11–22. [Google Scholar] [CrossRef]
- Levis, S. Crop heat stress in the context of Earth System modeling. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef] [Green Version]
- Jamieson, P.D.; Brooking, I.R.; Porter, J.R.; Wilson, D.R. Prediction of leaf appearance in wheat: A question of temperature. Field Crops Res. 1995, 41, 35–44. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: A review. J. Exp. Bot. 2012, 63, 4671–4712. [Google Scholar] [CrossRef] [PubMed]
- Amani, I.; Fischer, R.A.; Reynolds, M.P. Canopy temperature depression association with yield of irrigated spring wheat cultivars in a hot climate. J. Agron. Crop Sci. 1996, 176, 119–129. [Google Scholar] [CrossRef]
- Ayeneh, A.; van Ginkel, M.; Reynolds, M.P.; Ammar, K. Comparison of leaf, spike, peduncle and canopy temperature depression in wheat under heat stress. Field Crops Res. 2002, 79, 173–184. [Google Scholar] [CrossRef]
- Rebetzke, G.J.; Rattey, A.R.; Farquhar, G.D.; Richards, R.A.; Condon, A.G. Genomic regions for canopy temperature and their genetic association with stomatal conductance and grain yield in wheat. Funct. Plant Biol. 2012, 40, 14–33. [Google Scholar] [CrossRef]
- Gautam, A.; Prasad, S.V.S.; Jajoo, A.; Ambati, D. Canopy temperature as a selection parameter for grain yield and its components in durum wheat under terminal heat stress in late sown conditions. Agric. Res. 2015, 4, 238–244. [Google Scholar] [CrossRef]
- Fang, Q.X.; Ma, L.; Flerchinger, G.N.; Qi, Z.; Ahuja, L.R.; Xing, H.T.; Li, J.; Yu, Q. Modeling evapotranspiration and energy balance in a wheat–maize cropping system using the revised RZ-SHAW model. Agric. For. Meteorol. 2014, 194, 218–229. [Google Scholar] [CrossRef]
- Maruyama, A.; Kuwagata, T. Coupling land surface and crop growth models to estimate the effects of changes in the growing season on energy balance and water use of rice paddies. Agric. For. Meteorol. 2010, 150, 919–930. [Google Scholar] [CrossRef]
- Jackson, R.D.; Reginato, R.J.; Idso, S.B. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Yuan, G.; Luo, Y.; Sun, X.; Tang, D. Evaluation of a crop water stress index for detecting water stress in winter wheat in the North China Plain. Agric. Water Manag. 2004, 64, 29–40. [Google Scholar] [CrossRef]
- Bellvert, J.; Zarco-Tejada, P.J.; Marsal, J.; Girona, J.; González-Dugo, V.; Fereres, E. Vineyard irrigation scheduling based on airborne thermal imagery and water potential thresholds. Aust. J. Grape Wine Res. 2015. [Google Scholar] [CrossRef]
- Cohen, Y.; Alchanatis, V.; Sela, E.; Saranga, Y.; Cohen, S.; Meron, M.; Bosak, A.; Tsipris, J.; Ostrovsky, V.; Orolov, V.; et al. Crop water status estimation using thermography: Multi-year model development using ground-based thermal images. Precis. Agric. 2015, 16, 311–329. [Google Scholar] [CrossRef]
- Sieling, K.; Kage, H. N balance as an indicator of N leaching in an oilseed rape—Winter wheat—Winter barley rotation. Agric. Ecosyst. Environ. 2006, 115, 261–269. [Google Scholar] [CrossRef]
- Neukam, D.; Böttcher, U.; Kage, H. Modelling wheat stomatal resistance in hourly time steps from micrometeorological variables and soil water status. J. Agron. Crop Sci. 2015. [Google Scholar] [CrossRef]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Weigel, H.; Pacholski, A.; Burkart, S.; Helal, M.; Heinemeyer, O.; Kleikamp, B.; Manderscheid, R.; Frühauf, C.; Hendrey, G.; Lewin, K.; et al. Carbon turnover in a crop rotation under free air CO2 enrichment (FACE). Pedosphere 2005, 15, 728–738. [Google Scholar]
- Erbs, M.; Manderscheid, R.; Weigel, H.J. A combined rain shelter and free-air CO2 enrichment system to study climate change impacts on plants in the field. Methods Ecol. Evol. 2012, 3, 81–88. [Google Scholar] [CrossRef]
- Kage, H.S.; Stützel, H. HUME: An object oriented component library for generic modular modelling of dynamic systems. In Proceedings of the 1st Modelling Cropping System International Symposium, Lleida, Spain, 21–23 June 1999; pp. 299–300.
- Kage, H.; Kochler, M.; Stützel, H. Root growth and dry matter partitioning of cauliflower under drought stress conditions: Measurement and simulation. Eur. J. Agron. 2004, 20, 379–394. [Google Scholar] [CrossRef]
- Johnen, T.; Boettcher, U.; Kage, H. An analysis of factors determining spatial variable grain yield of winter wheat. Eur. J. Agron. 2014, 52, 297–306. [Google Scholar] [CrossRef]
- Li, K.Y.; Jong, R.D.; Boisvert, J.B. An exponential root-water-uptake model with water stress compensation. J. Hydrol. 2001, 252, 189–204. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. Closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; van Genuchten, M.T. Using texture and other soil properties to predict the unsaturated soil hydraulic functions. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Thom, A.; Oliver, H. Penmans Equation for estimating regional evaporation. Q. J. R. Meteorol. Soc. 1977, 103, 345–357. [Google Scholar] [CrossRef]
- Beese, F.; van der Ploeg, R.; Richter, W. Der Wasserhaushalt einer Löss-Parabraunerde unter Winterweizen und Brache. Z. Acker Pflanzenbau 1978, 146, 1–19. (In German) [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Pudoc, Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978. [Google Scholar]
- Ehlers, W.; Hamblin, A.P.; Tennant, D.; van der Ploeg, R.R. Root system parameters determining water uptake of field crops. Irrig. Sci. 1991, 12, 115–124. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Sestelo, M.; Villanueva, N.M.; Roca-Pardiñas, J. FWD select: An R package for selecting variables in regression models. Discuss. Papers Stat. Oper. Res. 2013, 13. Available online: http://depc05.webs.uvigo.es/reports/13_02.pdf (accessed on 21 January 2016). [Google Scholar]
- Grömping, U. Relative importance for linear regression in R: The package relaimpo. J. Stat. Softw. 2006, 17. [Google Scholar] [CrossRef]
- Zuur, A.; Ieno, E.N.; Walker, N.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer Science + Business Media: New York, NY, USA, 2009. [Google Scholar]
- Koenker, R.; Hallock, K.F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar] [CrossRef]
- Gobin, A. Impact of heat and drought stress on arable crop production in Belgium. Nat. Hazards Earth Syst. Sci. 2012, 12, 1911–1922. [Google Scholar] [CrossRef]
- Porter, J.R.; Gawith, M. Temperatures and the growth and development of wheat: A review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar] [CrossRef]
- Porter, J.R.; Semenov, M.A. Crop responses to climatic variation. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2021–2035. [Google Scholar] [CrossRef] [PubMed]
- Stöckle, C.O.; Nelson, R.L. Cropping Systems Simulation Model User’s Manual; Biological Systems Engineering Department, Washington State University: Pullman, WA, USA, 2013; Available online: https://nishat2013.files.wordpress.com/2013/11/cropping-system-manual-book.pdf (accessed on 21 October 2015).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neukam, D.; Ahrends, H.; Luig, A.; Manderscheid, R.; Kage, H. Integrating Wheat Canopy Temperatures in Crop System Models. Agronomy 2016, 6, 7. https://doi.org/10.3390/agronomy6010007
Neukam D, Ahrends H, Luig A, Manderscheid R, Kage H. Integrating Wheat Canopy Temperatures in Crop System Models. Agronomy. 2016; 6(1):7. https://doi.org/10.3390/agronomy6010007
Chicago/Turabian StyleNeukam, Dorothee, Hella Ahrends, Adam Luig, Remy Manderscheid, and Henning Kage. 2016. "Integrating Wheat Canopy Temperatures in Crop System Models" Agronomy 6, no. 1: 7. https://doi.org/10.3390/agronomy6010007
APA StyleNeukam, D., Ahrends, H., Luig, A., Manderscheid, R., & Kage, H. (2016). Integrating Wheat Canopy Temperatures in Crop System Models. Agronomy, 6(1), 7. https://doi.org/10.3390/agronomy6010007