Scaling of Thermal Images at Different Spatial Resolution: The Mixed Pixel Problem
Abstract
:1. Introduction

2. Impacts of Image Scale on Thermal Imaging for Plant Phenotyping
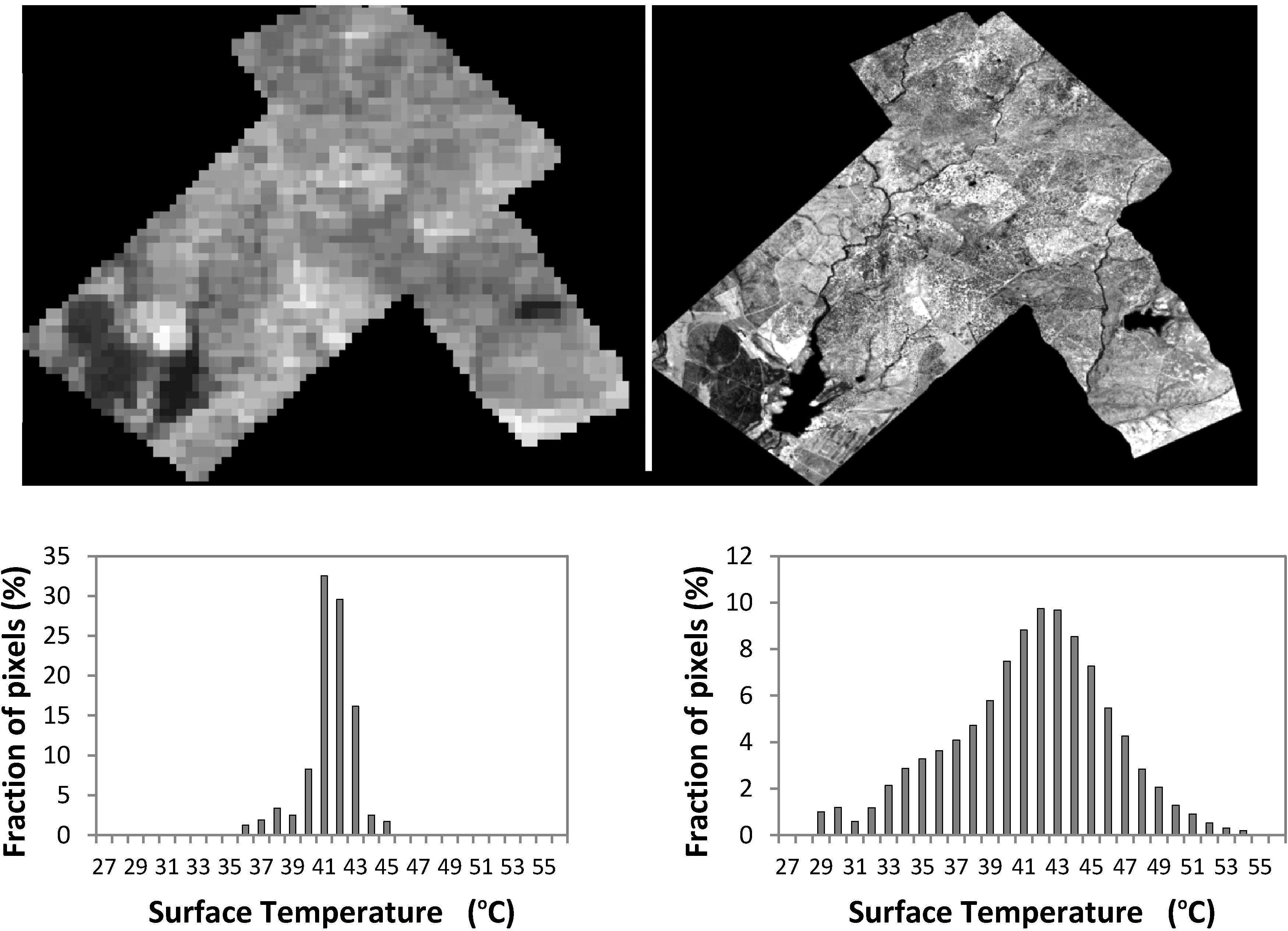
3. Review and Evaluation of Methods for Extraction of Component Temperatures
3.1. Whole Pixel Approaches to Extraction of True Leaf Temperatures
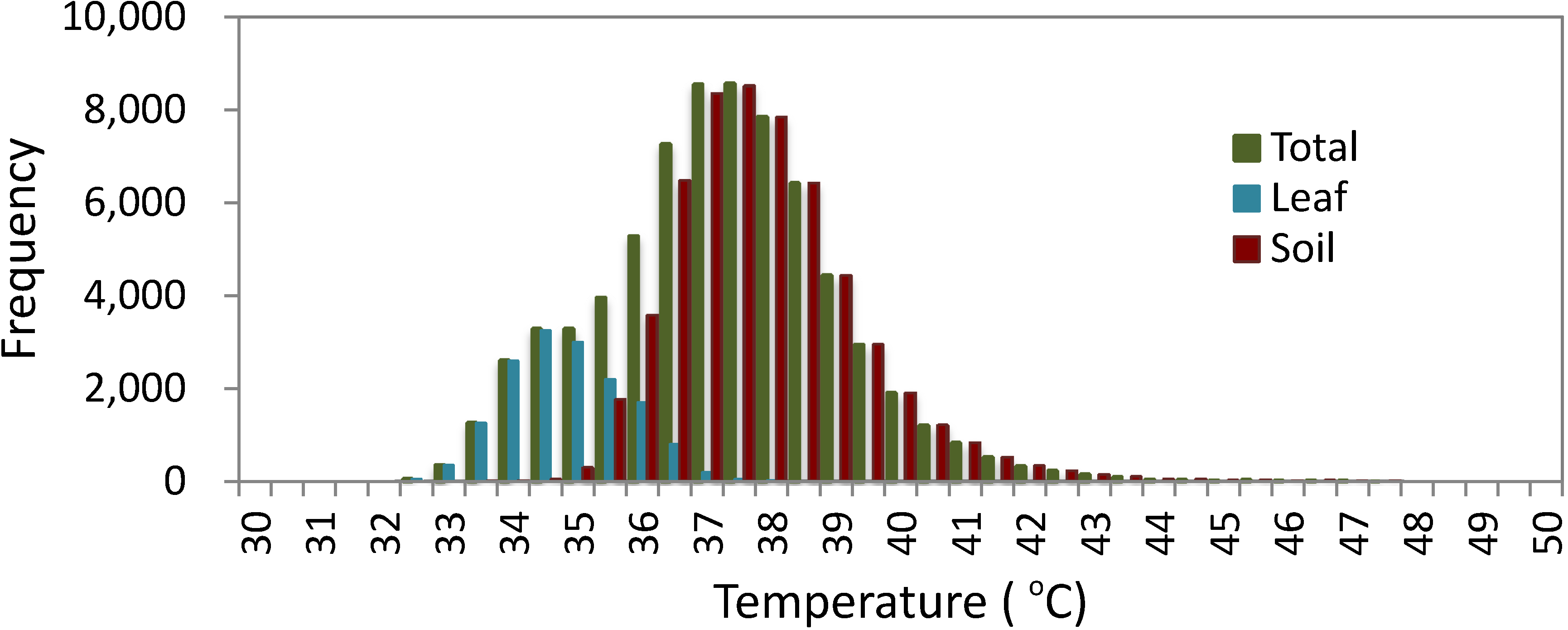
3.1.1. Histogram Analysis
3.1.2. Image Segmentation by Cross-Correlation with a Spectral Image

3.1.3. Mixed Pixels
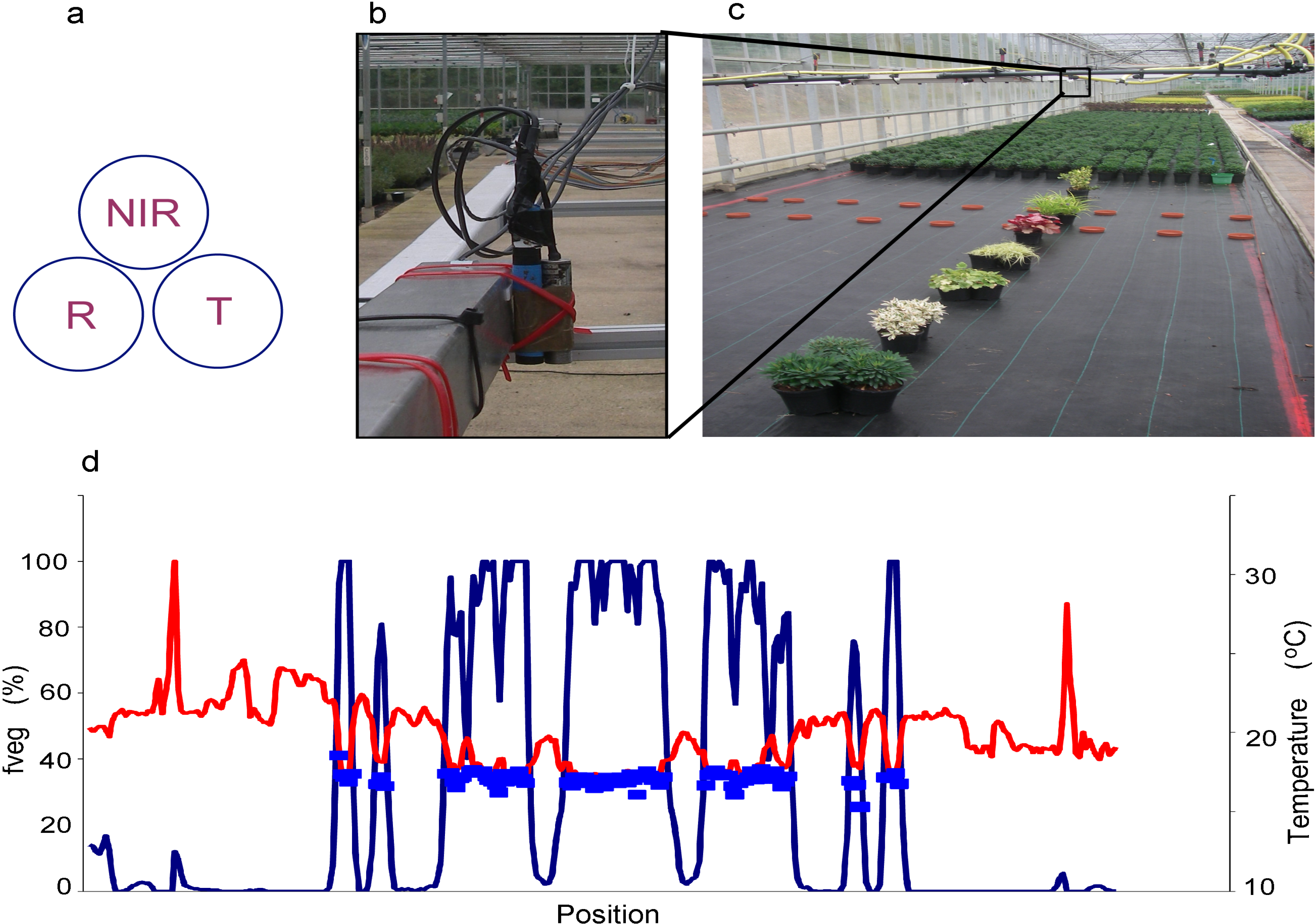
3.2. Spatially Precise Sub-Pixel Approaches (Dis-Aggregation)
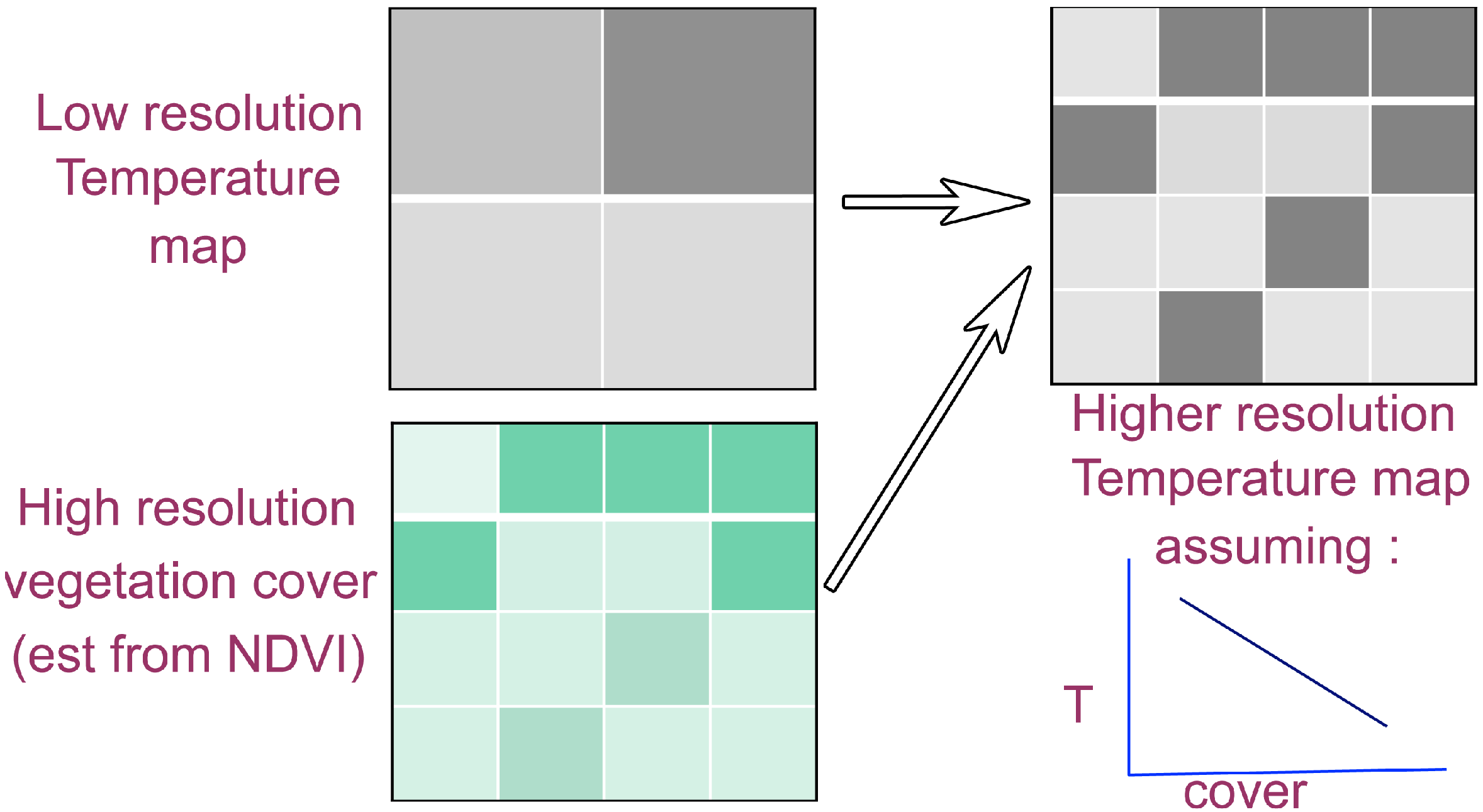
3.2.1. Data Fusion
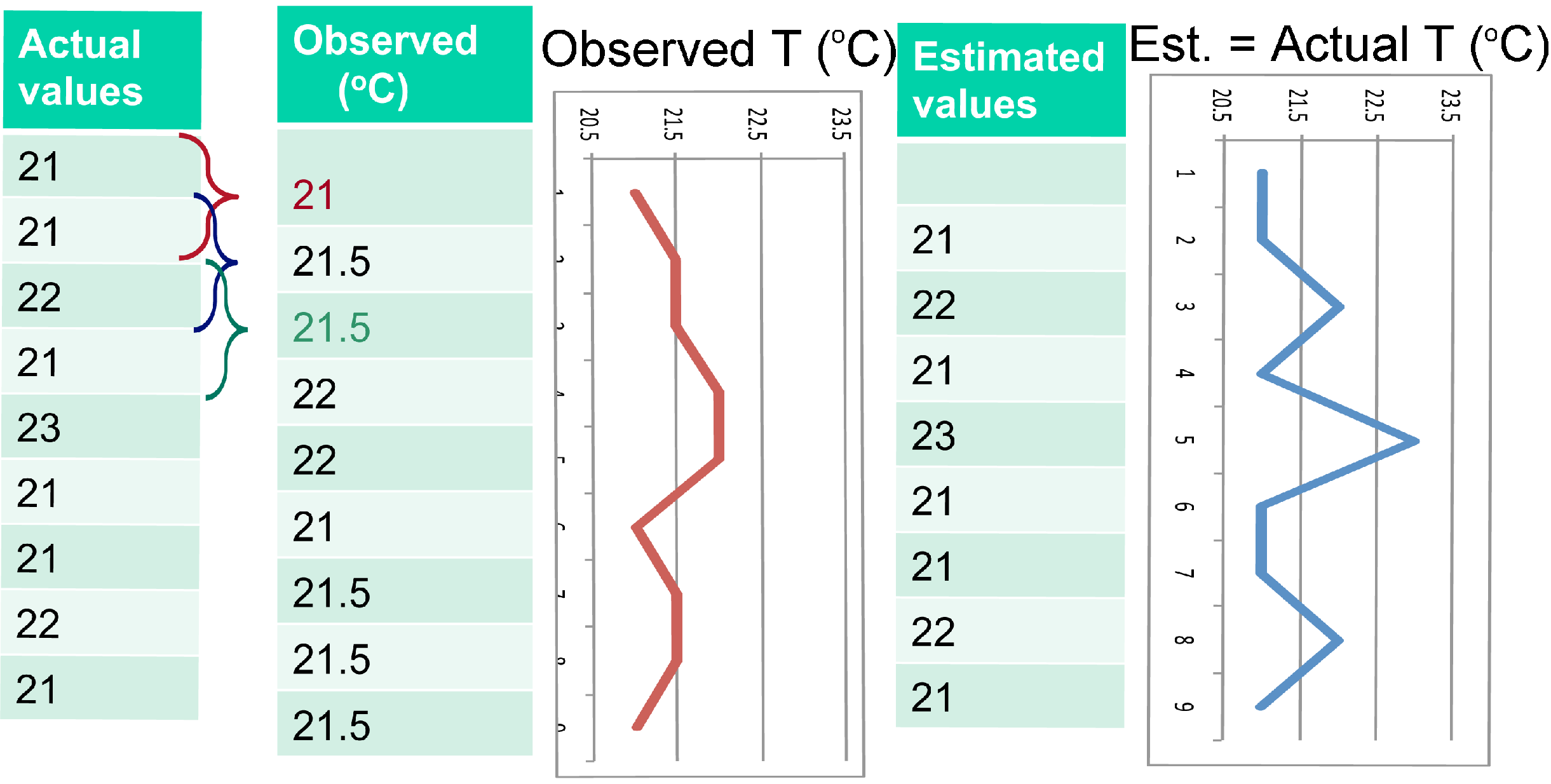
3.2.2. Oversampling (or Image Deconvolution)
4. Technical Aspects Relating to Choice of Sensor
4.1. Realistically Define the Objective of the Experiment and Define an Instrument Specification that Meets These Minimum Requirements
4.2. Determine the Required Speed of Response of the Sensor
4.3. Establish the Spatial Resolution of the Sensor (and Its Optics)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jones, H.G. Application of thermal imaging and infrared sensing in plant physiology and ecophysiology. Adv. Bot. Res. 2004, 41, 107–163. [Google Scholar] [CrossRef]
- Saint Pierre, C.; Crossa, J.; Manes, Y.; Reynolds, M.P. Gene action of canopy temperature in bread wheat under diverse environments. Theor. Appl. Genet. 2010, 120, 1107–1117. [Google Scholar] [CrossRef]
- Jones, H.G.; Serraj, R.; Loveys, B.R.; Xiong, L.; Wheaton, A.; Price, A.H. Thermal infrared imaging of crop canopies for the remote diagnosis and quantification of plant responses to water stress in the field. Funct. Plant Biol. 2009, 36, 978–989. [Google Scholar] [CrossRef]
- Romano, G.; Zia, S.; Spreer, W.; Sanchez, C.; Cairns, J.; Araus, J.L.; Müller, J. Use of thermography for high throughput phenotyping of tropical maize adaptation in water stress. Comput. Electron. Agric. 2011, 79, 67–74. [Google Scholar] [CrossRef]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press: Oxford, UK, 2010; p. 369. [Google Scholar]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Giuliani, R.; Flore, J.A. Potential use of infra-red thermometry for the detection of water stress in apple trees. Acta Hortic. 2000, 537, 383–392. [Google Scholar]
- Otsu, N. A threshold selection method from gray level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Guilioni, L.; Jones, H.G.; Leinonen, I.; Lhomme, J.P. On the relationships between stomatal resistance and leaf temperatures in thermography. Agric. For. Meteorol. 2008, 148, 1908–1912. [Google Scholar] [CrossRef]
- Leinonen, I.; Grant, O.M.; Tagliavia, C.P.P.; Chaves, M.M.; Jones, H.G. Estimating stomatal conductance with thermal imagery. Plant Cell Environ. 2006, 29, 1508–1518. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007; p. 592. [Google Scholar]
- Lillesand, T.M.; Kiefer, R.W.; Chipman, J.C. Remote Sensing and Image Interpretation, 6th ed.; John Wiley & Sons: New York, NY, USA, 2007; p. 768. [Google Scholar]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Observ. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Fiji Is Just ImageJ. Available online: http://fiji.sc/wiki/index.php/Fiji (accessed on 2 July 2014).
- Ridler, T.W.; Calvard, S. Picture thresholding using an iterative selection method. IEEE Trans. Syst. Man Cybern. 1978, 8, 630–632. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.C.K. A new method for gray-level picture thresholding using the entropy of the histogram. Graph. Model. Image Process. 1985, 29, 273–285. [Google Scholar]
- Li, C.H.; Tam, P.K.S. An iterative algorithm for minimum cross entropy thresholding. Pattern Recognit. Lett. 1998, 188, 771–776. [Google Scholar]
- Sirault, X.R.R.; James, R.A.; Furbank, R.T. A new screening method for osmotic component of salinity tolerance in cereals using infrared thermography. Funct. Plant Biol. 2009, 36. [Google Scholar] [CrossRef]
- Jones, H.G.; Stoll, M.; Santos, T.; de Sousa, C.; Chaves, M.M.; Grant, O.M. Use of infrared thermography for monitoring stomatal closure in the field: Application to grapevine. J. Exp. Bot. 2002, 53, 2249–2260. [Google Scholar] [CrossRef]
- Leinonen, I.; Jones, H.G. Combining thermal and visible imagery for estimating canopy temperature and identifying plant stress. J. Exp. Bot. 2004, 55, 1423–1431. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote Sensing—Principles and Interpretation; W. H. Freeman and Company: New York, NY, USA, 1997; p. 494. [Google Scholar]
- Rees, W.G. Physical Principles of Remote Sensing, 2nd ed.; Cambridge University Press: Cambridge, UK, 2001; p. 343. [Google Scholar]
- Möller, M.; Alchanatis, V.; Cohen, Y.; Meron, M.; Tsipris, J.; Naor, A.; Ostrovsky, V.; Sprintsin, M.; Cohen, S. Use of thermal and visible imagery for estimating crop water status of irrigated grapevine. J. Exp. Bot. 2007, 58, 827–838. [Google Scholar]
- Chaerle, L.; Leinonen, I.; Jones, H.G.; Van Der Straeten, D. Monitoring and screening plant populations with combined thermal and chlorophyll fluorescence imaging. J. Exp. Bot. 2007, 58, 773–784. [Google Scholar]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and cwsi in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- DeTar, W.R.; Penner, J.V. Airborne remote sensing used to estimate percent canopy cover and to extract canopy temperature from scene temperature in cotton. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 495–506. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Gillies, R.R.; Carlson, T.N.; Kustas, W.P.; Humes, K.S. A verification of the “triangle” method for obtaining surface soil water content and energy fluxes from remote measurements of the normalized difference vegetation index (NDVI) and surface radiant temperature. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar]
- Garcia, M.; Fernández, N.; Villagarcía, L.; Domingoe, F.; Puigdefábregas, J.; Sandholt, I. Accuracy of the temperature-vegetation dryness index using modis under water-limited vs. energy-limited evapotranspiration conditions. Remote Sens. Environ. 2014, 149, 100–117. [Google Scholar] [CrossRef]
- Jia, L.; Li, Z.-I.; Menenti, M.; Su, Z.; Verhoef, W.; Wan, Z. A practical algorithm to infer soil and foliage component temperatures from bi-angular ATSR-2 data. Int. J. Remote Sens. 2003, 24, 4739–4760. [Google Scholar] [CrossRef]
- Timmermans, J.; Verhoef, W.; van der Tol, C.; Su, Z. Retrieval of canopy temperature component temperatures through bayesian inversion of directional thermal measurements. Hydrol. Earth Syst. Sci. 2009, 13, 1249–1260. [Google Scholar] [CrossRef]
- Matson, M.; Dozier, J. Identification of subresolution high temperature sources using a thermal ir sensor. Photogramm. Eng. Remote Sens. 1981, 47, 1311–1318. [Google Scholar]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Cristobal, G.; Gil, E.; Sroubek, F. Superresolution imaging: A survey of current techniques. In Proceedings of the XVIII SPIE Conference on Advanced Signal Processing Algorithms, Architectures and Instrumentations, San Diego, CA, USA, 10 August 2008; Volume 7074.
- Choi, E.; Choi, J.; kang, M.G. Super-resolution approach to overcome physical limitations of imaging sensors: An overview. Int. J. Imaging Syst. Technol. 2004, 14, 36–46. [Google Scholar] [CrossRef]
- Farsiu, S.; Robinson, D.; Elad, M.; Milanfar, P. Advances and challenges in super-resolution. Int. J. Imaging Syst. Technol. 2004, 14, 47–57. [Google Scholar] [CrossRef]
- Prashar, A.; Jones, H.G. Infra-red thermography as a high throughput tool for phenotyping. Agronomy 2014, in press. [Google Scholar]
- Fuchs, M. Infrared measurement of canopy temperature and detection of plant water stress. Theor. Appl. Climatol. 1990, 42, 253–261. [Google Scholar] [CrossRef]
- Sirault, X.R.R.; Fripp, J.; Paproki, A.; Kuffner, P.; Nguyen, C.; Li, R.-R.; Daily, H.; Guo, J.; Furbank, R.T. Plantscan™: A three-dimensional phenotyping platform for capturing the structural dynamic of plant development and growth. In Proceedings of the 7th International Conference on Functional-Structural Plant Models, Saariselka, Finland, 9–14 June 2013; Sievänen, R., Nikinmaa, E., Godin, C., Lintunen, A., Nygren, P., Eds.; pp. 45–48.
- Prashar, A.; Yildiz, J.; McNicol, J.W.; Bryan, G.J.; Jones, H.G. Infra-red thermography for high throughput field phenotyping in Solanum tuberosum. PLoS One 2013, 8, e65816. [Google Scholar]
- Winterhalter, L.; Mistele, B.; Jampatong, S.; Schmidhalter, U. High throughput phenotyping of canopy water mass and canopy temperature in well-watered and drought stressed tropical maize hybrids in the vegetative stage. Eur. J. Agron. 2011, 35, 22–32. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jones, H.G.; Sirault, X.R.R. Scaling of Thermal Images at Different Spatial Resolution: The Mixed Pixel Problem. Agronomy 2014, 4, 380-396. https://doi.org/10.3390/agronomy4030380
Jones HG, Sirault XRR. Scaling of Thermal Images at Different Spatial Resolution: The Mixed Pixel Problem. Agronomy. 2014; 4(3):380-396. https://doi.org/10.3390/agronomy4030380
Chicago/Turabian StyleJones, Hamlyn G., and Xavier R. R. Sirault. 2014. "Scaling of Thermal Images at Different Spatial Resolution: The Mixed Pixel Problem" Agronomy 4, no. 3: 380-396. https://doi.org/10.3390/agronomy4030380
APA StyleJones, H. G., & Sirault, X. R. R. (2014). Scaling of Thermal Images at Different Spatial Resolution: The Mixed Pixel Problem. Agronomy, 4(3), 380-396. https://doi.org/10.3390/agronomy4030380




