Neural Network-Based Modeling for Precise Potato Yield Prediction Using Soil Parameters
Abstract
1. Introduction
- To develop an ANN model for precise prediction of potato yield intended for French fry production, based on 11 key soil parameters, which is the main technical and practical aim of the research.
- To identify the most important soil parameters influencing the yield and understand how these factors shape the predictive performance of the model—that is, the goal related to analyzing the impact of parameters on the outcome.
2. Materials and Methods
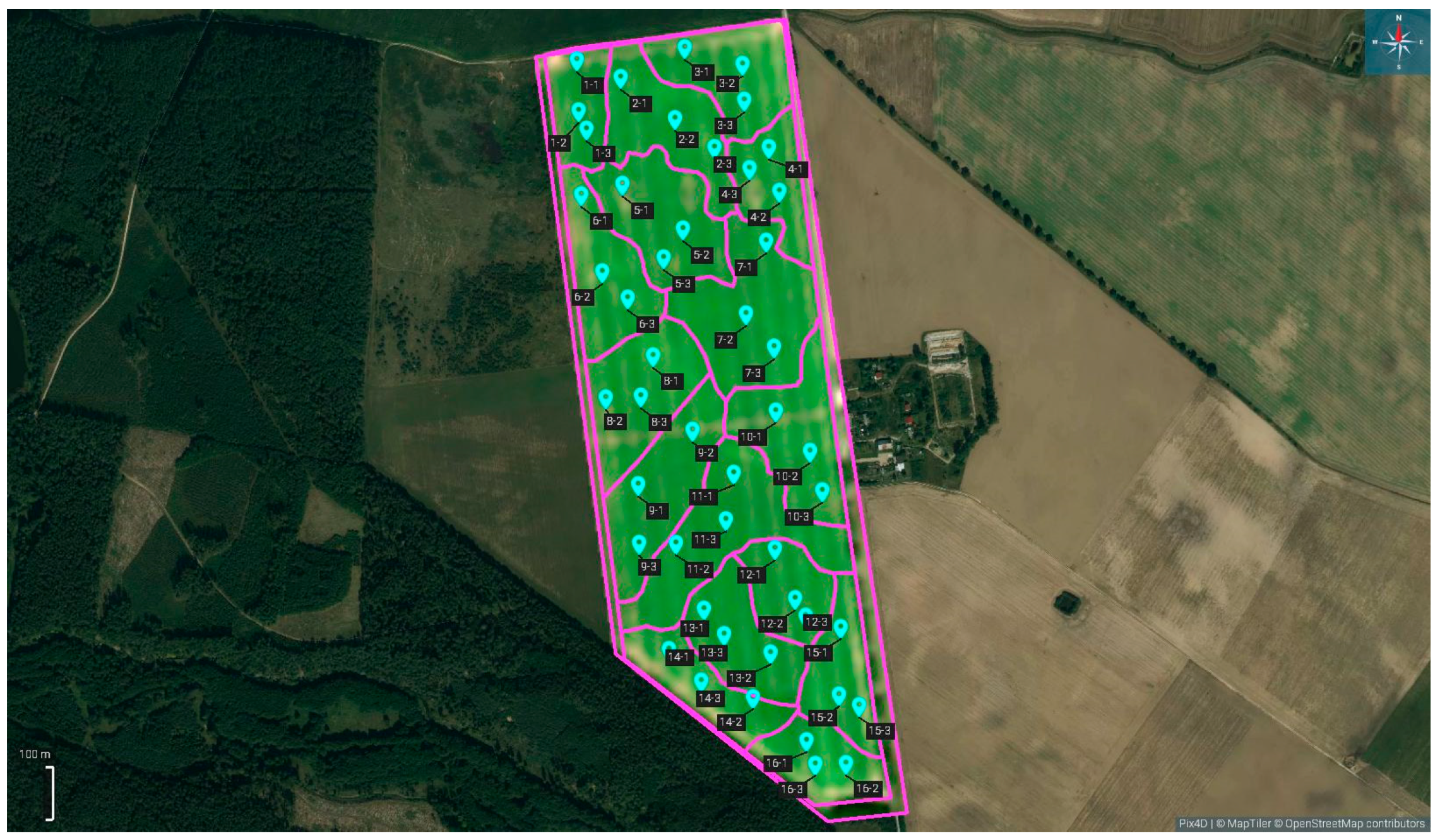
2.1. Field and Laboratory Research
2.1.1. Field Management Practices
2.1.2. Methodology for Soil Sampling and Preparation
2.1.3. Analysis of the Physicochemical Properties of Soil
2.1.4. Methodology for Sampling Potato Tubers Before Harvest
2.2. Data Analysis and Model Development
2.2.1. Dependent and Independent Variables for Building and Verifying a Neural Network Model
2.2.2. Correlation Analysis and Elimination of Collinearity
2.3. Data Preprocessing
2.3.1. Method of Creating a Neural Network Model
2.3.2. Model Evaluation
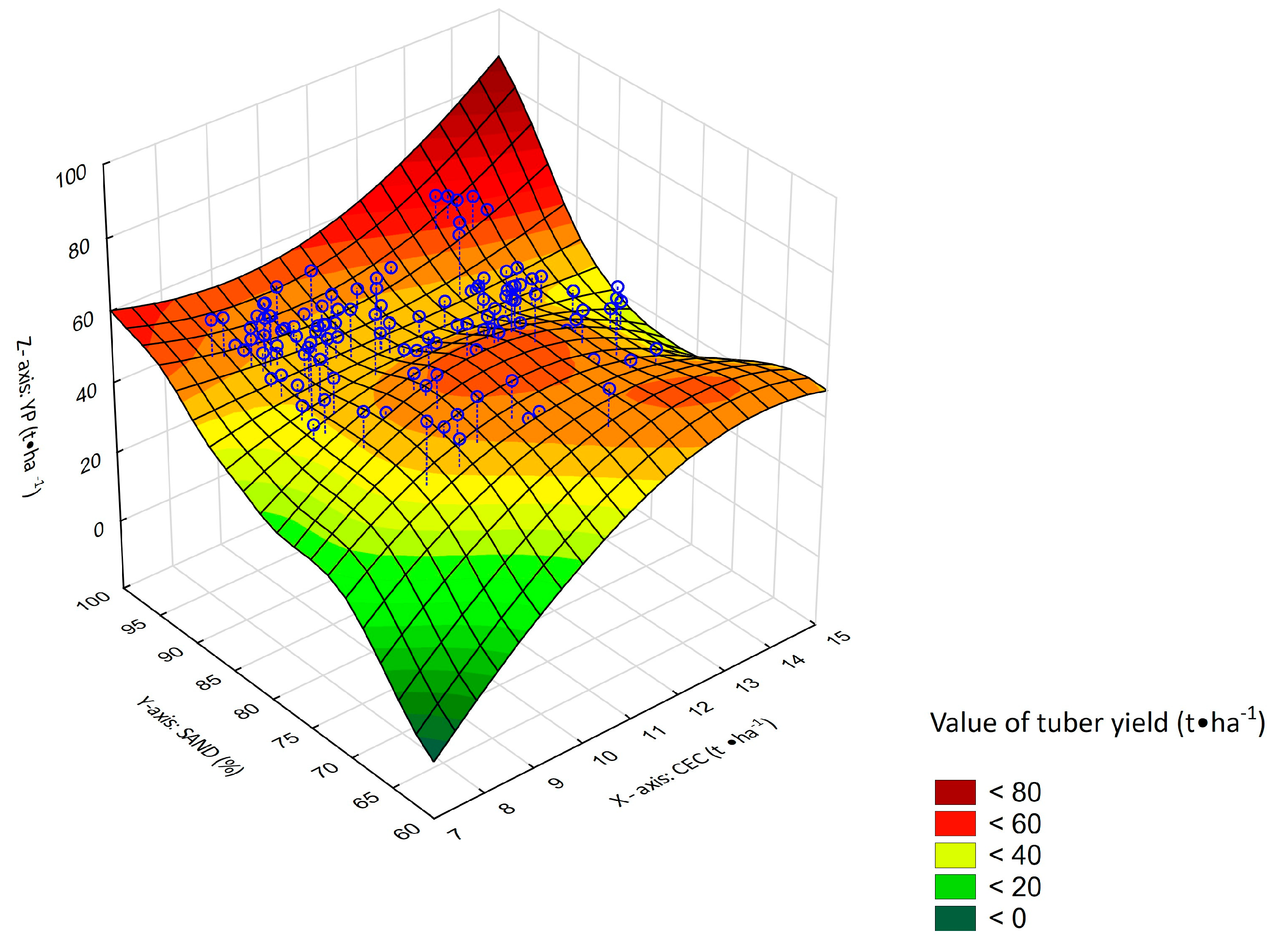
3. Results
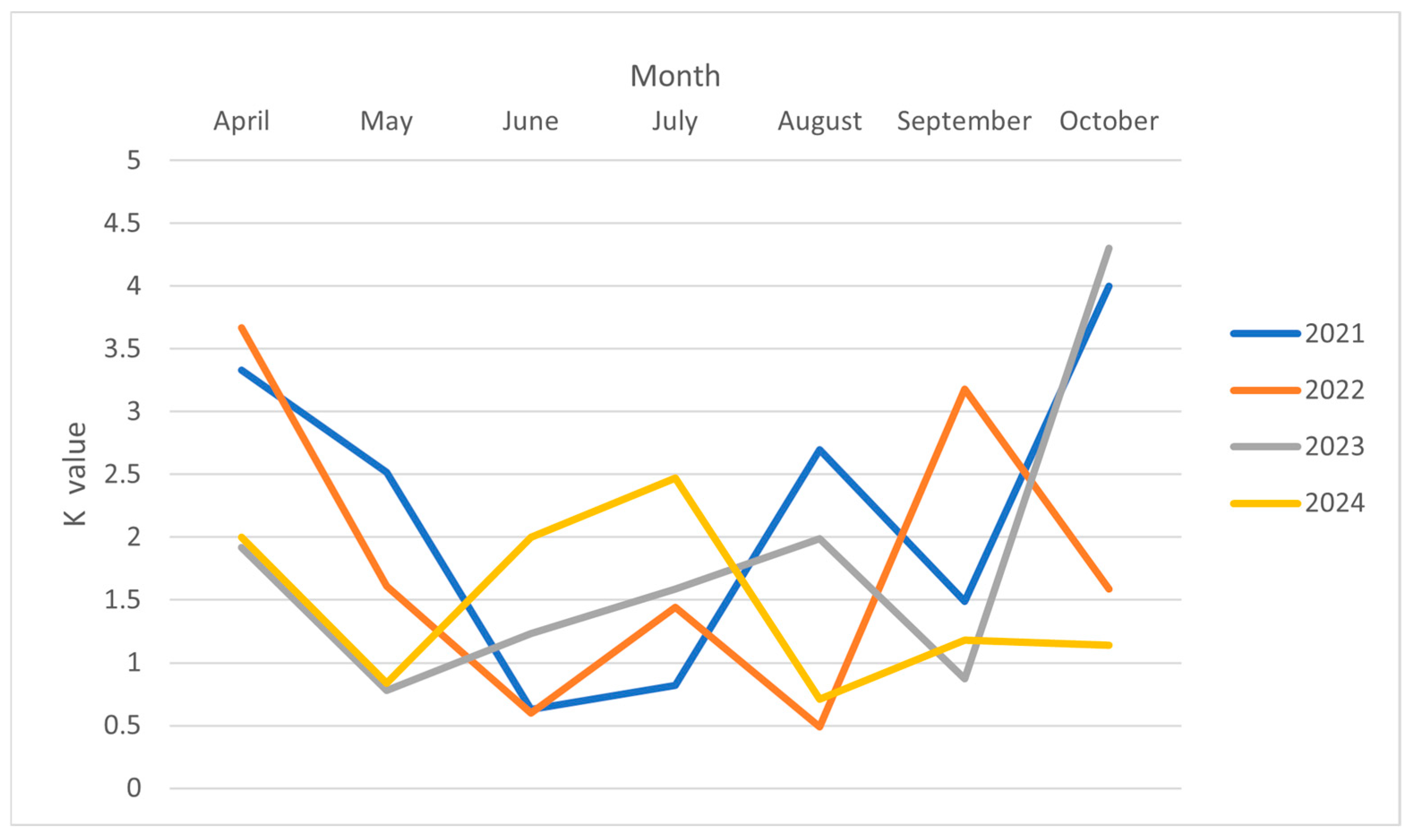
3.1. Basic Statistical Measures of Predictive Model Variables
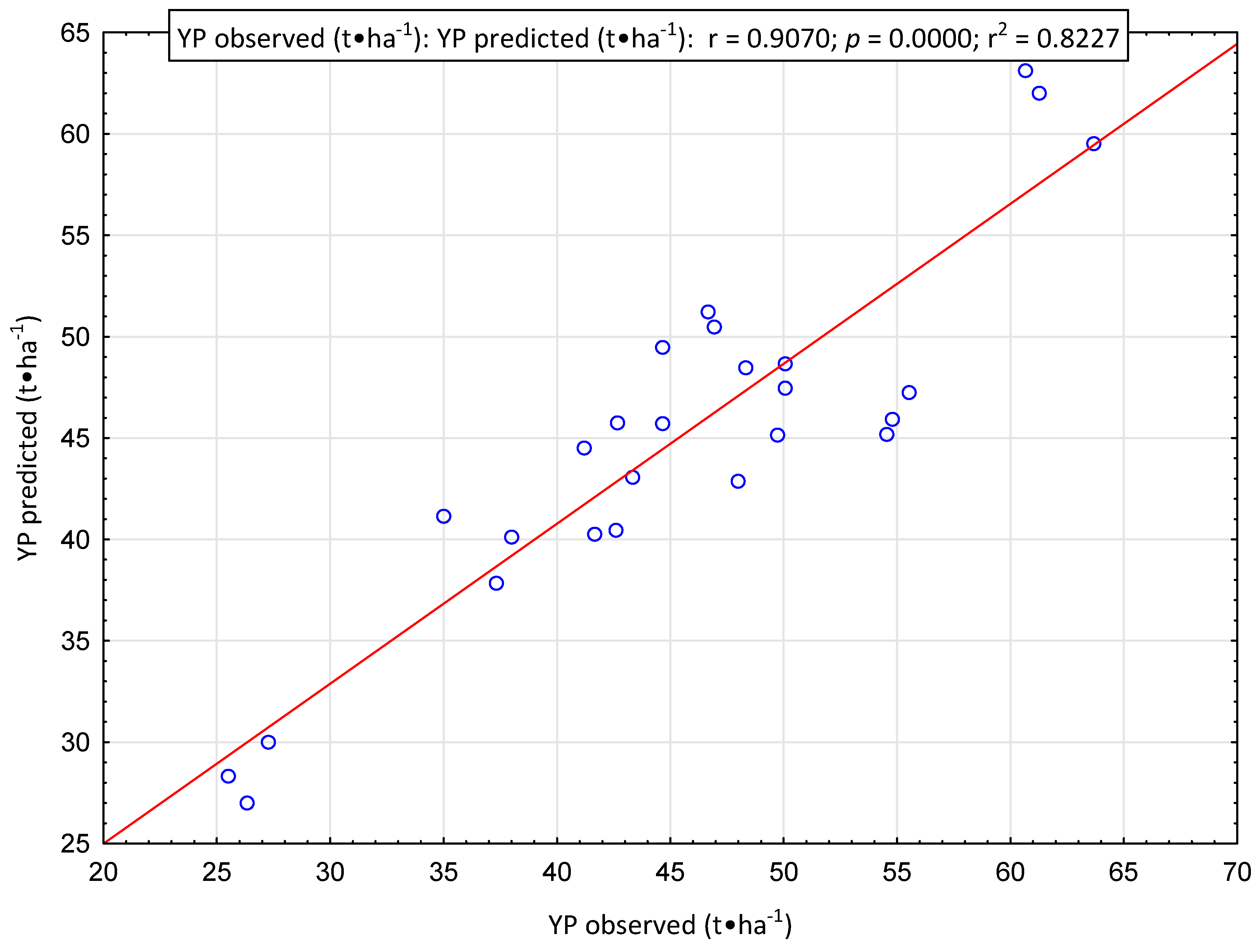
3.2. Forecasting Properties of Neural Model
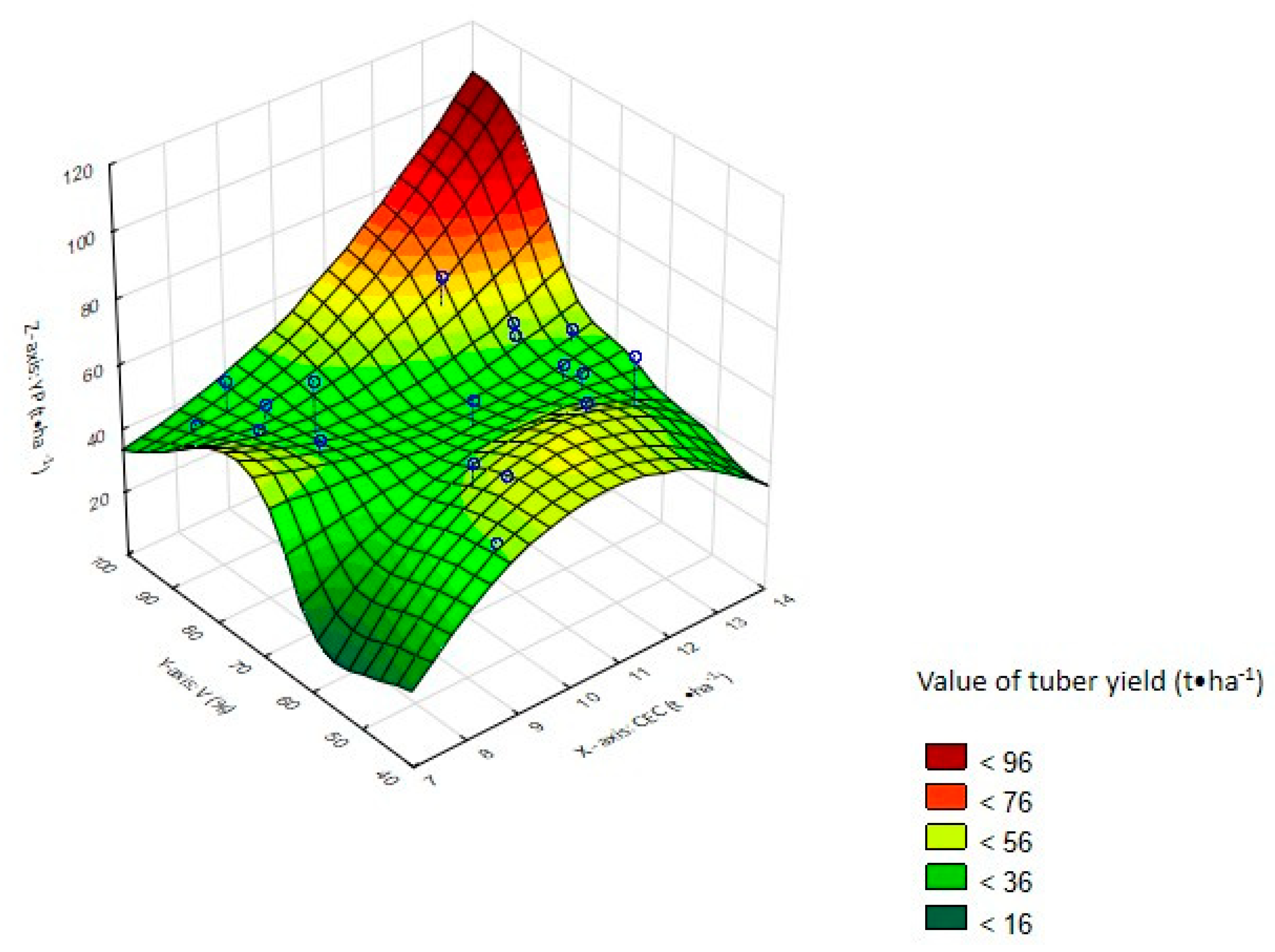
3.3. Sensitivity Analysis of MLP 11-5-1 Neural Network
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations (FAO). The State of Food and Agriculture 2023; FAO: Rome, Italy, 2023; ISBN 978-92-5-138167-0. [Google Scholar]
- Ray, D.K.; Mueller, N.D.; West, P.C.; Foley, J.A. Yield Trends Are Insufficient to Double Global Crop Production by 2050. PLoS ONE 2013, 8, e66428. [Google Scholar] [CrossRef]
- Lin, Y.; Li, S.; Duan, S.; Ye, Y.; Li, B.; Li, G.; Lyv, D.; Jin, L.; Bian, C.; Liu, J. Methodological Evolution of Potato Yield Prediction: A Comprehensive Review. Front. Plant Sci. 2023, 14, 1214006. [Google Scholar] [CrossRef]
- Kurek, J.; Niedbała, G.; Wojciechowski, T.; Świderski, B.; Antoniuk, I.; Piekutowska, M.; Kruk, M.; Bobran, K. Prediction of Potato (Solanum tuberosum L.) Yield Based on Machine Learning Methods. Agriculture 2023, 13, 2259. [Google Scholar] [CrossRef]
- Piekutowska, M. Using Artificial Intelligence for Sustainable Crop Production—A Comprehensive Review with a Focus on Potato Production. J. Water L. Dev. 2025. [Google Scholar] [CrossRef]
- Niedbała, G.; Piekutowska, M. Application of Artificial Neural Networks for the Prediction of Quality Characteristics Potato Tubers- Innovator Variety. J. Res. Appl. Agric. Eng. 2018, 64, 132–138. [Google Scholar]
- Wang, R.-F.; Su, W.-H. The Application of Deep Learning in the Whole Potato Production Chain: A Comprehensive Review. Agriculture 2024, 14, 1225. [Google Scholar] [CrossRef]
- Li, D.; Miao, Y.; Gupta, S.K.; Rosen, C.J.; Yuan, F.; Wang, C.; Wang, L.; Huang, Y. Improving Potato Yield Prediction by Combining Cultivar Information and UAV Remote Sensing Data Using Machine Learning. Remote Sens. 2021, 13, 3322. [Google Scholar] [CrossRef]
- Allal, L.G.; Bennekrouf, M.; Bettayeb, B.; Sahnoun, M. Technologies and Strategies for Optimizing the Potato Supply Chain: A Systematic Literature Review and Some Ideas for Application in the Algerian Context. Comput. Electron. Agric. 2025, 234, 110171. [Google Scholar] [CrossRef]
- Pszczółkowski, P.; Sawicka, B.; Skiba, D.; Barbaś, P. Enhancing Potato Quality in Fries Production Using Ultrasonic Techniques. Sustainability 2025, 17, 828. [Google Scholar] [CrossRef]
- Xing, Y.; Niu, X.; Wang, N.; Jiang, W.; Gao, Y.; Wang, X. The Correlation between Soil Nutrient and Potato Quality in Loess Plateau of China Based on PLSR. Sustainability 2020, 12, 1588. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Q.; de Vries, W.; Ros, G.H.; Chen, X.; Muneer, M.A.; Zhang, F.; Wu, L. Effects of Soil Amendments on Soil Acidity and Crop Yields in Acidic Soils: A World-Wide Meta-Analysis. J. Environ. Manag. 2023, 345, 118531. [Google Scholar] [CrossRef] [PubMed]
- Lipiec, J.; Kuś, J.; Słowińska-Jurkiewicz, A.; Nosalewicz, A. Soil Porosity and Water Infiltration as Influenced by Tillage Methods. Soil Tillage Res. 2006, 89, 210–220. [Google Scholar] [CrossRef]
- Khan, M.T.; Aleinikovienė, J.; Butkevičienė, L.-M. Innovative Organic Fertilizers and Cover Crops: Perspectives for Sustainable Agriculture in the Era of Climate Change and Organic Agriculture. Agronomy 2024, 14, 2871. [Google Scholar] [CrossRef]
- Zayed, O.; Hewedy, O.A.; Abdelmoteleb, A.; Ali, M.; Youssef, M.S.; Roumia, A.F.; Seymour, D.; Yuan, Z.-C. Nitrogen Journey in Plants: From Uptake to Metabolism, Stress Response, and Microbe Interaction. Biomolecules 2023, 13, 1443. [Google Scholar] [CrossRef]
- Ahmed, N.; Zhang, B.; Chachar, Z.; Li, J.; Xiao, G.; Wang, Q.; Hayat, F.; Deng, L.; Narejo, M.-N.; Bozdar, B.; et al. Micronutrients and Their Effects on Horticultural Crop Quality, Productivity and Sustainability. Sci. Hortic. 2024, 323, 112512. [Google Scholar] [CrossRef]
- Mazur, P.; Gozdowski, D.; Wójcik-Gront, E. Soil Electrical Conductivity and Satellite-Derived Vegetation Indices for Evaluation of Phosphorus, Potassium and Magnesium Content, PH, and Delineation of Within-Field Management Zones. Agriculture 2022, 12, 883. [Google Scholar] [CrossRef]
- Serrano, J.; Shahidian, S.; Marques da Silva, J.; Paniágua, L.L.; Rebollo, F.J.; Moral, F.J. Temporal Stability of Management Zone Patterns: Case Study with Contact and Non-Contact Soil Electrical Conductivity Sensors in Dryland Pastures. Sensors 2024, 24, 1623. [Google Scholar] [CrossRef]
- Hara, P.; Piekutowska, M.; Niedbała, G. Selection of Independent Variables for Crop Yield Prediction Using Artificial Neural Network Models with Remote Sensing Data. Land 2021, 10, 609. [Google Scholar] [CrossRef]
- Larkin, R.P.; Griffin, T.S.; Honeycutt, C.W.; Olanya, O.M.; He, Z. Potato Cropping System Management Strategy Impacts Soil Physical, Chemical, and Biological Properties over Time. Soil Tillage Res. 2021, 213, 105148. [Google Scholar] [CrossRef]
- Dubois, A.; Teytaud, F.; Verel, S. Short Term Soil Moisture Forecasts for Potato Crop Farming: A Machine Learning Approach. Comput. Electron. Agric. 2021, 180, 105902. [Google Scholar] [CrossRef]
- Khorramifar, A.; Rasekh, M.; Karami, H.; Malaga-Toboła, U.; Gancarz, M. A Machine Learning Method for Classification and Identification of Potato Cultivars Based on the Reaction of MOS Type Sensor-Array. Sensors 2021, 21, 5836. [Google Scholar] [CrossRef] [PubMed]
- Niedbała, G. Simple Model Based on Artificial Neural Network for Early Prediction and Simulation Winter Rapeseed Yield. J. Integr. Agric. 2019, 18, 54–61. [Google Scholar] [CrossRef]
- Verma, G.; Kumar, B. Multi-Layer Perceptron (MLP) Neural Network for Predicting the Modified Compaction Parameters of Coarse-Grained and Fine-Grained Soils. Innov. Infrastruct. Solut. 2022, 7, 78. [Google Scholar] [CrossRef]
- WRB. World Reference Base for Soil Resources. International Soil Classification Systems for Naming Soils and Creating Legends for Soil Maps, 4th ed.; Internationl Union of Soil Science IUSS: Vienna, Austria, 2022. [Google Scholar]
- Gudko, V.; Usatov, A.; Ioshpa, A.; Denisenko, Y.; Shevtsova, V.; Azarin, K. Agro-Climatic Conditions of the Southern Federal District of Russia in the Context of Climate Change. Theor. Appl. Clim. 2021, 145, 989–1006. [Google Scholar] [CrossRef]
- PN-R-04023:1996; Determination of Plant-Available Phosphorus in Mineral Soils—Methodology’. Polish Committee for Standardization: Warsaw, Poland, 1999.
- PN-R-04022:1996; Determination of Available Potassium in Soils—Extraction and Measurement Method. Polish Committee for Standardization: Warsaw, Poland, 1996.
- PB 31:2010; Soil—Determination of Available Magnesium by Extraction and Chemical Measurement’. Polish Committee for Standardization: Warsaw, Poland, 2010.
- Kabała, A.; Karczewski, C. Methodology of Laboratory Analysis of Soil and Plants; Wrocław University of Environmental and Life Sciences Publishing House: Wrocław, Poland, 2008. [Google Scholar]
- Piekutowska, M.; Niedbała, G.; Piskier, T.; Lenartowicz, T.; Pilarski, K.; Wojciechowski, T.; Pilarska, A.A.; Czechowska-Kosacka, A. The Application of Multiple Linear Regression and Artificial Neural Network Models for Yield Prediction of Very Early Potato Cultivars before Harvest. Agronomy 2021, 11, 885. [Google Scholar] [CrossRef]
- Piekutowska, M.; Hara, P.; Pentoś, K.; Lenartowicz, T.; Wojciechowski, T.; Kujawa, S.; Niedbała, G. Predicting Starch Content in Early Potato Varieties Using Neural Networks and Regression Models: A Comparative Study. Agronomy 2024, 14, 3010. [Google Scholar] [CrossRef]
- Hara, P.; Piekutowska, M.; Niedbała, G. Prediction of Protein Content in Pea (Pisum sativum L.) Seeds Using Artificial Neural Networks. Agriculture 2022, 13, 29. [Google Scholar] [CrossRef]
- Peng, J.; Kim, M.; Kim, Y.; Jo, M.; Kim, B.; Sung, K.; Lv, S. Constructing Italian Ryegrass Yield Prediction Model Based on Climatic Data by Locations in South Korea. Grassl. Sci. 2017, 63, 184–195. [Google Scholar] [CrossRef]
- Basir, M.S.; Chowdhury, M.; Islam, M.N.; Ashik-E-Rabbani, M. Artificial Neural Network Model in Predicting Yield of Mechanically Transplanted Rice from Transplanting Parameters in Bangladesh. J. Agric. Food Res. 2021, 5, 100186. [Google Scholar] [CrossRef]
- Bharti; Das, P.; Banerjee, R.; Ahmad, T.; Devi, S.; Verma, G. Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters. Horticulturae 2023, 9, 436. [Google Scholar] [CrossRef]
- Hara, P.; Piekutowska, M.; Niedbała, G. Prediction of Pea (Pisum sativum L.) Seeds Yield Using Artificial Neural Networks. Agriculture 2023, 13, 661. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and Its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Kley, T.; Preuß, P.; Fryzlewicz, P. Predictive, Finite-Sample Model Choice for Time Series under Stationarity and Non-Stationarity. Electron. J. Stat. 2019, 13, 3710–3774. [Google Scholar] [CrossRef]
- Hepp, T.; Schmid, M.; Gefeller, O.; Waldmann, E.; Mayr, A. Approaches to Regularized Regression—A Comparison between Gradient Boosting and the Lasso. Methods Inf. Med. 2016, 55, 422–430. [Google Scholar] [CrossRef] [PubMed]
- Niedbała, G.; Kurek, J.; Świderski, B.; Wojciechowski, T.; Antoniuk, I.; Bobran, K. Prediction of Blueberry (Vaccinium corymbosum L.) Yield Based on Artificial Intelligence Methods. Agriculture 2022, 12, 2089. [Google Scholar] [CrossRef]
- Rawal, A.; Chakraborty, S.; Li, B.; Lewis, K.; Godoy, M.; Paulette, L.; Weindorf, D.C. Determination of Base Saturation Percentage in Agricultural Soils via Portable X-Ray Fluorescence Spectrometer. Geoderma 2019, 338, 375–382. [Google Scholar] [CrossRef]
- Zhang, J.; Qu, X.; Song, X.; Xiao, Y.; Wang, A.; Li, D. Spatial Variation in Soil Base Saturation and Exchangeable Cations in Tropical and Subtropical China. Agronomy 2023, 13, 781. [Google Scholar] [CrossRef]
- Gupta, U.C.; WU, K.; LIANG, S. Micronutrients in Soils, Crops, and Livestock. Earth Sci. Front. 2008, 15, 110–125. [Google Scholar] [CrossRef]
- Mostofa, M.G.; Rahman, M.M.; Ghosh, T.K.; Kabir, A.H.; Abdelrahman, M.; Rahman Khan, M.A.; Mochida, K.; Tran, L.-S.P. Potassium in Plant Physiological Adaptation to Abiotic Stresses. Plant Physiol. Biochem. 2022, 186, 279–289. [Google Scholar] [CrossRef]
- Vreugdenhil, D.; Bradshaw, J.; Gebhardt, C.; Govers, F.; MacKerron, D.; Taylor, M.; Ross, H. Potato Biology and Biotechnology: Advances and Perspectives; Elsevier B.V.: Amsterdam, The Netherlands, 2007; ISBN 9780444510181. [Google Scholar]
- The Mechanisms of Absorption and Nutrients Transport in Plants: A Review. Trop. J. Nat. Prod. Res. 2022, 6, 8–14. [CrossRef]
- Khan, M.Z.; Akhtar, M.E.; Mahmood-ul-Hassan, M.; Mahmood, M.M.; Safdar, M.N. Potato tuber yield and quality as affected by rates and sources of potassium fertilizer. J. Plant Nutr. 2012, 35, 664–677. [Google Scholar] [CrossRef]
- Liszka-Skoczylas, M. Wpływ Nawożenia Roślin Ziemniaka (Solanum tuberosum L.) Na Zawartość i Jakość Skrobi w Bulwach. Zywn. Nauk. Technol. Jakosc/Food Sci. Technol. Qual. 2020, 122, 31–46. [Google Scholar] [CrossRef]
- Trawczyński, C. Wpływ Nawożenia Mineralnego Azotem Na Plon i Jakość Bulw Bardzo Wczesnych i Wczesnych Odmian Ziemniaka Uprawianych Na Wczesny Zbiór. Agron. Sci. 2023, 78, 81–96. [Google Scholar] [CrossRef]



| Symbol of Variable | Description | Data Range |
|---|---|---|
| INDEPENDENT VARIABLES | ||
| PH | Soil pH measured in KCl | 5.5–7.2 |
| P_SOIL | Soil content of P2O5 (mg/100 g) | 8.4–36.2 |
| K_SOIL | Soil content of K2O (mg/100 g) | 8.0–26.0 |
| Mg_SOIL | Soil content of Mg (mg/100 g) | 3.0–24.6 |
| HH | Hydrolytic acidity (cmol (+)∙kg−1) | 0.0–2.66 |
| S | Sum of exchangeable bases (cmol (+)∙kg−1) | 3.76–11.1 |
| CEC | Soil sorption capacity (cmol (+)∙kg−1) | 7.98–14.07 |
| V | Base saturation percentage (%) | 37.22–89.49 |
| SAND | Percentages of sand (%) | 65.24–96.16 |
| SILT | Percentages of silt (%) | 3.79–32.39 |
| CLAY | Percentages of clay (%) | 0.0–1.54 |
| OC | Organic carbon content (%) | 0.04–3.16 |
| H | Soil humus content (%) | 0.174–5.5 |
| TN | Total nitrogen (%) | 0.02–0.25 |
| DEPENDENT VARIABLE | ||
| YP | Yield of potato tubers (t∙ha−1) | 25.5–68.67 |
| CEC | PH | P_SOIL | K_SOIL | Mg_SOIL | HH | S | V | SAND | SILT | CLAY | OC | H | TN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC | 1.00 | −0.18 | 0.10 | 0.07 | −0.10 | −0.06 | 0.35 | −0.45 | −0.20 | 0.25 | 0.18 | −0.27 | −0.27 | −0.36 |
| PH | −0.18 | 1.00 | 0.37 | 0.07 | 0.13 | −0.67 | 0.31 | 0.45 | 0.07 | −0.15 | −0.04 | 0.17 | 0.17 | 0.14 |
| P_SOIL | 0.10 | 0.37 | 1.00 | 0.46 | 0.18 | −0.27 | 0.12 | 0.05 | −0.22 | 0.20 | 0.27 | 0.10 | 0.10 | −0.33 |
| K_SOIL | 0.07 | 0.07 | 0.46 | 1.00 | 0.35 | −0.04 | −0.07 | −0.09 | −0.44 | 0.45 | 0.42 | −0.08 | −0.08 | −0.34 |
| Mg_SOIL | −0.10 | 0.13 | 0.18 | 0.35 | 1.00 | −0.08 | −0.04 | 0.03 | −0.16 | 0.08 | 0.16 | 0.08 | 0.08 | −0.01 |
| HH | −0.06 | −0.67 | −0.27 | −0.04 | −0.08 | 1.00 | −0.60 | −0.51 | 0.04 | 0.03 | −0.09 | −0.17 | −0.17 | −0.11 |
| S | 0.35 | 0.31 | 0.12 | −0.07 | −0.04 | −0.60 | 1.00 | 0.67 | −0.16 | 0.13 | 0.19 | −0.01 | −0.01 | −0.11 |
| V | −0.45 | 0.45 | 0.05 | −0.09 | 0.03 | −0.51 | 0.67 | 1.00 | −0.01 | −0.06 | 0.05 | 0.20 | 0.20 | 0.16 |
| SAND | −0.20 | 0.07 | −0.22 | −0.44 | −0.16 | 0.04 | −0.16 | −0.01 | 1.00 | −0.92 | −0.91 | 0.22 | 0.22 | 0.35 |
| SILT | 0.25 | −0.15 | 0.20 | 0.45 | 0.08 | 0.03 | 0.13 | −0.06 | −0.92 | 1.00 | 0.93 | −0.28 | −0.28 | −0.43 |
| CLAY | 0.18 | −0.04 | 0.27 | 0.42 | 0.16 | −0.09 | 0.19 | 0.05 | −0.91 | 0.93 | 1.00 | −0.22 | −0.22 | −0.37 |
| OC | −0.27 | 0.17 | 0.10 | −0.08 | 0.08 | −0.17 | −0.01 | 0.20 | 0.22 | −0.28 | −0.22 | 1.00 | 1.00 | 0.21 |
| H | −0.27 | 0.17 | 0.10 | −0.08 | 0.08 | −0.17 | −0.01 | 0.20 | 0.22 | −0.28 | −0.22 | 1.00 | 1.00 | 0.21 |
| TN | −0.36 | 0.14 | −0.33 | −0.34 | −0.01 | −0.11 | −0.11 | 0.16 | 0.35 | −0.43 | −0.37 | 0.21 | 0.21 | 1.00 |
| Variable | Statistic | Training | Testing | Validation |
|---|---|---|---|---|
| pH | Min | 5.5 | 5.6 | 5.7 |
| Max | 7.2 | 6.6 | 7.1 | |
| Mean | 6.29 | 6.19 | 6.23 | |
| SD | 0.31 | 0.30 | 0.45 | |
| P_SOIL | Min | 8.4 | 8.4 | 8.9 |
| Max | 36.2 | 25.6 | 36.2 | |
| Mean | 17.96 | 17.46 | 17.36 | |
| SD | 4.66 | 3.44 | 7.20 | |
| K_SOIL | Min | 8 | 8 | 8 |
| Max | 26 | 22 | 24.6 | |
| Mean | 16.44 | 15.92 | 15.95 | |
| SD | 3.35 | 3.06 | 5.92 | |
| Mg_SOIL | Min | 3 | 3 | 3 |
| Max | 24.6 | 17 | 24.6 | |
| Mean | 6.31 | 5.95 | 6.35 | |
| SD | 2.60 | 2.43 | 6.37 | |
| HH | Min | 0.1 | 1 | 1 |
| Max | 2.66 | 2.5 | 2.24 | |
| Mean | 1.43 | 1.47 | 1.51 | |
| SD | 0.37 | 0.43 | 0.33 | |
| S | Min | 3.76 | 4 | 5 |
| Max | 11.1 | 10.3 | 10.4 | |
| Mean | 7.39 | 7.71 | 7.19 | |
| SD | 1.47 | 1.55 | 1.48 | |
| CEC | Min | 8 | 7.98 | 8 |
| Max | 14.07 | 13.5 | 14 | |
| Mean | 10.66 | 10.83 | 10.86 | |
| SD | 1.74 | 1.94 | 1.53 | |
| V | Min | 37.22 | 44.44 | 38.96 |
| Max | 89.49 | 85.86 | 89.05 | |
| Mean | 65.38 | 67.39 | 6265 | |
| SD | 14.25 | 14.75 | 15.08 | |
| SAND | Min | 65.24 | 71.04 | 76.28 |
| Max | 96.16 | 95.17 | 95.17 | |
| Mean | 85.74 | 85.12 | 87.09 | |
| SD | 7.11 | 6.25 | 11.16 | |
| OC | Min | 0.044 | 0.096 | 0.1 |
| Max | 1.36 | 1.16 | 3.16 | |
| Mean | 0.81 | 0.81 | 0.85 | |
| TN | Min | 0.01 | 0.01 | 0.01 |
| Max | 0.2549 | 0.126 | 0.138 | |
| Mean | 0.056 | 0.053 | 0.054 | |
| SD | 0.041 | 0.034 | 0.038 | |
| YP | Min | 26.6 | 27.13 | 27 |
| Max | 68.67 | 66.87 | 65.2 | |
| Mean | 46.83 | 46.44 | 51 | |
| SD | 9.21 | 9.16 | 8.00 |
| Abbreviation | Unit | Value |
|---|---|---|
| R2 | - | 0.8227 |
| RMSE | t∙ha−1 | 4.19 |
| MAE | t∙ha−1 | 3.35 |
| MAPE | % | 7.34 |
| MAX | t∙ha−1 | 9.35 |
| MAXP | % | 17.54 |
| Variable | Impact Value | Rank |
|---|---|---|
| CEC | 12.84 | 1 |
| V | 8.50 | 2 |
| S | 6.80 | 3 |
| K_SOIL | 2.97 | 4 |
| SAND | 1.69 | 5 |
| P_SOIL | 1.68 | 6 |
| PH | 1.15 | 7 |
| OC | 1.26 | 8 |
| HH | 1.19 | 9 |
| Mg_SOIL | 1.22 | 10 |
| TN | 1.00 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piekutowska, M.; Niedbała, G. Neural Network-Based Modeling for Precise Potato Yield Prediction Using Soil Parameters. Agronomy 2025, 15, 2156. https://doi.org/10.3390/agronomy15092156
Piekutowska M, Niedbała G. Neural Network-Based Modeling for Precise Potato Yield Prediction Using Soil Parameters. Agronomy. 2025; 15(9):2156. https://doi.org/10.3390/agronomy15092156
Chicago/Turabian StylePiekutowska, Magdalena, and Gniewko Niedbała. 2025. "Neural Network-Based Modeling for Precise Potato Yield Prediction Using Soil Parameters" Agronomy 15, no. 9: 2156. https://doi.org/10.3390/agronomy15092156
APA StylePiekutowska, M., & Niedbała, G. (2025). Neural Network-Based Modeling for Precise Potato Yield Prediction Using Soil Parameters. Agronomy, 15(9), 2156. https://doi.org/10.3390/agronomy15092156







