Monitoring Wolfberry (Lycium barbarum L.) Canopy Nitrogen Content with Hyperspectral Reflectance: Integrating Spectral Transformations and Multivariate Regression
Abstract
1. Introduction
2. Materials and Methods
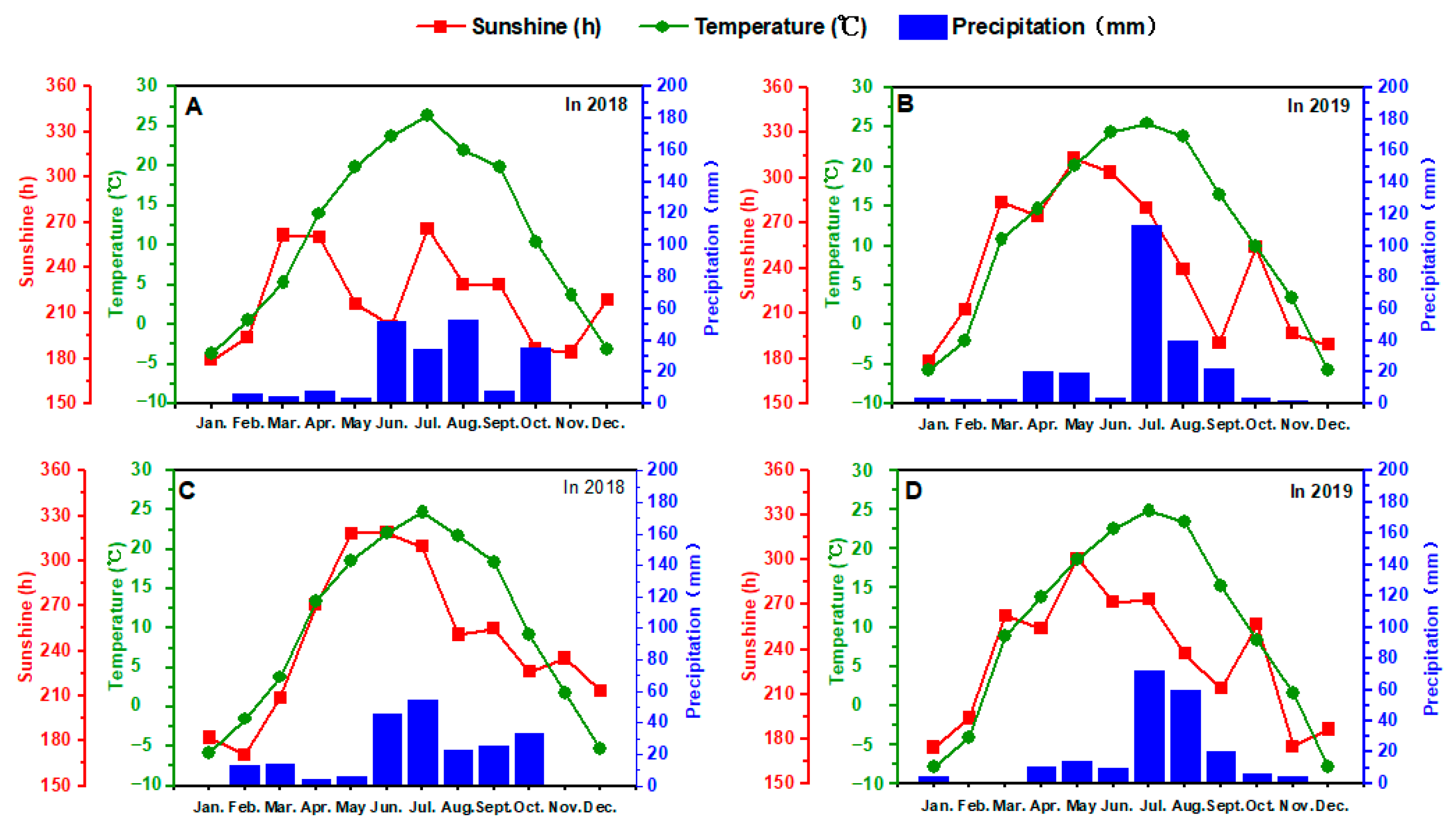
2.1. Study Area and Field Observation
2.2. Data Acquisition and Preprocessing
2.2.1. Canopy Hyperspectral Reflectance Acquisition
2.2.2. Canopy Nitrogen Content (CNC) Determination
2.2.3. Spectral Data Preprocessing
2.3. Spectral Variables and Extraction Method
2.3.1. Spectral Variables
2.3.2. Feature Spectral Variable Extraction Method
2.4. Prediction Models
3. Results
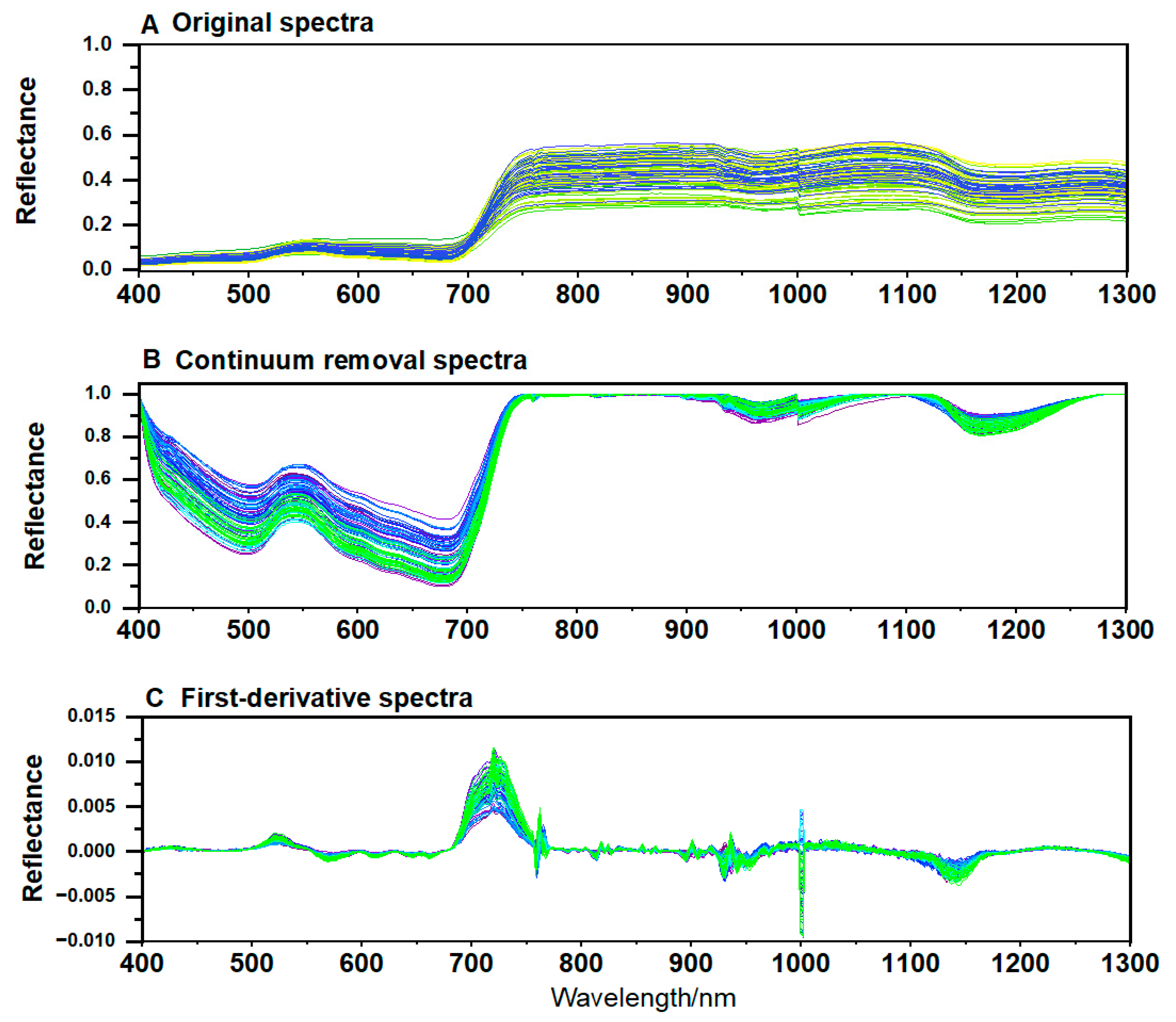
3.1. Canopy Spectral Analysis of Wolfberry Tree
3.2. Correlation Analysis Between Spectra Variables and Nitrogen Content
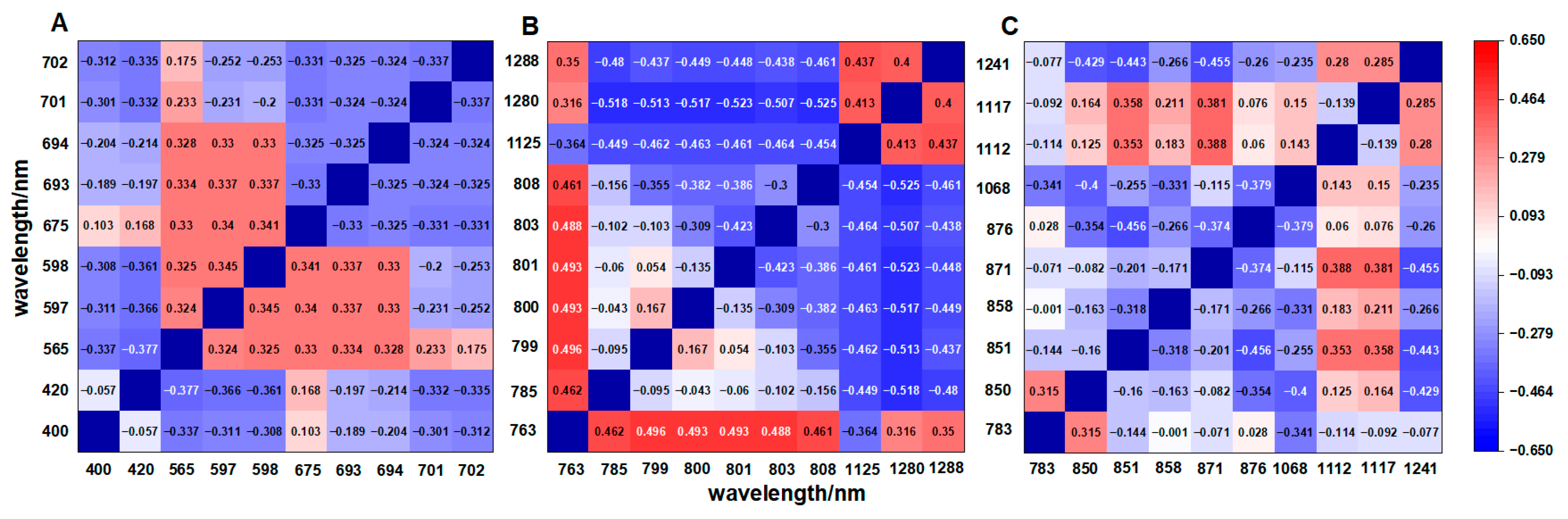
3.2.1. Correlation Between Spectral Wavelengths and Nitrogen Content
3.2.2. Correlation Between PVIs and Nitrogen Content
3.2.3. Correlation Between Ratio Spectral Index and Nitrogen Content
3.3. Feature Spectral Variables Selection
3.4. Multivariate Regression Model
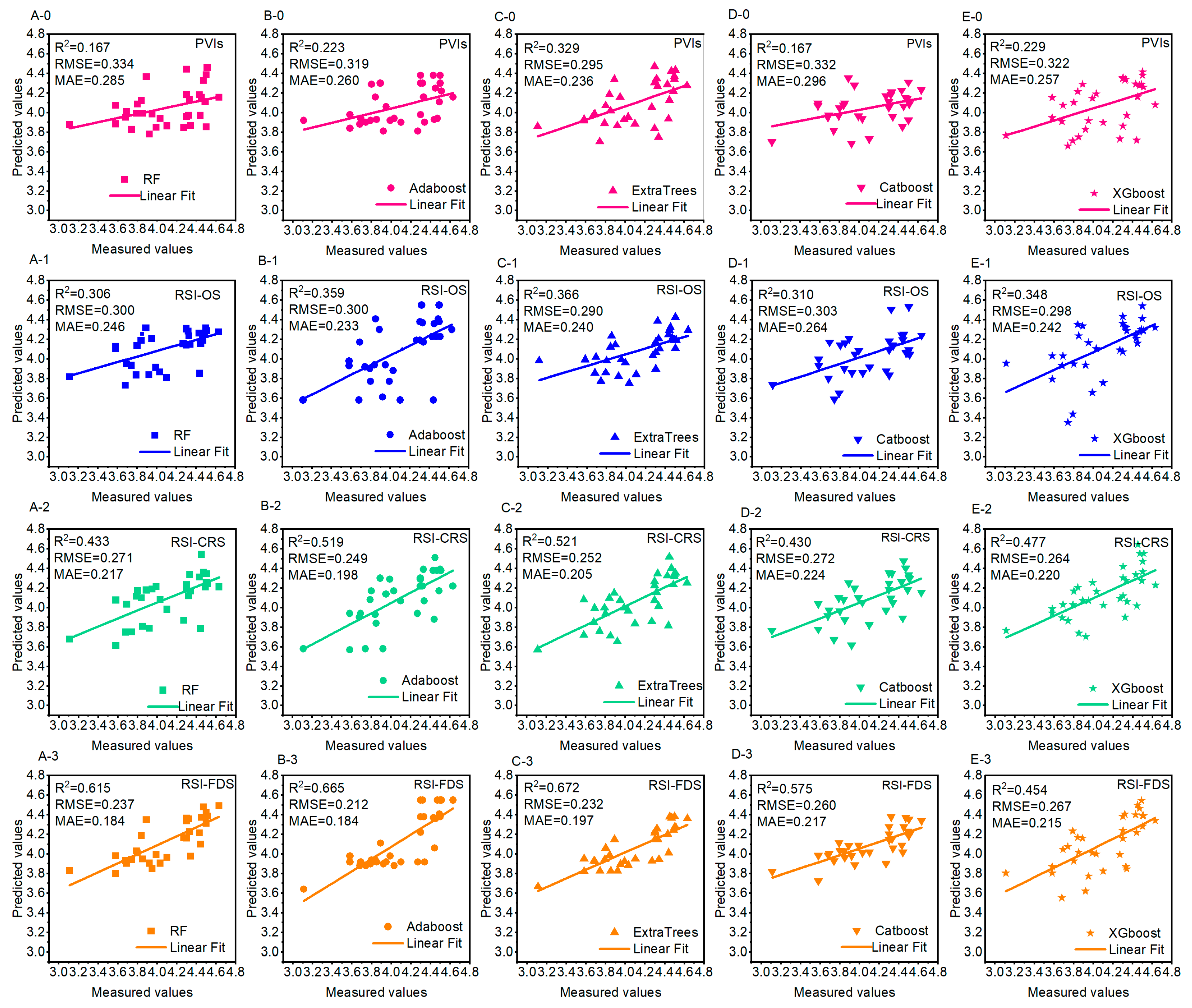
3.4.1. Model Construction
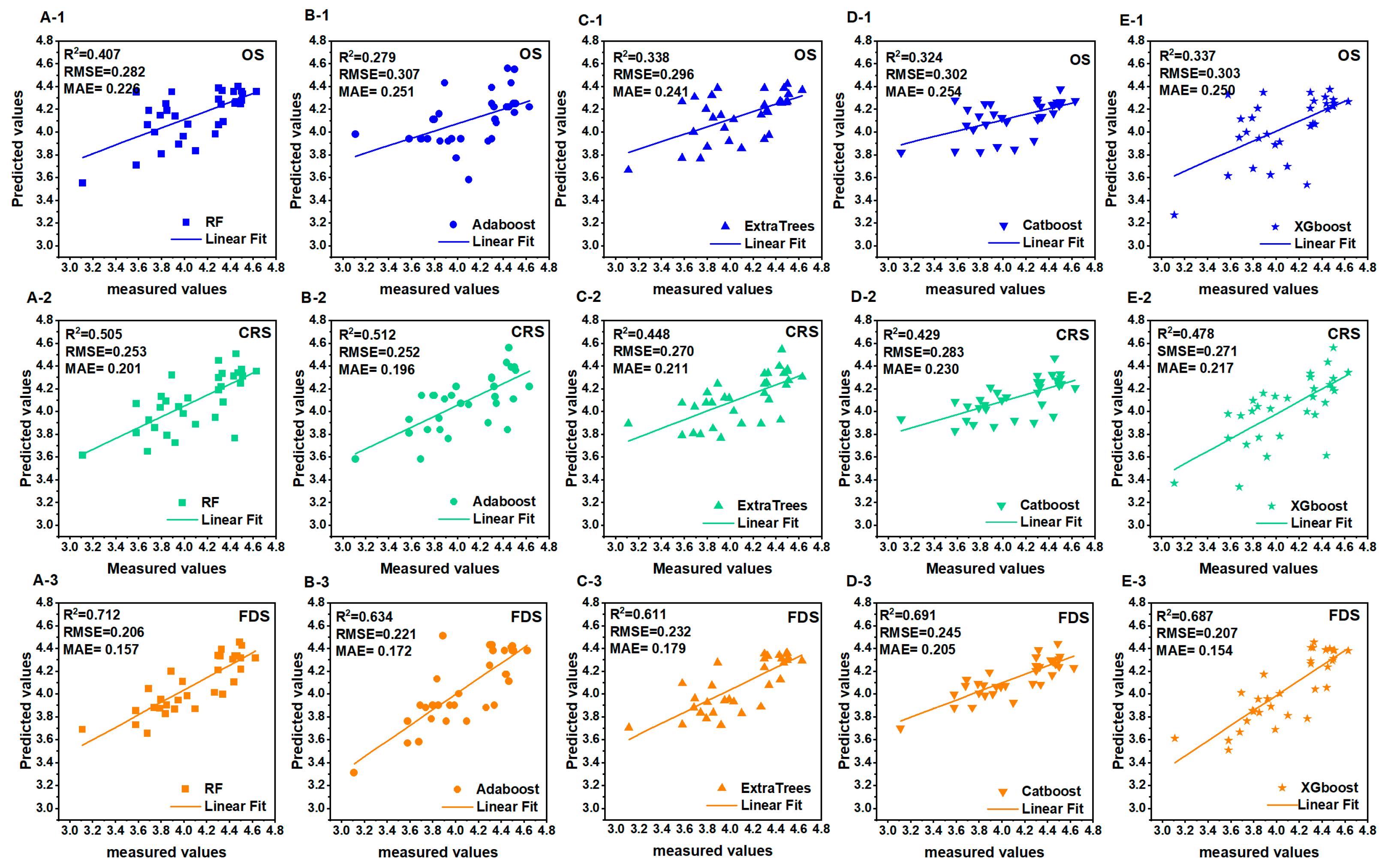
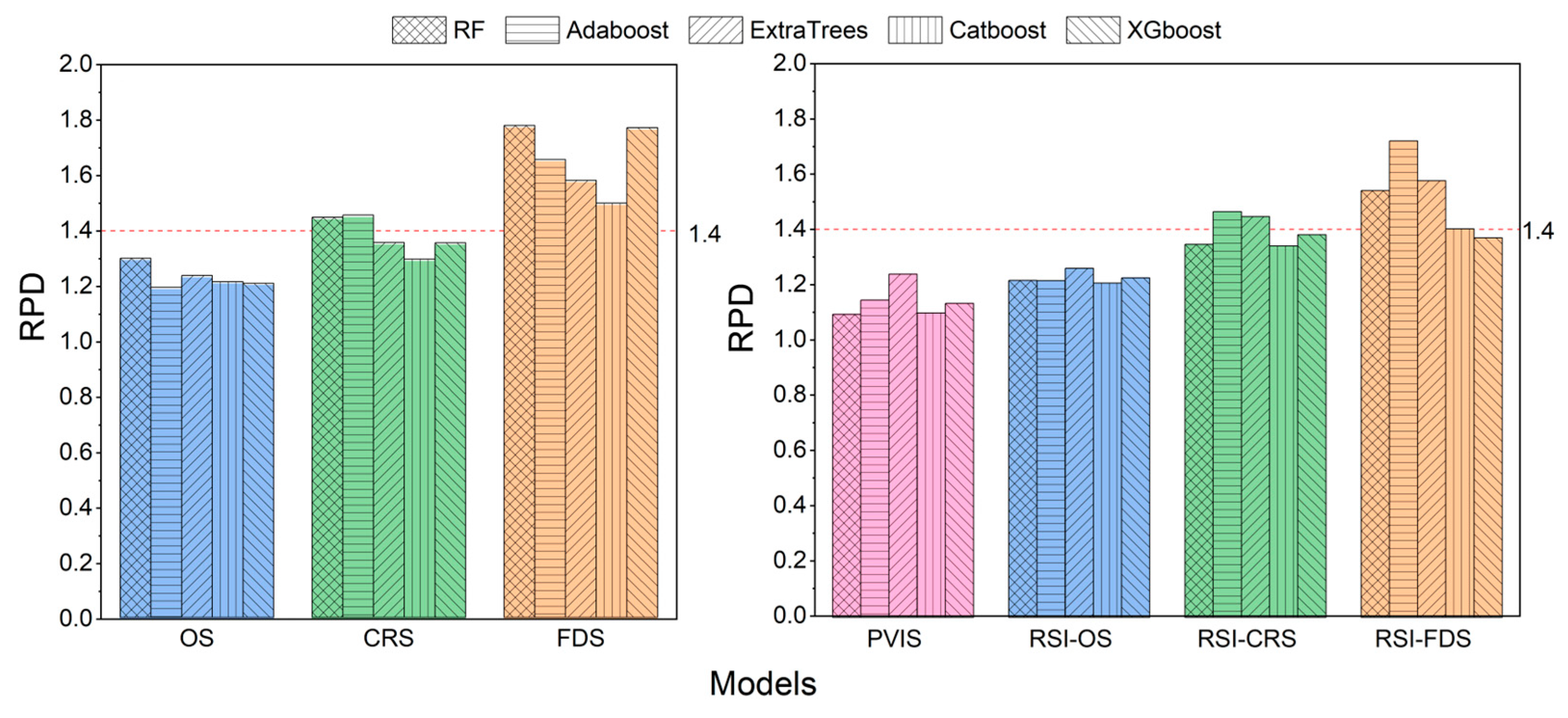
3.4.2. Model Validation
3.4.3. Model Accuracy Comparison
4. Discussion
4.1. Selection of the Research Spectral Range
4.2. Application of Mathematical Transformations
4.3. Feature Spectral Variable Screening
4.4. Superiority of Nonlinear Machine Learning Models
4.5. Comparison with Existing Literature and Study Significance
4.6. Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RFE | Recursive Feature Elimination |
| OS | original spectra |
| CRS | continuum-removed spectra |
| FDS | first-derivative spectra |
| PVIs | published vegetation indices |
| RSI | ratio spectral index |
| RSI-OS | ratio spectral indices from original spectra |
| RSI-CRS | ratio spectral indices from continuum-removed spectra |
| RSI-FDS | ratio spectral indices from first-derivative spectra |
References
- Ma, Y.P.; Wang, Z.J.; Li, Y.M.; Feng, X.R.; Song, L.H.; Gao, H.D.; Cao, B. Fruit morphological and nutritional quality features of goji berry (Lycium barbarum L.) during fruit development. Sci. Hortic. 2023, 308, 111555. [Google Scholar] [CrossRef]
- Yin, Z.R.; Huang, J.C.; Gui, L.G.; Zhao, Y.; Lei, J.Y. Characteristics of soil water movement in wolfberry fields under different drip irrigation amounts. Acta Agric. Boreali-Occident. Sin. 2020, 29, 1695–1702. [Google Scholar]
- Deng, Z.; Yin, J.; Eeswaran, R.; Gunaratnam, A.; Wu, J.; Zhang, H. Interacting effects of water and compound fertilizer on the resource use efficiencies and fruit yield of drip-fertigated Chinese wolfberry (Lycium barbar. L.). Technol. Hortic. 2024, 4, e019. [Google Scholar] [CrossRef]
- Li, L.; Li, F.; Liu, A.Y.; Wang, X.Y. The prediction model of nitrogen nutrition in cotton canopy leaves based on hyperspectral visible-near infrared band feature fusion. Biotechnol. J. 2023, 18, e2200623. [Google Scholar] [CrossRef]
- Peanusaha, S.; Pourreza, A.; Kamiya, Y.; Fidelibus, M.W.; Chakraborty, M. Nitrogen retrieval in grapevine (Vitis vinifera L.) leaves by hyperspectral sensing. Remote Sens. Environ. 2024, 302, 113966. [Google Scholar] [CrossRef]
- Han, M.X.; Zhang, L. Effects of fertilization methods and nitrogen content application on soil water and nitrogen distribution under microporous ceramic root irrigation of Lycium barbarum. Water Sav. Irrig. 2021, 1, 60–64. [Google Scholar]
- Li, M.X.; Zhu, X.C.; Li, W.; Tang, X.Y.; Yu, X.Y.; Jiang, Y.M. Retrieval of nitrogen content in apple canopy based on unmanned aerial vehicle hyperspectral images using a modified correlation coefficient method. Sustainability 2022, 14, 1992. [Google Scholar] [CrossRef]
- Shivashankar, K.; Potdar, P.M.; Gawdiya, S.; Golshetti, A.; Kanade, A.K.; Balol, G.; Biradar, D.P.; Math, K.K.; Al-Ansari, N.; El-Hendawy, S.; et al. SPAD dynamics in maize crop with precision nitrogen management under rain-fed and irrigated conditions. Sci. Rep. 2025, 15, 22842. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Jiang, J.; Fu, Z.; Wang, W.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Integrating phenology information with UAV multispectral data for rice nitrogen nutrition diagnosis. Eur. J. Agron. 2025, 169, 127696. [Google Scholar] [CrossRef]
- Ghazal, S.; Kommineni, N.; Munir, A. Comparative Analysis of Machine Learning Techniques Using RGB Imaging for Nitrogen Stress Detection in Maize. AI 2024, 5, 1286–1300. [Google Scholar] [CrossRef]
- Tang, Z.J.; Wang, X.; Xiang, Y.Z.; Liang, J.P.; Guo, J.J.; Li, W.Y.; Lu, J.S.; Du, R.Q.; Li, Z.J.; Zhang, F.C. Application of hyperspectral technology for leaf function monitoring and nitrogen nutrient diagnosis in soybean (Glycine max L.) production systems on the Loess Plateau of China. Eur. J. Agron. 2024, 154, 127098. [Google Scholar] [CrossRef]
- Wang, J.J.; Song, X.Y.; Mei, X.; Yang, G.J.; Li, Z.H.; Li, H.L.; Meng, Y. Sensitive bands selection and nitrogen content monitoring of rice based on Gaussian regression analysis. Spectrosc. Spectr. Anal. 2021, 41, 1722–1729. [Google Scholar]
- Fan, K.; Li, F.L.; Chen, X.K.; Li, Z.F.; Mulla David, J. Nitrogen balance index prediction of winter wheat by canopy hyperspectral transformation and machine learning. Remote Sens. 2022, 14, 3504. [Google Scholar] [CrossRef]
- Peng, Y.F.; Zhu, X.C.; Xiong, J.L.; Yu, R.Y.; Liu, T.L.; Jiang, Y.M.; Yang, G.J. Estimation of nitrogen content on apple tree canopy through red-edge parameters from fractional-order differential operators using hyperspectral reflectance. J. Indian Soc. Remote Sens. 2020, 49, 377–392. [Google Scholar] [CrossRef]
- Yu, F.H.; Bai, J.C.; Jin, Z.Y.; Zhang, H.G.; Yang, J.X.; Xu, T.Y. Estimating the rice nitrogen nutrition index based on hyperspectral transform technology. Front. Plant Sci. 2023, 14, 1118098. [Google Scholar] [CrossRef]
- Peng, Z.G.; Lin, S.Z.; Zhang, B.Z.; Wei, Z.; Liu, L.; Han, N.N.; Cai, J.B.; Chen, H. Winter Wheat Canopy Water Content Monitoring Based on Spectral Transforms and “Three-edge” Parameters. Agric. Water Manag. 2020, 240, 106306. [Google Scholar] [CrossRef]
- Zhou, X.T.; Yang, M.; Chen, X.Y.; Ma, L.L.; Yin, C.X.; Qin, S.Z.; Wang, L.; Lv, X.; Zhang, Z. Estimation of cotton nitrogen content based on multi-angle hyperspectral data and machine learning models. Remote Sens. 2023, 15, 955. [Google Scholar] [CrossRef]
- Song, X.; Xu, D.Y.; Huang, S.M.; Huang, C.C.; Zhang, S.Q.; Guo, D.D.; Zhang, K.K.; Yue, K. Nitrogen content inversion of wheat canopy leaf based on ground spectral reflectance data. J. Appl. Ecol. 2020, 31, 1636–1644. [Google Scholar]
- Li, H.; Li, D.; Xu, K.; Cao, W.; Jiang, X.; Ni, J. Monitoring of Nitrogen Indices in Wheat Leaves Based on the Integration of Spectral and Canopy Structure Information. Agronomy 2022, 12, 833. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2025, 108, 273–290. [Google Scholar] [CrossRef]
- Sahoo, R.N.; Rejith, R.G.; Gakhar, S.; Ranjan, R.; Meena, M.C.; Dey, A.; Mukherjee, J.; Dhakar, R.; Meena, A.; Daas, A.; et al. Drone remote sensing of wheat N using hyperspectral sensor and machine learning. Precis. Agric. 2023, 25, 704–728. [Google Scholar] [CrossRef]
- Yang, F.Q.; Dai, H.Y.; Feng, H.K.; Yang, G.J.; Li, Z.H.; Chen, Z.X. Hyperspectral estimation of plant nitrogen content based on Akaike’s information criterion. Trans. Chin. Soc. Agric. Eng. 2016, 32, 161–167. [Google Scholar]
- Feng, J.; Lu, Z.Y.; Ma, X.Y.; Chen, S.L.; Zhao, Q.H.; Wang, S.W. Crop canopy nitrogen inversion based on hyperspectral corn field geese model. J. Agric. Mech. Res. 2020, 42, 4–11. [Google Scholar]
- Wen, P.F.; Shi, Z.J.; Li, A.; Ning, F.; Zhang, Y.H.; Wang, R.; Li, J. Estimation of the vertically integrated leaf nitrogen content in maize using canopy hyperspectral red edge parameters. Precis. Agric. 2020, 22, 984–1005. [Google Scholar] [CrossRef]
- Shu, M.Y.; Zhu, J.Y.; Yang, X.H.; Gu, X.H.; Li, B.G.; Ma, Y.T. A spectral decomposition method for estimating the leaf nitrogen status of maize by UAV-based hyperspectral imaging. Comput. Electron. Agric. 2023, 212, 108100. [Google Scholar] [CrossRef]
- Alfadhl, A.; Townsend, P.A.; Wang, Y. Remote sensing for monitoring potato nitrogen status. Am. J. Potato Res. 2023, 100, 1–14. [Google Scholar] [CrossRef]
- Li, D.; Wang, C.Y.; Liu, W.; Peng, Z.P.; Huang, S.Y.; Huang, J.C.; Chen, S.S. Estimation of litchi (Litchi chinensis Sonn.) leaf nitrogen content at different growth stages using canopy reflectance spectra. Eur. J. Agron. 2016, 80, 182–194. [Google Scholar] [CrossRef]
- Adria, N.; Jun, S.; Zhong, Y. A Rapid Non-destructive Detection Method for Wolfberry Moisture Grade Using Hyperspectral Imaging Technology. J. Nondestruct. Eval. 2023, 42, 45. [Google Scholar]
- Zhao, J.; Liang, X.; Kang, X.; Li, Y.; An, W. Estimation of goji berry (Lycium barbarum L.) canopy water content based on optimal spectral indices. Sci. Hortic. 2024, 337, 113589. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Zhao, H.; Zhang, L. Predicting leaf nitrogen content in wolfberry trees by hyperspectral transformation and machine learning for precision agriculture. PLoS ONE 2024, 19, e0306851. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, G.; Qin, K.; Huang, T.; He, X.R.; Zhao, Q.F. Phenological characteristics of 42 wolfberry germplasm resources. Non-Wood For. Res. 2021, 39, 85–96. [Google Scholar]
- Abhiram, G.; Grafton, M.; Jeyakumar, P.; Bishop, P.; Davies, C.E.; McCurdy, M. The Nitrogen Dynamics of Newly Developed Lignite-Based Controlled-Release Fertilisers in the Soil-Plant Cycle. Plants 2022, 11, 3288. [Google Scholar] [CrossRef]
- Luo, S.J.; He, Y.B.; Duan, D.D.; Wang, Z.Z.; Zhang, J.K.; Zhang, Y.T.; Zhu, Y.Q.; Yu, J.K. Analysis of hyperspectral variation of different potato cultivars based on contiuum removed spectra. Spectrosc. Spectr. Anal. 2018, 38, 3231–3237. [Google Scholar]
- Luo, S.J.; He, Y.B.; Li, Q.; Jiao, W.H.; Zhu, Y.Q.; Yu, J.K.; Zhao, C.; Xu, R.Y.; Zhang, S.; Xu, F.; et al. Assessment of unified models for estimating potato leaf area index under water stress conditions across ground-based hyperspectral data. J. Appl. Remote Sens. 2020, 14, 014517. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the shortgrass prairie. Remote Sens. Environ. 1972, 1, 1355. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- López-Granados, F.; Peña-Barragán, J.M.; García-Torres, L.; Gómez-Casero, M.T.; Jurado-Expósito, M.; Fernández-Escobar, R. Assessing nitrogen and potassium deficiencies in olive orchards through discriminant analysis of hyperspectral data. J. Am. Soc. Hortic. Sci. 2007, 132, 611–618. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Moss, D.M. Spectral reflectance measurements in the genus sphagnum. Remote Sens. Environ. 1993, 45, 273–279. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Tian, Y.; Liu, X.; Cao, W. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and doublepeak red-edge effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Sims, D.A.; Luo, H.Y.; Hastings, S.; Oechel, W.C.; Rahman, A.F.; Gamon, J.A. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a Southern California chaparral ecosystem. Remote Sens. Environ. 2006, 103, 289–303. [Google Scholar] [CrossRef]
- Datt, B. Visible/near infrared reflectance and chlorophyll content in Eucalyptus leaves. Int. J. Remote Sens. 1999, 20, 2741–2759. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Metternicht, G. Vegetation indices derived from high-resolution airborne videography for precision crop management. Int. J. Remote Sens. 2003, 24, 2855–2877. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies. Remote Sens. Environ. 2010, 115, 281–297. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature analysis of leaf reflectance spectra: Algorithm development for remote sensing of chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen-and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Schleicher, T.D.; Bausch, W.C.; Delgado, J.A. Evaluation and refinement of the nitrogen reflectance index (NRI) for site-specific fertilizer management. In Proceedings of the ASAE Annual International Meeting, Sacramento, CA, USA, 30 July–1 August 2001; p. 011151. [Google Scholar]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess cartotenoids/chlorophyll-a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Hurcom, S.J.; Harrison, A.R. The NDVI and spectral decomposition for semi-arid vegetation abundance estimation. Int. J. Rem. Sens. 1998, 19, 3109–3125. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D.; Harlan, J. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; NASA/GSFC: Greenbelt, MD, USA, 1974; pp. 1–371. [Google Scholar]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Fitzgerald, G.J.; Rodriguez, D.; Christensen, L.K.; Belford, R.; Sadras, V.O.; Clarke, T.R. Spectral and thermal sensing for nitrogen and water status in rainfed and irrigated wheat environments. Precis. Agric. 2006, 7, 233–248. [Google Scholar] [CrossRef]
- Chen, S.M.; Hu, T.T.; Luo, L.H.; He, Q.; Zhang, S.W.; Li, M.Y.; Cui, X.L.; Li, H.X. Rapid estimation of leaf nitrogen content in apple-trees based on canopy hyperspectral reflectance using multivariate methods. Infrared Phys. Technol. 2020, 111, 103542. [Google Scholar] [CrossRef]
- Thorp, R.K. vegspec: A compilation of spectral vegetation indices and transformations in Python. SoftwareX 2024, 28, 101928. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.X.; Feng, G.H.; Yuan, F.; Yue, S.C.; Gao, X.W.; Liu, Y.Q.; Liu, B.; Ustin, S.L.; Chen, X.P. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Song, L.; Wang, L.Y.; Yang, Z.Q.; He, L.; Feng, Z.H.; Duan, J.Z.; Feng, W.; Guo, T.C. Comparison of algorithms for monitoring wheat powdery mildew using multi-angular remote sensing data. Crop J. 2022, 10, 1312–1322. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Yang, G.J.; Pu, R.L.; Li, Z.H.; Li, H.L.; Xu, X.G.; Song, X.Y.; Yang, X.D.; Zhao, C.J. An overview of crop nitrogen status assessment using hyperspectral remote sensing: Current status and perspectives. Eur. J. Agron. 2021, 124, 126241. [Google Scholar] [CrossRef]
- He, L.; Song, X.; Feng, W.; Guo, B.B.; Zhang, Y.S.; Wang, Y.H.; Wang, C.Y.; Guo, T.C. Improved remote sensing of leaf nitrogen concentration in winter wheat using multi-angular hyperspectral data. Remote Sens. Environ. 2016, 174, 122–133. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, W.J.; He, Y.; Wanger, T.C.; Cen, H.Y. Combining transfer learning and hyperspectral reflectance analysis to assess leaf nitrogen concentration across different plant species datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- Elvanidi, A.; Katsoulas, N.; Bartzanas, T.; Ferentinos, K.P.; Kittas, C. Crop water status assessment in controlled environment using crop reflectance and temperature measurements. Precis. Agric. 2017, 18, 332–349. [Google Scholar] [CrossRef]
- Berger, K.; Verrelst, J.; Féret, J.-B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef] [PubMed]
- Féret, J.-B.; Berger, K.; de Boissieu, F.; Malenovský, Z. PROSPECT-PRO for estimating content of nitrogen-containing leaf proteins and other carbon-based constituents. Remote Sens. Environ. 2021, 252, 112173. [Google Scholar] [CrossRef]
- Wang, C.; Qiao, X.X.; Li, G.X.; Feng, M.C.; Xie, Y.K.; Sun, H.; Zhang, M.J.; Song, X.Y.; Xiao, L.J.; Anwar, S.; et al. Hyperspectral estimation of soil organic matter and clay content in loess plateau of China. Agron. J. 2021, 113, 2506–2523. [Google Scholar] [CrossRef]
- Wei, H.; Grafton, M.; Bretherton, M.; Irwin, M.; Sandoval, E. Evaluation of Point Hyperspectral Reflectance and Multivariate Regression Models for Grapevine Water Status Estimation. Remote Sens. 2021, 13, 3198. [Google Scholar] [CrossRef]
- Ansardin, A.; Mamat, S.; Li, J.Z. Estimation of Chlorophyll Content of Long-Staple Cotton Based on Canopy Spectrum Characteristics. Laser Optoelectron. Prog. 2022, 59, 0530001. [Google Scholar]




| Date | Phenological Characteristics |
|---|---|
| Early April | The wolfberry tree begins to sprout and develop new leaves. |
| Late April to early May | New branches exhibit vigorous growth, with the emergence of buds and a few flowers. |
| Late May to early August | The period marks the flowering and fruiting phase for summer fruits. |
| Mid-August to September | As old leaves begin to fade, new buds open, and fresh branches extend, the plant enters the autumn flowering and fruiting stage. |
| October to November | Plants shed leaves and transition into dormancy. |
| Vegetation Indices | Calculation Formula | Reference |
|---|---|---|
| RVI | R800/R670 | [35] |
| GM | R750/R700 | [36] |
| SR705 | R750/R705 | [37] |
| SR550,670 | R550/R670 | [38] |
| Ratio vegetation index (VOG1) | R740/R720 | [39] |
| Ratio vegetation index (GM1) | R750/R550 | [40] |
| Ratio vegetation index (RVI1) | R950/R660 | [41] |
| RVI (R780,R550) | R780/R550 | [38] |
| RVI (R780,R670) | R780/R670 | [38] |
| GI (Greenness index) | R554/R677 | [42] |
| RVI (D705,D722) | D705/D722 | [43] |
| RVI (D730,D706) | D730/D706 | [43] |
| Canopy chlorophyll index (CCI) | D720/D700 | [44] |
| Datt derivative (DD) | D755/R705 | [45] |
| ND705 | (R750 − R705)/(R750 + R705) | [37] |
| NDVIgb | (R573 − R440)/(R573 + R440) | [46] |
| PPR | (R550 − R450)/(R550 + R450) | [47] |
| PRI | (R570 − R531)/(R570 + R531) | [48] |
| GNDVI | (R750 − R550)/(R750 + R550) | [49] |
| NPCI | (R430 − R680)/(R430 + R680) | [50] |
| NRI | (R570 − R670)/(R570 + R670) | [51] |
| SIPI | (R810 − R460)/(R810 + R460) | [52] |
| NDVI | (R800 − R670)/(R800 + R670) | [53] |
| Normalized difference vegetation index(NDVI1) | (R790 − R670)/(R790 + R670) | [54] |
| Normalized difference vegetation index (NDVI2) | (R1220 − R710)/(R1220 + R710) | [41] |
| Revised normalized difference vegetation index (ReNDVI) | (R755 − R705)/(R755 + R705) | [55] |
| Normalized difference red edge index (NDRE) | (R790 − R720)/(R790 + R720) | [56] |
| NDI | (R780 − R670)/(R780 + R670) | [38] |
| Sample Size | n | Maximum | Minimum | Mean | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Total set | 95 | 4.660 | 2.900 | 4.084 | 0.374 | 9.158% |
| Training set | 63 | 4.660 | 2.900 | 4.077 | 0.381 | 9.345% |
| Test set | 32 | 4.630 | 3.110 | 4.098 | 0.365 | 8.907% |
| Vegetation Index | Correlation Coefficient | Vegetation Index | Correlation Coefficient |
|---|---|---|---|
| RVI | 0.321 *** | ND705 | 0.319 *** |
| GM | 0.322 *** | NDVIgb | 0.366 *** |
| SR705 | 0.319 *** | PPR | 0.356 *** |
| SR(550 670) | 0.335 *** | PRI | −0.367 *** |
| VOG1 | 0.284 *** | GNDVI | 0.297 *** |
| GM1 | 0.297 *** | NPCI | 0.205 ** |
| RVI1 | 0.323 *** | NRI | 0.336 *** |
| RVI (R780 R550) | 0.300 *** | SIPI | 0.314 *** |
| RVI (R780 R670) | 0.323 *** | NDVI | 0.321 *** |
| GI (Greenness index) | 0.333 *** | NDVI1 | 0.321 *** |
| RVI (D705 D722) | −0.041 | NDVI2 | 0.282 *** |
| RVI (D730 D706) | 0.158 | ReNDVI | 0.319 *** |
| CCI | 0.223 ** | NDRE | 0.270 *** |
| DD | 0.202** | NDI | 0.323 *** |
| Model | Model Parameters |
|---|---|
| RF | n_estimators = 100, max_depth = 10, min_samples_split = 2, min_samples_leaf = 1 |
| AdaBoost | n_estimators = 100, learning_rate = 1, Loss function = square, base_estimator = Decision Tree Classifier |
| ExtraTrees | n_estimators = 100, max_depth = 10, min_samples_split = 2, min_samples_leaf = 1 |
| CatBoost | Iterations = 100, learning_rate = 0.06, depth = 10, l2_leaf_reg = 5 |
| XGBoost | max_depth = 10, learning_rate = 0.06, n_estimators = 100, l2_leaf_reg = 5 |
| GDLR | learning_rate = 0.05, max_iter = 100, batch_size = BGD, penalty = ‘l2’, alpha = 0.05, fit_intercept = True, tol = 1 × 10−4, |
| OLSLR | fit_intercept = True, normalize = False, copy_X = True, positive = False, |
| RR | alpha = 0.5, fit_intercept = True, max_iter = 300, solver = ‘cholesky’, tol = 1 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, H.; Zhao, H.; Zhang, L.; Xia, W. Monitoring Wolfberry (Lycium barbarum L.) Canopy Nitrogen Content with Hyperspectral Reflectance: Integrating Spectral Transformations and Multivariate Regression. Agronomy 2025, 15, 2072. https://doi.org/10.3390/agronomy15092072
Li Y, Wang H, Zhao H, Zhang L, Xia W. Monitoring Wolfberry (Lycium barbarum L.) Canopy Nitrogen Content with Hyperspectral Reflectance: Integrating Spectral Transformations and Multivariate Regression. Agronomy. 2025; 15(9):2072. https://doi.org/10.3390/agronomy15092072
Chicago/Turabian StyleLi, Yongmei, Hao Wang, Hongli Zhao, Ligen Zhang, and Wenjing Xia. 2025. "Monitoring Wolfberry (Lycium barbarum L.) Canopy Nitrogen Content with Hyperspectral Reflectance: Integrating Spectral Transformations and Multivariate Regression" Agronomy 15, no. 9: 2072. https://doi.org/10.3390/agronomy15092072
APA StyleLi, Y., Wang, H., Zhao, H., Zhang, L., & Xia, W. (2025). Monitoring Wolfberry (Lycium barbarum L.) Canopy Nitrogen Content with Hyperspectral Reflectance: Integrating Spectral Transformations and Multivariate Regression. Agronomy, 15(9), 2072. https://doi.org/10.3390/agronomy15092072






