Development of a Predictive Model Linking Electrical Characteristics to Semi-Lethal Temperature in Potted Apple Trees with Validation on Mature Specimens
Abstract
1. Introduction
2. Materials and Methods
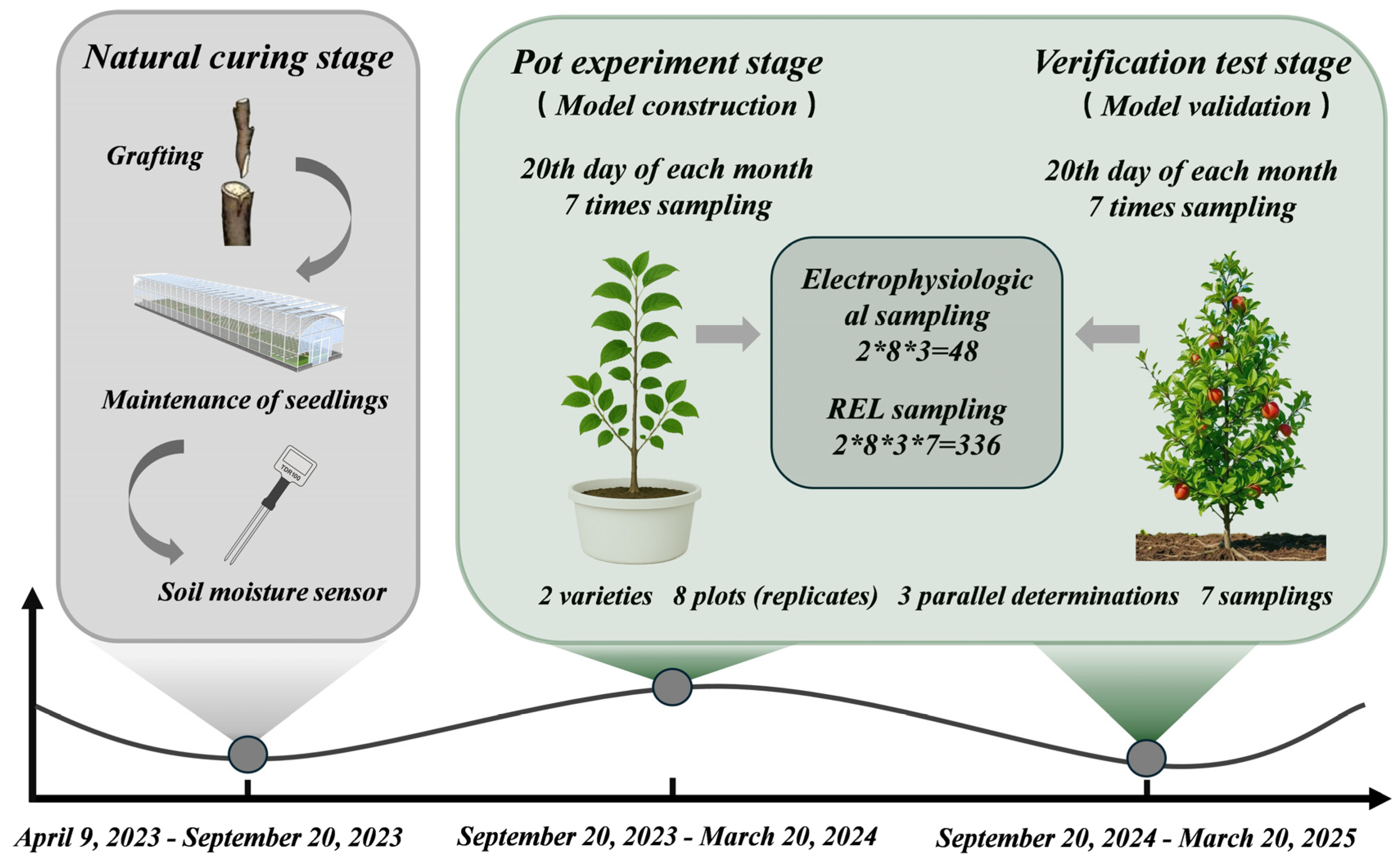
2.1. Experimental Design
2.1.1. Pot Experiment
2.1.2. Validation Experiment
2.2. Measurement Parameters
2.2.1. Low-Temperature Freezing Treatment
2.2.2. Measurement of Relative Electrolyte Leakage and Calculation of Semi-Lethal Temperature (LT50)
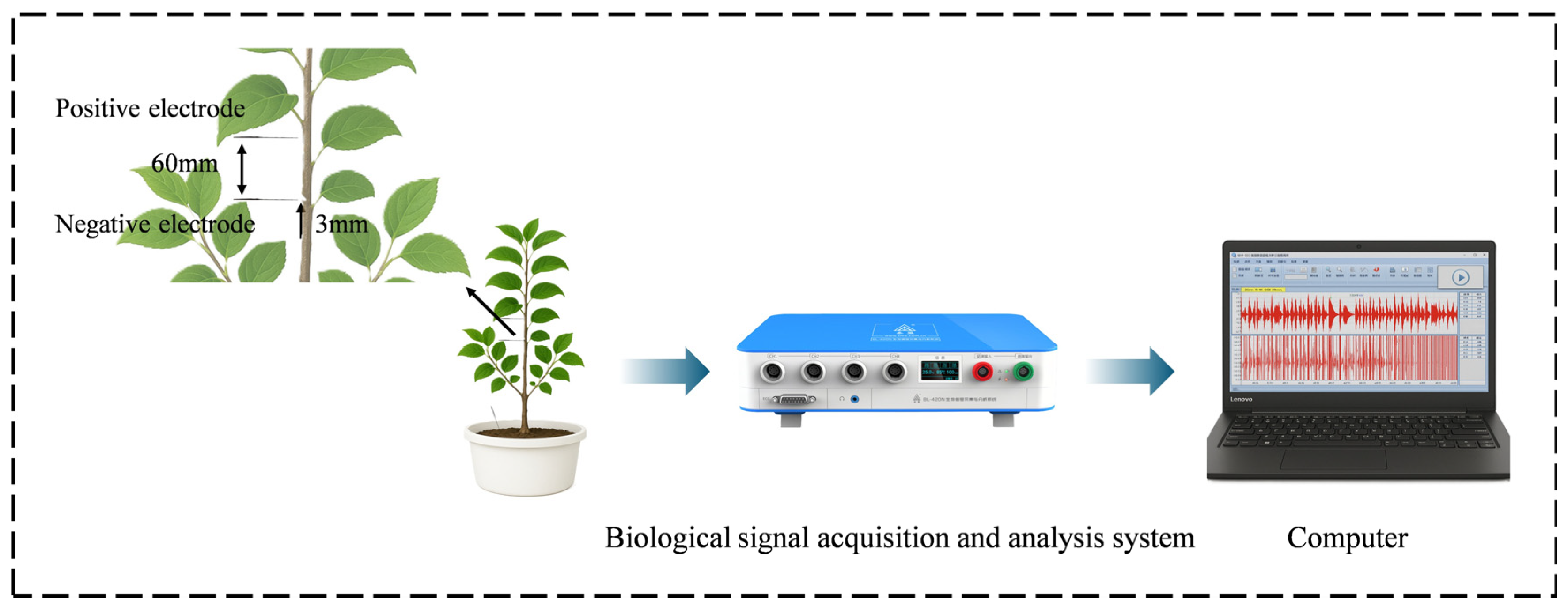
2.2.3. Acquisition of Electrical Properties
2.3. Statistic Analysis
2.3.1. Processing of Electrical Property Data
2.3.2. Construction and Evaluation of the Regression Model
3. Results
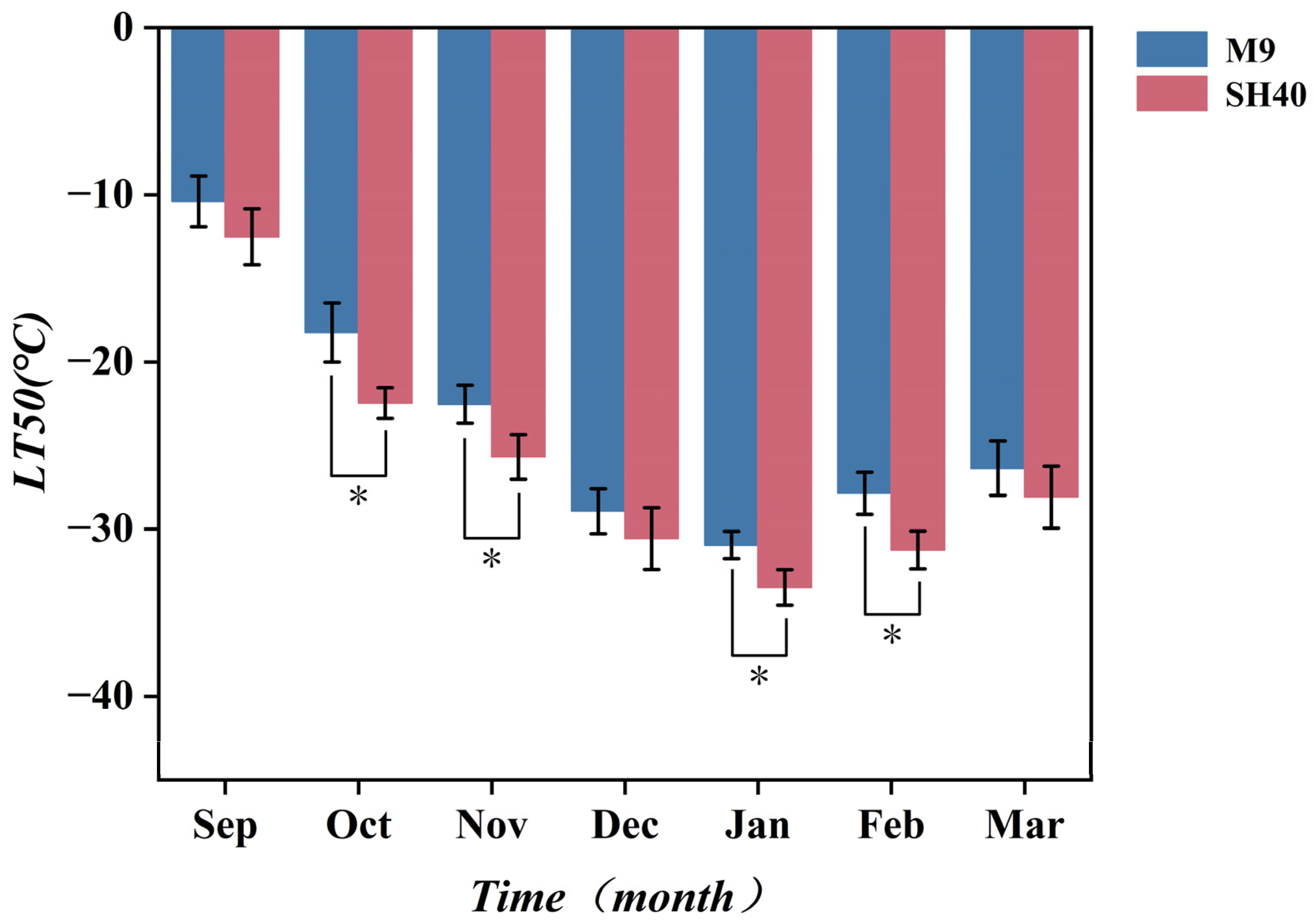
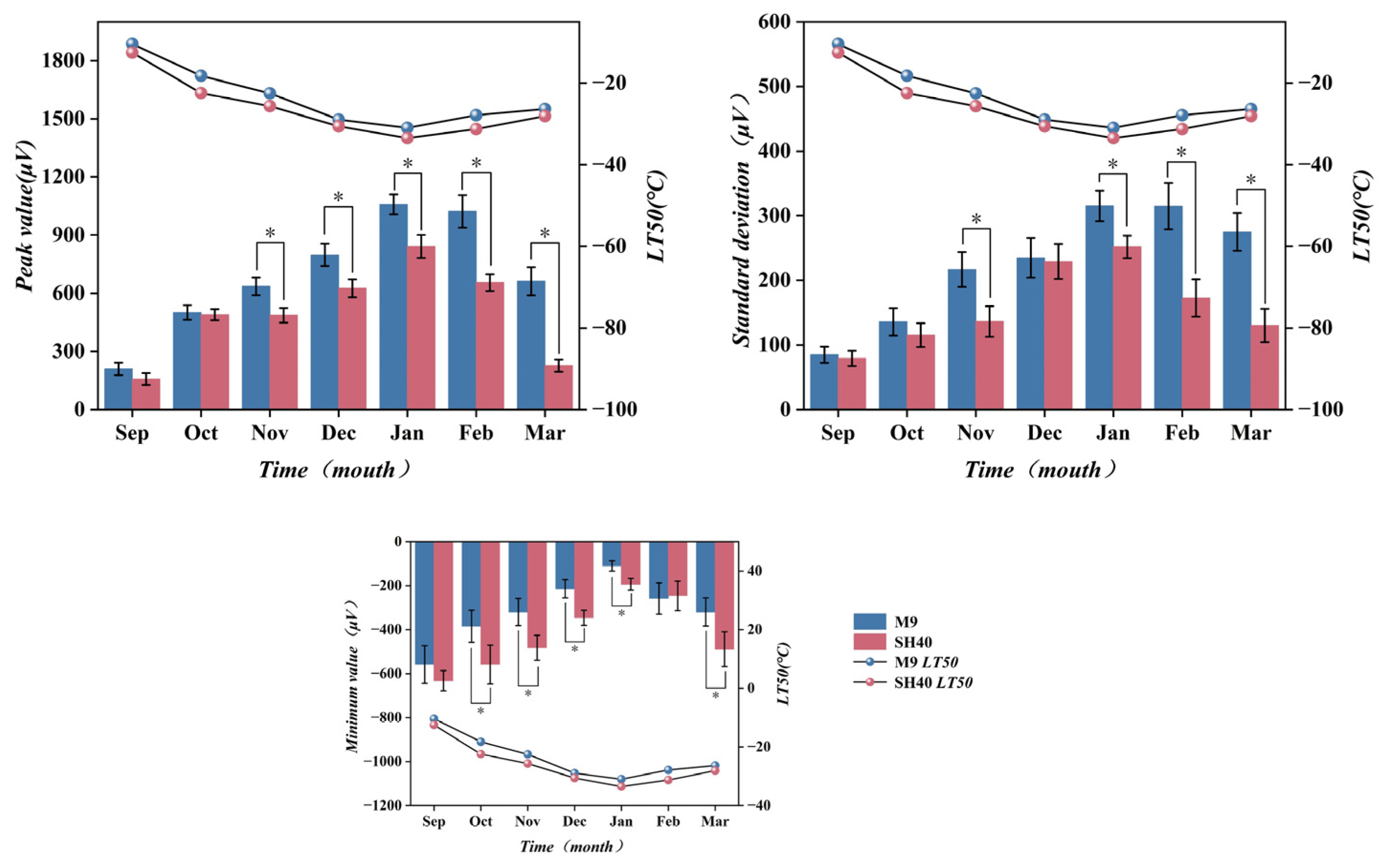
3.1. Variation in Semi-Lethal Temperature (LT50) of Potted Apple Rootstock
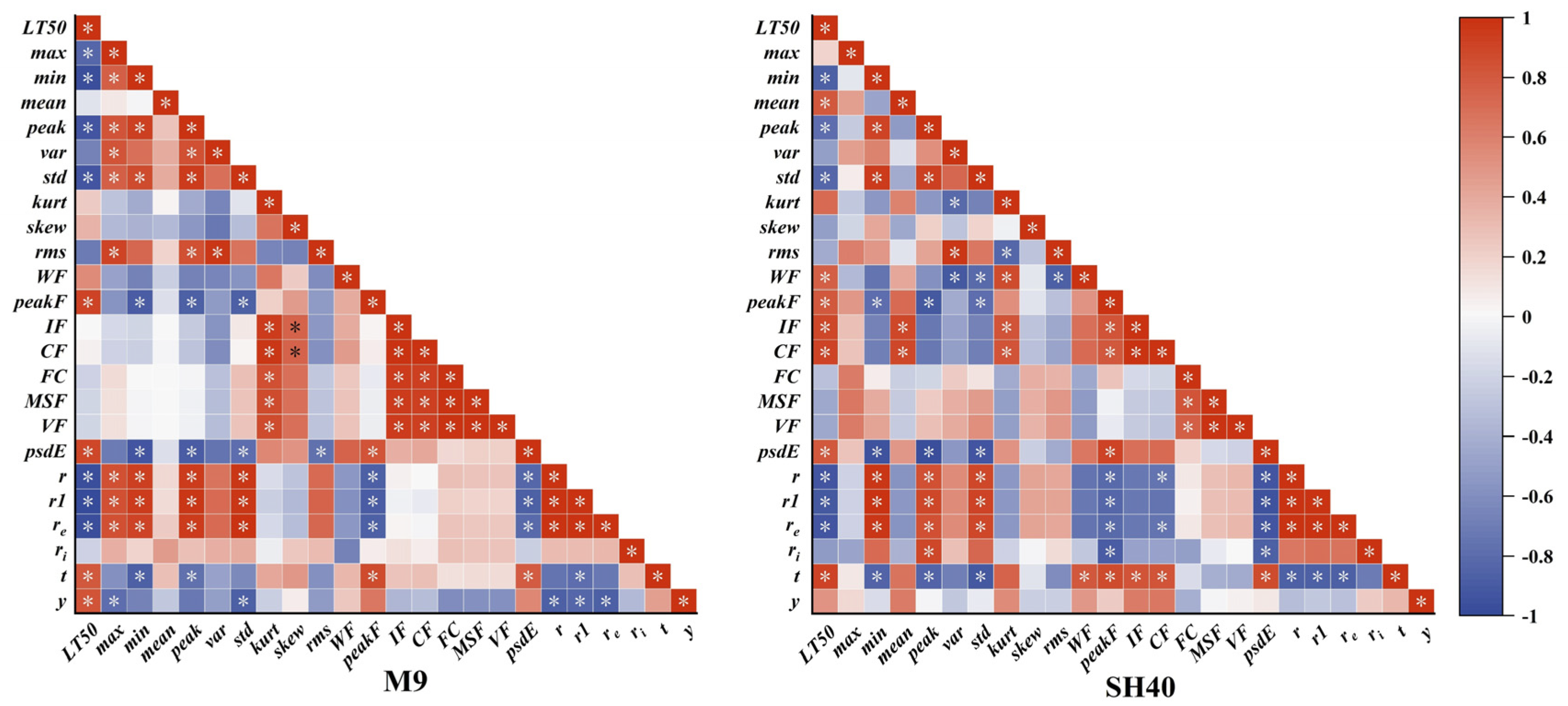
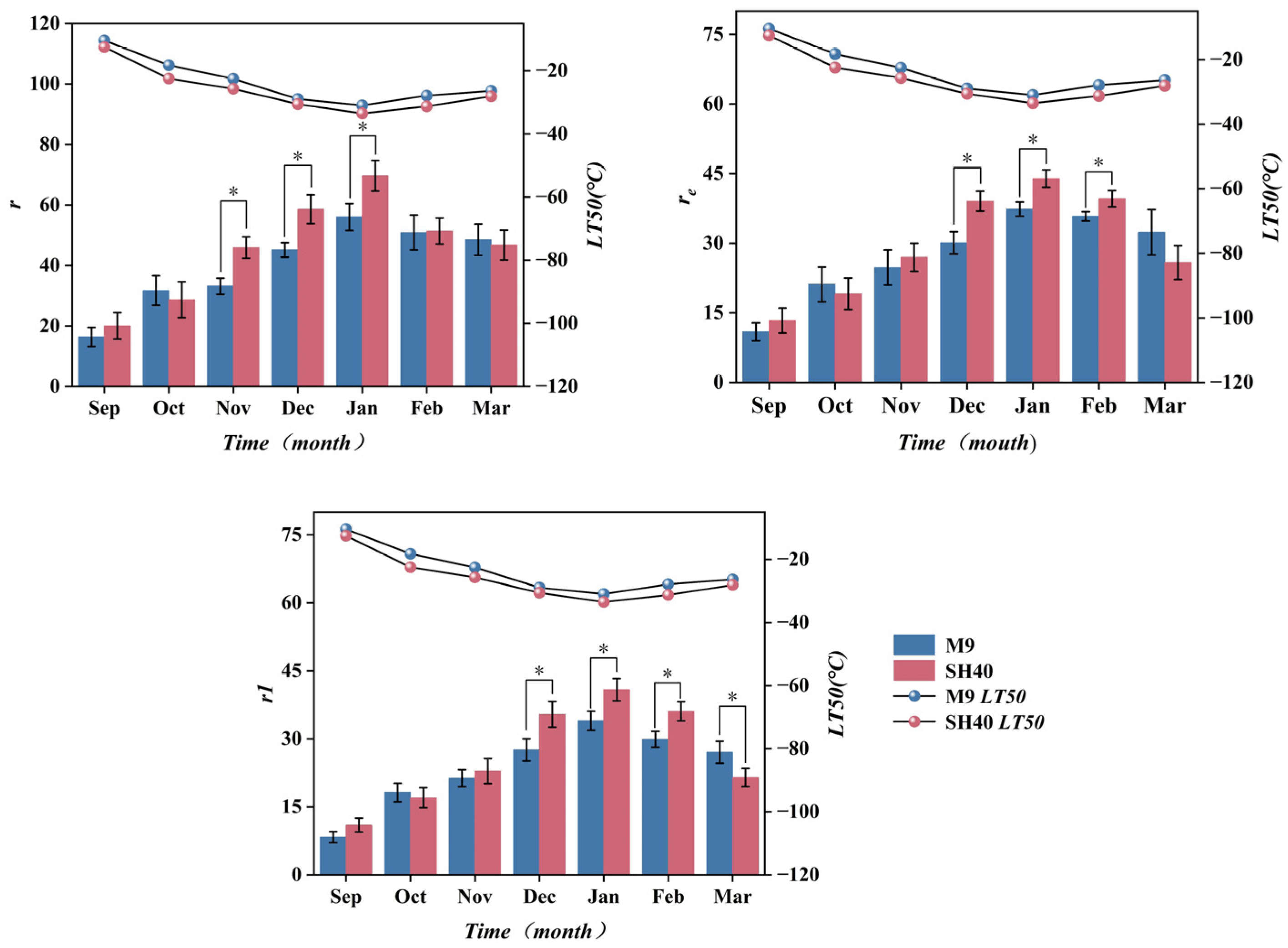
3.2. Correlation Analysis Between LT50 and Electrophysiological Features
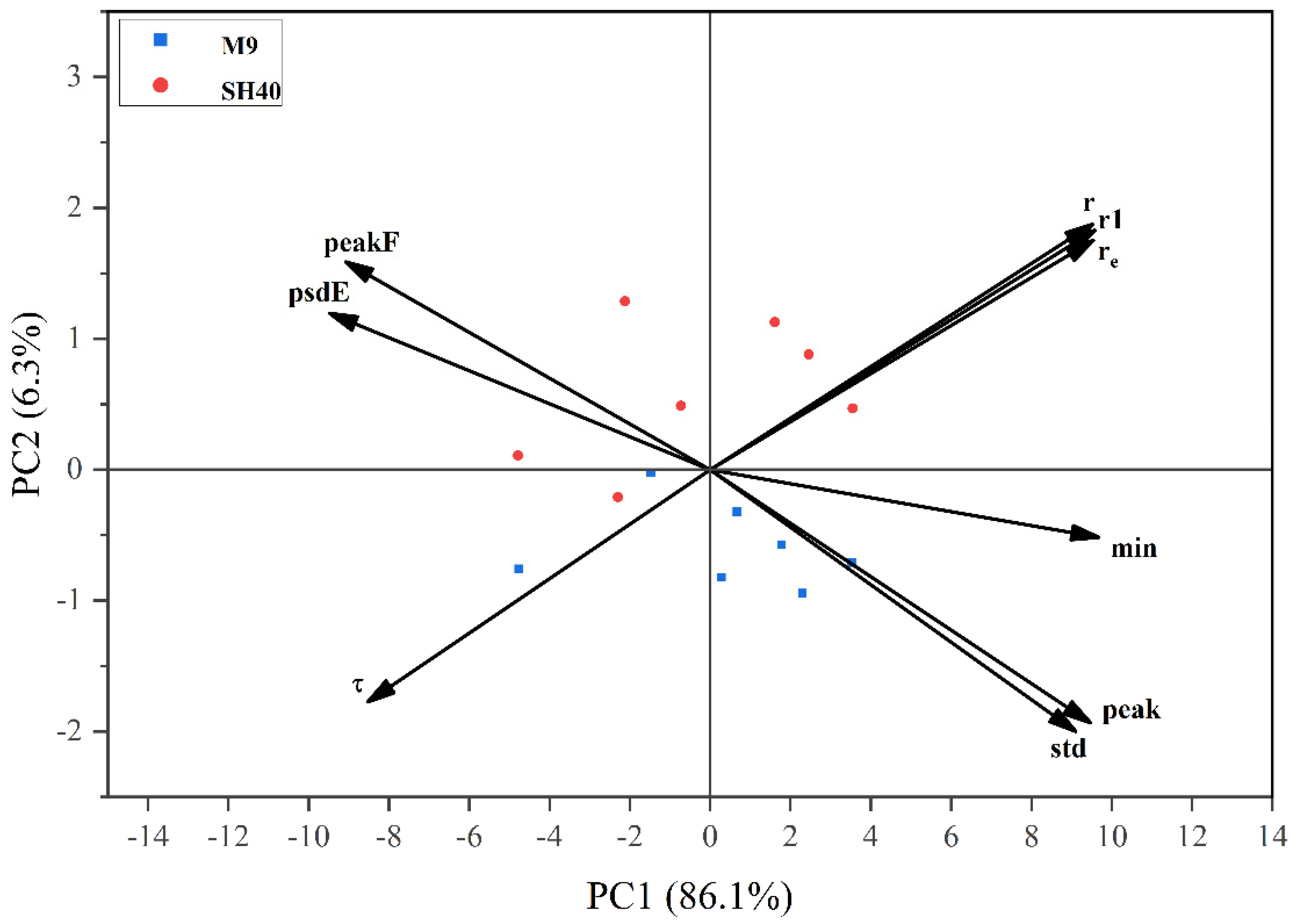
3.3. Principal Component Analysis (PCA) of Electrophysiological Features
3.4. Changes in Electrical Characteristics During Overwintering
3.5. LT50 and Optimal Indicators of Cold Tolerance Regression Modeling
3.5.1. Model Construction
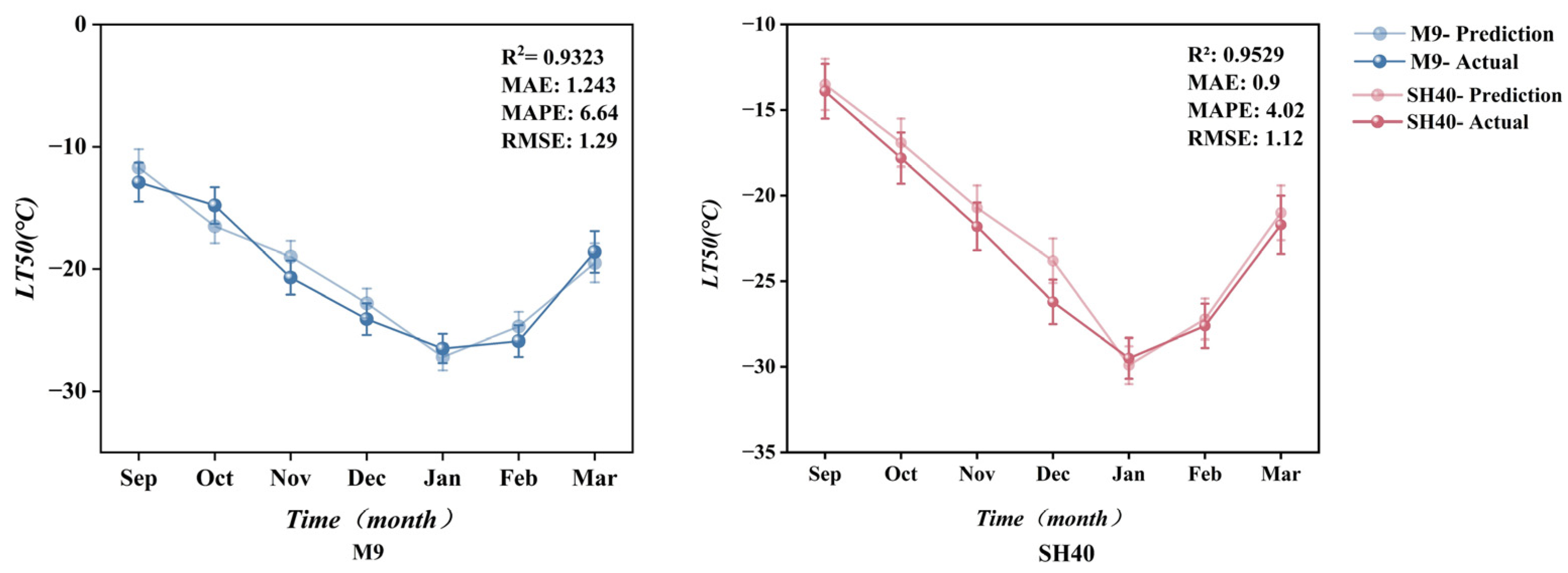
3.5.2. Model Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boinot, M.; Karakas, E.; Koehl, K.; Pagter, M.; Zuther, E. Cold stress and freezing tolerance negatively affect the fitness of Arabidopsis thaliana accessions under field and controlled conditions. Planta 2022, 255, 39. [Google Scholar] [CrossRef] [PubMed]
- Raza, A.; Charagh, S.; Najafi-Kakavand, S.; Abbas, S.; Shoaib, Y.; Anwar, S.; Sharifi, S.; Lu, G.; Siddique, K.H.M. Role of phytohormones in regulating cold stress tolerance: Physiological and molecular approaches for developing cold-smart crop plants. Plant Stress 2023, 8, 100152. [Google Scholar] [CrossRef]
- Powell, N.; Ji, X.; Ravash, R.; Edlington, J.; Dolferus, R. Yield stability for cereals in a changing climate. Funct. Plant Biol. 2012, 39, 539. [Google Scholar] [CrossRef] [PubMed]
- Ågren, J.; Schemske, D.W. Reciprocal transplants demonstrate strong adaptive differentiation of the model organism Arabidopsis thaliana in its native range. New Phytol. 2012, 194, 1112–1122. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.K. Cold stress tolerance mechanisms in plants. A review. Agron. Sustain. Dev. 2010, 30, 515–527. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ye, X.; Shen, Y.; Liu, H.; Zhao, X.; Guo, L.; Cao, L.; Du, Y.; Wu, W. A phylotranscriptomic dataset of angiosperm species under cold stress. Sci. Data 2023, 10, 399. [Google Scholar] [CrossRef]
- Ding, Y.; Shi, Y.; Yang, S. Advances and challenges in uncovering cold tolerance regulatory mechanisms in plants. New Phytol. 2019, 222, 1690–1704. [Google Scholar] [CrossRef]
- Chinnusamy, V.; Zhu, J.; Zhu, J.-K. Cold stress regulation of gene expression in plants. Trends Plant Sci. 2007, 12, 444–451. [Google Scholar] [CrossRef]
- Zhou, L.; Ullah, F.; Zou, J.; Zeng, X. Molecular and Physiological Responses of Plants that Enhance Cold Tolerance. Int. J. Mol. Sci. 2025, 26, 1157. [Google Scholar] [CrossRef]
- Qi, J.; Song, C.; Wang, B.; Zhou, J.; Kangasjärvi, J.; Zhu, J.; Gong, Z. Reactive oxygen species signaling and stomatal movement in plant responses to drought stress and pathogen attack. J. Integr. Plant Biol. 2018, 60, 805–826. [Google Scholar] [CrossRef]
- Anwar, M.P.; Khalid, M.A.I.; Islam, A.M.; Yeasmin, S.; Sharif, A.; Hadifa, A.; Ismail, I.A.; Hossain, A.; El Sabagh, A. Akbar Hossain Potentiality of Different Seed Priming Agents to Mitigate Cold Stress of Winter Rice Seedling. Phyton-Int. J. Exp. Bot. 2021, 90, 1491–1506. [Google Scholar] [CrossRef]
- Satyakam; Zinta, G.; Singh, R.K.; Kumar, R. Cold adaptation strategies in plants—An emerging role of epigenetics and antifreeze proteins to engineer cold resilient plants. Front. Genet. 2022, 13, 909007. [Google Scholar] [CrossRef] [PubMed]
- Qi, W.; Wang, F.; Ma, L.; Qi, Z.; Liu, S.; Chen, C.; Wu, J.; Wang, P.; Yang, C.; Wu, Y.; et al. Physiological and Biochemical Mechanisms and Cytology of Cold Tolerance in Brassica napus. Front. Plant Sci. 2020, 11, 1241. [Google Scholar] [CrossRef]
- Vuković Vimić, A.; Vujadinović Mandić, M.; Fotirić Akšić, M.; Vukićević, K.; Meland, M. Climate Potential for Apple Growing in Norway—Part 1: Zoning of Areas with Heat Conditions Favorable for Apple Growing under Observed Climate Change. Atmosphere 2023, 14, 993. [Google Scholar] [CrossRef]
- Pfleiderer, P.; Menke, I.; Schleussner, C.F. Increasing risks of apple tree frost damage under climate change. Clim. Change 2019, 157, 515–525. [Google Scholar] [CrossRef]
- Mei, C.; Yang, J.; Mei, Q.; Jia, D.; Yan, P.; Feng, B.; Mamat, A.; Gong, X.; Guan, Q.; Mao, K.; et al. MdNAC104 positively regulates apple cold tolerance via CBF-dependent and CBF-independent pathways. Plant Biotechnol. J. 2023, 21, 2057–2073. [Google Scholar] [CrossRef]
- Feng, X.-M.; Zhao, Q.; Zhao, L.-L.; Qiao, Y.; Xie, X.-B.; Li, H.-F.; Yao, Y.-X.; You, C.-X.; Hao, Y.-J. The cold-induced basic helix-loop-helix transcription factor gene MdCIbHLH1encodes an ICE-like protein in apple. BMC Plant Biol. 2012, 12, 22. [Google Scholar] [CrossRef]
- Yu, D.J.; Lee, H.J. Evaluation of freezing injury in temperate fruit trees. Hortic. Environ. Biotechnol. 2020, 61, 787–794. [Google Scholar] [CrossRef]
- Niu, Y.; Liu, Z.; He, H.; Han, X.; Qi, Z.; Yang, Y. Gene expression and metabolic changes of Momordica charantia L. seedlings in response to low temperature stress. PLoS ONE 2020, 15, e0233130. [Google Scholar] [CrossRef]
- Yu, J.; Cang, J.; Lu, Q.; Fan, B.; Xu, Q.; Li, W.; Wang, X. ABA enhanced cold tolerance of wheat ‘dn1’ via increasing ROS scavenging system. Plant Signal. Behav. 2020, 15, 1780403. [Google Scholar] [CrossRef]
- Strimbeck, G.R.; Schaberg, P.G.; Fossdal, C.G.; Schröder, W.P.; Kjellsen, T.D. Extreme low temperature tolerance in woody plants. Front. Plant Sci. 2015, 6, 884. [Google Scholar] [CrossRef] [PubMed]
- Kovaleski, A.P.; Grossman, J.J. Standardization of electrolyte leakage data and a novel liquid nitrogen control improve measurements of cold hardiness in woody tissue. Plant Methods 2021, 17, 53. [Google Scholar] [CrossRef]
- Lindén, L.; Palonen, P.; Lindén, M. Relating Freeze-induced Electrolyte Leakage Measurements to Lethal Temperature in Red Raspberry. J. Am. Soc. Hortic. Sci. 2000, 125, 429–435. [Google Scholar] [CrossRef]
- Wilson, B.C.; Jacobs, D.F. Effect of Storage Temperature and Duration on Cold Hardiness and Dormancy of Northern Red Oak Seedlings: Use of the Electrolyte Leakage Procedure; U.S. Department of Agriculture: Washington, DC, USA, 2005. [Google Scholar]
- Ilík, P.; Špundová, M.; Šicner, M.; Melkovičová, H.; Kučerová, Z.; Krchňák, P.; Fürst, T.; Večeřová, K.; Panzarová, K.; Benediktyová, Z.; et al. Estimating heat tolerance of plants by ion leakage: A new method based on gradual heating. New Phytol. 2018, 218, 1278–1287. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, G.; Que, S.; Zhu, L.; Di, B.; Jin, X. Relationship between parameters of electrical impedance spectroscopy and frost hardiness in stems and needles of Pinus bungeana. Front. For. China 2009, 4, 242–248. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.; Su, Y.; Xing, D.; Dai, Y.; Wu, Y.; Fang, L. A Plant’s Electrical Parameters Indicate Its Physiological State: A Study of Intracellular Water Metabolism. Plants 2020, 9, 1256. [Google Scholar] [CrossRef]
- Ruth Wairimu, N.; Kuria, K.P.; Tuwei, K.A. Action and variation potential electrical signals in higher plants. Afr. J. Biol. Sci. 2021, 3, 1–18. [Google Scholar] [CrossRef]
- Jócsák, I.; Végvári, G.; Vozáry, E. Electrical impedance measurement on plants: A review with some insights to other fields. Theor. Exp. Plant Physiol. 2019, 31, 359–375. [Google Scholar] [CrossRef]
- Hussain, M.I.; El-Keblawy, A.; Akhtar, N.; Elwakil, A.S. Electrical Impedance Spectroscopy in Plant Biology. In Sustainable Agriculture Reviews 52; Lichtfouse, E., Ed.; Springer International Publishing: Cham, Switzerland, 2021; Volume 52, pp. 395–416. [Google Scholar] [CrossRef]
- Dean, D.A.; Ramanathan, T.; Machado, D.; Sundararajan, R. Electrical impedance spectroscopy study of biological tissues. J. Electrost. 2008, 66, 165–177. [Google Scholar] [CrossRef]
- Abdelrady, W.A.; Ma, Z.; Elshawy, E.E.; Wang, L.; Askri, S.M.H.; Ibrahim, Z.; Dennis, E.; Kanwal, F.; Zeng, F.; Shamsi, I.H. Physiological and biochemical mechanisms of salt tolerance in barley under salinity stress. Plant Stress 2024, 11, 100403. [Google Scholar] [CrossRef]
- Bita, C.E.; Gerats, T. Plant tolerance to high temperature in a changing environment: Scientific fundamentals and production of heat stress-tolerant crops. Front. Plant Sci. 2013, 4, 273. [Google Scholar] [CrossRef] [PubMed]
- Saud, S.; Wang, D.; Fahad, S.; Javed, T.; Jaremko, M.; Abdelsalam, N.R.; Ghareeb, R.Y. The impact of chromium ion stress on plant growth, developmental physiology, and molecular regulation. Front. Plant Sci. 2022, 13, 994785. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wu, Y.; Xing, D.; Zhao, K.; Yu, R. Rapid Measurement of Drought Resistance in Plants Based on Electrophysiological Properties. Trans. ASABE 2015, 58, 1441–1446. [Google Scholar] [CrossRef]
- Liu, Y.; Li, D.; Qian, J.; Di, B.; Zhang, G.; Ren, Z. Electrical impedance spectroscopy (EIS) in plant roots research: A review. Plant Methods 2021, 17, 118. [Google Scholar] [CrossRef]
- Song, X.; Gao, T.; Ai, M.; Gao, S. Experimental investigation of freeze injury temperatures in trees and their contributing factors based on electrical impedance spectroscopy. Front. Plant Sci. 2024, 15, 1326038. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Pallicer, E.; Muñoz-Albero, M.; Pérez-Fuster, C.; Masot Peris, R.; Laguarda-Miró, N. Early Detection of Freeze Damage in Navelate Oranges with Electrochemical Impedance Spectroscopy. Sensors 2018, 18, 4503. [Google Scholar] [CrossRef]
- Zhang, G.; Xiao, J.; Chen, D. Electrical Impedance Spectroscopy Method for Determining Plant Cold Resistance. J. Plant Physiol. Mol. Biol. 2005, 31, 19–26. [Google Scholar]
- Romero Fogué, D.; Masot Peris, R.; Ibáñez Civera, J.; Contat Rodrigo, L.; Laguarda-Miro, N. Monitoring Freeze-Damage in Grapefruit by Electric Bioimpedance Spectroscopy and Electric Equivalent Models. Horticulturae 2022, 8, 218. [Google Scholar] [CrossRef]
- Mudrilov, M.; Ladeynova, M.; Grinberg, M.; Balalaeva, I.; Vodeneev, V. Electrical Signaling of Plants under Abiotic Stressors: Transmission of Stimulus-Specific Information. Int. J. Mol. Sci. 2021, 22, 10715. [Google Scholar] [CrossRef]
- Oyarce, P.; Gurovich, L. Electrical signals in avocado trees: Responses to light and water availability conditions. Plant Signal. Behav. 2010, 5, 34–41. [Google Scholar] [CrossRef]
- Wilner, J. Note on an electrolytic procedure for differentiating between frost injury of roots and shoots in woody plants. Can. J. Plant Sci. 1959, 39, 512–513. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Yang, L.T.; Li, Y.R. Physiological and Biochemical characteristics related to cold resistance in sugarcane. Sugar Tech 2015, 17, 49–58. [Google Scholar] [CrossRef]
- Verma, N.; Verma, A.K. Performance analysis of wavelet thresholding methods in denoising of audio signals of some Indian musical instruments. Int. J. Eng. Sci. Technol. 2012, 4, 6. [Google Scholar]
- Gao, X.; Xi, G.; Liu, K.; Liu, Q. The study of de-noising method about plant electrical signal based on wavelet. J. Xi’an Univ. Technol. 2013, 29, 92–97. [Google Scholar]
- Valencia, D.; Orejuela, D.; Salazar, J.; Valencia, J. Comparison analysis between rigrsure, sqtwolog, heursure and minimaxi techniques using hard and soft thresholding methods. In Proceedings of the 2016 XXI IEEE Symposium on Signal Processing, Images and Artificial Vision (STSIVA), Bucaramanga, Colombia, 31 August–2 September 2016; pp. 1–5. [Google Scholar]
- Zhou, J.; Yuan, W.; Di, B.; Zhang, G.; Zhu, J.; Zhou, P.; Ding, T.; Qian, J. Relationship among Electrical Signals, Chlorophyll Fluorescence, and Root Vitality of Strawberry Seedlings under Drought Stress. Agronomy 2022, 12, 1428. [Google Scholar] [CrossRef]
- Zhang, G.; Ryyppö, A.; Vapaavuori, E.; Repo, T. Quantification of additive response and stationarity of frost hardiness by photoperiod and temperature in Scots pine. Can. J. For. Res. 2003, 33, 1772–1784. [Google Scholar] [CrossRef]
- Serrano-Finetti, E.; Castillo, E.; Alejos, S.; León Hilario, L.M. Toward noninvasive monitoring of plant leaf water content by electrical impedance spectroscopy by electrical impedance spectroscopy. Comput. Electron. Agric. 2023, 210, 107907. [Google Scholar] [CrossRef]
- Repo, T.; Zhang, M.I.N.; Ryyppö, A.; Vapaavuori, E.; Sutinen, S. Effects of freeze-thaw injury on parameters of distributed electrical circuits of stems and needles of Scots pine seedlings at different stages of acclimation. J. Exp. Bot. 1994, 45, 823–833. [Google Scholar] [CrossRef]
- Uemura, M.; Steponkus, P.L. Cold Acclimation in Plants: Relationship Between the Lipid Composition and the Cryostability of the Plasma Membrane. J. Plant Res. 1999, 112, 245–254. [Google Scholar] [CrossRef]
- Moran, R.E.; Sun, Y.; Geng, F.; Zhang, D.; Fazio, G. Cold Temperature Tolerance of Trunk and Root Tissues in One- or Two-year-old Apple Rootstocks. HortScience 2011, 46, 1460–1464. [Google Scholar] [CrossRef]
- Zheng, G.; Li, L.; Li, W. Glycerolipidome responses to freezing- and chilling-induced injuries: Examples in Arabidopsis and rice. BMC Plant Biol. 2016, 16, 70. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Hoang, N.V.; Do, V.G.; Foster, T.M.; McGhie, T.K.; Kim, S.; Yang, S.J.; Park, J.-H.; Park, J.; Lee, J.-Y. Identification of genes associated with the regulation of cold tolerance and the RNA movement in the grafted apple. Sci. Rep. 2023, 13, 11583. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-L.; Meng, D.; Li, M.-J.; Zhou, J.; Yang, Y.-Z.; Zhou, B.-B.; Wei, Q.-P.; Zhang, J.-K. Transcription factors MhDREB2A/MhZAT10 play a role in drought and cold stress response crosstalk in apple. Plant Physiol. 2023, 192, 2203–2220. [Google Scholar] [CrossRef]
- Chen, X.; Yao, C.; Li, C.; Sun, C.; Mi, Y.; Li, C.; Hu, L. Frequency Response Model and Simulation of Transmembrane Potentials on Cellular Inner and Outer Membranes. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; pp. 5818–5821. [Google Scholar] [CrossRef]
- Alessandrini, A.; Facci, P. Changes in single K+ channel behavior induced by a lipid phase transition. Integr. Biol. 2010, 99, 3675–3683. [Google Scholar] [CrossRef][Green Version]
- Miura, K.; Furumoto, T. Cold Signaling and Cold Response in Plants. Int. J. Mol. Sci. 2013, 14, 5312–5337. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; He, L.; Li, F. Understanding cold stress response mechanisms in plants: An overview. Front. Plant Sci. 2024, 15, 1443317. [Google Scholar] [CrossRef]
- Zhang, M.I.N.; Willison, J.H.M. Electrical impedance analysis in plant tissues: In vivo detection of freezing injury. Can. J. Bot. 1992, 70, 2254–2258. [Google Scholar] [CrossRef]
- Isokawa, M. Membrane time constant as a tool to assess cell degeneration. Brain Res. Protoc. 1997, 1, 114–116. [Google Scholar] [CrossRef]
- Bañoc, D.M.; Yamauchi, A.; Kamoshita, A.; Wade, L.J.; Pardales, J.R. Genotypic Variations in Response of Lateral Root Development to Fluctuating Soil Moisture in Rice. Plant Prod. Sci. 2000, 3, 335–343. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, Z.; Zhu, X.; Hou, Y. Comprehensive evaluation of physiological response and cold tolerance of domesticated Cinnamomum camphora (L.) Presl under low temperature stress. PeerJ 2024, 12, e18590. [Google Scholar] [CrossRef]
- Campos, P.S.; Quartin, V.N.; Ramalho, J.C.; Nunes, M.A. Electrolyte leakage and lipid degradation account for cold sensitivity in leaves of Coffea sp. plants. J. Plant Physiol. 2003, 160, 283–292. [Google Scholar] [CrossRef] [PubMed]
| Date (Year-Month-Day) | Temperature (°C) | |||||
|---|---|---|---|---|---|---|
| 2023-09-20 | 4 | −10 | −20 | −30 | −35 | −45 |
| 2023-10-20 | 4 | −10 | −20 | −30 | −35 | −45 |
| 2023-11-20 | 4 | −10 | −20 | −30 | −35 | −45 |
| 2023-12-20 | 4 | −15 | −25 | −35 | −45 | −80 |
| 2024-01-20 | 4 | −15 | −25 | −35 | −45 | −80 |
| 2024-02-20 | 4 | −15 | −25 | −35 | −45 | −80 |
| 2024-03-20 | 4 | −10 | −20 | −30 | −45 | −80 |
| Principal Component | First Principal Component | Second Principal Component | |
|---|---|---|---|
| Eigenvalue | 15.503 | 1.127 | |
| Proportion (%) | 86.128 | 6.260 | |
| Cumulative (%) | 86.128 | 92.387 | |
| Eigenvector | Min | 0.244 | −0.073 |
| r1 | 0.242 | 0.259 | |
| re | 0.241 | 0.248 | |
| r | 0.240 | 0.265 | |
| std | −0.239 | 0.170 | |
| Peak | 0.239 | −0.273 | |
| psdE | 0.230 | −0.283 | |
| peakF | −0.229 | 0.224 | |
| t | −0.215 | −0.250 |
| Load Capacity | F1 × Y1 + F2 × Y2 | Weight | ||
|---|---|---|---|---|
| Indexes | Component | |||
| 1 | 2 | |||
| Min | 0.962 | −0.077 | 1.482 | 0.320 |
| r1 | 0.952 | 0.275 | 1.507 | 0.326 |
| re | 0.949 | 0.263 | 1.501 | 0.324 |
| r | 0.946 | 0.281 | 1.499 | 0.324 |
| std | −0.942 | 0.180 | −1.439 | −0.311 |
| Peak | 0.941 | −0.290 | 1.426 | 0.308 |
| psdE | 0.905 | −0.300 | 1.369 | 0.296 |
| peakF | −0.902 | 0.238 | −1.372 | −0.297 |
| t | −0.848 | −0.266 | −1.345 | −0.291 |
| Source | Degrees of Freedom | Sum of Squares | Mean Square Sum | F-Number | p-Number | |
|---|---|---|---|---|---|---|
| Model | 6 | 595.0042 | 99.1674 | 81.0923 | p < 0.0001 | |
| Error | 43 | 52.6674 | 1.2248 | |||
| Total | 49 | 647.6716 | ||||
| Variable | Degrees of Freedom | Estimated value | Standard error | t-value | p-value | |
| Constant | 1 | −3.9200 | 0.0086 | −455.81 | p < 0.0001 | |
| Min | 1 | 0.0013 | 0.0184 | 0.0701 | p < 0.0001 | |
| Peak | 1 | 0.0012 | 0.0198 | 0.0596 | p < 0.0001 | |
| Std | 1 | 0.0036 | 0.0210 | 0.1695 | p < 0.0001 | |
| r | 1 | −0.0331 | 0.0192 | −1.7240 | p < 0.0001 | |
| re | 1 | −0.1333 | 0.0202 | −6.5980 | p < 0.0001 | |
| r1 | 1 | −0.0711 | 0.0214 | −3.3234 | p < 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Wu, S.; Nie, X.; Jia, L.; Zhang, X.; Qian, J. Development of a Predictive Model Linking Electrical Characteristics to Semi-Lethal Temperature in Potted Apple Trees with Validation on Mature Specimens. Agronomy 2025, 15, 1458. https://doi.org/10.3390/agronomy15061458
Sun B, Wu S, Nie X, Jia L, Zhang X, Qian J. Development of a Predictive Model Linking Electrical Characteristics to Semi-Lethal Temperature in Potted Apple Trees with Validation on Mature Specimens. Agronomy. 2025; 15(6):1458. https://doi.org/10.3390/agronomy15061458
Chicago/Turabian StyleSun, Bo, Shuaiyang Wu, Xiaohang Nie, Linguang Jia, Xueying Zhang, and Ji Qian. 2025. "Development of a Predictive Model Linking Electrical Characteristics to Semi-Lethal Temperature in Potted Apple Trees with Validation on Mature Specimens" Agronomy 15, no. 6: 1458. https://doi.org/10.3390/agronomy15061458
APA StyleSun, B., Wu, S., Nie, X., Jia, L., Zhang, X., & Qian, J. (2025). Development of a Predictive Model Linking Electrical Characteristics to Semi-Lethal Temperature in Potted Apple Trees with Validation on Mature Specimens. Agronomy, 15(6), 1458. https://doi.org/10.3390/agronomy15061458






