Prediction of Spatial Winter Wheat Yield by Combining Multiscale Time Series of Vegetation and Meteorological Indices
Abstract
1. Introduction
2. Materials and Methods
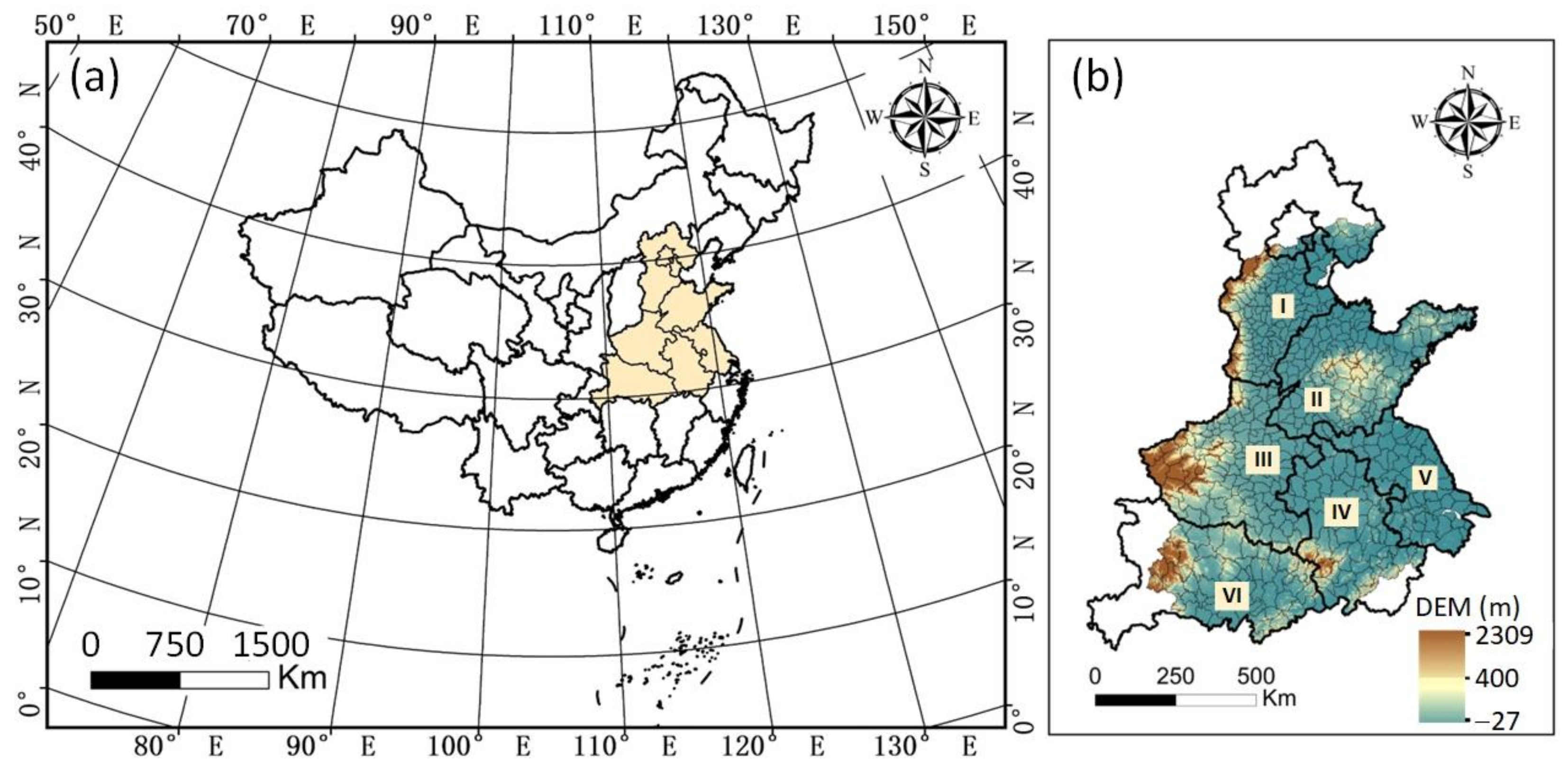
2.1. Study Area
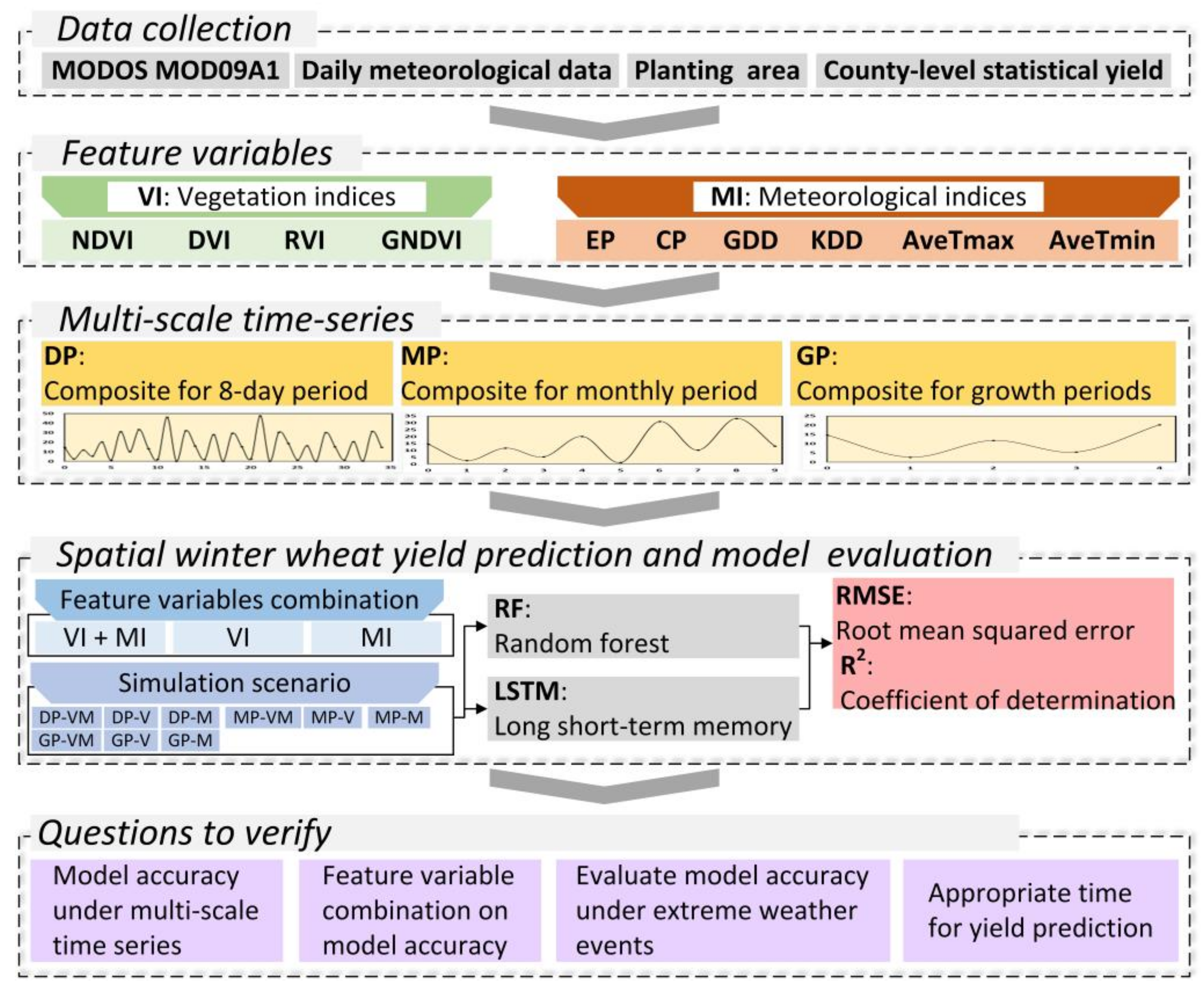
2.2. Analysis Workflow
2.3. Data Description
2.3.1. Data Collection and Preprocessing Steps
2.3.2. Calculation of Vegetation Indices
2.3.3. Calculation of Meteorological Indices
2.3.4. Construction of Multiple Time-Series Data
2.4. Yield Prediction Model and Accuracy Verification
3. Results
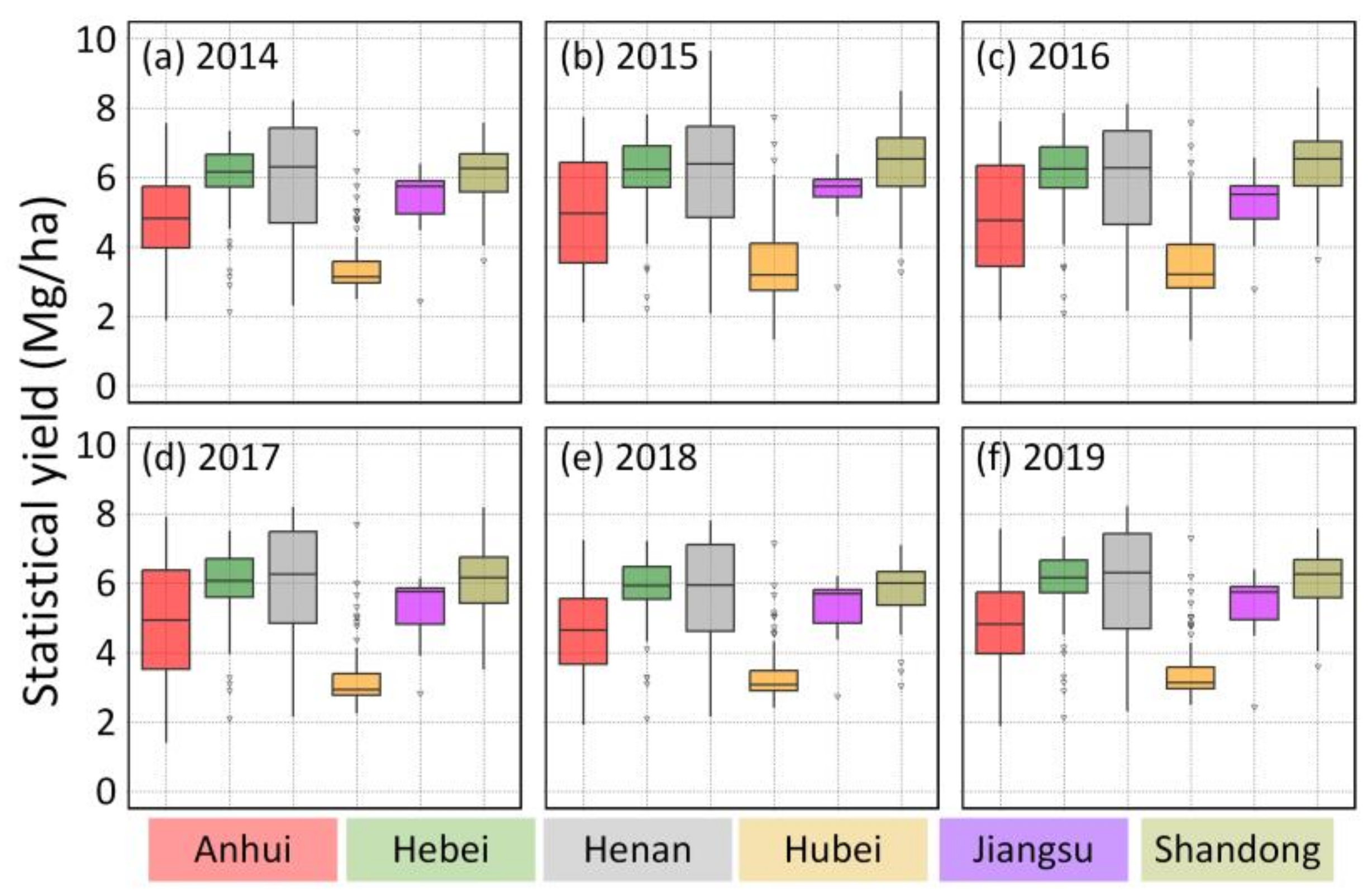
3.1. Descriptive Statistics
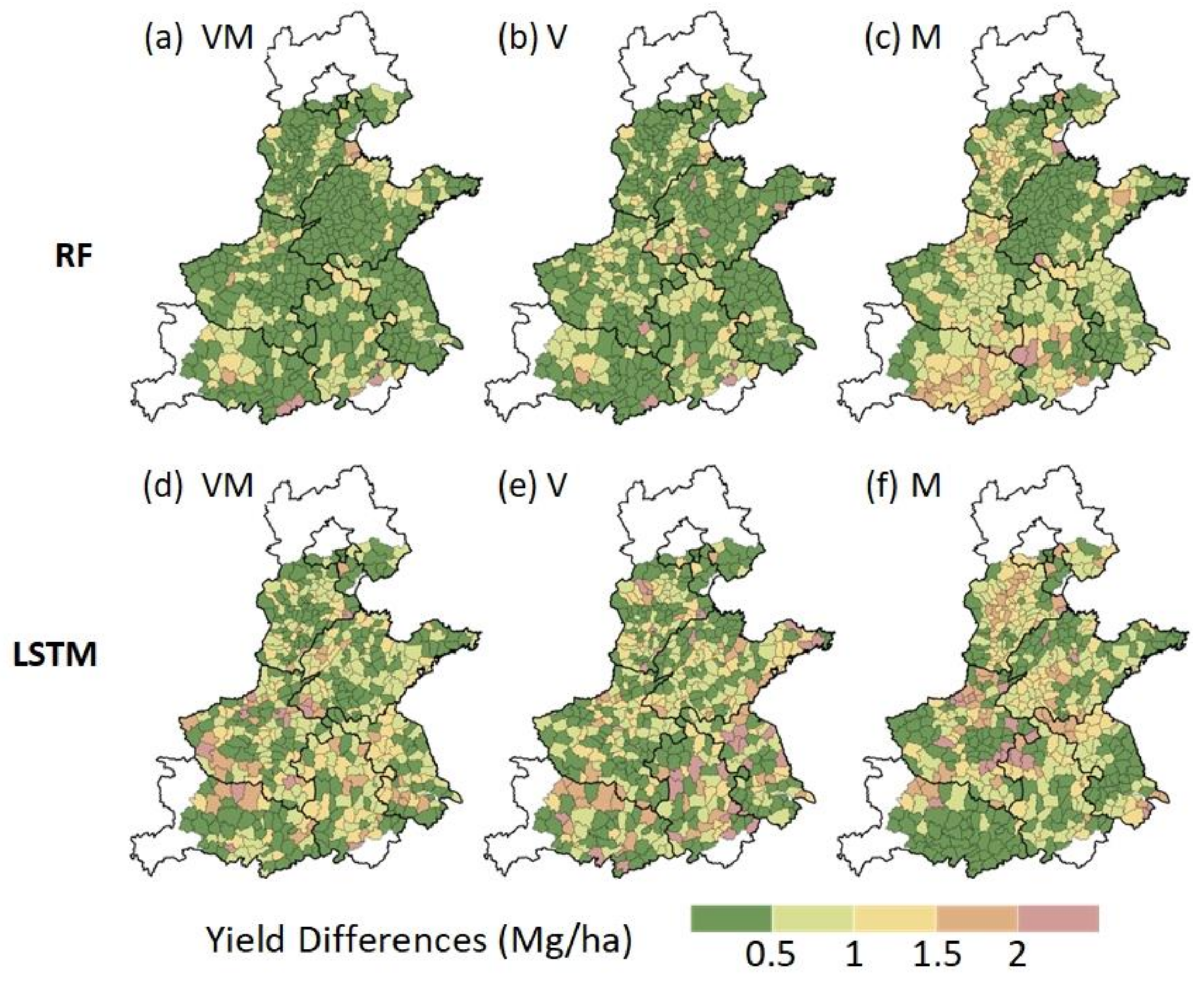
3.2. Model-Performance Evaluation
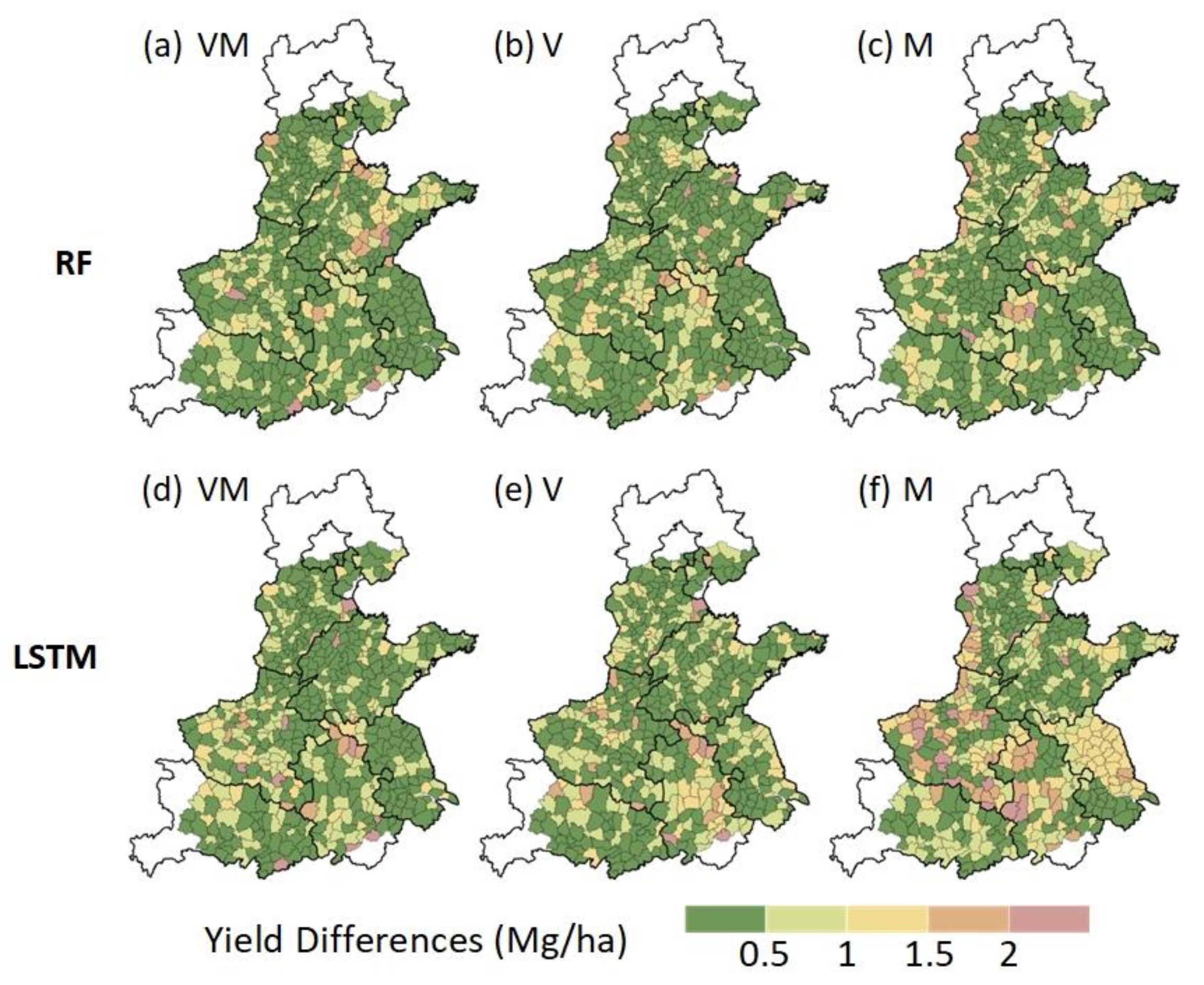
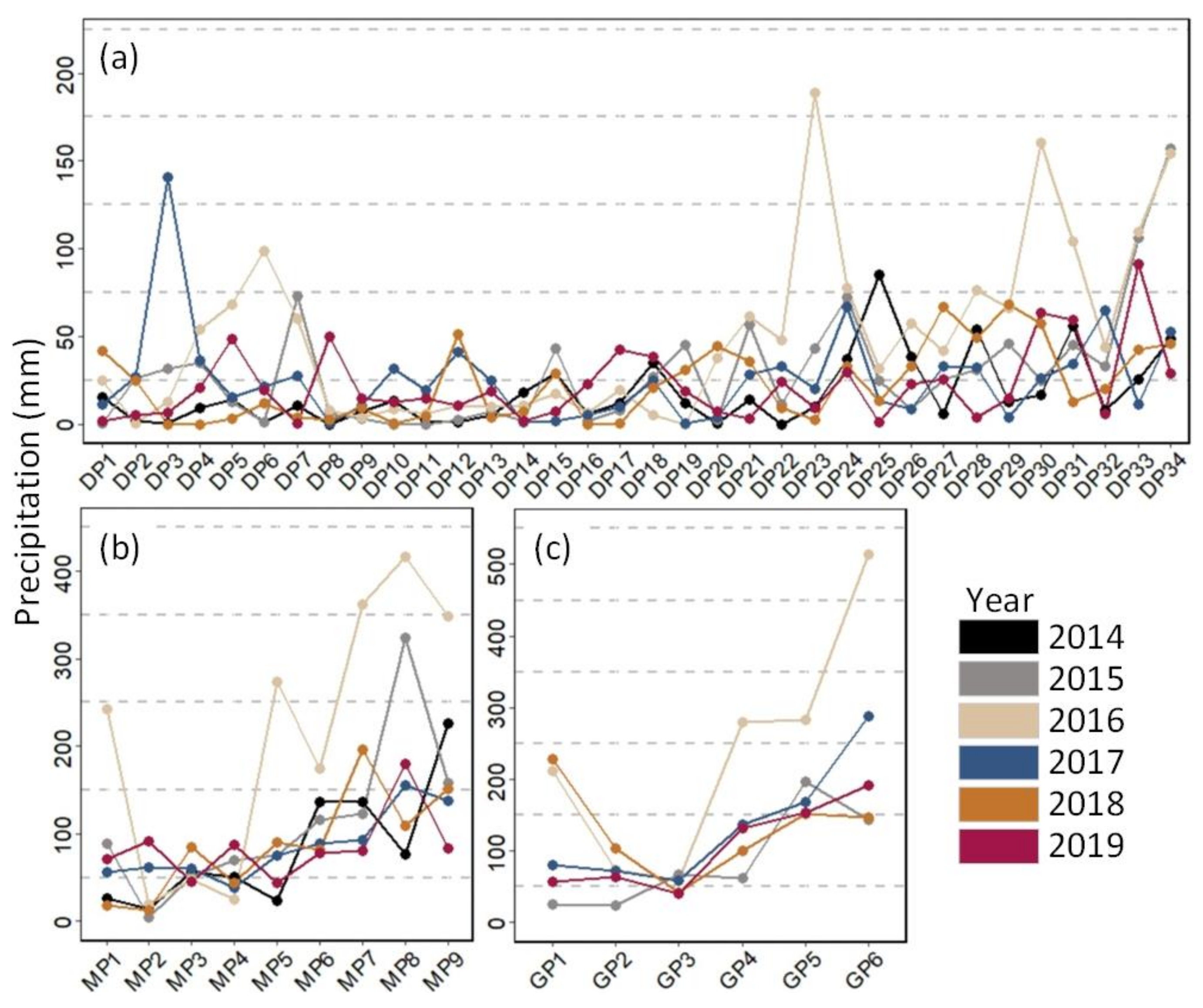
3.3. Model Performance Under Extreme Weather Conditions
3.4. Effects of Different Period Data on Model Accuracy
4. Discussion
4.1. Construction of the Time Series Prediction Model
4.2. Optimal Yield Prediction Time
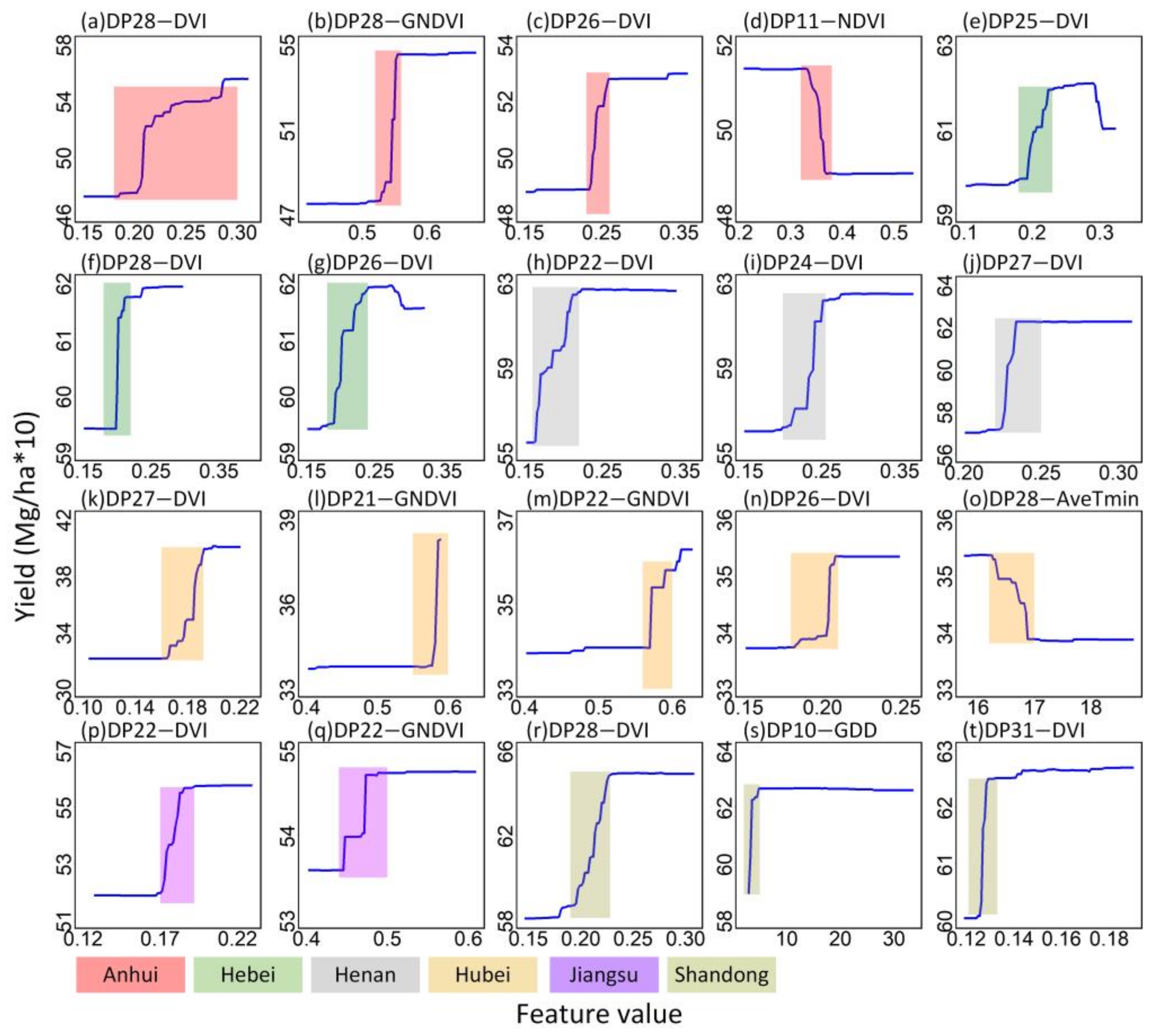
4.3. Nonlinear Relationship Between Feature Variables and Yield
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, H.; Zhang, X.; Ye, Z.; Jiang, L.; Qiu, X.; Tian, Y.; Zhu, Y.; Cao, W. Machine learning approaches can reduce environmental data requirements for regional yield potential simulation. Eur. J. Agron. 2021, 129, 126335. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, H.; Jiang, L.; Zhao, J.; Zuo, W.; Qiu, X.; Tian, Y.; Cao, W.; Zhu, Y. Selection of Appropriate Spatial Resolution for the Meteorological Data for Regional Winter Wheat Potential Productivity Simulation in China Based on WheatGrow Model. Agronomy 2018, 8, 198. [Google Scholar] [CrossRef]
- Klompenburg, T.V.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Zare, H.; Weber, T.K.; Ingwersen, J.; Nowak, W.; Gayler, S.; Streck, T. Within-season crop yield prediction by a multi-model ensemble with integrated data assimilation. Field Crops Res. 2024, 308, 109293. [Google Scholar] [CrossRef]
- Cheng, Z.; Gu, X.; Zhou, Z.; Zhang, Y.; Yin, H.; Li, W.; Chang, T.; Du, Y. Enhancing in-season yield forecast accuracy for film-mulched wheat: A hybrid approach coupling crop model and UAV remote-sensing data by ensemble learning technique. Eur. J. Agron. 2024, 156, 127174. [Google Scholar] [CrossRef]
- Sharafi, S.; Nahvinia, M. Sustainability insights: Enhancing rainfed wheat and barley yield prediction in arid regions. Agric. Water Manag. 2024, 299, 108857. [Google Scholar] [CrossRef]
- Perich, G.; Turkoglu, M.; Graf, L.; Wegner, J.; Aasen, H.; Walter, A.; Liebisch, F. Pixel-based yield mapping and prediction from Sentinel-2 using spectral indices and neural networks. Field Crops Res. 2023, 292, 108824. [Google Scholar] [CrossRef]
- Tanabe, R.; Matsui, T.; Tanaka, T. Winter wheat yield prediction using convolutional neural networks and UAV-based multispectral imagery. Field Crops Res. 2023, 291, 108786. [Google Scholar] [CrossRef]
- Arslan, N.; Sekertekin, A. Application of Long Short-Term Memory neural network model for the reconstruction of MODIS Land Surface Temperature images. J. Atmos. Solar-Terr. Phys. 2019, 194, 105100. [Google Scholar] [CrossRef]
- Clercq, D.; Mahdi, A. Feasibility of machine learning-based rice yield prediction in India at the district level using climate reanalysis and remote sensing data. Agric. Syst. 2024, 220, 104099. [Google Scholar] [CrossRef]
- Yin, X.; Peng, J.; Huang, S.; Leng, G. Aggravation of global maize yield loss risk under various hot and dry scenarios using multiple types of prediction approaches. Int. J. Clim. 2024, 44, 4. [Google Scholar] [CrossRef]
- Silva, J.; Heerwaarden, J.; Reidsma, P.; Laborte, A.; Tesfaye, K.; Ittersum, M. Big data, small explanatory and predictive power: Lessons from random forest modeling of on-farm yield variability and implications for data-driven agronomy. Field Crops Res. 2023, 302, 109063. [Google Scholar] [CrossRef] [PubMed]
- Apolo-Apolo, O.; Martínez-Guanter, J.; Egea, G.; Raja, P.; Perez-Ruiz, M. Deep learning techniques for estimation of the yield and size of citrus fruits using a UAV. Eur. J. Agron. 2020, 115, 126030. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Wang, L.; Li, D.; Li, H.; Gao, C.; Zhuang, M.; Zhuang, J.; Zhou, H.; Xu, S.; et al. Predicting maize yield in Northeast China by a hybrid approach combining biophysical modelling and machine learning. Field Crop. Res. 2023, 302, 109102. [Google Scholar] [CrossRef]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous corn and soybean yield prediction from remote sensing data using deep transfer learning. Sci. Rep. 2021, 11, 11132. [Google Scholar] [CrossRef]
- Lobell, D. The use of satellite data for crop yield gap analysis. Field Crops Res. 2013, 143, 56–64. [Google Scholar] [CrossRef]
- Richetti, J.; Lawes, R.; Whan, A.; Gaydon, D.; Thorburn, P. How well does APSIM NextGen simulate wheat yields across Australia using gridded input data? Validating Continental-Scale Crop Model Simulations. Eur. J. Agron. 2024, 158, 127212. [Google Scholar] [CrossRef]
- Li, S.; Jiang, S.; Song, N.; Han, Y.; Wang, J. Two-step fusion framework for generating 10 m resolution soil moisture with high accuracy in the cotton fields of southern Xinjiang. Ind. Crops Prod. 2025, 226, 120582. [Google Scholar] [CrossRef]
- Wang, M.; Ciais, P.; Frappart, F.; Tao, S.; Fan, L.; Sun, R.; Li, X.; Liu, X.; Wang, H.; Wigneron, J.P. A novel AMSR2 retrieval algorithm for global C-band vegetation optical depth and soil moisture (AMSR2 IB): Parameters’ calibration, evaluation and inter-comparison. Remote Sens. Environ. 2024, 313, 114370. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Tan, Z.; Yue, P.; Di, L.; Tang, J. Deriving High Spatiotemporal Remote Sensing Images Using Deep Convolutional Network. Remote Sens. 2018, 10, 1066. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, H.; Zhong, R.; Xu, J.; Xu, J.; Huang, J.; Wang, S.; Ying, Y.; Lin, T. A deep learning approach to conflating heterogeneous geospatial data for corn yield estimation: A case study of the US Corn Belt at the county level. Glob. Change Biol. 2020, 26, 1754–1766. [Google Scholar] [CrossRef] [PubMed]
- Ashapure, A.; Jung, J.; Chang, A.; Oh, S.; Yeom, J.; Maeda, M.; Maeda, A.; Dube, N.; Landivar, J.; Hague, S.; et al. Developing a machine learning based cotton yield estimation framework using multi-temporal UAS data. ISPRS J. Photogramm. Remote Sens. 2020, 169, 180–194. [Google Scholar] [CrossRef]
- Yang, G.; Yu, W.; Yao, X.; Zheng, H.; Cao, Q.; Zhu, Y.; Cao, W.; Cheng, T. AGTOC: A novel approach to winter wheat mapping by automatic generation of training samples and one-class classification on Google Earth. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102446. [Google Scholar] [CrossRef]
- Döll, P.; Siebert, S. Global modeling of irrigation water requirements. Water Resour. Res. 2002, 38, 8-1–8-10. [Google Scholar] [CrossRef]
- Martin, S. CROPWAT: A Computer Program for Irrigation Planning and Management. FAO Irrig. Drain. Pap. 1992, 46. [Google Scholar]
- Grogan, S.; Anderson, J.; Baenziger, P.; Frels, K.; Guttieri, M.; Haley, S.; Kim, K.; Liu, S.; McMaster, G.; Newell, M.; et al. Phenotypic Plasticity of Winter Wheat Heading Date and Grain Yield across the US Great Plains. Crop Sci. 2016, 56, 2223–2236. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, M.; Yin, X.; Zhang, H.; Chu, Q.; Wen, X.; Chen, F. Spatiotemporal change characteristics of heat and rainfall during the growth period of winter wheat in North China Plain from 1961 to 2010. J. China Agric. Univ. 2015, 20, 16–23. [Google Scholar] [CrossRef]
- He, X.; Luo, H.; Qiao, M.; Tian, Z.; Zhou, G. Yield estimation of winter wheat in China based on CNN-RNN network. TCSAE 2021, 37, 124–132. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gers, F.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zheng, Y.; Feng, L.; Chen, J.; Lakshmi, V.; Shi, H. Are only foods with large discharges threatening? Flood characteristics evolution in the Yangtze River Basin. Geosci. Lett. 2021, 8, 32. [Google Scholar] [CrossRef]
- Júnior, R.; Olivier, L.; Wallach, D.; Mullens, E.; Fraisse, C.; Asseng, S. A simple procedure for a national wheat yield forecast. Eur. J. Agron. 2023, 148, 126868. [Google Scholar] [CrossRef]
- Fan, G.; Yu, P.; Wang, Q.; Dong, Y. Short-term motion prediction of a semi-submersible by combining LSTM neural network and different signal decomposition methods. Ocean Eng. 2023, 267, 113266. [Google Scholar] [CrossRef]
- Maseko, S.; Laan, M.; Tesfamariam, E.; Delport, M.; Otterman, H. Evaluating machine learning models and identifying key factors influencing spatial maize yield predictions in data intensive farm management. Eur. J. Agron. 2024, 157, 127193. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Hong, Y.; Hu, B.; Peng, J.; Shi, Z. A comparison of multiple deep learning methods for predicting soil organic carbon in Southern Xinjiang, China. Comput. Electron. Agric. 2023, 212, 108067. [Google Scholar] [CrossRef]
- Jahromi, M.; Zand-Parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Pourghasemi, H. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
- Guo, Y.; Hao, F.; Zhang, X.; He, Y.; Fu, Y. Improving maize yield estimation by assimilating UAV-based LAI into WOFOST model. Field Crops Res. 2024, 315, 109477. [Google Scholar] [CrossRef]
- Chen, C.; Cao, G.; Li, Y.; Liu, D.; Ma, B.; Zhang, J.; Li, L.; Hu, J. Research on Monitoring Methods for the Appropriate Rice Harvest Period Based on Multispectral Remote Sensing. Discret. Dyn. Nat. Soc. 2022, 2022, 1519667. [Google Scholar] [CrossRef]
- Zare, H.; Viswanathan, M.; Weber, T.; Ingwersen, J.; Nowak, W.; Gayler, S.; Streck, T. Improving winter wheat yield prediction by accounting for weather and model parameter uncertainty while assimilating LAI and updating weather data within a crop model. Eur. J. Agron. 2024, 156, 127149. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Hajjarpoor, A.; Soltani, A.; Zeinali, E.; Kashiri, H.; Aynehband, A.; Vadez, V. Using boundary line analysis to assess the on-farm crop yield gap of wheat. Field Crops Res. 2018, 225, 64–73. [Google Scholar] [CrossRef]
- Bonneu, F.; Makowski, D.; Joly, J.; Allard, D. Machine learning based on functional principal component analysis to quantify the effects of the main drivers of wheat yields. Eur. J. Agron. 2024, 159, 127254. [Google Scholar] [CrossRef]





| Data Type | Element | Format | Source | Time Resolution | Spatial Resolution |
|---|---|---|---|---|---|
| Administrative | County | shp | National Earth System Science Data Center (www.geodata.cn (accessed on 1 January 2024)) | / | / |
| Meteorology | Tmax, Tmin, and PRE | tiff | Data Publisher for Earth & Environmental Science (https://pangaea.de/ (accessed on 19 December 2023)) | Daily | 1 km |
| Yield | Statistical yield | csv | Chinese Economic and Social Big DataResearch Platform(https://data.cnki.net/ (accessed on 1 April 2022)) | Yearly | / |
| Remote sensing | R, G, B, near infrared | tiff | MODIS Surface Reflectance products, Google Earth Engine (https://earthengine.google.com/ (accessed on 1 January 2024)) | 8 days | 500 m |
| Terrain | DEM | tiff | SRTMGL1_003 DEM (https://lpdaac.usgs.gov/products/srtmgl1v003/ (accessed on 19 December 2023)) | / | 30 m |
| Others | Planting area | tiff | National Ecosystem Science Data Center (https://www.nesdc.org.cn/ (accessed on 1 May 2024)) [24] | / | 10 m |
| Harvest Year | MODIS Image Time | |||
|---|---|---|---|---|
| Start Date | End Date | Time Interval | Image Number | |
| 2014 | 8 October 2013 | 26 June 2014 | 8 days | 34 |
| 2015 | 8 October 2014 | 26 June 2015 | ||
| 2016 | 8 October 2015 | 25 June 2016 | ||
| 2017 | 7 October 2016 | 26 June 2017 | ||
| 2018 | 8 October 2017 | 26 June 2018 | ||
| 2019 | 8 October 2018 | 26 June 2019 | ||
| Harvest Year | Growth Period | |||||
|---|---|---|---|---|---|---|
| GP1 | GP2 | GP3 | GP4 | GP5 | GP6 | |
| 2014 | 1 Oct. 2013– 11 Nov. 2013 | 12 Nov. 2013– 22 Dec. 2013 | 23 Dec. 2013– 1 Feb. 2014 | 2 Feb. 2014– 15 Mar. 2014 | 16 Mar. 2014– 26 Apr. 2014 | 27 Apr. 2014– 7 Jun. 2014 |
| 2015 | 1 Oct. 2014– 11 Nov. 2014 | 12 Nov. 2014– 22 Dec. 2014 | 23 Dec. 2014– 1 Feb. 2015 | 2 Feb. 2015– 14 Mar. 2015 | 15 Mar. 2015– 24 Apr. 2015 | 25 Apr. 2015– 5 Jun. 2015 |
| 2016 | 1 Oct. 2015– 11 Nov. 2015 | 12 Nov. 2015– 22 Dec. 2015 | 23 Dec. 2015– 1 Feb. 2016 | 2 Feb. 2016– 14 Mar. 2016 | 15 Mar. 2016– 24 Apr. 2016 | 25 Apr. 2016– 5 Jun. 2016 |
| 2017 | 1 Oct. 2016– 11 Nov. 2016 | 12 Nov. 2016– 22 Dec. 2016 | 23 Dec. 2016– 1 Feb. 2017 | 2 Feb. 2017– 15 Mar. 2017 | 16 Mar. 2017– 26 Apr. 2017 | 27 Apr. 2017– 7 Jun. 2017 |
| 2018 | 1 Oct. 2017– 11 Nov. 2017 | 12 Nov. 2017– 22 Dec. 2017 | 23 Dec. 2017– 1 Feb. 2018 | 2 Feb. 2018– 15 Mar. 2018 | 16 Mar. 2018– 26 Apr. 2018 | 27 Apr. 2018– 7 Jun. 2018 |
| 2019 | 1 Oct. 2018– 11 Nov. 2018 | 12 Nov. 2018– 22 Dec. 2018 | 23 Dec. 2018– 1 Feb. 2019 | 2 Feb. 2019– 15 Mar. 2019 | 16 Mar. 2019– 26 Apr. 2019 | 27 Apr. 2019– 7 Jun. 2019 |
| Province | Anhui | Hebei | Henan | Hubei | Jiangsu | Shandong | ||
|---|---|---|---|---|---|---|---|---|
| BSU.No | 57 | 112 | 111 | 52 | 63 | 117 | ||
| DP | RF | train | (285, 340) | (560, 340) | (555, 340) | (260, 340) | (315, 340) | (585, 340) |
| test | (57, 340) | (112, 340) | (111, 340) | (52, 340) | (63, 340) | (117, 340) | ||
| LSTM | train | (285, 34, 10) | (560, 34, 10) | (555, 34, 10) | (260, 34, 10) | (315, 34, 10) | (585, 34, 10) | |
| test | (57, 34, 10) | (112, 34, 10) | (111, 34, 10) | (52, 34, 10) | (63, 34, 10) | (117, 34, 10) | ||
| MP | RF | train | (285, 90) | (560, 90) | (555, 90) | (260, 90) | (315, 90) | (585, 90) |
| test | (57, 90) | (112, 90) | (111, 90) | (52, 90) | (63, 90) | (117, 90) | ||
| LSTM | train | (285, 9, 10) | (560, 9, 10) | (555, 9, 10) | (260, 9, 10) | (315, 9, 10) | (585, 9, 10) | |
| test | (57, 9, 10) | (112, 9, 10) | (111, 9, 10) | (52, 9, 10) | (63, 9, 10) | (117, 9, 10) | ||
| GP | RF | train | (285, 60) | (560, 60) | (555, 60) | (260, 60) | (315, 60) | (585, 60) |
| test | (57, 60) | (112, 60) | (111, 60) | (52, 60) | (63, 60) | (117, 60) | ||
| LSTM | train | (285, 6, 10) | (560, 6, 10) | (555, 6, 10) | (260, 6, 10) | (315, 6, 10) | (585, 6, 10) | |
| test | (57, 6, 10) | (112, 6, 10) | (111, 6, 10) | (52, 6, 10) | (63, 6, 10) | (117, 6, 10) | ||
| Province | Anhui | Hebei | Henan | Hubei | Jiangsu | Shandong |
|---|---|---|---|---|---|---|
| BSU.No | 57 | 112 | 111 | 52 | 63 | 117 |
| train | (285) | (560) | (555) | (260) | (315) | (585) |
| test | (57) | (112) | (111) | (52) | (63) | (117) |
| Province | ML | Variable | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DP-VM | DP-V | DP-M | MP-VM | MP-V | MP-M | GP-VM | GP-V | GP-M | ||
| Anhui | RF | 0.79 (0.56) | 0.82 (0.53) | 1.04 (0.46) | 0.73 (0.62) | 0.75 (0.6) | 0.83 (0.54) | 0.74 (0.6) | 0.79 (0.58) | 1.3 (0.58) |
| LSTM | 1.06 (0.36) | 1.87 (0.06) | 1.17 (0.2) | 0.95 (0.45) | 1.15 (0.55) | 1.12 (0.2) | 0.83 (0.53) | 1.09 (0.44) | 1.05 (0.64) | |
| Hebei | RF | 0.65 (0.51) | 0.66 (0.48) | 0.91 (0.07) | 0.6 (0.56) | 0.64 (0.5) | 0.87 (0.07) | 0.68 (0.46) | 0.63 (0.51) | 1.02 (0.05) |
| LSTM | 1.03 (0.22) | 1.09 (0.32) | 1.2 (0.05) | 0.72 (0.56) | 0.84 (0.49) | 0.99 (0.38) | 0.76 (0.41) | 0.71 (0.49) | 1.08 (0.06) | |
| Henan | RF | 0.49 (0.88) | 0.69 (0.82) | 0.97 (0.66) | 0.62 (0.83) | 0.72 (0.75) | 0.65 (0.82) | 0.59 (0.85) | 0.65 (0.83) | 0.62 (0.81) |
| LSTM | 1.32 (0.22) | 1.07 (0.47) | 1.92 (0.17) | 0.94 (0.56) | 0.98 (0.55) | 1.57 (0.16) | 0.97 (0.58) | 1.21 (0.47) | 1.13 (0.4) | |
| Hubei | RF | 0.71 (0.33) | 0.7 (0.35) | 1.19 (0.115) | 0.6 (0.41) | 0.67 (0.39) | 0.69 (0.43) | 0.75 (0.42) | 0.92 (0.25) | 1.23 (0.17) |
| LSTM | 1.33 (0.15) | 1.67 (0.02) | 0.95 (0.08) | 0.81 (0.28) | 0.87 (0.05) | 0.82 (0.08) | 0.84 (0.37) | 0.88 (0.21) | 0.88 (0.03) | |
| Jiangsu | RF | 0.52 (0.42) | 0.54 (0.38) | 0.66 (0.07) | 0.4 (0.66) | 0.45 (0.61) | 0.52 (0.47) | 0.63 (0.53) | 0.76 (0.15) | 0.5 (0.46) |
| LSTM | 1.15 (0.02) | 1.2 (0.15) | 0.97 (0.03) | 0.55 (0.51) | 0.64 (0.31) | 1.01 (0.16) | 0.55 (0.35) | 0.52 (0.38) | 0.8 (0.01) | |
| Shandong | RF | 0.67 (0.32) | 0.8 (0.41) | 0.76 (0.15) | 0.71 (0.67) | 0.67 (0.6) | 0.7 (0.44) | 0.62 (0.61) | 0.6 (0.42) | 0.67 (0.21) |
| LSTM | 1 (0.3) | 1.07 (0.1) | 0.82 (0.12) | 0.54 (0.46) | 0.57 (0.39) | 0.65 (0.16) | 0.51 (0.45) | 0.63 (0.38) | 0.7 (0.21) | |
| Province | ML | Monthly Periods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MP1 | MP2 | MP3 | MP4 | MP5 | MP6 | MP7 | MP8 | MP9 | ||
| Anhui | RF | 1.82 | 0.90 | 0.94 | 0.94 | 0.92 | 0.83 | 0.76 | 0.74 | 0.73 |
| LSTM | 1.37 | 1.02 | 1.22 | 1.50 | 1.54 | 1.07 | 0.83 | 1.05 | 0.95 | |
| Hebei | RF | 1.36 | 0.74 | 0.79 | 0.79 | 0.78 | 0.74 | 0.64 | 0.62 | 0.60 |
| LSTM | 0.94 | 0.81 | 0.80 | 0.80 | 0.79 | 0.78 | 0.74 | 0.68 | 0.71 | |
| Henan | RF | 1.29 | 1.23 | 1.21 | 1.13 | 1.16 | 1.11 | 1.09 | 0.78 | 0.62 |
| LSTM | 1.31 | 1.18 | 1.05 | 1.11 | 1.04 | 0.95 | 1.10 | 1.00 | 0.94 | |
| Hubei | RF | 1.09 | 0.90 | 0.85 | 0.78 | 0.84 | 0.76 | 0.71 | 0.71 | 0.70 |
| LSTM | 1.15 | 1.06 | 0.92 | 0.86 | 0.92 | 0.88 | 0.88 | 0.77 | 0.81 | |
| Jiangsu | RF | 0.94 | 0.62 | 0.60 | 0.60 | 0.57 | 0.53 | 0.53 | 0.48 | 0.40 |
| LSTM | 0.78 | 0.71 | 0.53 | 0.62 | 0.55 | 0.50 | 0.52 | 0.56 | 0.55 | |
| Shandong | RF | 1.40 | 1.32 | 0.94 | 0.93 | 0.92 | 0.80 | 0.75 | 0.78 | 0.74 |
| LSTM | 0.90 | 0.72 | 0.69 | 0.67 | 0.67 | 0.71 | 0.67 | 0.70 | 0.54 | |
| Province | ML | Growth Periods | |||||
|---|---|---|---|---|---|---|---|
| GP1 | GP2 | GP3 | GP4 | GP5 | GP6 | ||
| Anhui | RF | 0.92 | 0.84 | 0.83 | 0.77 | 0.76 | 0.74 |
| LSTM | 1.51 | 1.15 | 1.36 | 0.89 | 0.88 | 0.83 | |
| Hebei | RF | 0.79 | 0.78 | 0.80 | 0.77 | 0.77 | 0.68 |
| LSTM | 1.20 | 0.85 | 0.79 | 0.74 | 0.77 | 0.76 | |
| Henan | RF | 1.22 | 1.09 | 1.08 | 1.06 | 0.99 | 0.59 |
| LSTM | 1.41 | 1.07 | 1.01 | 0.99 | 0.97 | 0.97 | |
| Hubei | RF | 1.30 | 1.00 | 0.89 | 0.87 | 0.88 | 0.75 |
| LSTM | 1.13 | 0.99 | 0.91 | 0.88 | 0.87 | 0.84 | |
| Jiangsu | RF | 0.94 | 0.68 | 0.68 | 0.64 | 0.65 | 0.63 |
| LSTM | 0.88 | 0.698 | 0.568 | 0.558 | 0.60 | 0.55 | |
| Shandong | RF | 1.02 | 0.84 | 0.76 | 0.78 | 0.63 | 0.62 |
| LSTM | 0.72 | 0.60 | 0.65 | 0.57 | 0.56 | 0.51 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Yin, H.; Liu, J.; Wang, L.; Feng, W.; Song, H.; Fan, Y.; Qi, K.; Liang, Z.; Li, W.; et al. Prediction of Spatial Winter Wheat Yield by Combining Multiscale Time Series of Vegetation and Meteorological Indices. Agronomy 2025, 15, 1114. https://doi.org/10.3390/agronomy15051114
Xu H, Yin H, Liu J, Wang L, Feng W, Song H, Fan Y, Qi K, Liang Z, Li W, et al. Prediction of Spatial Winter Wheat Yield by Combining Multiscale Time Series of Vegetation and Meteorological Indices. Agronomy. 2025; 15(5):1114. https://doi.org/10.3390/agronomy15051114
Chicago/Turabian StyleXu, Hao, Hongfei Yin, Jia Liu, Lei Wang, Wenjie Feng, Hualu Song, Yangyang Fan, Kangkang Qi, Zhichao Liang, WenJie Li, and et al. 2025. "Prediction of Spatial Winter Wheat Yield by Combining Multiscale Time Series of Vegetation and Meteorological Indices" Agronomy 15, no. 5: 1114. https://doi.org/10.3390/agronomy15051114
APA StyleXu, H., Yin, H., Liu, J., Wang, L., Feng, W., Song, H., Fan, Y., Qi, K., Liang, Z., Li, W., Zhang, X., Zhang, R., & Wang, S. (2025). Prediction of Spatial Winter Wheat Yield by Combining Multiscale Time Series of Vegetation and Meteorological Indices. Agronomy, 15(5), 1114. https://doi.org/10.3390/agronomy15051114








