Computational Fluid Dynamics Simulation and Quantification of Solar Greenhouse Temperature Based on Real Canopy Structure
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Basic Control Equations
2.2.1. Energy Balance Equations
2.2.2. Radiation Model
2.2.3. Plant Porous Media Model
2.3. Model Establishment
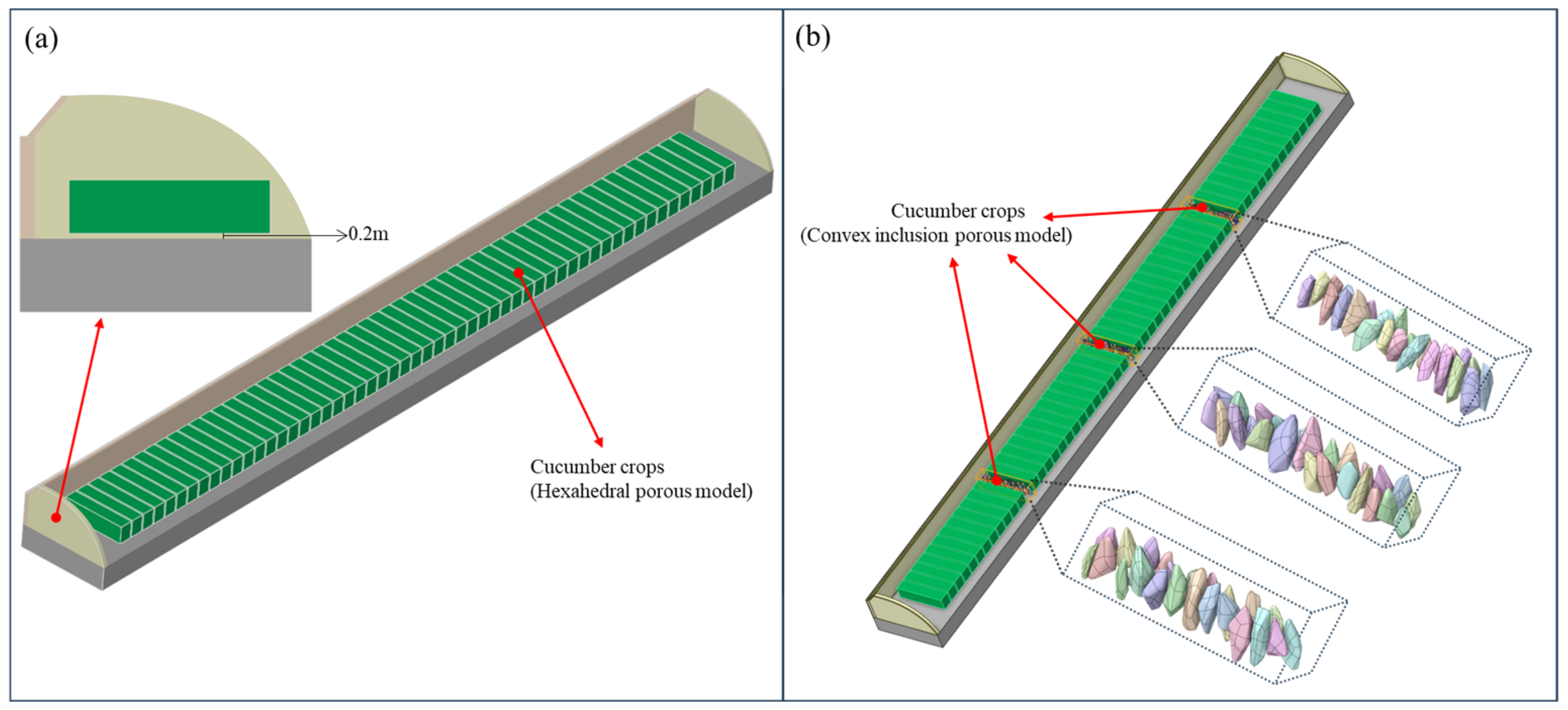
2.3.1. Real Greenhouse 3D Structural Model and Simplified Plant Model Assumptions
2.3.2. Small Greenhouse Model Considering the Fine 3D Structure of Plants
2.3.3. Grid Generation and Independence Verification
2.4. Boundary Conditions
2.5. Calculation Strategy
3. Results
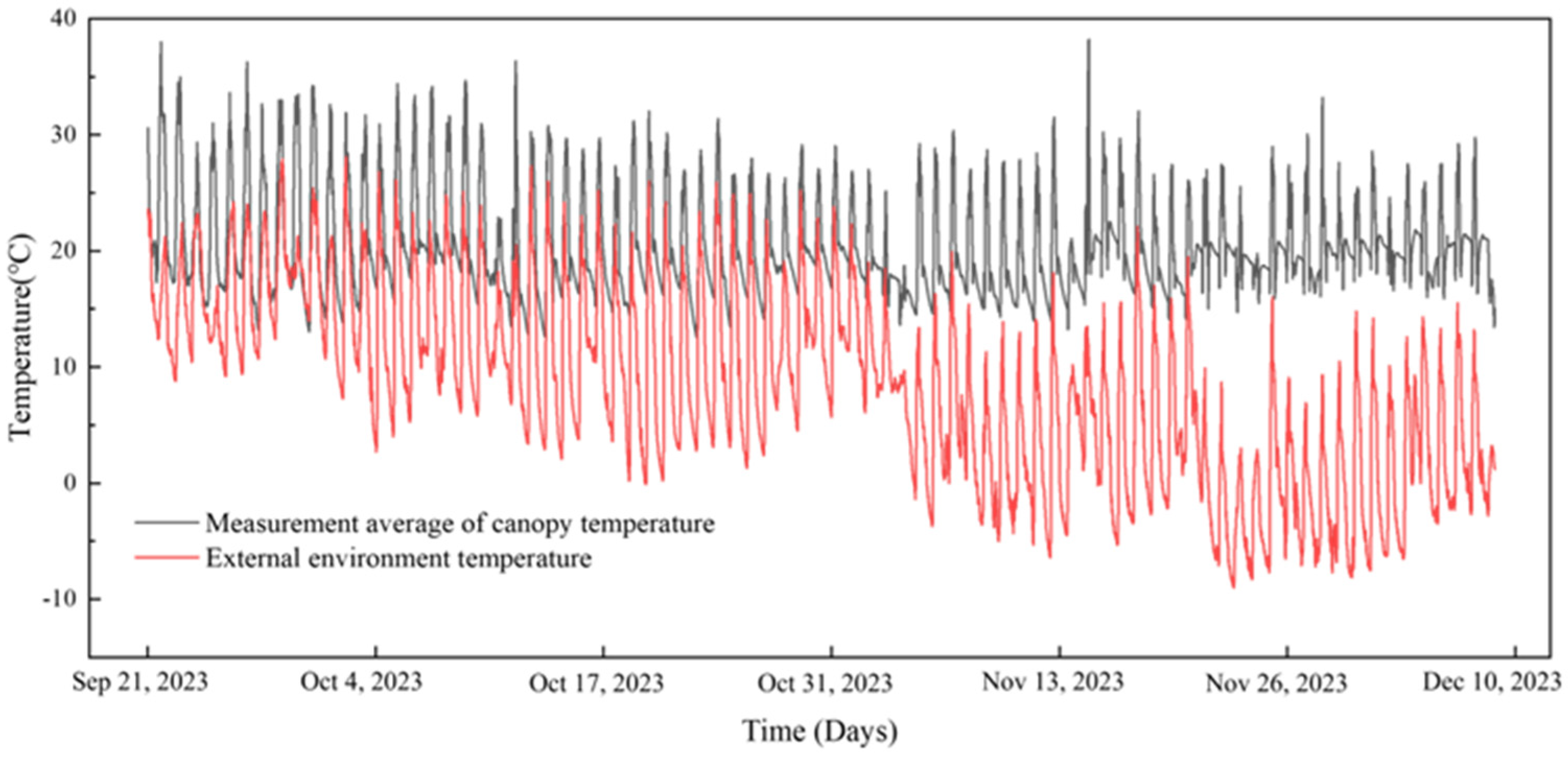
3.1. Experimental Data Analysis
3.2. CFD Grid Independence Verification Results
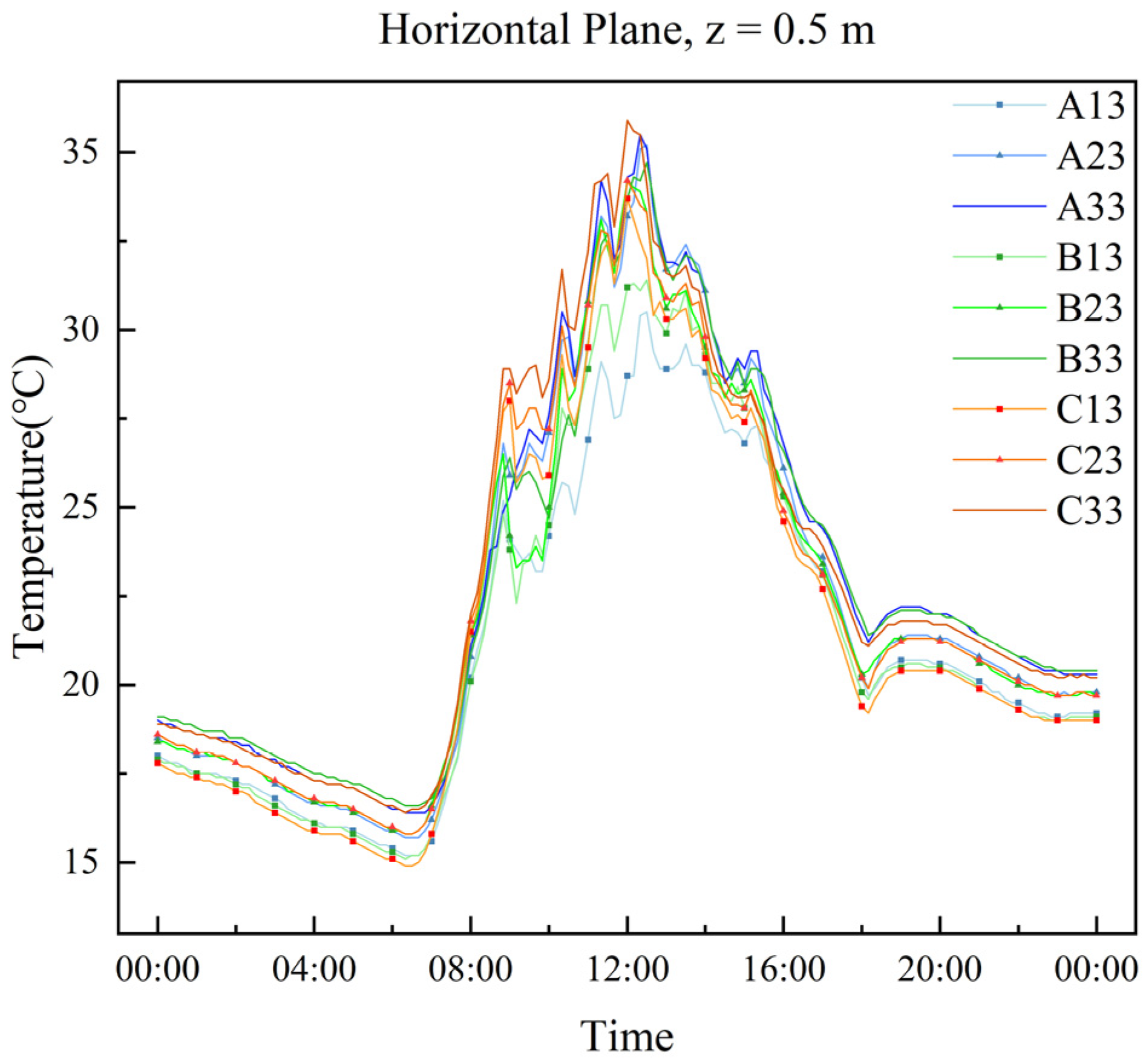
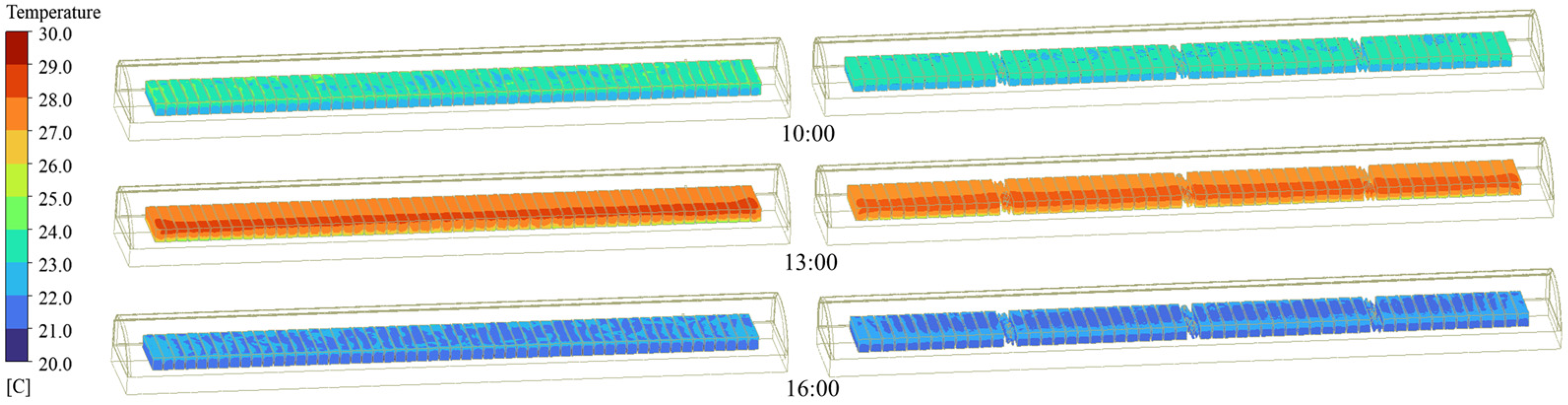
3.3. CFD Simulation Analysis of a Real Greenhouse
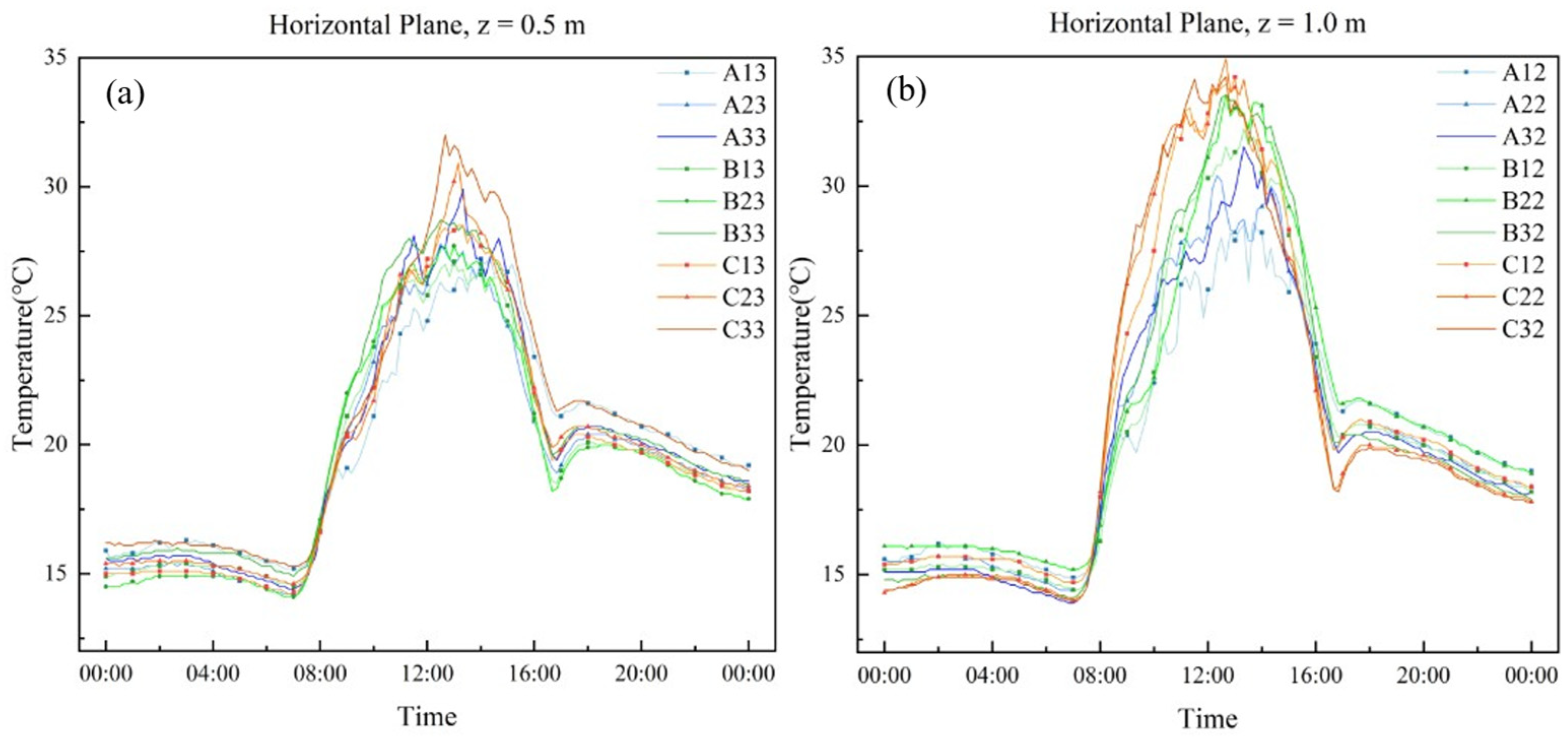
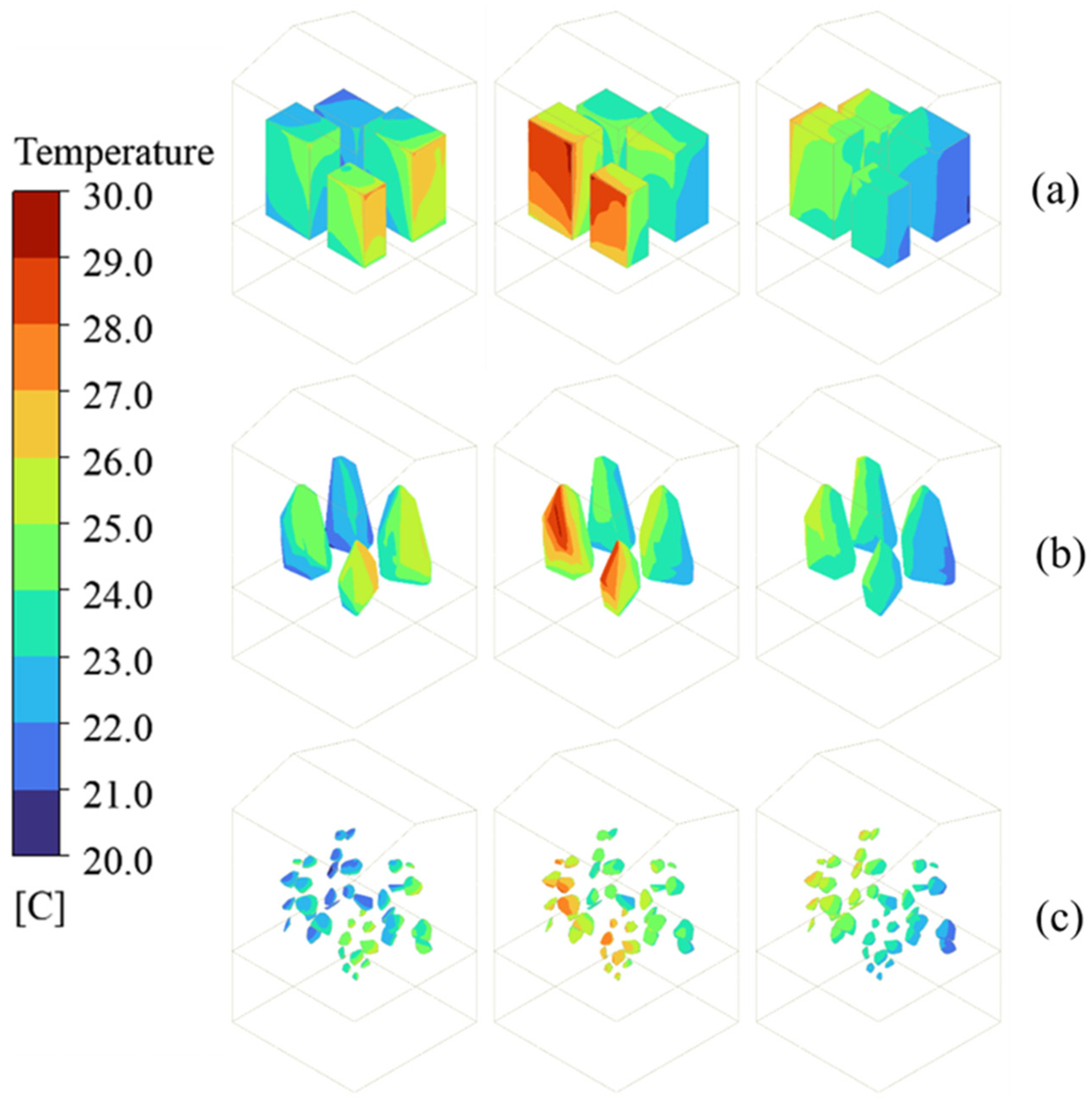
3.4. Comparative Analysis of CFD Simulation of a Small Virtual Greenhouse Model Considering the Fine 3D Structure of Plants
4. Discussion
4.1. Microclimate Distribution in Solar Greenhouse
4.2. Necessity of Applying Real Canopy Structure and Future Directions and Challenges
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Qi, M.; Meng, S. Sixty Years of Facility Horticulture Development in China: Achievements and Prospects. Acta Hortic. Sin. 2022, 10, 2119–2130. [Google Scholar] [CrossRef]
- Blum, A. Heterosis, Stress, and the Environment: A Possible Road Map towards the General Improvement of Crop Yield. J. Exp. Bot. 2013, 64, 4829–4837. [Google Scholar] [CrossRef]
- Chen, C.; Ling, H.; Zhai, Z.; Li, Y.; Yang, F.; Han, F.; Wei, S. Thermal Performance of an Active-Passive Ventilation Wall with Phase Change Material in Solar Greenhouses. Appl. Energy 2018, 216, 602–612. [Google Scholar] [CrossRef]
- Meng, L.; Yang, Q.; Bot, G.P.; Wang, N. Visual Simulation Model for Thermal Environment in Chinese Solar Greenhouse. Trans. Chin. Soc. Agric. Eng. 2009, 25, 164–170. [Google Scholar]
- Han, Y.; Xue, X.; Luo, X.; Guo, L.; Li, T. Establishment of Estimation Model of Solar Radiation within Solar Greenhouse. Trans. Chin. Soc. Agric. Eng. 2014, 30, 174–181. [Google Scholar]
- Bournet, P.E.; Rojano, F. Advances of Computational Fluid Dynamics (CFD) Applications in Agricultural Building Modelling: Research, Applications and Challenges. Comput. Electron. Agric. 2022, 201, 107277. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, S.; Zhou, J.; Hussain, S.A.; Liu, X.; Gao, J.; Huang, G. A Modelling Method for Large-Scale Open Spaces Orientated toward Coordinated Control of Multiple Air-Terminal Units. Build. Simul. 2023, 16, 225–241. [Google Scholar] [CrossRef]
- Guzmán, C.H.; Carrera, J.L.; Durán, H.A.; Berumen, J.; Ortiz, A.A.; Guirette, O.A.; Arroyo, A.; Brizuela, J.A.; Gómez, F.; Blanco, A.; et al. Implementation of Virtual Sensors for Monitoring Temperature in Greenhouses Using CFD and Control. Sensors 2019, 19, 60. [Google Scholar] [CrossRef] [PubMed]
- Bartzanas, T.; Boulard, T.; Kittas, C. Effect of Vent Arrangement on Windward Ventilation of a Tunnel Greenhouse. Biosyst. Eng. 2004, 88, 479–490. [Google Scholar] [CrossRef]
- Ould Khaoua, S.A.; Bournet, P.E.; Migeon, C.; Boulard, T.; Chassériaux, G. Analysis of Greenhouse Ventilation Efficiency Based on Computational Fluid Dynamics. Biosyst. Eng. 2006, 95, 83–98. [Google Scholar] [CrossRef]
- Saberian, A.; Sajadiye, S.M. The Effect of Dynamic Solar Heat Load on the Greenhouse Microclimate Using CFD Simulation. Renew. Energy 2019, 138, 722–737. [Google Scholar] [CrossRef]
- Liu, R.; Liu, J.; Liu, H.; Yang, X.; Bárcena, J.F.B.; Li, M. A 3-D Simulation of Leaf Condensation on Cucumber Canopy in a Solar Greenhouse. Biosyst. Eng. 2021, 210, 310–329. [Google Scholar] [CrossRef]
- Tong, G.; Christopher, D.M.; Zhang, G. New Insights on Span Selection for Chinese Solar Greenhouses Using CFD. Comput. Electron. Agric. 2018, 149, 3–15. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Jiang, L.; Wang, Y.; Liu, X.; Li, T. A Systematic Analysis of Multiple Structural Parameters of Chinese Solar Greenhouse Based on the Thermal Performance. Energy 2023, 273, 127193. [Google Scholar] [CrossRef]
- Fatnassi, H.; Bournet, P.E.; Boulard, T.; Roy, J.C.; Molina-Aiz, F.D.; Zaaboul, R. Use of Computational Fluid Dynamic Tools to Model the Coupling of Plant Canopy Activity and Climate in Greenhouses and Closed Plant Growth Systems: A Review. Biosyst. Eng. 2023, 230, 388–408. [Google Scholar] [CrossRef]
- Boulard, T.; Roy, J.C.; Pouillard, J.B.; Fatnassi, H.; Grisey, A. Modelling of Micrometeorology, Canopy Transpiration and Photosynthesis in a Closed Greenhouse Using Computational Fluid Dynamics. Biosyst. Eng. 2017, 158, 110–133. [Google Scholar] [CrossRef]
- Xiao, S.; Chai, H.; Shao, K.; Shen, M.; Wang, Q.; Wang, R.; Sui, Y.; Ma, Y. Image-Based Dynamic Quantification of Aboveground Structure of Sugar Beet in Field. Remote Sens. 2020, 12, 269. [Google Scholar] [CrossRef]
- Chen, B.; Shi, S.; Gong, W.; Zhang, Q.; Yang, J.; Du, L.; Sun, J.; Zhang, Z.; Song, S. Multispectral LiDAR Point Cloud Classification: A Two-Step Approach. Remote Sens. 2017, 9, 373. [Google Scholar] [CrossRef]
- Sultan Mahmud, M.; Zahid, A.; He, L.; Choi, D.; Krawczyk, G.; Zhu, H.; Heinemann, P. Development of a LiDAR-Guided Section-Based Tree Canopy Density Measurement System for Precision Spray Applications. Comput. Electron. Agric. 2021, 182, 106053. [Google Scholar] [CrossRef]
- Weiss, U.; Biber, P. Plant Detection and Mapping for Agricultural Robots Using a 3D LIDAR Sensor. Rob. Auton. Syst. 2011, 59, 265–273. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakabayashi, K.; Omasa, K. 3-D Modeling of Tomato Canopies Using a High-Resolution Portable Scanning Lidar for Extracting Structural Information. Sensors 2011, 11, 2166–2174. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.; Song, S.; Zhu, B.; Shi, S.; Li, F.; Cheng, X. Multi-Wavelength Canopy LiDAR for Remote Sensing of Vegetation: Design and System Performance. ISPRS J. Photogramm. Remote Sens. 2012, 69, 1–9. [Google Scholar] [CrossRef]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating Imaging Spectrometer Data: 3D Forest Modeling Based on LiDAR and in Situ Data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Bailey, B.N.; Mahaffee, W.F. Rapid Measurement of the Three-Dimensional Distribution of Leaf Orientation and the Leaf Angle Probability Density Function Using Terrestrial LiDAR Scanning. Remote Sens. Environ. 2017, 194, 63–76. [Google Scholar] [CrossRef]
- Omasa, K.; Ono, E.; Ishigami, Y.; Shimizu, Y.; Araki, Y. Plant Functional Remote Sensing and Smart Farming Applications. Int. J. Agric. Biol. Eng. 2022, 15, 1–6. [Google Scholar] [CrossRef]
- Xiao, S.; Ye, Y.; Fei, S.; Chen, H.; Zhang, B.; Li, Q.; Cai, Z.; Che, Y.; Wang, Q.; Ghafoor, A.Z.; et al. High-Throughput Calculation of Organ-Scale Traits with Reconstructed Accurate 3D Canopy Structures Using a UAV RGB Camera with an Advanced Cross-Circling Oblique Route. ISPRS J. Photogramm. Remote Sens. 2023, 201, 104–122. [Google Scholar] [CrossRef]
- Xiao, S.; Fei, S.; Ye, Y.; Xu, D.; Xie, Z.; Bi, K.; Guo, Y.; Li, B.; Zhang, R.; Ma, Y. 3D Reconstruction and Characterization of Cotton Bolls in Situ Based on UVA Technology. ISPRS J. Photogramm. Remote Sens. 2024, 209, 101–116. [Google Scholar] [CrossRef]
- Yu, G.; Zhang, S.; Li, S.; Zhang, M.; Benli, H.; Wang, Y. Numerical Investigation for Effects of Natural Light and Ventilation on 3D Tomato Body Heat Distribution in a Venlo Greenhouse. Inf. Process. Agric. 2023, 10, 535–546. [Google Scholar] [CrossRef]
- Gu, X.; Goto, E. Evaluation of Plant Canopy Microclimates with Realistic Plants in Plant Factories with Artificial Light Using a Computational Fluid Dynamics Model. Build. Environ. 2024, 264, 111876. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, D.; Lu, T.; Cao, L.; Ji, F.; Zhu, J.; Ma, Y. Quantification of Canopy Heterogeneity and Light Interception Difference within Greenhouse Cucumbers Based on Terrestrial Laser Scanning. Comput. Electron. Agric. 2025, 230, 109879. [Google Scholar] [CrossRef]
- Kichah, A.; Bournet, P.E.; Migeon, C.; Boulard, T. Corrigendum to “Measurement and CFD Simulation of Microclimate Characteristics and Transpiration of an Impatiens Pot Plant Crop in a Greenhouse” [Biosyst. Eng. 112 (1) (2012) 22–34]. Biosyst. Eng. 2012, 112, 252. [Google Scholar] [CrossRef]
- Majdoubi, H.; Boulard, T.; Fatnassi, H.; Bouirden, L. Airflow and Microclimate Patterns in a One-Hectare Canary Type Greenhouse: An Experimental and CFD Assisted Study. Agric. For. Meteorol. 2009, 149, 1050–1062. [Google Scholar] [CrossRef]
- Campen, J.B.; Bot, G.P.A. Determination of Greenhouse-Specific Aspects of Ventilation Using Three-Dimensional Computational Fluid Dynamics. Biosyst. Eng. 2003, 84, 69–77. [Google Scholar] [CrossRef]
- Nebbali, R.; Roy, J.C.; Boulard, T. Dynamic Simulation of the Distributed Radiative and Convective Climate within a Cropped Greenhouse. Renew. Energy 2012, 43, 111–129. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-Wave Radiation from Clear Skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Numerical Simulation of the Airflow and Temperature Distribution in a Tunnel Greenhouse Equipped with Insect-Proof Screen in the Openings. Comput. Electron. Agric. 2002, 34, 207–221. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Valera, D.L.; Álvarez, A.J.; Madueño, A. A Wind Tunnel Study of Airflow through Horticultural Crops: Determination of the Drag Coefficient. Biosyst. Eng. 2006, 93, 447–457. [Google Scholar] [CrossRef]
- Xu, D.; Henke, M.; Li, Y.; Zhang, Y.; Liu, A.; Liu, X.; Li, T. Optimal Design of Light Microclimate and Planting Strategy for Chinese Solar Greenhouses Using 3D Light Environment Simulations. Energy 2024, 302, 131805. [Google Scholar] [CrossRef]
- Zheng, S.; Cui, N.; Wei, X.; Wang, T.; Bai, Y.; Pei, D.; Fu, S.; Plauborg, F.; Jiao, P. Dynamics, Plant Physiological and Environmental Controls of Energy Exchange in a Grapevine Greenhouse in Northeast China. J. Hydrol. 2024, 637, 131395. [Google Scholar] [CrossRef]
- Baneshi, M.; Gonome, H.; Maruyama, S. Wide-Range Spectral Measurement of Radiative Properties of Commercial Greenhouse Covering Plastics and Their Impacts into the Energy Management in a Greenhouse. Energy 2020, 210, 118535. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, L.; Zhu, X.; He, B.; Chen, Y. Thermal Environment Model Construction of Chinese Solar Greenhouse Based on Temperature–Wave Interaction Theory. Energy Build. 2023, 279, 112648. [Google Scholar] [CrossRef]
- Li, Y.; Jian, Y.; Wang, S.; Liu, X.; Li, W.; Arıcı, M.; Zhang, L.; Li, W.; Cao, Y. Spatial Temperature Distribution and Ground Thermal Storage in the Plastic Greenhouse: An Experimental and Modeling Study. J. Energy Storage 2024, 77, 109938. [Google Scholar] [CrossRef]
- Mobtaker, H.G.; Ajabshirchi, Y.; Ranjbar, S.F.; Matloobi, M. Simulation of Thermal Performance of Solar Greenhouse in North-West of Iran: An Experimental Validation. Renew. Energy 2019, 135, 88–97. [Google Scholar] [CrossRef]
- Xu, K.; Guo, X.; He, J.; Yu, B.; Tan, J.; Guo, Y. A Study on Temperature Spatial Distribution of a Greenhouse under Solar Load with Considering Crop Transpiration and Optical Effects. Energy Convers. Manag. 2022, 254, 115277. [Google Scholar] [CrossRef]
- Mao, Q.; Li, H.; Ji, C.; Peng, Y.; Li, T. Experimental Study of Ambient Temperature and Humidity Distribution in Large Multi-Span Greenhouse Based on Different Crop Heights and Ventilation Conditions. Appl. Therm. Eng. 2024, 248, 123176. [Google Scholar] [CrossRef]
- Cui, H.; Wang, C.; Yu, S.; Xin, Z.; Liu, X.; Yuan, J. Two-Stage CFD Simulation of Droplet Deposition on Deformed Leaves of Cotton Canopy in Air-Assisted Spraying. Comput. Electron. Agric. 2024, 224, 109228. [Google Scholar] [CrossRef]






| Materials | Thickness (mm) | Density (kgm−3) | Specific Heat Capacity (J kg−1K−1) | Thermal Coefficient (Wm−1K−1) | Absorption Coefficient (m−1) | Scattering Coefficient (m−1) | Refractive Index |
|---|---|---|---|---|---|---|---|
| Air | - | 1.225 | 1006 | 0.02 | 0.15 | 0 | 1.0 |
| Brick wall | 350 | 1700 | 1050 | 0.81 | 0.5 | 0 | 1.2 |
| Polystyrene board | 80 | 50 | 1300 | 0.03 | 0.3 | 0 | 1.1 |
| Board | 60 | 550 | 2500 | 0.29 | 0.3 | 0 | 1.2 |
| Soil | - | 1860 | 1150 | 1.28 | 0.8 | 1.0 | 1.9 |
| Plastic film | 0.1 | 70 | 2300 | 0.19 | 0.1 | 0.3 | 1.2 |
| Heat preservation quilt | 40 | 950 | 1000 | 0.05 | 0.1 | 0 | 1.2 |
| Canopy | - | 1001 | 3300 | 0.4 | 0.6 | 0.1 | 1.5 |
| Greenhouse Models * | Total Number of Elements | Minimum Orthogonal Quality | Maximum Skewness | Average Minimum Air Temperature (°C) | |
|---|---|---|---|---|---|
| Coarse grid | a | 1,124,329 | 0.24 | 0.76 | 25.2 |
| b | 2,858,121 | 0.19 | 0.8 | 24.8 | |
| c | 53,676 | 0.23 | 0.78 | 24.9 | |
| d | 784,465 | 0.23 | 0.77 | 25.5 | |
| e | 1,058,893 | 0.21 | 0.79 | 25.8 | |
| Middle grid | a | 1,491,983 | 0.32 | 0.68 | 22.1 |
| b | 10,336,415 | 0.27 | 0.73 | 22.5 | |
| c | 96,911 | 0.34 | 0.66 | 22.3 | |
| d | 922,643 | 0.35 | 0.66 | 22.6 | |
| e | 1,544,039 | 0.29 | 0.72 | 22.5 | |
| Fine grid | a | 1,896,258 | 0.29 | 0.71 | 21.8 |
| b | 31,898,827 | 0.26 | 0.74 | 22.0 | |
| c | 128,674 | 0.29 | 0.7 | 22.1 | |
| d | 1,377,306 | 0.31 | 0.69 | 22.5 | |
| e | 2,021,265 | 0.25 | 0.75 | 22.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, M.; Xu, D.; Wang, Z.; Meng, L.; Wang, L.; Ma, Y.; Zhu, J.; Lv, C. Computational Fluid Dynamics Simulation and Quantification of Solar Greenhouse Temperature Based on Real Canopy Structure. Agronomy 2025, 15, 586. https://doi.org/10.3390/agronomy15030586
Hou M, Xu D, Wang Z, Meng L, Wang L, Ma Y, Zhu J, Lv C. Computational Fluid Dynamics Simulation and Quantification of Solar Greenhouse Temperature Based on Real Canopy Structure. Agronomy. 2025; 15(3):586. https://doi.org/10.3390/agronomy15030586
Chicago/Turabian StyleHou, Maolin, Demin Xu, Zhi Wang, Lei Meng, Liang Wang, Yuntao Ma, Jinyu Zhu, and Chunli Lv. 2025. "Computational Fluid Dynamics Simulation and Quantification of Solar Greenhouse Temperature Based on Real Canopy Structure" Agronomy 15, no. 3: 586. https://doi.org/10.3390/agronomy15030586
APA StyleHou, M., Xu, D., Wang, Z., Meng, L., Wang, L., Ma, Y., Zhu, J., & Lv, C. (2025). Computational Fluid Dynamics Simulation and Quantification of Solar Greenhouse Temperature Based on Real Canopy Structure. Agronomy, 15(3), 586. https://doi.org/10.3390/agronomy15030586







