Deep Reinforcement Learning-Based Cooperative Harvesting Strategy for Dual-Arm Robots in Apple Picking

Abstract

In the field of orchard harvesting, this study proposes a collaborative picking strategy for dual-arm robots, aiming to improve efficiency, reduce labor burden, and achieve precise automation. The strategy combines the Multi-Agent Proximal Policy Optimization (MAPPO) algorithm with the Multi-Objective Greedy Picking Strategy (MOGPS) algorithm. By centrally training the critic network and decentralizing the actor network, the robots can autonomously learn and precisely pick in a simulated environment. To address dynamic obstacle avoidance, a dynamic collision assessment strategy is proposed, and an improved MOGPS algorithm is used to consider the distribution of fruits and the complexity of the working environment, achieving adaptive path planning. Experimental results show that the MAPPO-MOGPS algorithm optimizes the picking path by 15.11%, with a picking success rate as high as 92.3% and an average picking error of only 0.014. Additionally, physical experiments in real-world settings demonstrate the algorithm’s practical effectiveness and generalization.

1. Introduction

With the tightening of the global agricultural labor market, the traditional labor-intensive agricultural operations can no longer meet the high-efficiency demands of modern agricultural production. The research and application of intelligent agricultural robot technology have become the key to agricultural modernization [1]. Among various agricultural picking environments, apple picking stands out as a challenging area for automation technology due to its strong seasonality, high labor demand, and complex working environment.

Zhao et al. [2] have developed a robotic device for apple picking, which consists of a manipulator, an end effector, and an image-based visual servo control system [3]. They have developed an apple recognition algorithm to achieve automatic detection and positioning during picking.

The motion control of dual-arm picking robots is more complex than that of a single mechanical arm [4]. In the field of robot path planning [5,6], numerous path planning algorithms have been introduced one after another [7,8]. For example, Shi et al. [9] proposed an obstacle avoidance path planning method for dual-arm robots, which introduces target probability bias and cost functions based on the Rapidly exploring Random Tree (RRT) algorithm [10] to reduce the randomness and blindness in the expansion process of the RRT algorithm. Long et al. [11] proposed a new motion planner named RRT*Smart-AD, which ensures that dual-arm robots can adapt to obstacle avoidance constraints and dynamic characteristics in dynamic environments. Zhang et al. [12] proposed a novel dual-arm robot obstacle avoidance strategy based on the Artificial Potential Field (APF) algorithm, which introduces an attractive function and a repulsive function to guide the movement of the mechanical arm towards the target object while avoiding obstacles [13]. These algorithms impose a significant computational burden in the complex picking environment of orchards, leading to insufficient real-time performance of the arm planning and difficulty in ensuring globally optimal paths. Additionally, the ability of these algorithms to process dynamic environmental information limits the effectiveness and reliability of the arm’s obstacle avoidance strategies.

Reinforcement learning is increasingly applied in the field of motion planning for dual-arm robots [14,15], enabling the learning of optimal behaviors to adapt to complex environments. James et al. [16] have employed the Deep Q-Network [17] to control the joint rotation of robot arms for grasping tasks. Prianto et al. [18] have utilized the Soft Actor-Critic (SAC) [19] method to plan the shortest paths for multiple robot arms. Ha et al. [20] have proposed the use of SAC for closed-loop decentralized planning of multiple robot arms. Zhao et al. [21] have applied Proximal Policy Optimization (PPO) [22] for cooperative planning of robot arms. The algorithm developed by Zhang et al. [23] integrates experience replay with shortest path constraints. Despite these methods enhancing adaptability and cooperative effects, their high computational cost limits their widespread application. Therefore, it is necessary to explore more efficient computational strategies to reduce resource consumption.

In unstructured environments of dense orchards, single-arm robots are often constrained by their inherent limitations in physical degrees of freedom and operational modes. When dealing with fruit clusters obscured by foliage or scenarios requiring simultaneous handling of multiple dispersed targets, they typically necessitate frequent repositioning and sequential operations to accomplish harvesting tasks. In contrast, dual-arm robots leverage their parallel processing capabilities in complex spaces to effectively overcome the limitations of single-arm systems in sequential harvesting, thereby significantly reducing the time required for individual fruit picking [24].

In this study, the underlying multi-agent coordination control employs the Multi-Agent Proximal Policy Optimization [25] algorithm, whose “centralized training with decentralized execution” framework is particularly suitable for dual robotic arm collaboration scenarios. Compared to fully distributed approaches, this framework leverages a centralized Critic network during the training phase to fully utilize global state information, effectively addressing non-stationarity issues in multi-agent environments and significantly enhancing the coordination and stability of policy learning. Meanwhile, in contrast to fully centralized methods, its decentralized execution mode ensures independent decision-making capability and scalability during real-world deployment, achieving an effective balance between sample efficiency and control performance.

At the top-level task allocation and path planning layer, we adopt an improved method based on Multi-Objective Greedy Policy Search [26]. This strategy conducts weighted evaluations of multiple objectives such as distance, obstacle distribution, and fruit density, enabling rapid generation of near-optimal task allocation schemes in dynamic environments [27]. Compared to swarm intelligence optimization methods like ant colony optimization [28] and genetic algorithms [29], the enhanced MOGPS algorithm leverages its single-step greedy selection mechanism and heuristic evaluation function to significantly reduce computational complexity while maintaining solution quality. This approach better aligns with the stringent real-time and computational efficiency requirements of fruit and vegetable harvesting tasks, effectively supporting the system’s online decision-making needs.

By hierarchically integrating MOGPS at the top level for macroscopic multi-objective optimization and path planning, the system’s global optimality is ensured. Concurrently, MAPPO operates at the bottom level, dedicated to executing local motion coordination and dynamic obstacle avoidance, thus establishing a closed-loop “global planning–local execution” mechanism. This collaborative paradigm effectively capitalizes on the strengths of both algorithms while mitigating their individual limitations, ultimately enhancing the intelligence and operational efficiency of the dual robotic arm system in complex agricultural settings.

This paper proposes a collaborative picking strategy for dual-arm robots in complex orchard environments, integrating the MAPPO [25] and MOGPS algorithms. The strategy enables the dual arms to autonomously perform precise picking through centralized training of the Critic network and distributed execution of the Actor network. To address dynamic obstacle avoidance during picking, a strategy for real-time monitoring and evaluation of collision risks is proposed [30], dynamically optimizing the picking path. The MOGPS algorithm considers the uneven distribution of fruit and the complexity of the working environment, dynamically allocating tasks and optimizing paths for the dual arms. Simulation experiments have verified the adaptability and path optimization capabilities of the MAPPO-MOGPS algorithm in a simulated apple picking environment. Additionally, experiments were conducted on the MAPPO-MOGPS algorithm in a real-world picking scenario, combined with a visual perception system [31], to validate its effectiveness.

2. Materials and Methods

To achieve efficient and safe dual-arm collaborative apple harvesting, this study designs an innovative strategy that integrates Multi-Agent Proximal Policy Optimization, a multi-objective greedy target selection mechanism, and a dynamic collision risk term. This section aims to outline the overall framework and the underlying rationale of the proposed methodology. Specifically, MAPPO serves as the underlying learning architecture, facilitating coordinated policy learning through parameter sharing between the agents. The multi-objective greedy selection mechanism is responsible for real-time task allocation and fruit target decision-making in complex environments. Meanwhile, the dynamic collision risk term is incorporated into the motion planning to explicitly avoid collisions between the arms and with environmental obstacles. Together, these components form a comprehensive decision-making system. By enabling real-time decision-making, the proposed approach enhances the coordination between the dual arms and their adaptability to dynamic environments.

2.1. MAPPO Algorithm

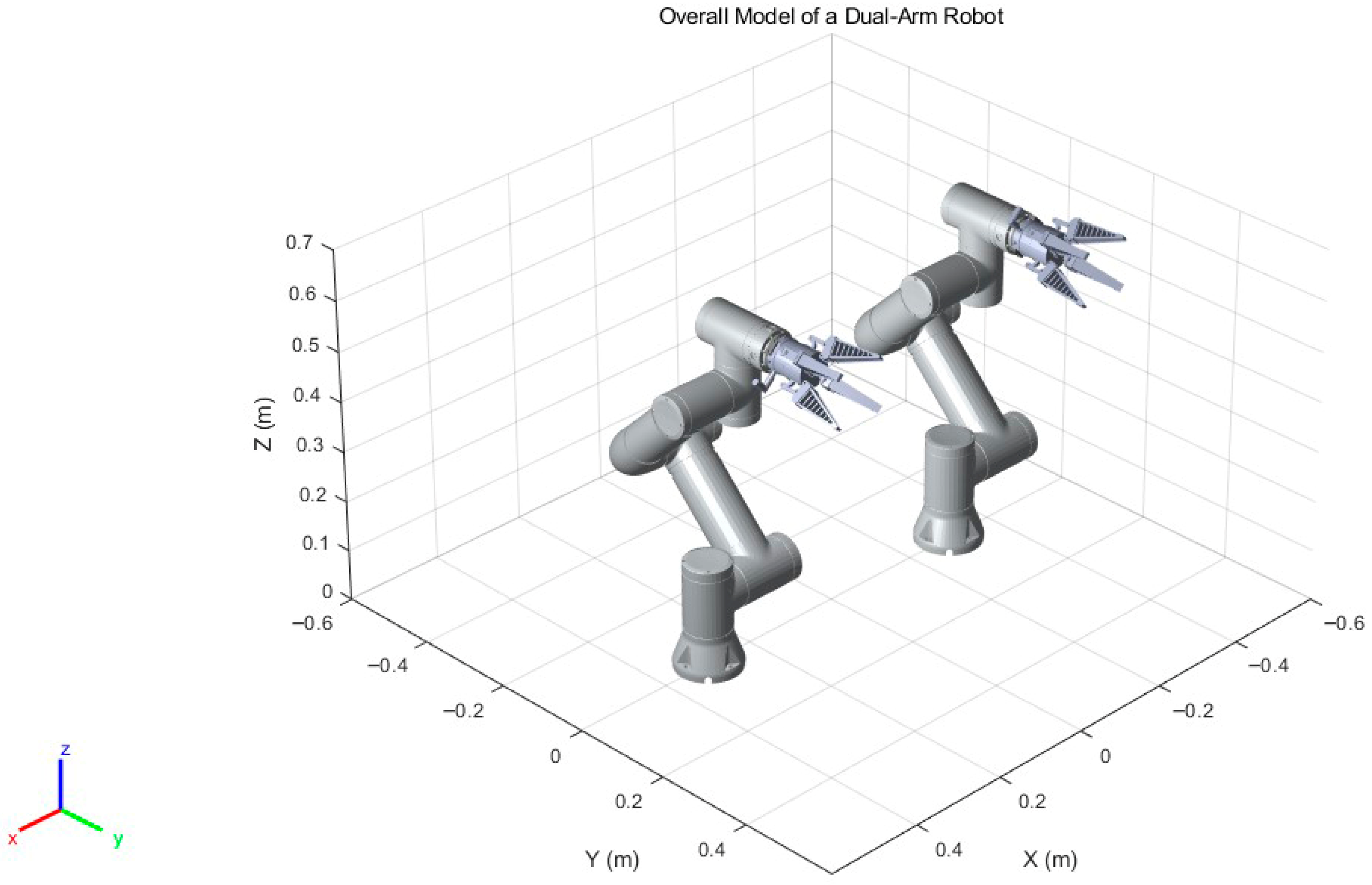
The PPO algorithm [32] is an on-policy reinforcement learning algorithm that stabilizes the learning process through trust region methods. Its policy update mechanism restricts the difference between the new and old policies, improving convergence and sample efficiency. MAPPO [22] is an extension of the PPO algorithm for multi-agent environments, adopting a centralized training with decentralized execution framework. Agents share information during training and make independent decisions during execution to achieve collaborative work. This study employs the Multi-Agent Proximal Policy Optimization (MAPPO) framework within a deep reinforcement learning context for a dual-arm apple harvesting robot. By jointly training the policy and value networks, we optimize the cooperative control strategy between the two arms, enabling enhanced collaborative performance. A physical simulation model of the robot developed for this research is presented in Figure 1.

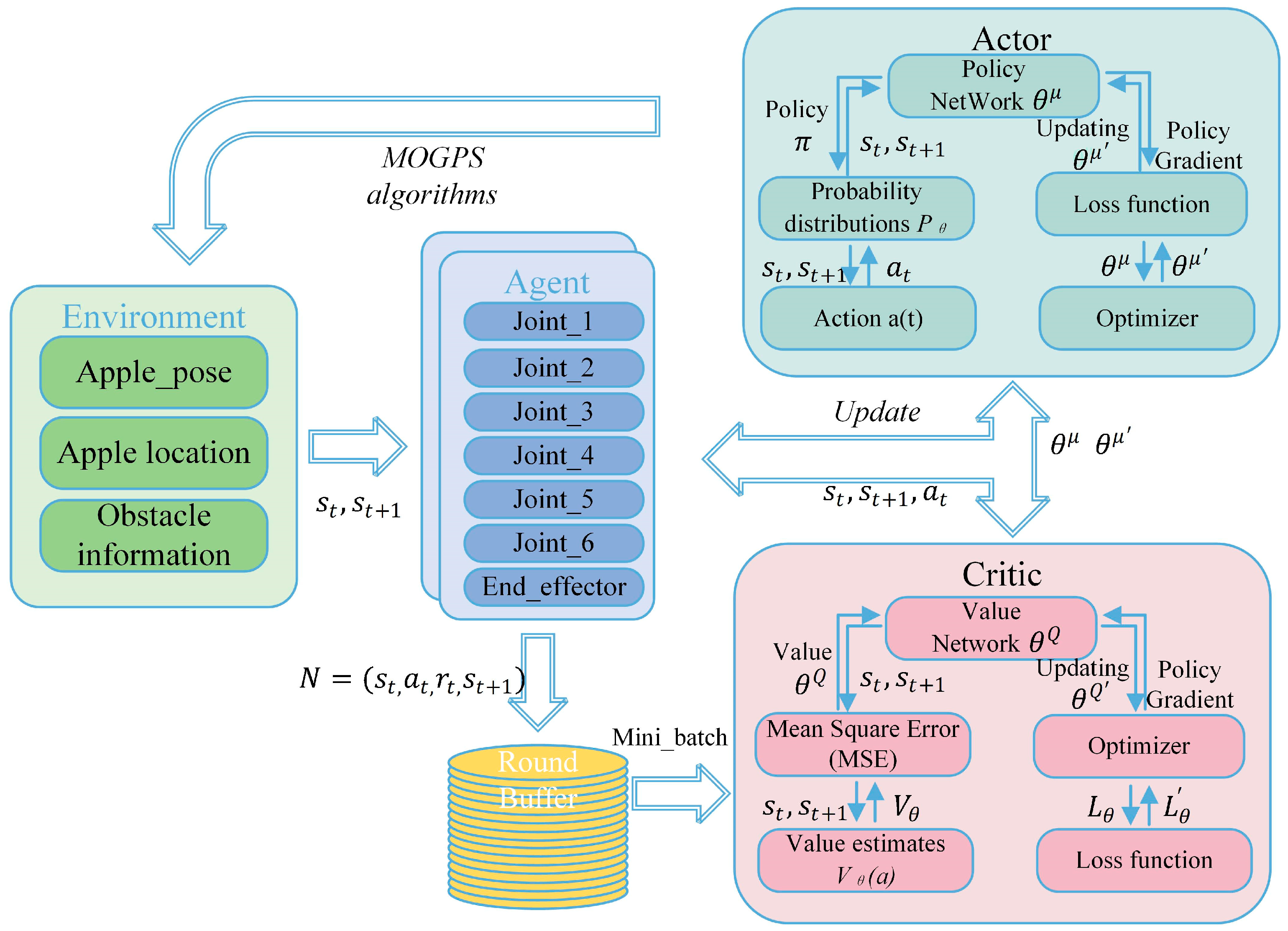
Within the MAPPO-MOGPS framework, the dual-arm picking robot system continuously monitors the operational environment to obtain the state $s_t$ of the target objects (such as apples, obstacles, etc.) at time $t$ as shown in Figure 2. This state consists of the position and orientation of the apples, as well as information about the obstacles. In the network architecture, two independent agents represent the left arm and the right arm, respectively. These agents read the joint state information of the dual-arm robot, denoted as ${joint}_t$, at time $t$, which includes joint coordinates, joint angles, and the coordinates and rotation pose of the end effector. Subsequently, the joint state information ${joint}_t$ is integrated into the environmental state $s_t$. Based on the current state information, the value $r_t$ of the actions produced is evaluated.

The dual-arm agent receives action commands $a_t$ from the Actor network and produces the next state $s_{t+1}$ through interaction with the environment. The experience tuple $N=\left(s_t,a_t,r_t,s_{t+1}\right)$ is stored in the round buffer. Meanwhile, the cumulative reward is used to calculate the return $r_t$ for each time step $t$ in the trajectory, and the Critic network is used to estimate the value function $V$ for each state $s_t$. The generalized advantage estimation function is shown in Equation (1).

$${A_i}^{\left(k\right)}={\sum }_{t=0}^{T-1}\gamma {\lambda }^t{{\delta }_i}^{(k+t)}$$

(1)

${{\delta }_i}^{(k+t)}$ is the temporal difference error for agent $i$ at time step $k$; $\gamma$ is the discount factor used to balance immediate rewards and future rewards. $\lambda$ is the hyperparameter of Generalized Advantage Estimation used to control the bias-variance trade-off in advantage estimation. The generalized advantage estimation function calculates the action advantage values and, by balancing the bias and variance in the estimation, provides stable and efficient directional guidance for the optimization of the policy network.

The advantage function of agent $i$ is used to calculate the target function of the Actor network. By computing the gradient of the policy loss, the Actor network is guided to update its parameters in the direction of gradient ascent. At the same time, the target function of the Critic network is calculated, and through the computation of the loss gradient, its parameters are optimized in the direction of gradient descent.

The optimization objective of the Actor network is:

$$\begin{gathered} L\left(\theta \right)=\left[{\displaystyle \frac{1}{Bn}}{\sum }_{i=1}^B{\sum }_{k=1}^{n}min\left(r_{\theta ,i}^{\left(k\right)}{A}_i^{\left(k\right)},Clip\left(r_{\theta ,i}^{\left(k\right)},1-\epsilon ,1+\epsilon \right)A_i^{\left(k\right)}\right) \\ +\sigma {\displaystyle \frac{1}{Bn}}{\sum }_{i=1}^B{\sum }_{k=1}^{n}S\left({\pi }_{\theta }\left(o_i^{\left(k\right)}\right)\right)\right] \end{gathered}$$

(2)

where $r_{\theta ,i}^{\left(k\right)}={\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{\theta old}\left(a_t|s_t\right)}}$ is the policy update ratio for agent $i$;$S$ represents the entropy parameter of the policy; $\sigma$ is the parameter used to control the entropy coefficient. $Clip\left(r_{\theta ,i}^{\left(k\right)},1-ϵ,1+ϵ\right)$ limits the magnitude of the policy update ratio $r_{\theta ,i}^{\left(k\right)}$, and $S\left({\pi }_{\theta }\left(o_i^{\left(k\right)}\right)\right)$ denotes the entropy of the policy ${\pi }_{\theta }$ under the observation $o_i^{\left(k\right)}$. $Bn$ denotes the number of batches.

The optimization objective of the Critic network is:

$$L\left(\phi \right)={\displaystyle \frac{1}{Bn}}{\sum }_{i=1}^B{\sum }_{k=1}^{N}max\left[{\left(V_{\phi }\left(s_i^{\left(k\right)}\right)-{\widehat{R}}_i\right)}^2,{\left(Clip\left(V_{\phi }\left(s_i^{\left(k\right)}\right),V_{\phi old}\left(s_i^{\left(k\right)}\right)-\epsilon ,V_{\phi old}\left(s_i^{\left(k\right)}\right)+\epsilon \right)-{\widehat{R}}_i\right)}^2\right]$$

(3)

where ${\widehat{R}}_i$ is the discounted reward. $B$ represents the size of the batch size; $V_{\phi }\left(s_i^{\left(k\right)}\right)$ is the state-value function, which is used to estimate the expected return of state $s_i^{\left(k\right)}$.

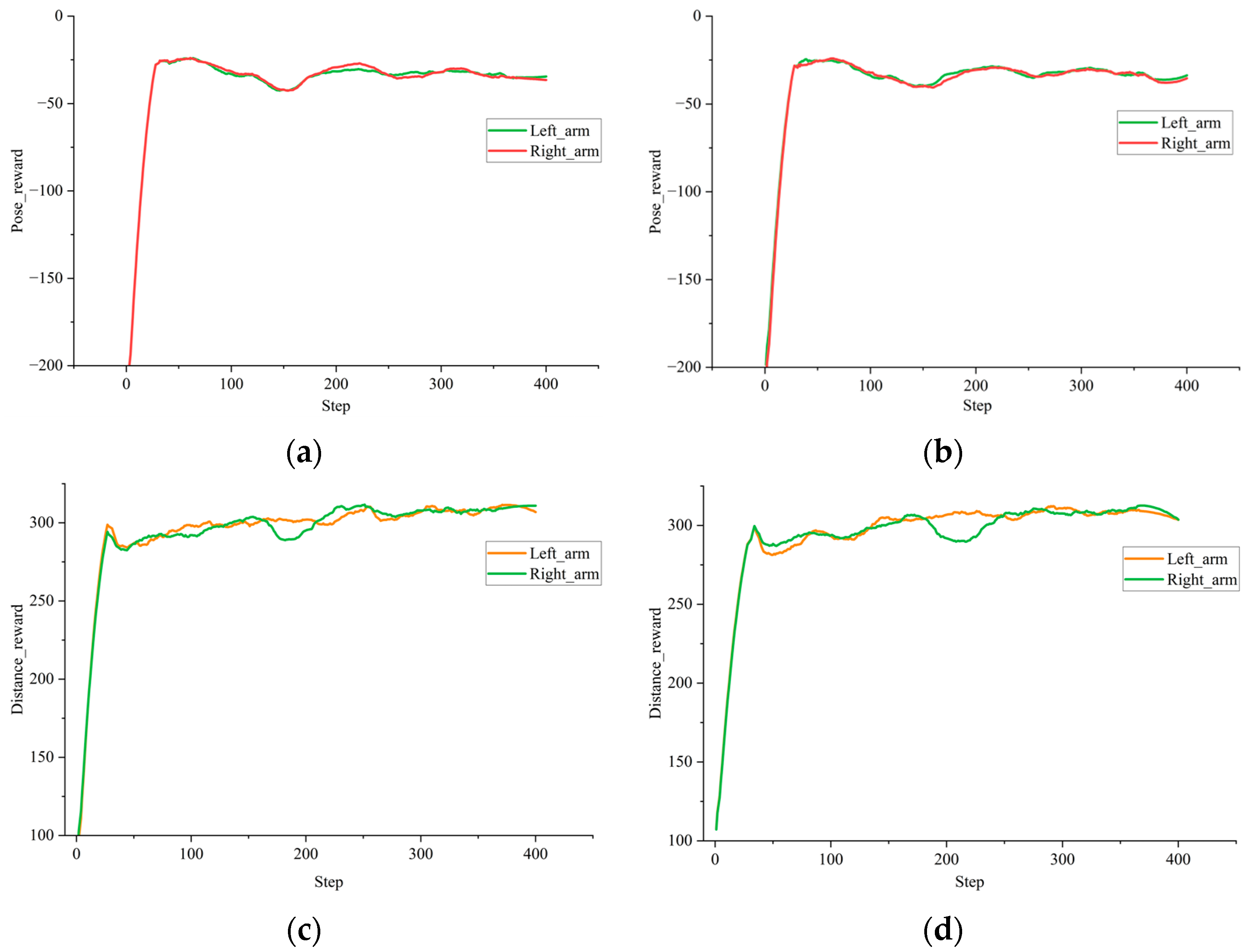
The two agents that make up the dual-arm picking robot system are isomorphic; they share a set of network parameters, forming a compact agent model. Based on this, the dual-arm agent undergoes coordinated training through the policy network and the value function network to achieve synchronized decision-making and action execution. The parameter sharing mechanism promotes policy consistency between the dual-arm agents, and through the iteration of picking strategies between the arms, it enhances the collective learning efficacy and action coordination of the dual-arm robot picking system.

2.2. Dual-Arm Dynamic Collision Assessment Strategy

In the complex orchard picking environment, the dual-arm picking robot system has extremely stringent requirements for obstacle avoidance precision during picking operations. To address the dynamic obstacle avoidance between the two arms during the operation of the dual-arm robot, as well as the static obstacle avoidance with branch obstacles, a dual-arm dynamic collision assessment strategy (DDC) based on the MAPPO reinforcement learning framework is proposed. By kinematically modeling the joints of the dual arms and real-time detecting and evaluating the risk of collision between the arms, the obstacle avoidance picking path of the dual-arm robot is optimized.

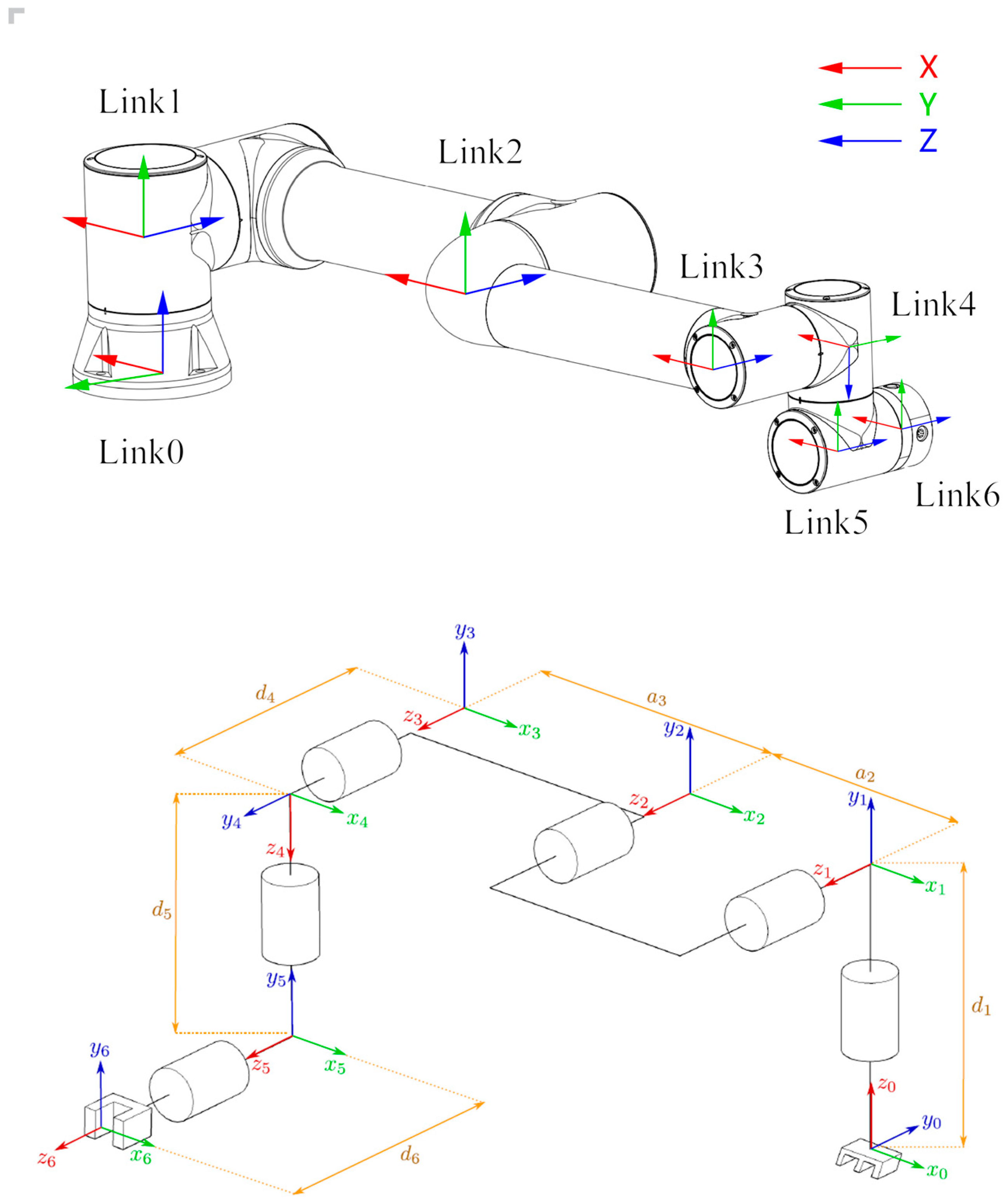
By using the DH modeling parameters as shown in

Table 1. DH Modeling Parameters.

Kinematics	θ (rad)	A (m)	D (m)	A (rad)	Mass (kg)
Joint 1	0	0	0.152	π/2	4.64
Joint 2	0	−0.425	0	0	10.08
Joint 3	0	−0.395	0	0	2.71
Joint 4	0	0	0.102	π/2	1.56
Joint 5	0	0	0.102	−π/2	1.56
Joint 6	0	0	0.100	0	0.36

, the transformation matrix for joint coordinates is constructed as shown in Figure 3, calculating the positions and orientations between each joint of the dual-arm robot as shown in Equation (4). Through the kinematic analysis of these parameters, a series of homogeneous transformation matrices are obtained to describe the entire motion chain of the robot from the base to the end effector.

$$T_i^{i+1}=\left(\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_i& 0& a_{i-1}\\ sin{\theta }_{i}cos{\alpha }_{i-1}& cos{\theta }_{i}cos{\alpha }_{i-1}& -sin{\alpha }_{i-1}& -sin{\alpha }_{i-1}{d}_i\\ sin{\theta }_{i}sin{\alpha }_{i-1}& cos{\theta }_{i}sin{\alpha }_{i-1}& cos{\alpha }_{i-1}& cos{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right)$$

(4)

In the DH parameters, $\theta$, $a$, $d$, and $\alpha$ denote the joint angle, link length, joint distance, and link twist angle, respectively.

Based on the kinematic analysis of the aforementioned dual-arm picking robot, a dual-arm dynamic obstacle avoidance assessment strategy is introduced. By analyzing the Euclidean distance between the robot’s end effector and the apples, as well as between the joints of the dual arms, the collision risk value is calculated to evaluate the robot’s action decisions in real-time as shown in Equation (10), and accordingly, the reward distribution is dynamically adjusted.

Based on the dynamic model of the dual-arm robot and the picking environment model, the collision risk for apple picking is calculated by predicting future states. Obtain the current state $s_t$ of the dual-arm robot (joint angles, angular velocities, angular accelerations) and the state of the environment (the positions of apples and branches), and predict the future state $s_{t+1}$ after the dual-arm performs the action $a_t$ by using the state transition model $P=\left(s_{t+1}|s_t,a_t\right)$. After obtaining the future joint states of the dual-arm robot, the potential for dynamic collisions between the arms and obstacles, as well as between the joints of the dual arms, is assessed based on the distances between them. In the MAPPO network, the expected collision risk $Ecrt$ is calculated based on real-time predictions of future states and collision detection results. 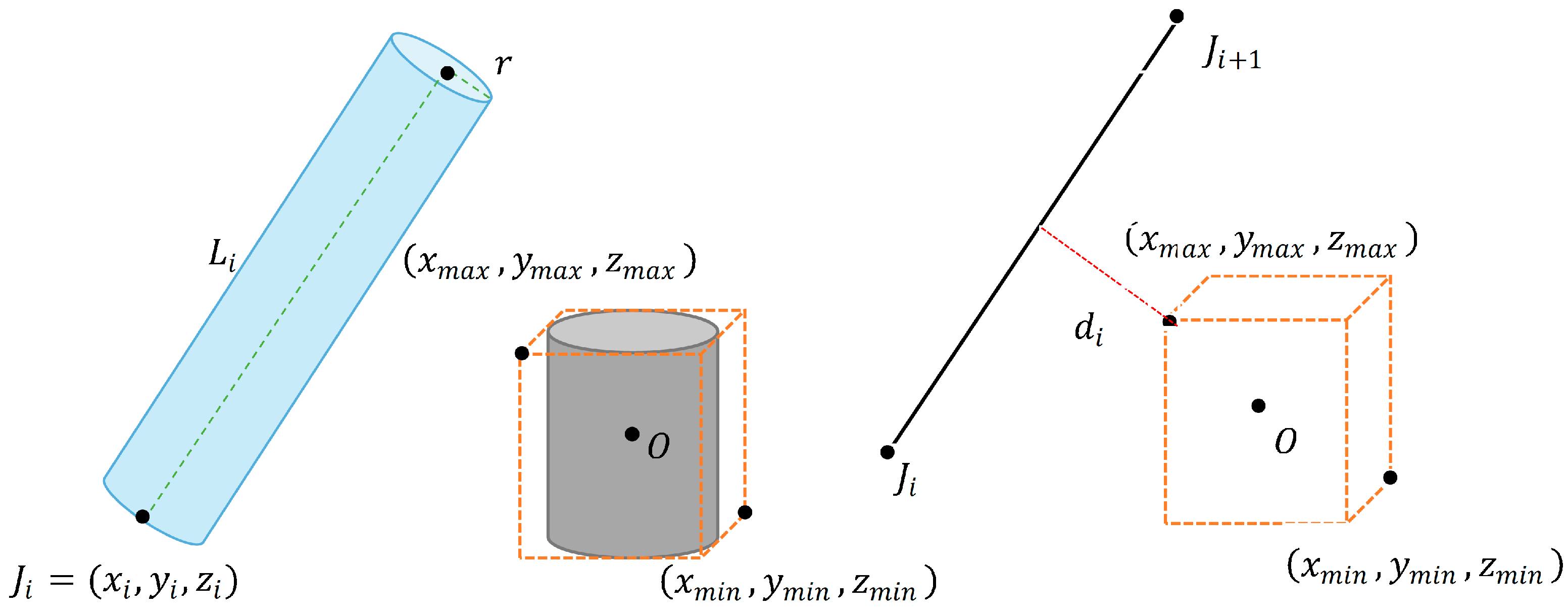As shown in Figure 4, for the sake of description, obstacles are defined as:

$$obstacle\left[\left(x_{min},y_{min},z_{min}\right)\le \left(x,y,z\right)\le \left(x_{max},y_{max},z_{max}\right)\right]$$

(5)

In collision detection algorithms, an axis-aligned bounding box model is employed to approximate obstacles for improved computational efficiency. This cuboid is uniquely defined by its minimum and maximum corner coordinates, which simplifies subsequent calculations

At time step $t$, the coordinate of the robot arm joint ${Link}_i$ is $P_i=\left(x_i,y_i,z_i\right)$, and the closest point between the robot arm and the obstacle is $P_{min}=\left(x_o,y_o,z_o\right)$. Then the direction vector of joint $i$ of the robot arm $\stackrel{⃑}{OD}$ is:

$$\stackrel{⃑}{OD}=P_{i+1}-P_i=\left({x_{i+1}-x}_i,{y_{i+1}-y}_i,z_{i+1}-z_i\right)$$

(6)

The vector from the nearest point of the tree branch obstacle $P_{min}$ to the robot arm joint ${Link}_i$ is:

$$\stackrel{⃑}{V}=P_{min}-P_i=\left({x_0-x}_i,{y_0-y}_i,z_0-z_i\right)$$

(7)

The shortest distance from an obstacle to joint $i$ of the robotic arm can be represented as $d_{min}$, which corresponds to the perpendicular component of the projection of vector $\stackrel{⃑}{V}$ onto the direction of $\stackrel{⃑}{OD}$.

$$d_{min}={\displaystyle \frac{\left|\stackrel{⃑}{V}\times \stackrel{⃑}{OD}\right|}{\left|\stackrel{⃑}{OD}\right|}}$$

(8)

Calculate the Euclidean distance between the coordinates of each joint of the dual arms, where $d_{ij}$ represents the Euclidean distance between the coordinate of the $i$ joint of the left arm and the $j$ joint of the right arm, and compute the potential collision risk between the joints of the dual arms.

$$d_{min}^{\prime }=min\left(d_{11},d_{12},\dots d_{ij}\right)$$

(9)

$$Ecrt=m·e^{-n\left(d_{min}\right)}$$

(10)

$Ecrt$ represents the Expected Collision Risk at time step $t$, which has an exponential relationship with the distance between the robot arm and the obstacle. The coefficient $m$ is used to limit the collision risk threshold:

$$R=R_t-\mu m·e^{-n\left(d_{min}\right)}$$

(11)

$\mu$ is a coefficient used to adjust the impact of the collision risk assessment on the total reward. This formula indicates that the reward function $R$ depends not only on the task completion status $R_t$ but also on the collision risk assessment $Ecrt$ based on the robot’s current state. Dynamically adjust the reward function based on the collision risk assessment $Ecrt$, so that the robot can optimize the obstacle-avoiding picking path during the harvesting process.

2.3. Multi-Target Dynamic Allocation Strategy

In the process of task allocation for dual-arm robots performing apple picking tasks in multi-target operational areas, it is necessary to consider the non-uniformity of fruit distribution within the dual-arm picking robot’s operational unit and the heterogeneity of the complexity of the working environment. Based on the greedy algorithm, a Multi-Objective Greedy Picking Strategy is proposed. This strategy divides the picking domain of the dual-arm robot into separate working areas and collaborative working areas. Within the independent working space, the objective function of the algorithm includes multiple dimensions. When determining the order of apple picking, various factors such as picking distance, obstacle influence, and the spatial distribution of the fruit are comprehensively considered.

The position of the robotic arm’s end effector in the world coordinate system is $P_e^k=\left(x_e^k,y_e^k,z_e^k\right)$, and the position of the $i$th apple in the world coordinate system is $P_i^k=\left(x_i^k,y_i^k,z_i^k\right)$. The calculation formula for the picking distance $D_i^k$ is:

$$D_i^k={\sum }_{i=1}^N\sqrt{{\left({x_e}^k-x_i^k\right)}^2+{\left({y_e}^k-y_i^k\right)}^2+{\left({z_e}^k-z_i^k\right)}^2}$$

(12)

By using the vector directional projection analysis method, the occupation ratio of obstacles on the projection interface in the direction of the projection vector is quantified to assess the obstacle-free degree of the path from the end effector of the dual-arm manipulator to the target fruit. When formulating the obstacle avoidance strategy $f_o$, priority should be given to maximizing the efficiency of obstacle avoidance to ensure the optimization of the picking path and the safety of the operation as shown in Equation (13).

$$f_o={\sum }_{i=1}^N{\displaystyle \frac{S_{obstacle}}{S_i}}$$

(13)

$S_{obstacle}$ represents the projected area of an obstacle on the projection plane in a specific projection direction $i$, and $S_i$ represents the total area of the projection plane.

Accurately analyze the distribution pattern of apples within the workspace, calculate the apple density in the space, and determine the picking priority of different areas based on the calculation results. This allows the dual-arm picking robot to prioritize visiting areas with high fruit density, reducing the empty travel distance of picking and enhancing the efficiency of path planning and resource utilization in the overall picking operation.

$${\rho }_i={\displaystyle \frac{N_i}{V_i}}$$

(14)

where ${\rho }_i$ represents the fruit density in the $i$th region, $N_i$ indicates the number of fruits within that region, and $V_i$ represents the volume of the region.

To integrate three distinct metrics of different dimensions distance, obstacle avoidance strategy, and density into a unified score for target ranking, a weighted summation method is employed to calculate the comprehensive score $G_i$ for each potential target $i$, as shown in Equation (15).

$$G_i=w_D·\widetilde{D_i^k}-w_f·f_o+w_{\rho }·\widetilde{{\rho }_i}$$

(15)

$\widetilde{D_i^k}$ and $\widetilde{{\rho }_i}$ represent the Min–Max normalized values of distance and density, respectively, while $w_D$, $w_f$, and $w_{\rho }$ denote the weight coefficients, satisfying $w_D{{+w}_f+w}_{\rho }=1$. The determination of the weight coefficients is based on task priority: in this work, priority is given to ensuring operational safety and efficiency. Therefore, parameter tuning was conducted through grid search, resulting in the final assignment of $w_D=0.5$, $w_f=0.3$, and $w_{\rho }=0.2$.

Under the multi-objective greedy grasping strategy, the dual-arm robot determines the grasping priority for spatially non-uniformly distributed apples based on their comprehensive scores $G_i$. As illustrated in Figure 5, targets located within the shared workspace of both arms are dynamically assigned to either the left or right arm for execution. The specific allocation rule is as follows: for the same target, the comprehensive scores derived from its interaction models with the left and right arms are compared, and the arm with the higher score is granted the grasping privilege for that target.

In summary, this study establishes a hierarchical decision-making system for dual-arm apple harvesting. The system comprises three core components: First, at the perception and decision-making layer, the Multi-Objective Greedy Picking Strategy Selection Mechanism comprehensively evaluates fruit spatial distribution, path length, and occlusion status to generate an optimal target assignment sequence. Subsequently, this command is transmitted to the control and execution layer, where the MAPPO algorithm, leveraging parameter sharing, decodes the abstract goals into specific joint control strategies for the dual-arm agents, accomplishing dynamic grasping tasks. Finally, the Dynamic Collision Risk Term is embedded into the motion planning process as an independent safety layer, enabling real-time trajectory adjustment through continuous risk assessment to achieve proactive obstacle avoidance. Collectively, these components ensure the high efficiency and robustness of the dual-arm apple harvesting operation.

3. Simulation

To accurately simulate the performance of the harvesting algorithm in real-world scenarios, this study established apple tree models with varying branch density levels based on the spatial distribution characteristics of branches under natural growth conditions, as shown in Figure 6. In the simulation environment, by incorporating the collision volume of branches, the occlusion and interference caused by apple branches to the robotic arm’s movement during actual harvesting were effectively simulated. This modeling approach enhances the realism of the simulation environment and the reliability of algorithm testing, while also providing a more physically authentic scenario for reinforcement learning training that closely resembles real harvesting tasks.

3.1. MAPPO- MOGPS Algorithm Simulation

In the simulation experiments, a dual-arm robotic harvesting system with six degrees of freedom was modeled within the PyBullet physics simulation platform. To more closely replicate real-world harvesting and grasping conditions, apple tree models exhibiting different canopy densities were incorporated into the simulated environment. A series of simulations were performed to assess the obstacle avoidance capacity and trajectory optimization effectiveness of the MAPPO-MOGPS algorithm during delicate picking operations carried out by the dual-arm robot. The experimental setup for the dual-arm harvesting and grasping tasks in the PyBullet simulation environment is illustrated in Figure 7.

Based on systematic tuning conducted in a simulation environment, this section identifies the key hyperparameters of the MAPPO-MOGPS algorithm during the centralized training phase to ensure a balance among learning stability, sample efficiency, and performance in dual-arm harvesting tasks. The finalized hyperparameter configuration is detailed in

Table 2. MAPPO-MOGPS Algorithm Training Hyperparameters.

Hyperparameter	MAPPO-MOGPS
Hidden layer size	128
Number of hidden layers	2
Learning rate	3 × 10−4
Cropping parameters	0.2
Discount factor	0.99
GAE Parameter	0.95
Entropy coefficient	0.005
Steps	16 × 107
Episode length	200
Number of parallel environments	16

.

The dual-arm robot was trained for apple picking tasks using the MAPPO-MOGPS algorithm. The experimental results, as shown in Figure 8, indicate that the distance reward quickly converges at step 3 × 10⁶ of the training, with a convergence value of about 300. This value reflects the distance reward between the robot’s end effector and the target apple. Meanwhile, the pose reward shows a trend of convergence after about 2.1 × 10⁶ iterations, with a convergence value of approximately −32. The reward function measures the relative pose between the end effector and the picking target point. The training results demonstrate enhanced distance reward and pose reward for the dual-arm picking robot in terms of target approaching efficiency and pose stability. The adaptability and motion planning capabilities of the dual-arm agent in complex picking environments have been improved.

3.2. Ablation Experiment

In the same simulation environment, a comparison was made between the MAPPO-MOGPS integrated with the MOGPS algorithm, the MAPPO-PSO using the Particle Swarm Optimization algorithm, and the experiment using only the basic MAPPO framework to evaluate the differences in the path optimization performance of these algorithms for a dual-arm six-degree-of-freedom picking robot, as shown in Figure 9.

This study systematically designed harvesting experiments under different fruit density conditions. First, 0–20 apples were randomly generated within 0–30 cm from the end of the fruit tree branches to simulate the spatial distribution randomness of apples under natural growth conditions. Based on this setup, 40 experimental trials were conducted to evaluate the basic performance of the three algorithms. Subsequently, the number of fruits was further divided into four density gradients (low, medium-low, medium-high, and high density), and 50 extended experiments were carried out to thoroughly investigate the influence of fruit quantity on algorithm performance.

As shown in

Table 3. Confidence Interval Analysis of Multi-Objective Path Algorithms Under Different Apple Densities.

Growth Density	Apple Count $\mathit{i}/{\mathbf{m}}^3$	Path Length 95% Confidence Interval (m)			Optimization
		MAPPO	MAPPO- PSO	MAPPO- MOGPS
Low	$0<i\le 5$	[2.5, 3.47]	[2.25, 3.04]	[2.16, 2.91]	4.25%
Medium-Low	$5<i\le 10$	[8.20, 9.46]	[6.78, 7.96]	[6.52, 7.24]	6.68%
Medium-High	$10<i\le 15$	[14.28, 15.62]	[11.76, 12.98]	[10.38, 11.05]	13.37%
High	$15<i\le 20$	[21.25, 25.23]	[16.66, 18.29]	[14.10, 15.56]	15.11%

, under low-density picking conditions, the path planning performance of the MAPPO, MAPPO-PSO, and MAPPO-MOGPS algorithms is comparable, with no statistically significant differences observed in the trajectory lengths of the dual robotic arms. The t-test results on the optimization rates across different density samples indicate that the MAPPO-MOGPS offers only limited improvement under these conditions, with an average enhancement of 4.25%. Although this improvement is statistically significant $(p=0.0077)$, its practical impact remains modest. As the fruit density increases, the MAPPO-MOGPS algorithm demonstrates superior performance. By comprehensively considering the spatial distribution of apples, branch collision constraints, and the Euclidean distance between the end-effector and the fruits, this algorithm achieves more efficient coordinated path planning for dual arms. Its path optimization performance shows a 15.11% improvement over the PSO algorithm, and this difference is highly statistically significant $(p<0.0001)$, indicating the substantial optimization capability of this strategy in complex picking environments. The experimental results confirm that the MAPPO-MOGPS algorithm can adapt to varying operational density conditions and effectively coordinate the motion trajectories of dual robotic arms in complex harvesting scenarios, thereby enhancing operational efficiency and obstacle avoidance capability.

By conducting ablation experiments on the MAPPO algorithm combined with the Dual-arm Dynamic Collision assessment function (DDC) and the MOGPS, a quantitative analysis of the differences in the obstacle avoidance capability and multi-target path optimization capability of the independently developed MAPPO-MOGPS algorithm was performed. The comprehensive evaluation of the MAPPO algorithm’s obstacle avoidance efficiency in complex environments and its path planning optimization capability in handling multi-target picking tasks was conducted.

As shown in the experimental data in

Table 4. Comparison of Algorithm Ablation Test Data.

Algorithms	DDC	MOGPS	Times	Success Rate
MAPPO	×	×	10	83.1%
	√	×	10	91.2%
	×	√	10	81.5%
	√	√	10	92.3%

, by integrating the MAPPO algorithm, the dual-arm dynamic obstacle avoidance strategy, and the MOGPS path planning strategy, the system’s operational success rate in harvesting tasks increased to 92.3%, with a significant enhancement in overall picking performance. In the comparative experiments, after removing the dual-arm dynamic obstacle avoidance strategy, the lack of dynamic collision constraints in the system led to frequent physical interference between the robotic arms and branches during simulated picking. This resulted in markedly reduced obstacle avoidance capability and an inability to perform real-time collision detection and response, ultimately causing the success rate to drop to 81.5%. In the experimental group without the MOGPS, the system exhibited deficiencies in dual-arm coordinated path planning, as evidenced by an increased average picking path length and reduced motion efficiency, which further compromised overall task performance.

3.3. Comparative Experiment

In this study, the hyperparameter configuration of the MAPPO algorithm in the simulation environment was adopted as the baseline, as outlined in Table 2. To ensure a fair comparison among the algorithms, both SAC and MADDPG followed the same key hyperparameter settings from this baseline during the centralized training phase under identical simulation conditions. A systematic comparison was conducted between MAPPO-MOGPS and the mainstream reinforcement learning algorithms SAC and MADDPG by evaluating three key metrics in the dual-arm apple grasping task: success rate, collision rate, and average error. A successful grasp was defined based on the opening and closing angle of the end-effector, with the specific criterion that if the positional deviation between the geometric center of the apple and that of the end-effector was less than 2 cm, the grasp was considered successful; otherwise, it was recorded as a failure. A collision was identified when the distance between the robotic arm and any obstacle surface was less than 2 mm.

The data results indicate that the MAPPO-MOGPS algorithm has demonstrated outstanding performance in the dual-arm robot picking tasks. As shown in

Table 5. Comparative Analysis of Multi-Agent Algorithm Performance in 1000 Episodes of Picking Trials.

Algorithms	Success Rate	Collision Rate	Average Error (m)
MAPPO-MOGPS	92.3%	5.42%	0.0146
SAC	87.52%	8.37%	0.0177
MADDPG	83.21%	14.64%	0.0188

, the dual-arm picking robot achieved a picking success rate of 92.3%, a collision rate of 5.42%, and an average error of 0.0146. Compared to the SAC and MADDPG algorithms, it showed advantages in terms of success rate, safety, and precision, verifying the efficiency and reliability of the MAPPO-MOGPS algorithm in complex environmental multi-target picking operations.

4. Experiment

To validate the transferability and effectiveness of the MAPPO-MOGPS from simulation to real-world scenarios after training, this study constructed a dual-arm robotic picking experimental platform. The core hardware configuration of the platform consists of two 6-DOF collaborative robotic arms (Fr3) and an Intel RealSense D455 depth camera. The specific parameters of these components are provided in

Table 6. Detailed Hardware Specifications of the Dual-Arm Apple Harvesting Robot.

Robot Parameters
Dual-Arm Parameters	Maximum working radius	0.62 m
	Joint maximum speed	180°/s
	Repeat positioning accuracy	±0.02 mm
	Maximum load weight	3 kg
End Effector	Drive mode	Servo Drive
	Maximum opening angle	135°
	Maximum Blessing Power	7 N
RealSense D455 Camera	Depth resolution	1280 × 720
	RGB resolution	1280 × 800
	Depth Frame Rate	90 Fps
	RGB Frame Rate	30 Fps
	Depth measurement range	87° × 58°
	Measurement range	0.6 m–6 m

. In this setup, the robotic arms serve as the actuators, while the depth camera is responsible for environmental perception and target localization. The software system is built on the Robot Operating System framework, integrating modules for visual perception, pose estimation, motion planning, and control, which achieves a complete closed loop for the algorithm from simulation to physical hardware. Furthermore, to minimize damage to the fruit during the picking process, the end-effector employs an adaptive gripper featuring compliant gripping characteristics.

To accurately identify apple targets and obtain their spatial pose information, this study employs a depth camera to capture RGB images of apples and trains a model on the image dataset based on an improved YOLO 11s neural network architecture. Examples of the training data are shown in Figure 10. This system integrates the SCH-YOLO11s [31] instance segmentation network to achieve simultaneous segmentation of the apple body and the calyx region. The network incorporates several structural improvements: embedding the C3k2_SimAM module to enhance feature extraction capabilities, using the CMUNeXt module to replace standard convolution operations in the backbone network to improve the model’s expressive efficiency, and fusing a Histogram Transformer (HTB) into the C2PSA module, thereby enhancing its adaptability to complex textures and lighting variations.

After obtaining the segmentation results, the 3D center point of the apple’s main body is fitted using the least squares method based on its point cloud data. Simultaneously, the geometric center of the calyx region is calculated by averaging its point cloud data. The spatial vector connecting the fruit center and the calyx center is then used to define the apple’s growth axis, which in turn determines its orientation and pose. The final, complete pose data output provides a precise input for subsequent robotic arm grasping path planning.

The evaluation of the SCH-YOLO11s model on an apple dataset demonstrates excellent performance. For the segmentation tasks, it achieved mean Average Precision of 97.1% for sound apples and 94.7% for their calyxes. Furthermore, in the vision-based pose estimation task, the model also exhibited high accuracy, with a mean angular error of 12.3° calculated over 100 independent tests.

To determine the relative pose of the apple in the dual-arm robot base frame, this study employs a hand-eye calibration method to establish the transformation relationship between the depth camera coordinate system and the robot base coordinate system. During the calibration process, a checkerboard calibration plate is attached to the robot end-effector, and the robot is controlled to assume multiple distinct poses. At each pose, stereo images are captured synchronously while the corresponding end-effector pose data in the base frame is recorded. Under the Eye-to-Hand configuration, the pose of the calibration plate in the camera coordinate system at each position is obtained through image processing. Based on multiple pose correspondences, a transformation matrix comprising rotation and translation is solved, which defines the fixed spatial transformation from the camera coordinate system to the robot base coordinate system. After calibration, this matrix enables accurate conversion of the apple’s initial pose measured in the camera coordinate system to the robot base coordinate system, thereby obtaining its three-dimensional position and orientation in the robot world coordinate system and providing a precise target localization basis for subsequent grasping tasks.

During the harvesting process, collaborative optimization of multi-target apple picking paths is achieved using the MAPPO-MOGPS algorithm. In this study, based on the acquired 3D pose information of the apples, a multi-objective optimization function is constructed, which integrates Euclidean distance, spatial distribution density, and the degree of occlusion by obstacles.

For quantitative evaluation, a spatial grid modeling method is employed to process the 3D poses of the identified apples. By extracting the coordinate extrema of each apple along the X, Y, and Z axes, a cubic bounding box that covers all targets is established and then discretized into uniform unit grids. The spatial distribution density is quantified based on the number of apples within each grid cell. Simultaneously, an occlusion weight coefficient is calculated for each apple to comprehensively assess its field-of-view completeness and picking accessibility. Based on these multi-dimensional evaluation results, a prioritized sequence of picking targets is generated.

The hardware system acquires joint angle information through the real-time collection of robotic arm joint encoder data, which is then fed into the pre-trained MAPPO-MOGPS algorithm. Based on historical picking experience and the current environmental state, the algorithm generates collaborative motion trajectories for the dual arms. These control commands are transmitted to the low-level driver modules of the robotic arms via the ROS (Robot Operating System) communication architecture to achieve precise motion control. Upon completion of the picking task, the harvested fruits are gathered by an automated collection system. The experimental workflow is illustrated in Figure 11.

To systematically evaluate the algorithm’s performance, experiments were conducted in an indoor environment with a simulated fruit tree, where simulated apples were randomly placed to mimic their natural growth distribution. For 10 target apples, four sets of 50 repetitive picking trials were performed in both the simulation environment and the physical system. The key performance metrics from these experiments were recorded and subsequently analyzed.

As shown in

Table 7. Comparison between simulated and actual harvesting performance.

Experimental Environment	Occlusion Conditions	Success Rate	Time (s/item)	Collision Rate	Average Error (m)
Simulation environment	Medium	92.3%	5.81	5.42%	0.0146
Real environment	No	87.62%	5.62	6.82%	0.0154
	Slight	82.47%	6.20	11.7%	0.0177
	Medium	81.14%	6.12	14.7%	0.0186

, this study observed a performance gap between the simulation environment and the physical system: while the success rate in the simulation reached 92.3%, the success rate in the physical experiments under moderate occlusion conditions was 81.4%, accompanied by numerous collisions with branches. This discrepancy primarily stems from two factors: the perception-reality gap and model mismatch.

At the perception level, the simulation provides ideal state information, whereas in the physical system, localization errors from the visual perception module are propagated to the motion planning layer. This causes pose deviations in the robotic arm as it approaches the target, leading to contact with surrounding branches, which, in turn, reduces the picking success rate and increases the risk of collisions. At the system modeling level, the dynamic models used in the simulation struggle to fully replicate complex physical properties of the real world, such as the flexibility of branches and the connection strength of fruit stems. This thereby limits the generalization performance of the purely simulation-trained strategy on the physical platform.

Nevertheless, in the presence of the aforementioned errors and uncertainties, the system still achieved a picking success rate of over 81% and maintained zero collisions between the dual arms throughout. Simultaneous collisions mainly occur between the robotic arm and branch obstacles. This demonstrates the effectiveness and robustness of the MAPPO-MOGPS algorithm in maintaining the safety of dual-arm collaborative operations in complex scenarios.

In summary, the physical experiments indicate that the primary bottlenecks of the current system are concentrated in visual perception accuracy and the capability for modeling and avoiding fine-grained obstacles. Future work will focus on enhancing perceptual robustness through multi-sensor fusion and performing closed-loop optimization of the simulation model using real physical interaction data, to further advance the cross-domain transfer performance from simulation to reality.

5. Results and Discussion

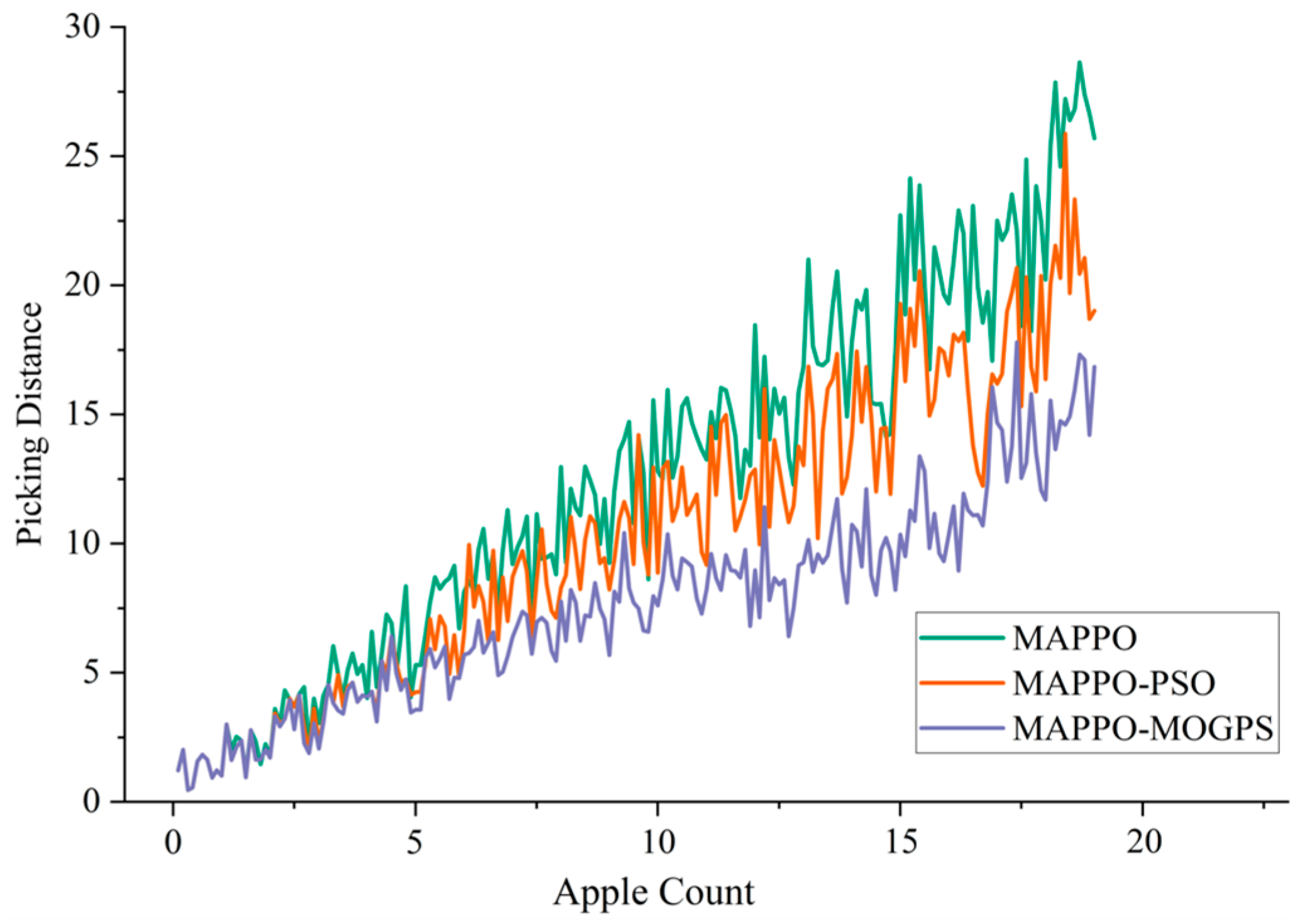
Simulation results demonstrate that the MAPPO-MOGPS proposed in this paper exhibits strong overall performance in the dual-arm apple harvesting task. According to statistical t-test results, the obstacle avoidance success rate reaches 92.3%, the mean positioning error of the end-effector is controlled within 0.014 m, and path planning efficiency is improved by 15.11% compared to baseline methods, fully validating the algorithm’s superiority in simulation environments. In practical dynamic harvesting validation, the success rate for apples in the outer canopy reaches 87.62%, with an average single-fruit harvesting time of 5.62 s, further proving the strategy’s good generalization capability in unobstructed scenarios.

Although the strategy performs well in simulation and simple scenarios, its performance in highly occluded complex environments still requires improvement, primarily due to challenges in simulation modeling and system implementation. At the simulation modeling level, to balance computational efficiency and realism, necessary simplifications were made to certain key physical properties: for instance, the flexible dynamics of fruit stems and branches were simplified as rigid bodies, ignoring elastic deformations in real environments; the visual perception module was built on ideal rendering without fully simulating disturbances such as sensor noise and variable lighting. Additionally, the contact model in the physics engine, as an approximation of real-world interactions, has inherent deviations in force transmission and friction characteristics. While these simplifications ensure training efficiency, they inevitably introduce systematic errors in the simulation-to-reality transfer. At the system implementation level, minor positioning errors in the visual perception stage are transmitted and amplified through the control chain, ultimately leading to pose deviations between the end-effector and the ideal harvesting point.

Furthermore, the current method still requires improvement in model uncertainty and risk assessment: for example, the one-step prediction model does not explicitly consider sensor noise and model mismatch; risk assessment also does not incorporate key factors such as relative velocity and time to collision. In addition, the biomechanical interactions during fruit harvesting and their potential damage have not been directly monitored or evaluated.

Based on the above analysis, future research will focus on the following directions: First, by integrating multi-sensor information and robust image algorithms, the perception accuracy of the system under complex conditions will be enhanced. Second, the introduction of flexible body dynamics and random disturbances into the simulation will help build a higher-fidelity virtual training environment. Finally, cross-crop adaptability studies will be expanded by establishing a physical parameter database for different fruits and optimizing grasping strategies, promoting the application of harvesting technology in diversified orchard scenarios. The advancement of these efforts will significantly enhance the operational robustness of the harvesting system in real-world complex environments and accelerate the transition of agricultural robotics from theoretical research to industrial application.

6. Conclusions

In the field of orchard harvesting, improving picking efficiency, reducing manual labor intensity, and achieving precise automated harvesting are critical challenges that require urgent solutions. This study proposes a dual-arm robot cooperative picking and obstacle avoidance strategy (MAPPO-MOGPS) that integrates the MAPPO algorithm with an improved MOGPS algorithm. This strategy leverages the MAPPO algorithm to enhance the autonomous learning capability of dual-arm harvesting robots in complex orchard environments. A dynamic collision assessment strategy for dual arms is established, which optimizes picking paths and reduces collision risks by dynamically monitoring and evaluating potential collision hazards during the harvesting process. The proposed improved MOGPS algorithm incorporates an apple harvesting priority evaluation mechanism to assess the non-uniform distribution of fruits and the complexity of the operational environment in real time, thereby dynamically adjusting the dual-arm harvesting strategy to achieve adaptive picking path planning for the dual-arm robot.