Abstract
Flax, an important oil and fiber crop, is widely cultivated in temperate and sub-frigid regions worldwide. China is one of the major producers of flax, with Gansu Province predominantly practicing cultivation in hilly areas. However, common issues such as feeding difficulties, stem entanglement, and low threshing efficiency significantly restrict the improvement of planting efficiency. This study addresses the key technical challenges in flax combine harvesting in hilly regions by developing a discrete element model of the flax plant and utilizing DEM-FEA co-simulation technology. The performance of two threshing drum models (T1 and T2) was analyzed, focusing on motion trajectory, stress distribution, and threshing effects. The simulation results show that the T2 model, with its combination of rib and rod tooth design, significantly improves threshing and separation efficiency. The loss rate was reduced from 5.6% in the T1 model to 1.78% in the T2 model, while the maximum stress and deformation were significantly lower, indicating higher structural stability and durability. Field validation results revealed that the T1 model had a total loss rate of 3.32%, an impurity rate of 3.57%, and an efficiency of 0.09 hm2/h. In contrast, the T2 model achieved a total loss rate of 2.29%, an impurity rate of 3.39%, and an efficiency of 0.22 hm2/h, representing a 144.4% improvement in working efficiency. These findings indicate that the T2 model has a higher potential for flax harvesting in hilly and mountainous regions, especially in improving threshing efficiency and operational stability, providing an important theoretical basis for optimizing threshing equipment design.
1. Introduction
Flax (Linum usitatissimum L.) serves as an important oil and fiber crop. Its seeds are rich in unsaturated fatty acids, linolenic acid, proteins, and dietary fiber, which have high nutritional value and a wide range of industrial uses [1]. Flax stems have a high fiber content and poor mobility but are widely used in textile and composite manufacturing due to their flexibility, moisture absorption, and lightweight [2]. Globally, flax is mainly distributed in temperate and subfreezing regions, including Canada, Russia, China, and other countries. China is an important cultivation and consumption country of flax, but also one of the main producing areas of flax in the world. China’s flax cultivation is mainly in the northern drylands; the planting area is mainly concentrated in Inner Mongolia, Gansu, Ningxia, Shaanxi, Xinjiang, and other provinces and regions [3]. Flax in China is both an important cash crop and an important part of dryland agriculture in the northwest.
Despite the significant economic importance of flax cultivation in China, harvesting flax in complex terrains such as hilly and mountainous regions still presents numerous challenges. These challenges, particularly the smooth feeding, stem wrapping, and low threshing efficiency during harvesting, severely hinder the improvement of mechanization levels and the modernization of the industry. At present, there are mainly axial flow and tangential flow threshing drums in grain combine harvesters [4]. The axial flow threshing drum has a high threshing rate due to the long contact time between the crop and the drum, but it consumes a lot of energy and has a lot of stems and broken grass; the tangential flow threshing drum has a short crop contact time and a better separation performance, but the threshing capacity is relatively low, and it is prone to the problem of entanglement [5]. In recent years, foreign countries have gradually developed a combination of tangential and axial flow threshing drums with adjustable threshing elements and step-less variable speed technology to adapt to the threshing needs of different crops [6]. However, small- and medium-sized combine harvesters in China are still dominated by single-axial-flow threshing drums, and transverse-axial-flow drums have certain limitations in their threshing capacity and adaptability due to structural limitations.
With the continuous development of grain threshing technology, foreign countries have gradually achieved multifunctionality and intelligence, such as adaptive adjustment of threshing gaps, step-less variable speed technology, and the design of combined drums, to meet the threshing requirements of different crops. However, research on the unique characteristics of flax plants in China remains limited. In particular, studies on the adaptability of flax plants under hilly and mountainous working conditions are still scarce. Improvements in threshing efficiency for some crops have been achieved by changing the form of threshing drums, adjusting feeding gaps, and optimizing cleaning methods [7]. Liu et al. [8] developed a variable-diameter threshing drum and monitoring method to improve threshing performance by enabling flexible adjustment of the threshing gap to prevent clogging at varying feeding rates. Sudajan et al. [9] studied the threshing efficiency of rice combine harvesters with different drum types, speeds, and feeding rates, providing technical support for optimal threshing device design. Liu et al. [10] used CFD-DEM-coupled simulation to analyze the structural parameters of cleaning devices and the flow dynamics of mixtures, offering a theoretical basis for cleaning device design. Wang et al. [11] proposed a DEM-based modeling and simulation method for dynamic threshing processes, enabling accurate performance analysis and optimization of threshing devices. Wu et al. [12,13] addressed issues of scavenging material accumulation and high scavenging loss during hilly operations by designing a self-leveling scavenging screen and control system, improving cleaning device performance in complex terrain. Xu et al. [14] took the flax threshing material as the research object and completed the calibration of six contact parameters, which provides an efficient and reliable method for the simulation and optimization of the agricultural machinery, especially in the modeling of flax threshing material and optimization of the design of the material, which has an important value in the application.
However, existing research on flax harvesting in complex terrains, such as those in Gansu Province, has not yet fully addressed the contradiction between smooth feeding and the separation performance of threshing [15]. The mechanization level of flax harvesting urgently needs to be improved. In this study, by combining the co-simulation technology of the discrete element method (DEM) and finite element method (FEA) [16], the interactions between the flax plant and threshing device were studied in depth, and the motion trajectories, stress distributions, and separation effects of the two drum models of T1 (full-rod-tooth transverse-axial-flow threshing drum, woven-screen concave plate) and T2 (striped-rod and rod-tooth combination transverse-axial-flow threshing drum, narrow-grid concave plate) were verified through a comparative study. A comparative study to verify the advantages of the model in improving threshing efficiency, reducing mechanical losses, and reducing entrainment losses, to provide a theoretical basis for the design and improvement of threshing devices for combined flax harvesting.
2. Materials and Methods
2.1. Analysis of Threshing Devices and Intercropping Processes
2.1.1. Threshing Device
As the flax stems contain a large number of fibers, resulting in their strength and poor mobility, flax plants intertwine with each other in a serious situation [17]. Field trials have shown that the hilly mountainous flax joint harvest, if the use of a full-rod tooth axial threshing drum, Jiangsu Wade Agricultural Machinery Co., Ltd., Danyang, China, often occurring flax plant entanglement threshing drum phenomenon, flax capsule cannot be completely threshed, resulting in the threshing drum clogging, conveying chain party clogging, threshing, and separation of the effect is not good, the full-rod tooth threshing drum cannot be adapted to the threshing and separation of the flax plant operation; if the use of a full-rod tooth axial threshing drum, due to the conveyor chain party The flax plant is transported to the threshing drum feed inlet, resulting in the flax plant being difficult to feed into the threshing drum, and the threshing drum feed inlet instantaneously feeding into the large amount, resulting in the threshing drum feed inlet withstanding the load being larger and the concave plate sieve being very easy to be damaged and deformed, and at the same time the full-rod threshing drum will be the flax stems kneaded finely. The formation of small, short stems is not conducive to the separation of the flax out of the material cleaned, accompanied by the phenomenon of damage to the flax seed grain, the full-rod axial flow threshing drum, Jiangsu Wade Agricultural Machinery Co., Ltd., Danyang, China. A full-ripple type threshing drum, Jiangsu Wade Agricultural Machinery Co., Ltd., Danyang, China is also not suitable for flax plant threshing separation operations. Hilly mountainous flax combined harvest threshing drum working conditions are hindered as shown in Figure 1.

Figure 1.
Obstruction of the working condition of the threshing drum during combined flax harvesting in hilly areas. (a) Clogging of full peg-tooth threshing drum; (b) difficulty in feeding full grain rod threshing drum; (c) damage and deformation of concave plate screen.
Based on the hilly and mountainous flax combine harvesting tests, this study investigates the interactions between flax plants and threshing devices using two models: T1 (full rod and tooth transverse axial flow threshing drum with a woven sieve concave plate, Jiangsu Wade Agricultural Machinery Co., Ltd., Danyang, China) and T2 (textured rod and rod-tooth combination transverse axial flow threshing drum with a narrow grid concave plate, Jiangsu Wade Agricultural Machinery Co., Ltd., Danyang, China). The T1 model consists of a detachment cover plate, crossbars, spike teeth, spatial discs, and a woven sieve concave plate, while the T2 model includes a threshing cover plate, textured rod threshing drum, rod-tooth threshing drum, spatial discs, and a narrow grid concave plate. The T1 and T2 models are shown in Figure 2. Experimental and theoretical analyses of the flax plant’s structural characteristics indicate that a larger detachment gap helps reduce mechanical damage and stem-wrapping issues. However, excessively large gaps may decrease threshing efficiency. Through tests conducted across various detachment gap ranges, the 20–40 mm gap setting for the T1 and T2 models effectively balances threshing efficiency and plant protection, ensuring a high threshing rate with minimal mechanical loss.
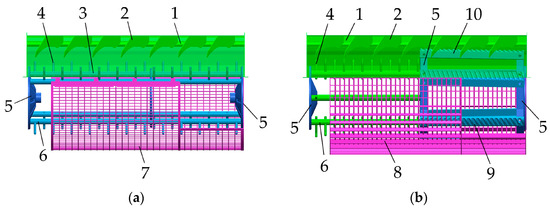
Figure 2.
T1 and T2 models. (a) T1 model; (b) T2 model. (1) Disengaging cover. (2) Grass guide. (3) Rod and tooth-threshing drum. (4) Spike teeth. (5) Spreader plate. (6) Crossbar. (7) Weave concave plate. (8) Narrow grid concave plate. (9) Ripple bar threshing drum. (10) Ripple bar.
2.1.2. Interaction Theory Analysis
The flax threshing separation process is mainly in the threshing drum striking, rubbing the role of several flax capsules rupture so that the flax seed grain reaches the surface layer of the concave plate, through the concave plate grid to achieve the separation of seeds and stems, then any seed grain in the concave plate at any location of the threshing and separation is random; if a single seed in the state of the feed inlet is equally likely, then any seed grain at any location in the concave plate will also be threshed or separated and will also be equiprobable [18]. Assuming that the flax plant entering the transaxial flow threshing and separating device consists of two parts, the unthreshed flax capsule and the free flax kernels, the flax kernel feeder quantity qj fed into the transaxial flow threshing and separating device is
where si is the number of free flaxseed grains that have been threshed but not separated into the transverse axial flow threshing device, %; sj is the number of free flaxseed grains entering the transverse axial flow threshing device that have not been threshed, %.
Setting the axial flow threshing device threshing coefficient as λ1 and separation coefficient as β1 within any small distance ∆x at any point x on the surface of the axial concave plate of the transverse axial flow threshing drum and denoting the probability of the occurrence of threshing in terms of frequency, the equation of the probability density function of the occurrence of threshing of the transverse axial flow drum, f(x), can be obtained [19] as
where x is the axial working distance from the starting point of the cross-axial flow drum grid concave plate screening, in mm; F(x) is the cumulative number of flax kernels threshed within the axial working distance of the screening start point of the cross-axial flow drum grid concave plate.
Morphing Equation (2) into a derivative and substituting it with the original equation yields
Integrating both sides of Equation (3) yields
The probability function of the occurrence of flax seed threshing in the axial direction x of the concave plate sieve of the transverse axial flow threshing and separation device can be obtained by substituting the deformation of Equation (2) into Equation (4) and then deriving the probability function as
Similarly, the probability function of the occurrence of flax seed separation in the axial direction x of the concave plate sieve of the transverse axial flow threshing and separation device can be obtained as
Then, the number of unthreshed flaxseed kernels in the range [0, L] was
When x = L, the unthreshed flax kernels are discharged with the flax stems out of the transverse axial flow threshing device, resulting in unthreshed loss; the unthreshed loss rate of the net is
The probability of flax kernel separation in a transverse axial flow threshing unit is the convolution of the probability density of flax kernel threshing and the probability of flax-free kernels passing through the concave plate grid; then the probability density function of flax kernel being separated is
Integration of Equation (9) yields the flax seed separation density function [20] for a transverse axial flow threshing unit as
Then, the density of separation of threshed and free seeds of flax in the threshing chamber of the transverse axial flow threshing device is
Then, the cumulative separation of flaxseed kernels H(x) below the transverse axial flow threshing drum is
Integration of Equation (12) yields the cumulative separation of flaxseed kernels under the transverse axial flow threshing drum as
The sum of cumulatively separated flax kernels H1(x), uncleaned flax kernels sn(x), and free flax kernels sf(x) in the transverse axial flow threshing unit is equal to the total amount of flax kernels qj in the threshing chamber; then the equilibrium equation for flax threshing and separation is
From Equation (14), the amount of flax-free seeds that are not separated after threshing and separation in the transverse axial flow threshing unit sf(x) can be obtained, and when x = L, the flax-free seeds that are not separated become entrainment loss, and the substitution of Equations (8) and (13) into Equation (14) results in the entrainment loss after threshing and separation in the transverse axial flow threshing unit [21] as
When all are fed into the flax plant in the flax-free seed, grain is zero, that is, si = 0, sj = 1, that is, a single transverse axial flow threshing drum threshing model, from Equation (15), can be obtained through single-axial threshing drum threshing after separation of entrainment loss sf(L), the cumulative amount of separated flax seeds H1(x), and the rate of unthreshed linseed grains sn(L) is
As can be seen from Equation (16), the cumulative separation of flax seed volume of the transverse axial flow threshing device rises in the form of an exponential curve at the feeder population, the initial section increases rapidly and tends to flatten out after reaching the maximum value; the amount of free flax seed volume by the transverse axial flow drum threshing separation continues to increase first and then decreases after reaching the maximum value, and then gradually decreases, to the transverse axial flow threshing drum discharge port when the corresponding value is the loss of entrainment; the amount of unthreshed net volume by the transverse axial flow roll simple threshing. After separation, the change was slow, with an exponentially decreasing trend, and became the number of unthreshed seeds at the discharge of the transaxial flow drum [22].
2.2. Joint DEM-FEA Simulation Modeling and Setup
2.2.1. DEM Modeling of Flax Plants
To ensure the simulation model accurately reflects the real flax plant while reducing computational load, the discrete element model (DEM) was simplified [23] using a segmented modeling approach (Figure 3). The flax plant was modeled as a Hertz–Mindlin bonding model, consisting of root stems, middle stems, neck stems, lateral branches, and capsules. The particles representing these parts were bonded in a single-sphere model, with diameters corresponding to the outer diameters of each part, and the centroids of the particles connected to form a line. The same bonding parameters were applied to the flax capsule, lateral branches, and neck stem. In EDEM software 2020, five new bulk materials were defined to represent the material properties of each flax plant part. The root stem is 21 mm long, 2.1 mm in diameter, with a bond radius of 1.3 mm; the middle stem is 15.2 mm long, 1.9 mm in diameter, with a bond radius of 1.2 mm; the neck stem is 10.5 mm long, 1.5 mm in diameter, with a bond radius of 1 mm; and the capsule is modeled as a single sphere with a diameter of 8 mm. The total length of the flax plant in the meta-particle module is 471 mm, with the root stem, middle stem, neck stem, and lateral branches measuring 168 mm, 152 mm, 147 mm, and 100 mm, respectively. Key parameters of the discrete element model are shown in Table 1, and the T1 and T2 model simulations are depicted in Figure 4.
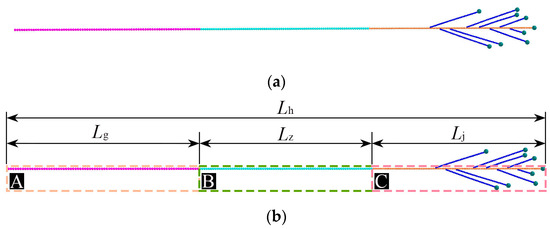
Figure 3.
Discrete metamodeling of flax plants. (a) Whole plant shape; (b) characteristic parameters of each part. A is the flax capsule, B is the lateral branches of the flax plant, and C is the neck stem of the flax.

Table 1.
Main parameters of the discrete element model.
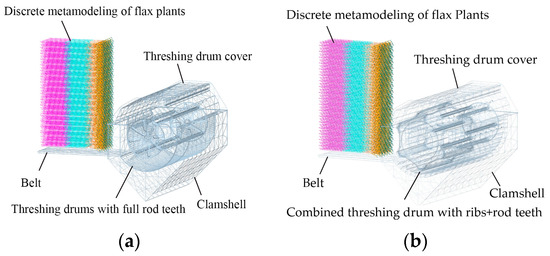
Figure 4.
Discrete element simulation models for T1 and T2 models. (a) T1 model; (b) T2 model.
2.2.2. Threshing Drum FEA Modeling
After the discrete element simulation calculations were completed, the format data files of flax plant particles with two threshing devices (rod and tooth threshing drum and woven concave plate and striped rod and rod and tooth combination threshing drum and narrow grid concave plate) were imported into the DEM Solutions module of the ANSYS Workbench software 2021, and a new static structural module was created, and the material properties were added to share the DEM Solutions module and static structural data for interaction analysis. Material properties share the DEM Solutions module and static structural data to analyze the interaction between particles and threshing drums and concave plates [24]. By adding constraints on the corresponding drum and concave plate geometric model, setting the deformation and stress calculation options in the static structural analysis, and completing the finite element solution process, the deformation and stress cloud diagrams of the drum and concave plate under the action of flax plant particles can be obtained intuitively [25]. At this time, the mesh parameters of the cylinder and concave geometry are derived from EDEM software, and the mesh is set in advance on its calculation interface, which can speed up the particle contact retrieval. Generally, the optimal mesh scale is twice the radius of the sphere of the smallest particle, which can provide reliable data support for analyzing the performance of the two threshing devices under different feeding conditions.
2.2.3. Parameter Settings
The T1 and T2 models are modeled by first drawing the T1 and T2 models in the 3D modeling software SolidWorks 2021 and simplifying the models. In the EDEM software for the T2 model threshing drum, to add rotary motion, set the speed to 800 r/min. In the T1 and T2 models, outside the setting of a cube as a particle plant, the use of directional generation technology to produce a sequential arrangement of the flax plant discrete metamodels, whose length × width × height spacing is 10 mm × 10 mm × 10 mm, set-up a conveyor belt to transport the flax plant discrete metamodel to the threshing device, and set the conveyor belt line speed to 2.5 m/s. The Bonding V2 model and Hertz–Mindlin (no slip) contact model were used in the particle-particle contact model in the EDEM software and added to the Bonding V2 model in the flax plant discrete metamodel in the EDEM software. Bonding V2 model to add flax plant bonding parameters, particles-geometry contact model using the Hertz–Mindlin (no slip) contact model, the time step using 25.81% of Rayleigh time, the time step is 3 × 10−7 s, the data saving interval is 0.01 s, a total of 1.5 s simulation. To reduce the computational load of the computer, following the principle of simplified analysis, set T1 and T2 model simulation calculations produced a total of 1.6 kg of flax plants.
3. Results
3.1. DEM-FEA Simulation Results Analysis
3.1.1. Analysis of T1 Model Simulation Results
After the simulation calculation, the T1 model’s flax plant movement during the process was obtained at the post-processing interface. As shown in Figure 5, the flax plant moves onto the conveyor belt, where neighboring flax capsules and stems cross and become entangled. Upon contact with the full-rod tooth threshing drum, the flax capsule and side branches are struck and fall off by the nail teeth. The nail teeth cause a shunting effect, separating areas where the strike is incomplete and complete. In the incomplete strike region, the flax plant’s stems and capsules rupture inadequately, resulting in poor seed threshing. In the complete strike region, the rupture is more thorough, yielding better threshing. The flax plants in the incomplete strike area continue into the threshing gap, where the crossbar’s striking effect is weaker than the nail teeth. However, the crossbar facilitates smoother feeding, allowing the flax plants to enter the threshing gap more smoothly under continuous action from both the nail teeth and the crossbar.
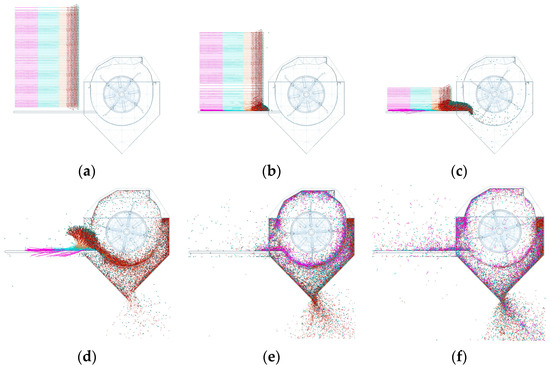
Figure 5.
T1 model flax plant movement process. (a) 0 s; (b) 0.15 s; (c) 0.3 s; (d) 0.45 s; (e) 0.6 s; (f) 0.75 s; (g) 0.9 s; (h) 1.05 s; (i) 1.2 s.
Figure 6 shows the shunting effect of the nail teeth on the flax plant. The rod tooth threshing drum improves the flax plant’s feeding mobility, but during the feeding process, the plant’s movement does not affect its axial direction. The flax plant relies mainly on the guiding plate’s inflow effect, with the guiding plate and threshing drum rotating together to discharge flax stems. However, when the flax stems move with the rod and tooth-type threshing drum, the guiding plate’s discharge function is limited, and the stems become entangled in the drum. This issue reduces the guiding plate’s efficiency and exacerbates entanglement problems. Consequently, the full-rod tooth threshing drum has limited effectiveness in threshing flax capsules, poor discharge performance, and frequent entanglement of the flax plant with the threshing drum.
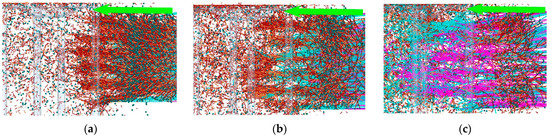
Figure 6.
Diversion of flax plants by peg teeth at different moments in the T1 model. (a) 0.41 s; (b) 0.45 s; (c) 0.51 s.
In the EDEM software post-processing module, there will be flax plant particles on the rod and tooth threshing drum, and the woven concave plate will play a role in data imported into ANSYS Workbench Static Structural module, in the rod and tooth threshing drum and woven concave plate geometric model to add constraints, in the calculation of the results of the addition of the deformation and stress options that can be obtained for the flax plant particles on the rod and tooth threshing drum and woven concave plate role of deformation and stress cloud diagrams. The braided concave plate is under the action of the deformation and stress cloud, as shown in Figure 7, Figure 8, Figure 9 and Figure 10.

Figure 7.
Deformation program of T1 model threshing drum. (a) 0.26 s; (b) 0.57 s; (c) 1 s.

Figure 8.
Stress program of T1 model threshing drum. (a) 0.26 s; (b) 0.57 s; (c) 1 s.

Figure 9.
Deformation of the woven concave plate in the T1 model. (a) 0.26 s; (b) 0.57 s; (c) 1 s.

Figure 10.
Stress program of the braided concave plate in the T1 model. (a) 0.26 s; (b) 0.57 s; (c) 1 s.
As shown in Figure 7 and Figure 8, the deformation of the T1 model full-rod tooth threshing drum primarily occurs in the threshing section, with the deformation decreasing sequentially from the threshing section to the haying section. The deformation is most pronounced at the nail teeth and crossbars, with the maximum deformation of 0.029 mm occurring at the nail teeth. The maximum stress in the T1 model full-rod tooth threshing drum is concentrated in the threshing section, particularly at the welding joints of the nail teeth and crossbar. The stress decreases from the threshing section to the haying section, with the maximum stress of 11.539 MPa occurring at the root of the nail teeth in the threshing section. As shown in Figure 9 and Figure 10, the deformation of the T1 model woven concave plate primarily occurs at the position where the threshing degree is the greatest in the threshing section, with the maximum deformation reaching 311 mm, which is in the damaged state. The maximum stress is also concentrated at the position with the highest threshing degree in the threshing section, mainly in the areas of the transverse and longitudinal screens, with the maximum stress of 1.13 MPa. The deformation and stress in the rod-tooth type threshing drum and the woven concave plate are attributed to the fact that the flax plants in the threshing section remain relatively intact and maintain high strength. During threshing, the flax plants directly contact the rod-tooth type threshing drum and woven concave plate, subjecting them to significant impacts from the nail teeth and crossbars. This results in large force being applied to the threshing drum and concave plate, causing deformation and stress concentration.
3.1.2. Analysis of T2 Model Simulation Results
After the T2 model simulation calculation is completed, the flax plant movement morphology process during the T2 model simulation time is obtained in the post-processing interface, as shown in Figure 11.
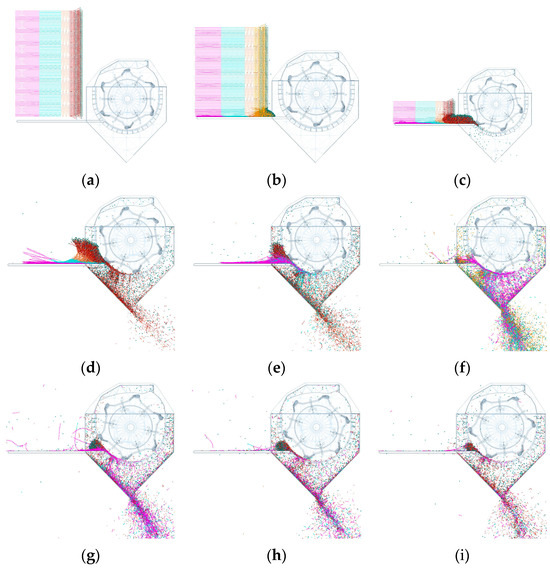
Figure 11.
T2 model flax plant movement process. (a) 0 s; (b) 0.15 s; (c) 0.3 s; (d) 0.45 s; (e) 0.6 s; (f) 0.75 s; (g) 0.9 s; (h) 1.05 s; (i) 1.2 s.
As can be seen from Figure 11, T2 models of flax plants fall into the conveyor belt with the conveyor belt’s forward movement, during which neighboring flax capsules and stems cross each other, accompanied by the phenomenon of entanglement. When the head of the flax plant and the combined threshing drum ribs section contact are instantaneous, the flax capsule by the ribs blow and rub, so that the flax capsule rupture, flax seeds are threshed, while the ribs section of the helical rotation of the flax plant has a channeling effect, the flax plant is struck by the ribs and rubbed to produce a tangential acceleration, the flax plant can quickly into the threshing drum, and the flax plant from the tangential movement into tangential and axial compound motion, at this time the flax plant in the grid concave plate by the double action from the tangential arc plate and axial bars, exacerbated the degree of rupture of the flax capsule, enhance the threshing capacity of the combined threshing drum. As shown in Figure 12, the contact area between the ribbed section and the flax plant is relatively large, and the duration of action is longer, allowing the flax plant to move a greater distance within the detachment gap. The cover plate’s internal guiding plate facilitates the rapid transport of the flax plant stems to the separation section, preventing them from entangling with the threshing drum. The rod-tooth section has a relatively minor effect on the flax plant’s threshing, primarily achieving stratification of the flax plant stems, seeds, husks, etc., through the picking and plucking action, with separation accomplished by the narrow grille concave plate. The ripple helix arrangement aids in the flow and threshing of the flax plant, but in the region with a larger detachment gap at the feed inlet, the flax plant’s mobility suddenly increases, accompanied by axial movement. This causes the flax plants in the larger detachment gap to move toward the smaller detachment gap, resulting in the aggregation of flax plants in the smaller detachment gap at the feed inlet, initiating a clogging phenomenon. After the clogging occurs, the flax plants in this region experience a reaction force after being struck by the ripple rods, making it more difficult to feed. The ripple and rod-tooth combination threshing drum enhances the threshing and separation effect of the flax plant, improves the threshing and separation capacity of the drum, and also improves the smoothness of flax stem discharge. However, the ripple and rod-tooth combination threshing drum operates more smoothly during feeding at small inclination angles, while local blockage is more likely to occur during feeding at large inclination angles.
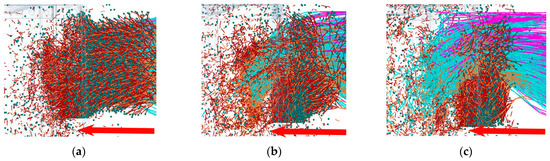
Figure 12.
Effect of stripe spiral on flax plants in the T2 model. (a) 0.39 s; (b) 0.48 s; (c) 0.56 s.
In the EDEM software post-processing module, there will be flax plant particles on the striped rod and rod tooth combination threshing drum and narrow grid concave plate role of data imported into the ANSYS Workbench Static Structural module, in the striped rod and rod tooth combination threshing drum and narrow grid concave plate geometric model to add constraints, add the deformation and stress options in the calculation results, and can be obtained flax. The deformation and stress of the plant particles on the ribs and rod teeth combination threshing drum and narrow grid concave plate under the action of the cloud, as shown in Figure 13, Figure 14, Figure 15 and Figure 16.

Figure 13.
Deformation program of the combined threshing drum in the T2 model. (a) 0.31 s; (b) 0.63 s; (c) 1 s.

Figure 14.
Stress program of the combined threshing drum in the T2 model. (a) 0.31 s; (b) 0.63 s; (c) 1 s.

Figure 15.
Deformation of narrow grid concave plate in the T2 model. (a) 0.31 s; (b) 0.63 s; (c) 1 s.

Figure 16.
Stress program of narrow lattice concave plate in T2 model. (a) 0.31 s; (b) 0.63 s; (c) 1 s.
Figure 13 and Figure 14 show that in the T2 model, the deformation of the striped rod and rod tooth combined threshing drum occurs mainly in the threshing section, with maximum deformation at the center of the striped rod section, decreasing towards the sides. The deformation in the middle causes the amplitude disk to deform, which in turn leads to the deformation of the rod tooth section crossbar, with the maximum deformation reaching 0.002 mm. Stress in the combined threshing drum is concentrated in the middle of the ribs, with a maximum stress value of 1.18 MPa. Figure 15 and Figure 16 show that the deformation of the narrow grid concave plate mainly occurs at the bottom of the threshing, separation, and grass discharge sections. The deformation manifests as axial deformation at the bottom of the narrow grid concave plate, with the transverse spacer plate showing the largest deformation. This deformation affects the grid strip, with a maximum deformation of 5.13 × 10−6 mm. The maximum stress in the narrow grid concave plate occurs at the bottom of the threshing, separation, and grass removal sections. Stress is transferred from the cross-partition plate to the grating, with the cross-partition plate experiencing higher stress (maximum stress of 0.2 MPa). The deformation and stress are mainly caused by the interaction between the flax plant’s root stems, central stems, and neck stems with the threshing drum and concave plate, particularly at the lower part of the concave plate. The cross-partition plate also bears significant reactions, leading to its deformation and the highest stress.
Comparing the full rod and tooth threshing drum and the striped rod and rod and tooth combination threshing drum in the T1 and T2 models, the maximum deformation of the former is much larger than that of the latter, and the difference between the two values is 0.027 mm, which is a large value; the maximum stress of the former is much larger than that of the latter, and the difference between the two values is 10.36 MPa, which is a large value; compared to the braided sieve concave plate and the narrow grid concave plate in the T1 and T2 models, the maximum deformation of the former is much larger than that of the latter, and the difference presents an order of magnitude multiple. The difference presents an order of magnitude multiple, and the difference value is extremely large; the maximum stress value of the former is much larger than that of the latter, and the difference value also presents an order of magnitude multiple, and the difference value is extremely large.
In summary, the T1 model of the rod and tooth threshing drum enhances the flax plant feeding mobility so that the flax plant is fed quickly, but the full rod and tooth threshing drum and woven sieve concave plate on the flax plant reaction force to withstand the weak, the rod and tooth and concave plate deformation is serious, continuous operation affects the operational efficiency, safety, and quality, nail teeth to hit the capsule and the neck of flax is not sufficient, large feeding volume of randomness, part of the flax plant failed to completely threshing, and at the same time, the maximum stress is much greater than the latter, the difference also shows an order of magnitude of the great difference. Plants cannot be completely threshed, and at the same time, it is easy for flax plants to wrap around the threshing drum phenomenon. The T2 model in the striped rod and rod tooth combination threshing drum striped rod section spiral is set to help the rapid flow of flax plants; the striped rod section and the flax plant have a larger contact area and can achieve complete threshed capsule flax; the rod tooth section enhances the separation of the effect of the flax stems, grains, and husks, but the striped rod and rod tooth combination in the form of a narrow grill concave plate brings a greater challenge; the narrow grid concave plate needs to withstand a great reaction force, while the helical setting of the ripple rod section leads to uneven feeding. In the feeding inlet shaft, the downward angle of the threshing gap’s small position is likely to produce a local accumulation of flax plants; a large feeding volume does not exist in this phenomenon; it is easy to exist in the small feeding volume.
3.2. Analysis of Flax Plant Movement
In the EDEM post-processing module, randomly selected T1 and T2 models of discrete element simulations of flax plant root stems, central stems, neck stems, lateral branches, capsules, and other particles were the object of data extraction to get the root stems of the flax plant, central stems, neck stems, lateral branches, capsules, and other particles of the group of trajectory map (Figure 17) [26].
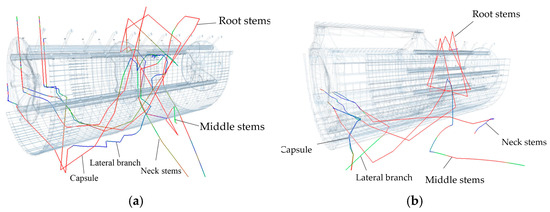
Figure 17.
T1 and T2 models of discrete element particle motion trajectories. (a) T1 model; (b) T2 model.
Figure 17a shows that in the T1 model, the discrete element simulation particle trajectory is complex, with the root, central, and neck stems of the flax plant performing spiral movements in the threshing chamber. These movements, influenced by the threshing drum and inner guide plate, result in the stems being discharged into the chamber, with the root stems having a significantly greater movement stroke than the central and neck stems. The lateral branches are broken and cyclically struck by the nail teeth, leading to their discharge after colliding with the concave plate. The flax capsules detach from the lateral branches upon impact and are discharged into the threshing chamber, though some capsules experience continuous impacts from the nail teeth. In Figure 17b, the T2 model shows a simpler particle trajectory. The root stems perform a spiral movement in the chamber and are discharged with the combined action of the threshing drum and guide plate. The central and neck stems follow incomplete spiral movements, with the central stems reaching the grass discharge port and the neck stems not, resulting in flax rejects. The flax capsules and lateral branches are discharged from the threshing chamber in the threshing section, forming two additional components of the flax rejects.
T1 model in the nail teeth constantly striking the various parts of the flax plant, resulting in the various parts of the flax plant movement and stroke with the different frequency of the nail teeth strikes are different changes, the frequency of changes in the movement of the material from the chamber is significantly accelerated, so that the flax plant after threshing stratified separation effect is better, the flax threshing material components are relatively simple, the threshing material in the root stem, the middle of the stems, the neck of the stems are less, the side branches are more, the rod tooth threshing drum. After threshing, flax threshing material components are relatively simple, greatly reducing the workload of the cleaning system. T2 model of the ripple rod section to enhance the ability of flax capsule threshing, but also increase the rubbing effect on the stems of the flax plant and capsule, after the ripple rod section of the kneading and squeezing of the stems of the flax plant to fracture, the most frequent fracture for the neck stems and side branches, while the rupture of the capsule of the flax is more complete, resulting in more shells, causing Linen out of the short stems, husk content increased, out of the material components of the degree of mixing further increased, the physical properties of the differences further reduced, resulting in increased workload of the cleaning system, cleaning further increase the difficulty.
3.3. Mechanism of Flax Plant Threshing
In the EDEM post-processing module in the T1 and T2 models of discrete metasimulation of the flax plant root stems, central stems, neck stems, lateral branches, capsules, and other particle groups were the object of data extraction. The extracted T1 and T2 models 1~1.5 s in the x-axis, z-axis average velocity of the particle groups, as shown in Figure 18 and Figure 19.
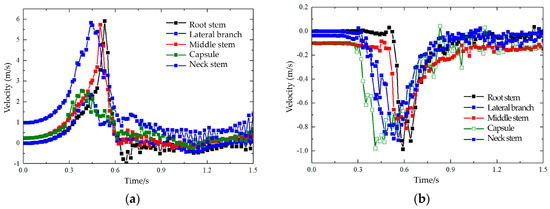
Figure 18.
Average x-axis and z-axis velocities of discrete element particle sets in the T1 model. (a) x-axis; (b) z-axis.
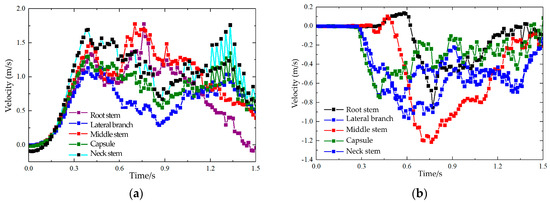
Figure 19.
Average x-axis and z-axis velocities of discrete element particle sets in the T2 model. (a) x-axis; (b) z-axis.
The x-axis is the feeding section of the flax plant movement direction; the x-axis velocity component can characterize the flax plant in different parts of the feeding process by the size of the action; the z-axis is the threshing section, and the separation section of the flax plant movement direction, the z-axis velocity component can characterize the flax plant in different parts of the threshing and separation of the size of the action taken by the role of the different parts of the flax plant.
Figure 18a shows the discrete elements of the T1 model. In the first 0.2 s, the average x-axis speed remains unchanged, indicating that the flax plant is in the free-fall phase after particle generation. After 0.2 s, the x-axis average speed of the particle group begins to change, with capsule particles changing first, followed by the lateral branches, neck stems, central stems, and root stems. This speed change occurs in the same order as the flax plant structure. In the prefeeding section, the flax capsule moves smoothly, and after being struck by the nail teeth, it accelerates to a maximum speed of 1.73 m/s at 0.42 s, then gradually decelerates, indicating that the capsule is the first to interact with the threshing drum. From 0.2 to 0.52 s, the flax capsule moves at high speed, followed by a decrease in speed as it exits the threshing chamber. The lateral branches move smoothly in the pre-feeding section. Upon detachment from the capsule and impact by the nail teeth, the lateral branches accelerate, reaching a maximum speed of 2.35 m/s at 0.44 s, then decelerate. This indicates that the lateral branches start moving as the capsule falls into the threshing chamber and are subjected to successive strikes by the nail teeth. From 0.2 to 0.5 s, the lateral branches move at high speed and are eventually ejected from the concave plate. The neck stems move smoothly during prefeeding, and after continuous impact by the nail teeth, they reach a maximum speed of 2.42 m/s at 0.44 s before gradually slowing down. This shows that the neck stems are impacted by the nail teeth upon entering the threshing chamber, moving at high speed from 0.2 to 0.53 s, then gradually slowing down as they exit the threshing chamber. The central stems are subject to continuous strikes by the nail teeth, reaching a maximum speed of 4.39 m/s at 0.5 s, then decelerating. The central stems move rapidly from 0.2 to 0.6 s, after which they enter the axial threshing separation stage. The root stems, impacted by the nail teeth, reach a maximum speed of 5.92 m/s at 0.53 s and then decelerate. From 0.2 to 0.6 s, the root stems move at high speed before gradually decelerating and transitioning into axial threshing separation. Similarly, as shown in Figure 18b, in the first 0.2 s, the average z-axis velocity remains unchanged, with the flax plant in the free-fall phase after particle generation. After 0.2 s, the z-axis average velocity begins to change, with the first change occurring in the capsule particles, followed by the lateral branches, neck stems, central stems, and root stems. The flax capsule reaches a maximum speed of 0.88 m/s at 0.41 s, lateral branches 0.85 m/s at 0.48 s, neck stems 0.73 m/s at 0.53 s, central stems 0.71 m/s at 0.61 s, and root stems 0.98 m/s at 0.59 s. From 0.2 to 1.02 s, all parts of the flax plant move at high speed. From 0.41 to 0.61 s, the interaction between the flax plant and the threshing device is strongest, with the axial movement of the plant parts being the most intense, leading to the best threshing and separation results.
Figure 19a shows the discrete elements of the T2 model. In the first 0.2 s, the average x-axis velocity remains unchanged, indicating the flax plant is in the free-fall phase after particle generation. From 0.2 to 0.42 s, the x-axis velocity of the particle group begins to change, with the first change occurring in the capsule particles, followed by the lateral branches, neck stems, central stems, and root stems. This change occurs in the same order as the flax plant structure. After 0.42 s, due to rib rubbing and squeezing, flax plant parts begin to separate, with the flax capsule and lateral branches being discharged from the threshing chamber by the concave plate. The root stems, central stems, and neck stems continue their tangential movement and are discharged through the grass outlet. From 0.2 to 0.42 s, the flax capsule moves smoothly during prefeeding, and after being struck by the ripple bar, it accelerates to a maximum speed of 1.11 m/s at 0.39 s, then gradually decelerates as it exits the threshing chamber. During the same period, the flax lateral branches are driven by the capsule’s movement and the ripple bar, reaching a maximum speed of 1.24 m/s at 0.42 s, then decelerating and being discharged from the threshing chamber. The flax neck stems also reach a maximum speed of 1.24 m/s at 0.42 s, followed by a gradual decrease in speed as they exit the threshing chamber. The central stems reach a maximum speed of 1.28 m/s at 0.41 s and move smoothly through the feeding section, transitioning from tangential to axial threshing separation. The root stems reach a maximum speed of 1.32 m/s at 0.42 s and also move from tangential to axial threshing separation. After 0.42 s, the flax plant parts exhibit differentiated feeding speeds. The capsule, lateral branches, and neck stems are extruded by the stripe rod and discharged by the concave plate, while the central and root stems continue moving with the threshing drum, following a trend of increasing and then decreasing feeding speed. They eventually exit through the discharge port. Similarly, Figure 19b shows that in the first 0.2 s, the average z-axis velocity remains unchanged, with the flax plant in free-fall after particle generation. After 0.2 s, the z-axis velocity of the particle group changes, with the capsule particles changing first, followed by the lateral branches, neck stems, central stems, and root stems. The order of change mirrors the flax plant structure. The flax capsule reaches a maximum speed of 0.75 m/s at 0.42 s, lateral branches 0.77 m/s at 0.56 s, neck stems 0.96 m/s at 0.61 s, central stems 1.21 m/s at 0.76 s, and root stems 0.86 m/s at 0.59 s. Between 0.2 and 0.42 s, the flax capsule, lateral branches, and neck stems move at high speed, resulting in effective threshing. However, the short stems formed by dislodged material from the neck stem and lateral branches increase the difficulty of clearing and loading. After 0.42 s, the root stems and central stems exhibit intense axial movement, resulting in optimal grass discharge and separation.
The maximum x-axis velocity capsule during feeding in T1 and T2 models was 1.73 m/s, 1.11 m/s, the maximum lateral branch velocity was 2.35 m/s, 1.24 m/s, the maximum neck stem velocity was 2.42 m/s, 1.24 m/s, the maximum central stem velocity was 4.39 m/s, 1.28 m/s, the maximum root stem velocity was were 5.92 m/s, 1.32 m/s; the maximum Z-axis velocity capsule during threshing and separation in T1 and T2 models were 0.88 m/s, 0.75 m/s, the maximum velocity of lateral branches were 0.85 m/s, 0.77 m/s, the maximum velocity of the neck stems were 0.73 m/s, 0.96 m/s, and the maximum velocity of the middle stem were 0.71 m/s, 1.21 m/s, and the maximum velocity of the root stem were 4.39 m/s, 1.28 m/s, and the maximum velocity of the root stem were 4.39 m/s, 1.28 m/s, and the maximum velocity of the root stem were 5.92 m/s, 1.32 m/s, respectively; 1.21 m/s, the maximum speed of the root stem was 0.98 m/s, 0.86 m/s, respectively; the difference in x-axis speeds of the capsule, lateral branches, neck stem, central stem, and root stem of the flax plant during the feeding process of T1 and T2 models were 0.62 m/s, 1.11 m/s, 1.18 m/s, 3.11 m/s, and 4.6 m/s, respectively, and the difference in the x-axis speeds of the threshing and separation process of the flax plant during the threshing of T1 and T2 models was 0.62 m/s, 1.11 m/s, 1.18 m/s, 3.11 m/s, and 4.6 m/s, respectively. Separation process of flax plant capsule, lateral branches, neck stems, central stems, root stems z-axis average speed difference of 0.13 m/s, 0.08 m/s, −0.23 m/s, −0.5 m/s, 0.12 m/s, respectively, it can be seen that in the process of feeding the T1 and T2 models flax plant x-axis average speed difference between various parts of the process is getting bigger and bigger, the T1 model feeding process faster than the T2 model fast, feeding section of the flax plant ministries and nail teeth between the action time is short, with the striker section of the action time is longer, while the threshing separation process T1 and T2 models flax plant ministries z-axis average speed difference first decreases and then increases, T1 model flax plant ministries in the threshing chamber movement is smoother, the T2 model flax plant ministries in the threshing chamber movement of the striker section of the helical settings and speed differences, in the threshing section and separation section speed is different in the threshing section and separation section, threshing and separation more thoroughly.
In summary, flax plant in the threshing room, flax plant stems entangled with each other, the flax capsule is the first to be threshing drum action leads to capsule rupture, flax seeds from the concave plate sieve fell into the cleaning system, at the same time, the threshing drum on the flax plant has a diversion, flax capsule by the action of the threshing drum caused by the side branches and the neck of the stems to accelerate the movement of the same time, while the threshing cylinder constantly acting on the flax plant, so that the flax plant in the tangential feed speed changes in the tangential direction, fast and smooth feeding, flax stems by the threshing drum and cover the joint action of the grass guide plate in the axial spiral movement, spiral movement during the flax seeds and stems accompanied by layered separation phenomenon, the seeds by the concave plate sieve falls into the cleaning system, stems in the grass section discharged from the threshing room. Rod tooth threshing drum on the flax plant feeding mobility is better, but feeding the process will not be on the flax plant’s movement and then have an impact on the flax plant; flax plant movement in the threshing drum mainly relies on the cover plate inside the grass guide plate flow. When the flax plant movement to the grass guide plate cannot be acted on, flax stems will not be along the axial movement, but entangled in the rod tooth threshing drum. This way, it will make the guide plate on the flax plant. This way makes the effect of the guide plate on the discharge of flax plant stems limited, exacerbating the flax plant entanglement threshing drum [27]. Ripple and rod tooth combination threshing drum increases the threshing and separation effect of the flax plant, enhances the threshing and separation capacity of the threshing drum, and at the same time enhances the discharge of the flax plant stems, but the ripple and rod tooth combination threshing drum is smoother in small taper feeding and prone to local blockage phenomenon in large taper feeding. The comprehensive comparison shows that to improve the flax threshing and separation capacity, reduce the flax winding threshing drum, and avoid feeding blockage, one should choose the ripple and rod tooth combination small taper transverse axial flow threshing drum with a narrow grid concave plate for the flax threshing operation.
4. Field Trial
4.1. Test Materials
The flax combine harvester threshing drum field performance test was carried out on 11–13 August 2022 in the village of Wenjiacha, Laojunpo Town, Huining County, Baiyin City, Gansu Province. The test model is a 4LZ-0.9 type hilly area hemp combine harvester, with a machine operating width of 1 m, a power feed of 0.9 kg/s, an operating speed of 0.4~0.7 m/s, a rated power of 13.4 kW, productivity 0.07~0.1 hm2/h, the test plot area is 0.667 hm2, the variety of flax is Longya 10, and the average height of the plant is 437.4 mm. The average plant height is 437.4 mm, the average number of capsules of a single plant is 6–11, planting density is 702 plants/m2, belonging to the typical dryland intensive planting of the flax planting mode. The experiment was carried out following the design parameters of the T1–T2 model of a hilly area combined harvester, and the total loss rate, the rate of impurity content, work efficiency, etc., were measured to verify the threshing effect.
4.2. Test Method
The test was conducted according to national standards. During the test, crop variety, conditions, and operating time were recorded, and the machine’s performance was observed. Key metrics, such as total loss rate, impurity content, and work efficiency, were determined. The test area was divided into six zones, each 1 m wide, with reserve areas at both ends no less than 500 mm. The machine operated at full width with a forward speed of 0.65 m/s over a 25 m test distance. The number of times the threshing drums of the T1–T2 model machines wrapped was noted, and the total time for harvesting was recorded to calculate efficiency. A minimum of 1000 g of grain was collected during the test, and the five-point sampling method was used to determine the seed loss per square meter. Clean woven bags were used for collection, and the samples were weighed using electronic scales with 0.001 g accuracy. The results are shown in Figure 20.

Figure 20.
Field tests.
4.3. Test Results
Combined with the characteristics of Gansu Province huisache planting, the requirements of crawler huisache combine harvester impurity rate and cleaning loss rate do not exceed 5%. Following the test standards and manual measurement by Formula (17), calculated by the value of the indicators, the results are shown in Table 2. From Table 2 it can be seen that the test indicators have reached the requirements of the relevant standards, the test process, the machine works smoothly, the threshing effect is better, the impurity content rate is low, the crushing rate is very low, and the total loss rate is small, in line with the requirements of the standard requirements of the flax joint harvesting can be carried out in hilly areas of flax combine harvester operations.
where m is the total mass of the small sample, g; Z is the impurity content, %; S is the loss rate, %. mz is the mass of impurities in the small sample, g; ms is the mass of caraway seeds per square, g.

Table 2.
Test results.
5. Discussion
The analysis of the study showed that the T2 model significantly outperforms the T1 model in the threshing and separation performance of flax plants. The T2 model, through the design of a combined roller with ribs and rod teeth, utilizes the spiral structure of the rib segment to apply rubbing and squeezing forces to the flax capsule, leading to a more complete rupture of the capsule. This allows the grains to quickly pass through the narrow grid concave plate for separation, which significantly reduces the entrainment loss rate. The data shows that the entrainment loss rate for the T2 model at 1.0 s was 1.78%, much lower than the 5.6% for the T1 model. Additionally, the T2 model demonstrated significant advantages in mechanical properties, with a maximum stress of 1.18 MPa and a maximum deformation of 0.002 mm, both significantly lower than the T1 model’s values of 11.539 MPa and 0.029 mm, indicating higher structural stability and durability. In summary, the T2 model shows clear superiority in threshing efficiency and reliability, making it more suitable for meeting the operational needs of combined flax harvesting in hilly and mountainous regions. However, the T2 model also exhibits some localized issues, especially when feeding plants with large inclination angles, which can lead to clogging. This may be related to the uneven distribution of the feeding gap caused by the spiral design of the rib section. In contrast, while the rod-tooth drum of the T1 model offers better feeding smoothness, the limitations of the nail-tooth striking method led to the problem of stems wrapping around the drum, which affects threshing efficiency and the performance of the subsequent cleaning system. Furthermore, the continuous striking of the nail teeth against the flax capsules and lateral branches in the T1 model results in a higher proportion of short stems and glumes in the threshed material, increasing the load on the cleaning system. To further improve the overall performance of the flax threshing machine, future research should focus on optimizing the design of the feeding inlet in the T2 model, improving the distribution of threshing gaps in combination with actual terrain conditions, and further enhancing feeding uniformity while reducing local blockages. At the same time, the separation capacity of the cleaning system should be improved to reduce the mixing of short stems and impurities, thereby increasing overall operational efficiency and stability.
In this study, a combined simulation method using the Discrete Element Method (DEM) and Finite Element Analysis (FEA) was employed, which provides an effective tool for modeling and performance evaluation of the flax threshing process. The advantage of the DEM-FEA method lies in its ability to realistically reproduce the interaction between flax plants and threshing devices, capturing complex physical phenomena such as collisions, compression, and friction through detailed particle-level simulations. Compared to traditional experimental methods, simulation approaches offer higher time and cost efficiency and allow for virtual testing under different design conditions, providing a scientific basis for design optimization. However, the DEM-FEA method also has some limitations. First, the accuracy of the simulations is constrained by the complexity of the modeling and computational resources. For the complex structure of flax plants and their irregular motion behaviors, there may be certain errors in the simulation results. Additionally, the DEM-FEA method relies on a large amount of experimental data and material parameters, which require considerable time and effort to obtain. Furthermore, material behavior may vary under different experimental conditions, limiting the reproducibility of the simulation results. Therefore, although the DEM-FEA method provides strong support for the design and optimization of threshing equipment, its results still need to be validated against actual experiments to ensure the reliability and applicability of the research findings. In conclusion, the DEM-FEA method provided powerful simulation support for this study but still requires further refinement and optimization, in conjunction with real operating conditions and additional experimental data, to improve its accuracy and application scope.
6. Conclusions
In this study, to address the problems of threshing device feeding difficulties, entangled drums, and low threshing efficiency in the process of combined harvesting of flax plants in hilly and mountainous areas, a discrete element flexible model of flax plants was established, and the performances and interactions of two threshing drum models (T1 and T2) were analyzed by using DEM-FEA co-simulation technology. Through the comparative study of the movement trajectory of the flax plant, mechanical stress distribution, and threshing effect, it verifies the advantages of the T2 model in improving threshing efficiency, reducing mechanical loss, and reducing entrainment loss, which provides a theoretical basis for the optimal design of threshing devices for flax combined harvesting. The main conclusions are as follows:
1. The T2 model demonstrates superior performance in terms of threshing efficiency, separation capacity, and mechanical stability compared to the T1 model. The T2 model incorporates a combination of ribbed rods and barbed rollers, utilizing the spiral structure of the ribbed section to apply a rubbing and squeezing effect. This significantly enhances the rupture of flax capsules and enables efficient seed separation through narrow grid concave plates. Simulation results indicate that the T2 model achieves a carryover loss rate of 1.78% at 1 s, much lower than the 5.6% of the T1 model, while improving the flowability of flax plants and reducing the generation of seed contaminants, thereby substantially enhancing both threshing and separation efficiencies. Additionally, the maximum stress (1.18 MPa) and maximum deformation (0.002 mm) in the T2 model are significantly lower than those of the T1 model (11.539 MPa and 0.029 mm), demonstrating superior mechanical stability and durability.
2. Field test results show that the T2 model offers clear advantages in practical applications. Field validation results reveal that the T2 model has a total loss rate of 2.29%, an impurity rate of 3.39%, and working efficiency of 0.22 hm2/h, representing a 144.4% improvement in working efficiency compared to the T1 model, which has a total loss rate of 3.32%, an impurity rate of 3.57%, and working efficiency of 0.09 hm2/h. These findings confirm the T2 model’s superior performance in real-world applications.
3. Further optimization is needed in the T2 model’s feeding flow and cleaning system. Although the spiral design of the ribbed rods improves the flowability of the flax plants, local blockages may still occur under high-angle feeding conditions, which may be attributed to the uneven distribution of the feeding gaps in the ribbed section. Additionally, while the T2 model shows significant advantages in threshing and separation, the flax plants, after being rubbed and squeezed, have a higher content of short stems and husks, which increases the load on the cleaning system. In contrast, the T1 model has a lower proportion of short stems but suffers from incomplete threshing, leading to higher contamination with impurities. Future designs should optimize the shape and gap distribution of the T2 model’s feeding inlet to improve feeding uniformity and reduce local blockages. At the same time, the cleaning system should be improved to enhance its ability to separate short stems and impurities.
Author Contributions
Conceptualization, R.S. and W.Z.; methodology, F.D.; software, R.S.; validation, L.C., F.D. and W.Z.; formal analysis, W.Z. and Z.L.; investigation, W.Z.; data curation, L.C.; writing—original draft preparation, R.S.; writing—review and editing, R.S.; visualization, R.S.; supervision, W.Z.; project administration, F.D.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Innovation Fund of Gansu Agricultural University-Public Recruitment Doctoral Research Start-up Fund, grant number GAU-KYQD-2023-09; Gansu Provincial Science and Technology Programme-Youth Science and Technology Fund; grant number 24JRRA659; Key Laboratory of Modern Agricultural Equipment and Technology (Jiangsu University) Ministry of Education and College of Agricultural Engineering, Jiangsu University, grant number MAET202316; China Agriculture Research System (CARS), grant number CARS-14-1-28; and Gansu Provincial Department of Education: Major Cultivation Project of Scientific Research and Innovation Platform for Universities, grant number 2024CXPT-15.
Data Availability Statement
Because of the need for follow-up research and to protect the scientific data of the author’s team, we will not disclose the data of this study for the time being, and the latest research results will be published later.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Čeh, B.; Štraus, S.; Hladnik, A.; Kušar, A. Impact of Linseed Variety, Location and Production Year on Seed Yield, Oil Content and Its Composition. Agronomy 2020, 10, 1770. [Google Scholar] [CrossRef]
- Rasheed, A.; He, P.; Long, Z.; Gillani, S.F.A.; Wang, Z.; Morsy, K.; Hashem, M.; Jie, Y. Cadmium (Cd) Tolerance and Phytoremediation Potential in Fiber Crops: Research Updates and Future Breeding Efforts. Agronomy 2024, 14, 2713. [Google Scholar] [CrossRef]
- Shi, R.; Dai, F.; Liu, X.; Zhao, W.; Qu, J.; Zhang, F.; Qing, D. Design and experiments of crawler-type hilly and mountainous flax combine harvester. Trans. Chin. Soc. Agric. Eng. 2021, 37, 59–67. [Google Scholar]
- Liang, Z.; Qin, Y.; Su, Z. Establishment of a Feeding Rate Prediction Model for Combine Harvesters. Agriculture 2024, 14, 589. [Google Scholar] [CrossRef]
- Wang, X.; Xie, F.; Ren, S.; Wang, X.; Zhang, Z. A mathematical model and test of the horizontal axial flow threshing separation device. Hunan Agric. Univ. (Nat. Sci.) 2020, 46, 480–487. [Google Scholar]
- Hussain, S.; Lei, X.; Wu, H.; Li, H.; Song, H.; Zheng, D.; Ghafoor, A. Optimizing the design of a multi-stage tangential roller threshing unit using CFD modeling and experimental studies. Comput. Electron. Agric. 2024, 226, 109400. [Google Scholar] [CrossRef]
- Liang, Z.; Million, E.W. Development of cleaning systems for combine harvesters: A. review. Biosyst. Eng. 2023, 236, 79–102. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Dong, Y.; Huang, M.; Zhang, T.; Cheng, J. Development of a variable-diameter threshing drum for rice combine harvester using MBD-DEM coupling simulation. Comput. Electron. Agric. 2022, 196, 106859. [Google Scholar] [CrossRef]
- Sudajan, S.; Salokhe, V.M.; Triratanasirichai, K. PM—Power and machinery: Effect of type of drum, drum speed and feed rate on sunflower threshing. Biosyst. Eng. 2002, 83, 413–421. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, S.; Chen, X. Design and experiment of spiral step cleaning device for ratooning rice based on CFD-DEM coupling. Comput. Electron. Agric. 2024, 224, 109207. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, H.; Li, Q. Modelling and simulation of the grain threshing process based on the discrete element method. Comput. Electron. Agric. 2020, 178, 105790. [Google Scholar] [CrossRef]
- Wu, J.; Tang, Q.; Mu, S.; Yang, X.; Jiang, L.; Hu, Z. Design and test of self-leveling system for cleaning screen of grain combine harvester. Agriculture 2023, 13, 377. [Google Scholar] [CrossRef]
- Que, K.; Tang, Z.; Wang, T.; Su, Z.; Ding, Z. Effects of Unbalanced Incentives on Threshing Drum Stability during Rice Threshing. Agriculture 2024, 14, 777. [Google Scholar] [CrossRef]
- Xu, P.; Dai, F.; Shi, R.; Zhao, W.; Song, X.; Zhao, Q.; Zhao, Y. Contact parameter calibration for flax threshing materials using machine learning and the Brazil nut effect. Powder Technol. 2024, 446, 120190. [Google Scholar] [CrossRef]
- Dai, F.; Xu, P.; Yuan, Z.; Shi, R.; Zhao, Y.; Song, X.; Zhao, W. Simulation and Optimization Experiment: Working Process of a Cleaning Device for Flax Combine Harvester. Agriculture 2023, 13, 2123. [Google Scholar] [CrossRef]
- Santiago, A.A.; Vargas, J.; Pérez, L.; Corona-García, C.; Alfonso, I. Mathematical and finite element analysis estimations of the reinforcement effect on Young’s modulus of polymer membrane/montmorillonite clay nanocomposites. Polym. Compos. 2021, 42, 2112–2121. [Google Scholar] [CrossRef]
- Foulk, J.A.; Akin, D.E.; Dodd, R.B. Processability of flax plant stems into functional bast fibers. Compos. Interfaces 2008, 15, 147–168. [Google Scholar] [CrossRef]
- Bu, L.; Chen, C.; Hu, G.; Zhou, J.; Adilet, S.; Chen, J. Investigating the dynamic behavior of an apple branch-stem-fruit model using experimental and simulation analysis. Comput. Electron. Agric. 2021, 186, 106224. [Google Scholar] [CrossRef]
- Zhang, D.; Yi, S.; Zhang, J.; Bao, Y. Establishment of millet threshing and separating model and optimization of harvester parameters. Alex. Eng. J. 2022, 61, 11251–11265. [Google Scholar] [CrossRef]
- Kunaev, V.; Bazarov, B.; Tavshanov, I.; Kadyrov, A.; Abdugaliyeva, G.; Kydyrbayeva, S. Evaluation of the effect of enrichment of slag aggregate for pavement subbase by grains density on its physical and mechanical characteristics. Results Eng. 2023, 18, 101181. [Google Scholar] [CrossRef]
- Feng, X.; Wang, L.; Bi, S.; Wang, B.; Ma, Z.; Gao, Y. Effects of Threshing Devices, Maize Varieties and Moisture Content of Grains on the Percentage of Maize Grains Broken in Harvesting. Agronomy 2023, 13, 1615. [Google Scholar] [CrossRef]
- Dai, F.; Song, X.; Guo, W.; Zhao, W.; Zhang, F.; Zhang, S. Simulation and test on separating cleaning process of flax threshing material based on gas-solid coupling theory. Int. J. Agric. Biol. Eng. 2020, 13, 73–81. [Google Scholar] [CrossRef]
- Xiao, F.; Luo, M.; Huang, F.; Zhou, M.; An, J.; Kuang, S.; Yu, A. CFD–DEM investigation of gas-solid flow and wall erosion of vortex elbows conveying coarse particles. Powder Technol. 2023, 424, 118524. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Zheng, M.; Ma, Z.; Zhao, Z.; Wang, C. Theoretical analysis and finite element simulation of a rice kernel obliquely impacted by a threshing tooth. Biosyst. Eng. 2013, 114, 146–156. [Google Scholar]
- Pérez, L.; Mercado, R.; Alfonso, I. Young’s modulus estimation for CNT reinforced metallic foams obtained using different space holder particles. Compos. Struct. 2017, 168, 26–32. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Wang, X.; Gu, X.; Zhang, B.; Liu, S. Rice threshing state prediction of threshing cylinder undergoing unbalanced harmonic response. Comput. Electron. Agric. 2023, 204, 107547. [Google Scholar] [CrossRef]
- Dudarev, I. A review of fiber flax harvesting: Conditions, technologies, processes and machines. J. Nat. Fibers 2022, 19, 4496–4508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).