3.1. Response Surface Analysis
The treatment combinations of the three factors investigated (
Table 1) were employed in the slow pyrolysis of the PKS to obtain the corresponding biochar yield, as defined in Equation (1) and summarized in
Table 2. Analysis of variance (ANOVA) was performed on the dataset summarized in
Table 2 to determine the significance of the model, individual factors, their interaction effect, the quadratic effect, and the cubic effect. The significance of the model and the effects were evaluated using probability (
p-value) and Fischer variation (F-value). The details of the ANOVA analysis are presented in
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7. The values in
Table 2 are presented in coded form, which refers to how the experimental variables (factors) were represented during the design and analysis process. The coded values −1, 0, and +1 are standardized values of the variables representing the low level, center point, and high level, respectively.
In order to determine the best model that fit the experimental data obtained from the BBD, five response models, namely, linear, two-factor-interaction (2FI), mean, quadratic, and cubic, were evaluated using ANOVA, as summarized in
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7. In
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7, the source of variation refers to the different components or factors that contributed to the total variability observed in the data. It identified where the variation came from in the dataset, allowing for the assessment of the impact of different factors on the dependent variables. The sum of squares is a term used to quantify the total variation in data, which it partitions into components attributed to different sources of variation. It measures how much variation exists due to specific factors or residual variability. The df, which stands for degree of freedom, denotes the number of independent values that can vary in the computation of a statistic estimate. In the context of ANOVA, it helps to partition the total variability into components attributed to a specific source. The mean square (MS) measures the average variation for a given source of variation. It is often employed to compare the variability explained by factors to the unexplained variability in the data. F-value is a test statistical parameter used to determine whether factors have a significant effect on the response. The
p-value denotes the probability of observing an F-statistic as extreme as the calculated F-value, assuming a null hypothesis is true. It is a measure of statistical significance for the factor being tested.
Table 3 summarizes the ANOVA results for the response surface linear model. It can be seen that the response surface linear model was significant, as indicated by the
p-values (<0.05). However, only the pyrolysis temperature was significant among the three factors. The significance of the lack of fit shows that the response surface linear model was not suitable for analyzing the dataset. The ANOVA result in
Table 4 indicates that the response surface 2FI model was also significant since the
p-value value was less than 0.05. The ANOVA also revealed that only the pyrolysis temperature was significant, while the flow rate of N
2 and the time on stream were not significant. The
p-value for the lack of fit of the response surface 2FI model was >0.05, which signifies that the model did not fit the dataset. The ANOVA result of the response surface mean model in
Table 5 shows that the model could not fit the dataset as there were no values obtained for the
p-value, which is also supported by the significant
p-value obtained for the lack of fit. In
Table 6, the ANOVA result of the response surface quadratic model shows that the model was significant since the
p-value was less than 0.05. Moreover, the three factors were statistically significant. The lack of fit was not significant; hence, the model was appropriate in explaining the effects of the factors on the biochar yield. Similarly, the ANOVA results of the response surface cubic model in
Table 7 show that the model was suitable for fitting the dataset.
The comparison between the five models based on the coefficient of determination (R
2), adjusted R
2, predicted R
2, adequate precision, and
p-value is summarized in
Table 8. The R
2 measured how well the statistical model explained the variation in the dependent variable. It helped to quantify the total variability in the response variable that was explained by the independent variable in the model. A value of R
2 close to 1 implied that the model explained a large proportion of the variability in the response variable. An R
2 close to 0 indicated that the model explained very little of the variability. The adjusted R
2 is a statistical parameter that helps to refine the R
2 metrics that adjust the number of predictors in a model. The adjusted R
2 accounted for the number of predictors and only increased if a new predictor improved the model significantly. The predicted R
2 measured how well the model predicted unseen data. The predicted R
2 focused on the model’s performance on validation or test data, providing an estimate of its predictive accuracy. Adequate precision helped to evaluate the quality of the model’s predictions relative to the noise in the data. It provided a signal-to-noise ratio, helping assess whether the model was sufficiently precise to navigate the design space. The comparison of the different models based on the values of the statistical parameters revealed that the response surface quadratic model was the best in modeling the datasets as indicated by bold text in
Table 8.
The response surface quadratic model, being the best, was further analyzed to determine the effect of interaction between the three factors, namely, pyrolysis temperature, flow rate of N
2, and time on stream. From the ANOVA analysis for the response surface quadratic model, it can be seen that the interaction effect between pyrolysis temperature and flow rate of N
2, pyrolysis temperature and time on stream, and flow rate of N
2 and time on stream were not significant since the
p-values were greater than 0.05. This implied that each of the factors had standalone effects on the biochar yield.
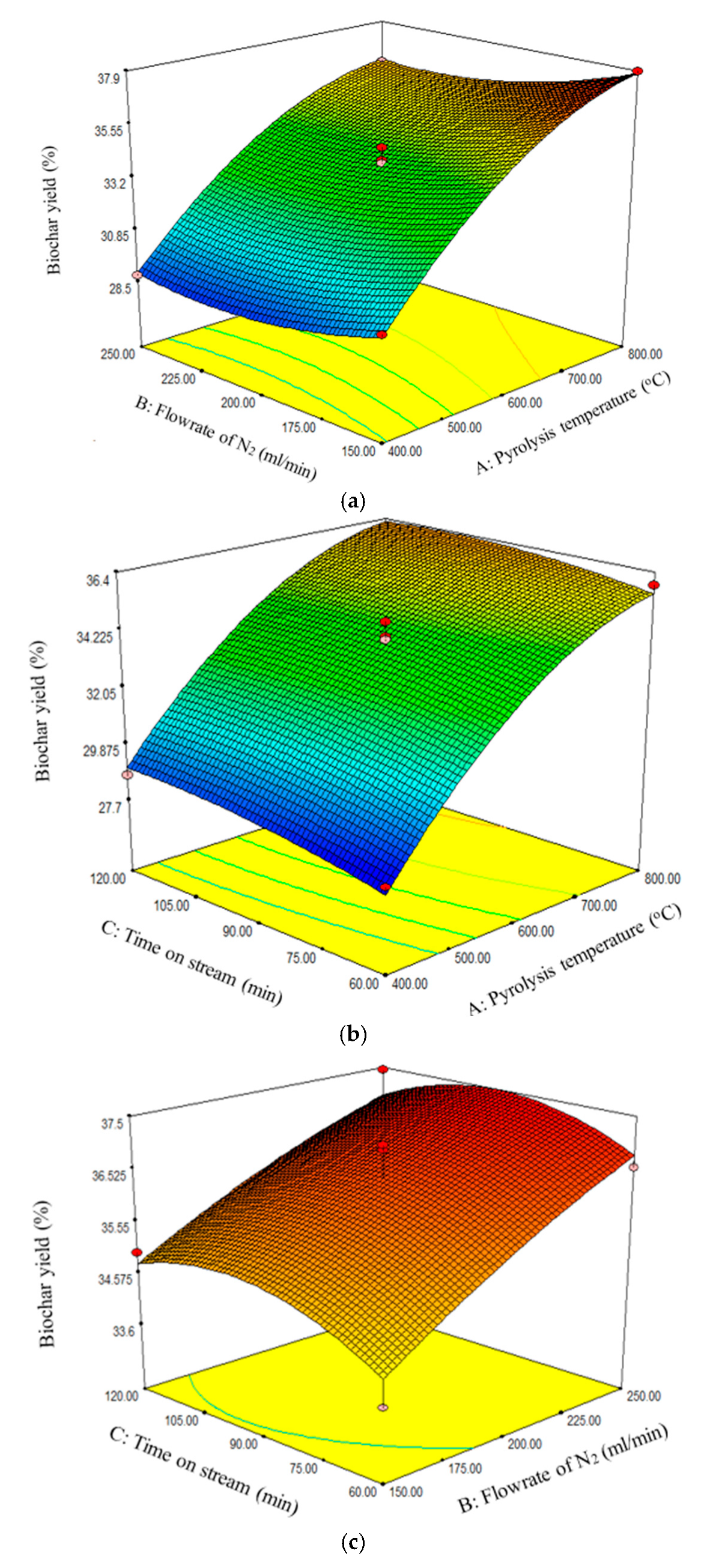
Figure 2a–c reveal that the biochar yield increased with increasing pyrolysis temperature and N
2 flow rate. However,
Figure 2c reveals that the biochar yield attained maximum value at 90 min.
3.3. Predictive Modeling
As shown in
Table 10, four ANN algorithms, namely, narrow, medium, wide, and optimized ANNs, were configured and employed to model biochar yield prediction from the pyrolysis process. The number of fully connected layers, iteration limit, regularization strength, standardized data, activation function, and size of the layers were considered the hyperparameters. The narrow ANN consisted of one fully connected layer with 10 hidden neurons. It can be seen that the biochar yield predicted, and the actual value were strongly correlated, as revealed by the R
2 of 0.900 and RMSE and MAE of 0.941 and 0.775, respectively. Both the medium ANN and the wide ANN, which consisted of 25 and 100 hidden neurons, respectively, also had robust but lower performance compared with the narrow and optimized ANNs. Amongst the four ANN models, the optimized architecture displayed the best performance, as indicated by the R
2, RMSE, and MAE values indicated by bold text in
Table 10. The predictive errors of the optimized ANN were slightly minimized, as indicated by the RMSE and MAE of 0.936 and 0.743, respectively. The performance of the optimized ANN can be attributed to a well-finetuned network architecture, the hyperparameters, and the training process resulting in higher accuracy on both training and unseen data.
The feature analysis shown in
Figure 4 revealed that the pyrolysis temperature significantly influenced the biochar yield. This was consistent with the ANOVA analysis for the response surface quadratic model, which had a
p-value far less than 0.05. The comparative analysis showed that the response surface quadratic model with an R
2 of 0.989 outperformed the optimized ANN, as indicated by the R
2 of 0.900.
3.4. Characterization of the Biochar
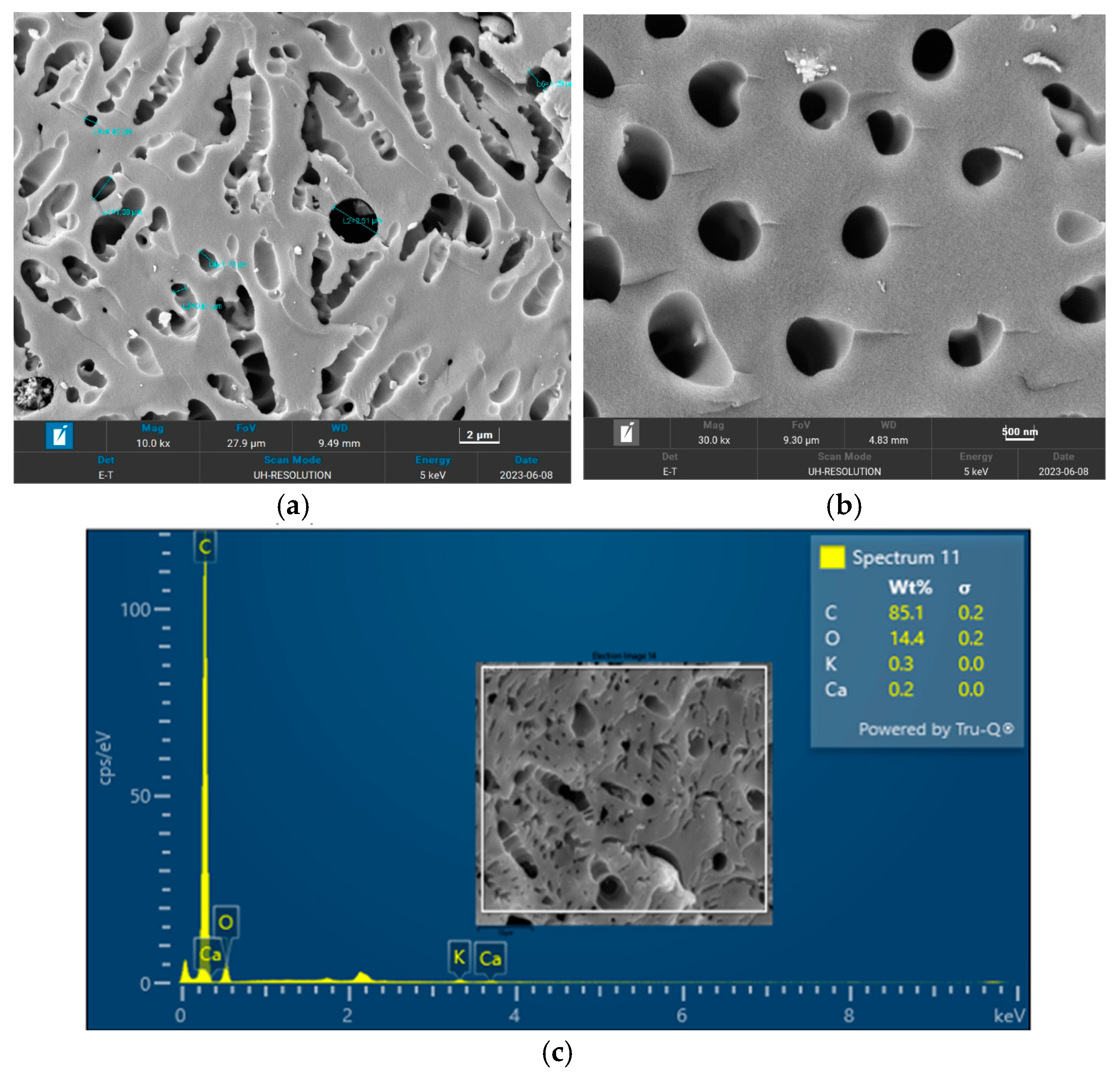
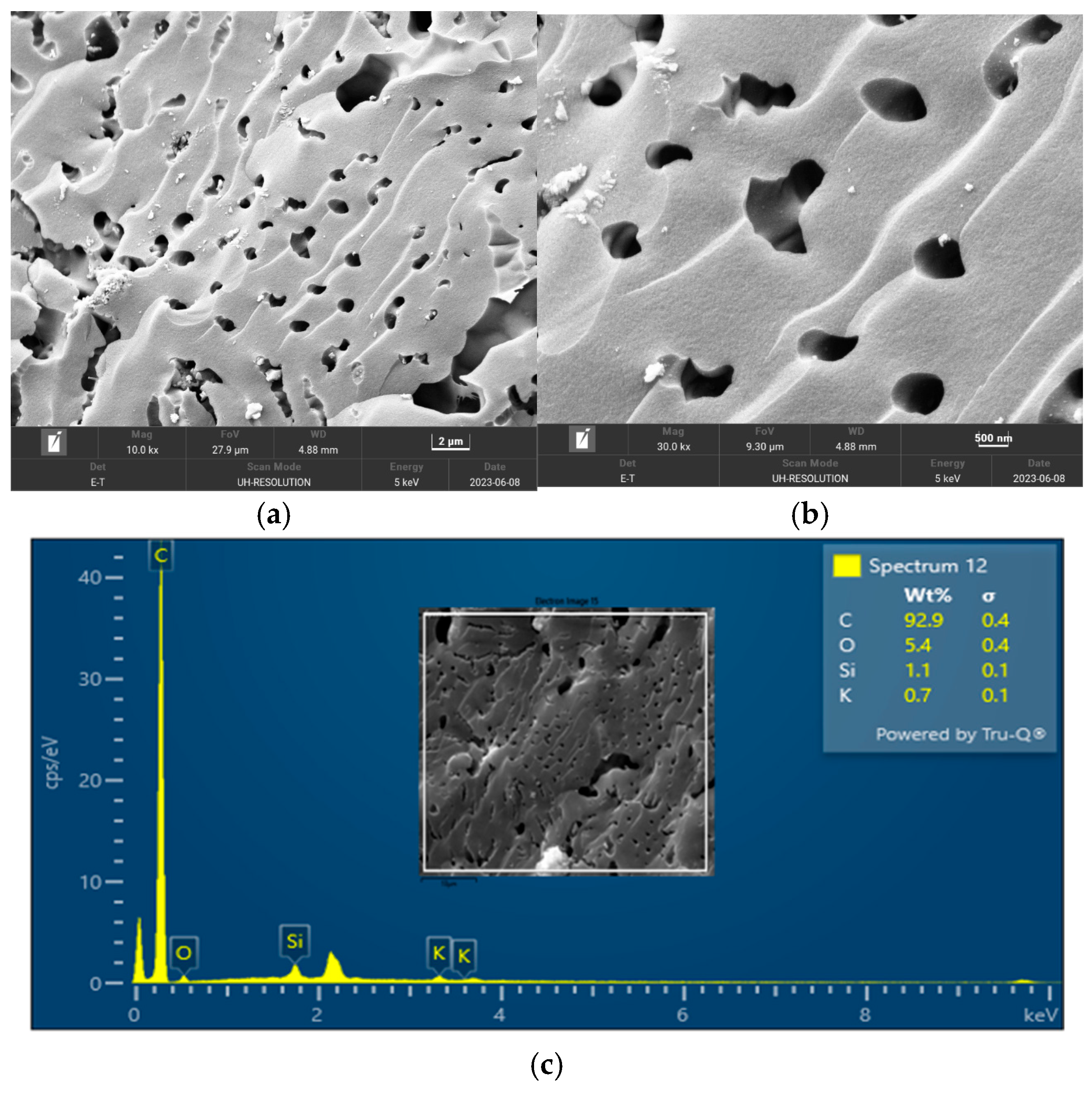
The surface morphology of biochar is an important characteristic that can be used to measure its adsorptive properties for onward applications as an adsorbent in wastewater treatment. The morphology of the biochar pyrolyzed at 400 °C, 600 °C, and 800 °C obtained from FESEM analysis are depicted in
Figure 5,
Figure 6 and
Figure 7, respectively. The biochar morphology pyrolyzed at a temperature range of 400–600 visibly showed the presence of pores with different dimensions. Studies have shown that the morphology of biochar is greatly influenced by the type of agricultural waste utilized for the slow pyrolysis process. Amongst the different biochars that have been produced from agricultural waste, biochar from PKS has demonstrated a high cavity or pore. The pyrolysis temperature can be seen to influence the pore distribution of the biochar as well as the elemental composition. The morphology of the biochar obtained in this study is consistent with that reported by Kassim et al. [
21] for a biochar nanocomposite prepared for the adsorptive removal of fluoroquinolones from an aqueous solution. At a pyrolysis temperature of 400 °C, the composition of carbon (C), oxygen, (O) potassium, and calcium (Ca) was obtained as 85.1%, 14.4%, 0.3%, and 0.3%, respectively. Also, at a pyrolysis temperature of 600 °C, the composition of C, O, K, and Ca was obtained as 92.1%, 7.2%, 0.5%, and 0.2%, respectively. At a pyrolysis temperature of 800 °C, the composition of C, O, K, and Ca were obtained as 92.9%, 5.4%, 1.1%, and 0.4%, respectively. It can be seen that the carbon content of the biochar from the pyrolysis increased with an increase in the pyrolysis temperature from 85.1% at 400 °C to 92.9% at 800 °C. Similarly, the composition of the K increased from 0.3% at 400 °C to 1.1% at 800 °C. The O composition in the biochar decreased from 14.4% at 400 °C to 5.4% at 600 °C. Studies have shown that elements such as C, O, K, and Ca have been detected in varying compositions in biochar produced from different agricultural wastes using EDX. Kong et al. [
22] reported compositions of approximately 88%, 17%, and 8% for biochar produced from PKS at 500 °C. Moreover, the elemental composition of the biochar obtained in this study is consistent with that reported by Giorcelli et al. [
23], who investigated biochar obtained from different pyrolysis temperatures and used as filler in epoxy resin composites.
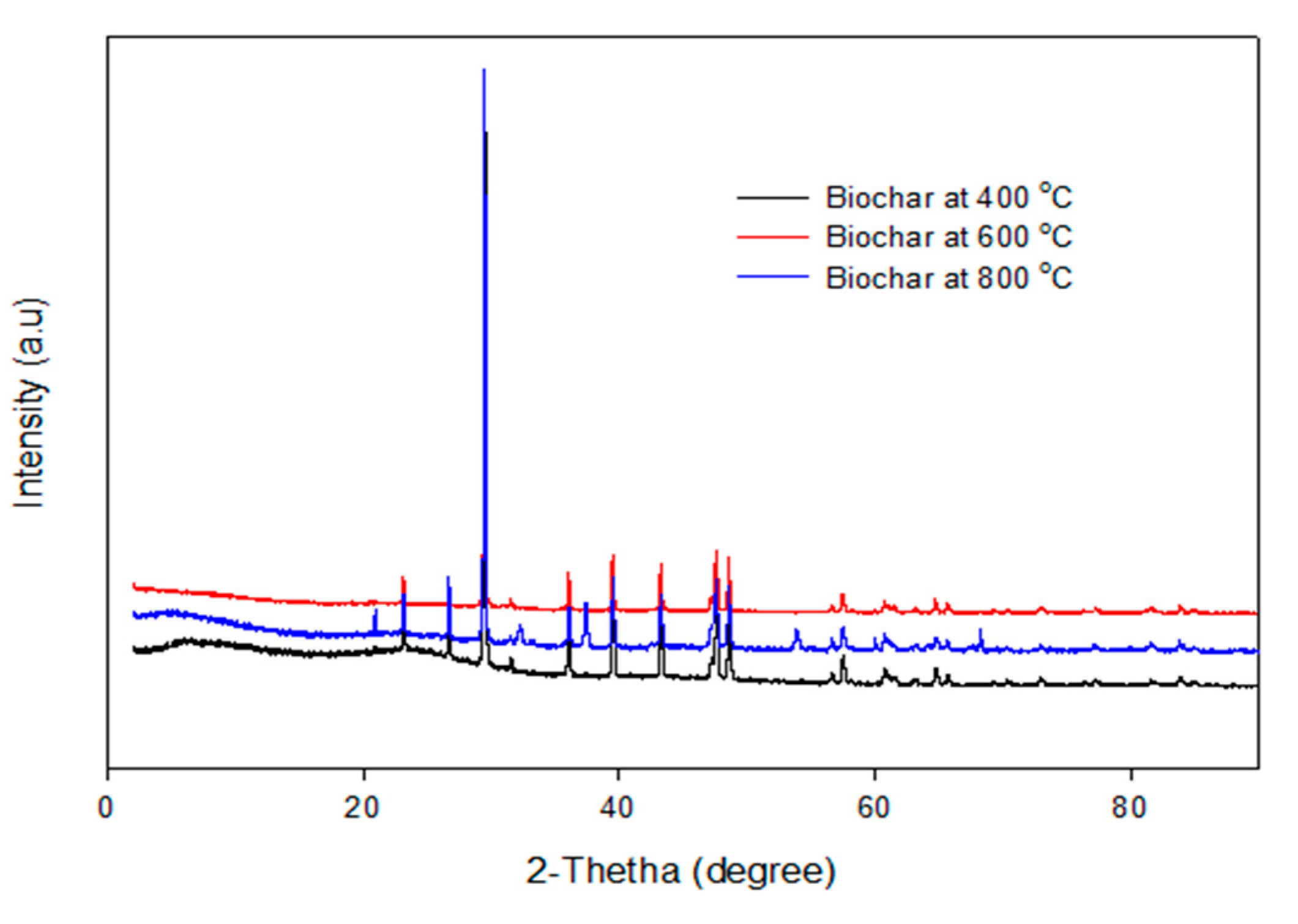
The XRD pattern of the biochars produced by the pyrolysis of PKS at 400 °C, 600 °C, and 800 °C are depicted in
Figure 8. It can be seen that the XRD pattern of the biochar obtained at temperatures of 400 °C, 600 °C, and 800 °C are identical, which implies that the crystallite makeup of the biochar was homogeneous, irrespective of the pyrolysis temperature. This is consistent with the EDX micrographs, which show identical elements obtained from the biochar obtained at different temperatures.
The N
2 physisorption analysis of the biochar obtained from the pyrolysis of the PKS at 400 °C, 600 °C, and 800 °C is depicted in
Figure 9. Although there are discrepancies in the adsorbed volumes, the isotherm’s shapes in the biochars produced at the same temperatures are comparable. It can be seen that the adsorption isotherms can be classified as type II. Adsorption isotherms of type II are commonly found in adsorbents characterized by a broad spectrum of pore sizes. The formation of the bilayer occurs after the complete formation of the monolayer, whereas the tri-layer is generated after the complete formation of the bilayer. The BET surface area, cumulative pore volume, and pore diameter of the biochar obtained at 400 °C were reported as 178.13 m
2/g, 0.020086 cm
3/g, and 5.6529 nm, respectively. Also, the BET surface area, cumulative pore volume, and pore diameter of the biochar obtained at 600 °C were reported as 146.22 m
2/gm
2/g, 0.026528 cm
3/g, and 5.5797 nm, respectively. For the biochar pyrolyzed at 800 °C, the BET surface area was estimated as 154.7591 m
2/g, cumulative pore volume was estimated as 0.032060 cm
3/g, and pore diameter was reported as 5.9025 nm. The pore diameters of the biochar greater than 2 nm were an indication that the biochar was a mesoporous material.
3.5. Potential Applications of the Biochar Produced
The characterization of the biochar obtained from the PKS pyrolysis revealed some impressive physicochemical properties, such as high porosity, high carbon content, and large surface area at the optimum conditions. Hence, the biochar can be used for many applications, such as soil amendment, carbon sequestration, water filtration, energy storage, and waste management. Brassard et al. [
24] and Adhikari et al. [
25] reported the potential of biochar obtained from the thermochemical valorization of different biomasses for soil amendment. The study revealed that the biochar derived from the pyrolysis of biomass such as palm kernel shell has the potential to enhance the chemical, physical, and biological properties of soil. Due to the high surface area recorded in this study, the biochar could help to remediate soil from any contamination, such as pesticides and heavy metals, through direct adsorption, thereby mitigating the leaching of such contaminants to water bodies. The leaching of ammonium and nitrate from Acrisol and Calcisol amended with holm oak biochar has been reported by Teutscherova et al. [
26]. Besides being used for soil amendment and the adsorption of organic contaminants, biochar derived from the pyrolysis of agricultural waste also finds wide application as a potential material for nutrient dynamics. Peiris et al. [
27] reported that biochar obtained from the pyrolysis of agriculture waste can help to enhance the retention of soil nutrients, thereby minimizing nutrient-leaching effects.