Comparison of the Soil Water, Vapor, and Heat Dynamics between Summer Maize and Bare Fields in Arid and Semi-Arid Areas
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site and Measurements
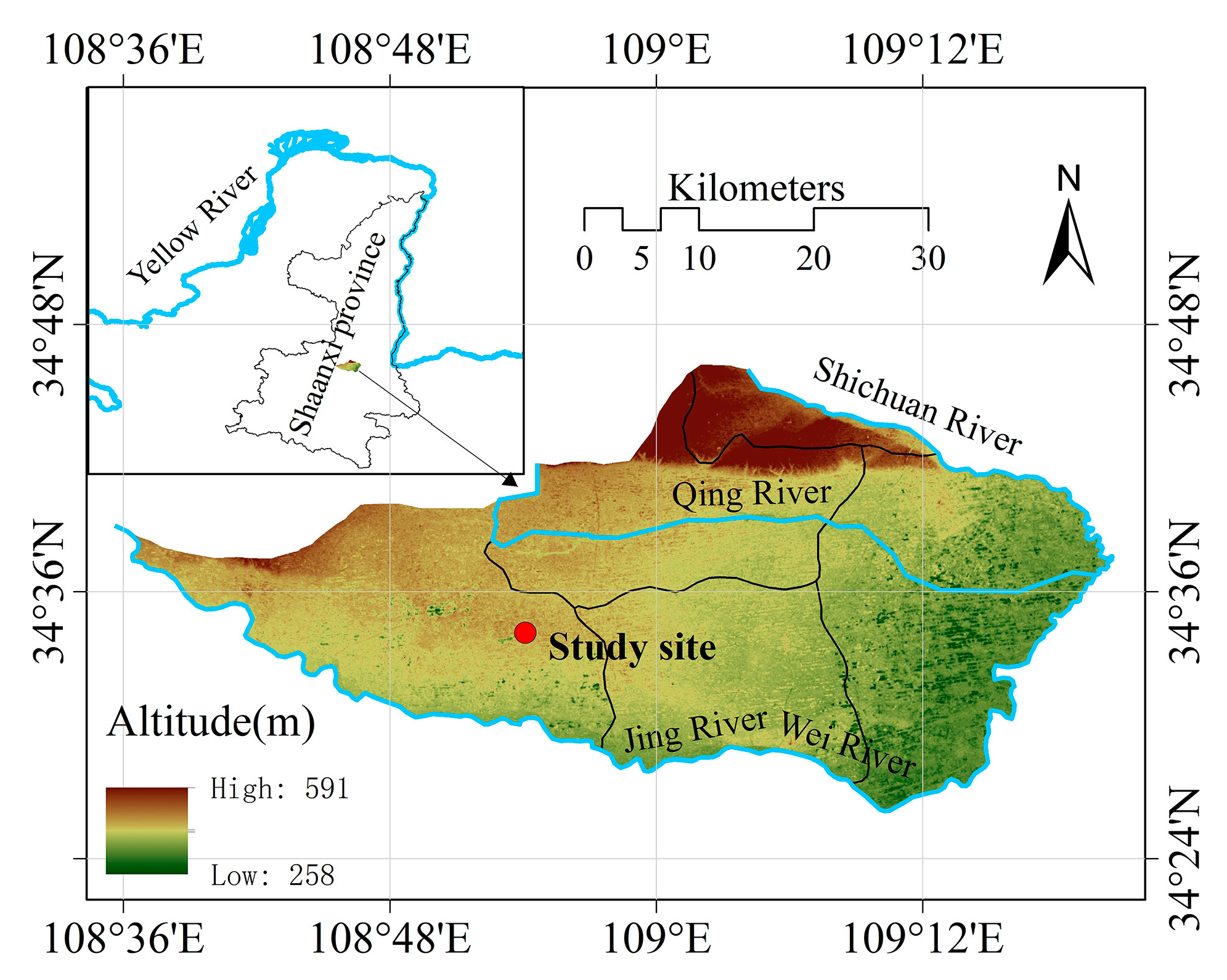
2.1.1. Study Site
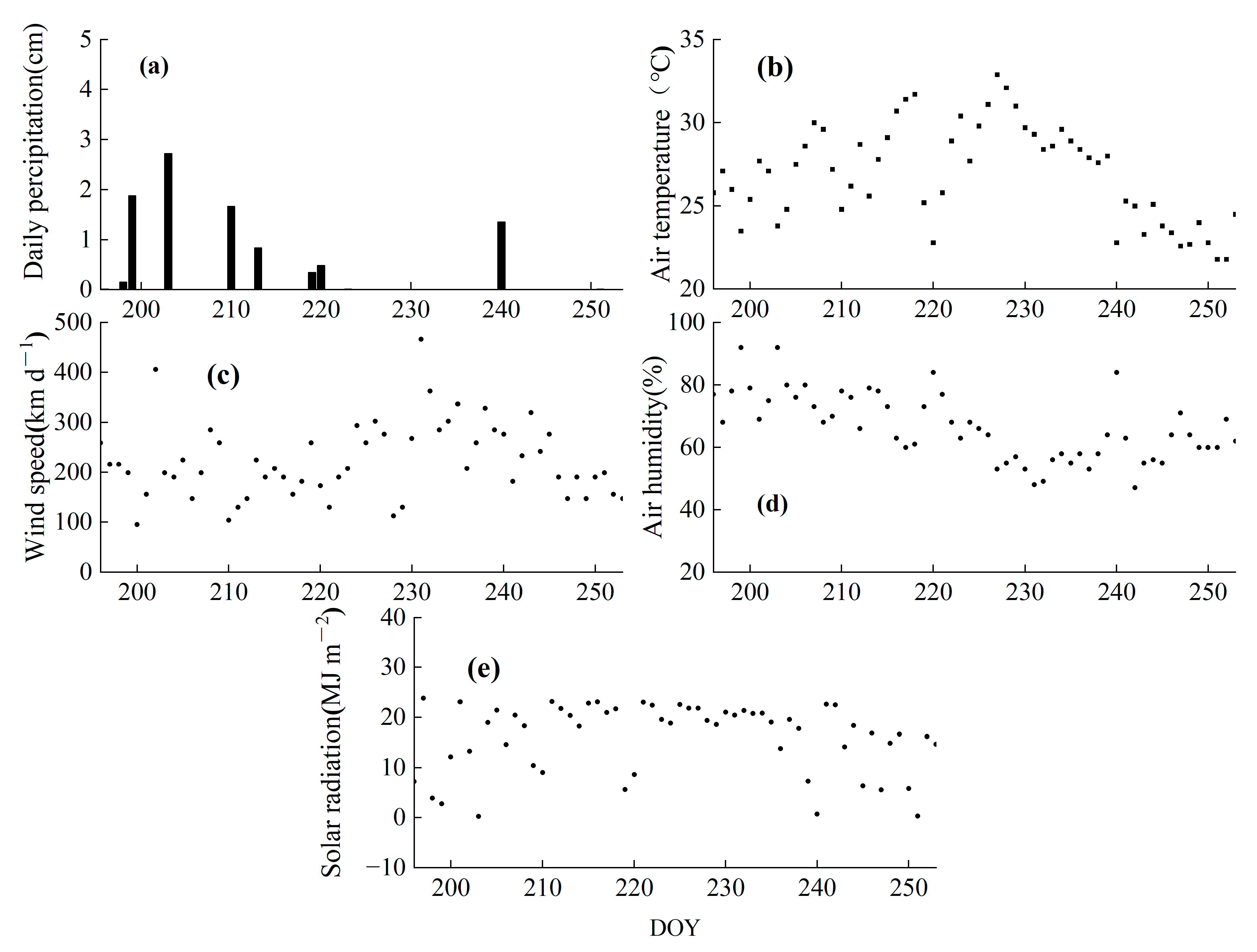
2.1.2. Field and Laboratory Measurements
2.2. Numerical Modeling
2.2.1. Liquid Water and Water Vapor Flow
2.2.2. Soil Heat Transport
2.2.3. Root Water Uptake Functions
2.2.4. Estimation of Potential ET
2.2.5. Initial and Boundary Conditions
2.2.6. Water Flow and Heat Transport Simulation
3. Results
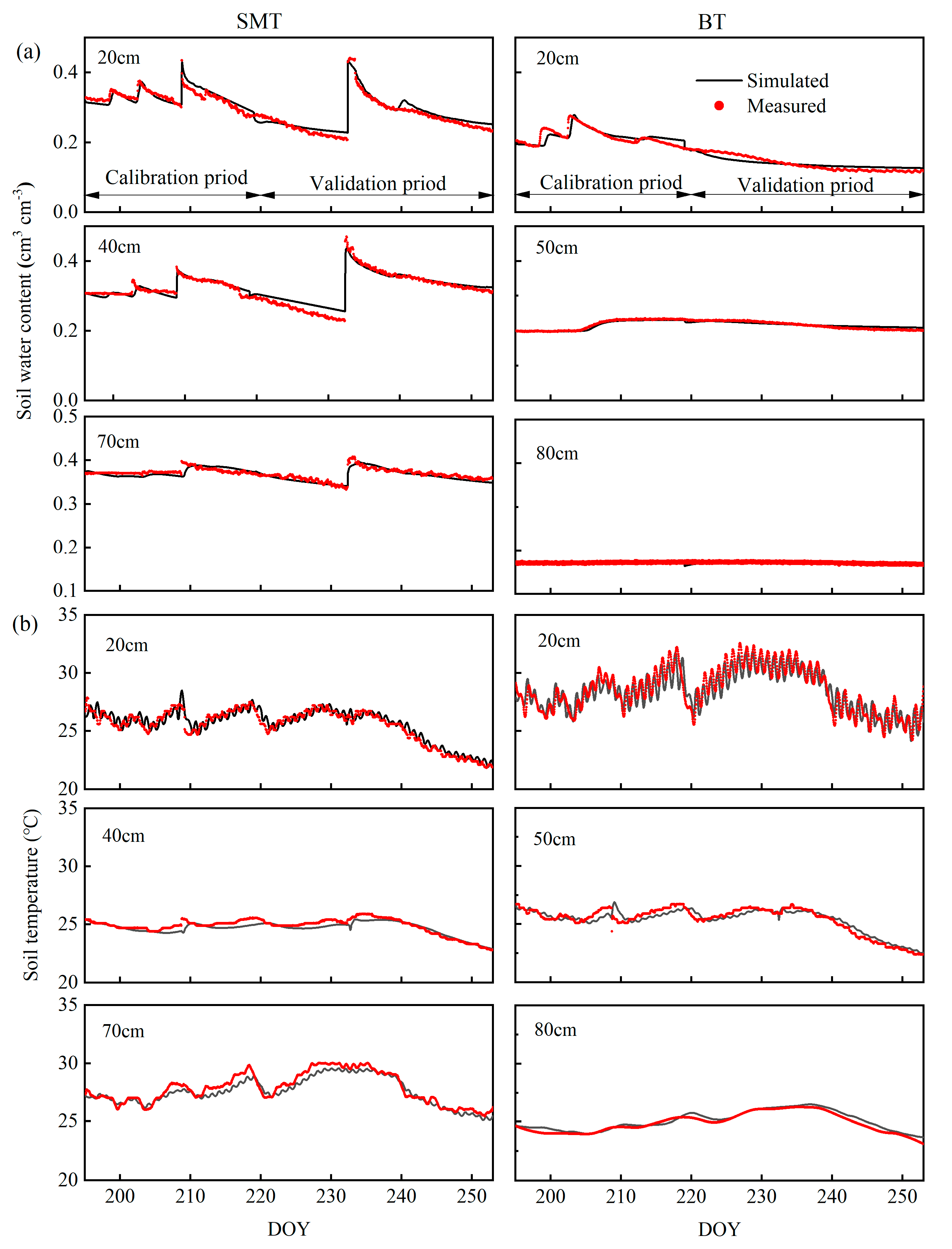
3.1. Model Calibration and Validation
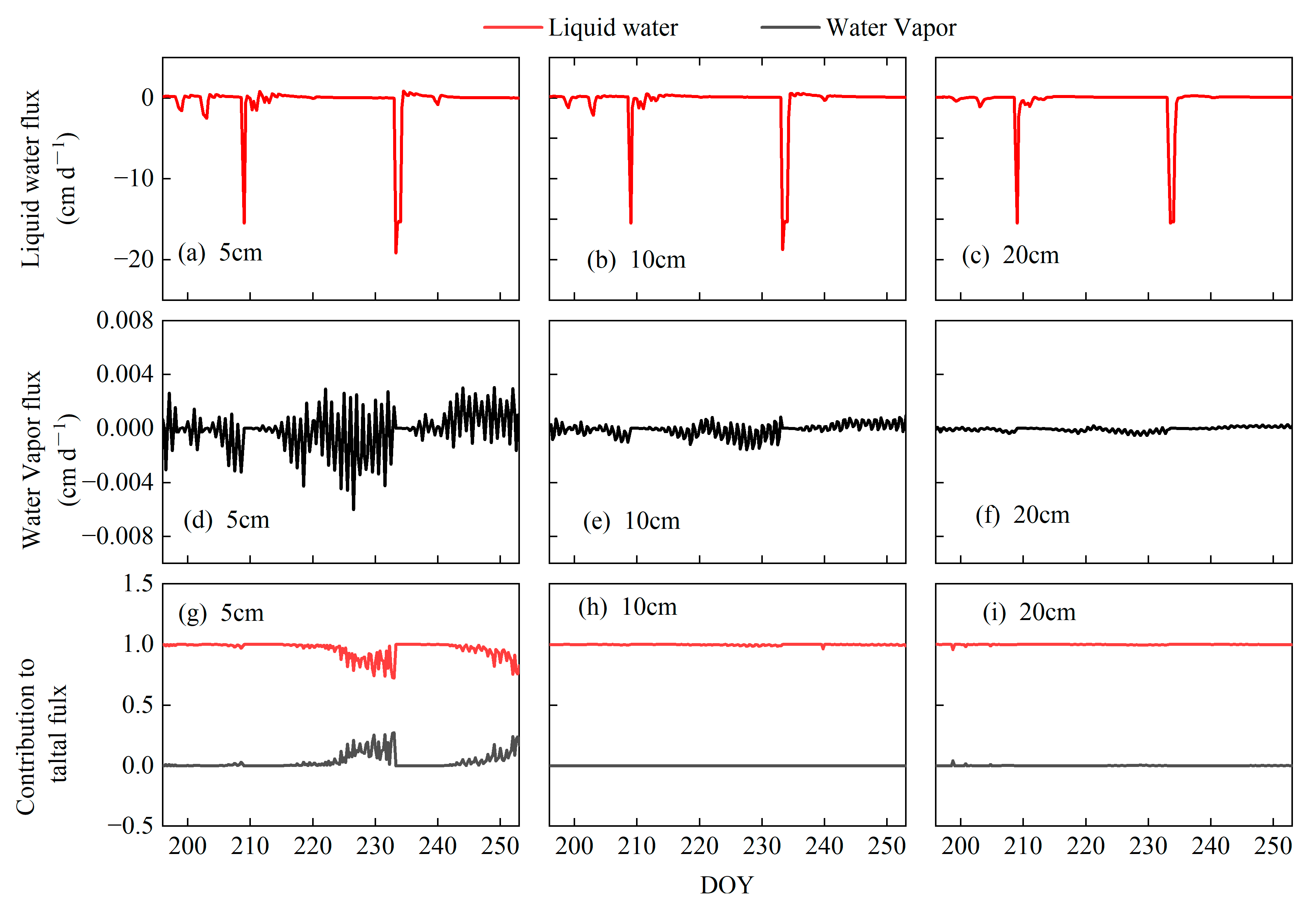
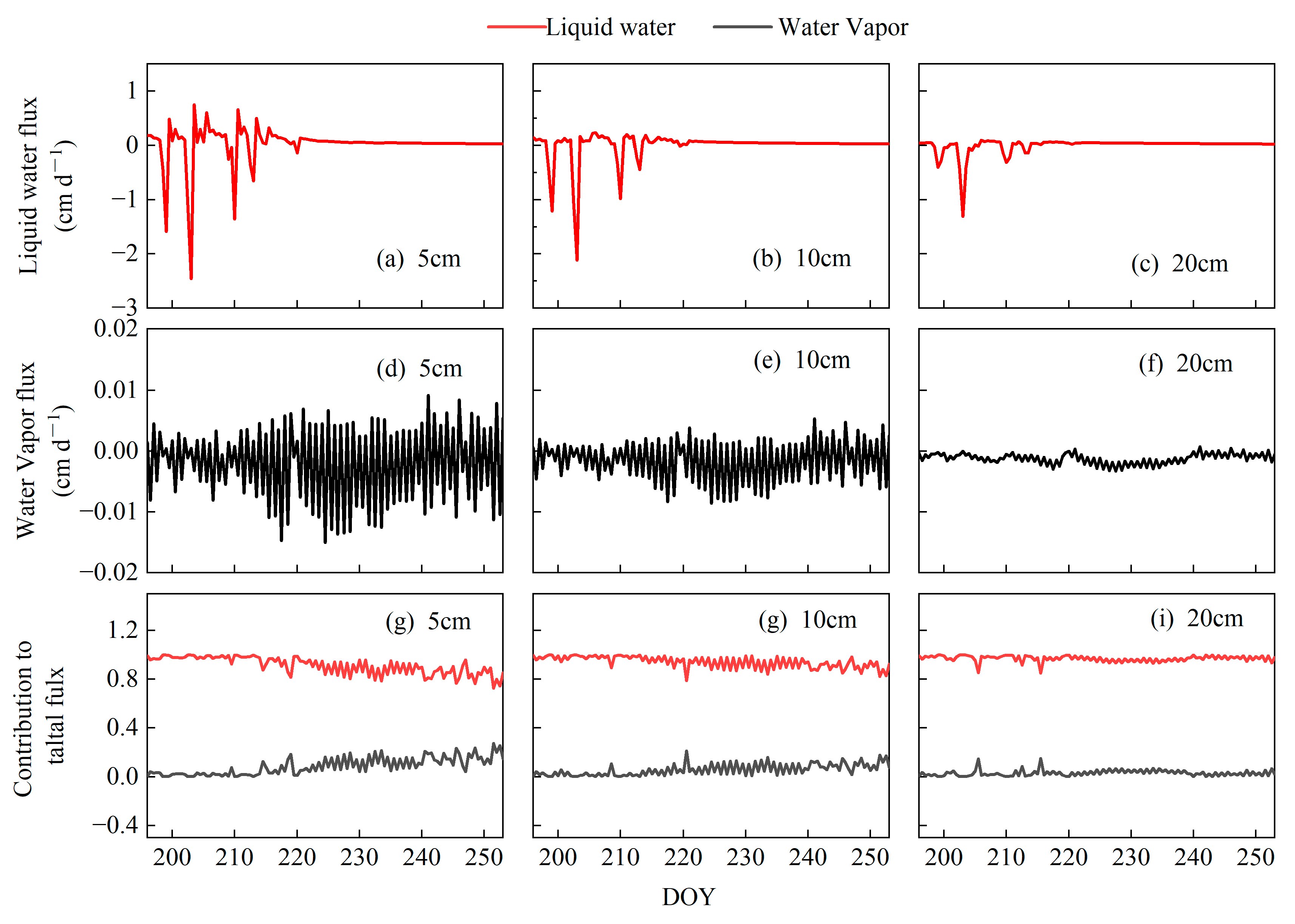
3.2. Liquid Water and Water Vapor during the Select Period
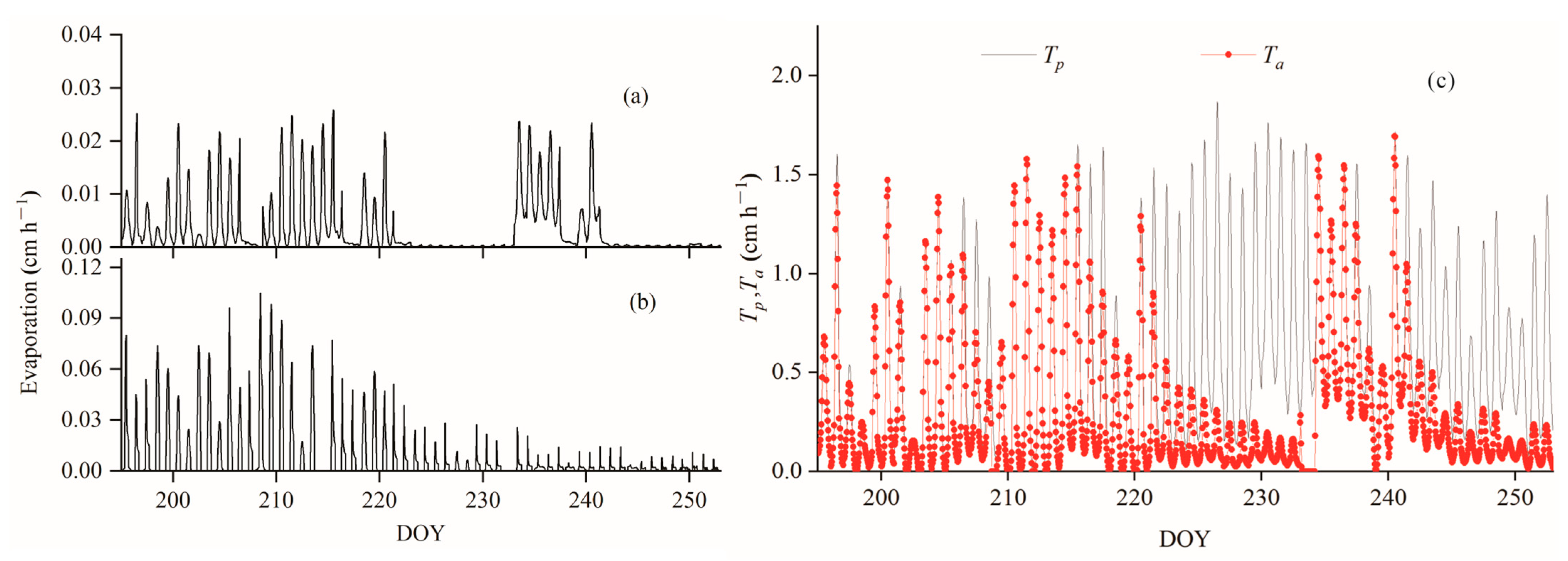
3.3. Evaporation and Transpiration
3.4. Water Dynamic in the Root Zone
4. Discussion
4.1. Modeling Implications
4.2. Influence of Irrigation on Water and Vapor Fluxes
4.3. Comparison of Water and Temperature Regimes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, P.; Ren, L. Evaluating the saline water irrigation schemes using a distributed agro-hydrological model. J. Hydrol. 2021, 594, 125688. [Google Scholar] [CrossRef]
- Nakayama, T. Simulation of the effect of irrigation on the hydrologic cycle in the highly cultivated Yellow River Basin. Agric. For. Meteorol. 2011, 151, 314–327. [Google Scholar] [CrossRef]
- Cahill, A.T.; Parlange, M.B. On water vapor transport in field soils. Water Resour. Res. 1998, 34, 731–739. [Google Scholar] [CrossRef]
- Parlange, M.B.; Cahill, A.T.; Nielsen, D.R.; Hopmans, J.W.; Wendroth, O. Review of heat and water movement in field soils. Soil Tillage Res. 1998, 47, 5–10. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, C.; Liu, X.; Lu, Y.; Chen, Y.; Wei, Y.; Ma, Y. NDVI-based vegetation dynamics and their responses to climate change and human activities from 1982 to 2020: A case study in the Mu Us Sandy Land, China. Ecol. Indic. 2022, 137, 108745. [Google Scholar] [CrossRef]
- Hou, L.; Wang, X.-S.; Hu, B.X.; Shang, J.; Wan, L. Experimental and numerical investigations of soil water balance at the hinterland of the Badain Jaran Desert for groundwater recharge estimation. J. Hydrol. 2016, 540, 386–396. [Google Scholar] [CrossRef]
- Huang, J.; Hou, R.; Yang, H. Diurnal pattern of liquid water and water vapor movement affected by rainfall in a desert soil with a high water table. Environ. Earth Sci. 2015, 75, 73. [Google Scholar] [CrossRef]
- Milly, P.C.D. A Linear Analysis of Thermal Effects on Evaporation From Soil. Water Resour. Res. 1984, 20, 1075–1085. [Google Scholar] [CrossRef]
- Saito, H.; Šimůnek, J.; Mohanty, B.P. Numerical Analysis of Coupled Water, Vapor, and Heat Transport in the Vadose Zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.; Reedy, R.C.; Simunek, J.; Andraski, B.J. Variations in flow and transport in thick desert vadose zones in response to paleoclimatic forcing (0-90 kyr): Field measurements, modeling, and uncertainties. Water Resour. Res. 2003, 39, 1179. [Google Scholar] [CrossRef]
- Schelde, K.; Thomsen, A.; Heidmann, T.; Schjønning, P.; Jansson, P.E. Diurnal fluctuations of water and heat flows in a bare soil. Water Resour. Res. 1998, 34, 2919–2929. [Google Scholar] [CrossRef]
- Gomez-Rey, M.X.; Couto-Vazquez, A.; Gonzalez-Prieto, S.J. Nitrogen transformation rates and nutrient availability under conventional plough and conservation tillage. Soil Tillage Res. 2012, 124, 144–152. [Google Scholar] [CrossRef]
- Sharratt, B.S.; Gesch, R.W. Emergence of Polymer-Coated Corn and Soybean Influenced by Tillage and Sowing Date. Agron. J. 2008, 100, 585–590. [Google Scholar] [CrossRef]
- Taylor, S.A.; Cavazza, L. The Movement of Soil Moisture in Response to Temperature Gradients1. Soil Sci. Soc. Am. J. 1954, 18, 351–358. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Philip, J.R.; De Vries, D.A. Moisture movement in porous materials under temperature gradients. Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Cass, A.; Campbell, G.S.; Jones, T.L. Enhancement of Thermal Water Vapor Diffusion in Soil. Soil Sci. Soc. Am. J. 1984, 48, 25–32. [Google Scholar] [CrossRef]
- Nassar, I.N.; Horton, R. Water Transport in Unsaturated Nonisothermal Salty Soil: II. Theoretical Development. Soil Sci. Soc. Am. J. 1989, 53, 1330–1337. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; Wan, L.; Wen, J. Numerical analysis of air-water-heat flow in unsaturated soil: Is it necessary to consider airflow in land surface models? J. Geophys. Res. 2011, 116, D20107. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; Wan, L.; Wen, J. A simulation analysis of the advective effect on evaporation using a two-phase heat and mass flow model. Water Resour. Res. 2011, 47, W10529. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z. Water Movement and Heat Transfer Simulations in a Soil under Ryegrass. Biosyst. Eng. 2006, 95, 127–138. [Google Scholar] [CrossRef]
- Dahiya, R.; Ingwersen, J.; Streck, T. The effect of mulching and tillage on the water and temperature regimes of a loess soil: Experimental findings and modeling. Soil Tillage Res. 2007, 96, 52–63. [Google Scholar] [CrossRef]
- Kader, M.A.; Nakamura, K.; Senge, M.; Mojid, M.A.; Kawashima, S. Numerical simulation of water- and heat-flow regimes of mulched soil in rain-fed soybean field in central Japan. Soil Tillage Res. 2019, 191, 142–155. [Google Scholar] [CrossRef]
- Zheng, C.; Šimůnek, J.; Lu, Y.; Liu, X.; Shi, C.; Li, H. Monitoring and modeling the coupled movement of water, vapor, and energy in arid areas. J. Hydrol. 2020, 590, 125528. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; Van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media. Version 4.17, HYDRUS Software Series 3; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Zhao, Y.; Peth, S.; Horn, R.; Krümmelbein, J.; Ketzer, B.; Gao, Y.; Doerner, J.; Bernhofer, C.; Peng, X. Modeling grazing effects on coupled water and heat fluxes in Inner Mongolia grassland. Soil Tillage Res. 2010, 109, 75–86. [Google Scholar] [CrossRef]
- Du, C.; Yu, J.; Wang, P.; Zhang, Y. Analysing the mechanisms of soil water and vapour transport in the desert vadose zone of the extremely arid region of northern China. J. Hydrol. 2018, 558, 592–606. [Google Scholar] [CrossRef]
- Liu, X.; Gao, W.; Sun, S.; Hu, A.; He, Y.; He, S.S. Responses of soil water dynamic processes and groundwater recharge to irrigation intensity and antecedent moisture in the vadose zone. Hydrol. Process. 2019, 33, 849–863. [Google Scholar] [CrossRef]
- Liu, X.; Guo, C.; He, S.; Zhu, H.; Li, J.; Yu, Z.; Qi, Y.; He, J.; Zhang, J.; Müller, C. Divergent gross nitrogen transformation paths in the topsoil and subsoil between abandoned and agricultural cultivation land in irrigated areas. Sci. Total Environ. 2020, 716, 137148. [Google Scholar] [CrossRef] [PubMed]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.J.; Heilman, J.L. Two-Dimensional Model for Water, Heat, and Solute Transport in Furrow-Irrigated Soil: II. Field Evaluation. Soil Sci. Soc. Am. J. 1996, 60, 1010–1021. [Google Scholar] [CrossRef]
- Chung, S.-O.; Horton, R. Soil heat and water flow with a partial surface mulch. Water Resour. Res. 1987, 23, 2175–2186. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements, FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; USA Salinity Laboratory, USDA, ARS: Riverside, CA, USA, 1991. [Google Scholar]
- Le Bourgeois, O.; Bouvier, C.; Brunet, P.; Ayral, P.A. Inverse modeling of soil water content to estimate the hydraulic properties of a shallow soil and the associated weathered bedrock. J. Hydrol. 2016, 541, 116–126. [Google Scholar] [CrossRef]
- Ket, P.; Oeurng, C.; Degré, A. Estimating Soil Water Retention Curve by Inverse Modelling from Combination of In Situ Dynamic Soil Water Content and Soil Potential Data. Soil Syst. 2018, 2, 55. [Google Scholar] [CrossRef]
- Asgarzadeh, H.; Mosaddeghi, M.R.; Dexter, A.R.; Mahboubi, A.A.; Neyshabouri, M.R. Determination of soil available water for plants: Consistency between laboratory and field measurements. Geoderma 2014, 226–227, 8–20. [Google Scholar] [CrossRef]
- Scharnagl, B.; Vrugt, J.A.; Vereecken, H.; Herbst, M. Inverse modelling of in situ soil water dynamics: Investigating the effect of different prior distributions of the soil hydraulic parameters. Hydrol. Earth Syst. Sci. 2011, 15, 3043–3059. [Google Scholar] [CrossRef]
- Mallants, D.; Mohanty, B.P.; Vervoort, A.; Feyen, J. Spatial analysis of saturated hydraulic conductivity in a soil with macropores. Soil Technol. 1997, 10, 115–131. [Google Scholar] [CrossRef]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 2003, 39, 1355. [Google Scholar] [CrossRef]
- Baroni, G.; Facchi, A.; Gandolfi, C.; Ortuani, B.; Horeschi, D.; van Dam, J.C. Uncertainty in the determination of soil hydraulic parameters and its influence on the performance of two hydrological models of different complexity. Hydrol. Earth Syst. Sci. 2010, 14, 251–270. [Google Scholar] [CrossRef]
- Werisch, S.; Grundmann, J.; Al-Dhuhli, H.; Algharibi, E.; Lennartz, F. Multiobjective parameter estimation of hydraulic properties for a sandy soil in Oman. Environ. Earth Sci. 2014, 72, 4935–4956. [Google Scholar] [CrossRef]
- Pinheiro, E.A.R.; de Jong van Lier, Q.; Inforsato, L.; Šimůnek, J. Measuring full-range soil hydraulic properties for the prediction of crop water availability using gamma-ray attenuation and inverse modeling. Agric. Water Manag. 2019, 216, 294–305. [Google Scholar] [CrossRef]
- Brunetti, G.; Šimůnek, J.; Bogena, H.; Baatz, R.; Huisman, J.A.; Dahlke, H.; Vereecken, H. On the Information Content of Cosmic-Ray Neutron Data in the Inverse Estimation of Soil Hydraulic Properties. Vadose Zone J. 2019, 18, 1–24. [Google Scholar] [CrossRef]
- Schelle, H.; Durner, W.; Iden, S.C.; Fank, J. Simultaneous Estimation of Soil Hydraulic and Root Distribution Parameters from Lysimeter Data by Inverse Modeling. Proc. Environ. Sci. 2013, 19, 564–573. [Google Scholar] [CrossRef]
- Eching, S.O.; Hopmans, J.W. Optimization of Hydraulic Functions from Transient Outflow and Soil Water Pressure Data. Soil Sci. Soc. Am. J. 1993, 57, 1167–1175. [Google Scholar] [CrossRef]
- Kool, J.B.; Parker, J.C.; van Genuchten, M.T. Determining Soil Hydraulic Properties from One-step Outflow Experiments by Parameter Estimation: I. Theory and Numerical Studies. Soil Sci. Soc. Am. J. 1985, 49, 1348–1354. [Google Scholar] [CrossRef]
- Milly, P.C.D. A Simulation Analysis of Thermal Effects on Evaporation From Soil. Water Resour. Res. 1984, 20, 1087–1098. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukla, M.K.; Mexal, J.G. Numerical Modeling of Water Fluxes in the Root Zone of a Mature Pecan Orchard. Soil Sci. Soc. Am. J. 2011, 75, 1667–1680. [Google Scholar] [CrossRef]
- Bittelli, M.; Ventura, F.; Campbell, G.S.; Snyder, R.L.; Gallegati, F.; Pisa, P.R. Coupling of heat, water vapor, and liquid water fluxes to compute evaporation in bare soils. J. Hydrol. 2008, 362, 191–205. [Google Scholar] [CrossRef]
- Jackson, R.D. Diurnal changes in soil water content during drying. In Field Soil Water Regime; Bruce, R.R., Ed.; Soil Science Society of America: Madison, WI, USA, 1973. [Google Scholar]
- Enz, J.W.; Brun, L.J.; Larsen, J.K. Evaporation and energy balance for bare and stubble covered soil. Agric. For. Meteorol. 1988, 43, 59–70. [Google Scholar] [CrossRef]
- Horton, R.; Bristow, K.L.; Kluitenberg, G.J.; Sauer, T.J. Crop residue effects on surface radiation and energy balance—Review. Theor. Appl. Climatol. 1996, 54, 27–37. [Google Scholar] [CrossRef]
- Heitman, J.L.; Xiao, X.; Horton, R.; Sauer, T.J. Sensible heat measurements indicating depth and magnitude of subsurface soil water evaporation. Water Resour. Res. 2008, 44, W00D05. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S.; Papendick, R.I.; Elliott, L.F. Simulation of heat and moisture transfer through a surface residue—Soil system. Agric. For. Meteorol. 1986, 36, 193–214. [Google Scholar] [CrossRef]
- Kader, M.A.; Senge, M.; Mojid, M.A.; Nakamura, K. Mulching type-induced soil moisture and temperature regimes and water use efficiency of soybean under rain-fed condition in central Japan. Int. Soil Water Conserv. Res. 2017, 5, 302–308. [Google Scholar] [CrossRef]


| Treatment | Soil Layer (cm) | Particle Size Distribution | Soil Texture | Bulk Density (g cm−3) | ||
|---|---|---|---|---|---|---|
| Sand (%) | Silt (%) | Clay (%) | ||||
| SMT | 0–30 | 10.04 | 74.89 | 15.07 | Silt Loam | 1.55 |
| 30–60 | 7.63 | 75.51 | 16.86 | Silt Loam | 1.57 | |
| 60–100 | 7.24 | 75.56 | 17.20 | Silt Loam | 1.66 | |
| BT | 0–30 | 9.7 | 74.1 | 16.2 | Silt Loam | 1.37 |
| 30–60 | 3.75 | 70.95 | 25.3 | Silt Loam | 1.54 | |
| 60–100 | 6.85 | 72.85 | 20.3 | Silt Loam | 1.44 | |
| Crop | Root Water Uptake Parameters | ||||||
|---|---|---|---|---|---|---|---|
| h0 (cm) | hopt (cm) | h2H (cm) | h2L (cm) | h3 (cm) | r2H (cm d−1) | r2L (cm d−1) | |
| Corn | −15 | −30 | −325 | −600 | −80,000 | 0.5 | 0.1 |
| Treatment | Soil Layer (cm) | θr | θs | α | n | Ks |
|---|---|---|---|---|---|---|
| SMT | 0–30 | 0.076 | 0.435 | 0.012 | 1.26 | 13.56 |
| 30–60 | 0.078 | 0.44 | 0.02 | 1.17 | 17.2 | |
| BT | 60–100 | 0.083 | 0.435 | 0.02 | 1.17 | 17.2 |
| 0–30 | 0.089 | 0.435 | 0.012 | 1.26 | 11.2 | |
| 30–60 | 0.086 | 0.446 | 0.011 | 1.4 | 15.6 | |
| 60–100 | 0.086 | 0.446 | 0.014 | 1.18 | 15.6 |
| Treatment | Soil Depth (cm) | Soil Water Content | Soil Temperature | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | ||||||
| RMSE (cm3 cm−3) | NSE | RMSE (cm3 cm−3) | NSE | RMSE (°C) | NSE | RMSE (°C) | NSE | ||
| SMT | 20 | 0.014 | 0.641 | 0.012 | 0.93 | 0.588 | 0.379 | 0.404 | 0.939 |
| 40 | 0.01 | 0.749 | 0.015 | 0.923 | 0.467 | 0.077 | 0.323 | 0.942 | |
| 70 | 0.008 | −0.618 | 0.006 | 0.776 | 0.355 | −0.317 | 0.284 | 0.888 | |
| BT | 20 | 0.014 | 0.611 | 0.01 | 0.788 | 0.995 | 0.534 | 1.064 | 0.784 |
| 50 | 0.003 | 0.963 | 0.005 | 0.778 | 0.524 | 0.681 | 0.48 | 0.907 | |
| 80 | 0.001 | −0.152 | 0.002 | −0.12 | 0.218 | 0.772 | 0.272 | 0.906 | |
| Treatment | Soil Depth (cm) | qlh | qvh | qlT | qvT |
|---|---|---|---|---|---|
| SMT | 2 | 99.4% | 0.0% | 0.5% | 0.1% |
| 5 | 99.6% | 0.0% | 0.4% | 0.0% | |
| 10 | 99.4% | 0.0% | 0.6% | 0.0% | |
| 20 | 99.6% | 0.0% | 0.4% | 0.0% | |
| 50 | 97.7% | 0.0% | 2.3% | 0.0% | |
| 100 | 98.4% | 0.0% | 1.6% | 0.0% | |
| BT | 2 | 81.9% | 0.7% | 0.4% | 17.0% |
| 5 | 84.6% | 0.1% | 1.5% | 13.8% | |
| 10 | 86.2% | 0.0% | 3.0% | 10.8% | |
| 20 | 90.2% | 0.0% | 3.8% | 6.0% | |
| 50 | 94.5% | 0.0% | 3.1% | 2.4% | |
| 100 | 78.5% | 0.0% | 15.5% | 6.0% |
| Treatment | P | I | DP | E | T | ∆S |
|---|---|---|---|---|---|---|
| SMT | 89.3 | 310 | 174.9 | 50.1 | 178.9 | −42.41 |
| BT | 89.3 | 0 | 0.1617 | 104.39 | 0 | −15.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Liu, X.; Zheng, C.; Lu, Y.; He, J.; He, Y. Comparison of the Soil Water, Vapor, and Heat Dynamics between Summer Maize and Bare Fields in Arid and Semi-Arid Areas. Agronomy 2023, 13, 1171. https://doi.org/10.3390/agronomy13041171
Gao W, Liu X, Zheng C, Lu Y, He J, He Y. Comparison of the Soil Water, Vapor, and Heat Dynamics between Summer Maize and Bare Fields in Arid and Semi-Arid Areas. Agronomy. 2023; 13(4):1171. https://doi.org/10.3390/agronomy13041171
Chicago/Turabian StyleGao, Wande, Xiuhua Liu, Ce Zheng, Yudong Lu, Junqi He, and Yi He. 2023. "Comparison of the Soil Water, Vapor, and Heat Dynamics between Summer Maize and Bare Fields in Arid and Semi-Arid Areas" Agronomy 13, no. 4: 1171. https://doi.org/10.3390/agronomy13041171
APA StyleGao, W., Liu, X., Zheng, C., Lu, Y., He, J., & He, Y. (2023). Comparison of the Soil Water, Vapor, and Heat Dynamics between Summer Maize and Bare Fields in Arid and Semi-Arid Areas. Agronomy, 13(4), 1171. https://doi.org/10.3390/agronomy13041171









