The Effect of Plug Height and Inflow Rate on Water Flow Characteristics in Furrow Irrigation
Abstract
:1. Introduction
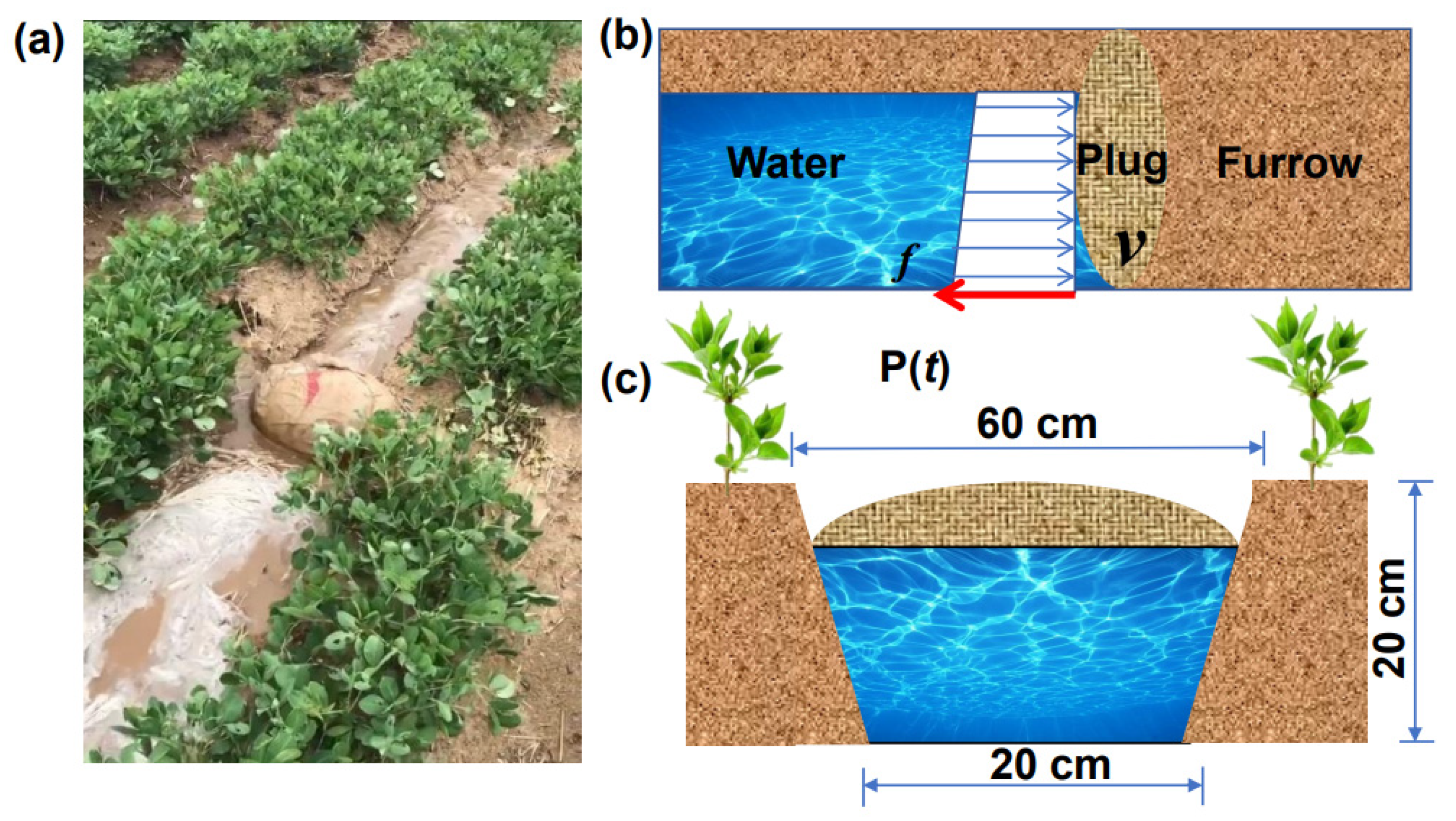
2. Materials and Methods
2.1. FLOW-3D Simulation
2.1.1. Governing Equations
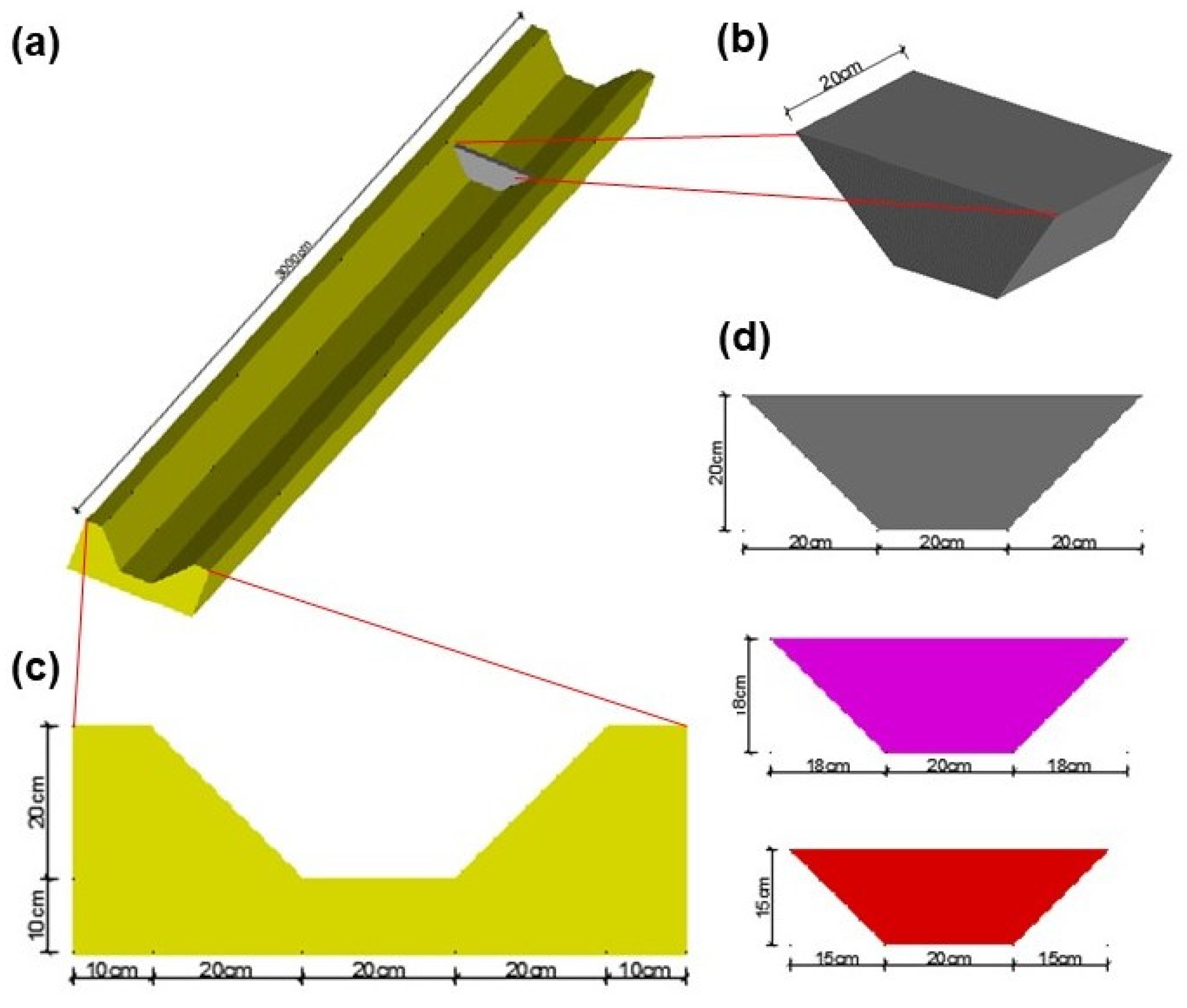
2.1.2. Grid Division
2.1.3. Boundary Conditions
2.1.4. Working Conditions
2.2. HYDRUS-2D Simulation
2.2.1. Governing Equations
2.2.2. Boundary Conditions and Initial Conditions
2.3. Irrigation Uniformity
2.4. Cumulative Infiltration
3. Results and Discussion
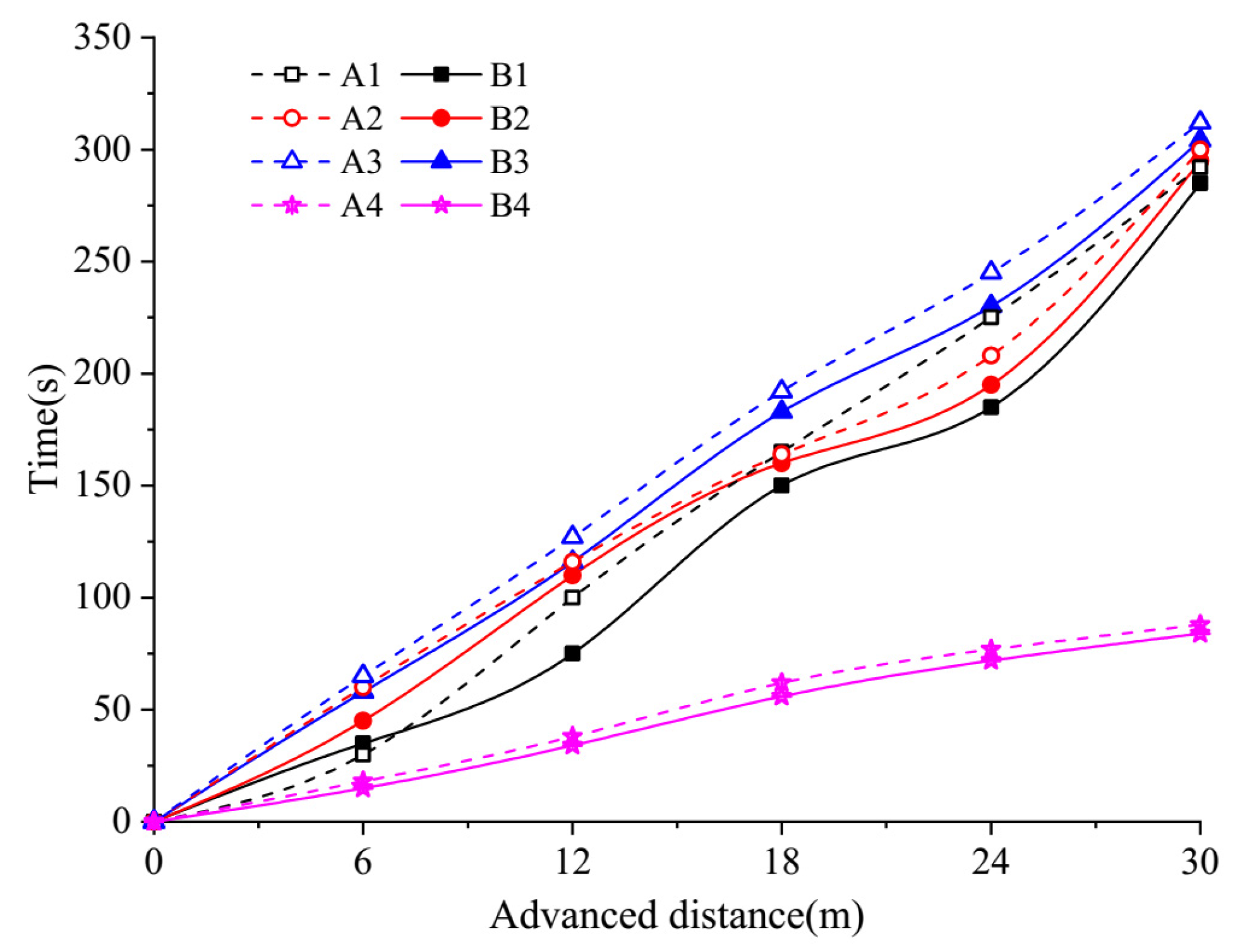
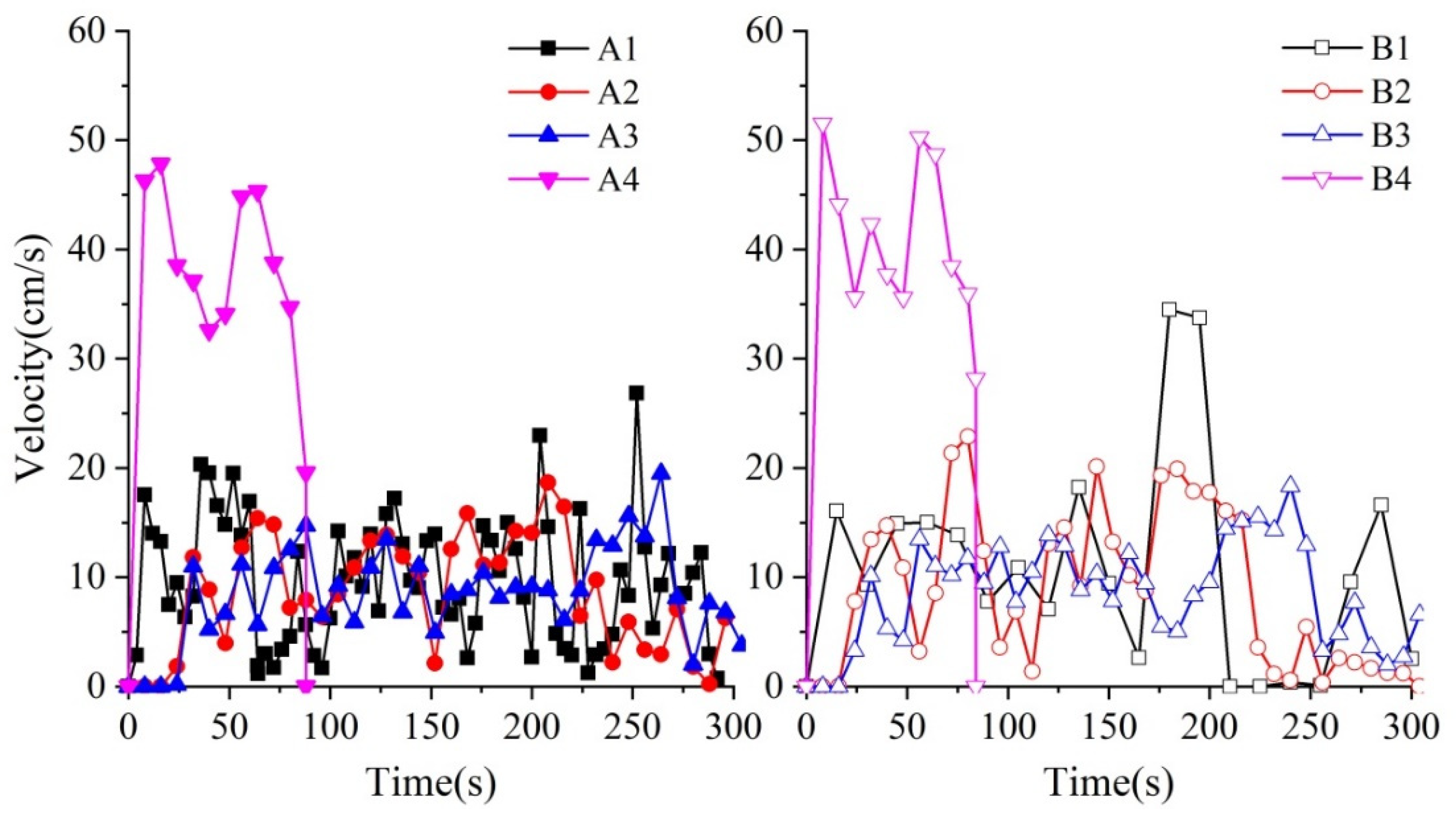
3.1. Water Advancement in the Furrow and Plug Operating Speed
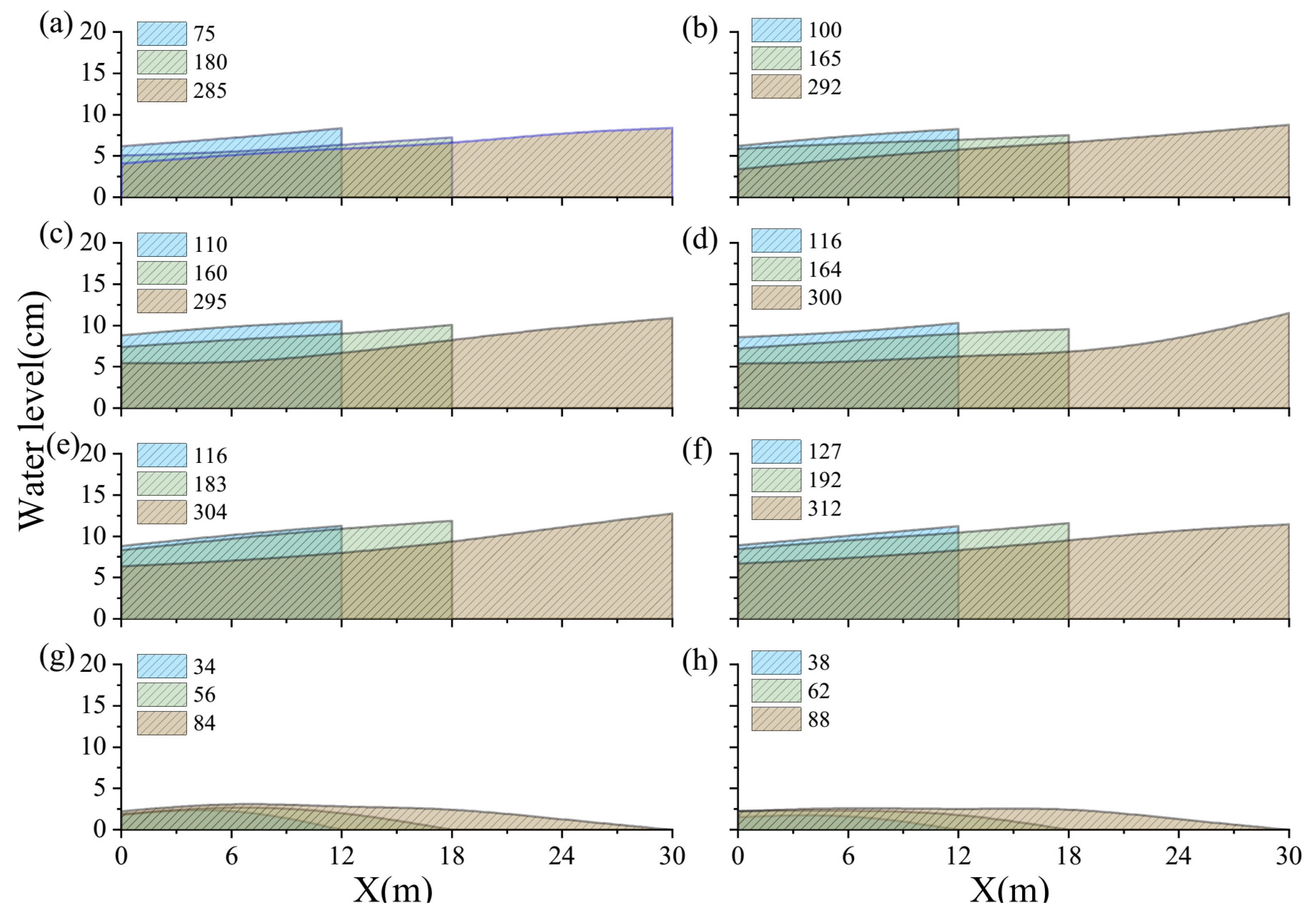
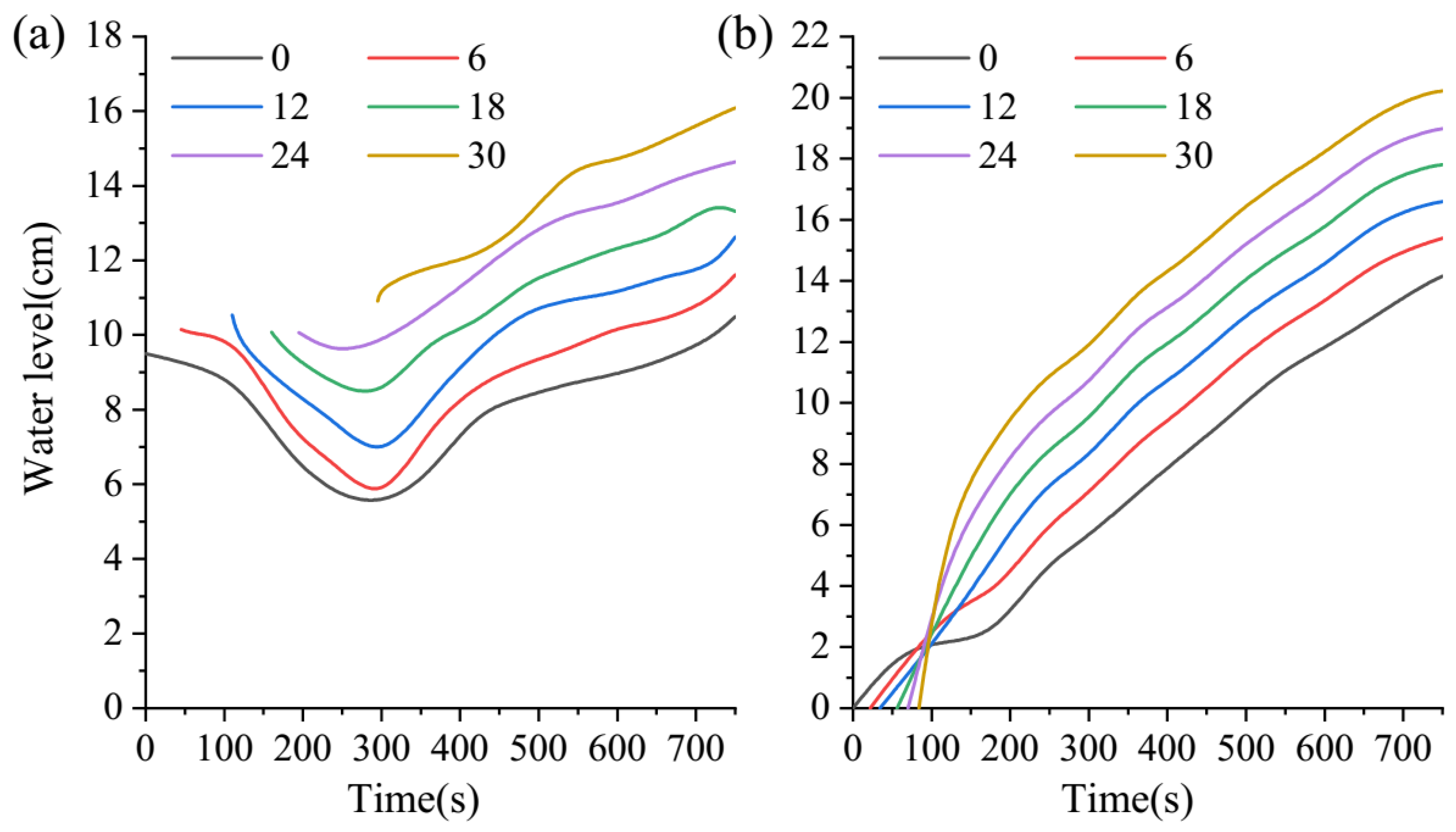
3.2. Water Levels
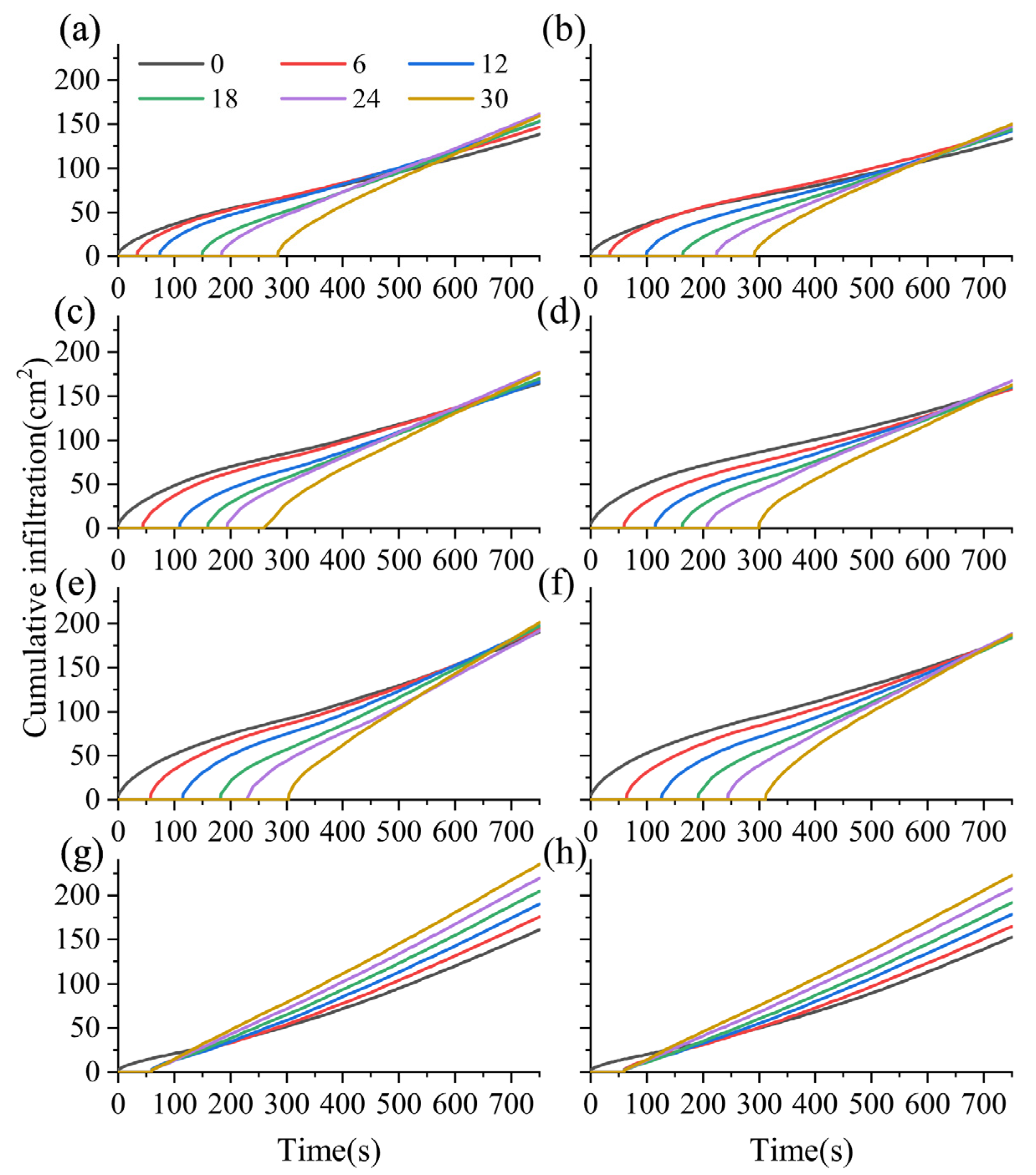
3.3. Cumulative Infiltration
3.4. Uniformity Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IFPRI. Global Report on Food Crises; International Food Policy Research Institute (IFPRI): Washington, DC, USA, 2019. [Google Scholar]
- Sulser, T.B.; Nestorova, B.; Rosegrant, M.W.; van Rheenen, T. The future role of agriculture in the Arab region’s food security. Food Secur. 2011, 3, 23–48. [Google Scholar] [CrossRef]
- Bailey-Serres, J.; Parker, J.E.; Ainsworth, E.A.; Oldroyd, G.E.D.; Schroeder, J.I. Genetic strategies for improving crop yields. Nature 2019, 575, 109–118. [Google Scholar] [CrossRef]
- Frona, D.; Szenderak, J.; Harangi-Rakos, M. The challenge of feeding the world. Sustainability 2019, 11, 5816. [Google Scholar] [CrossRef]
- Wang, F.T.; Yu, C.; Xiong, L.C.; Chang, Y. How can agricultural water use efficiency be promoted in China? A spatial-temporal analysis. Resour. Conserv. Recycl. 2019, 145, 411–418. [Google Scholar] [CrossRef]
- Carr, M.K.V.; Knox, J.W. The water relations and irrigation requirements of sugar cane (Saccharum officinarum): A review. Exp. Agric. 2011, 47, 1–25. [Google Scholar] [CrossRef]
- Sarker, K.K.; Hossain, A.; Timsina, J.; Biswas, S.K.; Kundu, B.C.; Barman, A.; Ibn Murad, K.F.; Akter, F. Yield and quality of potato tuber and its water productivity are influenced by alternate furrow irrigation in a raised bed system. Agric. Water Manag. 2019, 224, 105750. [Google Scholar] [CrossRef]
- Teffera, Z.L.; Li, J.H.; Astatkie, T.; Gebru, Z.M. Effects of irrigation systems on physicochemical properties of soil at different depths: A case study at a farm near Ziway Lake, Ethiopia. Irrig. Drain. 2019, 68, 165–175. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Keshavarz, M.R.; Playan, E. Surface fertigation: A review, gaps and needs. Span. J. Agric. Res. 2014, 12, 820–837. [Google Scholar] [CrossRef]
- Abbasi, F.; Adamsen, F.J.; Hunsaker, D.J.; Feyen, J.; Shouse, P.; van Genuchten, M.T. Effects of flow depth on water flow and solute transport in furrow irrigation: Field data analysis. J. Irrig. Drain. Eng. 2003, 129, 237–246. [Google Scholar] [CrossRef]
- Mazarei, R.; Mohammadi, A.S.; Naseri, A.; Ebrahimian, H.; Izadpanah, Z. Optimization of furrow irrigation performance of sugarcane fields based on inflow and geometric parameters using WinSRFR in Southwest of Iran. Agric. Water Manag. 2020, 228, 105899. [Google Scholar] [CrossRef]
- Sayari, S.; Rahimpour, M.; Zounemat-Kermani, M. Assessment of straight and meandering furrow irrigation strategies under different inflow rates. Water SA 2019, 45, 685–690. [Google Scholar] [CrossRef]
- Mohammadi, A.; Besharat, S.; Abbasi, F. Effects of irrigation and fertilization management on reducing nitrogen losses and increasing corn yield under furrow irrigation. Agric. Water Manag. 2019, 213, 1116–1129. [Google Scholar] [CrossRef]
- Wang, W.-Y.; Luo, W.; Wang, Z.-R. Surge flow irrigation with sediment-laden water in northwestern China. Agric. Water Manag. 2005, 75, 1–9. [Google Scholar] [CrossRef]
- Younts, C.D.; Eisenhauer, D.E.; Fekersillassie, D. Impact of Surge Irrigation on Furrow Water Advance. Trans. ASAE 1996, 39, 973–979. [Google Scholar] [CrossRef]
- Onishi, J.; Ikeura, H.; Paluashova, G.K.; Shirokova, Y.I.; Kitamura, Y.; Fujimaki, H. Suitable inflow rate and furrow length for simplified surge flow irrigation. Paddy Water Environ. 2019, 17, 185–193. [Google Scholar] [CrossRef]
- Jiang, H.G.; Liu, Y.C.; Li, C.D.; Liu, L.T.; Sheng, L.L.; Liu, H.Q. Analysis of the uniformity of cotton growth and yield in furrow irrigation along the irrigation trench. J. Hebei Agric. Univ. 2016, 39, 105–111. [Google Scholar]
- Wu, D.; Xue, J.; Bo, X.; Meng, W.; Wu, Y.; Du, T. Simulation of Irrigation Uniformity and Optimization of Irrigation Technical Parameters Based on the SIRMOD Model under Alternate Furrow Irrigation. Irrig. Drain. 2017, 66, 478–491. [Google Scholar] [CrossRef]
- Mulubrehan, K.; Gebremicael, T.G.; Abbadi, G.; Teferi, G. Effect of surge flow and alternate irrigation on the irrigation efficiency and water productivity of onion in the semi-arid areas of North Ethiopia. Agric. Water Manag. 2017, 187, 69–76. [Google Scholar]
- Liu, K.; Xiong, Y.; Xu, X.; Huang, Q.; Huo, Z.; Huang, G. Modified Model for Simulating Water Flow in Furrow Irrigation. J. Irrig. Drain. Eng. 2020, 146, 06020002. [Google Scholar] [CrossRef]
- Bristow, K.L.; Šimůnek, J.; Helalia, S.A.; Siyal, A.A. Numerical simulations of the effects furrow surface conditions and fertilizer locations have on plant nitrogen and water use in furrow irrigated systems. Agric. Water Manag. 2020, 232, 106044. [Google Scholar] [CrossRef]
- Li, X.; Jin, L.; Engel, B.A.; Yang, Z.; Wang, W.; He, W.; Wang, Y. Influence of the structure of cylindrical mobile flumes on hydraulic performance characteristics in U-shaped channels. Flow Meas. Instrum. 2020, 72, 101708. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; MacVicar, B.; Ghodsian, M.; Mehraein, M.; Torabi, M.; Savage, B.M. Evaluation of flow characteristics in labyrinth weirs using response surface methodology. Flow Meas. Instrum. 2019, 69, 101617. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Liaghat, A.; Parsinejad, M.; Playán, E.; Abbasi, F.; Navabian, M. Simulation of 1D surface and 2D subsurface water flow and nitrate transport in alternate and conventional furrow fertigation. Irrig. Sci. 2013, 31, 301–316. [Google Scholar] [CrossRef]
- Iqbal, S.; Guber, A.K.; Khan, H.Z. Estimating nitrogen leaching losses after compost application in furrow irrigated soils of Pakistan using HYDRUS-2D software. Agric. Water Manag. 2016, 168, 85–95. [Google Scholar] [CrossRef]
- Naghedifar, S.M.; Ziaei, A.N.; Ansari, H. Simulation of irrigation return flow from a Triticale farm under sprinkler and furrow irrigation systems using experimental data: A case study in arid region. Agric. Water Manag. 2018, 210, 185–197. [Google Scholar] [CrossRef]
- Qiu, R.; Du, T.; Kang, S. Root length density distribution and associated soil water dynamics for tomato plants under furrow irrigation in a solar greenhouse. J. Arid Land 2017, 9, 637–650. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, 7. [Google Scholar] [CrossRef]
- Nie, W.B.; Huang, H.; Ma, X.Y.; Fei, L.J. Evaluation of closed-end border irrigation accounting for soil infiltration variability. J. Irrig. Drain Eng. 2017, 143, 1. [Google Scholar] [CrossRef]
- Bautista, E.; Schlegel, J. Estimation of Infiltration and Hydraulic Resistance in Furrow Irrigation, with Infiltration Dependent on Flow Depth. Trans. ASABE 2017, 60, 1873–1884. [Google Scholar] [CrossRef]
- Lei, T.W.; Yuan, P.J.; Huang, X.F.; Zhan, W.H.; Yu, J. Laboratory Simulated Experiments on Control Over Furrow-Irrigation Induced Soil Erosion. Trans. Chin. Soc. Agric. Eng. 2002, 18, 26–30. [Google Scholar]
- Dibal, J.M.; Ramalan, A.A.; Mudiare, O.J.; Igbadun, H.E. Scenario Studies on Effects of Soil Infiltration Rates, Land Slope, and Furrow Irrigation Characteristics on Furrow Irrigation-Induced Erosion. Int. Sch. Res. Not. 2014, 2014, 942732. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Zhang, Y.X.; Cheng, D.J.; Wang, L.S.; Hu, H.Y.; Li, F.; Zhang, C. The Effects of Infiltration Heads on the Soil Water Movements Under Film Mulched Ridge-furrow Irrigation with Small Tubes. China Rural Water Hydropower 2017, 12, 22–26. [Google Scholar]
- Keshavarz, M.S.; Ebrahimian, H.; Abbasi, F.; Playán, E. Effect of micro-dams on water flow characteristics in furrow irrigation. Irrig. Sci. 2020, 38, 307–319. [Google Scholar] [CrossRef]

| Treatments | Flow Rate (L/s) | Field Slope | Height of Plug (cm) |
|---|---|---|---|
| A1 | 2.8 | 0.002 | 15 |
| A2 | 2.8 | 0.002 | 18 |
| A3 | 2.8 | 0.002 | 21 |
| A4 | 2.8 | 0.002 | 0 (no plug) |
| B1 | 3.0 | 0.002 | 15 |
| B2 | 3.0 | 0.002 | 18 |
| B3 | 3.0 | 0.002 | 21 |
| B4 | 3.0 | 0.002 | 0 (no plug) |
| Soil | θr | θs | α | n | Ks |
|---|---|---|---|---|---|
| (cm3 cm−3) | (cm3 cm−3) | (m−1) | (-) | (cm h−1) | |
| Sandy loam | 0.065 | 0.41 | 0.075 | 1.89 | 4.42 |
| Loam | 0.078 | 0.43 | 0.036 | 1.56 | 1.04 |
| Soil Texture | Irrigation Uniformity | |||||||
|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | B1 | B2 | B3 | B4 | |
| Sandy loam | 97.30% | 98.60% | 99.22% | 88.72% | 95.81% | 97.49% | 98.36% | 88.84% |
| Loam | 90.18% | 96.02% | 96.01% | 89.44% | 93.11% | 94.97% | 96.72% | 89.58% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Liu, K.; Li, A.; Yang, M.; Gao, X.; Zhao, X.; Cai, Y. The Effect of Plug Height and Inflow Rate on Water Flow Characteristics in Furrow Irrigation. Agronomy 2022, 12, 2225. https://doi.org/10.3390/agronomy12092225
Yu J, Liu K, Li A, Yang M, Gao X, Zhao X, Cai Y. The Effect of Plug Height and Inflow Rate on Water Flow Characteristics in Furrow Irrigation. Agronomy. 2022; 12(9):2225. https://doi.org/10.3390/agronomy12092225
Chicago/Turabian StyleYu, Juan, Keyao Liu, Anbin Li, Mingfei Yang, Xiaodong Gao, Xining Zhao, and Yaohui Cai. 2022. "The Effect of Plug Height and Inflow Rate on Water Flow Characteristics in Furrow Irrigation" Agronomy 12, no. 9: 2225. https://doi.org/10.3390/agronomy12092225
APA StyleYu, J., Liu, K., Li, A., Yang, M., Gao, X., Zhao, X., & Cai, Y. (2022). The Effect of Plug Height and Inflow Rate on Water Flow Characteristics in Furrow Irrigation. Agronomy, 12(9), 2225. https://doi.org/10.3390/agronomy12092225






