Global Sensitivity Analysis of Key Parameters in the APSIMX-Sugarcane Model to Evaluate Nitrate Balance via Treed Gaussian Process
Abstract
1. Introduction
2. Materials and Methods
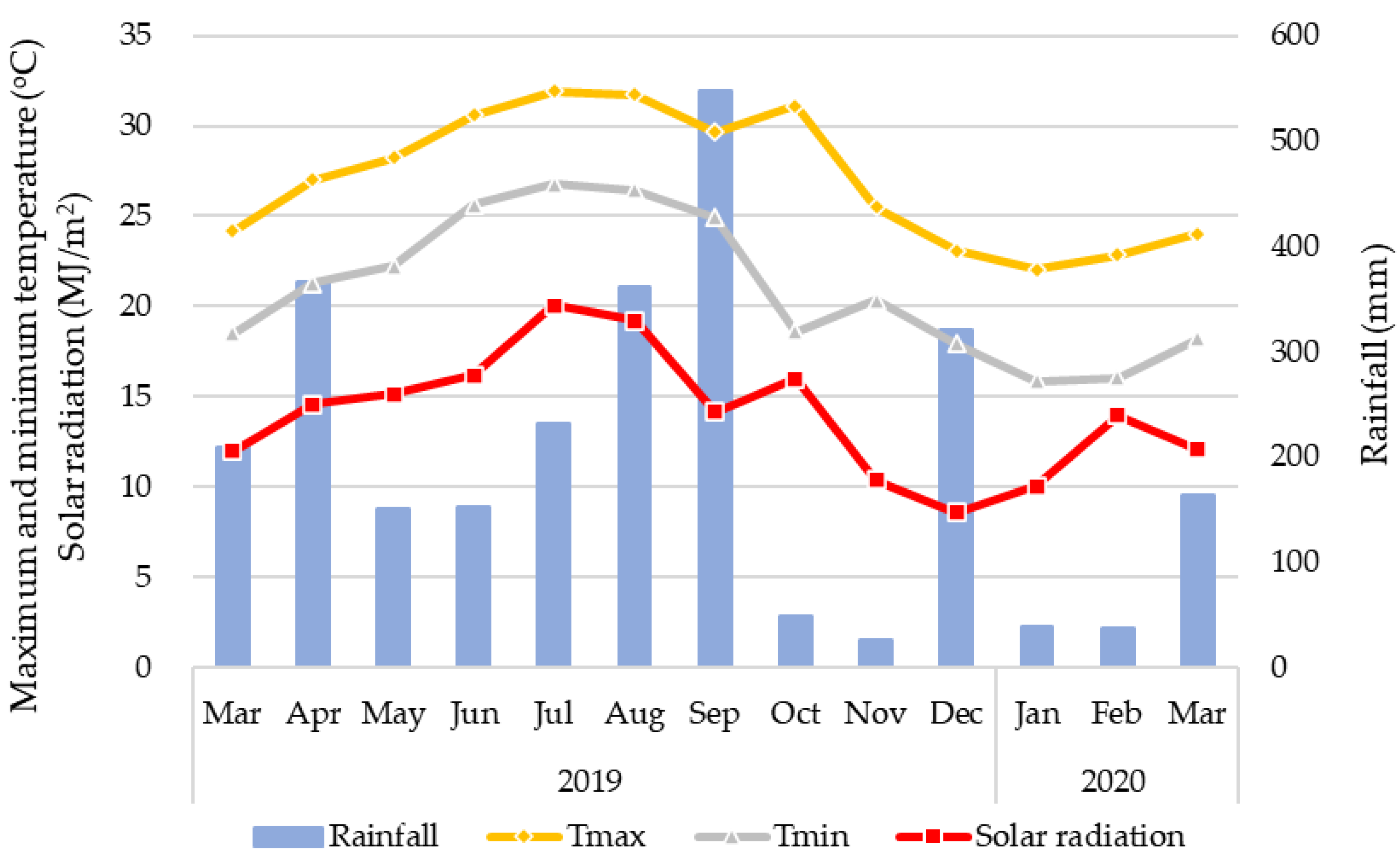
2.1. Study Field
2.2. APSIMX Simulation
2.3. Sensitivity Analysis
2.3.1. Parameters Used for GSA
2.3.2. Training Design Point Generation
2.3.3. Treed Gaussian Process
3. Results and Discussion
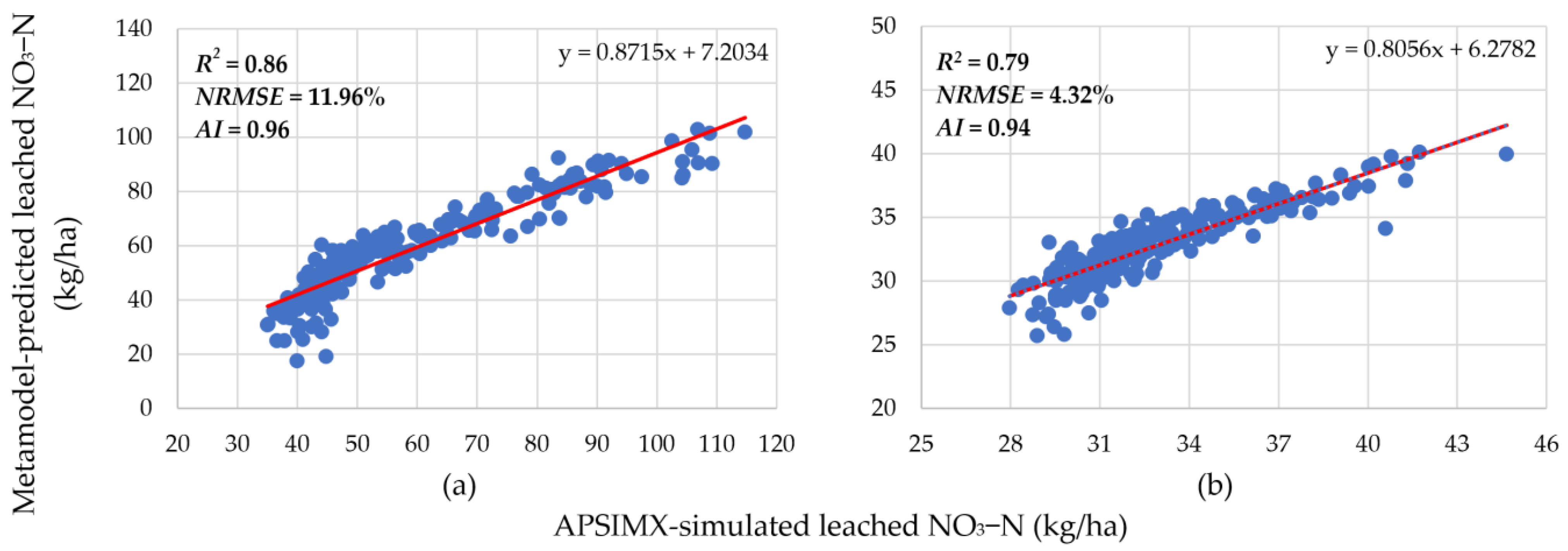
3.1. Meta-Model Accuracy
3.2. Sensitivity Analysis
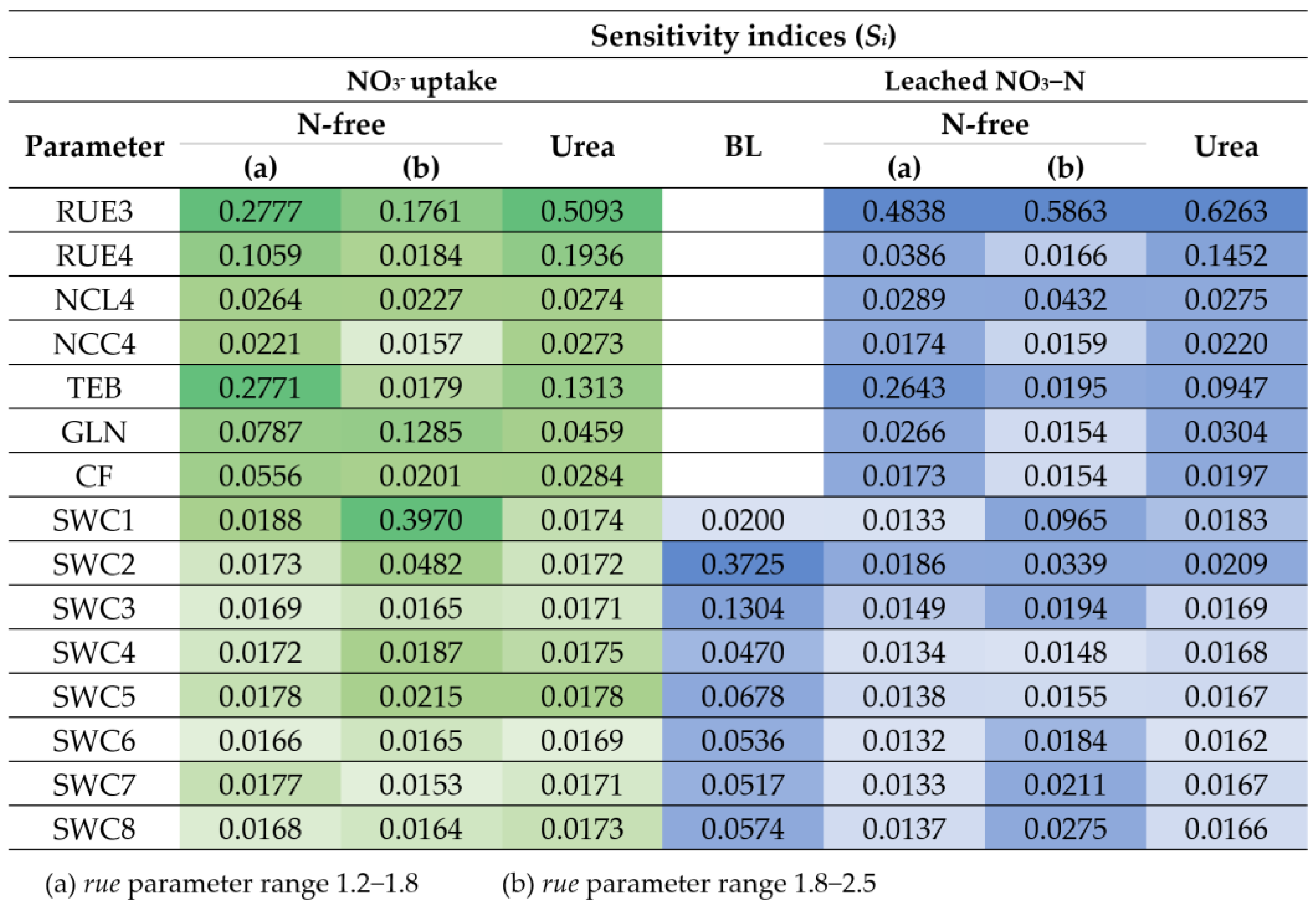
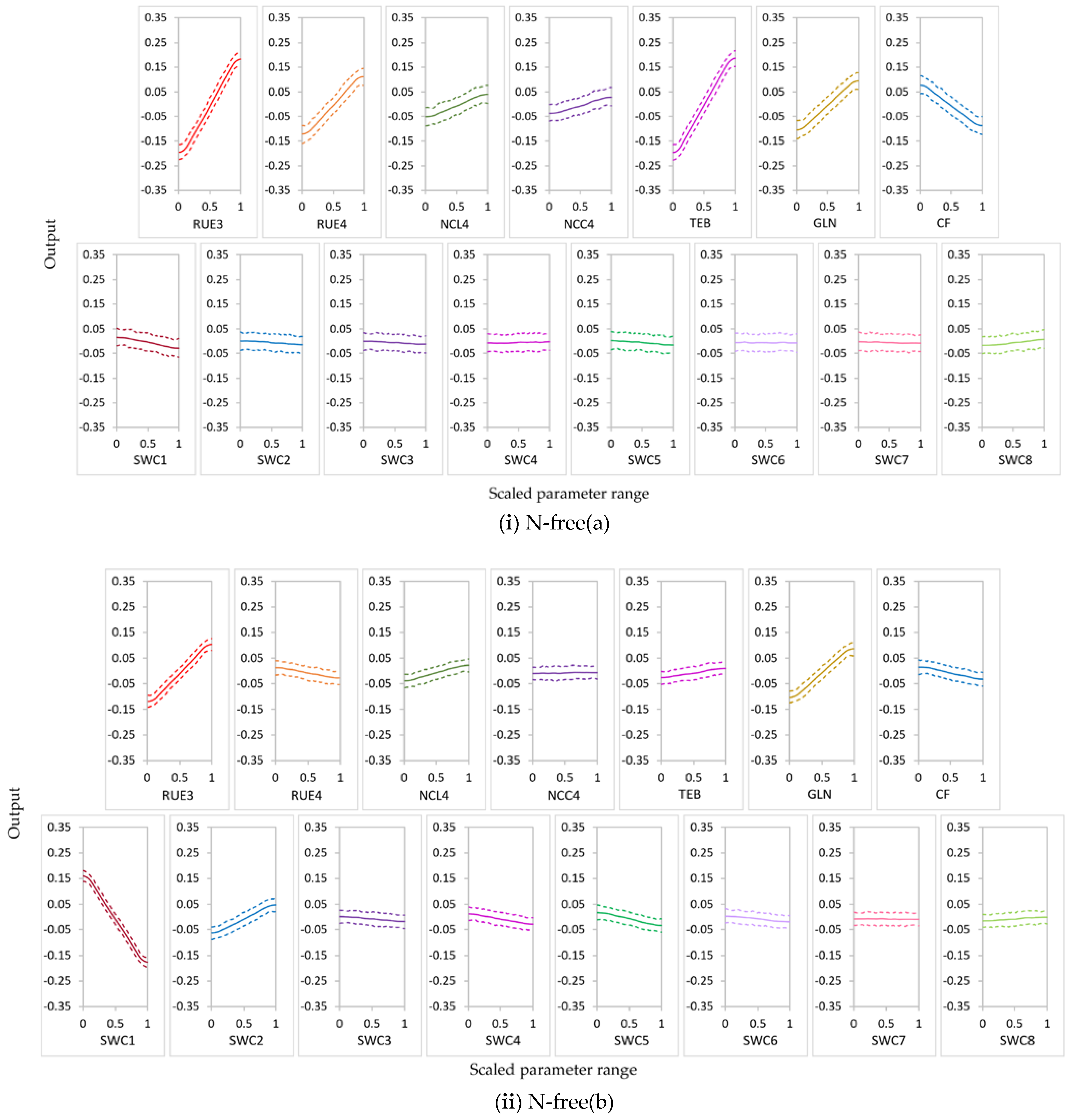
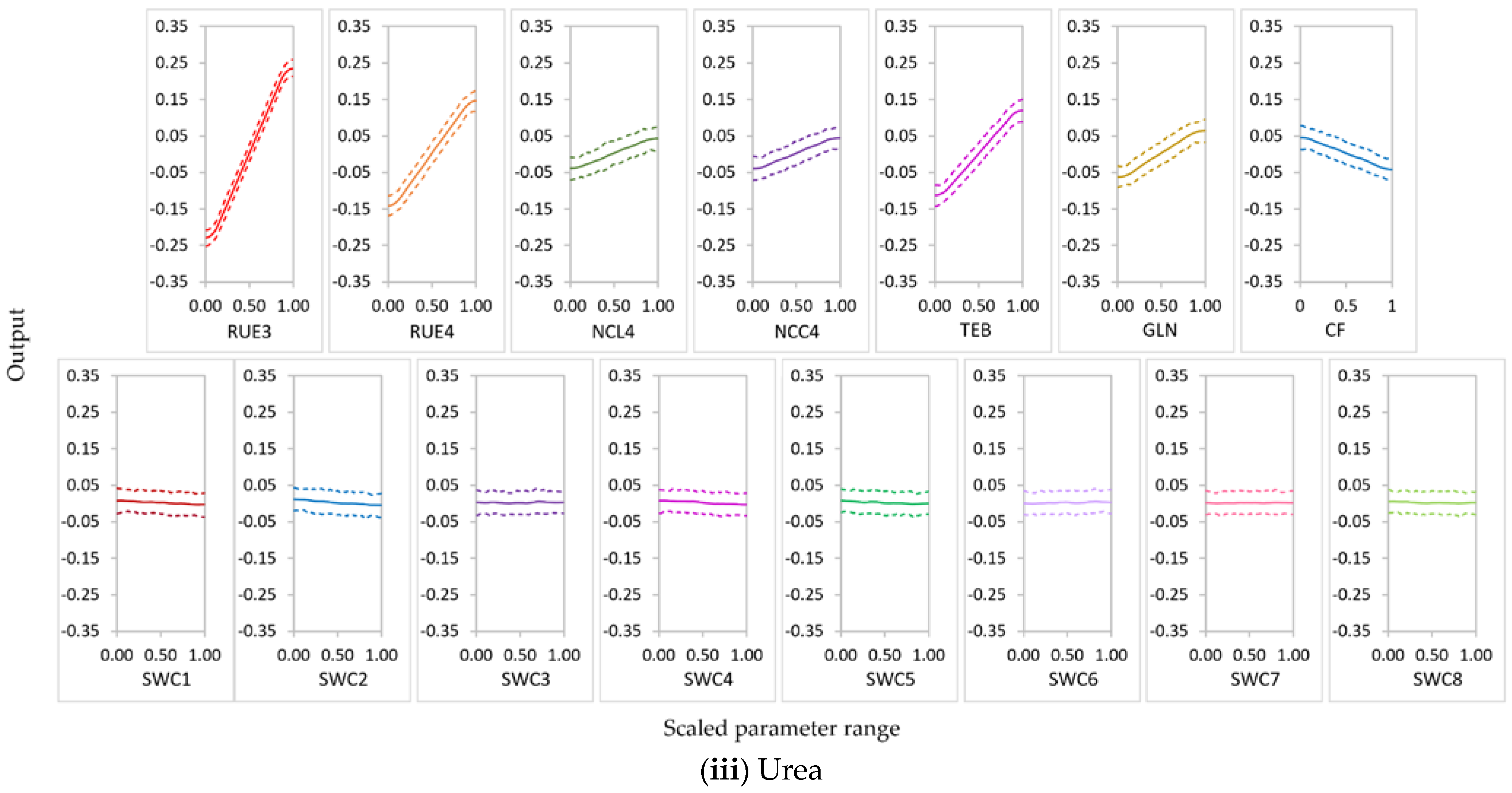
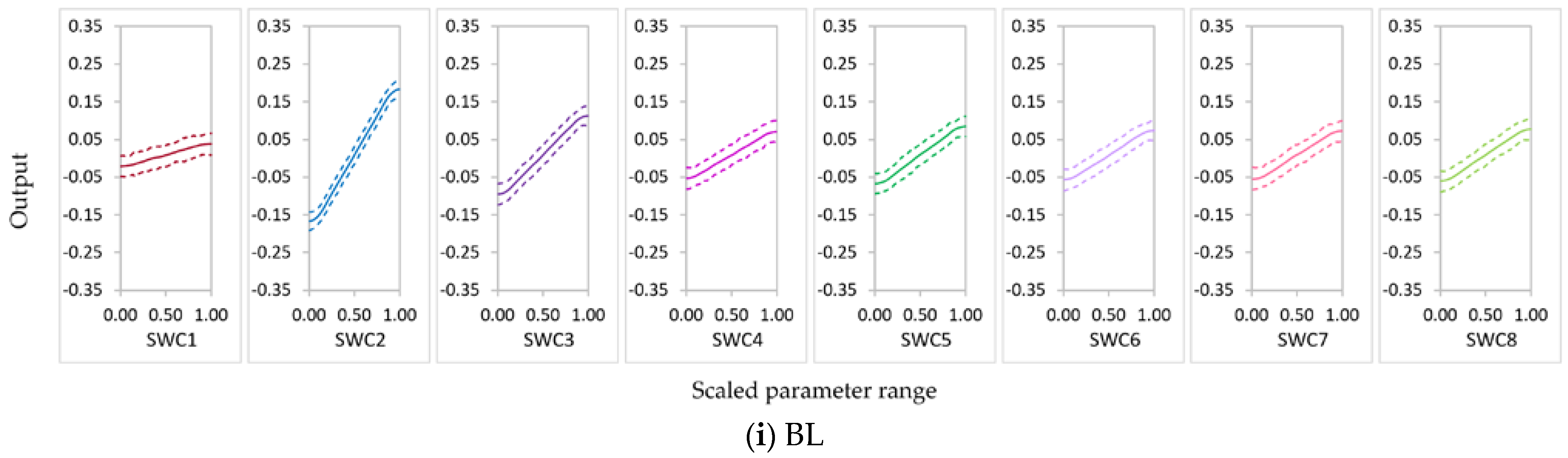
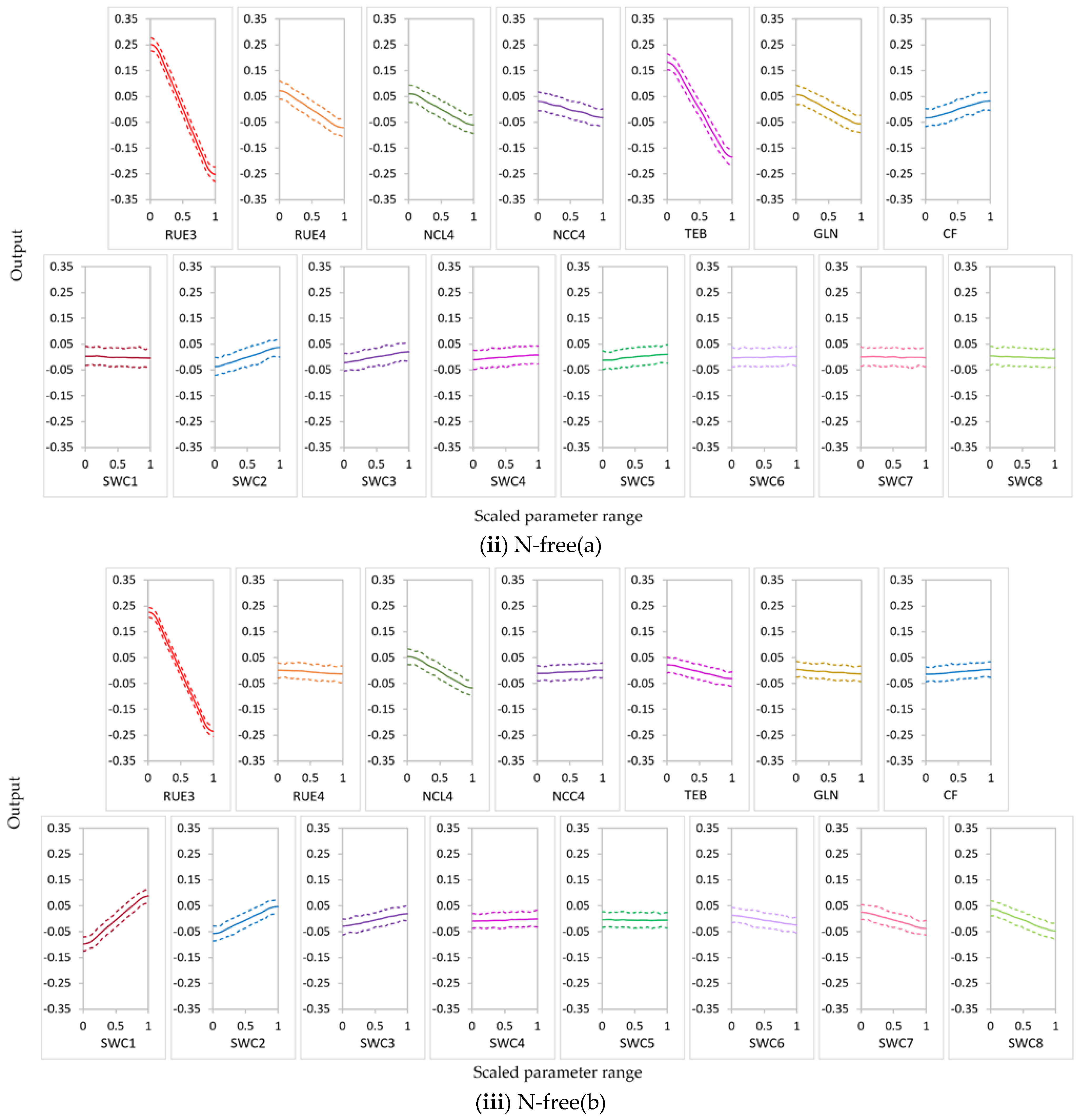
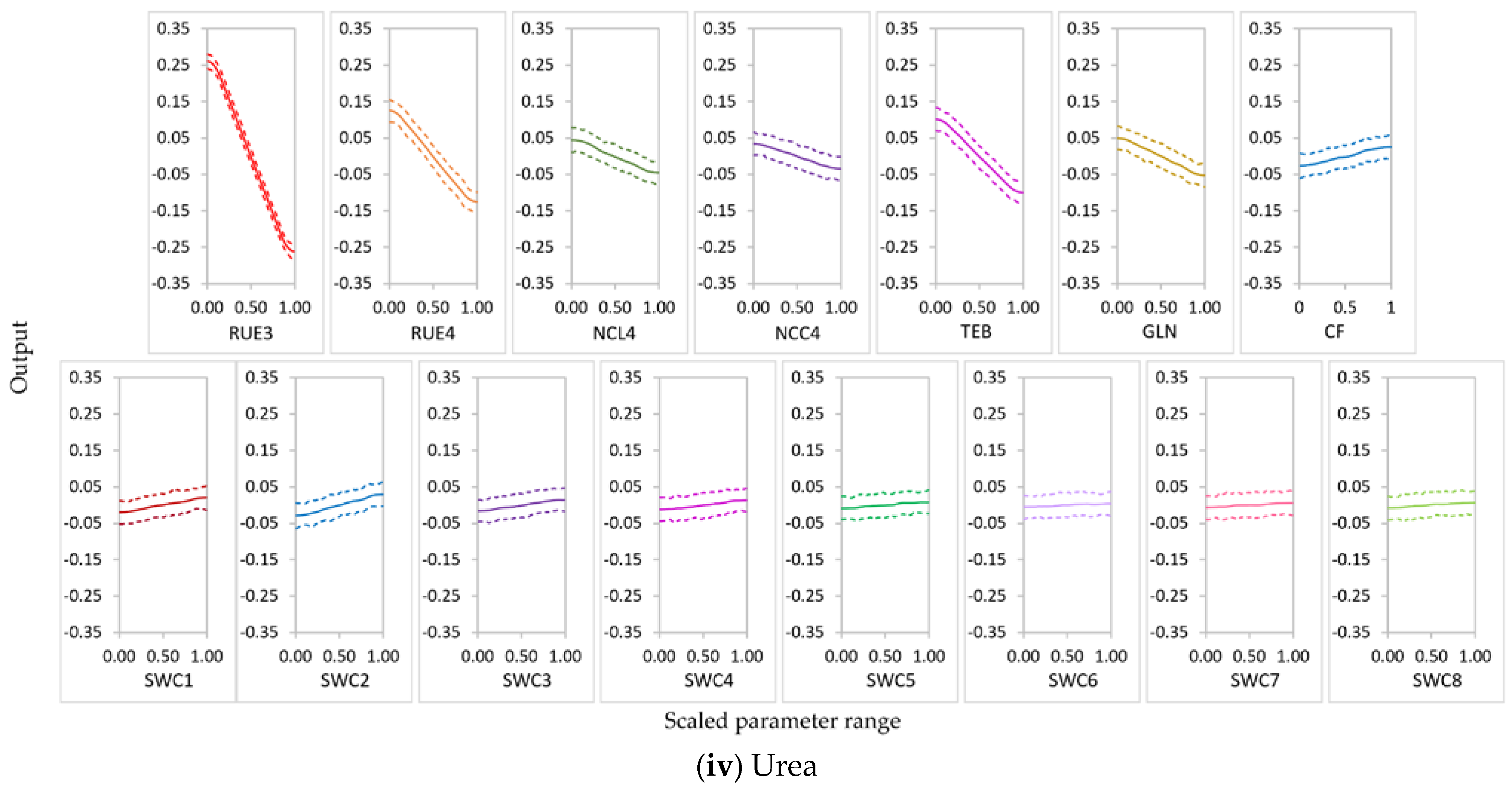
3.2.1. Parameter Sensitivity
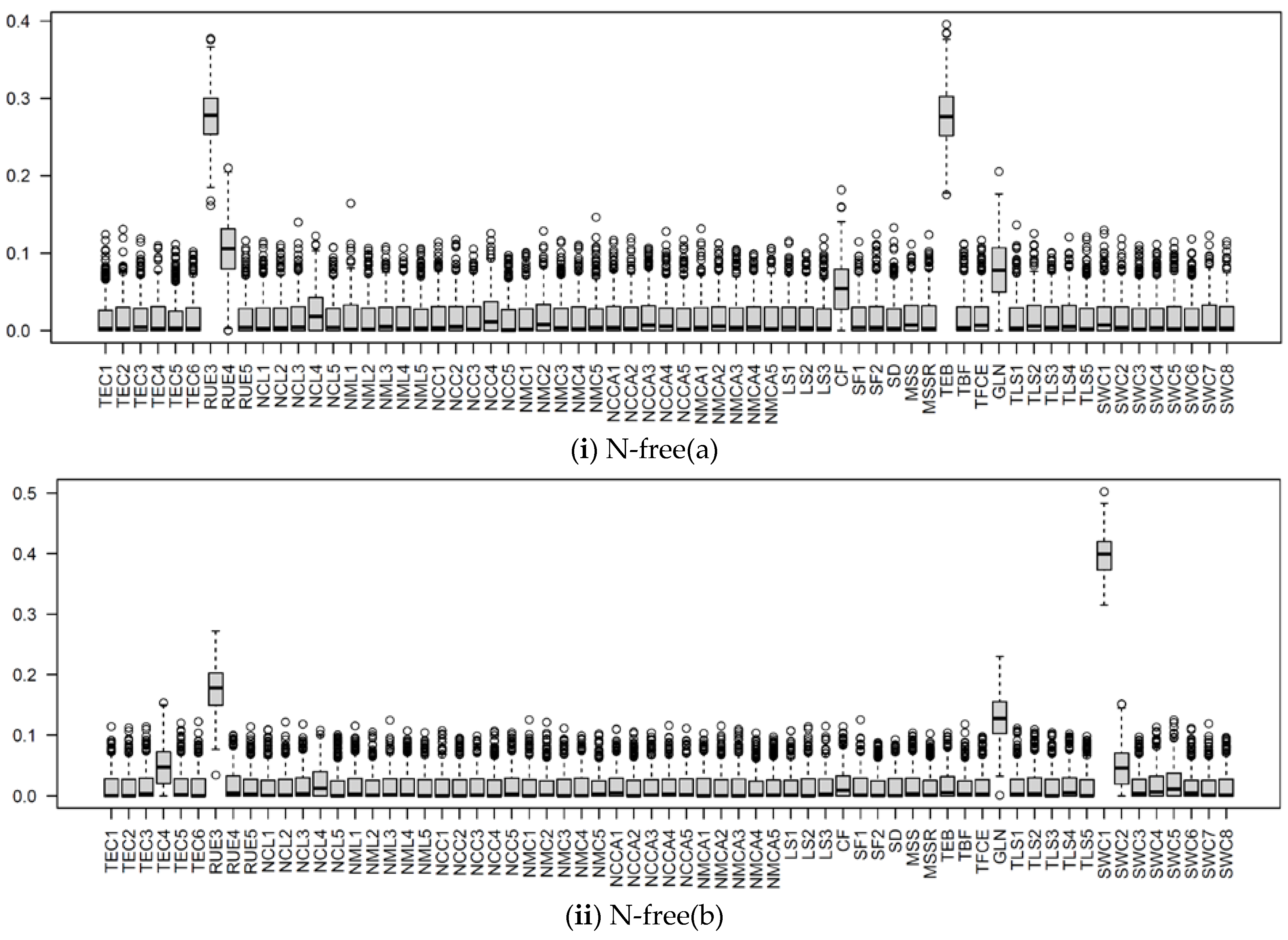
3.2.2. Behavior of Highly Influential Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matsuoka, M. Sugarcane cultivation and sugar industry in Japan. Sugar Tech. 2006, 8, 3–9. [Google Scholar] [CrossRef]
- Department of Agriculture, Forestry and Fisheries, Okinawa Prefectural Government. Manual Guide for Sugarcane Cultivation; Okinawa Prefectural Government: Okinawa, Japan, 2018; pp. 10–12. (In Japanese)
- Kingstone, G. Mineral nutrition of sugarcane. In Sugarcane: Physiology, Biochemistry, and Functional Biology, 1st ed.; Moore, P.H., Botha, F.C., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; Volume 1, pp. 85–120. [Google Scholar]
- Agata, S.; Satake, H.; Tokuyama, A. Chemical characteristics and isotopic compositions of spring and river waters in Okinawa Island. Chikyukagaku 2001, 35, 27–41. (In Japanese) [Google Scholar] [CrossRef]
- Nakanishi, Y. Correlation between actual fertilizing to sugarcane and nitrate concentration in groundwater of Miyako Island, Okinawa. Jpn. J. Soil Sci. Plant. Nutr. 2001, 72, 499–504. (In Japanese) [Google Scholar]
- Shuhei, Y. Dynamics of Groundwater Nitrates in Limestone Aquifer of the Southern Okinawa Island. Bull. Natl. Inst. Rural Eng. Jpn. 2013, 52, 59–110. [Google Scholar]
- Holzworth, D.; Huth, N.I.; Fainges, J.; Brown, H.; Zurcher, E.; Cichota, R.; Verrall, S.; Herrmann, N.I.; Zheng, B.; Snow, V. APSIM Next Generation: Overcoming challenges in modernising a farming systems model. Environ. Model. Softw. 2018, 103, 43–51. [Google Scholar] [CrossRef]
- Keating, B.A.; Robertson, M.J.; Muchow, R.C.; Huth, N.I. Modelling sugarcane production systems I. Development and performance of the sugarcane module. Field Crop Res. 1999, 61, 253–271. [Google Scholar] [CrossRef]
- Martiné, J.F.; Todoroff, P. Le Modèle de Croissance Mosicas et Sa Plateforme de Simulation Simulex:État Des Lieux et Perspectives. Rev. Agric. Sucr. Maurice 2002, 80, 133–147. [Google Scholar]
- Jones, M.R.; Singels, A. Refining the Canegro Model for Improved Simulation of Climate Change Impacts on Sugarcane. Eur. J. Agron. 2018, 100, 76–86. [Google Scholar] [CrossRef]
- Liu, D.L.; Bull, T.A. Simulation of Biomass and Sugar Accumulation in Sugarcane Using a Process-Based Model. Ecol. Modell. 2001, 144, 181–211. [Google Scholar] [CrossRef]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An Overview of the Crop Model. Stics. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Peng, T.; Fu, J.; Jiang, D.; Du, J. Simulation of the Growth Potential of Sugarcane as an Energy Crop Based on the APSIM Model. Energies 2020, 13, 2173. [Google Scholar] [CrossRef]
- Dias, H.B.; Inman-Bamber, G.; Everingham, Y.; Sentelhas, P.C.; Bermejo, R.; Christodoulou, D. Traits for Canopy Development and Light Interception by Twenty-Seven Brazilian Sugarcane Varieties. Field Crop Res. 2020, 249, 107716. [Google Scholar] [CrossRef]
- Shan, Y.; Huang, M.; Harris, P.; Wu, L.A. Sensitivity analysis of the SPACSYS model. Agriculture 2021, 11, 624. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Y.; Shi, X.; Liu, Y.; Wang, S.; Yu, D. Sensitivity and uncertainty analysis of CENTURY-modeled SOC dynamics in upland soils under different climate-soil-management conditions: A case study in China. J. Soils Sediments 2016, 17, 85–96. [Google Scholar] [CrossRef]
- Krishnan, P.; Aggarwal, P. Global sensitivity and uncertainty analyses of a web based crop simulation model (web InfoCrop wheat) for soil parameters. Plant Soil 2018, 423, 443–463. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. Water Resource Systems Modeling: Its Role in Planning and Management. In Water Resource Systems Planning and Management; Springer: Cham, Switzerland, 2017; pp. 51–71. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Sexton, J.; Everingham, Y.L.; Inman-Bamber, G. A global sensitivity analysis of cultivar trait parameters in a sugarcane growth model for contrasting production environments in Queensland, Australia. Eur. J. Agron. 2017, 88, 96–105. [Google Scholar] [CrossRef]
- Confalonieri, R. Monte Carlo based sensitivity analysis of two crop simulators and considerations on model balance. Eur. J. Agron. 2010, 33, 89–93. [Google Scholar] [CrossRef]
- Specka, X.; Nendel, C.; Wieland, R. Analysing the parameter sensitivity of the agro-ecosystem model MONICA for different crops. Eur. J. Agron. 2015, 71, 73–87. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Willems, P. Global sensitivity analysis of yield output from the water productivity model. Environ. Model. Softw. 2014, 51, 323–332. [Google Scholar] [CrossRef]
- Dzotsi, K.A.; Basso, B.; Jones, J.W. Development, uncertainty and sensitivity analysis of the simple SALUS crop model in DSSAT. Ecol. Modell. 2013, 260, 62–76. [Google Scholar] [CrossRef]
- Song, X.; Zhan, C.; Kong, F.; Xia, J. Advances in the study of uncertainty quantification of large-scale hydrological modeling system. J. Geogr. Sci. 2011, 21, 801–819. [Google Scholar] [CrossRef]
- Cariboni, J.; Gatelli, D.; Liska, R.; Saltelli, A. The role of sensitivity analysis in ecological modelling. Ecol. Modell. 2007, 203, 167–182. [Google Scholar] [CrossRef]
- Liang, H.; Qi, Z.; DeJonge, K.C.; Hu, K.; Li, B. Global sensitivity and uncertainty analysis of nitrate leaching and crop yield simulation under different water and nitrogen management practices. Comput. Electron. Agric. 2017, 142, 201–210. [Google Scholar] [CrossRef]
- Yang, S.; Tian, W.; Cubi, E.; Meng, Q.; Liu, Y.; Wei, L. Comparison of Sensitivity Analysis Methods in Building Energy Assessment. Procedia Eng. 2016, 146, 174–181. [Google Scholar] [CrossRef]
- Sobol’, L.M. On sensitivity estimation for nonlinear mathematical models. Matem. Mod. 1990, 2, 112–118. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Mara, T.A.; Tarantola, S. Application of global sensitivity analysis of model output to building thermal simulations. Build. Simul. 2008, 1, 290–302. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, F.; Shen, H.; Xing, X.; Xiaoyi, M. global sensitivity analysis and evaluation of the DSSAT model for summer maize (Zea mays L.) under irrigation and fertilizer stress. Int. J. Plant Prod. 2021, 15, 523–539. [Google Scholar] [CrossRef]
- Dejonge, K.C.; Ascough, J.C., II; Ahmadi, M.; Andales, A.A.; Arabi, M. Global sensitivity and uncertainty analysis of a dynamic agroecosystem model under different irrigation treatments. Ecol. Modell. 2012, 231, 113–125. [Google Scholar] [CrossRef]
- Kumar, S.; Niwas, R.; Khichar, M.L.; Kumar, Y.; Premdeep, A.S. Sensitivity analysis of DSSAT CROPGRO-Cotton model for cotton under different growing environments. Indian J. Ecol. 2017, 44, 237–241. [Google Scholar]
- Xu, M.; Wang, C.; Ling, L.; Batchelor, W.D.; Zhang, J.; Kuai, J. Sensitivity analysis of the CROPGRO-Canola model in China: A case study for rapeseed. PLoS ONE 2021, 16, 17. [Google Scholar] [CrossRef] [PubMed]
- Varella, H.; Guérif, M.; Buis, S. Global sensitivity analysis measures the quality of parameter estimation: The case of soil parameters and a crop model. Environ. Model. Softw. 2010, 25, 310–319. [Google Scholar] [CrossRef]
- Zhao, G.; Bryan, B.A.; Song, X. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar, environmental, and management parameters. Ecol. Modell. 2014, 279, 1–11. [Google Scholar] [CrossRef]
- Qin, F.; Zhao, Y.; Shi, X.; Xu, S.; Yu, D. Sensitivity and uncertainty analysis for the DeNitrification–DeComposition model, a case study of modeling soil organic carbon dynamics at a long-term observation site with a rice–bean rotation. Comput. Electron. Agric. 2016, 124, 263–272. [Google Scholar] [CrossRef]
- Gramacy, R.B.; Taddy, M. Categorical Inputs, Sensitivity Analysis, Optimization and Importance Tempering with tgp Version 2, an R Package for Treed Gaussian Process Models. J. Stat. Softw. 2010, 33, 1–48. [Google Scholar] [CrossRef]
- Bandara, W.B.M.A.C.; Sakai, K.; Nakandakari, T.; Kapetch, P.; Rathnappriya, R.H.K. A Gaussian-Process-Based Global Sensitivity Analysis of Cultivar Trait Parameters in APSIM-Sugar Model: Special Reference to Environmental and Management Conditions in Thailand. Agronomy 2020, 10, 984. [Google Scholar] [CrossRef]
- Gunarathna, M.H.J.P.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.K.N. Sensitivity Analysis of Plant- and Cultivar-Specific Parameters of APSIM-Sugar Model: Variation between Climates and Management Conditions. Agronomy 2019, 9, 242. [Google Scholar] [CrossRef]
- Bandara, W.B.M.A.C.; Sakai, K.; Nakandakari, T.; Kapetch, P.; Anan, M.; Nakamura, S.; Setouchi, H.; Rathnappriya, R.H.K. Global Optimization of Cultivar Trait Parameters in the Simulation of Sugarcane Phenology Using Gaussian Process Emulation. Agronomy 2021, 11, 1379. [Google Scholar] [CrossRef]
- Rathnappriya, R.H.K.; Sakai, K.; Okamoto, K.; Kimura, S.; Haraguchi, T.; Nakandakari, T.; Setouchi, H.; Bandara, W.B.M.A.C. Examination of the Effectiveness of Controlled Release Fertilizer to Balance Sugarcane Yield and Reduce Nitrate Leaching to Groundwater. Agronomy 2022, 12, 695. [Google Scholar] [CrossRef]
- Okamoto, K.; Goto, S.; Anzai, T.; Ando, S. Nitrogen Leaching and Nitrogen Balance under Differing Nitrogen Fertilization for Sugarcane Cultivation on a Subtropical Island. Water 2021, 13, 740. [Google Scholar] [CrossRef]
- Iwata, Y.; Miyamoto, T.; Kameyama, K.; Nishiya, M. Effect of sensor installation on the accurate measurement of soil water content. Eur. J. Soil Sci. 2017, 68, 817–828. [Google Scholar] [CrossRef]
- Kubotera, H. Analysis of problems in certain soils of the Kyushu Okinawa region for suitable management. Soil Sci. Plant Nutr. 2020, 66, 15–20. [Google Scholar] [CrossRef]
- Shinogi, Y.; Miyamoto, T.; Kameyama, K.; Yan, C. Optimal use of biomass in an isolated environment: Case study at Miyako Island, Japan. In Proceedings of the 27th International Society of Sugar Cane Technologists Congress, Veracruz, Mexico, 7–11 March 2010. [Google Scholar]
- Kameyama, K.; Miyamoto, T.; Shinogi, Y. Increases in available water content of soils by applying bagasse-charcoals. In Proceedings of the 19th World Congress of Soil Science, Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010. [Google Scholar]
- Sakai, K.; Nakamura, S. N2O emissions from shimajiri-maji (calcaric dark red soil) after applying two chemical fertilizers. Appl. Ecol. Environ. Res. 2015, 13, 339–348. [Google Scholar] [CrossRef]
- Singels, A. Crop Models. In Sugarcane: Physiology, Biochemistry, and Functional Biology; Moore, P.H., Botha, F.C., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2013; pp. 541–577. [Google Scholar]
- Everingham, Y.L.; Inman-Bamber, N.G.; Thorburn, P.J.; McNeill, T.J. A Bayesian modelling approach for long lead sugarcane yield forecasts for the Australian sugar industry. Aust. J. Agric. Res. 2007, 58, 87–94. [Google Scholar] [CrossRef]
- Inman-Bamber, N.G.; Attard, S.A.; Baillie, C.; Lawson, D.; Simpson, L. A web-based system for planning use of limited irrigation water in sugarcane. Proc. Aust. Soc. Sugar Cane Technol. 2005, 27, 170–181. [Google Scholar]
- Everingham, Y.; Baillie, C.; Inman-Bamber, G.; Baillie, J. Forecasting water allocations for Bundaberg sugarcane farmers. Clim. Res. 2008, 36, 231–239. [Google Scholar] [CrossRef][Green Version]
- Marin, F.R.; Jones, J.W.; Singels, A.; Royce, F.; Assad, E.D.; Pellegrino, G.Q.; Justino, F. Climate change impacts on sugarcane attainable yield in southern Brazil. Clim. Chang. 2013, 117, 227–239. [Google Scholar] [CrossRef]
- Thorburn, P.J.; Antwerpen, R.V.A.N.; Meyer, J.H.; Bezuidenhout, C.N. The impact of trash management on soil carbon and nitrogen: I Modelling long-term experimental results in the South African sugar industry. Proc. S. Afr. Sug Technol. Ass. 2002, 76, 260–268. [Google Scholar]
- SoilN. Available online: https://www.apsim.info/documentation/model-documentation/soil-modules-documentation/soiln/ (accessed on 2 August 2022).
- Catchpoole, V.R.; Keating, B.A. Sugarcane yield and nitrogen uptake in relation to profiles of mineral-nitrogen in the soil. In Proceedings of the 17th Conference of the Australian Society of Sugar Cane Technologists, Bundaberg, Australia, 2–5 May 1995. [Google Scholar]
- Muchow, R.C.; Robertson, M.J. Relating crop nitrogen uptake to sugarcane yield. In Proceedings of the 16th Conference of the Australian Society of Sugar Cane Technologists, Townsville, Australia, 26–29 April 1994. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 2 August 2022).
- Miguez, F. Inspect, Read, Edit and Run ‘APSIM’ “Next Generation” and ‘APSIM’ Classic. Available online: https://cran.r-project.org/package=apsimx (accessed on 2 August 2022).
- Wickham, H.; Müller, K. R Database Interface. Available online: https://cran.r-project.org/package=DBI (accessed on 2 August 2022).
- Müller, K.; Wickham, H.; James, D.A.; Falcon, S.; Hipp, D.R.; Kennedy, D.; Mistachkin, J.; Healy, L.; SQLite Authors; R Consortium. RStudio SQLite Interface for R. Available online: https://cran.r-project.org/package=RSQLite (accessed on 2 August 2022).
- Ooms, J. The Jsonlite Package: A Practical and Consistent Mapping between JSON Data and R Objects. arXiv 2022, arXiv:1403.2805. [Google Scholar]
- Gramacy, R.B.; Taddy, M.A. Bayesian Treed Gaussian Process Models. R Package Version 2.4-18. 2022. Available online: https://cran.r-project.org/web/packages/tgp/index.html (accessed on 2 August 2022).
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, S.; Yang, Y.; Tian, W.; Sun, Y.; Lyu, M. Global sensitivity analysis on borehole thermal energy storage performances under intermittent operation mode in the first charging phase. Renew. Energy 2019, 143, 183–198. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.-S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd.: Chichester, UK, 2008; p. 305. [Google Scholar]
- Gramacy, R.B. tgp: An R Package for Bayesian Nonstationary, Semiparametric Nonlinear Regression and Design by Treed Gaussian Process Models. J. Stat. Softw. 2007, 19, 1–46. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Massmann, C.; Holzmann, H. Analysis of the behavior of a rainfall–runoff model using three global sensitivity analysis methods evaluated at different temporal scales. J. Hydrol. 2012, 475, 97–110. [Google Scholar] [CrossRef]
- Svenson, J.; Santner, T.; Dean, A.; Moon, H. Estimating sensitivity indices based on Gaussian process metamodels with compactly supported correlation functions. J. Stat. Plan. Inference 2014, 144, 160–172. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Li, H.; Wang, X. Sensitivity analysis of thermal performance of granary building based on machine learning. In Proceedings of the 24th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Hong Kong; 2019. Available online: http://papers.cumincad.org/data/works/att/caadria2019_245.pdf (accessed on 2 August 2022).
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Liu, S.; Yang, J.Y.; Zhang, X.Y.; Drury, C.F.; Reynolds, W.D.; Hoogenboom, G. Modelling crop yield, soil water content and soil temperature for a soybean–maize rotation under conventional and conservation tillage systems in Northeast China. Agric. Water Manag. 2013, 123, 32–44. [Google Scholar] [CrossRef]
- Probert, M.E.; Dimes, J.P.; Keating, B.A.; Dalal, R.C.; Strong, W.M. APSIM’s Water and Nitrogen Modules and Simulation of the Dynamics of Water and Nitrogen in Fallow Systems. Agric. Syst. 1998, 56, 28. [Google Scholar] [CrossRef]
- Cichota, R.; Vogeler, I.; Sharp, J.; Verburg, K.; Huth, N.; Holzworth, D.; Dalgliesh, N.; Snow, V. A protocol to build soil descriptions for APSIM simulations. MethodsX 2021, 8, 101566. [Google Scholar] [CrossRef]
- Elli, E.F.; Huth, N.; Sentelhas, P.C.; Carneiro, R.L.; Alvares, C.A. Global sensitivity-based modelling approach to identify suitable Eucalyptus traits for adaptation to climate variability and change. In Silico Plants 2020, 2, diaa003. [Google Scholar] [CrossRef]
- Casadebaig, P.; Chapman, S.; Huth, N.; Faivre, R.; Chenu, K. Assessment of the Potential Impacts of Wheat Plant Traits across Environments by Combining Crop Modeling and Global Sensitivity Analysis. PLoS ONE 2016, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Robertson, M.J.; Wood, A.W.; Muchow, R.C. Growth of sugarcane under high input conditions in tropical Australia. I. Radiation use, biomass accumulation and partitioning. Field Crop Res. 1996, 48, 11–25. [Google Scholar] [CrossRef]
- Wajid, N.; Ashfaq, A.; Asad, A.; Muhammad, T.; Muhammad, A.; Muhammad, S.; Jabran, K.; Shah, G.M.; Sultana, S.R.; Hammad, H.M.; et al. Radiation efficiency and nitrogen fertilizer impacts on sunflower crop in contrasting environments of Punjab, Pakistan. Environ. Sci. Pollut. Res. 2018, 25, 1822–1836. [Google Scholar] [CrossRef]
- Dias, H.B.; Inman-Bamber, G.; Bermejo, R.P.; Sentelhas, C.; Christodoulou, D. New APSIM-Sugar features and parameters required to account for high sugarcane yields in tropical environments. Field Crop Res. 2019, 235, 38–53. [Google Scholar] [CrossRef]
- Inman-Bamber, N.G. Temperature and seasonal effects on canopy development and light interception of sugarcane. Field Crop. Res. 1994, 36, 41–51. [Google Scholar] [CrossRef]
- De Oliveira, E.C.A.; De Castro Gava, G.J.; Trivelin, P.C.O.; Otto, R.; Franco, H.C.J. Determining a critical nitrogen dilution curve for sugarcane. J. Plant Nutr. Soil Sci. 2013, 176, 712–723. [Google Scholar] [CrossRef]
- Muchow, R.C.; Robertson, M.J.; Wood, A.W. Growth of sugarcane under high input conditions in tropical Australia. II. Sucrose accumulation and partitioning, and commercial yield. Field Crop Res. 1996, 48, 11–25. [Google Scholar] [CrossRef]
- Dalgliesh, N.; Hochman, Z.; Huth, N.; Holzworth, D. Field Protocol to APSoil Characterisations; Version 4; CSIRO: Perth, Australia, 2016; p. 25. [Google Scholar]
- van Heerden, P.D.R.; Donaldson, R.A.; Watt, D.A.; Singels, A. Biomass accumulation in sugarcane: Unravelling the factors underpinning reduced growth phenomena. J. Exp. Bot. 2010, 61, 2877–2887. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, R.A.; Redshaw, K.A.; Rhodes, R.; Van Antwerpen, R. Season effects on productivity of some commercial south African sugarcane cultivars, I: Biomass and Radiation Use Efficiency. In Proceedings of the 81st Annual Congress of South African Sugar Technologists’ Association, Durban, South Africa, 29–31 July 2008. [Google Scholar]
- Park, S.E.; Robertson, M.; Inman-Bamber, N.G. Decline in the growth of a sugarcane crop with age under high input conditions. Field Crop. Res. 2005, 92, 305–320. [Google Scholar] [CrossRef]
- Thorburn, P.; Biggs, J.; Jones, M.R.; Singels, A.; Marin, F.; Martine, J.F.; Chinorumba, S.; Viator, R.; Nunez, O. Evaluation of the APSIM-Sugar model for simulating sugarcane yield at sites in seven countries: Initial results. In Proceedings of the 87th Annual Congress of South African Sugar Technologists’ Association, Pietermaritzburg, South Africa, 17–22 August 2014. [Google Scholar]
- Romero, E.R.; Scandaliaris, J.; Rufino, M.; Zamora, F.P. Biothermal models to predict plant cane emergence. In Proceedings of the XXIV International Society of Sugar Cane Technologists Congress, Brisbane, Australia, 17–21 September 2001. [Google Scholar]
- De Santana, A.C.; De Oliveira, E.C.A.; Da Silva, V.S.G.; Dos Santos, R.L.; Da Silva, M.A.; Freire, F.J. Critical nitrogen dilution curves and productivity assessments for plant cane. Rev. Bras. Eng. Agric. Ambient. 2020, 24, 244–251. [Google Scholar] [CrossRef]








| Soil Depth (cm) | BD (g/cm3) | Air Dry (mm/mm) | LL15 (mm/mm) | DUL (mm/mm) | SAT (mm/mm) | KS (mm/day) | Sugarcane LL (mm/mm) | Sugarcane KL (/day) | Sugarcane XF (0–1) | Sugarcane PAWC (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0–15 | 1.530 | 0.056 | 0.111 | 0.207 | 0.365 | 11051.8 | 0.131 | 0.1 | 1 | 11.3 |
| 15–30 | 1.520 | 0.086 | 0.108 | 0.198 | 0.365 | 9287.7 | 0.127 | 0.1 | 1 | 10.6 |
| 30–60 | 1.340 | 0.125 | 0.125 | 0.225 | 0.42 | 13572.1 | 0.148 | 0.08 | 1 | 23 |
| 60–90 | 1.260 | 0.126 | 0.126 | 0.205 | 0.471 | 8129.8 | 0.150 | 0.06 | 1 | 16.4 |
| 90–120 | 1.340 | 0.142 | 0.142 | 0.209 | 0.454 | 4780.7 | 0.176 | 0.04 | 1 | 10 |
| 120–150 | 1.340 | 0.142 | 0.142 | 0.209 | 0.454 | 4780.7 | 0.176 | 0.01 | 1 | 10 |
| 150–180 | 1.340 | 0.142 | 0.142 | 0.209 | 0.454 | 4780.7 | 0.176 | 0.01 | 0 | 0 |
| 180–200 | 1.340 | 0.142 | 0.142 | 0.209 | 0.454 | 4780.7 | 0.176 | 0.01 | 0 | 0 |
| Depth (cm) | Carbon (Total %) | C:N (g/g) | FOM (kg/ha) | NO3−N (ppm) | NH4−N (ppm) | pH |
|---|---|---|---|---|---|---|
| 0–20 | 1.30 | 11 | 343.139 | 2 | 1.00 | 6 |
| 20–40 | 0.90 | 11 | 245.870 | 2 | 1.00 | 6 |
| 40–60 | 0.54 | 11 | 176.174 | 1 | 1.00 | 6 |
| 60–90 | 0.40 | 11 | 106.855 | 1 | 0.50 | 6 |
| 90–120 | 0.40 | 11 | 64.811 | 1 | 0.50 | 6 |
| 120–150 | 0.40 | 11 | 39.310 | 1 | 0.50 | 6 |
| 150–180 | 0.40 | 11 | 23.842 | 1 | 0.50 | 6 |
| Function of Parameters | Parameter Name | Description | Level | Code | Units | Range |
|---|---|---|---|---|---|---|
| Canopy development | leaf_size | Area of the respective leaf | leaf_size_no = 1 | LS1 | mm2 | 500–2000 |
| leaf_size_no = 14 | LS2 | mm2 | 25,000–70,000 | |||
| leaf_size_no = 20 | LS3 | mm2 | 25,000–70,000 | |||
| green_leaf_no | Maximum number of fully expanded green leaves | GLN | No. | 9–14 | ||
| tillerf_leaf_size | Tillering factors according to the leaf numbers | Tiller_leaf_size_no = 1 | TLS1 | mm2/mm2 | 1–6 | |
| Tiller_leaf_size_no = 4 | TLS2 | mm2/mm2 | 1–6 | |||
| Tiller_leaf_size_no = 10 | TLS3 | mm2/mm2 | 1–6 | |||
| Tiller_leaf_size_no = 16 | TLS4 | mm2/mm2 | 1–6 | |||
| Tiller_leaf_size_no = 26 | TLS5 | mm2/mm2 | 1–6 | |||
| Partitioning of assimilates | cane_fraction | Fraction of accumulated biomass partitioned to cane | CF | g/g | 0.65–0.80 | |
| sucrose_fraction_stalk | Fraction of accumulated biomass partitioned to sucrose | SF1 | g/g | 0.50–0.70 | ||
| stress_factor_stalk | Stress factor for sucrose accumulation | SF2 | n/a | 0.2–1.0 | ||
| sucrose_delay | Sucrose accumulation delay | SD | g/m2 | 0–600 | ||
| min_sstem_sucrose | Minimum stem biomass before partitioning to sucrose commences | MSS | g/m2 | 450–1500 | ||
| Phenological development based on thermal time | min_sstem_sucrose_redn | Reduction to minimum stem sucrose under stress | MSSR | g/m2 | 0–20 | |
| tt_emerg_to_begcane | Accumulated thermal time from emergence to beginning of cane | TEB | °C day | 1200–1900 | ||
| tt_begcane_to_flowering | Accumulated thermal time from beginning of cane to flowering | TBF | °C day | 5500–6500 | ||
| tt_flowering_to_crop_end | Accumulated thermal time from flowering to end of the crop | TFCE | °C day | 1750–2250 | ||
| Dry matter assimilation | transp_eff_cf | Transpiration efficiency coefficient | From sowing to sprouting | TEC1 | kg kPa/kg | 0.008–0.014 |
| From sprouting to emergence | TEC2 | |||||
| From emergence to the beginning of cane growth | TEC3 | |||||
| From the beginning of cane growth to flowering | TEC4 | |||||
| From flowering to the end of the crop | TEC5 | |||||
| At the end of the crop | TEC6 | |||||
| rue | Radiation use efficiency | From emergence to the beginning of cane growth | RUE3 | g/MJ | 1.2–2.5 | |
| From the beginning of cane growth to flowering | RUE4 | |||||
| From flowering to the end of the crop | RUE5 | |||||
| Influencing the sugarcane growth process | y_n_conc_crit_leaf | Critical N concentration in leaves | From sowing to sprouting | NCL1 | g/g | 0.0175–0.0325 |
| From sprouting to emergence | NCL2 | g/g | 0.0175–0.0325 | |||
| From emergence to the beginning of cane growth | NCL3 | g/g | 0.0105–0.0195 | |||
| From the beginning of cane growth to flowering | NCL4 | g/g | 0.0105–0.0195 | |||
| From flowering to the end of the crop | NCL5 | g/g | 0.0035–0.0065 | |||
| y_n_conc_min_leaf | Minimum N concentration in leaves | From sowing to sprouting | NML1 | g/g | 0.0105–0.0195 | |
| From sprouting to emergence | NML2 | g/g | 0.0105–0.0195 | |||
| From emergence to the beginning of cane growth | NML3 | g/g | 0.0035–0.0065 | |||
| From the beginning of cane growth to flowering | NML4 | g/g | 0.0035–0.0065 | |||
| From flowering to the end of the crop | NML5 | g/g | 0.0028–0.0052 | |||
| y_n_conc_crit_cane | Critical N concentration in cane | From sowing to sprouting | NCC1 | g/g | 0.0063–0.0117 | |
| From sprouting to emergence | NCC2 | g/g | 0.0063–0.0117 | |||
| From emergence to the beginning of cane growth | NCC3 | g/g | 0.0063–0.0117 | |||
| From the beginning of cane growth to flowering | NCC4 | g/g | 0.0042–0.0078 | |||
| From flowering to the end of the crop | NCC5 | g/g | 0.00035–0.00065 | |||
| y_n_conc_min_cane | Minimum N concentration in cane | From sowing to sprouting | NMC1 | g/g | 0.0014–0.0026 | |
| From sprouting to emergence | NMC2 | g/g | 0.0014–0.0026 | |||
| From emergence to the beginning of cane growth | NMC3 | g/g | 0.00035–0.00065 | |||
| From the beginning of cane growth to flowering | NMC4 | g/g | 0.00035–0.00065 | |||
| From flowering to the end of the crop | NMC5 | g/g | 0.00035–0.00065 | |||
| y_n_conc_crit_cabbage | Critical N concentration in cabbage | From sowing to sprouting | NCCA1 | g/g | 0.0133–0.0247 | |
| From sprouting to emergence | NCCA2 | g/g | 0.0133–0.0247 | |||
| From emergence to the beginning of cane growth | NCCA3 | g/g | 0.0042–0.0078 | |||
| From the beginning of cane growth to flowering | NCCA4 | g/g | 0.0042–0.0078 | |||
| From flowering to the end of the crop | NCCA5 | g/g | 0.0007–0.0013 | |||
| y_n_conc_min_cabbage | Minimum N concentration in cabbage | From sowing to sprouting | NMCA1 | g/g | 0.007–0.013 | |
| From sprouting to emergence | NMCA2 | g/g | 0.007–0.013 | |||
| From emergence to the beginning of cane growth | NMCA3 | g/g | 0.0021–0.0039 | |||
| From the beginning of cane growth to flowering | NMCA4 | g/g | 0.0021–0.0039 | |||
| From flowering to the end of the crop | NMCA5 | g/g | 0.00056–0.00104 | |||
| The rate of flow of water undersaturated conditions | SWCON | Parameter rerated to saturated flow-proportion of water between saturation and field capacity (Whole profile drainage rate coefficient) | Soil layer 0–15 cm | SWC1 | /day | 0.2–0.8 |
| Soil layer 15–30 cm | SWC2 | |||||
| Soil layer 30–60 cm | SWC3 | |||||
| Soil layer 60–90 cm | SWC4 | |||||
| Soil layer 90–120 cm | SWC5 | |||||
| Soil layer 120–150 cm | SWC6 | |||||
| Soil layer 150–180 cm | SWC7 | |||||
| Soil layer 180–200 cm | SWC8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathnappriya, R.H.K.; Sakai, K.; Okamoto, K.; Kimura, S.; Haraguchi, T.; Nakandakari, T.; Setouchi, H.; Bandara, W.B.M.A.C. Global Sensitivity Analysis of Key Parameters in the APSIMX-Sugarcane Model to Evaluate Nitrate Balance via Treed Gaussian Process. Agronomy 2022, 12, 1979. https://doi.org/10.3390/agronomy12081979
Rathnappriya RHK, Sakai K, Okamoto K, Kimura S, Haraguchi T, Nakandakari T, Setouchi H, Bandara WBMAC. Global Sensitivity Analysis of Key Parameters in the APSIMX-Sugarcane Model to Evaluate Nitrate Balance via Treed Gaussian Process. Agronomy. 2022; 12(8):1979. https://doi.org/10.3390/agronomy12081979
Chicago/Turabian StyleRathnappriya, R. H. K., Kazuhito Sakai, Ken Okamoto, Sho Kimura, Tomokazu Haraguchi, Tamotsu Nakandakari, Hideki Setouchi, and W. B. M. A. C. Bandara. 2022. "Global Sensitivity Analysis of Key Parameters in the APSIMX-Sugarcane Model to Evaluate Nitrate Balance via Treed Gaussian Process" Agronomy 12, no. 8: 1979. https://doi.org/10.3390/agronomy12081979
APA StyleRathnappriya, R. H. K., Sakai, K., Okamoto, K., Kimura, S., Haraguchi, T., Nakandakari, T., Setouchi, H., & Bandara, W. B. M. A. C. (2022). Global Sensitivity Analysis of Key Parameters in the APSIMX-Sugarcane Model to Evaluate Nitrate Balance via Treed Gaussian Process. Agronomy, 12(8), 1979. https://doi.org/10.3390/agronomy12081979








