An Agricultural Event Prediction Framework towards Anticipatory Scheduling of Robot Fleets: General Concepts and Case Studies
Abstract
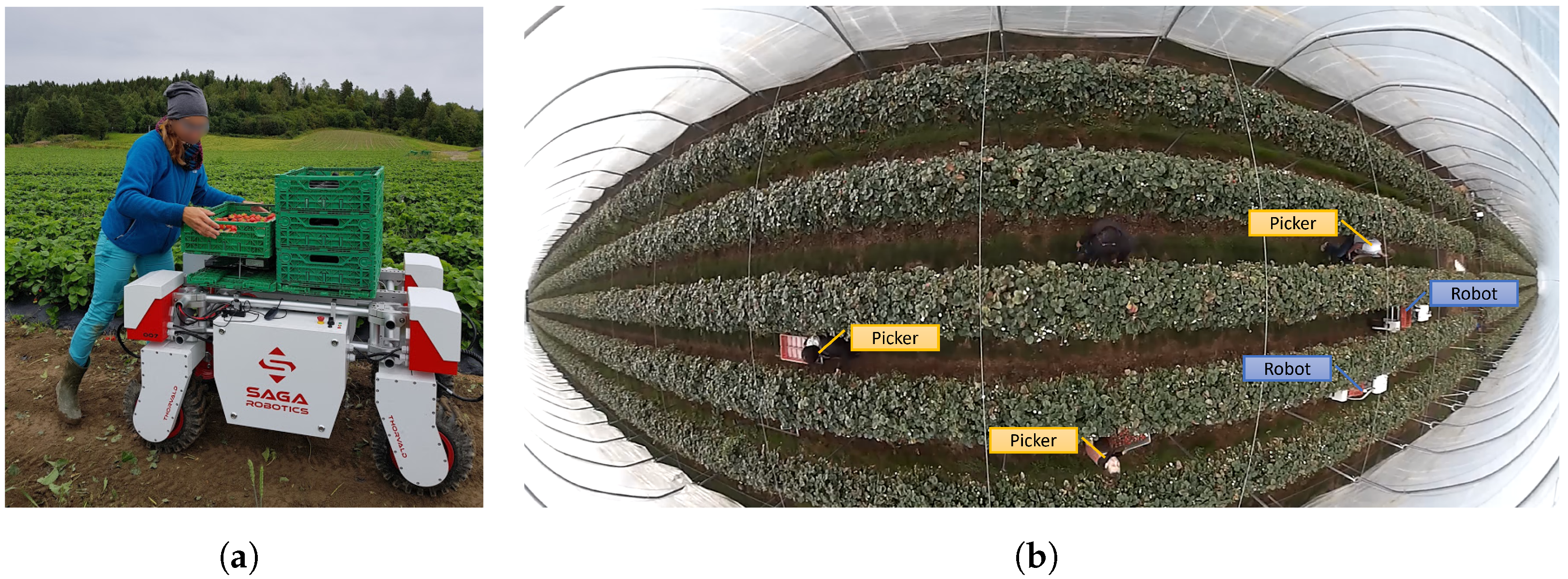
:1. Introduction
1.1. Problem Formulation
1.2. Related Works
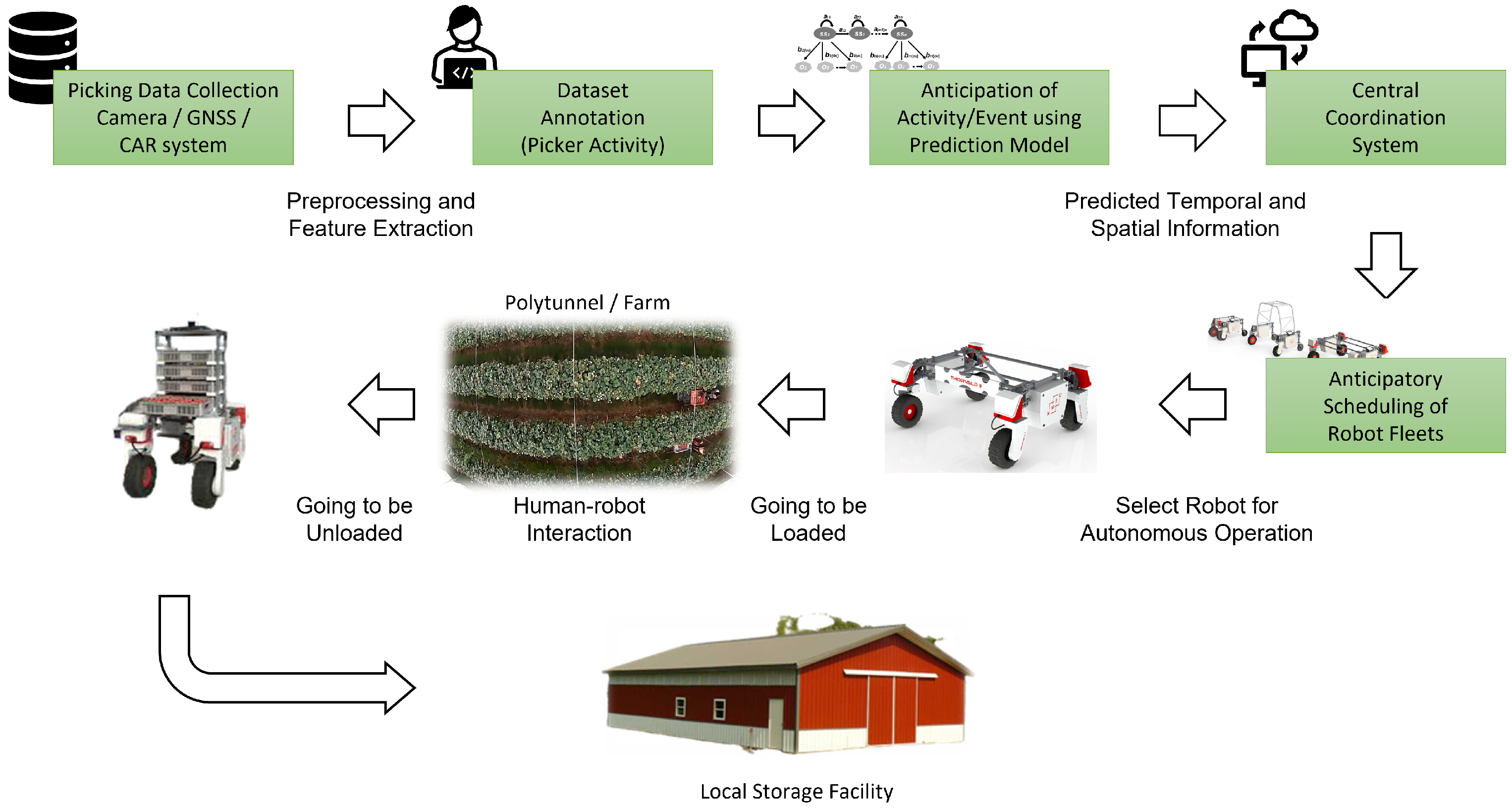
1.3. Our Proposal and Contribution
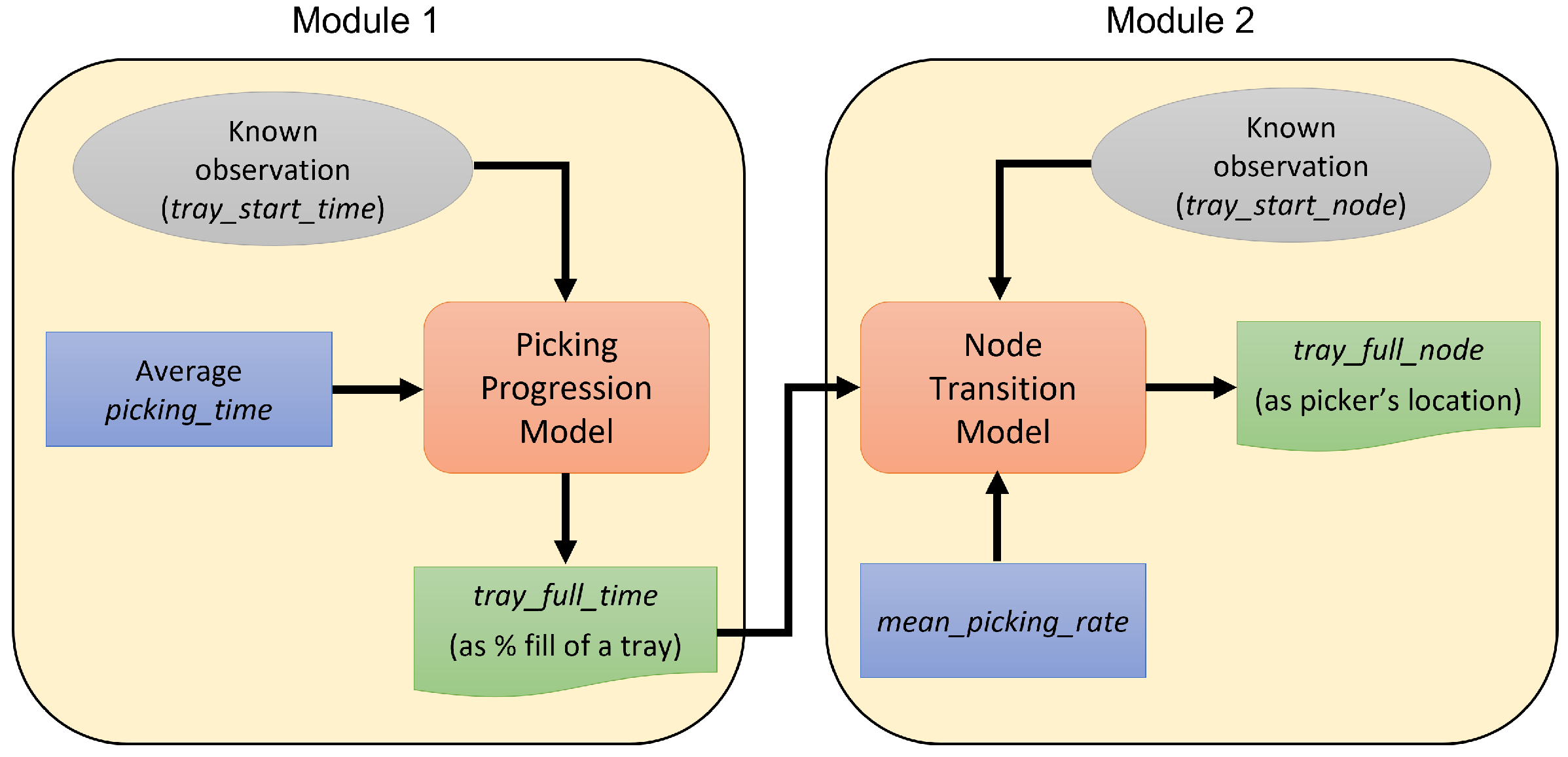
2. System Overview
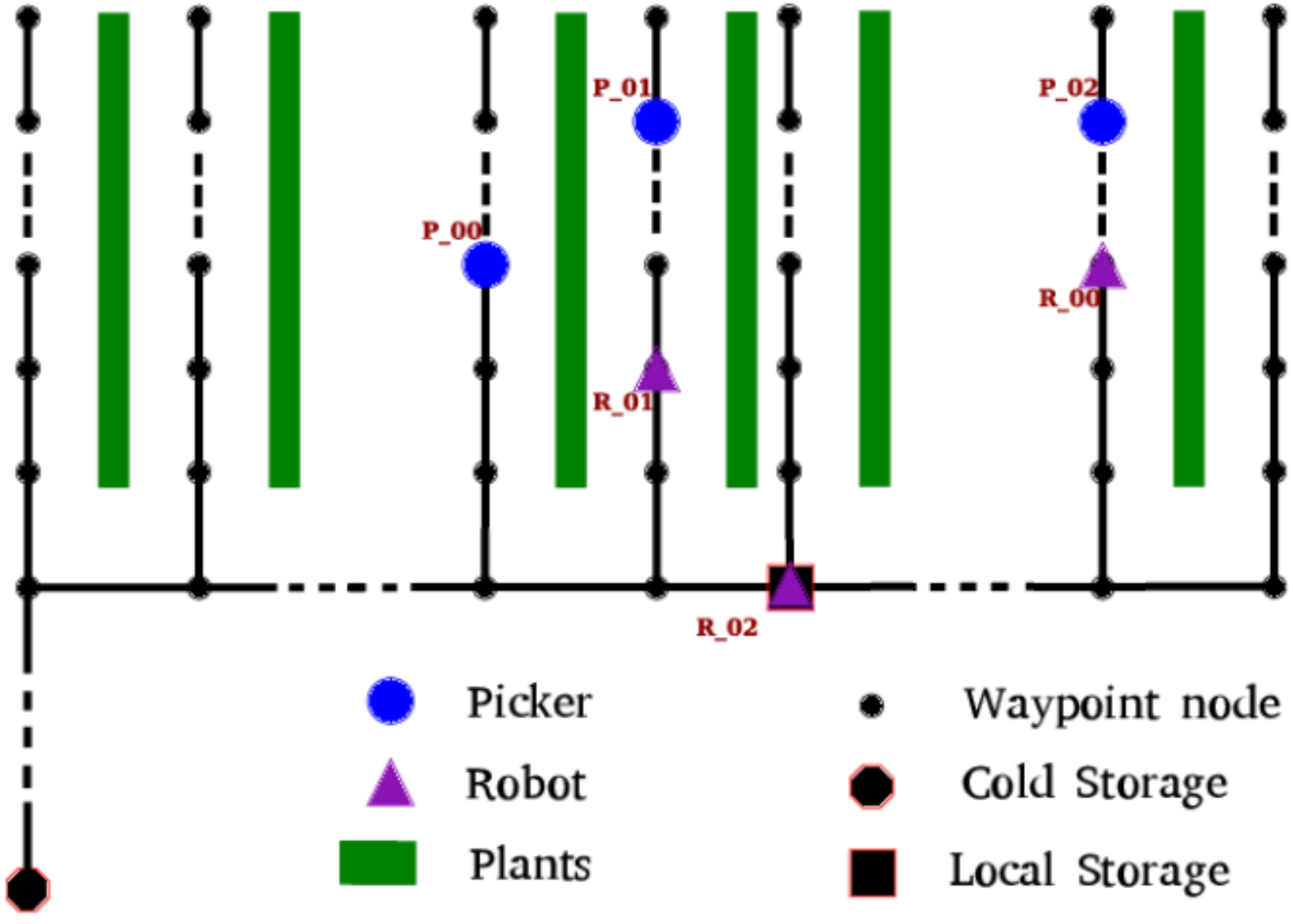
2.1. The Topological Map
2.2. A State Abstraction for Picking Operation
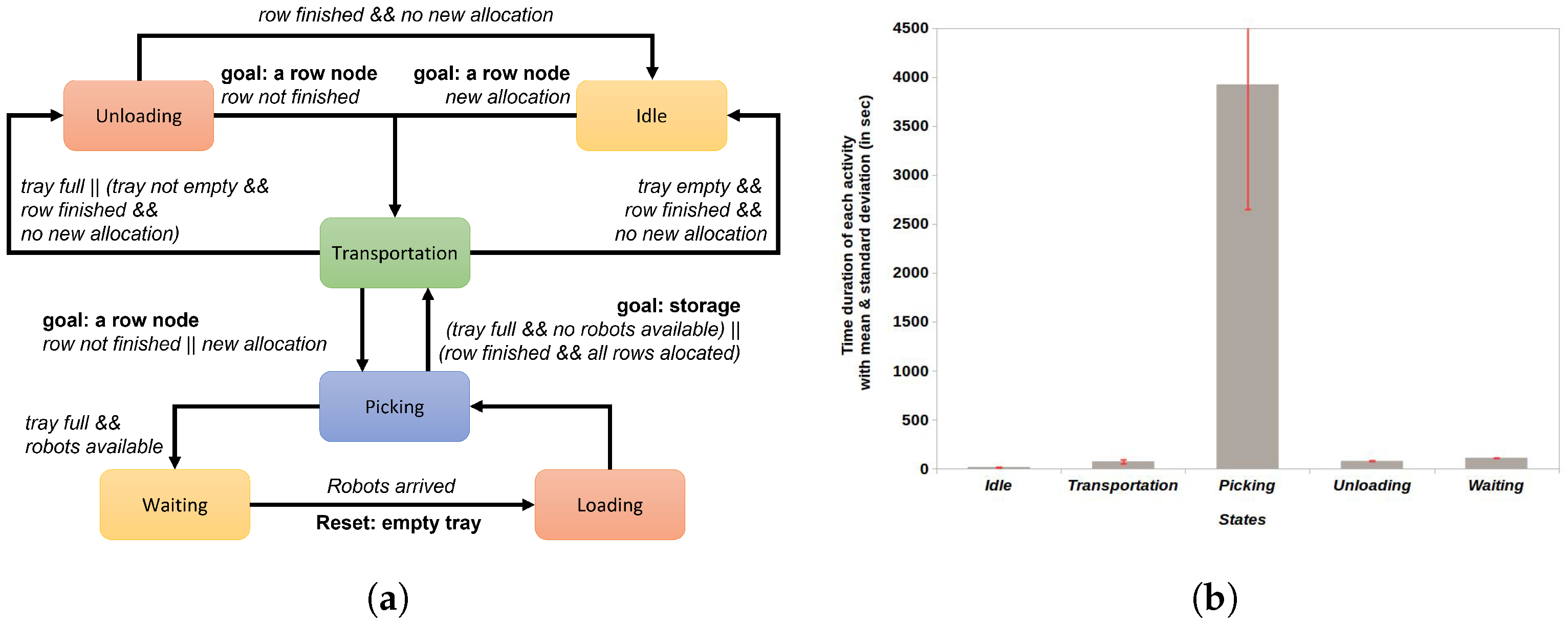
Categorizing the Picker’s States
3. A Topological Map-Based Spatio-Temporal Prediction Framework
3.1. Spatio-Temporal Prediction Modules
3.2. Design of Individual CtHMMs
3.3. Predictions from the CtHMMs
4. Experimental Evaluation
4.1. Test Case 1: To Choose an Optimal Picking_State_Progression Model
4.2. Test Case 2: Spatio-Temporal Predictions of the Picker’s Motion
4.2.1. Analysis for a Single Picker
4.2.2. Analysis for an Overall Picking Operation
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srinivasan, A. (Ed.) Handbook of Precision Agriculture: Principles and Applications; Food Products Press, An Imprint of the Haworth Press, Inc.: Binghamton, NY, USA, 2006. [Google Scholar]
- Bechar, A.; Vigneault, C. Agricultural Robots for Field Operations: Concepts and Components. Biosyst. Eng. 2016, 149, 94–111. [Google Scholar] [CrossRef]
- Vasconez, J.P.; Kantor, G.A.; Auat Cheein, F.A. Human-robot Interaction in Agriculture: A Survey and Current Challenges. Biosyst. Eng. 2019, 179, 35–48. [Google Scholar] [CrossRef]
- Das, G.; Cielniak, G.; From, P.; Hanheide, M. Discrete Event Simulations for Scalability Analysis of Robotic in-Field Logistics in Agriculture—A Case Study. In Proceedings of the IEEE International Conference on Robotics and Automation, Workshop on Robotic Vision and Action in Agriculture, Brisbane, Australia, 21–26 May 2018; pp. 1–6. [Google Scholar]
- Achillas, C.; Bochtis, D.; Aidonis, D.; Marinoudi, V.; Folinas, D. Voice-driven Fleet Management System for Agricultural Operations. Inf. Process. Agric. 2019, 6, 471–478. [Google Scholar] [CrossRef]
- Bochtis, D.; Benos, L.; Lampridi, M.; Marinoudi, V.; Pearson, S.; Sørensen, C.G. Agricultural Workforce Crisis in Light of the COVID-19 Pandemic. Sustainability 2020, 12, 8212. [Google Scholar] [CrossRef]
- From, P.J.; Grimstad, L.; Hanheide, M.; Pearson, S.; Cielniak, G. Rasberry—Robotic and Autonomous Systems for Berry Production. ASME Mech. Eng. 2018, 140, S14–S18. [Google Scholar] [CrossRef] [Green Version]
- Grimstad, L.; From, P. The Thorvald II Agricultural Robotic System. Robotics 2017, 6, 24. [Google Scholar] [CrossRef] [Green Version]
- Baxter, P.; Cielniak, G.; Hanheide, M.; From, P. Safe Human-Robot Interaction in Agriculture. In Proceedings of the Companion of the 2018 ACM/IEEE International Conference on Human-Robot Interaction, Chicago, IL, USA, 5–8 March 2018; pp. 59–60. [Google Scholar]
- Sørensen, C.; Bochtis, D. Conceptual Model of Fleet Management in Agriculture. Biosyst. Eng. 2010, 105, 41–50. [Google Scholar] [CrossRef]
- Emmi, L.; Gonzalez-de Soto, M.; Gonzalez-de Santos, P. Configuring a Fleet of Ground Robots for Agricultural Tasks. In ROBOT2013: First Iberian Robotics Conference: Advances in Robotics; Armada, M.A., Sanfeliu, A., Ferre, M., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 505–517. [Google Scholar]
- de Santos, P.G.; Ribeiro, A.; Fernandez-Quintanilla, C.; Lopez-Granados, F.; Brandstoetter, M.; Tomic, S.; Pedrazzi, S.; Peruzzi, A.; Pajares, G.; Kaplanis, G.; et al. Fleets of Robots for Environmentally-safe Pest Control in Agriculture. Precis. Agric. 2017, 18, 574–614. [Google Scholar] [CrossRef]
- Huuskonen, J.; Oksanen, T. Augmented Reality for Supervising Multirobot System in Agricultural Field Operation. In Proceedings of the 6th IFAC Conference on Sensing, Control and Automation Technologies for Agriculture, Sydney, Australia, 4–6 December 2019; pp. 367–372. [Google Scholar]
- Wu, C.; Chen, Z.; Wang, D.; Song, B.; Liang, Y.; Yang, L.; Bochtis, D.D. A Cloud-Based in-field Fleet Coordination System for Multiple Operations. Energies 2020, 13, 775. [Google Scholar] [CrossRef] [Green Version]
- Wurman, P.R.; D’Andrea, R.; Mountz, M. Coordinating Hundreds of Cooperative, Autonomous Vehicles in Warehouses. AI Mag. 2008, 29, 9–20. [Google Scholar]
- Ball, D.; Ross, P.; English, A.; Milani, P.; Richards, D.; Bate, A.; Upcroft, B.; Wyeth, G.; Corke, P. Farm Workers of the Future: Vision-Based Robotics for Broad-Acre Agriculture. IEEE Robot. Autom. Mag. 2017, 24, 97–107. [Google Scholar] [CrossRef]
- Bochtis, D.; Sørensen, C.; Vougioukas, S. Path Planning for In-field Navigation-aiding of Service Units. Comput. Electron. Agric. 2010, 74, 80–90. [Google Scholar] [CrossRef]
- Conesa-Muñoz, J.; Bengochea-Guevara, J.M.; Andujar, D.; Ribeiro, A. Efficient Distribution of a Fleet of Heterogeneous Vehicles in Agriculture: A Practical Approach to Multi-path Planning. In Proceedings of the IEEE International Conference on Autonomous Robot Systems and Competitions, Vila Real, Portugal, 8–10 April 2015; pp. 56–61. [Google Scholar]
- Xu, W.; Wang, Q.; Chen, R. Spatio-temporal Prediction of Crop Disease Severity for Agricultural Emergency Management based on Recurrent Neural Networks. GeoInformatica 2018, 22, 363–381. [Google Scholar] [CrossRef]
- Ozaki, V.A.; Ghosh, S.K.; Goodwin, B.K.; Shirota, R. Spatio-temporal Modeling of Agricultural Yield Data with an Application to Pricing Crop Insurance Contracts. Am. J. Agric. Econ. 2008, 90, 951–961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tokovenko, O.; Dorfman, J.H.; Gunter, L.F. A Spatio-temporal Model for Agricultural Yield Prediction. In Proceedings of the Annual Meeting: Agricultural and Applied Economics Association, Denver, CO, USA, 25–27 July 2010; pp. 1–17. [Google Scholar]
- Khan, M.W.; Das, G.P.; Hanheide, M.; Cielniak, G. Incorporating Spatial Constraints into a Bayesian Tracking Framework for Improved Localisation in Agricultural Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020; pp. 2440–2445. [Google Scholar]
- Martinez, J.; Black, M.J.; Romero, J. On Human Motion Prediction using Recurrent Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4674–4683. [Google Scholar]
- Cheng, Y.; Sun, L.; Liu, C.; Tomizuka, M. Towards Efficient Human-Robot Collaboration With Robust Plan Recognition and Trajectory Prediction. IEEE Robot. Autom. Lett. 2020, 5, 2602–2609. [Google Scholar] [CrossRef]
- Callens, T.; van der Have, T.; Rossom, S.V.; De Schutter, J.; Aertbeliën, E. A Framework for Recognition and Prediction of Human Motions in Human-Robot Collaboration Using Probabilistic Motion Models. IEEE Robot. Autom. Lett. 2020, 5, 5151–5158. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, Y.; Wang, J.; Zhang, W. Optimal Collision-Free Robot Trajectory Generation Based on Time Series Prediction of Human Motion. IEEE Robot. Autom. Lett. 2018, 3, 226–233. [Google Scholar] [CrossRef]
- Unhelkar, V.V.; Lasota, P.A.; Tyroller, Q.; Buhai, R.; Marceau, L.; Deml, B.; Shah, J.A. Human-Aware Robotic Assistant for Collaborative Assembly: Integrating Human Motion Prediction With Planning in Time. IEEE Robot. Autom. Lett. 2018, 3, 2394–2401. [Google Scholar] [CrossRef] [Green Version]
- Rabiner, L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.Y.; Li, S.; Li, F.; Song, L.; Rehg, J.M. Efficient Learning of Continuous-time Hidden Markov Models for Disease Progression. Adv. Neural Inf. Process. Syst. 2015, 28, 3600–3608. [Google Scholar]
- Bartolomeo, N.; Trerotoli, P.; Serio, G. Progression of Liver Cirrhosis to HCC: An Application of Hidden Markov Model. BMC Med. Res. Methodol. 2011, 11, 38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.Y.; Ishikawa, H.; Chen, M.; Wollstein, G.; Schuman, J.S.; Rehg, J.M. Longitudinal Modeling of Glaucoma Progression using 2-Dimensional Continuous-Time Hidden Markov Model. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Nagoya, Japan, 22–26 September 2013; pp. 444–451. [Google Scholar]
- Hulme, W.J.; Martin, G.P.; Sperrin, M.; Casson, A.J.; Bucci, S.; Lewis, S.; Peek, N. Adaptive Symptom Monitoring Using Hidden Markov Models – An Application in Ecological Momentary Assessment. IEEE J. Biomed. Health Inform. 2021, 25, 1770–1780. [Google Scholar] [CrossRef] [PubMed]
- Vasquez, D.; Fraichard, T.; Laugier, C. Growing Hidden Markov Models: An Incremental Tool for Learning and Predicting Human and Vehicle Motion. Int. J. Robot. Res. 2009, 28, 1486–1506. [Google Scholar] [CrossRef] [Green Version]
- BolaBola, J.Z.; Wang, Y.; Wu, S.; Qin, H.; Niu, J. Application of Hidden Markov Model in Human Motion Recognition by Using Motion Capture Data. In Advances in Physical Ergonomics and Human Factors; Goonetilleke, R., Karwowski, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 21–28. [Google Scholar]
- Varadarajan, K.M. Topological Mapping for Robot Navigation using Affordance Features. In Proceedings of the 6th International Conference on Automation, Robotics and Applications, Queenstown, New Zealand, 17–19 February 2015; pp. 42–49. [Google Scholar]
- Binch, A.; Das, G.P.; Fentanes, J.P.; Hanheide, M. Context Dependant Iterative Parameter Optimisation for Robust Robot Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 3937–3943. [Google Scholar]
- Visser, I. Seven Things to Remember about Hidden Markov Models: A Tutorial on Markovian Models for Time Series. J. Math. Psychol. 2011, 55, 403–415. [Google Scholar] [CrossRef]
- Perduca, V.; Nuel, G. Measuring the influence of observations in HMMs through the Kullback–Leibler distance. IEEE Signal Process. Lett. 2012, 20, 145–148. [Google Scholar] [CrossRef] [Green Version]
- Allahverdyan, A.; Galstyan, A. Comparative Analysis of Viterbi Training and Maximum Likelihood Estimation for HMMs. In Advances in Neural Information Processing Systems; ISMANS: Granada, Spain, 2011; pp. 1674–1682. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A. ROS: An Open-Source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kebo, Japan, 12–17 May 2009; pp. 1–6. [Google Scholar]




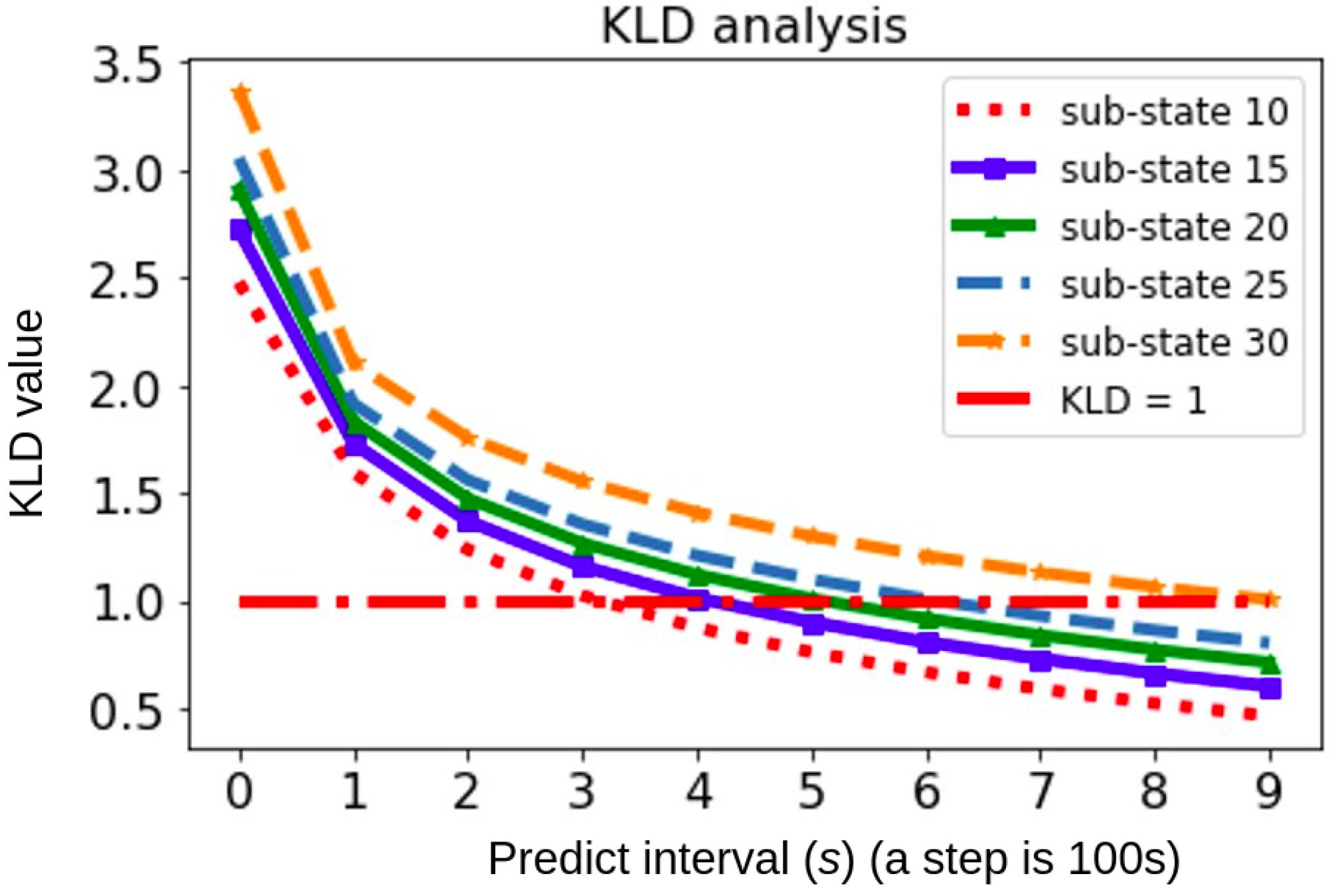
| Number of Sub-States | 10 | 15 | 20 | 25 | 30 |
| KLD Value | 0.46 | 0.60 | 0.71 | 0.92 | 1.006 |
| Acronym | Definition | Description |
|---|---|---|
| TFT | Tray Full Time | Time taken to fill a tray, denoted by tray_full_time. |
| PTE | Prediction Time Error | Difference between actual and predicted (TFT), denoted by prediction_time_error. |
| TTT | Transportation Time per Tray | Travel time taken by picker to unload a full fruit tray to the local storage, denote by transportation_time. |
| ANCT | Average Nodes Covered per “tray-full event” | Nodes distance on an average a picker covers for filling up a tray. |
| NTT | Node Transition Time | Time taken by a picker while picking, to move from one node to its subsequent node. |
| ATT | Average “tray-full event” Time | For overall process, an average time taken by a picker to fill a tray. |
| APCT | Average Process Completion Time | For overall process, an average time taken to pick a complete farm. |
| STT | Save on Transportation Time | Based on the usage of the prediction model, a reduction in transportation time. |
| FoO | Frequency of Occurrence | Likeliness of an event to occur. |
| PAE | Percentage Average Error | For overall process, the absolute difference between actual and predicted values in percent. |
| Start | Prediction | Actual | PTE per Tray | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| End | End | End | End | prediction_time_error | |||||||||
| ray No. | row_ID | node_ID | Time (s) | Direction | row_ID | node_ID | Time (s) | Direction | row_ID | node_ID | Time (s) | Direction | Time (s) |
| 1 | 00 | 00 | 1.9 | F | 00 | 16 | 2096.7 | F | 00 | 16 | 2114.9 | F | 18.9 |
| 2 | 00 | 16 | 2393.6 | F | 02 | 08 | 4630.3 | F | 02 | 07 | 4475.5 | F | −154.5 |
| 3 | 02 | 07 | 4664.7 | F | 02 | 23 | 6764.5 | F | 02 | 22 | 6641.3 | F | −123.2 |
| 4 | 02 | 22 | 6978.1 | F | 02 | 11 | 8949.0 | R | 02 | 11 | 8935.6 | R | −13.4 |
| 5 | 02 | 11 | 9163.8 | R | 04 | 04 | 11,138.5 | F | 04 | 04 | 11,150.2 | F | 11.7 |
| 6 | 04 | 04 | 11,311.9 | F | 04 | 19 | 13,281.5 | F | 04 | 20 | 13,399.4 | F | 117.9 |
| 7 | 04 | 20 | 13,718.8 | F | 04 | 13 | 15,680.1 | R | 04 | 13 | 15,686.2 | R | 6.1 |
| Class | Pred. | Act. | PTE | Who’s | Empirical | FoO |
|---|---|---|---|---|---|---|
| Node | Node | per Tray (s) | Waiting | % STT (Approx.) | ||
| 1 | same | same | PTE ⋘ TTT | Robot | 100 | High |
| 2 | behind | ahead | PTE ≤ TTT | Robot | ) | High |
| 3 | ahead | behind | −2TTT ⋘−PTE <−TTT | Picker | Not Applicable | Medium |
| 4 | same | same | −TTT ⋘ PTE | Picker | ) | Low |
| Prediction | Actual | PAE | |
|---|---|---|---|
| APCT (s) | 15,787.85 | 15,726.02 | |
| ANCT | |||
| ATT (s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, A.; Das, G.; Hanheide, M.; Candea Leite, A.; From, P.J. An Agricultural Event Prediction Framework towards Anticipatory Scheduling of Robot Fleets: General Concepts and Case Studies. Agronomy 2022, 12, 1299. https://doi.org/10.3390/agronomy12061299
Pal A, Das G, Hanheide M, Candea Leite A, From PJ. An Agricultural Event Prediction Framework towards Anticipatory Scheduling of Robot Fleets: General Concepts and Case Studies. Agronomy. 2022; 12(6):1299. https://doi.org/10.3390/agronomy12061299
Chicago/Turabian StylePal, Abhishesh, Gautham Das, Marc Hanheide, Antonio Candea Leite, and Pål Johan From. 2022. "An Agricultural Event Prediction Framework towards Anticipatory Scheduling of Robot Fleets: General Concepts and Case Studies" Agronomy 12, no. 6: 1299. https://doi.org/10.3390/agronomy12061299
APA StylePal, A., Das, G., Hanheide, M., Candea Leite, A., & From, P. J. (2022). An Agricultural Event Prediction Framework towards Anticipatory Scheduling of Robot Fleets: General Concepts and Case Studies. Agronomy, 12(6), 1299. https://doi.org/10.3390/agronomy12061299







