Abstract
Reference crop evapotranspiration (ETo) is an important component of the hydrological cycle that is used for water resource planning, irrigation, and agricultural management, as well as in other hydrological processes. The aim of this study was to estimate the ETo based on limited meteorological data using an artificial neural network (ANN) method. The daily data of minimum temperature (Tmin), maximum temperature (Tmax), mean temperature (Tmean), solar radiation (SR), humidity (H), wind speed (WS), sunshine hours (Ssh), maximum global radiation (gradmax), minimum global radiation (gradmin), day length, and ETo data were obtained over the long-term period from 1969 to 2019. The analysed data were divided into two parts from 1969 to 2007 and from 2008 to 2019 for model training and testing, respectively. The optimal ANN for forecasting ETo included Tmax, Tmin, H, and SR at hidden layers (4, 3); gradmin, SR, and WS at (6, 4); SR, day length, Ssh, and Tmean at (3, 2); all collected parameters at hidden layer (5, 4). The results showed different alternative methods for estimation of ETo in case of a lack of climate data with high performance. Models using ANN can help promote the decision-making for water managers, designers, and development planners.
1. Introduction
Increased water consumption due to rapid population growth has necessitated expanding food production through irrigation and industrial output to meet basic human needs [1]. The fundamental goal of irrigation is to apply water to maintain crop evapotranspiration when rainfall is insufficient [2,3]. Evapotranspiration (ET) is a connection between the energy and water cycles, and climate is the primary source of water vapor in the atmosphere [4,5,6,7]. It regulates the quantity of water needed for vegetation development, surface runoff, water loss from water bodies, and water requirements for ecological sustainability. As a result, it is one of the most important hydro-meteorological factors for irrigation and water resource management, as well as ecological monitoring [8,9,10,11]. Evapotranspiration, like other hydro-meteorological variables, has changed all over the world because of global warming. Changes in ET must be assessed to plan adaptation and mitigation to combat climate change’s effects on water supplies, agriculture, and ecology [12]. Evapotranspiration is one of the most essential components of hydrological and climatological processes, accounting for roughly 70% of precipitation falling on land and consuming more than 50% of the solar energy collected by the earth [13,14]. As a result, ET is a particularly valuable indicator for analysing the hydrologic regime’s changing behaviour [15].
Evapotranspiration, on the other hand, is difficult to quantify. Although lysimeters are commonly used to directly measure ET, they are poorly spread over the world due to their high cost and time-consuming management [16,17]. Therefore, ET is generally estimated by various empirical models that assess either potential evapotranspiration (ETp) or reference crop evapotranspiration (ETo) [18,19]. The factor ETo is the highest rate of evapotranspiration that a well-watered vegetative grass surface can produce [5,20,21]. It is thought to be the most accurate way to quantify evaporative demand from real-world land surfaces under certain meteorological conditions [22]. In fact, ETo (rather than actual ET) has long been a key input into numerous hydrological models [23,24]. The ETo is a key factor in the hydrological process used for the calculation of the water requirement, based on the meteorological parameters [25] and quantification in agriculture and precision farming [26]. In addition to empirical ETo models, newly emerging artificial intelligence and machine learning techniques have recently been used to estimate ETo [27,28,29,30].
Intelligent computer models, such as the artificial neural network (ANN) methodology have been created as alternate ways for calculating ET throughout the last decade [31]. Because of its broad use in a variety of scientific fields, ANNs have shown significant progress in the studies on hydrology and water resources [27,28]. Artificial neural networks are large, parallel-distributed processors made up of basic processing units that have a natural proclivity for storing and making available experimental information. They are useful tools for modelling nonlinear processes because they require minimal inputs and can map input-output connections without requiring any prior knowledge of the process [32]. As an efficient soft calculation technology for estimating ETo based on accessible and quantified climatic variables, artificial intelligence models (AI) have been widely applied [33,34].
Neural Networks are frequently used in anticipating lumpy demand, which is characterized by periods of no demand and times of high demand. Traditional time-series approaches may be unable to capture data with a nonlinear pattern. To get over these restrictions, NN modelling is a potential option. Without requiring a priori function forms of models, neural networks can be used to model time series data. Many neural network algorithms have been suggested, explored, and successfully applied to time series prediction and causal prediction, including Multilayer Feed-forward NN, Recurrent NN, Time delay NN, and Nonlinear Autoregressive exogenous NN [35].
The corrosion rate and residual strength of un-stiffened aluminium panels with corrosion thinning and MSD were predicted using ANN by Pidaparti et al. [36,37]. When the ANN residual strength forecasts were compared to the experimental findings, the mean absolute error was found to be around 12%. Even when compared to some of the other very simple engineering models presented in the literature, such an error level is considered to be relatively high.
Hijazi et al. [38] recently used ANN modelling to forecast the residual strength of panels using MSD. A dataset of 147 alternative configurations was compiled from a variety of literature sources, with 97 data points utilized for training, 25 for validation, and 25 for testing. Three different aluminium alloys (2024-T3, 2524-T3, and 7075-T6), four different test panel configurations (un-stiffened, stiffened, stiffened with broken middle stiffener, and lap-joints), and several panel and crack geometries were included in the dataset.
An advantage of ANN models, is that attribute-value pairs can be used to represent problems in ANN. The output of ANNs can be discrete-valued, real-valued, or a vector of many real or discrete-valued attributes, while the target function can be discrete-valued, real-valued, or a vector of numerous real or discrete-valued attributes. Noise in the training data is not a problem for ANN learning algorithms. There may be faults in the training samples, but they will have no effect on the final output. It is employed when a quick assessment of the learnt target function is necessary. The number of weights in the network, the number of training instances considered, and the settings of various learning algorithm parameters can all contribute to long training durations for ANNs [39].
The ANN model used by De and Debnath [40] to compute the maximum and minimum temperatures over India throughout the summer is improved herein. For the years 1901 to 2003, this program used the data for three months to predict the mean monthly surface temperature in the monsoon months (June, July and August) over India, using a Multilayer Perceptron Neural Network (MLPNN). As a result, three models for maximum and lowest temperature for each monsoon month were developed for the period 1901–2003. In all situations, the estimate error was less than 5%. Hasmat Malikand Savita [41], for example, proposes an artificial neural network (ANN) for long-term wind velocity prediction.
In this research, we have tested an artificial neural network intelligence technique (ANN) as a first choice software for the prediction of the ETo with partial climate data and assessed its accuracy with reference information [42]. The fundamental advantage of this network is that no arithmetic model is needed, so an ANN is prepared on examples and trends using a big number of independent and dependent information without past hypotheses about their natural distribution and interactions [43]. The ANNs lack the limitations of other methods of prediction as they finding the needed data through the observed data. Using the ANN techniques, it is essential to have adequate input and output data that is symmetrical [44]. Previous studies have used various AI algorithms and models for computing the ETo [45]. For example, Yin et al. [46] used various regular metrological variables, including Tmax, Tmin, wind speed, relative humidity, and solar radiation, to model daily evapotranspiration in China. The results depended upon the machine learning techniques of a hereditary model, or an algorithm such as the kernel model, i.e., the support vector machine (GA-SVM). The artificial neural network and SVM models were compared; the researchers applied the GA-SVM models for the predication of the ETo. An estimate of ETo using eight climatic variables was proposed by Jovic et al. [47] using a hybrid method called the genetic programming (GP).
The main aim of this study was to develop estimation models for ETo using ANN techniques with limited available climatic data to support farmers, water managers, designers, and development planners. Furthermore, in the research area, to the best of our knowledge, there are no studies in the literature that use artificial intelligence methods to predict ETo based on limited climate data. Given the availability of data and the complexity of computing ETo using the Penman Monteith technique, which requires multiple parameters, the steps of this research were: (1) to model reference crop evaporation ETo in a particular area using some of the variables in the climate data, and to compute the performance of ANN model results, and (2) to select the best developed ANN model for estimation of ETo based on performance metrics. The study outcomes and discussion are described, analysed, and the performance of the ANN in the projection of ETo is compared to observation data.
2. Materials and Methods
2.1. Study Site
The study area is located in the eastern part of Hungary (Hajdú-Bihar County), between 47.5° N and 21.5° E (Figure 1) [48]. In this part of Hungary, the climate is classified as a continental one with a hot summer and a cold rainy winter [49]. The total sunshine hours are 2000 h y−1, with 810 h in summer and 175–180 h in winter. The average annual temperature is 9.6–9.8 °C. Homogenized data for the average, the minimum and the maximum daily air temperature values at 2 m above the ground, and the daily sum of precipitation for the period of 1901–2010, were used. The average daily sum of sunshine hours from 1920 to 2010 was used for the calculations with no data gaps. Considering the wind conditions, north-eastern winds are dominant in Hungary, and based on the dataset for 110 years, the average wind velocity was 3 m s−1. As a yearly average, winds higher than 10 m s−1 occurred in 122 days per year. The most variable climate element in the plain site was precipitation. The annual precipitation was 560–590 mm; however, the spatial distribution of precipitation varies widely. In the vegetation growing period of 1st April to 30th September, its average is around 350 mm, but differences between years and the seasonal distribution are extreme. For example, based on the dataset for Debrecen, which is in the middle of the lowland of the Carpathian basin, the minimum and maximum annual precipitations between years 1901 and 2010 were 321 mm and 953 mm, respectively. The mean annual potential evapotranspiration was 918 mm year−1, though in the first decade of the 1900s, it was 883 mm year−1, while in the first decade of the 2000s, it was 953 mm year−1. In terms of land use, the proportion of arable land was about 50% of the total area, with maize and wheat among the main crops [50].
Figure 1.
Map of the study area within Hungary.
2.2. Data Sources
In this research, the weather station of Debrecen city, which is situated in the central part of the study area, was chosen to collect the historical meteorological data for modelling. The weather station is one of the official stations of the Hungarian Weather Service and is located in a reference site as required based on Allen et al. [5]. The daily data of minimum temperature (Tmin), maximum temperature (Tmax), mean temperature (Tmean), solar radiation (SR), relative humidity (H), wind speed (WS), sunshine hours (Ssh), were obtained from the open access meteorological database of the Hungarian Meteorological Service (https://odp.met.hu/climate/station_data_series/ accessed: 03 December 2021), over the long-term period from 1969 to 2019. The downloaded data were already homogenized and adjusted by the National Weather Service. Day length, and minimum and maximum global radiation values were modelled using latitude values and the calendar day. Maximum global radiation (gradmax) (known as well: clear-sky solar radiation) was calculated based on the 37th equation in the FAO 56 paper [5]. The fraction of extraterrestrial radiation that reaches the earth’s surface ranges from 0.25 on a day with dense cloud cover to about 0.75 on a cloudless day with clear sky [5]. Therefore, minimum global radiation (gradmin) referring to solar radiation assuming dense cloud cover was calculated as follows:
where: gradmin: Minimum global radiation; and Ra: extraterrestrial radiation (MJ m−2 d−1).
The FAO-endorsed Penman–Monteith parameterization [5] was used for estimating reference crop evapotranspiration which calculates reference crop evapotranspiration. The albedo used was 0.23, whilst the aerodynamic resistance was 70 s m−1.
where:
ETo: reference crop evapotranspiration (mm day−1),
Rn: net radiation at the crop surface (MJ m−2 day−1),
G: soil heat flux density (MJ m−2 day−1),
T: mean daily air temperature at 2 m height (°C),
u2: wind speed at 2 m height (m s−1),
es: saturation vapour pressure (kPa),
ea: actual vapour pressure (kPa),
es – ea: saturation vapour pressure deficit (kPa),
Δ: slope vapour pressure curve (kPa °C−1),
γ: psychrometric constant (kPa °C−1).
The analysed data were divided into two parts, from 1969 to 2007, and from 2008 to 2019, for model training and testing, respectively.
2.3. Application of the Artificial Neural Network method (ANN)
The artificial neural networks (ANN) provide a technique with features in common with the analysis process of the neural network [51]. A multi-layered structure is among the most common models for feed-forward ANN. The input, hidden and output layers comprise the easy network architecture of ANN. The input group is transferred to the network on the input layer. The number of nodes in this layer defines the number of inputs. In addition, every input variable is calculated by one neuron, and each neuron is related to those neurons of the other layer by their weights. The hidden layer is that which performs the essential principle of the network and divides the most essential information from the input layer and converts it to the next layer. Difficulties may arise in the processing of new data groups in the same network if more neurons are used than necessary. The most generally used methods for calculating the number of hidden layer neurons and layer are trial and error techniques. Their performance is very useful to increase the accuracy of the study results.
Recently, artificial technology has been successfully applied for predicting the ETo and other climate factors. As a result, many researchers have achieved highly accurate results and provided valuable predication data that was helpful for the future planning and development and accorded with observed data [44,45,46].
Our data sets were studied using a technique of artificial intelligence. The ANN is a type with three layers, as illustrated in Figure 2. The input layer is the initial data of the neural network, the hidden input network is the intermediate input layer, where all the computations are made, the output layer produces the result (output) for each input. To improve the neural network’s performance, multiple combinations of input variables with a number of hidden neurons for each layer were applied using an automatic loop to adjust the ANN design. As a result, the optimal combination of factors for forecasting ETo and architecture was chosen based on statistical analysis indicators.
Figure 2.
ANN structure.
2.4. Performance Evaluation
The actual ETo and the modelled values were compared throughout the study period. To evaluate the accuracy of the models, the following statistical indicators were selected: root mean square error (RMSE), normalized root mean square error (NRMSE), mean absolute percentage error (MAPE), accuracy, and the coefficient of determination (R2) [3,52,53]. All the parameters are defined as follows: is the observed or actual value, is the simulated value, is the mean value, and N is the total number of data points.
RMSE:
NRMSE:
where SD is the standard deviation of the observed or actual ETo values
Mean absolute percentage error:
R2:
Accuracy:
3. Results
3.1. Calculated ETo
There was a considerable increasing trend in ETo values over the 50 years of data (Figure 3). The increase corresponds with the increasing trend of temperature at the study site, explored by Juhász et al. [54].
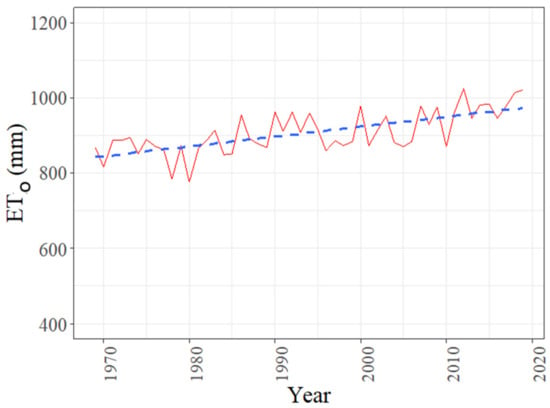
Figure 3.
Yearly values of ETo (1969–2019).
3.2. Data Fusion of Climatic Factors for Modelling the ETo
There are two approaches to choosing the appropriate climatic variables in ANNs for forecasting ETo. The first approach relies on training and testing various variable combinations in the ANN in the study, to arrive at the optimal or best combination with high accuracy, performance, and less error. The second strategy employs dimensionality reduction algorithms, such as principal component analysis (PCA), which find patterns in data based on the correlation between features and pick the best variables as inputs to the ANNs. The five combinations in the hidden layer (4, 3), (6, 4), (3, 2), (4, 2), and (5, 4) were used for the development of the ANN models. The input variables were used such as daily of minimum temperature (Tmin), maximum temperature (Tmax), mean temperature (Tmean), solar radiation (SR), Humidity (H), wind speed (WS), and sunshine hours (Ssh), maximum global radiation (gradmax), minimum global radiation (gradmin), and day length. Different scenarios were formed using these input variables and it was examined which one was the most suitable at different layers.
Table 1 lists the top five hidden configurations from the different combinations of input variables based on values of the root mean square error (RMSE), mean absolute percentage error (MAPE), the normalized root mean square error (NRMSE), the accuracy (ACC), and the coefficient of determination (R2) during testing phases. The first combination (C1), consisting of Tmean + Sun shine hours + CWB, showed that values of RMSE, MAPE, NRMSE, ACC and R2 were obtained in the range of 0.071–0.257 mm, 0.005–0.072%, 0.032–0.425%, 0.986–0.997% and 0.85–0.98%, respectively. In order to find the most accurate model, the model must have low RMSE, MAPE, NRMSE values and high ACC and R2 values [52,53]. For the C1 combination, the most accurate model was the ANN model having hidden layer (5, 4).

Table 1.
Top five architectures of hidden configurations from different variable combinations: with RMSE (mm), MAPE (%), NRMSE (%), ACC (%), and R2 for the study area.
The values of R2 for the C2 combination (Tmax + Tmin + Humidity + Solar Radiation) were obtained as 0.99 for all (among all hidden layers) developed models of ANN. Whereas, the values of RMSE, MAPE, NRMSE and ACC were obtained in the range of 0.008–0.019 mm, 0.000–0.0014%, 0.000–0.003%, and 0.998–0.999%, respectively for C2. The most accurate model was found at hidden layer (4, 3) where values of RMSE, MAPE, NRMSE, ACC and R2 were 0.008 mm, 0.000%, 0.000% and 0.999%, and 0.99%, respectively.
The values of RMSE (mm), MAPE (%), NRMSE (%), ACC (%) and R2 for the C3 combination (Gradmax + Sun shine hours + Windspeed) did not vary too much and were obtained in the ranges of 0.548–0.549, 0.315–0.318, 1.943–2.038, 0.994–0.996, and 0.30–0.31, respectively. Further, the combination C4 (Gradmin + Solar Radiation +Windspeed) showed good results in the hidden layer (6, 4) of the ANN model with the lowest values of RMSE, MAPE, NRMSE as 0.010 (mm), 0.000 (%), and 0.0001 (%) and highest values of ACC and R2 as 0.999% and 0.99.
It is seen from Table 1 that the combination C5 (Climate Water Balance (CWB) + Humidity + Windspeed) performed poorly along with C3. The values of ACC (0.998% in the (4, 3) and (4, 2) neurons) and R2 (0.94 in (5, 4) neuron) in the C6 combination (including just CWB parameter) showed good results. The C6 combination had the ranges of 0.155–0.372 mm for RMSE, 0.022–0.140% for MAPE and 0.087–0.690% for NRMSE. The best results in this combination were seen in the (5, 4) hidden layer. Furthermore, for the combination C7 (Solar Radiation + daylength+ Sun shine hours + Tmean), the values of R2 (0.99) were the same for all developed models of the ANN. Whereas, the values of RMSE, MAPE, NRMSE and ACC were found to be 0.0147–0.0345 mm, 0.0003–0.0025%, 0.001–0.004%, and 0.997–0.999%, respectively. The most accurate results were found at hidden layer (3, 2) with minimum values of RMSE (%), MAPE (%), and NRMSE (%) and highest values of ACC (%) and R2 for C7.
The last combination, C8, included all parameters and values in the ranges of 0.0170–0.330, 0.0006–0.0019, and 0.001–0.004 were found for RMSE (mm), MAPE (%), and NRMSE (%), respectively. The values of ACC (0.999%) and R2 (0.99) were the same at all developed models of ANN. From Table 1, it is concluded that the most accurate model was obtained at hidden layer (5, 4) for C8.
Table 2 shows the results of the most accurate developed models for all the given combinations. Thus, it is clear from Table 2 that the most accurate results were obtained for the combination C2 (4, 3). The values for RMSE, MAPE, NRMSE were found to be the lowest at 0.008 mm, 0.000%, and 0.000%, respectively, of all the combinations, whereas values for ACC, and R2 of 0.999%, and 0.99, respectively, were the highest of all the combinations. The next best result was obtained for the C4 (6, 4) followed by C7 (3, 2), C8 (5, 4), C1 (5, 4), and C6 (6, 4). The results show the combination C3 had the worst performance followed by C5. Thus, the C2 combination (Tmax + Tmin + Humidity + Solar Radiation) at hidden neurons (4, 3) can be used to develop the models.

Table 2.
The most accurate results at given hidden neurons among all developed models of ANN for all combinations at given site.
3.3. Structural Network Design of the Superior Models
The results of the training data from 1969 to 2007 are presented in Figure 4, showing the optimum structure of the trained neural network. Basic information such as training synaptic weights, the number of hidden neuron layers, convergence steps, and overall errors are all conveyed by each network topology. The threshold for partial derivatives of the error function was chosen at 0.01 for the purposes of this research.
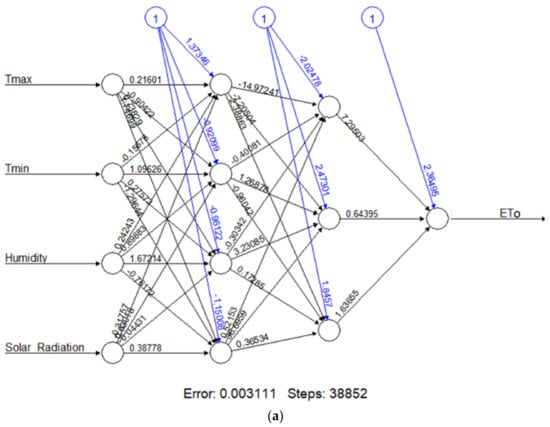
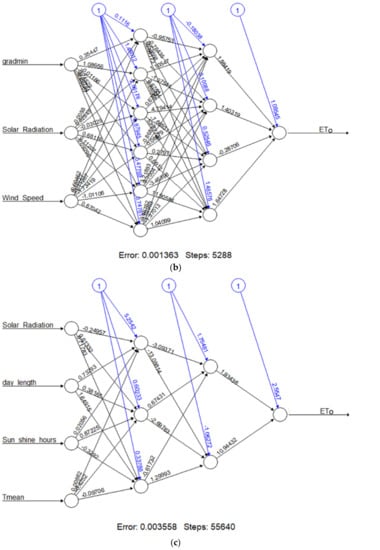
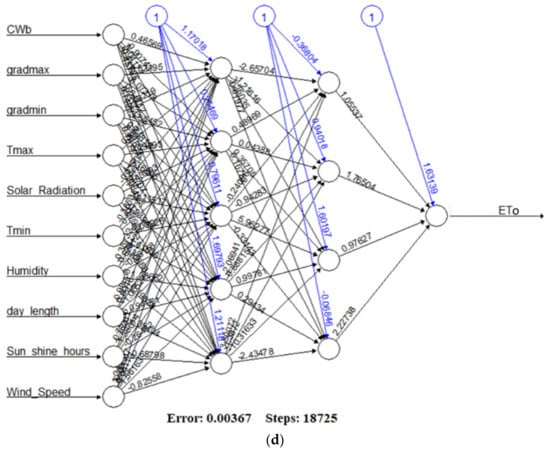
Figure 4.
Neural network layouts for the optimal combined variables for predicting the ETo in Debrecen (a) Structural Network Design of the Superior Model—Hidden Layers (4, 3); (b) Structural Network Design of the Superior Model—Hidden Layers (6, 4); (c) Structural Network Design of the Superior Model—Hidden Layers (3, 2); (d) Structural Network Design of the Superior Model — Hidden Layers (5, 4).
All the superior models had different combinations of inputs variables with a variable number of hidden neuron layers. The first three Superior Models contained limited meteorological data (A: Tmax, Tmin, humidity, solar radiation; B: gradmin, solar radiation, wind speed; C: solar radiation, day length, sunshine hours, Tmean). The fourth model (D) contained all the inputs: CWB, gradmax, gradmin, Tmax, Tmin, humidity, solar radiation, day length, sunshine hours, wind speed.
Model A had hidden neuron layers (4, 3), the training process needed 38,852 steps to achieve the least error. The process has an overall error of about 0.003. Model B had hidden neuron layers (6, 4) and the training process needed 5288 steps with an overall error of about 0.001. Furthermore, in Model C with hidden neuron layers (3, 2), the training process needed 55,640 steps until all absolute partial derivatives of the error function were smaller than the default threshold of 0.01, with the process having an overall error of about 0.004. Model D required 18,725 steps in the training process until all absolute partial derivatives of the error function were smaller than the default threshold of 0.01 and had an overall error was 0.004.
3.4. ETo Prediction and Validation for Superlative ANN Models
After training the neural networks with data from the 39 years from 1969 to 2007 for both the meteorological dataset and ETo and selecting the best model with hidden neuron layers, the prediction of ETo, based on each model, was performed for the same period using the testing data (2008–2019). The predicted values of the ETo were then compared with the reserved data (the tested years) that were not executed for the machine learning model. The results for each model are presented in Figure 5. The deterministic coefficient varies for each model, but in each case, it was greater than 0.998. Although there are ignorable differences (0.07%) in the deterministic coefficients amongst the models containing limited meteorological data, the best performed model was the one which had hidden layers (3, 2), with solar radiation, day length, sunshine hours, Tmean input parameters.
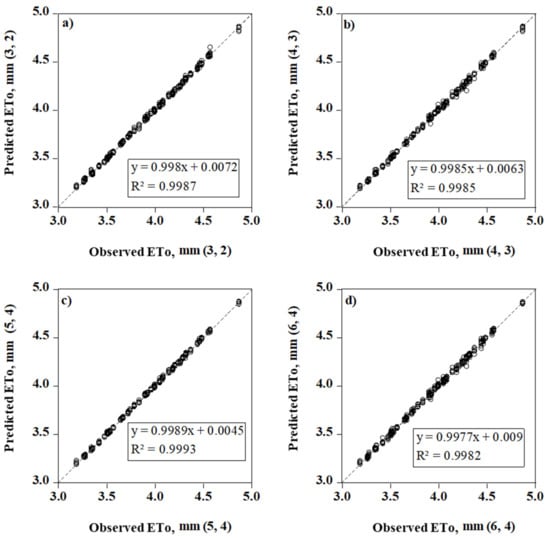
Figure 5.
Comparison between model prediction and observed ETo values for the optimal ANNs at the different hidden layers for Debrecen (a) performance of model with hidden layers (3, 2); (b) performance of model with hidden layers (4, 3); (c) performance of model with hidden layers (5, 4); (d) performance of model with hidden layers (6, 4).
Based on the above results, it was found that scenario C2 had higher accuracy (ACC) with the best correlation (R2) and, at the same time, the least error, of all the scenarios. According to the parameters used in this scenario, it was observed that the minimum and maximum temperature and solar radiation were the most effective parameters in the evapotranspiration occurrence. The results showed that the scenario C2 is almost consistent with the scenario C4, with very slight differences. By comparing Scenario C2 with Scenario C1, it was clear that replacing the Tmean with the Tmax and Tmin reduces the accuracy of the model. Also, the poor performance of the scenario C3 showed that the Gradmax parameter had the least impact on this process, because by eliminating this factor in other scenarios, the accuracy of the models was improved compared to this scenario. In scenario C3 and C5, the accuracy of the model was reduced by removing each of the Tmax,Tmin and solar radiation parameters. In the C8 scenario, although the accuracy of the model was high, using the many parameters made the model more complex. In other words, it was appropriate to have a model with fewer parameters and high accuracy (such as scenario C2). The values of R2 also show the correlation between the amount of real and estimated evapotranspiration, which accorded with the results, in all scenarios except C3 and C5; a high correlation was observed between these two values. In general, based on the significant accuracy of the Scenarios C2 and C4, the estimated evapotranspiration can be predicted with very high accuracy with the minimum dataset (Tmax, Tmin and solar radiation), and the results can be used where data collecting (field survey or measurement) is not possible.
4. Discussion
Rapid climate change around the world poses major challenges against sustainability of ecosystems and human lives and welfare [55,56,57]. Recently, the earth surface temperature was increased significantly [58,59], and is projected to increase in the future [60,61]. These rapid changes have altered the process of the global hydrological cycle and its component [59,62]. However, these changes along with extreme drought cycles have badly affected soil moisture regimes and inhibited different functions of the soil system [63,64]. In this sense, evapotranspiration, is one of the main components of the hydrological cycle that is directly influenced by climate change, due to the dynamic interaction between different climate components (temperature, radiation, rainfall) and water storage. Thus, tracking changes in ET is an essential tool for ensuring sustainability and profitability of agricultural systems. Hence, ET is the main link between the availability of water for agricultural system and atmospheric demands.
Although many kinds of equipment, models and equations have been developed for measuring or simulating ET, has all have their own drawbacks. Thus, new trends in the application of different models of ANNs for ET calculation could produce a reliable output, which can help promote the decision-making for water managers, designers, and development planners. In this context, the main aim of this research was to evaluate the performance of different scenarios with ANN models in ET prediction for eastern Hungary. In the training stage of the ANN models, the Superior Models contained varied components of meteorological data. The first model used Tmax, Tmin, humidity, solar radiation; the second adopted gradmin, solar radiation, wind speed; while the third employed solar radiation, day length, sunshine hours, Tmean. However, the fourth model contained all the inputs: CWB, gradmax, gradmin, Tmax, Tmin, humidity, solar radiation, day length, sunshine hours, and wind speed. For the prediction phase, the best performed model was the one which had hidden layers (3, 2) with solar radiation, day length, sunshine hours, Tmean as input parameters. Remarkably, it seems that in both steps, temperature and solar radiation were an important factor that influenced the simulation process via the ANN models. In this sense, the C2 scenario indicated that Tmax, Tmin and solar radiation were the most effective parameters in the evapotranspiration occurrence.
Previously, Alsafadi et al. [65] pointed out an increase of drought events across Hungary, and also, Mohammed et al. [48] detected more than 103 event (1950–2010) of severe agricultural drought in Debrecen (eastern Hungary). However, Matyasovszky et al. [66] reported a warmer climate condition across Hungary. Lockwood [67] indicated the influence of solar activity on winter temperature across the Eurasian region, while Mares et al. [68] showed a good concordance between drought and solar/geomagnetic activities in central Europe. All these conclusions, directly or indirectly, support our finding, especially for the C2 scenario, where frequent drought events (i.e., less propagation of soil moisture) in Debrecen, warmer climate conditions (increase of Tmax, Tmin) and increase of solar/geomagnetic activities (i.e., solar radiation) enhanced ET process and increased the water demanded by atmosphere.
Agricultural activities, especially maize production, are the main economic activity in the study area [48,49]. Thus, modelling and reduction of ET is a vital issue for sustainably of agribusiness, taking into consideration the sensitivity of maize to water deficit and drought events. Climate change along with decreasing rainfall and increasing ET creates new unsuitable conditions for crop and fruit production [69]. This vulnerability is also explained by the difference between annual precipitation and annual evapotranspiration. It is well known that in mid-season, the potential evapotranspiration is high and precipitation does not meet it, and so there is a shortage of soil moisture for crops, furthermore the high clay content can be also a huge problem concerning readily available water content of soils [70]. Unfortunately, future climate change is predicted to cause more serious drought and extreme events in the Tisza River basin, which includes Debrecen [54,71]. According to statistical data, droughts occur every second or third year during summer, especially in July and August. Therefore, summer crops, such as maize are more affected by the drought than crops harvested in early summer, like wheat [72]. The vital interaction between the different climate parameters (Tmax, Tmin, humidity, solar radiation) and the ecosystem component accelerates the development of research on AI and ML algorithms to support decision makers. However, adaptation of the ANN methods could support policy makers and stockholders for the future planning and development.
5. Conclusions
Although the accurate determination of ETo is of great importance for water and water resources management, its estimation is a challenge. The experimental objectives of this study were achieved by estimating ETo based on limited meteorological data using an artificial neural network method for a particular area. Alternative methods were found for the estimation of ETo where there is a lack of climate data with high accuracy, nevertheless the best developed ANN model in ETo estimation was selected based on performance metrics. We established that the optimal ANN for forecasting ETo included Tmax, Tmin, H, and SR at hidden layers (4, 3); gradmin, SR, and WS at (6, 4); SR, day length, Ssh, and Tmean at (3, 2); all collected parameters at (5, 4). The calculated ETo values achieved a high statistical significance versus those simulated with the lowest distributional variations, and the accuracy and coefficients of determination were close to 1. ANN models produced relatively satisfactory outputs, and after developing an easy-to-use modelling platform, could be advanced to promote the decision-making for farmers, water managers, designers, and development planners at the study site. Nevertheless, the application of ANNs also proved to be an appropriate tool in ETo estimation, therefore, there is a potential to develop models for a larger climatic region (i.e., Pannonian region) that involve more accurate climate data for prediction.
Author Contributions
Conceptualization, A.E. and C.J.; data curation, L.H.; formal analysis, A.E.; funding acquisition, E.H.; investigation, S.M., C.B.P., M.K., S.A.B., J.Z. and L.H.; methodology, A.E., A.N. and L.H.; resources, A.E. and L.H.; supervision, A.N., J.T. and C.J.; validation, S.M., C.B.P., M.K. and S.A.B.; visualization, L.H.; writing—original draft, A.E., A.N., J.Z. and E.K.; writing—review and editing, A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Institutes for Agricultural Research and Educational Farm, University of Debrecen.
Data Availability Statement
Not applicable.
Acknowledgments
This research was funded by the National Research, Development and Innova- tion Fund of Hungary, 2020-4.1.1-TKP2020 funding scheme, grant number TKP2020-IKA-04, and 441 the TKP2021-NKTA funding scheme, grant number TKP2021-NKTA-32.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhat, S.A.; Pandit, B.A.; Khan, J.N.; Kumar, R.; Jan, R. Water requirements and irrigation scheduling of maize crop using CROPWAT model. Int. J. Curr. Microbiol. Appl. Sci. 2017, 6, 1662–1670. [Google Scholar] [CrossRef]
- Bhat, S.A.; Pandit, B.; Dar, M.U.D.; Jan, R.; Khan, S.; Mehraj, K. Statistical Comparison of Reference Evapotranspiration Methods: A Case Study from Srinagar in J&K, India. Int. J. Curr. Microbiol. App. Sci. 2017, 6, 3731–3737. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Zhang, L.; Deng, J.; Juma, A.; Wang, K. Modeling monthly crop coefficients of maize based on limited meteorological data: A case study in Nile Delta, Egypt. Comput. Electron. Agric. 2020, 173, 105368. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Elbeltagi, A.; Rizwan, M.; Mokhtar, A.; Deb, P.; Abdullahi, G.; Kushwaha, N.L.; Peroni, L.; Malik, A.; Kumar, N.; Deng, J. Spatial and temporal variability analysis of green and blue evapotranspiration of wheat in the Egyptian Nile Delta from 1997 to 2017. J. Hydrol. 2020, 594, 125662. [Google Scholar] [CrossRef]
- Jerin, J.N.; Islam, H.M.T.; Islam, T.; Shahid, S.; Zhenghua, H.; Mehnaz, B.; Ronghao, C.; Ahmed, E. Spatiotemporal trends in reference evapotranspiration and its driving factors in Bangladesh. Theor. Appl. Climatol. 2021, 144, 793–808. [Google Scholar] [CrossRef]
- Bhat, S.A.; Pandit, B.; Dar, M.U.D.; Rouhullah, S.A.; Jan, R.; Khan, S. Comparative study of different methods of evapotranspiration estimation in Kashmir Valley. J. Agrometeorol. 2017, 19, 383–384. [Google Scholar]
- Mahdi, D.; Sanaz, J.; Samad, E. Climate change impacts on spatial-temporal variations of reference evapotranspiration in Iran. Water Harvest. Res. 2017, 2, 13–23. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Islam, A.R.M.T. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Total Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef]
- Chu, R.; Li, M.; Islam, A.R.M.T.; Fei, D.; Shen, S. Attribution analysis of actual and potential evapotranspiration changes based on the complementary relationship theory in the Huai River Basin of eastern China. Int. J. Clim. 2019, 39, 4072–4090. [Google Scholar] [CrossRef]
- Pour, S.H.; Wahab, A.K.A.; Shahid, S.; Ismail, Z.B. Changes in reference evapotranspiration and its driving factors in peninsular Malaysia. Atmos. Res. 2020, 246, 105096. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. Sensitivity of potential evapotranspiration to changes in climate variables for different Australian climatic zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Tian, H.; Dangal, S.R.S.; Yang, Q.; Yang, J.; Lu, C.; Tao, B.; Ren, W.; Ouyang, Z. Responses of global terrestrial evapotranspiration to climate change and increasing atmospheric CO2 in the 21st century. Earth’s Future 2015, 3, 15–35. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Xing, W.; Fu, J. Projecting the potential evapotranspiration by coupling different formulations and input data reliabilities: The possible uncertainty source for climate change impacts on hydrological regime. J. Hydrol. 2017, 555, 298–313. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, D.; Chen, X.; Zhang, J. A simple method for estimating field crop evapotranspiration from pot experiments. Water 2018, 10, 1823. [Google Scholar] [CrossRef] [Green Version]
- Ünlü, M.; Kanber, R.; Kapur, B. Comparison of soybean evapotranspirations measured by weighing lysimeter and Bowen ratio-energy balance methods. Afr. J. Biotechnol. 2010, 9, 4700–4713. [Google Scholar] [CrossRef]
- Başağaoğlu, H.; Chakraborty, D.; Winterle, J. Reliable evapotranspiration predictions with a probabilistic machine learning framework. Water 2021, 13, 557. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Reference Evapotranspiration (ETo) Methods Implemented as ArcMap Models with Remote-Sensed and Ground-Based Inputs, Examined along with MODIS ET, for Peloponnese, Greece. ISPRS Int. J. Geo-Inf. 2021, 10, 390. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Chang. 2016, 6, 946–949. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Tan, J. Interannual variations of evapotranspiration and water use efficiency over an oasis cropland in arid regions of North-Western China. Water 2020, 12, 1239. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef] [Green Version]
- Bai, P.; Liu, X.; Yang, T.; Li, F.; Liang, K.; Hu, S.; Liu, C. Assessment of the influences of different potential evapotranspiration inputs on the performance of monthly hydrological models under different climatic conditions. J. Hydrometeorol. 2016, 17, 2259–2274. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Xu, C.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Jing, W.; Yaseen, Z.M.; Shahid, S.; Saggi, M.K.; Tao, H.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Chau, K.W. Implementation of evolutionary computing models for reference evapotranspiration modeling: Short review, assessment and possible future research directions. Eng. Appl. Comput. Fluid Mech. 2019, 13, 811–823. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Qu, Z.; Martins, D.S.; Paredes, P.; Pereira, L.S. Daily reference evapotranspiration for hyper-arid to moist sub-humid climates in inner mongolia, China: I. Assessing temperature methods and spatial variability. Water Resour. Manag. 2016, 30, 3769–3791. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Adnan, R.M. Three different adaptive neuro fuzzy computing techniques for forecasting long-period daily streamflows. In Big Data in Engineering Applications; Roy, S.S., Samui, P., Deo, R., Ntalampiras, S., Eds.; Springer: Singapore, 2018; pp. 303–321. [Google Scholar]
- Khosravinia, P.; Nikpour, M.R.; Kisi, O.; Yaseen, Z.M. Application of novel data mining algorithms in prediction of discharge and end depth in trapezoidal sections. Comput. Electron. Agric. 2020, 170, 105283. [Google Scholar] [CrossRef]
- Torres, A.F.; Walker, W.R.; McKee, M. Forecasting daily potential evapotranspiration using machine learning and limited climatic data. Agric. Water Manag. 2011, 98, 553–562. [Google Scholar] [CrossRef]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Gorka, L.; Amais, O.B.; Jose, J.L. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks. A Comprehensive Foundation; Prentice Hall International Inc.: Hoboken, NJ, USA, 1999; p. 823. [Google Scholar]
- Alizamir, M.; Kisi, O.; Muhammad Adnan, R.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Elragal, H.M. Improving neural networks prediction accuracy using particle swarm optimization combiner. Int. J. Neural Syst. 2009, 19, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Pidaparti, R.M.; Jayanti, S.; Palakal, M.J. Residual Strength and Corrosion Rate Predictions of Aging Aircraft Panels: Neural Network Study. J. Aircr. 2002, 39, 175–180. [Google Scholar] [CrossRef]
- Pidaparti, R. Aircraft structural integrity assessment through computational intelligence techniques. Struct. Durab. Health Monit. 2006, 2, 131–148. [Google Scholar] [CrossRef]
- Hijazi, A.; Al-Dahidi, S.; Altarazi, S. Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks. Materials 2020, 13, 5216. [Google Scholar] [CrossRef]
- Ince, R. Prediction of fracture parameters of concrete by Artificial Neural Networks. Eng. Fract. Mech. 2004, 71, 2143–2159. [Google Scholar] [CrossRef]
- De, S.; Debnath, A. Artificial neural network based prediction of maximum and minimum temperature in the summer monsoon months over India. Appl. Phys. Res. 2009, 1, 37. [Google Scholar] [CrossRef] [Green Version]
- Malik, H.; Singh, S. Application of artificial neural network for long term wind speed prediction. In Proceedings of the Conference on Advances in Signal Processing (CASP), Pune, India, 9–11 June 2016; Institute of Electrical and Electronics Engineers: New Jersey, NJ, USA, 2016; pp. 217–222. [Google Scholar] [CrossRef]
- Adisa, O.M.; Botai, J.O.; Adeola, A.M.; Hassen, A.; Botai, C.M.; Darkey, D.; Tesfamariam, E. Application of artificial neural network for predicting maize production in South Africa. Sustainability 2019, 11, 1145. [Google Scholar] [CrossRef] [Green Version]
- Moghaddam, M.G.; Ahmad, F.B.H.; Basri, M.; Rahman, M.B.A. Artificial neural network modeling studies to predict the yield of enzymatic synthesis of betulinic acid ester. Electron. J. Biotechnol. 2010, 13, 3–4. [Google Scholar] [CrossRef]
- Nema, M.K.; Khare, D.; Chandniha, S.K. Application of artificial intelligence to estimate the reference evapotranspiration in sub-humid Doon valley. Appl. Water Sci. 2017, 7, 3903–3910. [Google Scholar] [CrossRef] [Green Version]
- Adnan, R.M.; Chen, Z.; Yuan, X.; Kisi, O.; El-Shafie, A.; Kuriqi, A.; Ikram, M. Reference Evapotranspiration Modeling Using New Heuristic Methods. Entropy 2020, 22, 547. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Wen, X.; Feng, Q.; He, Z.; Zou, S.; Yang, L. Integrating genetic algorithm and support vector machine for modeling daily reference evapotranspiration in a semi-arid mountain area. Hydrol. Res. 2016, 48, 1177–1191. [Google Scholar] [CrossRef]
- Jovic, S.; Nedeljkovic, B.; Golubovic, Z.; Kostic, N. Evolutionary algorithm for reference evapotranspiration analysis. Comput. Electron. Agric. 2018, 150, 1–4. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsafadi, K.; Daher, H.; Gombos, B.; Mahmood, S.; Harsányi, E. Precipitation pattern changes and response of vegetation to drought variability in the eastern Hungary. Bull. Natl. Res. Cent. 2020, 44, 55. [Google Scholar] [CrossRef] [Green Version]
- Takács, I.; Amiri, M.; Károly, K.; Mohammed, S. Assessing soil quality changes after 10 years of agricultural activities in eastern Hungary. Irrig. Drain. 2021, 70, 1116–1128. [Google Scholar] [CrossRef]
- Mohammed, S.; Mirzaei, M.; Pappné Törő, Á.; Anari, M.G.; Moghiseh, E.; Asadi, H.; Harsányi, E. Soil carbon dioxide emissions from maize (Zea mays L.) fields as influenced by tillage management and climate. Irrig. Drain. 2021, 71, 228–240. [Google Scholar] [CrossRef]
- Keskin, T.E.; Düğenci, M.; Kaçaroğlu, F. Prediction of water pollution sources using artificial neural networks in the study areas of Sivas, Karabuk and Bartın (Turkey). Environ. Earth Sci. 2015, 73, 5333–5347. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Deng, J.; Wang, K.; Hong, Y. Crop Water footprint estimation and modeling using an arti fi cial neural network approach in the Nile Delta, Egypt. Agric. Water Manag. 2020, 235, 106080. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Deng, J.; Wang, K.; Malik, A.; Maroufpoor, S. Modeling long-term dynamics of crop evapotranspiration using deep learning in a semi-arid environment. Agric. Water Manag. 2020, 241, 106334. [Google Scholar] [CrossRef]
- Juhász, C.; Gálya, B.; Kovács, E.; Nagy, A.; Tamás, J.; Huzsvai, L. Seasonal predictability of weather and crop yield in regions of Central European continental climate. Comput. Electron. Agric. 2020, 173, 105400. [Google Scholar] [CrossRef]
- Celik, S. The effects of climate change on human behaviors. In Environment, Climate, Plant and Vegetation Growth; Fahad, S., Hasanuzzaman, M., Alam, M., Ullah, H., Saeed, M., Khan, I.A., Adnan, M., Eds.; Springer: Cham, Switzerland, 2020; pp. 577–589. [Google Scholar]
- Mupedziswa, R.; Kubanga, K.P. Climate change, urban settlements and quality of life: The case of the Southern African Development Community region. Dev. S. Afr. 2017, 34, 196–209. [Google Scholar] [CrossRef]
- Pecl, G.T.; Araújo, M.B.; Bell, J.D.; Blanchard, J.; Bonebrake, T.C.; Chen, I.C.; Williams, S.E. Biodiversity redistribution under climate change: Impacts on ecosystems and human well-being. Science 2017, 355, eaai9214. [Google Scholar] [CrossRef] [PubMed]
- Cane, M.A.; Clement, A.C.; Kaplan, A.; Kushnir, Y.; Pozdnyakov, D.; Seager, R.; Murtugudde, R. Twentieth-century sea surface temperature trends. Science 1997, 275, 957–960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maček, U.; Bezak, N.; Šraj, M. Reference evapotranspiration changes in Slovenia, Europe. Agric. For. Meteorol. 2018, 260, 183–192. [Google Scholar] [CrossRef]
- Hari, V.; Rakovec, O.; Markonis, Y.; Hanel, M.; Kumar, R. Increased future occurrences of the exceptional 2018–2019 Central European drought under global warming. Sci. Rep. 2020, 10, 12207. [Google Scholar] [CrossRef] [PubMed]
- Hassan, W.H.; Nile, B.K. Climate change and predicting future temperature in Iraq using CanESM2 and HadCM3 modeling. Modeling Earth Syst. Environ. 2021, 7, 737–748. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Dinpashoh, Y. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416, 182–205. [Google Scholar] [CrossRef]
- Wang, H.; Rogers, J.C.; Munroe, D.K. Commonly used drought indices as indicators of soil moisture in China. J. Hydrometeorol. 2015, 16, 1397–1408. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wen, F.; Wood, E.F. A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. Atmos. 2004, 109, D24108. [Google Scholar] [CrossRef]
- Alsafadi, K.; Mohammed, S.; Ayugi, B.; Sharaf, M.; Harsányi, E. Spatial–temporal evolution of drought characteristics over Hungary between 1961 and 2010. Pure Appl. Geophys. 2020, 177, 3961–3978. [Google Scholar] [CrossRef] [Green Version]
- Matyasovszky, I.; Weidinger, T.; Bartholy, J.; Barcza, Z. Current regional climate 652 change studies in Hungary: A review. Geogr. Helv. 1999, 54, 138–146, 653. [Google Scholar] [CrossRef] [Green Version]
- Lockwood, M.; Owens, M.; Barnard, L.; Davis, C.; Thomas, S. Solar cycle 24: What is the Sun up to? Astron. Geophys. 2012, 53, 3.9–3.15. [Google Scholar] [CrossRef] [Green Version]
- Mares, I.; Dobrica, V.; Mares, C.; Demetrescu, C. Assessing the solar variability signature in climate variables by information theory and wavelet coherence. Sci. Rep. 2021, 11, 11337. [Google Scholar] [CrossRef] [PubMed]
- Bakucs, Z.; Fertő, I.; Vígh, E. Crop Productivity and Climatic Conditions: Evidence from Hungary. Agriculture 2020, 10, 421. [Google Scholar] [CrossRef]
- Nagy, A.; Tamás, J. Integrated airborne and field methods to characterize soil water regime. In Peer-Reviewed Contributions, Transport of Water, Chemicals and Energy in the Soil-Plant-Atmosphere System; Celkova, A., Ed.; Institute of Hydrology, Slovak Academy of Sciences: Bratislava, Slovakia, 2009; pp. 412–420. [Google Scholar]
- Szalmáné Csete, M.; Buzási, A. Hungarian regions and cities towards an adaptive future-analysis of climate change strategies on different spatial levels. Időjárás/Q. J. Hung. Meteorol. Serv. 2020, 124, 253–276. [Google Scholar] [CrossRef]
- Tamás, J.; Nagy, A.; Fehér, J. Agricultural biomass monitoring on watersheds based on remote sensed data. Water Sci. Technol. 2015, 72, 2212–2220. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).