Determination of Cassava Leaf Area for Breeding Programs
Abstract
:1. Introduction
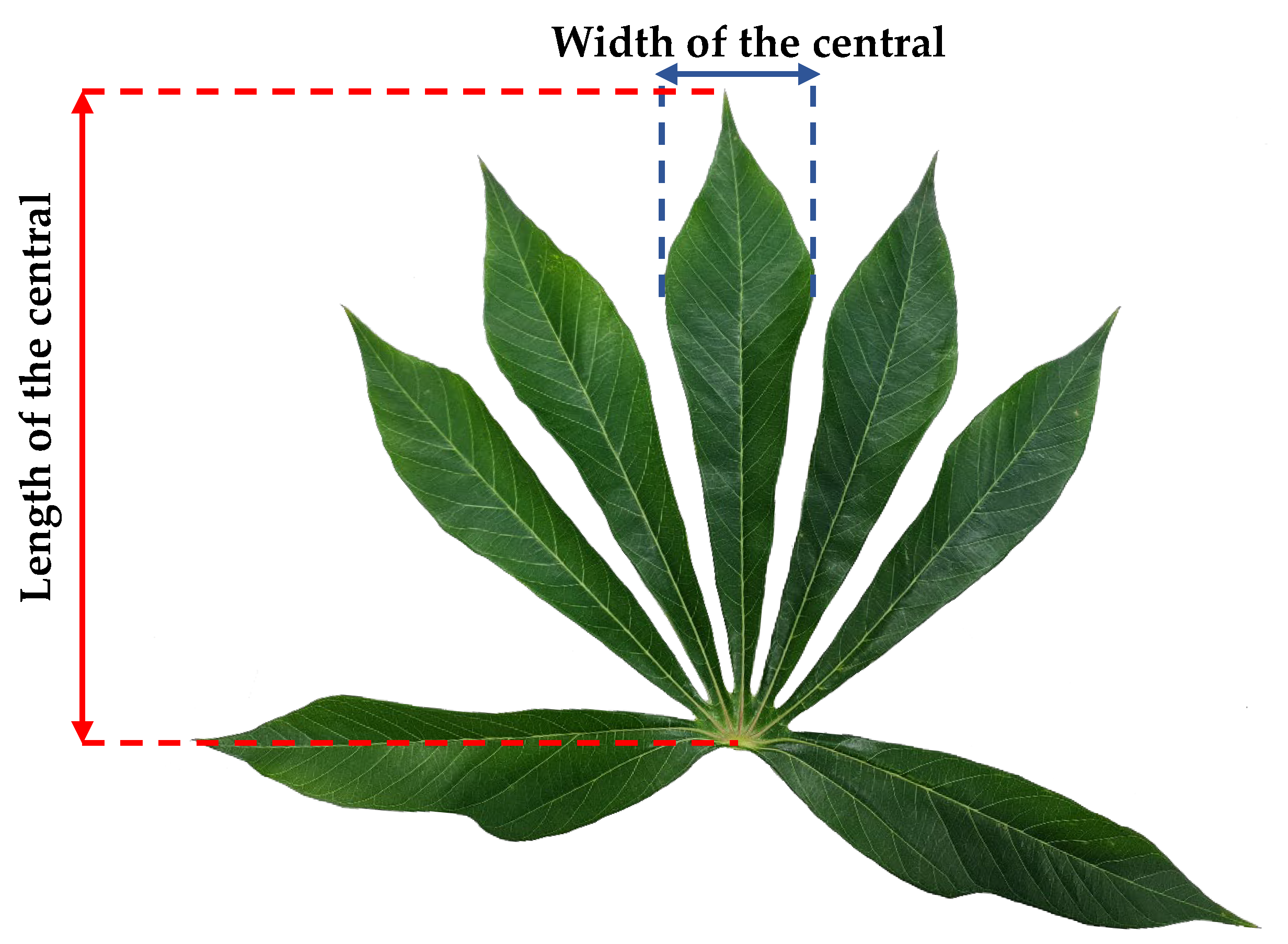
2. Materials and Methods
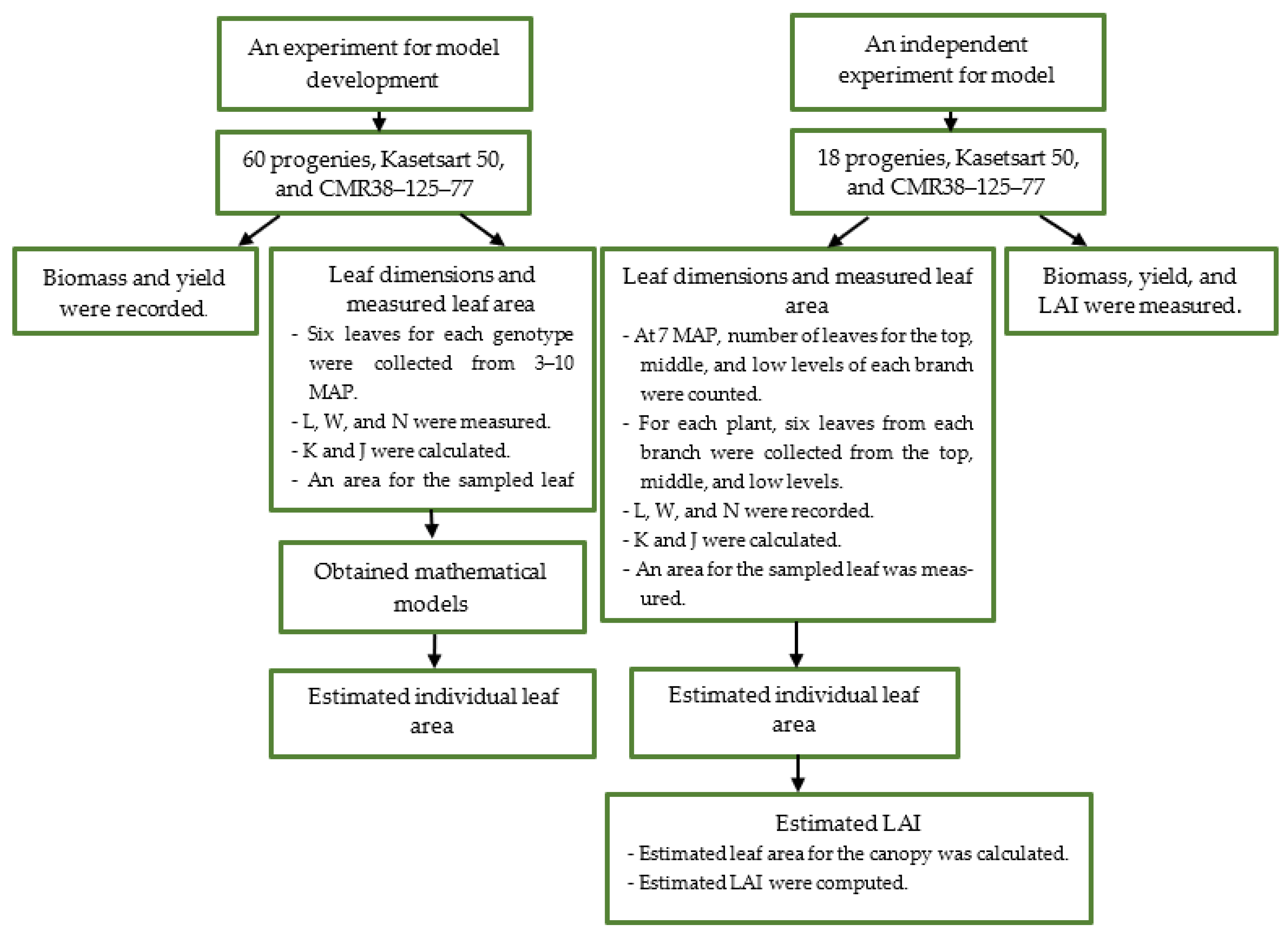
2.1. An Experiment for Model Development
2.2. An Independent Experiment for Model Evaluation
3. Results and Discussion
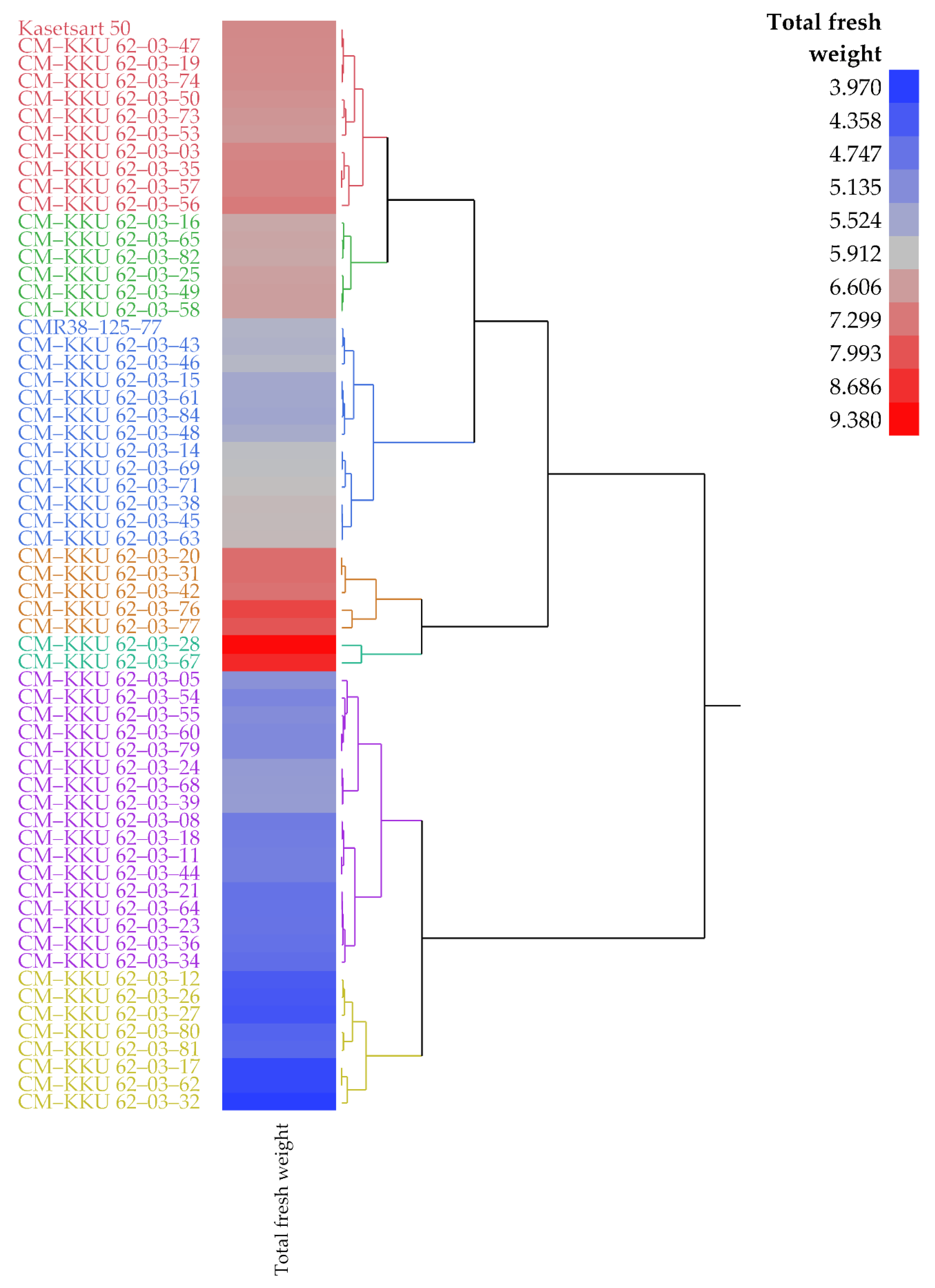
3.1. Measured Leaf Area and Final Fresh Weights
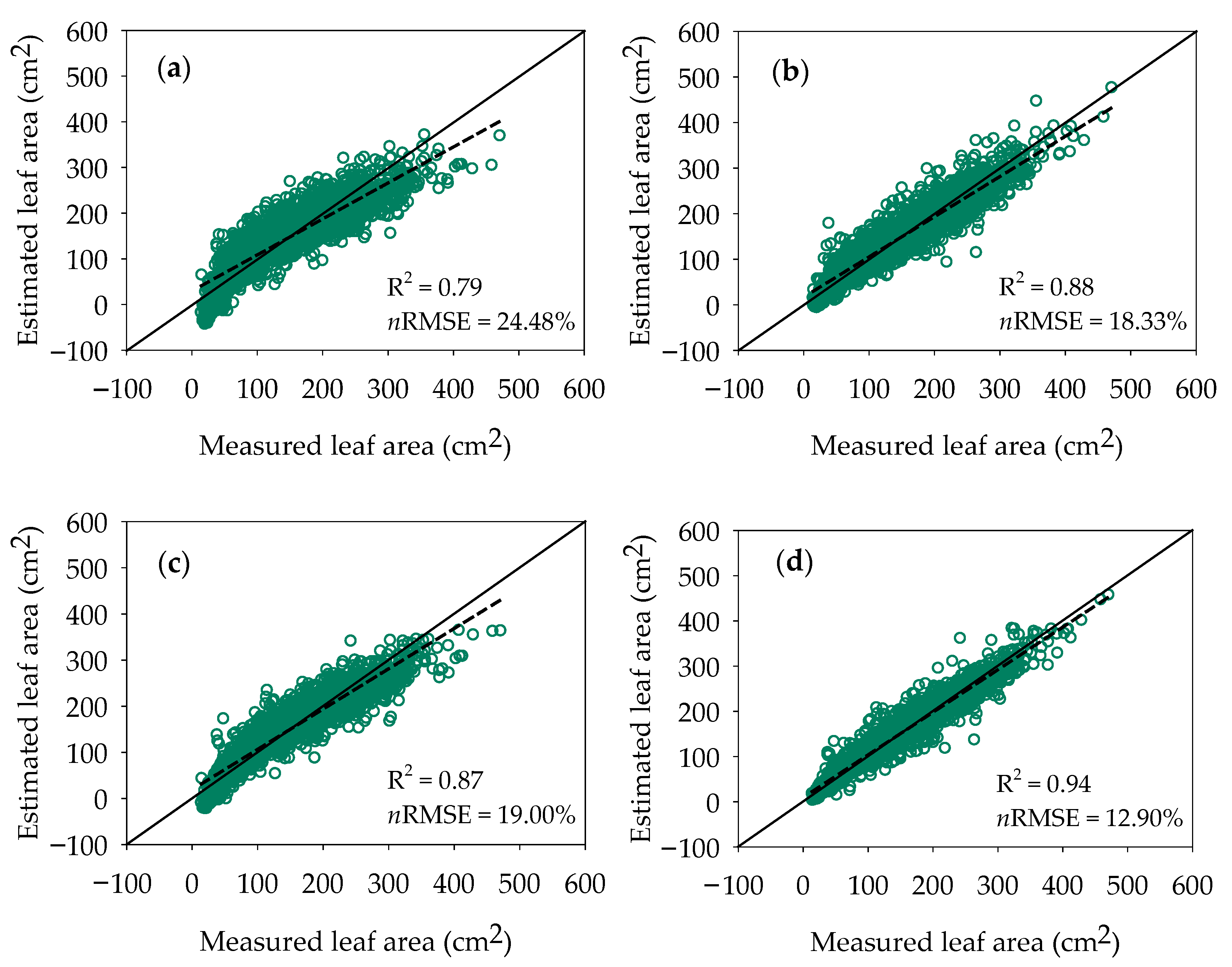
3.2. The Mathematical Model of Linear Regression for Estimating Leaf Area
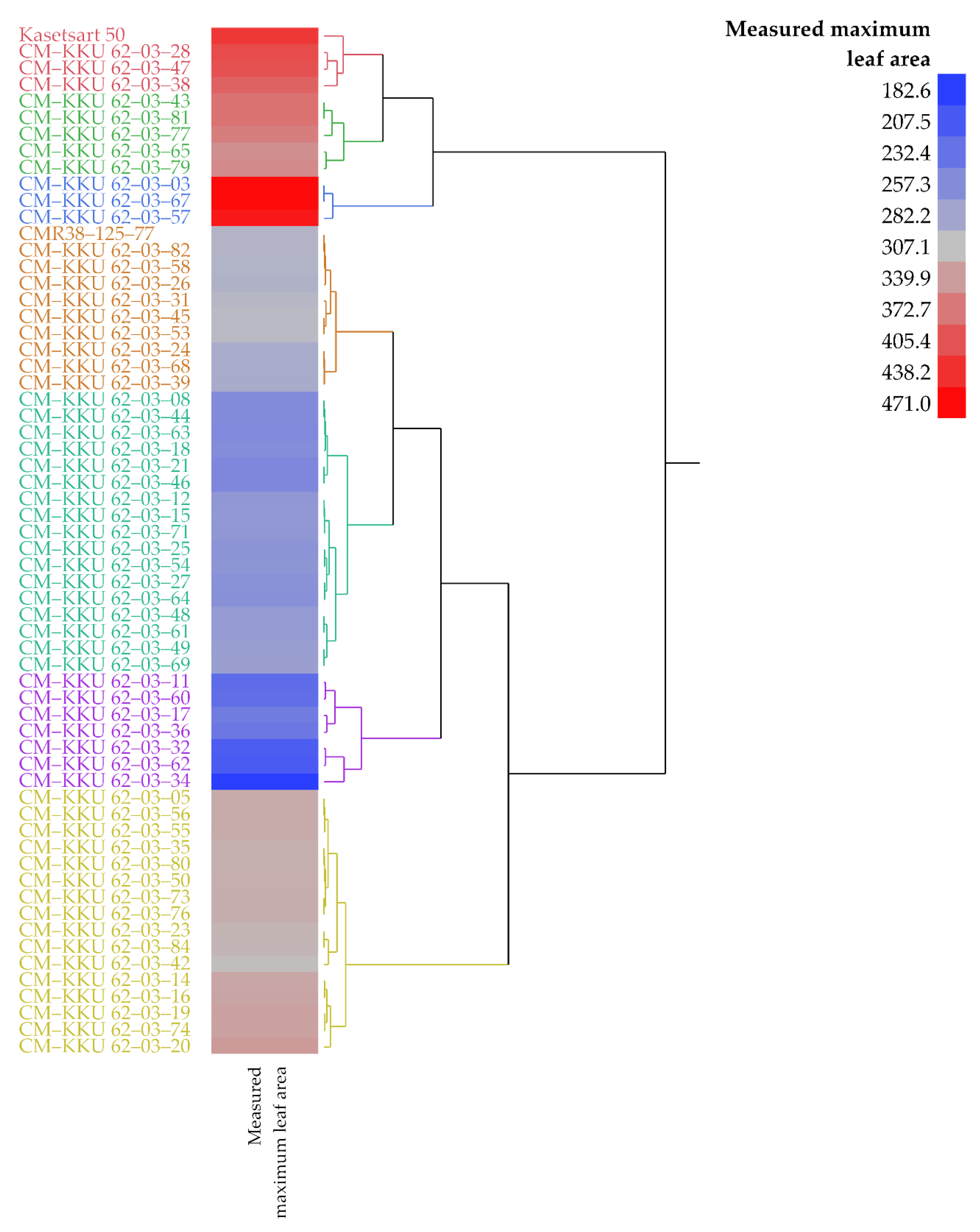
3.3. Correlation between Estimated Maximum Individual Leaf Area and Biomass
3.4. Evaluation of the Mathematical Models with Independent Data Set
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Genotype | Total Fresh Weight (kg Plant−1) | Storage Root Fresh Weight (kg Plant−1) | Measured Maximum Individual Leaf Area (cm2) | Estimated Maximum Individual Leaf Area (cm2) | |||
|---|---|---|---|---|---|---|---|
| L | L, K | L, J | L, K, J | ||||
| Kasetsart 50 | 6.96 | 4.65 | 429.15 | 297.13 | 360.45 | 354.51 | 401.26 |
| CMR38–125–77 | 5.72 | 4.32 | 295.45 | 257.91 | 272.16 | 265.26 | 272.21 |
| CM–KKU 62–03–03 | 7.04 | 3.72 | 470.98 | 240.26 | 238.27 | 268.44 | 457.27 |
| CM–KKU 62–03–05 | 5.21 | 3.53 | 326.35 | 263.79 | 325.24 | 270.42 | 313.90 |
| CM–KKU 62–03–08 | 4.88 | 3.37 | 255.90 | 218.69 | 217.42 | 225.71 | 214.01 |
| CM–KKU 62–03–11 | 4.93 | 3.32 | 225.59 | 263.79 | 239.52 | 245.00 | 226.61 |
| CM–KKU 62–03–12 | 4.39 | 3.00 | 267.81 | 234.38 | 255.21 | 244.62 | 241.13 |
| CM–KKU 62–03–14 | 5.86 | 4.26 | 330.84 | 287.33 | 303.66 | 340.81 | 333.57 |
| CM–KKU 62–03–15 | 5.54 | 3.87 | 268.31 | 263.79 | 291.76 | 219.58 | 250.69 |
| CM–KKU 62–03–16 | 6.37 | 3.86 | 332.17 | 320.66 | 340.93 | 320.28 | 337.17 |
| CM–KKU 62–03–17 | 4.11 | 2.42 | 241.84 | 206.92 | 221.99 | 220.55 | 231.53 |
| CM–KKU 62–03–18 | 4.90 | 3.02 | 257.57 | 263.79 | 250.55 | 245.00 | 257.16 |
| CM–KKU 62–03–19 | 6.93 | 5.09 | 335.89 | 273.60 | 339.15 | 279.01 | 335.29 |
| CM–KKU 62–03–20 | 7.50 | 4.84 | 341.46 | 279.48 | 271.26 | 336.90 | 321.37 |
| CM–KKU 62–03–21 | 4.74 | 2.95 | 252.43 | 238.30 | 233.78 | 248.06 | 241.51 |
| CM–KKU 62–03–23 | 4.76 | 3.15 | 316.79 | 253.99 | 322.22 | 261.82 | 319.36 |
| CM–KKU 62–03–24 | 5.34 | 3.66 | 288.10 | 312.82 | 323.99 | 279.01 | 290.38 |
| CM–KKU 62–03–25 | 6.53 | 4.39 | 263.93 | 216.73 | 166.56 | 229.15 | 183.47 |
| CM–KKU 62–03–26 | 4.35 | 3.05 | 293.17 | 204.96 | 277.03 | 218.83 | 279.55 |
| CM–KKU 62–03–27 | 4.30 | 2.98 | 262.33 | 230.46 | 327.96 | 225.71 | 284.52 |
| CM–KKU 62–03–28 | 9.38 | 4.45 | 412.77 | 306.94 | 380.46 | 308.25 | 371.92 |
| CM–KKU 62–03–31 | 7.50 | 3.11 | 298.50 | 253.99 | 282.01 | 282.13 | 285.07 |
| CM–KKU 62–03–32 | 3.97 | 2.36 | 211.84 | 226.53 | 227.04 | 232.59 | 225.31 |
| CM–KKU 62–03–34 | 4.67 | 2.45 | 182.64 | 234.38 | 209.85 | 198.19 | 181.39 |
| CM–KKU 62–03–35 | 7.10 | 4.74 | 322.14 | 332.43 | 392.40 | 330.60 | 383.07 |
| CM–KKU 62–03–36 | 4.72 | 2.33 | 237.04 | 210.85 | 232.80 | 223.99 | 240.76 |
| CM–KKU 62–03–38 | 6.06 | 3.86 | 391.96 | 265.75 | 332.05 | 309.52 | 368.52 |
| CM–KKU 62–03–39 | 5.37 | 3.93 | 287.25 | 320.66 | 306.56 | 299.65 | 283.36 |
| CM–KKU 62–03–42 | 7.41 | 5.15 | 310.28 | 287.33 | 319.63 | 264.21 | 295.71 |
| CM–KKU 62–03–43 | 5.69 | 4.09 | 377.93 | 253.99 | 360.80 | 297.78 | 382.37 |
| CM–KKU 62–03–44 | 4.93 | 2.93 | 255.96 | 273.60 | 241.13 | 261.82 | 240.93 |
| CM–KKU 62–03–45 | 6.05 | 4.39 | 301.18 | 253.99 | 286.93 | 261.82 | 289.36 |
| CM–KKU 62–03–46 | 5.77 | 3.99 | 252.61 | 214.77 | 217.74 | 227.43 | 227.98 |
| CM–KKU 62–03–47 | 6.95 | 4.56 | 407.35 | 306.94 | 335.98 | 364.29 | 381.20 |
| CM–KKU 62–03–48 | 5.59 | 4.01 | 271.84 | 244.18 | 269.26 | 253.22 | 273.74 |
| CM–KKU 62–03–49 | 6.56 | 4.33 | 274.97 | 220.65 | 271.81 | 232.59 | 275.10 |
| CM–KKU 62–03–50 | 6.81 | 4.56 | 323.13 | 255.95 | 295.46 | 288.00 | 336.20 |
| CM–KKU 62–03–53 | 6.67 | 4.62 | 301.61 | 253.99 | 282.01 | 212.16 | 242.66 |
| CM–KKU 62–03–54 | 5.03 | 3.47 | 265.44 | 252.03 | 252.97 | 260.10 | 259.65 |
| CM–KKU 62–03–55 | 5.13 | 3.71 | 327.33 | 275.56 | 302.91 | 286.05 | 303.03 |
| CM–KKU 62–03–56 | 7.25 | 4.80 | 326.23 | 265.75 | 321.92 | 272.14 | 320.10 |
| CM–KKU 62–03–57 | 7.10 | 4.66 | 458.80 | 304.98 | 411.82 | 362.33 | 446.98 |
| CM–KKU 62–03–58 | 6.57 | 4.03 | 294.48 | 242.22 | 261.44 | 251.50 | 266.69 |
| CM–KKU 62–03–60 | 5.09 | 2.33 | 228.27 | 222.61 | 209.02 | 234.31 | 232.99 |
| CM–KKU 62–03–61 | 5.53 | 3.57 | 271.64 | 277.52 | 301.05 | 261.82 | 276.49 |
| CM–KKU 62–03–62 | 4.11 | 2.56 | 208.84 | 224.57 | 203.32 | 236.03 | 215.86 |
| CM–KKU 62–03–63 | 6.07 | 4.08 | 254.42 | 204.96 | 230.48 | 175.84 | 203.97 |
| CM–KKU 62–03–64 | 4.75 | 2.99 | 260.94 | 207.51 | 209.02 | 221.06 | 220.39 |
| CM–KKU 62–03–65 | 6.43 | 5.00 | 351.82 | 312.82 | 329.62 | 313.41 | 327.95 |
| CM–KKU 62–03–67 | 8.81 | 2.38 | 470.98 | 371.65 | 476.58 | 363.27 | 457.27 |
| CM–KKU 62–03–68 | 5.35 | 3.42 | 287.86 | 259.87 | 281.77 | 266.98 | 285.01 |
| CM–KKU 62–03–69 | 5.88 | 3.67 | 275.20 | 316.74 | 298.75 | 296.21 | 271.39 |
| CM–KKU 62–03–71 | 5.96 | 4.05 | 267.13 | 240.26 | 247.09 | 249.78 | 254.34 |
| CM–KKU 62–03–73 | 6.74 | 4.05 | 324.11 | 275.56 | 294.28 | 280.73 | 296.28 |
| CM–KKU 62–03–74 | 6.91 | 4.51 | 334.04 | 273.60 | 287.56 | 279.01 | 290.38 |
| CM–KKU 62–03–76 | 8.26 | 5.02 | 324.23 | 289.29 | 289.19 | 292.77 | 292.18 |
| CM–KKU 62–03–77 | 7.96 | 4.50 | 366.45 | 346.16 | 323.98 | 342.64 | 322.70 |
| CM–KKU 62–03–79 | 5.09 | 3.07 | 355.67 | 293.21 | 378.47 | 296.21 | 370.00 |
| CM–KKU 62–03–80 | 4.52 | 2.98 | 322.39 | 263.79 | 279.86 | 321.25 | 326.86 |
| Genotype | Total Fresh Weight (kg Plant−1) | Storage Root Fresh Weight (kg Plant−1) | Measured LAI | Estimated LAI | |||
|---|---|---|---|---|---|---|---|
| L | L, K | L, J | L, K, J | ||||
| Kasetsart 50 | 4.09 | 0.51 | 1.25 | 1.52 | 1.34 | 1.55 | 1.39 |
| CMR38–125–77 | 1.25 | 0.32 | 0.03 | 0.08 | 0.08 | 0.09 | 0.09 |
| CM–KKU 62–03–05 | 2.18 | 0.47 | 0.77 | 0.97 | 1.02 | 1.03 | 1.07 |
| CM–KKU 62–03–14 | 5.81 | 3.64 | 0.55 | 0.90 | 0.79 | 0.97 | 0.86 |
| CM–KKU 62–03–15 | 2.19 | 0.37 | 0.55 | 0.71 | 0.69 | 0.64 | 0.63 |
| CM–KKU 62–03–20 | 4.28 | 1.60 | 0.73 | 1.15 | 0.91 | 1.21 | 1.00 |
| CM–KKU 62–03–25 | 6.63 | 3.43 | 1.24 | 1.65 | 1.25 | 1.82 | 1.45 |
| CM–KKU 62–03–34 | 4.09 | 0.07 | 1.22 | 1.67 | 1.36 | 1.61 | 1.35 |
| CM–KKU 62–03–42 | 4.62 | 1.06 | 2.38 | 2.08 | 2.36 | 2.33 | 2.54 |
| CM–KKU 62–03–44 | 5.00 | 0.21 | 1.66 | 2.65 | 2.13 | 2.41 | 1.99 |
| CM–KKU 62–03–46 | 5.87 | 3.41 | 0.60 | 1.08 | 1.11 | 1.22 | 1.23 |
| CM–KKU 62–03–47 | 6.61 | 3.77 | 1.37 | 1.94 | 1.93 | 2.15 | 2.10 |
| CM–KKU 62–03–53 | 7.18 | 4.46 | 0.78 | 1.22 | 1.14 | 1.23 | 1.16 |
| CM–KKU 62–03–56 | 6.17 | 3.21 | 1.47 | 1.63 | 1.79 | 1.74 | 1.86 |
| CM–KKU 62–03–57 | 6.88 | 4.23 | 0.89 | 0.92 | 0.96 | 1.05 | 1.07 |
| CM–KKU 62–03–58 | 2.46 | 0.25 | 0.73 | 1.08 | 1.06 | 1.11 | 1.09 |
| CM–KKU 62–03–77 | 5.83 | 2.89 | 1.30 | 1.87 | 1.70 | 1.93 | 1.77 |
| CM–KKU 62–03–79 | 7.65 | 3.54 | 1.71 | 2.57 | 2.56 | 2.63 | 2.61 |
| CM–KKU 62–03–81 | 7.58 | 4.26 | 1.97 | 2.55 | 2.18 | 2.28 | 2.00 |
| CM–KKU 62–03–82 | 4.59 | 2.28 | 0.50 | 1.01 | 1.18 | 1.05 | 1.19 |
References
- Howeler, R.H. Sustainable Soil and Crop Management of Cassava in Asia; CIAT Publication: Hanoi, Vietnam, 2014. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Food Outlook-Biannual Report on Global Food Markets–November 2018; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- Food and Agriculture Organization of the United Nations. FAOSTAT–Crops. Available online: http://www.fao.org/faostat/en/#data/QC/ (accessed on 3 March 2022).
- Kawano, K.; Narintaraporn, K.; Narintaraporn, P.; Sarakarn, S.; Limsila, A.; Limsila, J.; Suparhan, D.; Sarawat, V.; Watananonta, W. Yield improvement in a multistage breeding program for cassava. Crop Sci. 1998, 38, 325–332. [Google Scholar] [CrossRef]
- Ceballos, H.; Iglesias, C.A.; Pérez, J.C.; Dixon, A.G. Cassava breeding: Opportunities and challenges. Plant Mol. Biol. 2004, 56, 503–516. [Google Scholar] [CrossRef] [PubMed]
- Ceballos, H.; Pérez, J.C.; Joaqui Barandica, O.; Lenis, J.I.; Morante, N.; Calle, F.; Pino, L.; Hershey, C.H. Cassava breeding I: The value of breeding value. Front. Plant Sci. 2016, 7, 1227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ceballos, H.; Hershey, C.; Iglesias, C.; Zhang, X. Fifty years of a public cassava breeding program: Evolution of breeding objectives, methods, and decision–making processes. Theor. Appl. Genet. 2021, 134, 2335–2353. [Google Scholar] [CrossRef] [PubMed]
- El–Sharkawy, M.A. Cassava biology and physiology. Plant Mol. Biol. 2004, 56, 481–501. [Google Scholar] [CrossRef]
- Cock, J.H.; Franklin, D.; Sandoval, G.; Juri, P. The ideal cassava plant for maximum yield. Crop Sci. 1979, 19, 271–279. [Google Scholar] [CrossRef]
- Fukai, S.; Alcoy, A.B.; Llamelo, A.B.; Patterson, R.D. Effects of solar radiation on growth of cassava (Manihot esculenta Crantz.). I. Canopy development and dry matter growth. Field Crops Res. 1984, 9, 347–360. [Google Scholar] [CrossRef]
- El-Sharkawy, M.A. International research on cassava photosynthesis, productivity, eco-physiology, and responses to environmental stresses in the tropics. Photosynthetica 2006, 44, 481–512. [Google Scholar] [CrossRef]
- Mahakosee, S.; Jogloy, S.; Vorasoot, N.; Theerakulpisut, P.; Banterng, P.; Kesmala, T.; Holbrook, C.; Kvien, C. Seasonal variations in canopy size and yield of Rayong 9 cassava genotype under rainfed and irrigated conditions. Agronomy 2019, 9, 362. [Google Scholar] [CrossRef] [Green Version]
- Phoncharoen, P.; Banterng, P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P.; Hoogenboom, G. Growth rates and yields of cassava at different planting dates in a tropical savanna climate. Sci. Agric. 2019, 76, 376–388. [Google Scholar] [CrossRef]
- Phoncharoen, P.; Banterng, P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P.; Hoogenboom, G. The impact of seasonal environments in a tropical savanna climate on forking, leaf area index, and biomass of cassava genotypes. Agronomy 2019, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Phosaengsri, W.; Banterng, P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P. Leaf performances of cassava genotypes in different seasons and its relationship with biomass. Turk. J. Field Crops 2019, 24, 54–64. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Cadena, L.P.; Hoogenboom, G.; Fisher, M.J.; Ramirez-Villegas, J.; Prager, S.D.; Becerra Lopez–Lavalle, L.A.; Pypers, P.; Mejia de Tafur, M.S.; Wallach, D.; Muñoz–Carpena, R.; et al. Importance of genetic parameters and uncertainty of MANIHOT, a new mechanistic cassava simulation model. Eur. J. Agron. 2020, 115, 126031. [Google Scholar] [CrossRef]
- Phoncharoen, P.; Banterng, P.; Moreno Cadena, L.P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P.; Hoogenboom, G. Performance of the CSM–MANIHOT–Cassava Model for Simulating Planting Date Response of Cassava Genotypes. Field Crops Res. 2021, 264, 108073. [Google Scholar] [CrossRef]
- Phoncharoen, P.; Banterng, P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P.; Hoogenboom, G. Identifying suitable genotypes for different cassava production environments—A modeling approach. Agronomy 2021, 11, 1372. [Google Scholar] [CrossRef]
- Sawatraksa, N.; Banterng, P.; Jogloy, S.; Vorasoot, N.; Moreno Cadena, L.P.; Hoogenboom, G. Performance of a model in simulating growth and stability for cassava grown after rice. Agron. J. 2021, 113, 2335–2348. [Google Scholar] [CrossRef]
- He, J.; Reddy, G.V.; Liu, M.; Shi, P. A general formula for calculating surface area of the similarly shaped leaves: Evidence from six Magnoliaceae species. Glob. Ecol. Conserv. 2020, 23, e01129. [Google Scholar] [CrossRef]
- Toebe, M.; Souza, R.R.D.; Mello, A.C.; Melo, P.J.D.; Segatto, A.; Castanha, A.C. Leaf area estimation of squash ‘Brasileirinha’ by leaf dimensions. Cienc. Rural. 2019, 49, e20180932. [Google Scholar] [CrossRef] [Green Version]
- Koubouris, G.; Bouranis, D.; Vogiatzis, E.; Nejad, A.R.; Giday, H.; Tsaniklidis, G.; Ligoxigakis, E.K.; Blazakis, K.; Kalaitzis, P.; Fanourakis, D. Leaf area estimation by considering leaf dimensions in olive tree. Sci. Hortic. 2018, 240, 440–445. [Google Scholar] [CrossRef]
- Rouphael, Y.; Colla, G.; Fanasca, S.; Karam, F. Leaf area estimation of sunflower leaves from simple linear measurements. Photosynthetica 2007, 45, 306–308. [Google Scholar] [CrossRef]
- Peksen, E. Non–destructive leaf area estimation model for faba bean (Vicia faba L.). Sci. Hortic. 2007, 113, 322–328. [Google Scholar] [CrossRef]
- Serdar, Ü.; Demirsoy, H. Non–destructive leaf area estimation in chestnut. Sci. Hortic. 2006, 108, 227–230. [Google Scholar] [CrossRef]
- Pandey, S.K.; Singh, H. A simple, cost-effective method for leaf area estimation. J. Bot. 2011, 2011, 658240. [Google Scholar] [CrossRef] [Green Version]
- Zanetti, S.; Pereira, L.F.; Sartori, M.M.P.; Silva, M.A. Leaf area estimation of cassava from linear dimensions. An. Acad. Bras. Cienc. 2017, 89, 1729–1736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trachta, M.A.; Junior, A.Z.; Alves, A.F.; Freitas, C.P.D.O.D.; Streck, N.A.; Cardoso, P.D.S.; Santos, A.T.L.; Nascimento, M.D.F.D.; Rossato, I.G.; Simões, G.P.; et al. Leaf area estimation with nondestructive method in cassava. Bragantia 2020, 79, 472–484. [Google Scholar] [CrossRef]
- Malik, A.I.; Kongsil, P.; Nguyễn, V.A.; Ou, W.; Srean, P.; López–Lavalle, L.A.B.; Utsumi, Y.; Lu, C.; Kittipadakul, P.; Nguyễn, H.H.; et al. Cassava breeding and agronomy in Asia: 50 years of history and future directions. Breed. Sci. 2020, 70, 145–166. [Google Scholar] [CrossRef] [Green Version]
- Department of Agriculture. Good Agricultural Practices for Cassava; National Bureau of Agricultural Commodity and Food Standards Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2008.
- Analytical Software. Statistix, version 10; Analytical Software: Tallahassee, FL, USA, 2013.
- Wallach, D.; Goffinet, B. Mean squared error of prediction as a criterion for evaluating and comparing system models. Ecol. Modell. 1989, 44, 299–306. [Google Scholar] [CrossRef]
- Irikura, V.; Cock, J.H.; Kawano, K. The physiological basis of genotype–temperature interactions in cassava. Field Crops Res. 1979, 2, 227–239. [Google Scholar] [CrossRef]
- Alves, A.A.C. Cassava botany and physiology. In Cassava: Biology, Production and Utilization; Hillocks, R.J., Thresh, J.M., Bellotti, A.C., Eds.; CABI Publishing: New York, NY, USA, 2002; pp. 67–89. [Google Scholar]
- Joaqui Barandica, O.; Pérez, J.C.; Lenis, J.I.; Calle, F.; Morante, N.; Pino, L.; Hershey, C.H.; Ceballos, H. Cassava breeding II: Phenotypic correlations through the different stages of selection. Front. Plant Sci. 2016, 7, 1649. [Google Scholar] [CrossRef] [Green Version]
- Kawano, K. Thirty years of cassava breeding for productivity–biological and social factors for success. Crop Sci. 2003, 43, 1325–1335. [Google Scholar] [CrossRef]
- Ojulong, H.F.; Labuschagne, M.T.; Herselman, L.; Fregene, M. Yield traits as selection indices in seedling populations of cassava. Crop Breed. Appl. Biotechnol. 2010, 10, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Tan, S.L.; Cock, J.H. Branching habit as a yield determinant in cassava. Field Crops Res. 1979, 2, 281–289. [Google Scholar] [CrossRef]

| Age | Variable | n | Minimum | Maximum | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 3 MAP | LA (cm2) | 372 | 90.67 | 458.80 | 212.33 | 206.47 | 60.61 |
| L (cm) | 372 | 12.40 | 24.00 | 17.40 | 17.20 | 2.09 | |
| W (cm) | 372 | 2.40 | 7.00 | 4.45 | 4.40 | 0.94 | |
| N | 372 | 5.00 | 9.00 | 6.84 | 7.00 | 0.91 | |
| K (cm2) | 372 | 33.28 | 160.48 | 78.51 | 76.55 | 23.44 | |
| J (cm2) | 372 | 71.50 | 212.40 | 119.38 | 119.00 | 23.43 | |
| 4 MAP | LA (cm2) | 372 | 83.74 | 412.77 | 209.35 | 206.39 | 61.47 |
| L (cm) | 372 | 11.60 | 25.70 | 18.17 | 18.20 | 2.54 | |
| W (cm) | 372 | 2.20 | 6.30 | 4.21 | 4.20 | 0.72 | |
| N | 372 | 3.00 | 9.00 | 6.61 | 7.00 | 1.01 | |
| K (cm2) | 372 | 33.58 | 147.42 | 77.58 | 75.60 | 21.74 | |
| J (cm2) | 372 | 45.00 | 204.30 | 120.20 | 121.80 | 25.32 | |
| 5 MAP | LA (cm2) | 372 | 76.15 | 470.98 | 193.20 | 184.79 | 62.25 |
| L (cm) | 372 | 11.60 | 27.00 | 17.95 | 18.00 | 2.47 | |
| W (cm) | 372 | 2.50 | 6.80 | 4.14 | 4.10 | 0.72 | |
| N | 372 | 3.00 | 9.00 | 6.24 | 7.00 | 1.08 | |
| K (cm2) | 372 | 34.80 | 182.92 | 75.46 | 73.32 | 21.39 | |
| J (cm2) | 372 | 44.10 | 213.30 | 112.48 | 112.00 | 27.09 | |
| 6 MAP | LA (cm2) | 372 | 38.07 | 374.58 | 166.21 | 159.26 | 68.30 |
| L (cm) | 372 | 11.00 | 24.70 | 17.16 | 17.00 | 2.64 | |
| W (cm) | 372 | 1.80 | 5.90 | 3.93 | 3.90 | 0.75 | |
| N | 372 | 3.00 | 9.00 | 6.02 | 6.00 | 1.13 | |
| K (cm2) | 372 | 21.24 | 143.26 | 68.83 | 66.60 | 21.81 | |
| J (cm2) | 372 | 37.20 | 202.50 | 104.55 | 105.00 | 29.96 | |
| 7 MAP | LA (cm2) | 372 | 25.25 | 342.37 | 134.10 | 123.28 | 61.24 |
| L (cm) | 372 | 8.00 | 24.50 | 15.48 | 15.00 | 2.93 | |
| W (cm) | 372 | 1.80 | 5.60 | 3.60 | 3.50 | 0.73 | |
| N | 372 | 3.00 | 9.00 | 5.40 | 5.00 | 1.35 | |
| K (cm2) | 372 | 18.60 | 129.85 | 57.42 | 52.50 | 21.44 | |
| J (cm2) | 372 | 24.00 | 204.30 | 85.36 | 80.00 | 32.43 | |
| 8 MAP | LA (cm2) | 372 | 27.63 | 308.38 | 106.73 | 93.09 | 53.63 |
| L (cm) | 372 | 8.50 | 21.40 | 14.00 | 13.95 | 2.59 | |
| W (cm) | 372 | 1.80 | 5.60 | 3.34 | 3.20 | 0.71 | |
| N | 372 | 2.00 | 9.00 | 4.97 | 5.00 | 1.46 | |
| K (cm2) | 372 | 17.85 | 109.20 | 48.09 | 44.84 | 18.19 | |
| J (cm2) | 372 | 21.00 | 181.80 | 71.20 | 67.25 | 29.12 | |
| 9 MAP | LA (cm2) | 372 | 14.09 | 322.14 | 77.35 | 67.75 | 45.25 |
| L (cm) | 372 | 6.00 | 25.00 | 12.38 | 12.10 | 2.73 | |
| W (cm) | 372 | 1.20 | 6.00 | 3.00 | 2.90 | 0.72 | |
| N | 372 | 1.00 | 8.00 | 4.61 | 5.00 | 1.55 | |
| K (cm2) | 372 | 9.36 | 150.00 | 38.52 | 35.48 | 17.21 | |
| J (cm2) | 372 | 9.50 | 175.00 | 58.48 | 52.65 | 27.93 | |
| 10 MAP | LA (cm2) | 372 | 14.63 | 246.23 | 74.98 | 64.77 | 41.66 |
| L (cm) | 372 | 5.90 | 20.00 | 11.74 | 11.40 | 2.82 | |
| W (cm) | 372 | 1.40 | 5.60 | 2.98 | 2.90 | 0.73 | |
| N | 372 | 2.00 | 7.00 | 4.64 | 5.00 | 1.33 | |
| K (cm2) | 372 | 10.03 | 100.24 | 36.46 | 33.70 | 16.70 | |
| J (cm2) | 372 | 18.60 | 137.90 | 55.90 | 52.00 | 24.86 |
| Independent Variable | Function | R2 |
|---|---|---|
| L | LA = 19.61L − 157.83 | 0.79 |
| L, K | LA = 3.68 L + 2.35K − 51.31 | 0.88 |
| L, J | LA = 8.92L + 1.18J − 99.29 | 0.87 |
| L, K, J | LA = −3.39L + 2.04K + 1.01J − 15.10 | 0.94 |
| Leaf Area | Total Fresh Weight | Storage Root Fresh Weight |
|---|---|---|
| Estimated maximum leaf area (L) | 0.50 ** | 0.31 * |
| Estimated maximum leaf area (L, K) | 0.50 ** | 0.32 * |
| Estimated maximum leaf area (L, J) | 0.51 ** | 0.35 ** |
| Estimated maximum leaf area (L, K, J) | 0.54 ** | 0.33 ** |
| Estimated LAI | Measured LAI | Total Fresh Weight | Storage Root Fresh Weight |
|---|---|---|---|
| Estimated LAI (L) | 0.93 ** | 0.65 ** | 0.44 ** |
| Estimated LAI (L, K) | 0.94 ** | 0.58 ** | 0.41 ** |
| Estimated LAI (L, J) | 0.95 ** | 0.64 ** | 0.46 ** |
| Estimated LAI (L, K, J) | 0.96 ** | 0.59 ** | 0.43 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phoncharoen, P.; Banterng, P.; Vorasoot, N.; Jogloy, S.; Theerakulpisut, P. Determination of Cassava Leaf Area for Breeding Programs. Agronomy 2022, 12, 3013. https://doi.org/10.3390/agronomy12123013
Phoncharoen P, Banterng P, Vorasoot N, Jogloy S, Theerakulpisut P. Determination of Cassava Leaf Area for Breeding Programs. Agronomy. 2022; 12(12):3013. https://doi.org/10.3390/agronomy12123013
Chicago/Turabian StylePhoncharoen, Phanupong, Poramate Banterng, Nimitr Vorasoot, Sanun Jogloy, and Piyada Theerakulpisut. 2022. "Determination of Cassava Leaf Area for Breeding Programs" Agronomy 12, no. 12: 3013. https://doi.org/10.3390/agronomy12123013
APA StylePhoncharoen, P., Banterng, P., Vorasoot, N., Jogloy, S., & Theerakulpisut, P. (2022). Determination of Cassava Leaf Area for Breeding Programs. Agronomy, 12(12), 3013. https://doi.org/10.3390/agronomy12123013







