Identification, Interaction, Expression, and Function of QTLs on Leaf Numbers with Single-Segment Substitution Lines in Rice
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Mapping of the Population
2.2. Field Experiments and Measurement of the Leaf Numbers
2.3. QTL Analysis
3. Results and Analysis
3.1. Phenotypic Variation in the Leaf Number
3.2. QTL Identification of the Leaf Numbers
3.3. QTL Epistatic Interactions and Their Effects on the Leaf Numbers
3.4. QTL Expressions on Leaf Numbers
3.5. QTL Functions on Leaf Numbers
4. Discussion
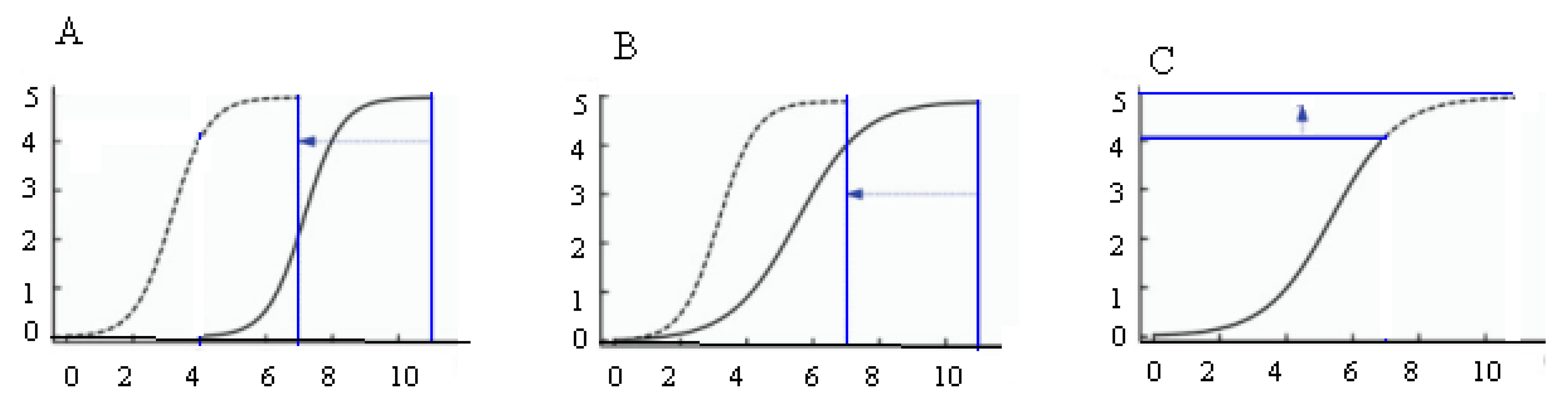
4.1. Dynamic Expression of the QTL on the Leaf Number
4.2. Advantages of SSSLs for QTL Analysis
4.3. The Approaches to the Dynamic Analysis of QTLs
4.4. Impact of Epistasis on the Leaf Number
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Itoh, J.; Nonomura, K.; Ikeda, K.; Yamaki, S.; Inukai, Y.; Yamagishi, H.; Kitano, H.; Nagato, Y. Rice plant development: From zygote to spikelet. Plant Cell Physiol. 2005, 46, 23–47. [Google Scholar]
- Du, F.; Guan, C.; Jiao, Y. Molecular mechanisms of leaf morphogenesis. Mol. Plant 2018, 11, 1117–1134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uzair, M.; Long, H.; Zafar, S.; Suyash, B.; Chun, Y.; Li, L.; Fang, J.; Zhao, J.; Peng, L.; Yuan, S.; et al. Narrow Leaf21, encoding ribosomal protein RPS3A, controls leaf development in rice. Plant Physiol. 2021, 186, 497–518. [Google Scholar] [CrossRef] [PubMed]
- Khush, G.S. Green revolution: The way forward. Nat. Rev. Genet. 2001, 2, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.B.; Khush, G.S.; Virk, P.D.; Tang, Q.Y.; Zou, Y.B. Progress in ideotype breeding to increase rice yield potential. Field Crop. Res. 2008, 108, 32–38. [Google Scholar] [CrossRef]
- Fei, C.; Xu, Q.; Xu, Z.J.; Chen, W.F. The effect of rice breeding process on improvement of yield and quality in China. Rice Sci. 2020, 27, 363–367. [Google Scholar]
- Wang, J.J.; Xu, J.; Qian, Q.; Zhang, G.H. Development of rice leaves: How histiocytic cells modulate leaf polarity establishment. Rice Sci. 2020, 27, 468–479. [Google Scholar]
- Mayi, M.; Takanori, Y.; Yutaka, S.; Jun-Ichi, I. Genome-wide analysis of spatiotemporal expression patterns during rice leaf development. BMC Genom. 2021, 22, 169. [Google Scholar]
- Nikolov, L.A.; Runions, A.; Gupta, M.D.; Tsiantis, M. Leaf development and evolution. Curr. Top. Dev. Biol. 2019, 131, 109–139. [Google Scholar]
- Lee, J.; Park, J.J.; Kim, S.L.; Yim, J.; An, G. Mutations in the rice liguleless gene result in a complete loss of the auricle, ligule, and laminar joint. Plant Mol. Biol. 2007, 65, 487–499. [Google Scholar] [CrossRef]
- Jackson, D. Double labeling of KNOTTED1 mRNA and protein reveals multiple potential sites of protein trafficking in the shoot apex. Plant Physiol. 2002, 129, 1423–1429. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.F.; Li, M.; Wen, J.; Du, Y.; Zhang, Y.M. Functional mapping of quantitative trait loci associated with rice tillering. Mol. Genet. Genom. 2010, 284, 263–271. [Google Scholar] [CrossRef]
- Liu, G.F.; Zhu, H.T.; Liu, S.W.; Zeng, R.Z.; Zhang, Z.M.; Li, W.T.; Ding, X.H.; Zhao, F.M.; Zhang, G.Q. Unconditional and conditional QTL mapping for the developmental behavior of tiller number in rice (Oryza sativa L.). Genetica 2010, 138, 885–893. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, W.; Ma, S.; Luan, X.; Zhu, H.; Wang, A.; Huang, C.; Rong, B.; Dong, S.; Meng, L.; et al. Unconditional and conditional analysis of epistasis between tillering QTLs based on single segment substitution lines in rice. Sci. Rep. 2020, 10, 5912. [Google Scholar] [CrossRef]
- Luan, X.; Xiong, L.; Xu, H.; Zhu, H.; Bu, S.; Meng, L.; Liu, G.; Wang, S. Functional mapping of tillering QTLs using the Wang–Lan–Ding model and a SSSL population. Mol. Genet. Genom. 2021, 296, 1279–1286. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, H.; Huang, J.; Zhu, H.; Luan, X.; Bu, S.; Liu, Z.; Wang, X.; Peng, Z.; Meng, L.; et al. Dynamic analysis of QTLs on plant height with single segment substitution lines in rice. Sci. Rep. 2022, 12, 5465. [Google Scholar] [CrossRef]
- Zhang, G.Q. The platform of breeding by design based on the SSSL library in rice. Hereditas 2019, 41, 754–760. (In Chinese) [Google Scholar]
- Zhu, J. Analysis of conditional genetic effects and variance components in developmental genetics. Genetics 1995, 141, 1633–1639. [Google Scholar] [CrossRef]
- Zhu, J. Mixed model approaches of mapping genes for complex quantitative traits. J. Zhejiang Univ. 1999, 33, 327–335. [Google Scholar]
- Xu, H.M.; Zhu, J. Statistical approaches in QTL mapping and molecular breeding for complex traits. Chin. Sci. Bull. 2012, 57, 2637–2644. [Google Scholar]
- Ma, C.X.; Casella, G.; Wu, R.L. Functional mapping of quantitative trait loci underlying the character process: A theoretical framework. Genetics 2002, 161, 1751–1762. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.L.; Ma, C.X.; Lin, M.; Wang, Z.H.; Casella, G. Functional mapping of quantitative trait loci underlying growth trajectories using a transform-both-sides logistic model. Biometrics 2004, 60, 729–738. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.L.; Lin, M. Opinion-functional mapping-how to map and study the genetic architecture of dynamic complex traits. Nat. Rev. Genet. 2006, 7, 229–237. [Google Scholar] [CrossRef]
- Cui, Y.H.; Zhu, J.; Wu, R.L. Functional mapping for genetic control of programmed cell death. Physiol. Genom. 2006, 25, 458–469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, Y.H.; Li, S.Y.; Li, G.X. Functional mapping imprinted quantitative trait loci underlying developmental characteristics. Theor. Biol. Med. Model. 2008, 5, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, R.S.; Lan, Z.X.; Ding, Y.X. Studies on mathematical models of the relationship between insect development and temperature. Acta Ecol. Sin. 1982, 2, 47–57. [Google Scholar]
- Zhang, G.Q.; Zeng, R.Z.; Zhang, Z.M.; Ding, X.H.; Li, W.T.; Liu, G.M.; He, F.H.; Tulukdar, A.; Huang, C.E.; Xi, Z.Y.; et al. The construction of a library of single segment substitution lines in rice (Oryza sativa L.). Rice Genet. Newsl. 2004, 21, 85–87. [Google Scholar]
- Xi, Z.Y.; He, F.H.; Zeng, R.Z.; Zhang, Z.M.; Ding, X.H.; Li, W.T.; Zhang, G.Q. Development of a wide population of chromosome single segment substitution lines in the genetic background of an elite cultivar of rice (Oryza sativa L.). Genome 2009, 49, 476–484. [Google Scholar] [CrossRef]
- Atchley, W.R.; Zhu, J. Developmental quantitative genetics, conditional epigenetic variability and growth in mice. Genetics 1997, 147, 765–776. [Google Scholar] [CrossRef]
- Wu, W.R.; Li, W.M.; Tang, D.Z.; Lu, H.R.; Worland, A.J. Time-related mapping of quantitative trait loci underlying tiller number in rice. Genetics 1999, 151, 297–303. [Google Scholar] [CrossRef]
- Yan, J.; Zhu, J.; He, C.X.; Benmoussa, M.; Wu, P. Molecular dissection of developmental behavior of plant height in rice (Oryza sativa L.). Genetics 1998, 150, 1257–1265. [Google Scholar] [CrossRef]
- Cao, G.; Zhu, J.; He, C.; Gao, Y.; Yan, J.; Wu, P. Impact of epistasis and QTL×environment interaction on the developmental behavior of plant height in rice (Oryza sativa L.). Theor. Appl. Genet. 2001, 103, 153–160. [Google Scholar] [CrossRef]
- Yang, G.; Xing, Y.; Li, S.; Ding, J.; Yue, B.; Deng, K.; Li, Y.; Zhu, Y. Molecular dissection of developmental behavior of tiller number and plant height and their relationship in rice (Oryza sativa L.). Hereditas 2006, 143, 236–245. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, L.; Guo, L.; Gao, Z.; Zeng, D.; Zhu, L.; Liang, G.; Qian, Q. Conditional and unconditional mapping of quantitative trait loci underlying plant height and tiller number in rice (Oryza sativa L.) grown at two nitrogen levels. Prog. Nat. Sci.-Mater. 2008, 18, 1539–1547. [Google Scholar] [CrossRef]
- Örjan, C.; Chris, S.H. Epistasis: Too often neglected in complex trait studies? Nat. Rev. Genet. 2004, 5, 618–625. [Google Scholar]
- Mackay, T.F.C.; Stone, E.A.; Ayroles, J.F. The genetics of quantitative traits: Challenges and prospects. Nat. Rev. Genet. 2009, 10, 565–577. [Google Scholar] [CrossRef]
- Mackay, T.F.C. Epistasis and quantitative traits: Using model organisms to study gene-gene interactions. Nat. Rev. Genet. 2014, 15, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Eshed, Y.; Zamir, D. An introgression line population of Lycopersicon pennellii in the cultivated tomato enables the identification and fine mapping of yield-associated QTL. Genetics 1995, 141, 1147–1162. [Google Scholar] [CrossRef]
- Eshed, Y.; Zamir, D. Less-than-additive epistatic interactions of quantitative trait loci in tomato. Genetics 1996, 143, 1807–1817. [Google Scholar] [CrossRef]
- Lin, H.X.; Yamamoto, T.; Sasaki, T.; Yano, M. Characterization and detection of epistatic interactions of 3 QTLs, Hd1, Hd2, and Hd3, controlling heading date in rice using nearly isogenic lines. Theor. Appl. Genet. 2000, 101, 1021–1028. [Google Scholar] [CrossRef]
- Zhu, H.T.; Li, Y.; Liang, J.Y.; Luan, X.; Xu, P.; Wang, S.K.; Zhang, G.Q.; Liu, G.F. Analysis of QTLs on heading date based on single segment substitution lines in rice (Oryza Sativa L.). Sci. Rep. 2018, 8, 13232. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Jin, L.; Zhu, H.T.; Wang, S.K.; Zhang, G.Q.; Liu, G.F. QTL epistatic analysis for yield components with single-segment substitution lines in rice. Plant Breed. 2018, 137, 346–354. [Google Scholar] [CrossRef]
- Yang, Z.F.; Jin, L.; Zhu, H.T.; Wang, S.K.; Zhang, G.Q.; Liu, G.F. Analysis of epistasis among QTLs on heading date based on single segment substitution lines in rice. Sci. Rep. 2018, 8, 3059. [Google Scholar] [CrossRef] [PubMed]
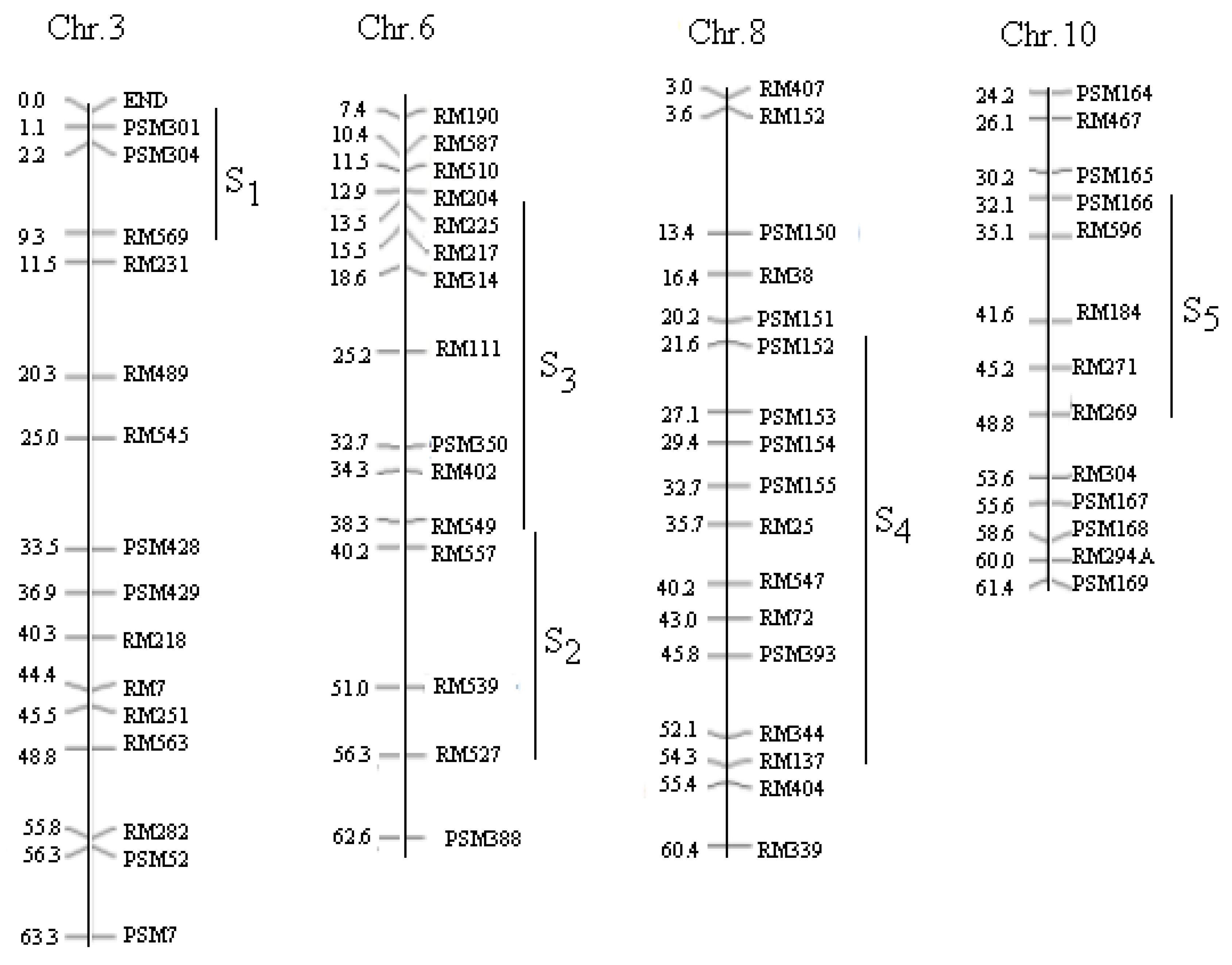
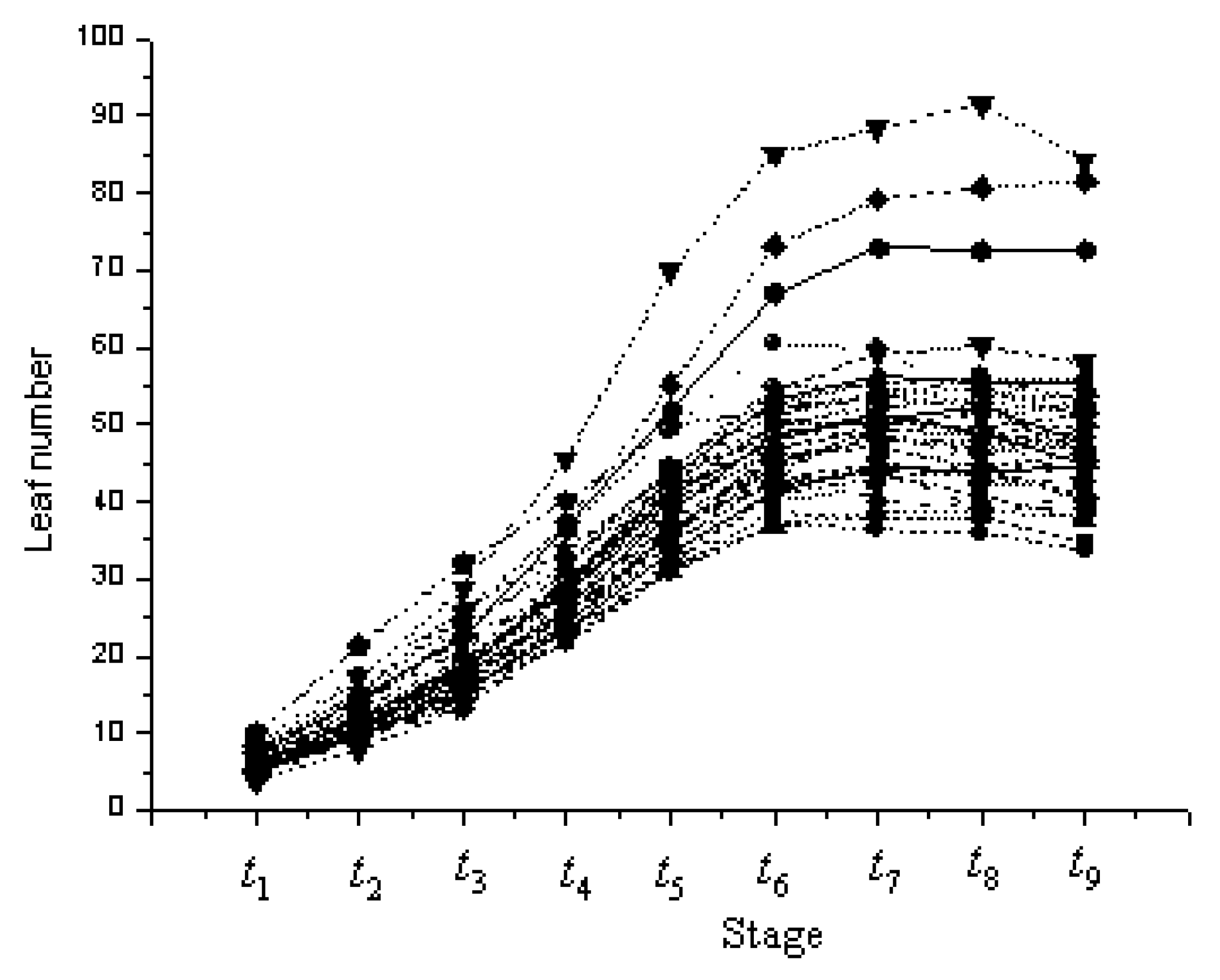
| SSSL | Code | Chr | Marker on Substituted Segment | Donor Parent |
|---|---|---|---|---|
| W23-03-08-09-27-82 | S1 | 3 | End--PSM301-PSM304--RM569 | Lemont |
| W08-18-09-09-06-02 | S2 | 6 | RM549-RM136-RM527 | IR64 |
| W04-47-68-05-04-04-02-02 | S3 | 6 | RM510--RM204--RM50--RM549 | BG367 |
| W06-26-35-01-05-02 | S4 | 8 | PSM152--PSM154-RM72--RM404 | Katy |
| W11-17-03-07-05-08 | S5 | 10 | PSM166--RM596-RM271--RM269 | Basmati 370 |
| SSSL | Effect | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | a | −7.8 * | −11.6 * | −14.4 ** | −16.5 ** | −13.8 ** | ||||
| d | 3.0 ** | 4.2 ** | 7.3 ** | |||||||
| S2 | a | 3.9 ** | 5.7 ** | 7.2 * | ||||||
| d | 4.7 ** | 11.0 ** | 14.5 ** | 14.1 ** | 11.3 ** | |||||
| S3 | a | 11.1 * | ||||||||
| d | 10.6 * | 15.7 ** | 14.6 ** | 21.6 ** | ||||||
| S4 | d | 5.3 ** | 8.2 ** | 7.6 * | ||||||
| S5 | d | 3.3 ** | 7.2 ** | 8.5 ** | 10.5 ** | 10.5 ** | 11.6 * | 9.0 * |
| SSSL Combination | Epistatic Component | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 |
|---|---|---|---|---|---|---|---|---|---|---|
| S1/S2 | aa | −5.1 * | −6.8 * | |||||||
| ad | −2.4 * | −11.5 ** | −10.9 ** | 19.0 ** | 25.6 ** | 24.4 ** | ||||
| da | −3.2 ** | −5.9 ** | −12.3 ** | −12.1 * | ||||||
| dd | −7.3 ** | −13.8 ** | −21.1 ** | −16.4 ** | −11.9 * | |||||
| S1/S3 | ad | −15.0 * | ||||||||
| da | −2.4 * | −5.2 * | −8.0 ** | |||||||
| dd | −3.6 ** | −5.6 ** | −10.5 ** | −9.9 * | −10.8 * | −17.9 * | −16.5 * | −17.7 ** | −28.2 ** | |
| S1/S4 | ad | −4.9 * | −4.9 * | 13.5 * | 19.2 ** | 18.5 ** | ||||
| da | 18.2 * | 25.0 ** | 31.6 ** | 22.3 ** | ||||||
| dd | −4.8 ** | −10.6 ** | −18.7 ** | −20.3 ** | −14.5 * | |||||
| S1/S5 | ad | −2.9 * | −6.2 ** | −5.2 * | 15.4 * | |||||
| da | −2.8 * | −6.5 * | ||||||||
| dd | −6.1 ** | −11.4 ** | −17.0 ** | −16.3 ** | −17.5 ** | −18.4 * | ||||
| S2/S3 | aa | −4.1 * | −5.6 * | |||||||
| ad | −15.5 * | −15.0 * | ||||||||
| da | −4.3 ** | −11.3 ** | −13.4 ** | −11.6 ** | −13.0 * | |||||
| dd | −4.5 * | 25.1 ** | 35.1 ** | 32.4 ** | 38.8 ** | 26.6 ** | ||||
| S2/S4 | aa | −4.8 * | −7.9 ** | −11.7 ** | −14.2 * | −14.9 * | −13.7 * | |||
| ad | −10.0 ** | −14.4 ** | −15.6 ** | |||||||
| da | −4.5 ** | −10.5 ** | −14.4 ** | −12.1 ** | −11.1 * | |||||
| dd | −6.3 ** | −16.8 ** | −24.5 ** | −24.0 ** | −18.4 ** | |||||
| S2/S5 | aa | −5.6 ** | −8.8 ** | −9.6 * | −10.9 * | |||||
| ad | −5.3 ** | −13.7 ** | −18.2 ** | −21.8 ** | −23.1 ** | −22.9 ** | −19.3 ** | |||
| da | −5.9 ** | −13.2 ** | −17.1 ** | −16.5 ** | −16.7 ** | |||||
| dd | −9.0 ** | −19.8 ** | −25.9** | −24.1 ** | −23.2 ** | −15.7 * |
| SSSL | Effect | t1|t0 | t2|t1 | t3|t2 | t4|t3 | t5|t4 | t6|t5 | t7|t6 | t8|t7 | t9|t8 |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | a | −2.9 * | ||||||||
| d | 3.0 ** | −5.6 * | −6.4 * | 5.5 * | ||||||
| S2 | a | 2.8 * | −4.2 * | |||||||
| d | 4.7 ** | 3.0 * | −7.4 ** | −10.0 ** | ||||||
| S3 | d | 4.5 * | 6.2 ** | |||||||
| S4 | a | 5.5 * | ||||||||
| d | 1.4 * | 2.9 * | −5.2 * | −6.5 * | −4.8 * | 4.2 * | ||||
| S5 | a | 5.4 * | ||||||||
| d | 3.3 ** | −8.2 ** | 7.0 ** |
| SSSL Combination | Epistatic Component | t1|t0 | t2|t1 | t3|t2 | t4|t3 | t5|t4 | t6|t5 | t7|t6 | t8|t7 | t9|t8 |
|---|---|---|---|---|---|---|---|---|---|---|
| S1/S2 | ad | −9.3 ** | 5.4 ** | 8.1 * | 7.5 * | 11.4 ** | ||||
| da | −3.2 ** | 8.2 ** | ||||||||
| dd | −7.3 ** | 8.4 ** | 11.0 ** | 7.5 * | 7.9 * | |||||
| S1/S3 | ad | −7.5 * | ||||||||
| da | −2.4 * | |||||||||
| dd | −3.6 ** | −10.4 * | ||||||||
| S1/S4 | ad | 8.8 * | ||||||||
| da | 6.3 * | 8.2 * | ||||||||
| dd | −4.8 ** | 9.3 ** | ||||||||
| S1/S5 | ad | −2.9 ** | 4.0 * | |||||||
| da | −2.8 ** | −6.8 * | ||||||||
| dd | −6.1 ** | 10.0 * | 7.8 * | −10.5 ** | ||||||
| S2/S3 | ad | −6.7 * | 6.7 * | |||||||
| da | −4.3 ** | 9.4 * | ||||||||
| dd | 3.9 * | 13.2 ** | ||||||||
| S2/S4 | ad | −7.1 ** | 10.7 ** | 8.9 * | ||||||
| da | −4.5 ** | 8.4 * | ||||||||
| dd | −6.3 ** | −6.0 ** | 13.6 ** | 15.3 ** | ||||||
| S2/S5 | ad | −5.3 ** | −4.3 * | 6.2 * | 10.5 ** | |||||
| da | −5.9 ** | 10.3 ** | ||||||||
| dd | −9.0 ** | 9.1 ** | 11.3 ** | 10.1 ** |
| SSSL | Effect | t0 | r | K | c |
|---|---|---|---|---|---|
| S1 | a | −13.2 * | 0.235 * | ||
| d | −1.29 ** | −15.5 * | |||
| S2 | a | −0.57 * | |||
| d | −1.43 ** | 0.397 ** | |||
| S3 | a | 13.5 * | 0.209 * | ||
| d | 22.3 ** | ||||
| S4 | a | ||||
| d | −1.05 ** | ||||
| S5 | a | 0.227 * | |||
| d | 12.2 * | 0.403 ** |
| Epistasis | Epistatic Component | ||||
|---|---|---|---|---|---|
| S1/S2 | ad | 1.55 ** | −0.716 ** | ||
| da | 1.54 ** | ||||
| dd | 2.61 ** | ||||
| S1/S3 | aa | −0.364 * | |||
| da | 0.93 * | ||||
| S1/S4 | ad | 1.08 * | 20.3 * | ||
| da | 1.28 ** | 42.8 ** | |||
| dd | 2.52 ** | ||||
| S1/S5 | aa | 0.394 * | −0.365 * | ||
| ad | −0.373 * | ||||
| dd | 1.59 ** | −0.299 * | |||
| S2/S3 | da | 0.92 * | −0.476 ** | ||
| dd | 1.47 ** | −0.415 ** | |||
| S2/S4 | ad | 1.74 ** | |||
| da | 1.10 * | −0.449 ** | |||
| dd | 2.82 ** | ||||
| S2/S5 | ad | 1.14 ** | −21.1 * | −0.467 ** | |
| da | 1.95 ** | −0.380 * | |||
| dd | 1.94 ** | −23.0 * | −0.654 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, S.; Zhan, P.; Huang, L.; Tang, J.; Chen, L.; Zhu, H.; Liu, Z.; Meng, L.; Liu, G.; Wang, S. Identification, Interaction, Expression, and Function of QTLs on Leaf Numbers with Single-Segment Substitution Lines in Rice. Agronomy 2022, 12, 2968. https://doi.org/10.3390/agronomy12122968
Bu S, Zhan P, Huang L, Tang J, Chen L, Zhu H, Liu Z, Meng L, Liu G, Wang S. Identification, Interaction, Expression, and Function of QTLs on Leaf Numbers with Single-Segment Substitution Lines in Rice. Agronomy. 2022; 12(12):2968. https://doi.org/10.3390/agronomy12122968
Chicago/Turabian StyleBu, Suhong, Penglin Zhan, Lilong Huang, Jichun Tang, Leyi Chen, Haitao Zhu, Zupei Liu, Lijun Meng, Guifu Liu, and Shaokui Wang. 2022. "Identification, Interaction, Expression, and Function of QTLs on Leaf Numbers with Single-Segment Substitution Lines in Rice" Agronomy 12, no. 12: 2968. https://doi.org/10.3390/agronomy12122968
APA StyleBu, S., Zhan, P., Huang, L., Tang, J., Chen, L., Zhu, H., Liu, Z., Meng, L., Liu, G., & Wang, S. (2022). Identification, Interaction, Expression, and Function of QTLs on Leaf Numbers with Single-Segment Substitution Lines in Rice. Agronomy, 12(12), 2968. https://doi.org/10.3390/agronomy12122968






