Temperature-Based Grapevine Ripeness Modeling for cv. Touriga Nacional and Encruzado in the Dão Wine Region, Portugal
Abstract
1. Introduction
2. Materials and Methods
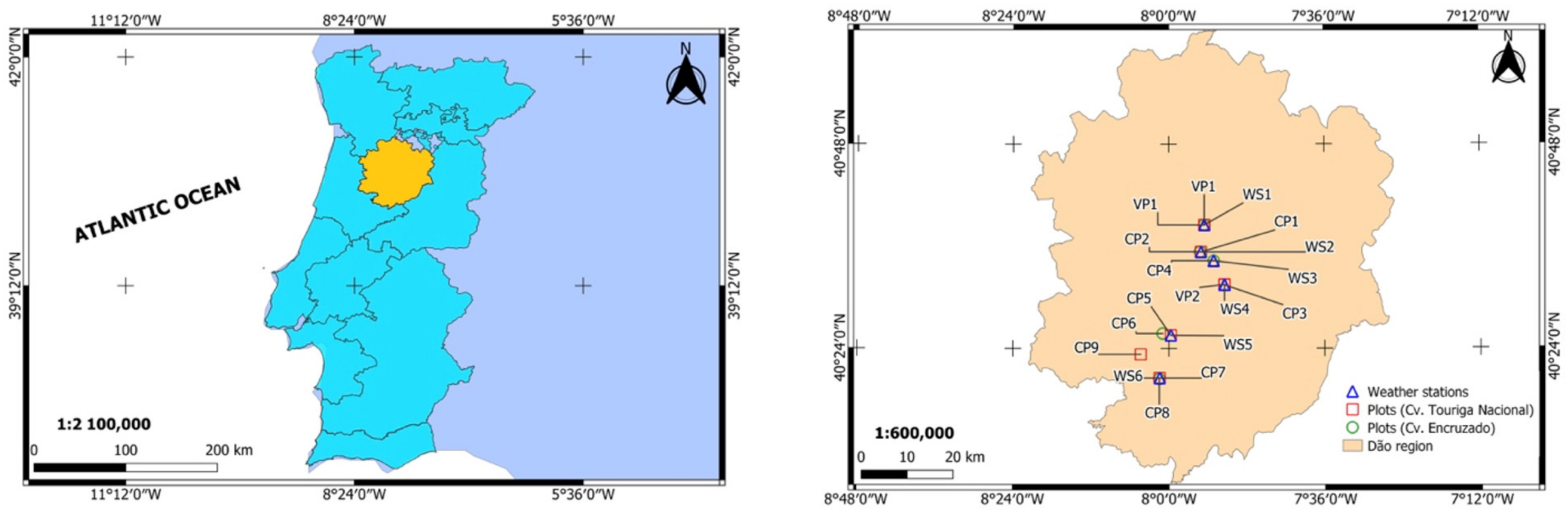
2.1. Study Area
2.2. Phenological Data
2.3. Berry Quality Monitoring and Maturity Stages
2.4. Temperature Dataset
2.5. Models Selection and Evaluation
- (a)
- The Degree Day function (DD) that determine the RF through the daily temperature (Ti) and a fitted temperature threshold (T0), often referred to as base temperature:
- (b)
- The Sigmoid function (SM) that calculates the RF from the Ti and two fit parameters, e and d, which correspond to the location and sharpness of the curve, respectively:
3. Results
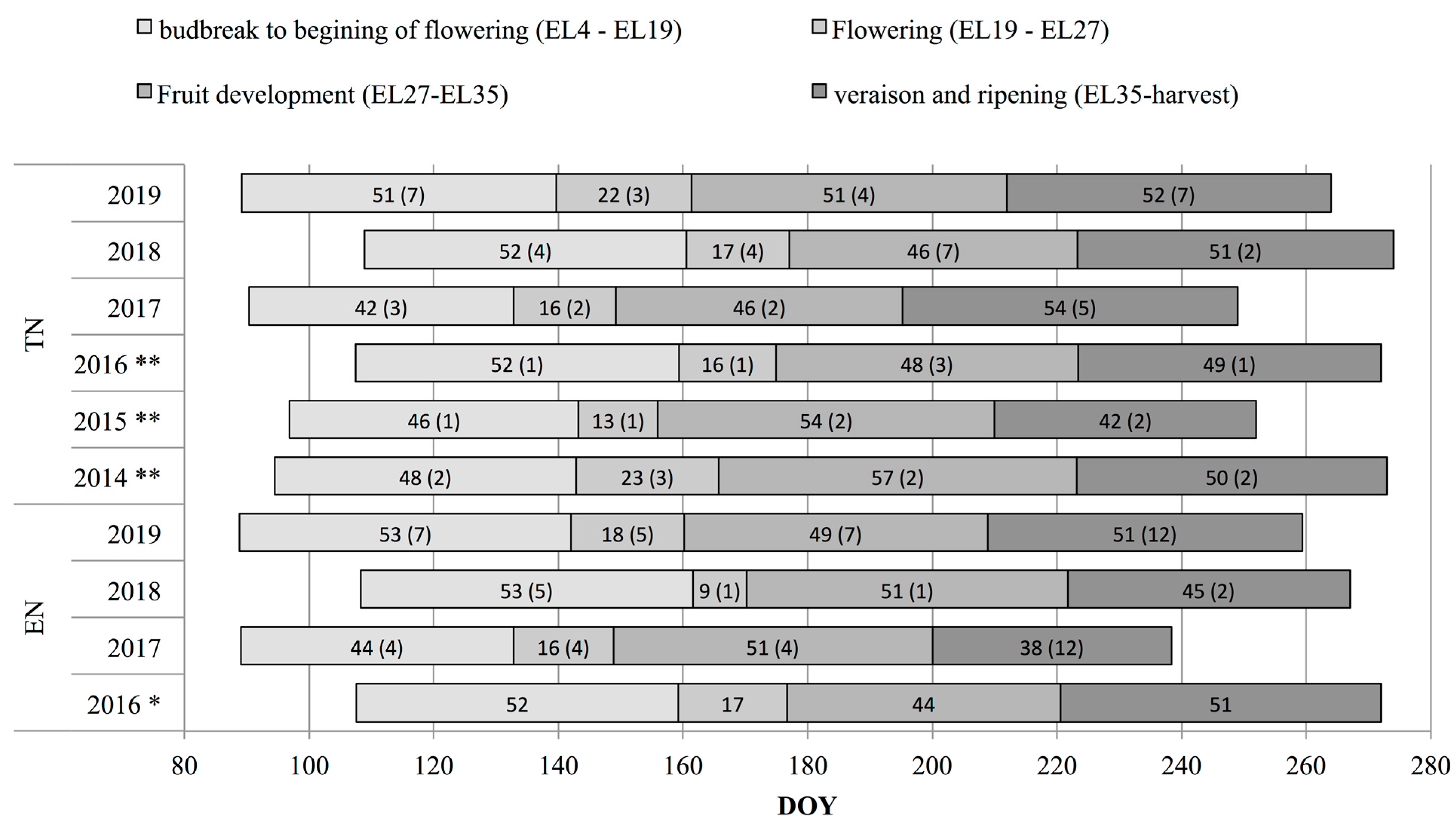
3.1. Phenological, Ripening and Climate Data
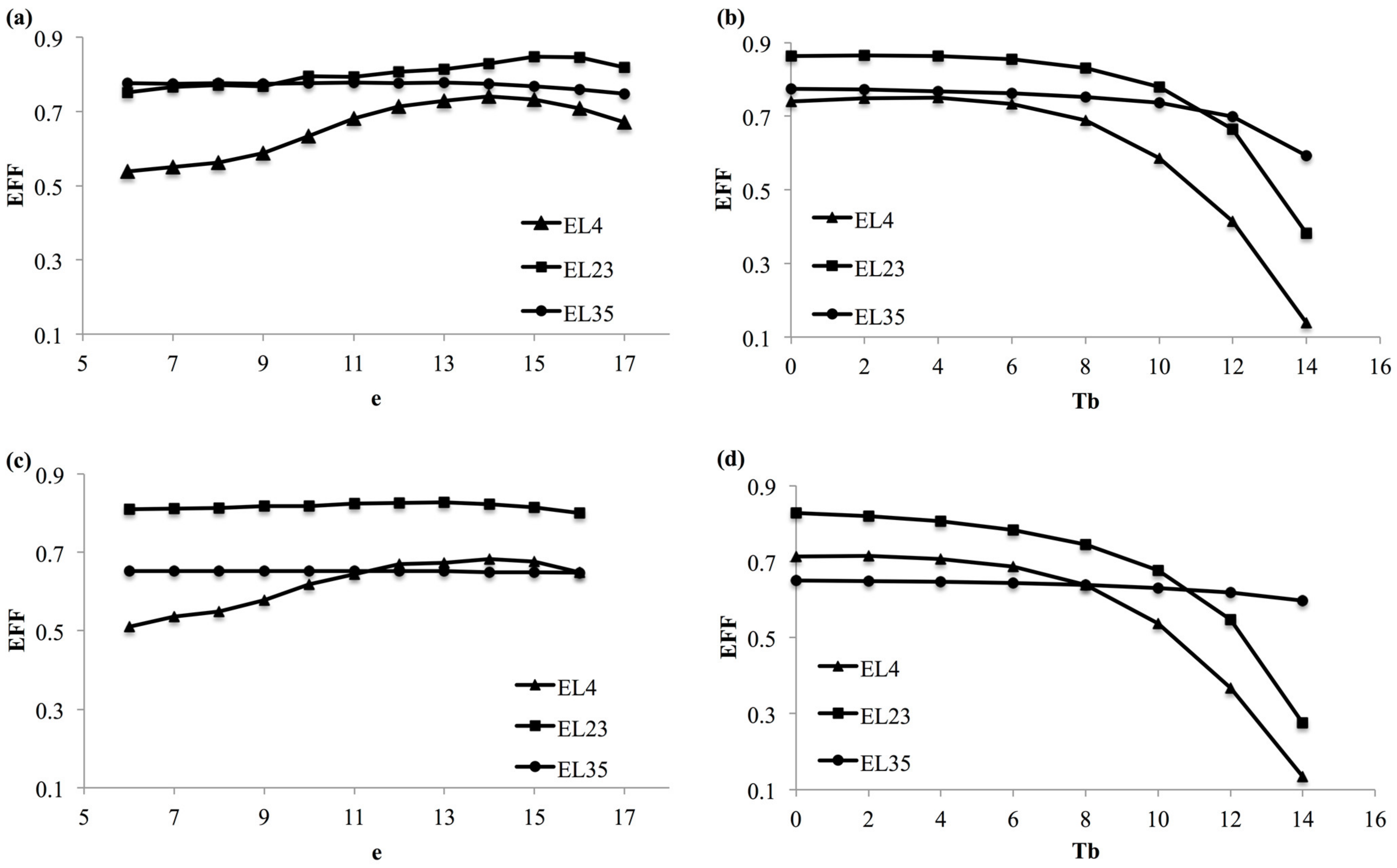
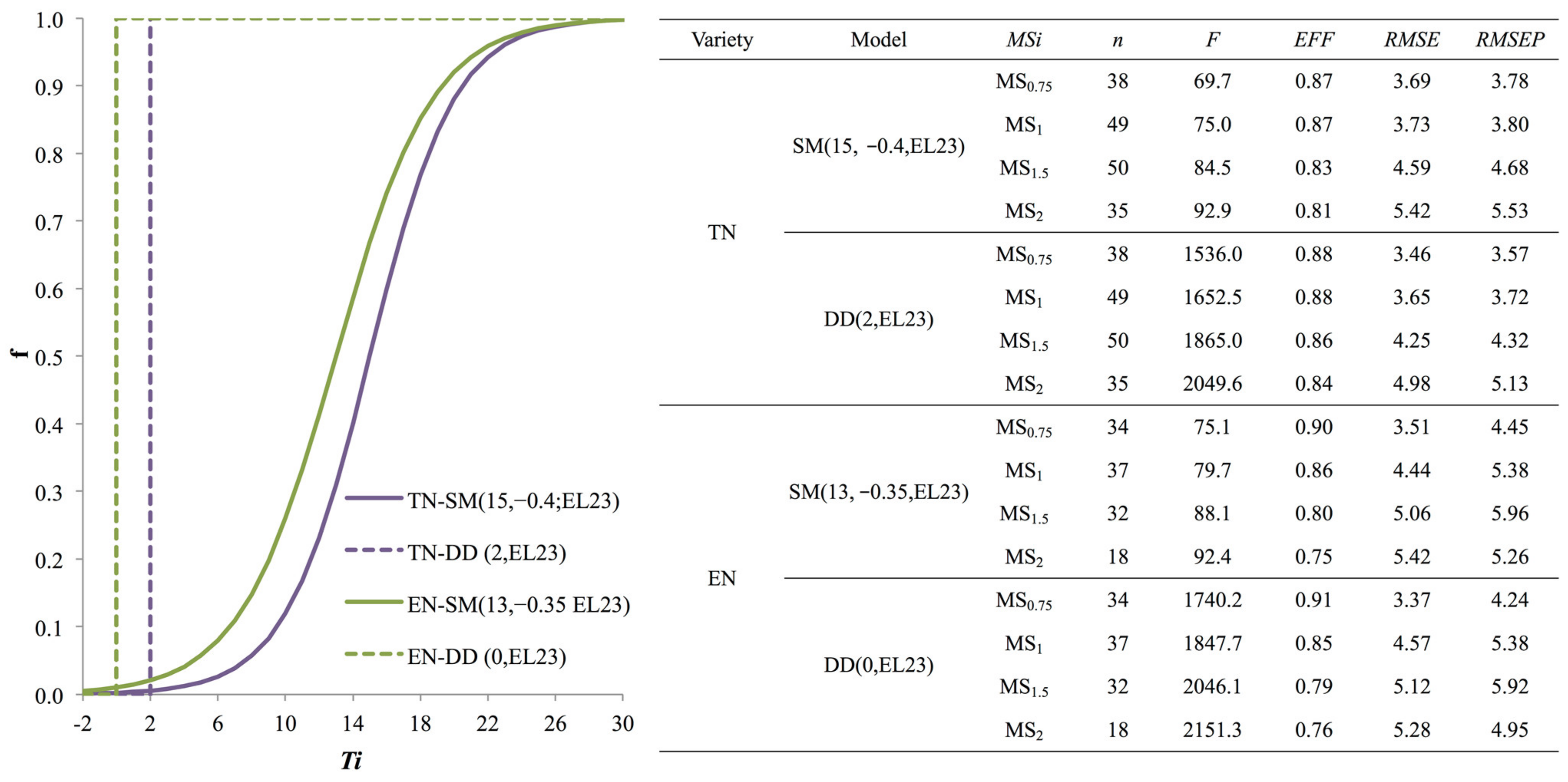
3.2. Model Selection
3.3. Model Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bashir, S.; Kaur, N. The Biochemistry of Grape Berry Development. Int. J. Curr. Microbiol. Appl. Sci. 2018, 7, 1692–1699. [Google Scholar] [CrossRef]
- Conde, C.; Silva, P.; Fontes, N.; Dias, A.; Tavares, R.; Sousa, M.; Agasse, A.; Delrot, S.; Gerós, H. Biochemical Changes throughout Grape Berry Development and Fruit and Wine Quality. Food 2007, 1, 1–22. [Google Scholar]
- Dokoozlian, N.K. Grape Berry Growth and Development. In Raisin Production Manual; Christensen, L.P., Ed.; Agriculture and Natural Resources at University of California: Davis, CA, USA, 2000; pp. 30–37. [Google Scholar] [CrossRef]
- Letchov, G.; Roychev, V. Growth Kinetics of Grape Berry Density (Vitis Vinifera L. ’Black Corinth’). Vitis-J. Grapevine Res. 2017, 56, 155–159. [Google Scholar] [CrossRef]
- Ollat, N.; Diakou-Verdin, P.; Carde, J.P.; Barrieu, F.; Gaudillère, J.P.; Moing, A. Grape berry development: A review. J. Int. Sci. Vigne Vin. 2002, 36, 109–131. [Google Scholar]
- Suter, B.; Destrac Irvine, A.; Gowdy, M.; Dai, Z.; van Leeuwen, C. Adapting Wine Grape Ripening to Global Change Requires a Multi-Trait Approach. Front. Plant Sci. 2021, 12, 36. [Google Scholar] [CrossRef] [PubMed]
- Du Plessis, C.S. Optimum Maturity and Quality Parameters in Grapes: A Review. S. Afr. J. Enol. Vitic. 1984, 5, 35–42. [Google Scholar] [CrossRef]
- Du Plessis, C.S.; Van Rooyen, P.C. Grape Maturity and Wine Quality. S. Afr. J. Enol. Vitic. 1982, 3, 41–45. [Google Scholar] [CrossRef][Green Version]
- Meléndez, E.; Ortiz, M.C.; Sarabia, L.A.; ÍÑiguez, M.; Puras, P. Modelling Phenolic and Technological Maturities of Grapes by Means of the Multivariate Relation between Organoleptic and Physicochemical Properties. Anal. Chim. Acta 2013, 761, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Van Rooyen, P.C.; Ellis, L.P.; Du Plessis, C.S. Interactions between Grape Maturity Indices and Quality for Pinotage and Cabernet Sauvignon Wines from Four Localities. S. Afr. J. Enol. Vitic. 1984, 5, 29–34. [Google Scholar] [CrossRef][Green Version]
- Cameron, W.; Petrie, P.R.; Barlow, E.W.R.; Patrick, C.J.; Howell, K.; Fuentes, S. Is Advancement of Grapevine Maturity Explained by an Increase in the Rate of Ripening or Advancement of Veraison? Aust. J. Grape Wine Res. 2021, 27, 334–347. [Google Scholar] [CrossRef]
- Costa, C.; Graça, A.; Fontes, N.; Teixeira, M.; Gerós, H.; Santos, J.A. The Interplay between Atmospheric Conditions and Grape Berry Quality Parameters in Portugal. Appl. Sci. 2020, 10, 4943. [Google Scholar] [CrossRef]
- Fernández-González, M.; Rodríguez-Rajo, F.J.; Escuredo, O.; Aira, M.J. Influence of Thermal Requirement in the Aerobiological and Phenological Behavior of Two Grapevine Varieties. Aerobiologia 2013, 29, 523–535. [Google Scholar] [CrossRef]
- Lucchetta, V.; Volta, B.; Tononi, M.; Zanotelli, D.; Andreotti, C. Effects of Pre-Harvest Techniques in the Control of Berry Ripening in Grapevine Cv. Sauvignon Blanc. In BIO Web of Conferences; EDP Sciences: Ulis, France, 2019; Volume 13, p. 04016. [Google Scholar] [CrossRef]
- Zheng, W.; García, J.; Balda, P.; Martínez De Toda, F. Effects of Severe Trimming after Fruit Set on the Ripening Process and the Quality of Grapes. Vitis 2017, 56, 27–33. [Google Scholar] [CrossRef]
- Feller, U.; Lovisolo, C.; Narayan Misra, A.; Zarrouk, O.; Pinheiro, C.; Brunetti, C.; Egipto, R.; Genebra, T.; Gori, A.; Lopes, C.M.; et al. Grape Ripening Is Regulated by Deficit Irrigation/Elevated Temperatures According to Cluster Position in the Canopy. Front. Plant Sci. 2016, 7, 1640. [Google Scholar] [CrossRef]
- Costa, R.; Fraga, H.; Fonseca, A.; De Cortázar-Atauri, I.G.; Val, M.C.; Carlos, C.; Reis, S.; Santos, J.A. Grapevine Phenology of Cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections. Agronomy 2019, 9, 210. [Google Scholar] [CrossRef]
- Leolini, L.; Costafreda-Aumedes, S.; Santos, J.A.; Menz, C.; Fraga, H.; Molitor, D.; Merante, P.; Junk, J.; Kartschall, T.; Destrac-Irvine, A.; et al. Phenological Model Intercomparison for Estimating Grapevine Budbreak Date (Vitis Vinifera L.) in Europe. Appl. Sci. 2020, 10, 3800. [Google Scholar] [CrossRef]
- Parker, A.K.; De Cortázar-Atauri, I.G.; Van Leeuwen, C.; Chuine, I. General Phenological Model to Characterise the Timing of Flowering and Veraison of Vitis Vinifera L. Aust. J. Grape Wine Res. 2011, 17, 206–216. [Google Scholar] [CrossRef]
- Reis, S.; Fraga, H.; Carlos, C.; Silvestre, J.; Eiras-Dias, J.; Rodrigues, P.; Santos, J.A. Grapevine Phenology in Four Portuguese Wine Regions: Modeling and Predictions. Appl. Sci. 2020, 10, 3708. [Google Scholar] [CrossRef]
- Mariani, L.; Alilla, R.; Cola, G.; Monte, G.D.; Epifani, C.; Puppi, G.; Osvaldo, F. IPHEN-a Real-Time Network for Phenological Monitoring and Modelling in Italy. Int. J. Biometeorol. 2013, 57, 881–893. [Google Scholar] [CrossRef]
- Molitor, D.; Junk, J.; Evers, D.; Hoffmann, L.; Beyer, M. A High-Resolution Cumulative Degree Day-Based Model to Simulate Phenological Development of Grapevine. Am. J. Enol. Vitic. 2014, 65, 72–80. [Google Scholar] [CrossRef]
- Ortega-Farías, S.O.; Lozano, P.; Moreno, Y.; León, L. Development of Models for Predicting Phenology and Evolution of Maturity in Cv. Cabernet Sauvignon and Chardonnay Grapevines. Agric. Técnica 2002, 62, 27–37. [Google Scholar]
- Rodrigues, P.; Prata, P.; Gouveia, J.P.; Pedroso, V.; Marques, F.; Rouxinol, N.; Pinto, S.; Moura, P.; Carvalho, J.; Gaião, D.; et al. Modelos Fenológicos Para as Castas Touriga Nacional, Jaen e Alfrocheiro Na Região Demarcada Do Dão. In Proceedings of the 10o Simpósio de Vitivinicultura do Alentejo, Évora, Portugal, 4–6 May 2016; Volume II, pp. 127–135. [Google Scholar]
- Verdugo-Vásquez, N.; Pañitrur-De La Fuente, C.; Ortega-Farías, S. Model Development to Predict Phenological Scales of Table Grapes (Cvs. Thompson, Crimson and Superior Seedless and Red Globe) Using Growing Degree Days. OENO One 2017, 51, 277–288. [Google Scholar] [CrossRef]
- Coombe, B.G. Growth Satges of the Grapevine: Adoption of a System for Identifying Grapevine Growth Stages. Aust. J. Grape Wine Res. 1995, 1, 104–110. [Google Scholar] [CrossRef]
- Parker, A.K.; de Cortázar-Atauri, I.G.; Gény, L.; Spring, J.L.; Destrac, A.; Schultz, H.; Molitor, D.; Lacombe, T.; Graça, A.; Monamy, C.; et al. Temperature-Based Grapevine Sugar Ripeness Modelling for a Wide Range of Vitis Vinifera L. Cultivars. Agric. For. Meteorol. 2020, 285, 107902. [Google Scholar] [CrossRef]
- Michelini, S.; Tomada, S.; Kadison, A.E.; Pichler, F.; Hinz, F.; Zejfart, M. Modeling Malic Acid Dynamics to Ensure Quality, Aroma and Freshness of Pinot Blanc Wines in South Tyrol (Italy). OENO One 2021, 55, 159–179. [Google Scholar] [CrossRef]
- Sadras, V.O.; Collins, M.; Soar, C.J. Modelling Variety-Dependent Dynamics of Soluble Solids and Water in Berries of Vitis Vinifera. Aust. J. Grape Wine Res. 2008, 14, 250–259. [Google Scholar] [CrossRef]
- De Cortázar-Atauri, I.G.; Brisson, N.; Ollat, N.; Jacquet, O.; Payan, J.-C. Asynchronous Dynamics of Grapevine (“Vitis Vinifera”) Maturation: Experimental Study for a Modelling Approach. OENO One 2009, 43, 83–97. [Google Scholar] [CrossRef]
- Andreoli, V.; Cassardo, C.; Iacona, T.L.; Spanna, F. Description and Preliminary Simulations with the Italian Vineyard Integrated Numerical Model for Estimating Physiological Values (IVINE). Agronomy 2019, 9, 94. [Google Scholar] [CrossRef]
- Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Jones, G.V.; Alves, F.; Pinto, J.G.; Santos, J.A. Very High Resolution Bioclimatic Zoning of Portuguese Wine Regions: Present and Future Scenarios. Reg. Environ. Chang. 2014, 14, 295–306. [Google Scholar] [CrossRef]
- Chuine, I.; De Cortazar-Atauri, I.G.; Kramer, K.; Hänninen, H. Plant Development Models. In Phenology: An Integrative Environmental Science; Schwartz, M., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 275–293. [Google Scholar] [CrossRef]
- Barnuud, N.N.; Zerihun, A.; Gibberd, M.; Bates, B. Berry Composition and Climate: Responses and Empirical Models. Int. J. Biometeorol. 2014, 58, 1207–1223. [Google Scholar] [CrossRef]
- Cogato, A.; Meggio, F.; Pirotti, F.; Cristante, A.; Marinello, F. Analysis and Impact of Recent Climate Trends on Grape Composition in North-East Italy. BIO Web Conf. 2019, 13, 04014. [Google Scholar] [CrossRef]
- Jones, G.V.; Davis, R.E. Climate Influences on Grapevine Phenology, Grape Composition, and Wine Production and Quality for Bordeaux, France. Am. J. Enol. Vitic. 2000, 51, 249–261. [Google Scholar]
- Williams, D.W.; Andris, H.L.; Beede, R.H.; Luvisi, D.A.; Norton, M.V.K.; Williams, L.E. Validation of a Model for the Growth and Development of the Thompson Seedless Grapevine. II. Phenology. Am. J. Enol. Vitic. 1985, 36, 283–289. [Google Scholar]
- Cameron, W.; Petrie, P.R.; Barlow, E.W.R.; Patrick, C.J.; Howell, K.; Fuentes, S.; Cameron, W. Advancement of Grape Maturity: Comparison between Contrasting Cultivars and Regions. Aust. J. Grape Wine Res. 2019, 26, 53–67. [Google Scholar] [CrossRef]
- Cosme, F.; Gonçalves, B.; Ines, A.; Jordão, A.M.; Vilela, A. Grape and Wine Metabolites: Biotechnological Approaches to Improve Wine Quality. In Grape Wine Biotechnol; Morara, A., Ed.; IntechOpen: London, UK, 2016. [Google Scholar] [CrossRef]
- De Orduña, R.M. Climate Change Associated Effects on Grape and Wine Quality and Production. Food Res. Int. 2010, 43, 1844–1855. [Google Scholar] [CrossRef]
| (a) | Year | |||||||||||||||||
| 2014 * | 2015 * | 2016 * | 2017 | 2018 | 2019 | |||||||||||||
| 1 Jan to EL4 | 9.4 | ± | 0.3 | 9.0 | ± | 0.2 | 9.1 | ± | 0.2 | 10.0 | ± | 0.6 | 9.2 | ± | 0.3 | 10.3 | ± | 0.4 |
| EL4 to EL19 | 15.5 | ± | 0.4 | 14.9 | ± | 0.5 | 14.5 | ± | 0.2 | 16.0 | ± | 0.8 | 15.5 | ± | 0.3 | 14.3 | ± | 0.8 |
| EL19 to EL27 | 15.6 | ± | 1.5 | 19.8 | ± | 0.5 | 18.4 | ± | 0.2 | 19.2 | ± | 0.9 | 18.9 | ± | 2.1 | 18.6 | ± | 1.0 |
| EL27 to EL35 | 19.7 | ± | 0.1 | 21.4 | ± | 0.1 | 23.7 | ± | 0.1 | 21.4 | ± | 0.5 | 21.7 | ± | 0.2 | 19.7 | ± | 0.6 |
| EL35 to Harvest | 19.6 | ± | 0.3 | 20.6 | ± | 0.4 | 21.3 | ± | 0.2 | 21.9 | ± | 0.4 | 23.0 | ± | 0.3 | 21.4 | ± | 0.5 |
| GSL (EL4-harvest) | 18.0 | ± | 0.4 | 19.1 | ± | 0.3 | 19.5 | ± | 0.2 | 19.8 | ± | 0.6 | 19.9 | ± | 0.4 | 18.5 | ± | 0.7 |
| (b) | Weather station | |||||||||||||||||
| WS1 | WS2 ** | WS3 ** | WS4 | WS5 ** | WS6 ** | |||||||||||||
| 1 Jan to EL4 | 9.1 | ± | 0.3 | 9.7 | ± | 0.5 | 9.9 | ± | 0.4 | 9.6 | ± | 0.5 | 10.1 | ± | 0.6 | 10.3 | ± | 0.5 |
| EL4 to EL19 | 14.2 | ± | 0.7 | 15.2 | ± | 0.8 | 15.2 | ± | 0.7 | 15.1 | ± | 0.9 | 15.6 | ± | 0.9 | 15.8 | ± | 0.7 |
| EL19 to EL27 | 17.8 | ± | 1.5 | 18.7 | ± | 1.2 | 18.6 | ± | 1.0 | 18.6 | ± | 1.1 | 18.2 | ± | 1.1 | 20.4 | ± | 1.3 |
| EL27 to EL35 | 20.8 | ± | 1.9 | 21.3 | ± | 0.9 | 21.0 | ± | 0.8 | 21.3 | ± | 1.4 | 20.7 | ± | 0.8 | 21.1 | ± | 0.7 |
| EL35 to Harvest | 20.8 | ± | 0.6 | 22.6 | ± | 0.6 | 21.7 | ± | 0.6 | 21.4 | ± | 1.0 | 21.9 | ± | 0.6 | 22.3 | ± | 0.7 |
| GSL (EL4-harvest) | 18.6 | ± | 1.2 | 19.7 | ± | 0.8 | 19.2 | ± | 0.7 | 19.3 | ± | 1.1 | 19.2 | ± | 0.8 | 19.8 | ± | 0.8 |
| Variety | Grape Maturity Stages | tx | DD Model | SM Model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T0 | EFF | RMSE | F | e | d | EFF | RMSE | F | |||
| EN | MS0.75 | EL4 | 6.16 | 0.79 | 5.0 | 1743.6 | 16.3 | −39.93 | 0.87 | 4.0 | 100.7 |
| EL23 | 0.03 | 0.91 | 3.4 | 1738.1 | 15.8 | −0.51 | 0.91 | 3.3 | 71.8 | ||
| EL35 | 0.02 | 0.73 | 5.8 | 458.0 | 15.8 | −0.26 | 0.73 | 5.8 | 17.0 | ||
| MS1.00 | EL4 | 2.44 | 0.72 | 6.3 | 2333.3 | 16.2 | −40.00 | 0.74 | 6.1 | 105.3 | |
| EL23 | 0.01 | 0.85 | 4.6 | 1846.5 | 14.5 | −40.00 | 0.86 | 4.4 | 84.9 | ||
| EL35 | 0.02 | 0.71 | 6.4 | 571.7 | 11.6 | −27.90 | 0.72 | 6.4 | 25.8 | ||
| MS1.50 | EL4 | 0.07 | 0.67 | 6.4 | 2878.3 | 13.2 | −0.19 | 0.66 | 6.5 | 110.3 | |
| EL23 | 0.01 | 0.79 | 5.1 | 2045.5 | 12.6 | −0.49 | 0.80 | 5.0 | 92.3 | ||
| EL35 | 0.03 | 0.60 | 7.0 | 764.5 | 9.1 | −0.14 | 0.61 | 7.0 | 29.8 | ||
| MS2.00 | EL4 | 0.01 | 0.71 | 5.9 | 2970.8 | 10.6 | −0.17 | 0.64 | 6.5 | 123.6 | |
| EL23 | 0.01 | 0.76 | 5.3 | 2150.3 | 11.2 | −0.09 | 0.78 | 5.1 | 72.0 | ||
| EL35 | 0.01 | 0.56 | 7.2 | 888.8 | 6.9 | −15.28 | 0.56 | 7.2 | 39.9 | ||
| TN | MS0.75 | EL4 | 3.04 | 0.83 | 4.2 | 2143.1 | 15.3 | −36.49 | 0.87 | 3.7 | 105.2 |
| EL23 | 3.85 | 0.89 | 3.4 | 1386.5 | 16.2 | −0.27 | 0.88 | 3.6 | 60.6 | ||
| EL35 | 7.78 | 0.90 | 3.2 | 302.8 | 17.2 | −0.57 | 0.90 | 3.3 | 18.9 | ||
| MS1.00 | EL4 | 2.19 | 0.73 | 5.4 | 2360.8 | 14.5 | −0.31 | 0.74 | 5.4 | 104.0 | |
| EL23 | 0.03 | 0.88 | 3.6 | 1823.3 | 15.8 | −39.17 | 0.88 | 3.7 | 81.5 | ||
| EL35 | 0.01 | 0.75 | 5.2 | 575.7 | 10.0 | −0.21 | 0.75 | 5.2 | 24.0 | ||
| MS1.50 | EL4 | 4.17 | 0.72 | 5.9 | 2273.4 | 14.9 | −0.44 | 0.70 | 6.2 | 116.2 | |
| EL23 | 2.32 | 0.86 | 4.2 | 1834.4 | 15.7 | −0.41 | 0.84 | 4.5 | 81.7 | ||
| EL35 | 0.02 | 0.75 | 5.7 | 801.0 | 12.3 | −0.23 | 0.74 | 5.7 | 32.6 | ||
| MS2.00 | EL4 | 3.00 | 0.73 | 6.5 | 2614.6 | 12.2 | −40.00 | 0.71 | 6.7 | 150.6 | |
| EL23 | 2.81 | 0.84 | 5.0 | 1962.5 | 16.2 | −38.96 | 0.82 | 5.3 | 99.8 | ||
| EL35 | 0.01 | 0.70 | 6.8 | 999.1 | 11.1 | −28.11 | 0.73 | 6.5 | 45.6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, P.; Pedroso, V.; Gonçalves, F.; Reis, S.; Santos, J.A. Temperature-Based Grapevine Ripeness Modeling for cv. Touriga Nacional and Encruzado in the Dão Wine Region, Portugal. Agronomy 2021, 11, 1777. https://doi.org/10.3390/agronomy11091777
Rodrigues P, Pedroso V, Gonçalves F, Reis S, Santos JA. Temperature-Based Grapevine Ripeness Modeling for cv. Touriga Nacional and Encruzado in the Dão Wine Region, Portugal. Agronomy. 2021; 11(9):1777. https://doi.org/10.3390/agronomy11091777
Chicago/Turabian StyleRodrigues, Pedro, Vanda Pedroso, Fernando Gonçalves, Samuel Reis, and João A. Santos. 2021. "Temperature-Based Grapevine Ripeness Modeling for cv. Touriga Nacional and Encruzado in the Dão Wine Region, Portugal" Agronomy 11, no. 9: 1777. https://doi.org/10.3390/agronomy11091777
APA StyleRodrigues, P., Pedroso, V., Gonçalves, F., Reis, S., & Santos, J. A. (2021). Temperature-Based Grapevine Ripeness Modeling for cv. Touriga Nacional and Encruzado in the Dão Wine Region, Portugal. Agronomy, 11(9), 1777. https://doi.org/10.3390/agronomy11091777






