Canopy Temperature as a Key Physiological Trait to Improve Yield Prediction under Water Restrictions in Potato
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Plant Material
2.2. Experimental Conditions and Crop Management
2.3. Crop Measurements
2.4. Potato Yield Simulation
2.4.1. Potential Yield Modeling Calibration
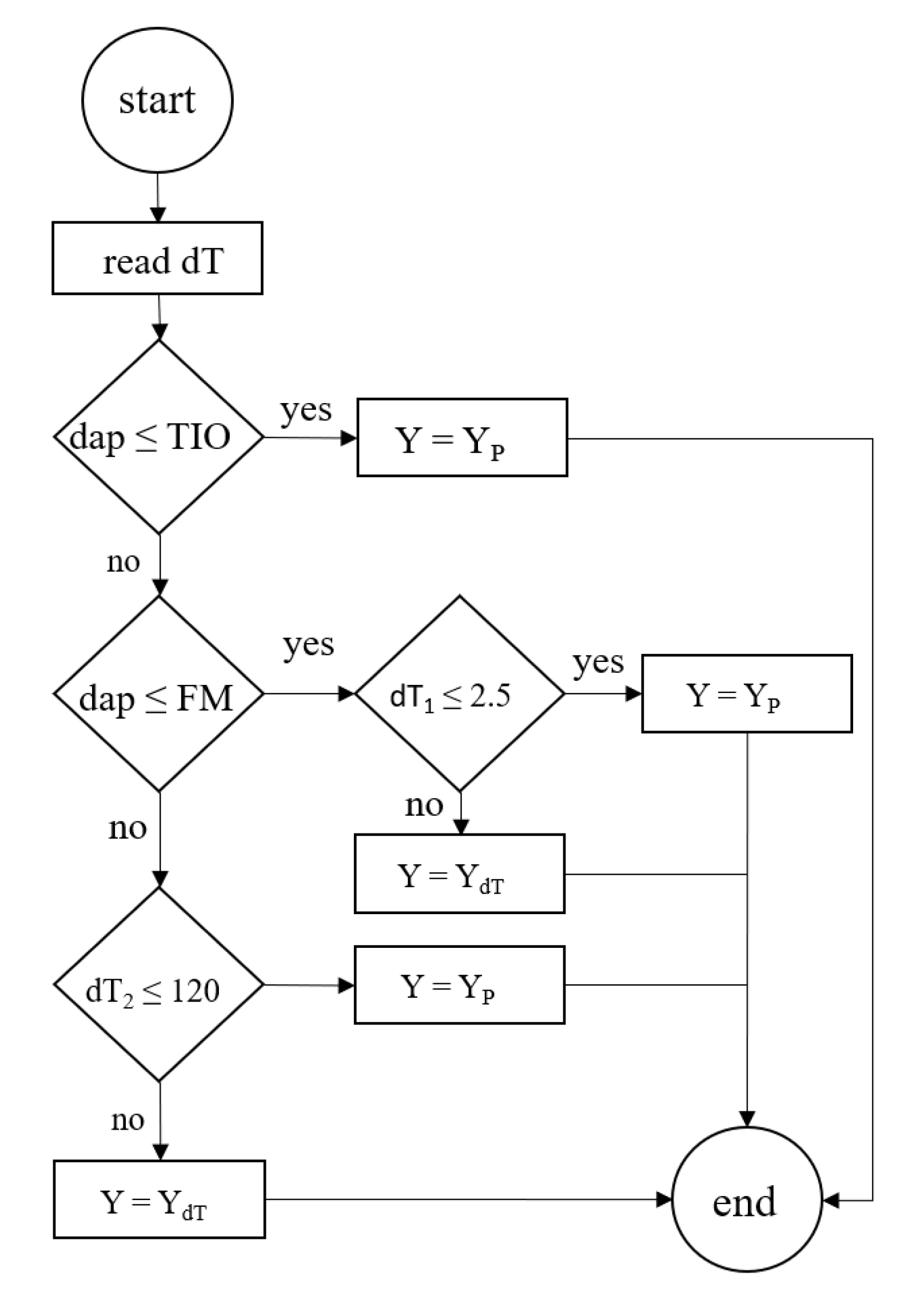
2.4.2. Yield Prediction under Water-Limited Conditions
2.4.3. Evaluation of the Crop Models’ Performance
3. Results
3.1. Sensitivity Analysis, Model Parameters’ Calibration, and Reduction Functions’ Calculation
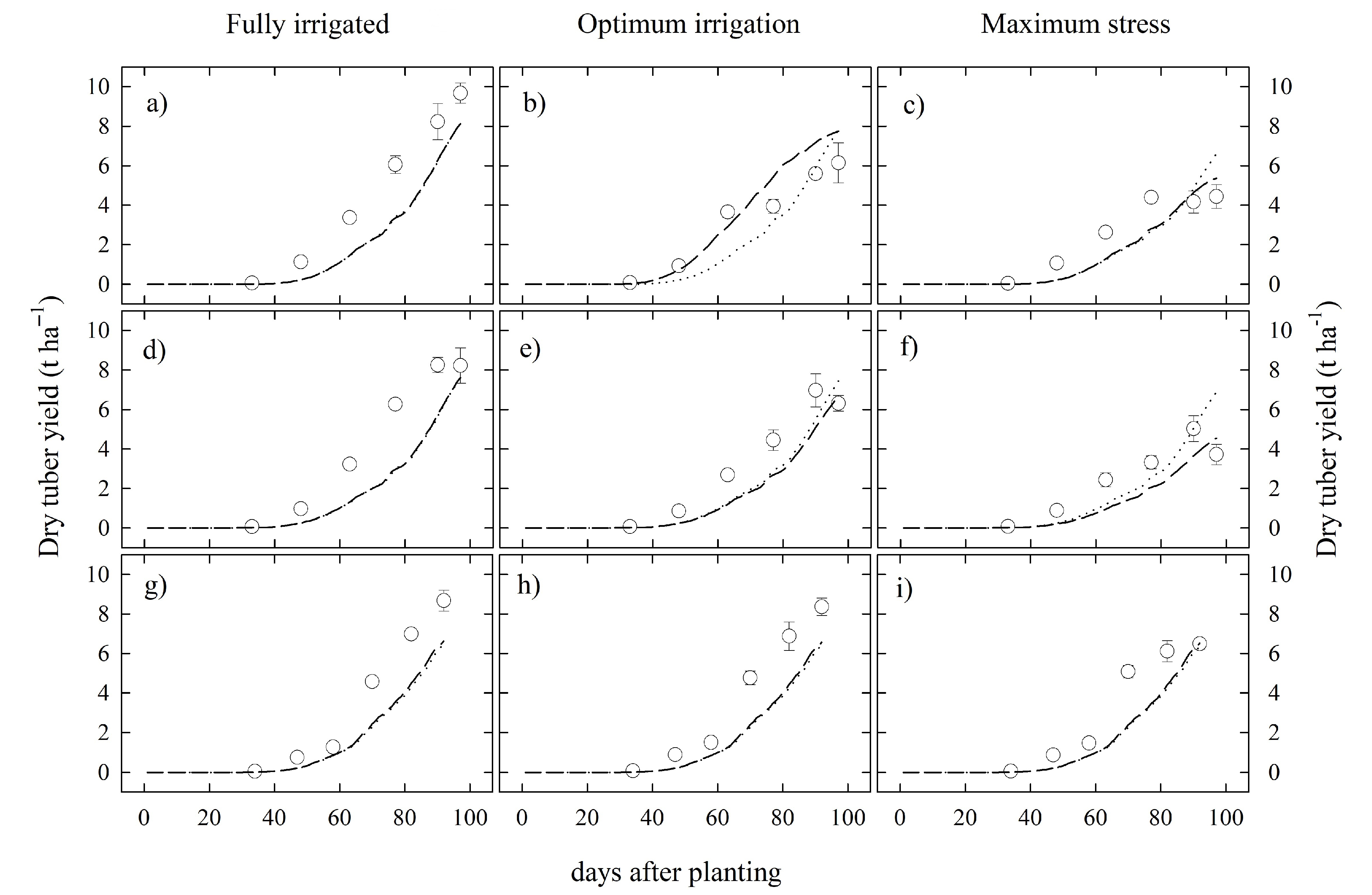
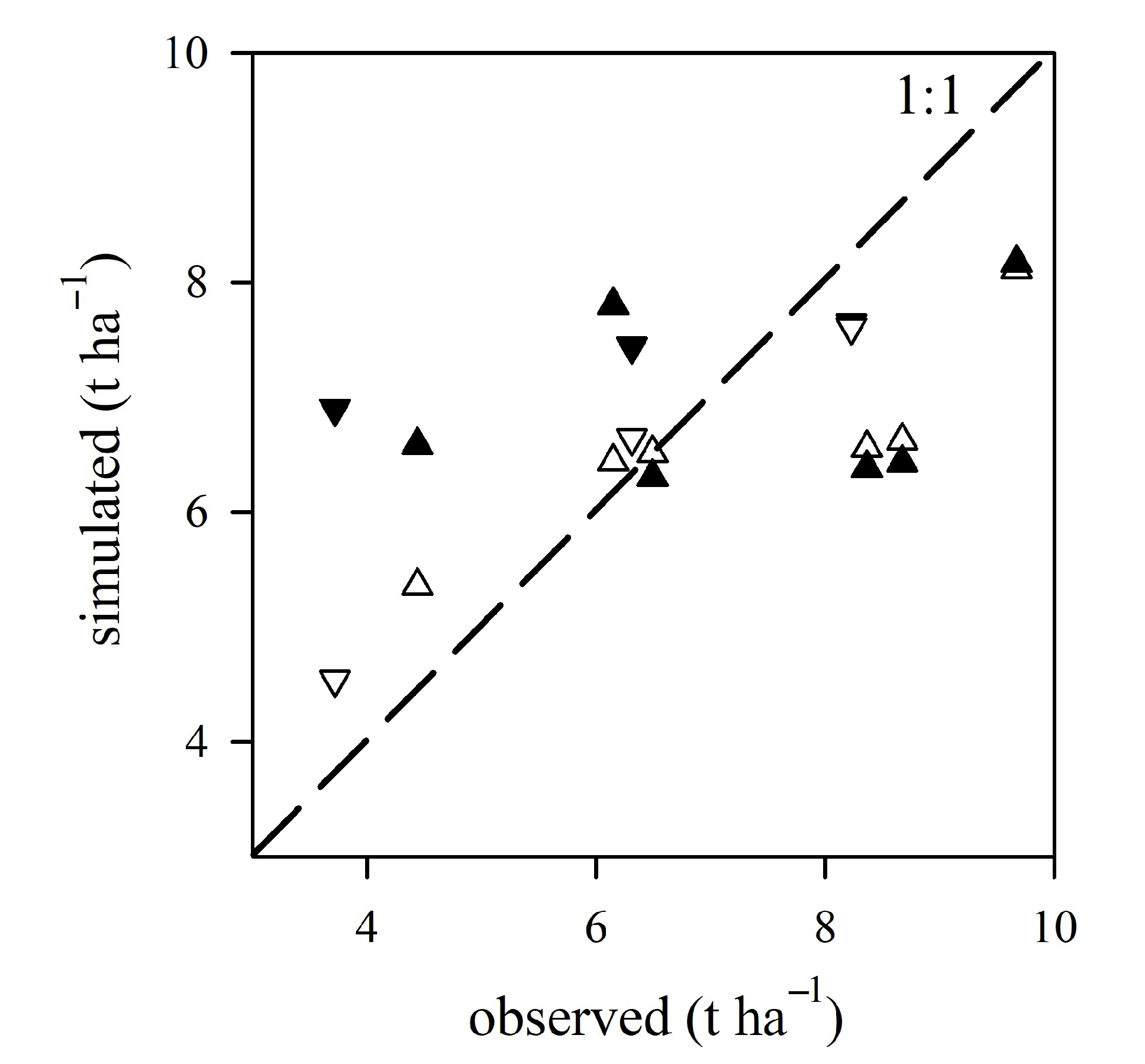
3.2. Model Performances and Validation
4. Discussion
4.1. Canopy Temperature Incorporation Improved Yield Prediction under Water Restriction
4.2. Modeling Performance under Water Restriction Depends on the Irrigation Type
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dinar, A.; Tieu, A.; Huynh, H. Water scarcity impacts on global food production. Glob. Food Sec. 2019, 23, 212–226. [Google Scholar] [CrossRef] [Green Version]
- Mancosu, N.; Snyder, R.L.; Kyriakakis, G.; Spano, D. Water Scarcity and Future Challenges for Food Production. Water 2015, 7, 975–992. [Google Scholar] [CrossRef]
- Renault, D.; Wallender, W.W. Nutritional water productivity and diets. Agric. Water Manag. 2000, 45, 275–296. [Google Scholar] [CrossRef]
- DeFauw, S.L.; He, Z.; Larkin, R.P.; Mansour, S.A. Sustainable potato production and global food security. In Sustainable Potato Production: Global Case Studies; He, Z., Larkin, R., Honeycutt, W., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 3–19. [Google Scholar] [CrossRef]
- Devaux, A.; Kromann, P.; Ortiz, O. NPotatoes for sustainable global food security. Potato Res. 2014, 57, 185–199. [Google Scholar] [CrossRef]
- Sood, M.C.; Singh, N. Water management. In The Potato: Production and Utilization in Sub-Tropics; Khurana, S.M.P., Minhas, J.S., Pandey, S.K., Eds.; Mehta Publishers: New Dehli, India, 2003; pp. 111–112. [Google Scholar]
- Monneveux, P.; Ramírez, D.A.; Pino, M.T. Drought tolerance in potato (S. tuberosum L.): Can we learn from drought tolerance research in cereals? Plant Sci. 2013, 205–206, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Obidiegwu, J.E.; Bryan, G.J.; Jones, H.G.; Prashar, A. Coping with drought: Stress and adaptive responses in potato and perspectives for improvement. Front. Plant Sci. 2015, 6, 542. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.B.; Wang, C.Y.; Zhang, H.; Dong, F.; Zheng, X.F.; Gale, W.; Li, S.X. Effect of water saving management practices and nitrogen fertilizer rate on crop yield and water use efficiency in a winter wheat–summer maize cropping system. Field Crops Res. 2011, 122, 157–163. [Google Scholar] [CrossRef]
- Ramírez, D.A.; Yactayo, W.; Rens, L.R.; Rolando, J.L.; Palacios, S.; De Mendiburu, F.; Mares, V.; Barreda, C.; Loayza, H.; Monneveux, P.; et al. Defining biological thresholds associated to plant water status for monitoring water restriction effects: Stomatal conductance and photosynthesis recovery as key indicators in potato. Agric. Water Manag. 2016, 177, 369–378. [Google Scholar] [CrossRef]
- Silva-Díaz, C.; Ramírez, D.A.; Rodríguez-Delfín, A.; De Mendiburu, F.; Rinza, J.; Ninanya, J.; Loayza, H.; Quiroz, R. Unraveling Ecophysiological Mechanisms in Potatoes under Different Irrigation Methods: A Preliminary Field Evaluation. Agronomy 2020, 10, 827. [Google Scholar] [CrossRef]
- Jones, H.G.; Hutchinson, P.A.; May, T.; Jamali, H.; Deery, D.M. A practical method using a network of fixed infrared sensors for estimating crop canopy conductance and evaporation rate. Biosyst. Eng. 2018, 165, 59–69. [Google Scholar] [CrossRef] [Green Version]
- Rinza, J.; Ramírez, D.A.; García, J.; De Mendiburu, F.; Yactayo, W.; Barreda, C.; Velasquez, T.; Mejía, A.; Quiroz, R. Infrared radiometry as a tool for early water deficit detection: Insights into its use for establishing irrigation calendars for potatoes under humid conditions. Potato Res. 2019, 62, 109–122. [Google Scholar] [CrossRef] [Green Version]
- Jones, H.G. Application of thermal imaging and infrared sensing in plant physiology and ecophysiology. Adv. Bot. Res. 2004, 41, 107–163. [Google Scholar] [CrossRef]
- Raymundo, R.; Asseng, S.; Cammarano, D.; Quiroz, R. Potato, sweet potato, and yam models for climate change: A review. Field Crops Res. 2014, 166, 173–185. [Google Scholar] [CrossRef]
- Fleisher, D.H.; Dathe, A.; Timlin, D.J.; Reddy, V.R. Improving potato drought simulations: Assessing water stress factors using a coupled model. Agric. For. Meteorol. 2015, 200, 144–155. [Google Scholar] [CrossRef]
- Gu, Z.; Qi, Z.; Burghate, R.; Yuan, S.; Jiao, X.; Xu, J. Irrigation scheduling approaches and applications: A review. J. Irrig. Drain. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Webber, H.; Ewert, F.; Kimball, B.A.; Siebert, S.; White, J.W.; Wall, G.W.; Ottman, M.J.; Trawally, D.; Gaiser, T. Simulating canopy temperature for modelling heat stress in cereals. Environ. Model. Softw. 2016, 77, 143. [Google Scholar] [CrossRef] [Green Version]
- Webber, H.; Martre, P.; Asseng, S.; Kimball, B.; White, J.; Ottman, M.; Wall, G.; De Sanctis, G.; Doltra, J.; Grant, R.; et al. Canopy temperature for simulation of heat stress in irrigated wheat in a semi-arid environment: A multi-model comparison. Field Crops Res. 2017, 202, 21–35. [Google Scholar] [CrossRef]
- Webber, H.; White, J.W.; Kimball, B.A.; Ewert, F.; Asseng, S.; Rezaei, E.E.; Pinter, P.J., Jr.; Hatfield, J.L.; Reynolds, M.P.; Ababaei, B.; et al. Physical robustness of canopy temperature models for crop heat stress simulation across environments and production conditions. Field Crops Res. 2018, 216, 75–88. [Google Scholar] [CrossRef] [Green Version]
- Cucho-Padin, G.; Rinza, J.; Ninanya, J.; Loayza, H.; Quiroz, R.; Ramírez, D.A. Development of an open-source thermal image processing software for improving irrigation management in potato crops (Solanum tuberosum L.). Sensors 2020, 20, 472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Shaughnessy, S.A.; Evett, S.R.; Colaizzi, P.D.; Howell, T.A. A crop water stress index and time threshold for automatic irrigation scheduling of grain sorghum. Agric. Water Manag. 2012, 107, 122–132. [Google Scholar] [CrossRef] [Green Version]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Chen, X.; Qi, Z.; Gui, D.; Gu, Z.; Ma, L.; Zeng, F.; Li, L.; Sima, M.W. A model-based real-time decision support system for irrigation scheduling to improve water productivity. Agronomy 2019, 9, 686. [Google Scholar] [CrossRef] [Green Version]
- Servicio Nacional de Meteorología e Hidrología (SENAMHI). Reporte Ejecutivo–Climas del Perú: Mapas de Clasificación Nacional Peru. 2020; p. 5. Available online: https://idesep.senamhi.gob.pe/geonetwork/srv/api/records/9f18b911-64af-4e6b-bbef-272bb20195e4/attachments/Resumen%20ejecutivo%20Climas%20del%20Peru%CC%81.pdf (accessed on 15 March 2021).
- Gutiérrez-Rosales, R.O.; Espinoza-Trelles, J.A.; Bonierbale, M. UNICA: Variedad Peruana para mercado fresco y papa frita con tolerancia y resistencia para condiciones climáticas adversas. Rev. Latinoam. Papa 2017, 14, 41–50. [Google Scholar] [CrossRef]
- Rol, J.L.; Ramírez, D.A.; Yactayo, W.; Monneveux, P.; Quiroz, R. Leaf greenness as a drought tolerance related trait in potato (Solanum Tuberosum L.). Environ. Exp. Bot. 2015, 110, 27–35. [Google Scholar] [CrossRef]
- Quiroz, R.; Chujoy, E.; Mares, V. Papa o potato. In Respuesta del Rendimiento de los Cultivos al Agua; Steduto, P., Hsiao, T.C., Fereres, E., Raes, D., Eds.; Estudio FAO: Roma, Italy, 2012; pp. 190–195. Available online: https://agris.fao.org/agris-search/search.do?recordID=XF2015001461 (accessed on 15 April 2021).
- Quiroz, R.; Loayza, H.; Barreda, C.; Gavilán, C.; Posadas, A.; Ramírez, D.A. Linking process-based potato models with light reflectance data: Does model complexity enhance yield prediction accuracy? Eur. J. Agron. 2017, 82, 104–112. [Google Scholar] [CrossRef]
- Production Systems and the Environment (PSE); International Potato Center (CIP). Protocol for Designing and Conducting Potato Field Experiments for Modeling Purposes; International Potato Center: Lima, Peru, 2013; p. 16. [Google Scholar] [CrossRef]
- Condori, B.; Hijmans, R.J.; Quiroz, R.; Ledent, J.F. Quantifying the expression of potato genetic diversity in the high Andes through growth analysis and modeling. Field Crops Res. 2010, 119, 135–144. [Google Scholar] [CrossRef]
- Harahagazwe, D.; Condori, B.; Barreda, C.; Bararyenya, A.; Byarugaba, A.A.; Kude, D.A.; Lung’aho, C.; Martinho, C.; Mbiri, D.; Nasona, B.; et al. How big is the potato ( Solanum tuberosum L.) yield gap in Sub-Saharan Africa and why? A participatory approach. Open Agric. 2018, 3, 180–189. [Google Scholar] [CrossRef]
- Yin, X.; Goudriaan, J.A.N.; Lantinga, E.A.; Vos, J.A.N.; Spiertz, H.J. A flexible sigmoid function of determinate growth. Ann. Bot. 2003, 91, 361–371. [Google Scholar] [CrossRef]
- R Core Team. R Software, Version, 5.3.3.; Available online: https://www.r-project.org/ (accessed on 20 November 2020).
- Kooman, P.L.; Fahem, M.; Tegera, P.; Haverkort, A.J. Effects of climate on different potato genotypes 1. Radiation interception, total and tuber dry matter production. Eur. J. Agron. 1996, 5, 193–205. [Google Scholar] [CrossRef]
- Carli, C.; Yuldashev, F.; Khalikov, D.; Condori, B.; Mares, V.; Monneveux, P. Effect of different irrigation regimes on yield, water use efficiency and quality of potato (Solanum Tuberosum L.) Lowl. Tashkent, Uzb. A Field Model. Perspective. Field Crops Res. 2014, 163, 90–99. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Evapotranspiración del Cultivo: Guías para la Determinación de los Requerimientos de Agua de los Cultivos; Estudio FAO: Roma, Italy, 2006; p. 298. Available online: http://www.fao.org/3/x0490s/x0490s00.htm (accessed on 15 April 2021).
- Spitters, C.J.T.; Schapendonk, A.H.C.M. Evaluation of breeding strategies for drought tolerance in potato by means of crop growth simulation. In Genetic Aspects of Plant Mineral Nutrition. Developments in Plant and Soil Sciences; El Bassam, N., Dambroth, M., Loughman, B.C., Eds.; Springer: Dordrecht, The Netherlands, 1990; pp. 151–161. [Google Scholar] [CrossRef]
- Rab, M.A.; Chandra, S.; Fisher, P.D.; Robinson, N.J.; Kitching, M.; Aumann, C.D.; Imhof, M. Modelling and prediction of soil water contents at field capacity and permanent wilting point of dryland cropping soils. Soil Res. 2011, 49, 90–99. [Google Scholar] [CrossRef]
- Raymundo, R.; Asseng, S.; Prassad, R.; Kleinwechter, U.; Concha, J.; Condori, B.; Bowen, W.; Wolf, J.; Olesen, J.E.; Dong, Q.; et al. Performance of the SUBSTOR-potato model across contrasting growing conditions. Field Crops Res. 2017, 202, 57–76. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.H.; Sang, W.G.; Baek, J.K.; Kim, J.H.; Shin, P.; Seo, M.C.; Cho, J.I. The effect of concurrent elevation in CO2 and temperature on the growth, photosynthesis, and yield of potato crops. PLoS ONE 2020, 15, e0241081. [Google Scholar] [CrossRef] [PubMed]
- Kingra, P.K.; Mahey, R.K.; Gill, K.K.; Mukherjee, J.; Bal, S.K. Prediction of grain yield of wheat using canopy temperature based indices. J. Agromet. 2010, 12, 61–63. Available online: https://www.researchgate.net/profile/Pavneet-Kingra/publication/288973076_Prediction_of_grain_yield_of_wheat_using_canopy_temperature_based_indices/links/5a1fe5c5aca272cbfbc33f39/Prediction-of-grain-yield-of-wheat-using-canopy-temperature-based-indices.pdf (accessed on 15 April 2015).
- Conaty, W.C.; Mahan, J.R.; Neilsen, J.E.; Tan, D.K.; Yeates, S.J.; Sutton, B.G. The relationship between cotton canopy temperature and yield, fibre quality and water-use efficiency. Field Crops Res. 2015, 183, 329–341. [Google Scholar] [CrossRef]
- Hou, M.; Tian, F.; Zhang, T.; Huang, M. Evaluation of canopy temperature depression, transpiration, and canopy greenness in relation to yield of soybean at reproductive stage based on remote sensing imagery. Agric. Water Manag. 2019, 222, 182–192. [Google Scholar] [CrossRef]
- Balota, M.; Payne, W.A.; Evett, S.R.; Lazar, M.D. Canopy temperature depression sampling to assess grain yield and genotypic differentiation in winter wheat. Crop Sci. 2007, 47, 1518–1529. [Google Scholar] [CrossRef]
- Thapa, S.; Jessup, K.E.; Pradhan, G.P.; Rudd, J.C.; Liu, S.; Mahan, J.R.; Devkota, R.N.; Baker, J.A.; Xue, Q. Canopy temperature depression at grain filling correlates to winter wheat yield in the US Southern High Plains. Field Crops Res. 2018, 217, 11–19. [Google Scholar] [CrossRef]
- Ajayi, A.E.; Olufayo, A.A. Evaluation of two temperature stress indices to estimate grain sorghum yield and evapotranspiration. Agron. J. 2004, 96, 1282–1287. [Google Scholar] [CrossRef]
- Erdem, T.; Orta, A.H.; Erdem, Y.; Okursoy, H. Crop water stress index for potato under furrow and drip irrigation systems. Potato Res. 2005, 48, 49–58. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Šťastná, M.; Toman, F.; Dufkova, J. Usage of SUBSTOR model in potato yield prediction. Agric. Water Manag. 2010, 97, 286–290. [Google Scholar] [CrossRef]
- Hill, D.; Nelson, D.; Hammond, J.; Bell, L. Morphophysiology of Potato (Solanum Tuberosum) Response Drought Stress. Paving Way Forward. Front. Plant Sci. 2020, 11. [Google Scholar] [CrossRef]
- Haverkort, A.J.; Franke, A.C.; Steyn, J.M.; Pronk, A.A.; Caldiz, D.O.; Kooman, P.L. A Robust Potato Model: LINTUL-Potato-DSS. Potato Res. 2015, 58, 313–327. [Google Scholar] [CrossRef] [Green Version]
- Minda, T.T.; Van Der Molen, M.K.; de Arellano Vilà-Guerau, J.; Chulda, K.C.; Struik, P.C. Responses of Canopy Growth and Yield of Potato Cultivars to Weather Dynamics in a Complex Topography: Belg Farming Seasons in the Gamo Highlands, Ethiopia. Agronomy 2019, 9, 163. [Google Scholar] [CrossRef] [Green Version]
- Neukam, D.; Ahrends, H.; Luig, A.; Manderscheid, R.; Kage, H. Integrating wheat canopy temperatures in crop system models. Agronomy 2016, 6, 7. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Evaluation, Analysis, Parameterization, and Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; p. 462. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Purdy, A.J.; Fisher, J.B.; Goulden, M.L.; Colliander, A.; Halverson, G.; Tu, K.; Famiglietti, J.S. SMAP soil moisture improves global evapotranspiration. Remote Sens. Environ. 2018, 219, 1–14. [Google Scholar] [CrossRef]
- Kasampalis, D.A.; Alexandridis, T.K.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of remote sensing on crop models: A review. J. Imaging 2018, 4, 52. [Google Scholar] [CrossRef] [Green Version]
- Shao, Q.; Bange, M.; Mahan, J.; Jin, H.; Jamali, H.; Zheng, B.; Chapman, S.C. A new probabilistic forecasting model for canopy temperature with consideration of periodicity and parameter variation. Agric. For. Meteorol. 2019, 265, 143. [Google Scholar] [CrossRef]
- Mahan, J.R.; Conaty, W.; Neilsen, J.; Payton, P.; Cox, S.B. Field performance in agricultural settings of a wireless temperature monitoring system based on a low-cost infrared sensor. Comput. Electron. Agric. 2010, 71, 176–181. [Google Scholar] [CrossRef]
- Payero, J.O.; Mirzakhani-Nafchi, A.; Khalilian, A.; Qiao, X.; Davis, R. Development of a low-cost Internet-of-Things (IoT) system for monitoring soil water potential using Watermark 200SS sensors. Adv. Internet Things 2017, 7, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Noguera, M.; Millán, B.; Pérez-Paredes, J.J.; Ponce, J.M.; Aquino, A.; Andújar, J.M. A new low-cost device based on thermal infrared sensors for olive tree canopy temperature measurement and water status monitoring. Remote Sens. 2020, 12, 723. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Shi, B.; Yao, Z.; Shukla, M.K.; Du, T. Energy partitioning and microclimate of solar greenhouse under drip and furrow irrigation systems. Agric. Water Manag. 2020, 234, 106096. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Shen, Y.; Zhang, X.; Lei, Y. Web-based irrigation decision support system with limited inputs for farmers. Agric. Water Manag. 2018, 210, 279–285. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigation scheduling focusing on the FAO-56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop—the FAO crop model to simulate yield response to water: II. Main algorithms and software description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Sammis, T.; Sharma, P.; Shukla, M.K.; Wang, J.; Miller, D. A water-balance drip-irrigation scheduling model. Agric. Water Manag. 2012, 113, 30–37. [Google Scholar] [CrossRef]
- Fernández, J.E. Plant-based methods for irrigation scheduling of woody crops. Horticulturae 2012, 3, 35. [Google Scholar] [CrossRef] [Green Version]
- Veysi, S.; Naseri, A.A.; Hamzeh, S.; Bartholomeus, H. A satellite based crop water stress index for irrigation scheduling in sugarcane fields. Agric. Water Manag. 2017, 189, 70–86. [Google Scholar] [CrossRef]
- Chauhan, Y.S.; Wright, G.C.; Holzworth, D.; Rachaputi, R.C.; Payero, J.O. AQUAMAN: A web-based decision support system for irrigation scheduling in peanuts. Irrig. Sci. 2013, 31, 271–283. [Google Scholar] [CrossRef]
- Wang, E.; Attard, S.; Linton, A.; McGlinchey, M.; Xiang, W.; Philippa, B.; Everingham, Y. Development of a closed-loop irrigation system for sugarcane farms using the Internet of Things. Comput. Electron. Agric. 2020, 172, 105376. [Google Scholar] [CrossRef]
- Simionesei, L.; Ramos, T.B.; Palma, J.; Oliveira, A.R.; Neves, R. IrrigaSys: A web-based irrigation decision support system based on open source data and technology. Comput. Electron. Agric. 2020, 178, 105822. [Google Scholar] [CrossRef]
- Lasage, R.; Verburg, P.H. IrrigaSys: Evaluation of small scale water harvesting techniques for semi-arid environments. J. Arid Environ. 2015, 118, 48–57. [Google Scholar] [CrossRef]
- Grum, B.; Hessel, R.; Kessler, A.; Woldearegay, K.; Yazew, E.; Ritsema, C.; Geissen, V. A decision support approach for the selection and implementation of water harvesting techniques in arid and semi-arid regions. Agric. Water Manag. 2016, 173, 35–47. [Google Scholar] [CrossRef]
| Trial | Plot Size (m) | # of Plants per Plot | TO (dap) | N×M | Irrigation Indicator | Irrigation Thresholds | Irrigation Type | Fertilizer Dose (kg ha ) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| A | 3.6 × 12.5 | 120 | 30 | 3 × 4 | 0.15 and 0.05 | DI and FI | 180:100:160 | 31.8 | |
| B | 3.6 × 12.5 | 120 | 34 | 4 × 5 | CWSI | 0.4, 0.6 and 0.7 | DI and FI | 180:100:160 | 32.8 |
| C | 4.5 × 15.8 | 180 | 36 | 3 × 5 | CWSI | 0.4 and 0.6 | DI | 160:80:180 | 28.4 |
| Physiological Process | Crop Parameters | Symbol | DI | FI | Sensitivity Analysis |
|---|---|---|---|---|---|
| Light interception | Maximum canopy cover index (fraction) | W | 1.0 | 1.0 | 0.99 |
| TT time at the maximum canopy cover (°C day) | t | 971.3 | 1023.0 | 1.70 | |
| TT at the maximum canopy cover growth rate (°C day) | t | 332.3 | 272.9 | −0.79 | |
| Light conversion | Radiation use efficiency (g MJ) | RUE | 2.47 | 2.80 | 0.99 |
| Biomass translocation | Maximum harvest index (fraction) | A | 0.76 | 0.73 | 0.99 |
| TT at the maximum tuber partition rate (°C day) | t | 642.1 | 659.5 | ∼0 | |
| TT just before the tuber initiation process (°C day) | b | 222.2 | 286.6 | ∼0 | |
| Dry matter concentration of tubers (fraction) | DMc | 0.21 | 0.18 |
| TCP | Value | a () | b () | c | R |
|---|---|---|---|---|---|
| RUE | 2.64 | −0.81 | −2.56 | 1.41 | 0.92 |
| 1.00 | −3.69 | −0.75 | 1.24 | 0.84 | |
| 997.2 | −1.91 | −0.04 | 1.08 | 0.73 | |
| A | 0.75 | −4.05 | 0.82 | 1.02 | 0.53 |
| Metrics | Drip Irrigation | Furrow Irrigation | Overall | |||
|---|---|---|---|---|---|---|
| P1 | P2 | P1 | P2 | P1 | P2 | |
| R | 0.94 | 0.97 | 0.91 | 0.99 | 0.93 | 0.98 |
| m | 1.05 | 1.12 | 0.84 | 0.99 | 0.97 | 1.08 |
| RMSE | 1.76 | 1.34 | 1.98 | 0.62 | 1.84 | 1.15 |
| NRMSE | 0.24 | 0.18 | 0.33 | 0.10 | 0.27 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ninanya, J.; Ramírez, D.A.; Rinza, J.; Silva-Díaz, C.; Cervantes, M.; García, J.; Quiroz, R. Canopy Temperature as a Key Physiological Trait to Improve Yield Prediction under Water Restrictions in Potato. Agronomy 2021, 11, 1436. https://doi.org/10.3390/agronomy11071436
Ninanya J, Ramírez DA, Rinza J, Silva-Díaz C, Cervantes M, García J, Quiroz R. Canopy Temperature as a Key Physiological Trait to Improve Yield Prediction under Water Restrictions in Potato. Agronomy. 2021; 11(7):1436. https://doi.org/10.3390/agronomy11071436
Chicago/Turabian StyleNinanya, Johan, David A. Ramírez, Javier Rinza, Cecilia Silva-Díaz, Marcelo Cervantes, Jerónimo García, and Roberto Quiroz. 2021. "Canopy Temperature as a Key Physiological Trait to Improve Yield Prediction under Water Restrictions in Potato" Agronomy 11, no. 7: 1436. https://doi.org/10.3390/agronomy11071436
APA StyleNinanya, J., Ramírez, D. A., Rinza, J., Silva-Díaz, C., Cervantes, M., García, J., & Quiroz, R. (2021). Canopy Temperature as a Key Physiological Trait to Improve Yield Prediction under Water Restrictions in Potato. Agronomy, 11(7), 1436. https://doi.org/10.3390/agronomy11071436











