Capturing GEI Patterns for Quality Traits in Biparental Wheat Populations
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Description of Field Trials
2.3. Phenotyping
2.4. Statistical Analysis
3. Results
3.1. The First Stage of the Analysis
3.2. Transgressive Segregation in Quality Traits
3.3. Phenotypic Correlations between Quality Traits
3.4. Selection of the Appropriate AMMI Model
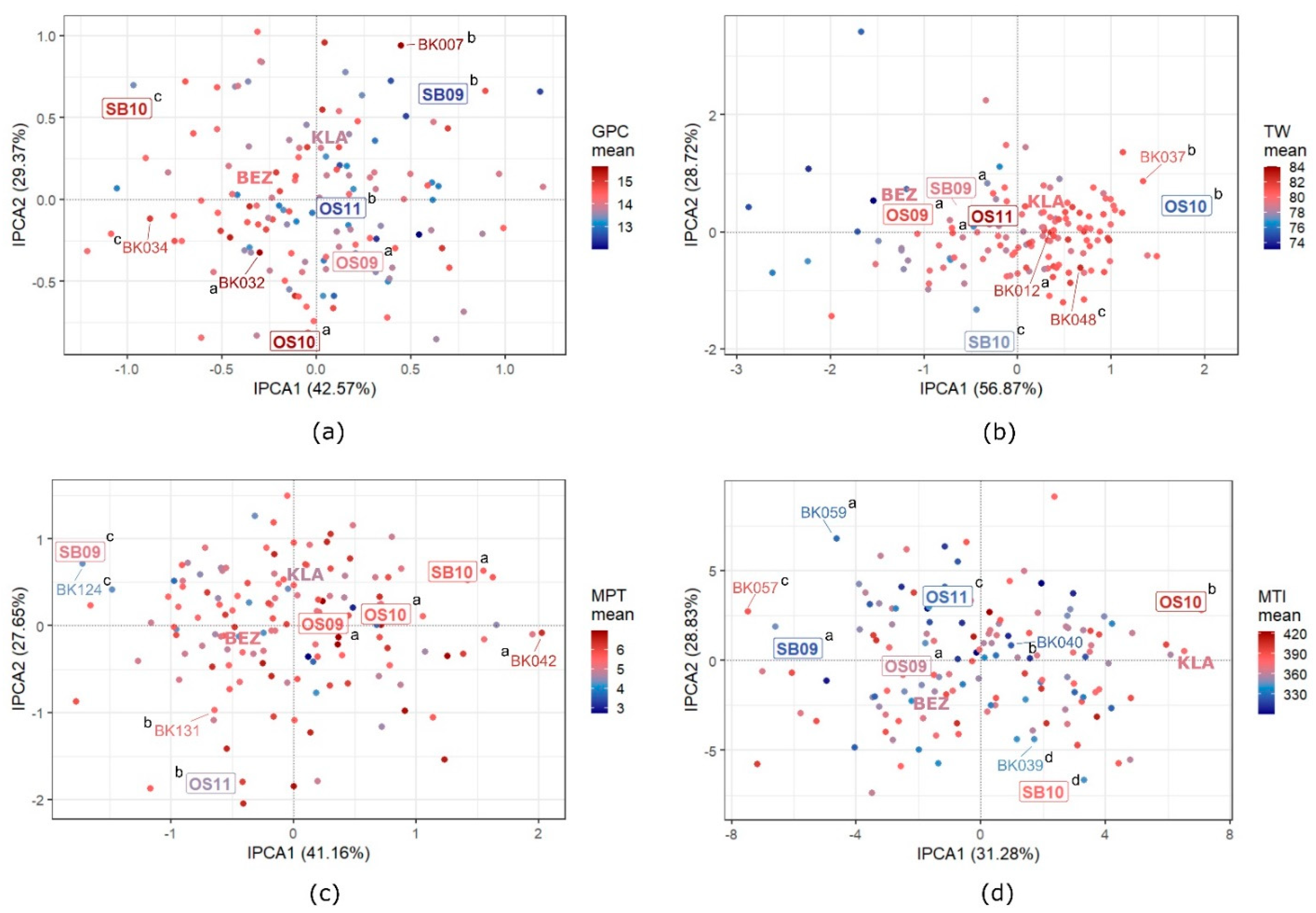
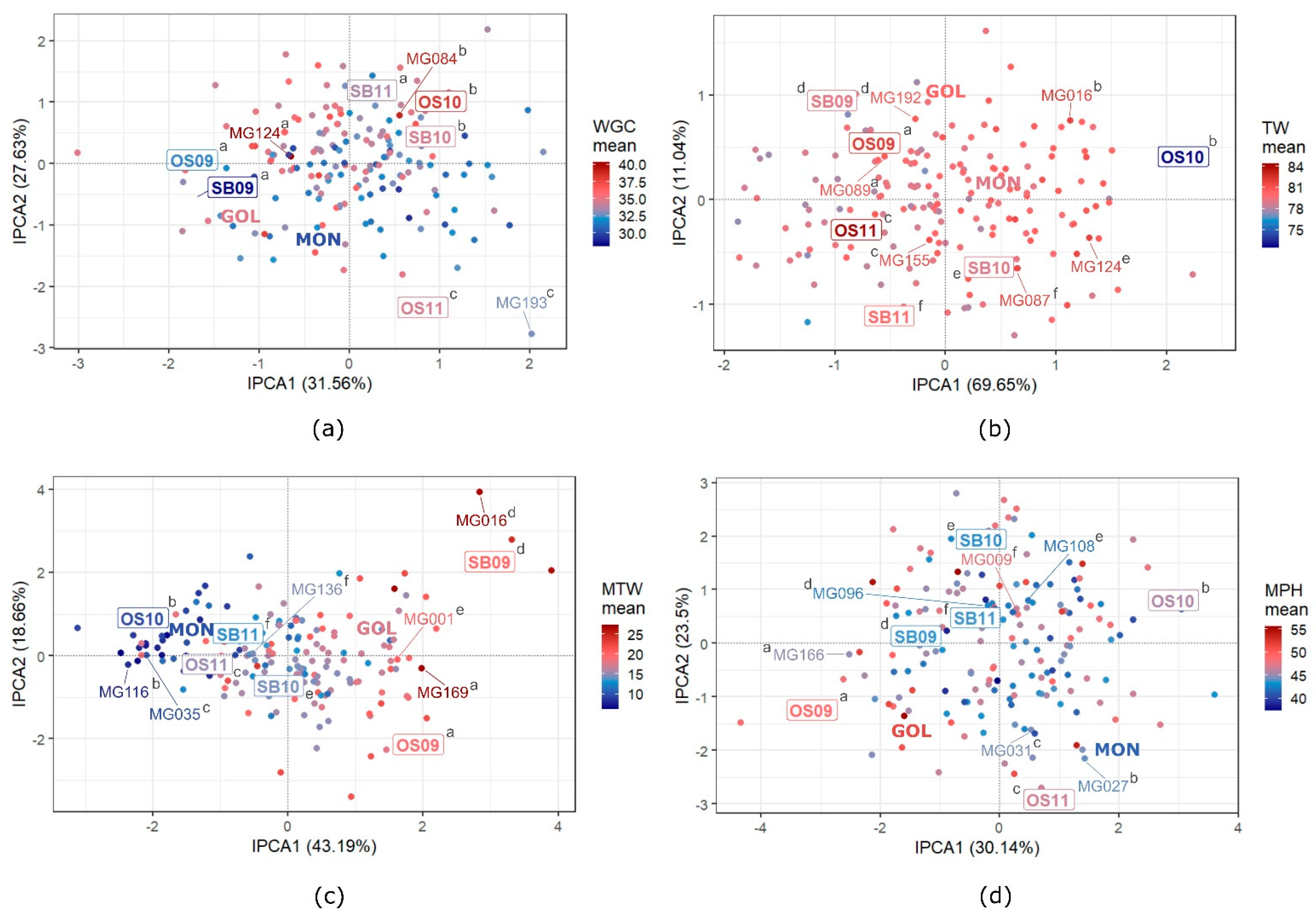
3.5. GEI Patterns in Quality Traits
4. Discussion
4.1. Transgressive Segregation and Phenotypic Correlations among Quality Traits
4.2. Selection of the Appropriate AMMI Model
4.3. GEI Patterns
4.4. Consequences for a Breeding Program
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bordes, J.; Ravel, C.; Le Gouis, J.; Lapierre, A.; Charmet, G.; Balfourier, F. Use of a global wheat core collection for association analysis of flour and dough quality traits. J. Cereal Sci. 2011, 54, 137–147. [Google Scholar] [CrossRef]
- Payne, P.I. Genetics of wheat storage proteins and the effect of allelic variation on bread-making quality. Annu. Rev. Plant Physiol. 1987, 38, 141–153. [Google Scholar] [CrossRef]
- Shewry, P.R. Improving the Protein Content and Quality of Temperate Cereals: Wheat, Barley and Rye. In Impacts of Agriculture on Human Health and Nutrition; Cakmak, I., Welch, R., Eds.; USDA, ARS, U.S. Plant, Soil and Nutrition Laboratory, Cornell University: Ithaca, NY, USA, 2004; Volume 2. [Google Scholar]
- Kristensen, P.S.; Jahoor, A.; Andersen, J.R.; Cericola, F.; Orabi, J.; Janss, L.L.; Jensen, J. Genome-wide association studies and comparison of models and cross-validation strategies for genomic prediction of quality traits in advanced winter wheat breeding lines. Front. Plant Sci. 2018, 9, 69. [Google Scholar] [CrossRef]
- Laidig, F.; Piepho, H.P.; Rentel, D.; Drobek, T.; Meyer, U.; Huesken, A. Breeding progress, environmental variation and correlation of winter wheat yield and quality traits in German official variety trials and on-farm during 1983–2014. Theor. Appl. Genet. 2017, 130, 223–245. [Google Scholar] [CrossRef]
- Elli, L.; Villalta, D.; Roncoroni, L.; Barisani, D.; Ferrero, S.; Pellegrini, N.; Bardella, M.T.; Valiante, F.; Tomba, C.; Carroccio, A.; et al. Nomenclature and diagnosis of gluten-related disorders: A position statement by the Italian Association of Hospital Gastroenterologists and Endoscopists (AIGO). Dig. Liver Dis. 2017, 49, 138–146. [Google Scholar] [CrossRef]
- Shewry, P.R.; Tatham, A.S.; Barro, F.; Barcelo, P.; Lazzeri, P. Biotechnology of breadmaking: Unraveling and manipulating the multi-protein gluten complex. Bio/Technology 1995, 13, 1185–1190. [Google Scholar] [CrossRef]
- Payne, P.I.; Nightingale, M.A.; Krattiger, A.F.; Holt, L.M. The Relationship between HMW Glutenin Subunit Composition and the Bread-making Quality of British-grown Wheat Varieties. J. Sci. Food Agric. 1987, 40, 51–65. [Google Scholar] [CrossRef]
- MacRitchie, F. Physicochemical properties of wheat proteins in relation to functionality. Adv. Food Nutr. Res. 1992, 36, 1–87. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, Y.; Gowda, M.; Longin, C.F.H.; Reif, J.C.; Mette, M.F. Predicting hybrid performances for quality traits through genomic-assisted approaches in Central European wheat. PLoS ONE 2016, 11, e0158635. [Google Scholar] [CrossRef] [PubMed]
- Lado, B.; Vázquez, D.; Quincke, M.; Silva, P.; Aguilar, I.; Gutiérrez, L. Resource allocation optimization with multi-trait genomic prediction for bread wheat (Triticum aestivum L.) baking quality. Theor. Appl. Genet. 2018, 131, 2719–2731. [Google Scholar] [CrossRef]
- Hook, S.C.W. Specific weight and wheat quality. J. Sci. Food Agric. 1984, 35, 1136–1141. [Google Scholar] [CrossRef]
- Békés, F. New aspects in quality related wheat research: 1. Challenges and achievements. Cereal Res. Commun. 2012, 40, 159–184. [Google Scholar] [CrossRef]
- Hayes, B.J.; Panozzo, J.; Walker, C.K.; Choy, A.L.; Kant, S.; Wong, D.; Tibbits, J.; Daetwyler, H.D.; Rochfort, S.; Hayden, M.J.; et al. Accelerating wheat breeding for end-use quality with multi-trait genomic predictions incorporating near infrared and nuclear magnetic resonance-derived phenotypes. Theor. Appl. Genet. 2017, 130, 2505–2519. [Google Scholar] [CrossRef] [PubMed]
- Graybosch, R.A.; Peterson, C.J.; Hareland, G.A.; Shelton, D.R.; Olewnik, M.C.; He, H.; Stearns, M.M. Relationships between small-scale wheat quality assays and commercial test bakes. Cereal Chem. 1999, 76, 428–433. [Google Scholar] [CrossRef]
- Swanson, C. Testing of the quality of flour by the recording dough mixer. Cereal Chem. 1993, 10, 1–29. [Google Scholar]
- Johnson, J.A.; Swanson, C.O.; Bayfield, E.G. The correlation of mixogram with baking results. Cereal Chem. 1943, 20, 625–644. [Google Scholar]
- Gras, P.W.; O’Brien, L. Application of a 2-gram mixograph to early generation selection for dough strength. Cereal Chem. 1992, 69, 254–257. [Google Scholar]
- Bustos-Korts, D.; Romagosa, I.; Borràs-Gelonch, G.; Slafer, G.; Eeuwijk, F. Genotype by Environment Interaction and Adaptation. In Crop Science. Encyclopedia of Sustainability Science and Technology Series; Savin, R., Slafer, G., Eds.; Springer: New York, NY, USA, 2019; pp. 29–71. [Google Scholar]
- Grausgruber, H.; Oberforster, M.; Werteker, M.; Ruckenbauer, P.; Vollmann, J. Stability of quality traits in Austrian-grown winter wheats. Field Crop. Res. 2000, 66, 257–267. [Google Scholar] [CrossRef]
- Robert, N.; Denis, J.B. Stability of baking quality in bread wheat using several statistical parameters. Theor. Appl. Genet. 1996, 93, 172–178. [Google Scholar] [CrossRef]
- Battenfield, S.D.; Guzmán, C.; Chris Gaynor, R.; Singh, R.P.; Peña, R.J.; Dreisigacker, S.; Fritz, A.K.; Poland, J.A. Genomic selection for processing and end-use quality traits in the CIMMYT spring bread wheat breeding program. Plant Genome 2016, 9, 1–12. [Google Scholar] [CrossRef]
- Peterson, C.J.; Graybosch, R.A.; Shelton, D.R.; Baenziger, P.S. Baking quality of hard winter wheat: Response of cultivars to environment in the Great Plains. Euphytica 1998, 100, 157–162. [Google Scholar] [CrossRef]
- Simmonds, N.W. The relation between yield and protein in cereal grain. J. Sci. Food Agric. 1995, 67, 309–315. [Google Scholar] [CrossRef]
- Groos, C.; Robert, N.; Bervas, E.; Charmet, G. Genetic analysis of grain protein-content, grain yield and thousand-kernel weight in bread wheat. Theor. Appl. Genet. 2003, 106, 1032–1040. [Google Scholar] [CrossRef]
- Šimić, G.; Horvat, D.; Jurković, Z.; Drezner, G.; Novoselović, D.; Dvojković, K. The genotype effect on the ratio of wet gluten content to total wheat grain protein. J. Cent. Eur. Agric. 2006, 7, 13–18. [Google Scholar] [CrossRef]
- Williams, R.M.; O’Brien, L.; Eagles, H.A.; Solah, V.A.; Jayasena, V. The influences of genotype, environment, and genotype × environment interaction on wheat quality. Aust. J. Agric. Res. 2008, 59, 95–111. [Google Scholar] [CrossRef]
- Hernández-Espinosa, N.; Mondal, S.; Autrique, E.; Gonzalez-Santoyo, H.; Crossa, J.; Huerta-Espino, J.; Singh, R.P.; Guzmán, C. Milling, processing and end-use quality traits of CIMMYT spring bread wheat germplasm under drought and heat stress. Field Crop. Res. 2018, 215, 104–112. [Google Scholar] [CrossRef]
- Drezner, G.; Gunjača, J.; Novoselović, D.; Horvat, D. Interpretation of GEI effect analysis for some agronomic and quality traits in ten winter wheat (Triticum aestivum L.) cultivars. Cereal Res. Commun. 2010, 38, 259–265. [Google Scholar] [CrossRef]
- Gauch, H.G. Statistical Analysis of Regional Yield Trials: AMMI Analysis of Factorial Designs; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Mani, E. Molecular Dissection of Breadmaking Quality in Wheat (Triticum aestivum L.). Ph.D. Thesis, University of Pune, Pune, India, October 2007. [Google Scholar]
- Mut, Z.; Aydin, N.; Orhan Bayramoglu, H.; Ozean, H. Stability of some quality traits in bread wheat (Triticum aestivum) genotypes. J. Environ. Biol. 2010, 31, 489–495. [Google Scholar]
- Khan, M.A.U.; Mohammad, F.; Khan, F.U.; Ahmad, S.; Ullah, I. Additive main effect and multiplicative interaction analysis for grain yield in bread wheat. J. Anim. Plant Sci. 2020, 30, 677–684. [Google Scholar] [CrossRef]
- Sardouei-Nasab, S.; Mohammadi-Nejad, G.; Nakhoda, B. Yield stability in bread wheat germplasm across drought stress and non-stress conditions. Agron. J. 2019, 111, 175–181. [Google Scholar] [CrossRef]
- Khan, M.A.U.; Mohammad, F.; Khan, F.U.; Ahmad, S.; Raza, M.A.; Kamal, T. Comparison among different stability models for yield in bread wheat. Sarhad J. Agric. 2020, 36, 282–290. [Google Scholar] [CrossRef]
- Rodriguez, M.; Rau, D.; Papa, R.; Attene, G. Genotype by environment interactions in barley (Hordeum vulgare L.): Different responses of landraces, recombinant inbred lines and varieties to Mediterranean environment. Euphytica 2008, 163, 231–247. [Google Scholar] [CrossRef]
- Groos, C.; Bervas, E.; Charmet, G. Genetic analysis of grain protein content, grain hardness and dough rheology in a hard X hard bread wheat progeny. J. Cereal Sci. 2004, 40, 93–100. [Google Scholar] [CrossRef]
- Krishnappa, G.; Ahlawat, A.K.; Shukla, R.B.; Singh, S.K.; Singh, S.K.; Singh, A.M.; Singh, G.P. Multi-environment analysis of grain quality traits in recombinant inbred lines of a biparental cross in bread wheat (Triticum aestivum L.). Cereal Res. Commun. 2019, 47, 334–344. [Google Scholar] [CrossRef]
- Elangovan, M.; Dholakia, B.B.; Rai, R.; Lagu, M.D.; Tiwari, R.; Gupta, R.K.; Gupta, V.S. Mapping QTL associated with agronomic traits in bread wheat (Triticum aestivum L.). J Wheat Res. 2011, 3, 14–23. [Google Scholar]
- Prashant, R.; Mani, E.; Rai, R.; Gupta, R.K.; Tiwari, R.; Dholakia, B.; Oak, M.; Röder, M.; Kadoo, N.; Gupta, V. Genotype × environment interactions and QTL clusters underlying dough rheology traits in Triticum aestivum L. J. Cereal Sci. 2015, 64, 82–91. [Google Scholar] [CrossRef]
- Elangovan, M.; Rai, R.; Dholakia, B.B.; Lagu, M.D.; Tiwari, R.; Gupta, R.K.; Rao, V.S.; Röder, M.S.; Gupta, V.S. Molecular genetic mapping of quantitative trait loci associated with loaf volume in hexaploid wheat (Triticum aestivum). J. Cereal Sci. 2008, 47, 587–598. [Google Scholar] [CrossRef]
- Horvat, D.; Drezner, G.; Jurković, Z.; Šimić, G.; Magdić, D.; Dvojković, K. The importance of high-molecular-weight glutenin subunits for wheat quality evaluation. Poljoprivreda 2006, 12, 53–57. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: http://www.R-project.org (accessed on 20 May 2021).
- Butler, D.G.; Cullis, B.R.; Gilmour, A.R.; Gogel, B.J.; Thompson, R. ASReml-R Reference Manual Version 4; VSN International Ltd.: Hemel Hempstead, UK, 2017. [Google Scholar]
- Brien, M.C. asremlPlus: Augments ‘ASReml-R’ in Fitting Mixed Models and Packages Generally in Exploring Prediction Differences. 2021. R Package Version 4.2-32. Available online: https://cran.r-project.org/web/packages/asremlPlus/index.html (accessed on 20 May 2021).
- Gauch, H.G. Model Selection and Validation for Yield Trials with Interaction. Biometrics 1988, 44, 705–715. [Google Scholar] [CrossRef]
- Gauch, H.G. A simple protocol for AMMI analysis of yield trials. Crop Sci. 2013, 53, 1860–1869. [Google Scholar] [CrossRef]
- Paderewski, J. An R function for imputation of missing cells in two-way data sets by EM-AMMI algorithm. Commun. Biometry Crop Sci. 2013, 8, 60–69. [Google Scholar]
- Forkman, J.; Piepho, H.P. Parametric bootstrap methods for testing multiplicative terms in GGE and AMMI models. Biometrics 2014, 70, 639–647. [Google Scholar] [CrossRef]
- Piepho, H.P. Robustness of statistical tests for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trials. Theor. Appl. Genet. 1995, 90, 438–443. [Google Scholar] [CrossRef]
- Tarakanovas, P.; Ruzgas, V. Additive main effect and multiplicative interaction analysis of grain yield of wheat varieties in Lithuania. Agron. Res. 2006, 4, 91–98. [Google Scholar]
- Wei, T.; Simko, V. corrplot: Visualization of a Correlation Matrix 2017. R Package Version 0.84. Available online: https://cran.r-project.org/web/packages/corrplot/index.html (accessed on 20 May 2021).
- Harrell, F.E. Hmisc: Harrell Miscellaneous. 2021. R Package Version 4.4-2. Available online: https://CRAN.R-project.org/package=Hmisc (accessed on 20 May 2021).
- Wickham, H. Reshaping Data with the reshape Package. J. Stat. Softw. 2007, 21, 1–20. [Google Scholar] [CrossRef]
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation 2020. R Package Version 1.0.2. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 20 May 2021).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Slowikowski, K. ggrepel: Automatically Position Non-Overlapping Text Labels with “ggplot2” 2020. R Package Version 0.8.2. Available online: https://CRAN.R-project.org/package=ggrepel (accessed on 20 May 2021).
- Gollob, H.F. A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika 1968, 33, 73–115. [Google Scholar] [CrossRef] [PubMed]
- Turner, A.S.; Bradburne, R.P.; Fish, L.; Snape, J.W. New quantitative trait loci influencing grain texture and protein content in bread wheat. J. Cereal Sci. 2004, 40, 51–60. [Google Scholar] [CrossRef]
- Singh, B.; Singh, N. Physico-chemical, water and oil absorption and thermal properties of gluten isolated from different indian wheat cultivars. J. Food Sci. Technol. 2006, 43, 251–255. [Google Scholar]
- Campbell, K.G.; Finney, P.L.; Bergman, C.J.; Gualberto, D.G.; Anderson, J.A.; Giroux, M.J.; Siritunga, D.; Zhug, J.; Gendre, F.; Roué, C.; et al. Quantitative trait loci associated with milling and baking quality in a soft × hard wheat cross. Crop Sci. 2001, 41, 1275–1285. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Xiao, Y.; Yan, J.; Zhang, Y.; Zhang, Y.; Ma, C.; Xia, X.; He, Z. QTL mapping for milling, gluten quality, and flour pasting properties in a recombinant inbred line population derived from a Chinese soft × hard wheat cross. Crop Pasture Sci. 2009, 60, 587–597. [Google Scholar] [CrossRef]
- Zheng, F.; Deng, Z.; Shi, C.; Zhang, X.; Tian, J. QTL Mapping for Dough Mixing Characteristics in a Recombinant Inbred Population Derived from a Waxy × Strong Gluten Wheat (Triticum aestivum L.). J. Integr. Agric. 2013, 12, 951–961. [Google Scholar] [CrossRef]
- Gauch, H.G.; Zobel, R.W. Imputing missing yield trial data. Theor. Appl. Genet. 1990, 79, 753–761. [Google Scholar] [CrossRef] [PubMed]
- Paderewski, J.; Rodrigues, P.C. The Usefulness of EM-AMMI to Study the Influence of Missing Data Pattern and Application to Polish Post-Registration Winter Wheat Data. Aust. J. Crop Sci. 2014, 8, 640–645. [Google Scholar]
- Arciniegas-Alarcón, S.; García-Peña, M.; Rodrigues, P.C. New Multiple Imputation Methods for Genotype-by-Environment Data That Combine Singular Value Decomposition and Jackknife Resampling or Weighting Schemes. Comput. Electron. Agric. 2020, 176, 105617. [Google Scholar] [CrossRef]
- Echeverry-Solarte, M.; Kumar, A.; Kianian, S.; Simsek, S.; Alamri, M.S.; Mantovani, E.E.; McClean, P.E.; Deckard, E.L.; Elias, E.; Schatz, B.; et al. New QTL alleles for quality-related traits in spring wheat revealed by RIL population derived from supernumerary × non-supernumerary spikelet genotypes. Theor. Appl. Genet. 2015, 128, 893–912. [Google Scholar] [CrossRef]
- Goel, S.; Singh, K.; Singh, B.; Grewal, S.; Dwivedi, N.; Alqarawi, A.A.; Abd Allah, E.F.; Ahmad, P.; Singh, N.K. Analysis of genetic control and QTL mapping of essential wheat grain quality traits in a recombinant inbred population. PLoS ONE 2019, 14, e0200669. [Google Scholar] [CrossRef]
- Jin, H.; Wen, W.; Liu, J.; Zhai, S.; Zhang, Y.; Yan, J.; Liu, Z.; Xia, X.; He, Z. Genome-wide QTL mapping for wheat processing quality parameters in a Gaocheng 8901/Zhoumai 16 recombinant inbred line population. Front. Plant Sci. 2016, 7, 1032. [Google Scholar] [CrossRef] [PubMed]
- Merrick, L.F.; Lyon, S.R.; Balow, K.A.; Murphy, K.M.; Jones, S.S.; Carter, A.H. Utilization of evolutionary plant breeding increases stability and adaptation of winter wheat across diverse precipitation zones. Sustainability 2020, 12, 9728. [Google Scholar] [CrossRef]
- Sjoberg, S.M.; Carter, A.H.; Steber, C.M.; Garland-Campbell, K.A. Unraveling complex traits in wheat: Approaches for analyzing genotype × environment interactions in a multienvironment study of falling numbers. Crop Sci. 2020, 60, 3013–3026. [Google Scholar] [CrossRef]

| Trait | Parental Cultivars Mean | RILs | Positive Transgressive Segregants 3 | Negative Transgressive Segregants 4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| P1 1 | P2 2 | Min | Mean | Max | N | % | N | % | |
| BK population | |||||||||
| GPC 5 | 14.3 | 13.9 | 10.6 | 14.0 | 17.5 | 55 | 38.5 | 60 | 42.0 |
| WGC | 34.7 | 34.1 | 20.5 | 34.1 | 43.9 | 61 | 42.7 | 62 | 43.4 |
| TW | 79.1 | 79.8 | 64.8 | 79.5 | 86.9 | 71 | 49.7 | 46 | 32.2 |
| MPT | 5.2 | 4.6 | 1.3 | 5.4 | 10.0 | 86 | 60.1 | 19 | 13.3 |
| MTW | 20.1 | 18.8 | 10.8 | 21.3 | 35.1 | 111 | 77.6 | 8 | 5.6 |
| MTI | 359.6 | 367.2 | 237.3 | 361.3 | 504.9 | 65 | 45.5 | 66 | 46.2 |
| MPH | 41.6 | 42.4 | 25.5 | 41.8 | 58.9 | 66 | 46.2 | 67 | 46.9 |
| MG population | |||||||||
| GPC | 13.0 | 14.1 | 11.0 | 13.8 | 17.3 | 56 | 32.4 | 21 | 12.1 |
| WGC | 29.9 | 35.3 | 21.8 | 33.5 | 43.9 | 27 | 15.6 | 5 | 2.9 |
| TW | 79.3 | 80.4 | 65.7 | 79.6 | 86.2 | 46 | 26.6 | 70 | 40.5 |
| MPT | 4.6 | 4.9 | 1.6 | 4.8 | 9.1 | 95 | 54.9 | 63 | 36.4 |
| MTW | 9.3 | 17.9 | 4.4 | 15.2 | 45.9 | 46 | 26.6 | 19 | 11.0 |
| MTI | 347.5 | 438.8 | 285.5 | 382.8 | 527.8 | 3 | 1.7 | 10 | 5.8 |
| MPH | 41.5 | 52.2 | 30.8 | 45.4 | 73.2 | 5 | 2.9 | 18 | 10.4 |
| IPCA | Sum of Squares | Simple Bootstrap | FR-Test | Cross-Validation | ||||
|---|---|---|---|---|---|---|---|---|
| IPCA SS | % | Total % | T | p Value | F | p Value | RMSPD | |
| GPC | ||||||||
| 0 | 14.7 | |||||||
| 1 | 58.0 | 42.6 | 42.6 | 0.43 | 0.000 | 2.16 | 0.000 | 21.1 |
| 2 | 40.0 | 29.4 | 71.9 | 0.51 | 0.000 | 2.05 | 0.000 | 49.9 |
| 3 | 21.6 | 15.8 | 87.8 | 0.57 | 0.315 | 1.27 | 0.076 | 52.0 |
| 4 | 16.7 | 12.3 | 100.0 | |||||
| WGC | ||||||||
| 0 | 44.4 | |||||||
| 1 | 524.7 | 42.2 | 42.2 | 0.42 | 0.000 | 2.13 | 0.000 | 54.1 |
| 2 | 343.1 | 27.6 | 69.8 | 0.48 | 0.001 | 1.79 | 0.000 | 105.9 |
| 3 | 192.8 | 15.5 | 85.3 | 0.51 | 0.955 | 1.04 | 0.413 | 197.9 |
| 4 | 183.2 | 14.7 | 100.0 | |||||
| TW | ||||||||
| 0 | 39.6 | |||||||
| 1 | 562.4 | 56.9 | 56.9 | 0.57 | 0.000 | 3.85 | 0.000 | 94.1 |
| 2 | 284.1 | 28.7 | 85.6 | 0.67 | 0.000 | 3.91 | 0.000 | 97.7 |
| 3 | 89.9 | 9.1 | 94.7 | 0.63 | 0.007 | 1.69 | 0.001 | 118.0 |
| 4 | 52.5 | 5.3 | 100.0 | |||||
| MPT | ||||||||
| 0 | 39.3 | |||||||
| 1 | 400.2 | 41.2 | 41.2 | 0.41 | 0.000 | 2.05 | 0.000 | 46.9 |
| 2 | 268.8 | 27.7 | 68.8 | 0.47 | 0.001 | 1.73 | 0.000 | 102.3 |
| 3 | 209.9 | 21.6 | 90.4 | 0.69 | 0.000 | 2.23 | 0.000 | 108.8 |
| 4 | 93.3 | 9.6 | 100.0 | |||||
| MTW | ||||||||
| 0 | 74.1 | |||||||
| 1 | 1774.3 | 48.7 | 48.7 | 0.48 | 0.000 | 2.68 | 0.000 | 102.0 |
| 2 | 800.3 | 22.0 | 70.7 | 0.43 | 0.061 | 1.46 | 0.003 | 119.9 |
| 3 | 571.6 | 15.7 | 86.4 | 0.54 | 0.684 | 1.14 | 0.215 | 235.5 |
| 4 | 496.8 | 13.6 | 100.0 | |||||
| MTI | ||||||||
| 0 | 796.8 | |||||||
| 1 | 126404.6 | 31.3 | 31.3 | 0.32 | 0.255 | 1.37 | 0.009 | 1043.1 |
| 2 | 116513.4 | 28.8 | 60.1 | 0.41 | 0.210 | 1.35 | 0.016 | 1983.6 |
| 3 | 94460.8 | 23.4 | 83.5 | 0.59 | 0.120 | 1.40 | 0.024 | 133.1 |
| 4 | 66703.0 | 16.5 | 100.0 | |||||
| MPH | ||||||||
| 0 | 102.6 | |||||||
| 1 | 1999.9 | 30.2 | 30.2 | 0.30 | 0.606 | 1.27 | 0.036 | 128.3 |
| 2 | 1866.4 | 28.1 | 58.3 | 0.40 | 0.296 | 1.32 | 0.026 | 157.6 |
| 3 | 1466.6 | 22.1 | 80.4 | 0.53 | 0.792 | 1.11 | 0.275 | 252.0 |
| 4 | 1300.9 | 19.6 | 100.0 | |||||
| IPCA | Sum of Squares | Simple Bootstrap | FR-Test | Cross-Validation | ||||
|---|---|---|---|---|---|---|---|---|
| IPCA SS | % | Total % | T | p Value | F | p Value | RMSPD | |
| GPC | ||||||||
| 0 | 20.7 | |||||||
| 1 | 108.2 | 36.6 | 36.6 | 0.37 | 0.000 | 2.25 | 0.000 | 42.2 |
| 2 | 71.9 | 24.4 | 61.0 | 0.38 | 0.000 | 1.83 | 0.000 | 69.2 |
| 3 | 45.1 | 15.3 | 76.3 | 0.39 | 0.376 | 1.26 | 0.035 | 84.0 |
| 4 | 40.5 | 13.7 | 90.0 | 0.58 | 0.124 | 1.35 | 0.024 | 75.1 |
| 5 | 29.6 | 10.0 | 100.0 | |||||
| WGC | ||||||||
| 0 | 62.8 | |||||||
| 1 | 855.4 | 31.6 | 31.5 | 0.32 | 0.000 | 1.79 | 0.000 | 69.3 |
| 2 | 748.9 | 27.6 | 59.2 | 0.40 | 0.000 | 1.99 | 0.000 | 178.6 |
| 3 | 432.3 | 15.9 | 75.1 | 0.39 | 0.385 | 1.26 | 0.036 | 295.1 |
| 4 | 405.4 | 15.0 | 90.1 | 0.60 | 0.028 | 1.49 | 0.005 | 262.5 |
| 5 | 268.4 | 9.9 | 100.0 | |||||
| TW | ||||||||
| 0 | 44.7 | |||||||
| 1 | 957.0 | 69.7 | 69.7 | 0.70 | 0.000 | 8.92 | 0.000 | 48.6 |
| 2 | 151.6 | 11.0 | 80.7 | 0.36 | 0.001 | 1.68 | 0.000 | 69.2 |
| 3 | 116.9 | 8.5 | 89.2 | 0.44 | 0.009 | 1.55 | 0.000 | 90.3 |
| 4 | 77.3 | 5.6 | 94.8 | 0.52 | 0.864 | 1.07 | 0.319 | 115.7 |
| 5 | 71.1 | 5.2 | 100.0 | |||||
| MPT | ||||||||
| 0 | 35.6 | |||||||
| 1 | 352.0 | 39.8 | 39.8 | 0.40 | 0.000 | 1.93 | 0.000 | 50.4 |
| 2 | 154.0 | 17.4 | 57.2 | 0.29 | 0.817 | 0.80 | 0.953 | 162.4 |
| 3 | 149.7 | 16.9 | 74.1 | 0.40 | 0.302 | 0.65 | 0.998 | 185.4 |
| 4 | 128.2 | 14.5 | 88.6 | 0.56 | 0.283 | 2.54 | 0.000 | 175.8 |
| 5 | 100.6 | 11.4 | 100.0 | |||||
| MTW | ||||||||
| 0 | 114.4 | |||||||
| 1 | 3996.4 | 43.2 | 43.2 | 0.43 | 0.000 | 2.24 | 0.000 | 114.3 |
| 2 | 1726.7 | 18.7 | 61.9 | 0.31 | 0.402 | 0.87 | 0.858 | 385.1 |
| 3 | 1391.4 | 15.0 | 76.9 | 0.39 | 0.332 | 0.64 | 0.998 | 336.6 |
| 4 | 1165.1 | 12.6 | 89.5 | 0.54 | 0.563 | 2.34 | 0.000 | 454.4 |
| 5 | 973.6 | 10.5 | 100.0 | |||||
| MTI | ||||||||
| 0 | 1078.0 | |||||||
| 1 | 255111.6 | 32.0 | 32.0 | 0.32 | 0.000 | 1.38 | 0.003 | 1182.6 |
| 2 | 195556.4 | 24.5 | 56.5 | 0.36 | 0.001 | 1.11 | 0.211 | 1473.6 |
| 3 | 137022.0 | 17.2 | 73.7 | 0.40 | 0.311 | 0.65 | 0.998 | 2656.3 |
| 4 | 114022.2 | 14.3 | 88.0 | 0.54 | 0.509 | 2.38 | 0.000 | 2750.6 |
| 5 | 95698.0 | 12.0 | 100.0 | |||||
| MPH | ||||||||
| 0 | 150.9 | |||||||
| 1 | 4709.2 | 30.1 | 30.1 | 0.30 | 0.001 | 1.26 | 0.025 | 172.8 |
| 2 | 3671.7 | 23.5 | 53.6 | 0.34 | 0.027 | 1.00 | 0.506 | 217.1 |
| 3 | 2779.2 | 17.8 | 71.4 | 0.38 | 0.535 | 0.61 | 0.999 | 494.6 |
| 4 | 2562.1 | 16.4 | 87.8 | 0.57 | 0.155 | 2.68 | 0.000 | 684.3 |
| 5 | 1903.4 | 12.2 | 100.0 | |||||
| Trait | BK Population | MG Population | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Contribution to Total SS (%) | Contribution to GEI (%) | Contribution to Total SS (%) | Contribution to GEI (%) | |||||||
| G | E | GEI | IPCA1 | IPCA1 + IPCA2 | G | E | GEI | IPCA1 | IPCA1 + IPCA2 | |
| GPC | 17.7 | 74.9 | 7.4 | 42.6 | 71.9 | 36.1 | 42.3 | 21.6 | 36.6 | 61.0 |
| WGC | 17.6 | 75.9 | 6.5 | 42.2 | 69.8 | 24.7 | 59.7 | 15.7 | 31.6 | 59.2 |
| TW | 18.3 | 71.6 | 10.2 | 56.9 | 85.6 | 6.9 | 84.9 | 8.1 | 69.7 | 80.7 |
| MPT | 26.8 | 11.0 | 62.2 | 41.2 | 68.8 | 47.1 | 12.6 | 40.4 | 39.8 | 57.2 |
| MTW | 39.8 | 9.2 | 50.9 | 48.7 | 70.7 | 45.5 | 33.7 | 20.8 | 43.2 | 61.9 |
| MTI | 29.9 | 45.9 | 24.2 | 31.3 | 60.1 | 31.2 | 23.7 | 45.2 | 32.0 | 56.5 |
| MPH | 30.7 | 40.3 | 29.0 | 30.2 | 58.3 | 36.7 | 15.7 | 47.5 | 30.1 | 53.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plavšin, I.; Gunjača, J.; Šimek, R.; Novoselović, D. Capturing GEI Patterns for Quality Traits in Biparental Wheat Populations. Agronomy 2021, 11, 1022. https://doi.org/10.3390/agronomy11061022
Plavšin I, Gunjača J, Šimek R, Novoselović D. Capturing GEI Patterns for Quality Traits in Biparental Wheat Populations. Agronomy. 2021; 11(6):1022. https://doi.org/10.3390/agronomy11061022
Chicago/Turabian StylePlavšin, Ivana, Jerko Gunjača, Ruđer Šimek, and Dario Novoselović. 2021. "Capturing GEI Patterns for Quality Traits in Biparental Wheat Populations" Agronomy 11, no. 6: 1022. https://doi.org/10.3390/agronomy11061022
APA StylePlavšin, I., Gunjača, J., Šimek, R., & Novoselović, D. (2021). Capturing GEI Patterns for Quality Traits in Biparental Wheat Populations. Agronomy, 11(6), 1022. https://doi.org/10.3390/agronomy11061022






