Farm-Scale Crop Yield Prediction from Multi-Temporal Data Using Deep Hybrid Neural Networks
Abstract
:1. Introduction
1.1. Problem Statement and Hypotheses
- H1: Satellite images of farms and their surroundings can be used to accurately predict farm-scale crop yields.The first hypothesis assumes that farm-scale crop yield prediction is possible given the availability of enough per-farm crop yield data in Norway and satellite images. We will then do a comparative analysis with the preliminary experiment using weather data to predict crop yield production. This is a prerequisite for the subsequent hypotheses, assuming that satellite data contains independent variables affecting crop yield.
- H2: Accurate field boundaries along with satellite images increase crop yield accuracy significantly.This hypothesis assumes that differences between field conditions and management decisions in neighbouring farms can effect crop yield, which could be difficult for a model to learn unless accurate field boundaries are provided. If the hypothesis is correct, it may show that satellite images can explain differences in crop yield between neighbouring farms and that such models can aid in decision-making at a farm level.
- H3: Prediction accuracy can be further increased by combining satellite images and weather data.It is assumed that weather data and satellite images contain some different and independent variables. We hypothesise that a deep learning model can learn features from both datasets effectively and that this provides better performance than models using the two data sources separately. Higher prediction accuracy makes the prediction model more helpful in aiding farmers and subsequent industries.
- H4: It is possible to predict farm-scale crop yield earlier in the growing season with some reduced accuracy.The most accurate crop yield predictions will likely be when there is as much data available as possible, meaning at the end of the growing season. However, getting accurate estimates for deliveries earlier allows mills and administrative authorities to prepare in advance.
1.2. State-of-the-Art Approaches to Crop Yield Prediction
1.2.1. Origins and Early Use of Remote Spectral Observations
1.2.2. Deriving Values from Vegetation Indices
1.2.3. Machine Learning Applied to Remotely Sensed Data
2. Related Work
2.1. Norwegian Agriculture and Grain Production
2.2. Plant Growth Factors
- Light: Light is a component of photosynthesis and is essential for overall plant growth. In Norwegian crops, the duration of light is particularly relevant; according to Åssveen and Abrahamsen, the duration of light in a day (day length) is more influential than temperature as growth factors [33].
- Temperature: temperature affects growth in several ways. A rise in temperature triggers the germination process, so the temperature controls when the seedlings initially sprout [34]. The temperature also affects when crops such as winter wheat break dormancy to resume the growth in spring [35]. A typical measurement using temperature to estimate plant growth is the so-called sum degrees, meaning the sum of mean daily temperatures for the period. Crops will have different requirements for how much sum degrees are needed before it is ripe for harvest [31,32].
- Nutrition: plants need in total 17 essential chemical elements to grow. Three of the required components are found in air and water (carbon, hydrogen, and oxygen), while the soil must provide the rest [36]. Farmers can fertilise the soil, which adds materials containing nutrients to make these available to the plants. The roots absorb approximately 98% of the nutrients through soil water [37]. If the plant is under stress by extreme temperatures, drought, or low light, this can lower the plants’ ability to absorb nutrients efficiently [38].
2.3. Deep Learning Models in Crop Yield Prediction
2.3.1. Convolutional Neural Networks
2.3.2. Recurrent Neural Networks
2.4. Remote Sensing Technique in Crop Yield Prediction
Identifying Vegetation Index
- 1.
- The leaves of plants contain chlorophyll pigments, which is an essential factor in photosynthesis and ultimately makes the leaves green. Chlorophyll pigments make the leaves absorb a lot of the red and blue regions of the visible and near-infrared (VNIR) spectrum, but not in the green region. The number of chlorophyll pigments can indicate health in vegetation; thus, measuring the amount of reflection in the red spectrum can estimate vegetation health. Low reflectance in the red spectrum shows healthy vegetation.
- 2.
- Leaves have evolved to scatter solar radiation in the Near-Infrared (NIR) part of the spectrum, as it is difficult to extract the energy at these wavelengths efficiently (longer than 700 nm). This implies that healthy vegetation will have higher reflectance of NIR.
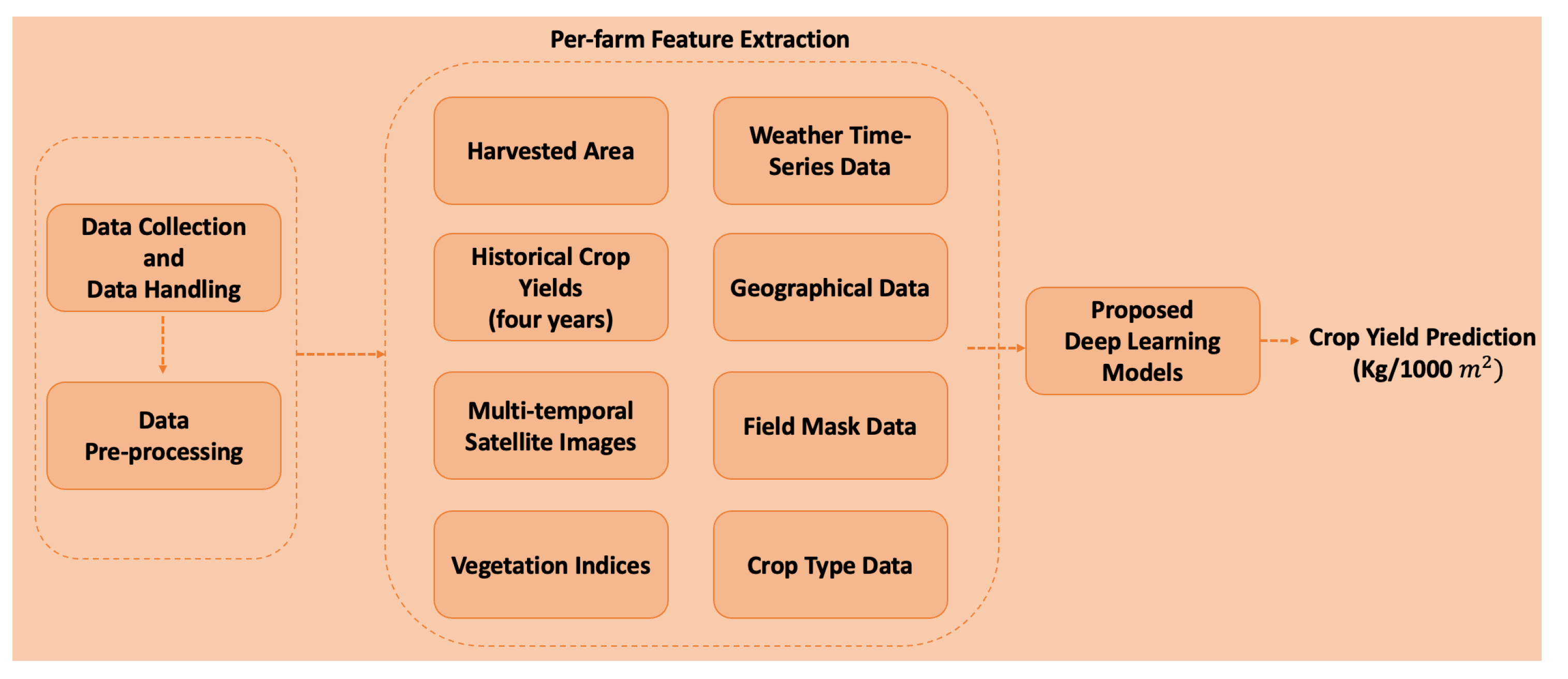
3. Material and Methods
3.1. Multi-Temporal Data Collection and Data Handling
3.1.1. Norwegian Agriculture Agency
3.1.2. Geographical Data
3.1.3. Weather Data
3.1.4. Satellite Image Data
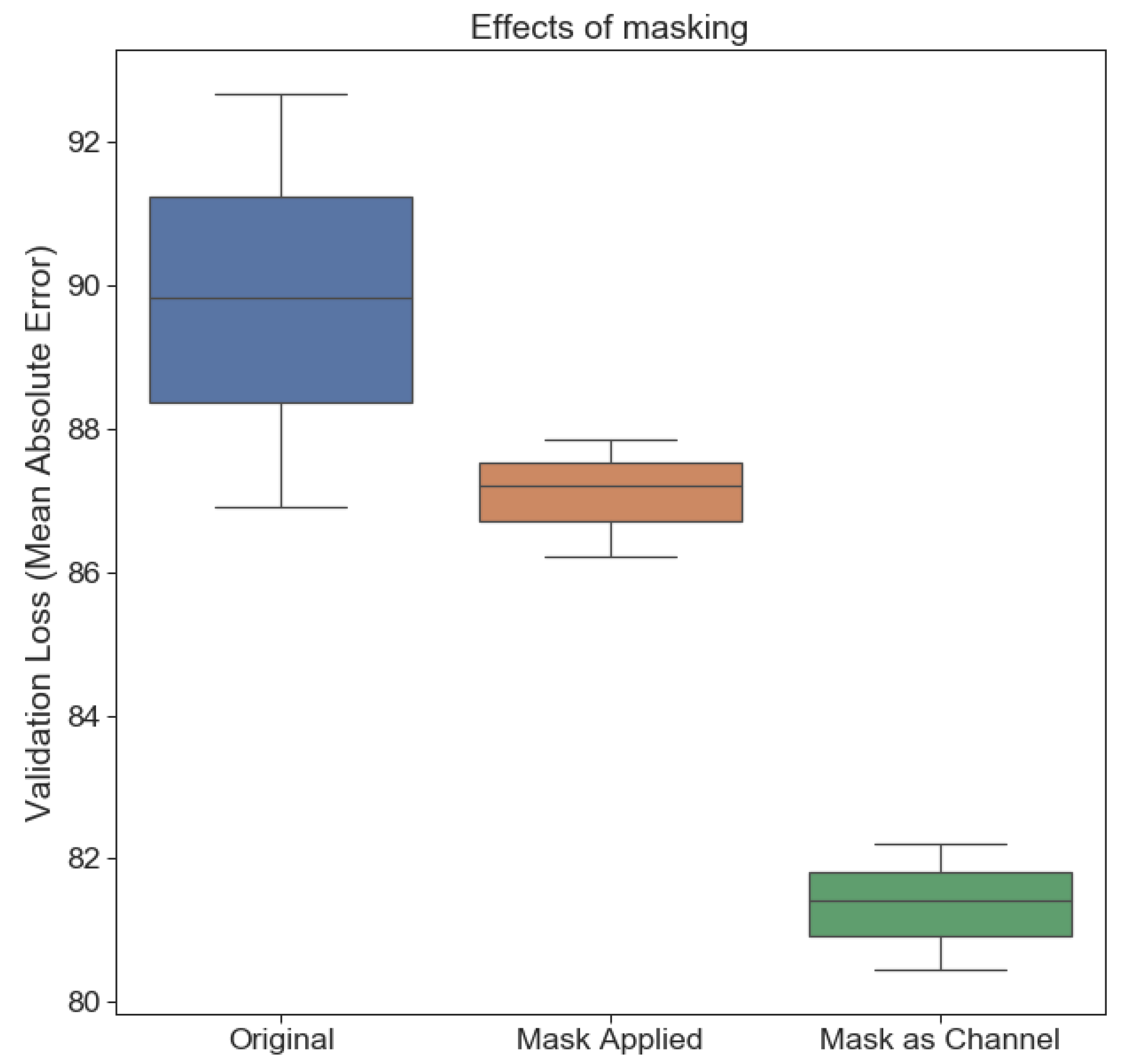
3.1.5. Data Handling Using Image Masking
- 1.
- Generating masks: the image masks are generated in three steps:
- Intersect the bounding box and the cultivated fields for each farm, leaving only the coordinates for cultivated fields inside the satellite images.
- Convert the geographic map coordinates of longitude and latitude to corresponding pixel locations of the satellite images. Given that the images are 100 × 100, the bounding boxes represent the borders of these images (top left 0,0 and bottom right 100,100). Convert each field point within the bounding box to pixel coordinates based on relative position within the bounding box.
- Generate a matrix of zeros and ones based on where the cultivated fields are located, resulting in a 100 × 100 matrix.
- 2.
- Applying masks: we implemented two methods of applying masks to the images; applied or added as a channel. In the first method, i.e., applied mask, the mask is multiplied by each image channel. The result is an image where only the cultivated fields remain, and all other pixel values are zero. In the second method, i.e., added a mask, the mask is added to the image as a separate channel. The mask channel will add some information to the image so that it can highlight which parts of the image are cultivated fields.
3.1.6. Time Spans of Satellite and Weather Data
3.2. Data Preprocessing
3.2.1. Normalisation
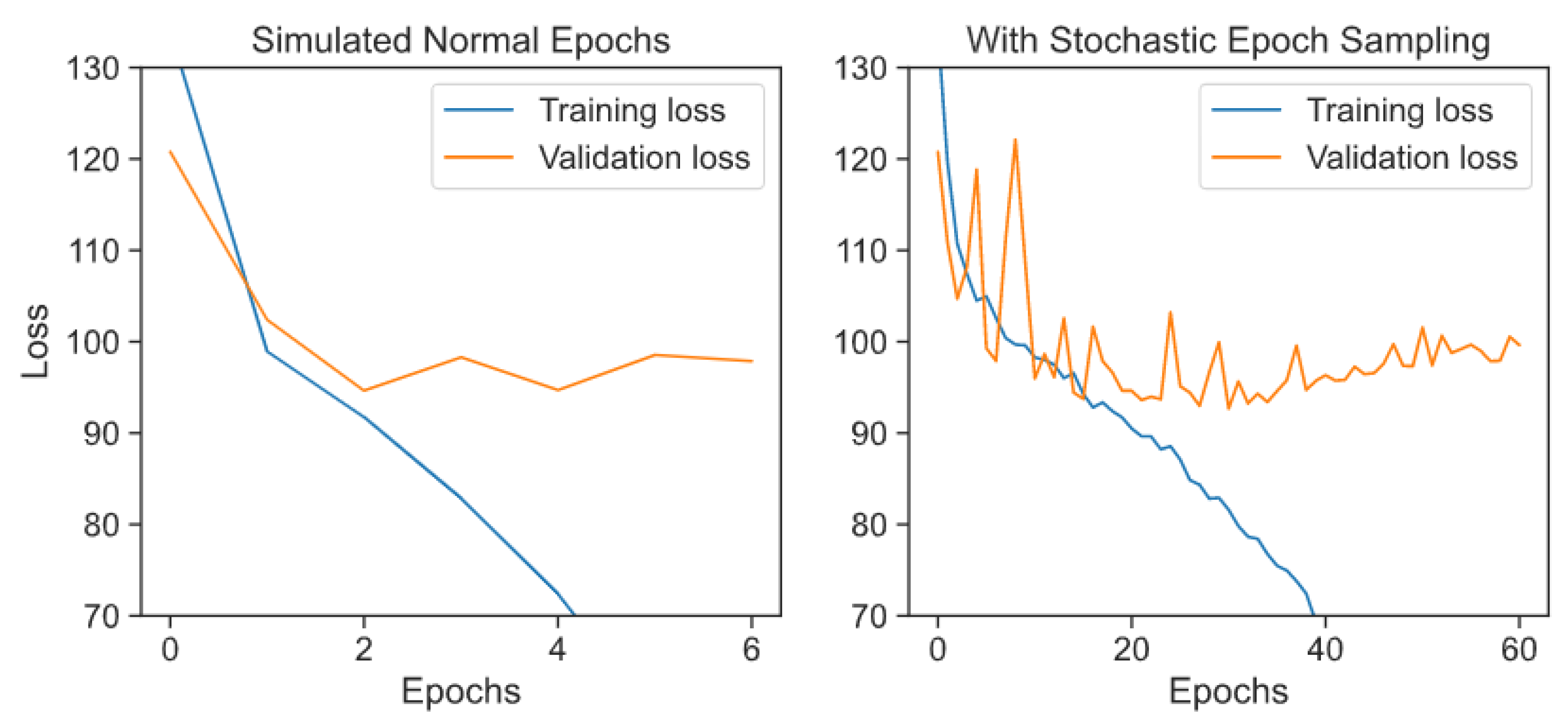
3.2.2. Implementing Data Augmentation to Reduce Overfitting
- Cropping: the cropping augmentation is a method to extend the dataset. Initially, the images are 100 × 100 pixels, and by cropping these to 90 × 90 pixels, we extend the dataset by a factor of five, with minimal loss of information. Each training sample is cropped five times, such that the resulting dataset has five entries for the same farm. The crops are done top-left, top-right, centre, bottom-left, and bottom-right.
- Rotation: another standard method of increasing the number of training samples is to apply image rotation, which forces the models to learn features not purely based on the location of certain specific patterns in an image. We extensively apply image rotation to all image samples by selecting a random rotation angle for each image. The rotation angle is also different for images in the same time series, which produces a unique image time series every time. Image dimensions are kept unchanged, meaning that any corners rotated out of the image are discarded. Black pixels are used to pad any empty corners of the image.
- Pixel noise: to increase the variability of images, we introduce some augmentation through the noise, using a simple salt-and-pepper method. Applying salt-and-pepper noise is a process of changing a fraction of the pixels in the image to their minimum or maximum values (0 or 1) [59]. The vast majority of the image remains unchanged. In contrast, approximately 1% of the pixels (chosen at random) were altered to either 0 or 1. The images in the dataset are multispectral (i.e., containing 12 channels). A pixel was chosen to be altered, the value of all the channels was updated at the same pixel.
3.2.3. Identifying Crop Yield Prediction Targets
3.3. Prediction Model Using Weather Data
Baseline Approach: The Weather DNN Model
3.4. Prediction Models Using Satellite Images
3.4.1. Initial Experiment 1: The Single Image CNN Model
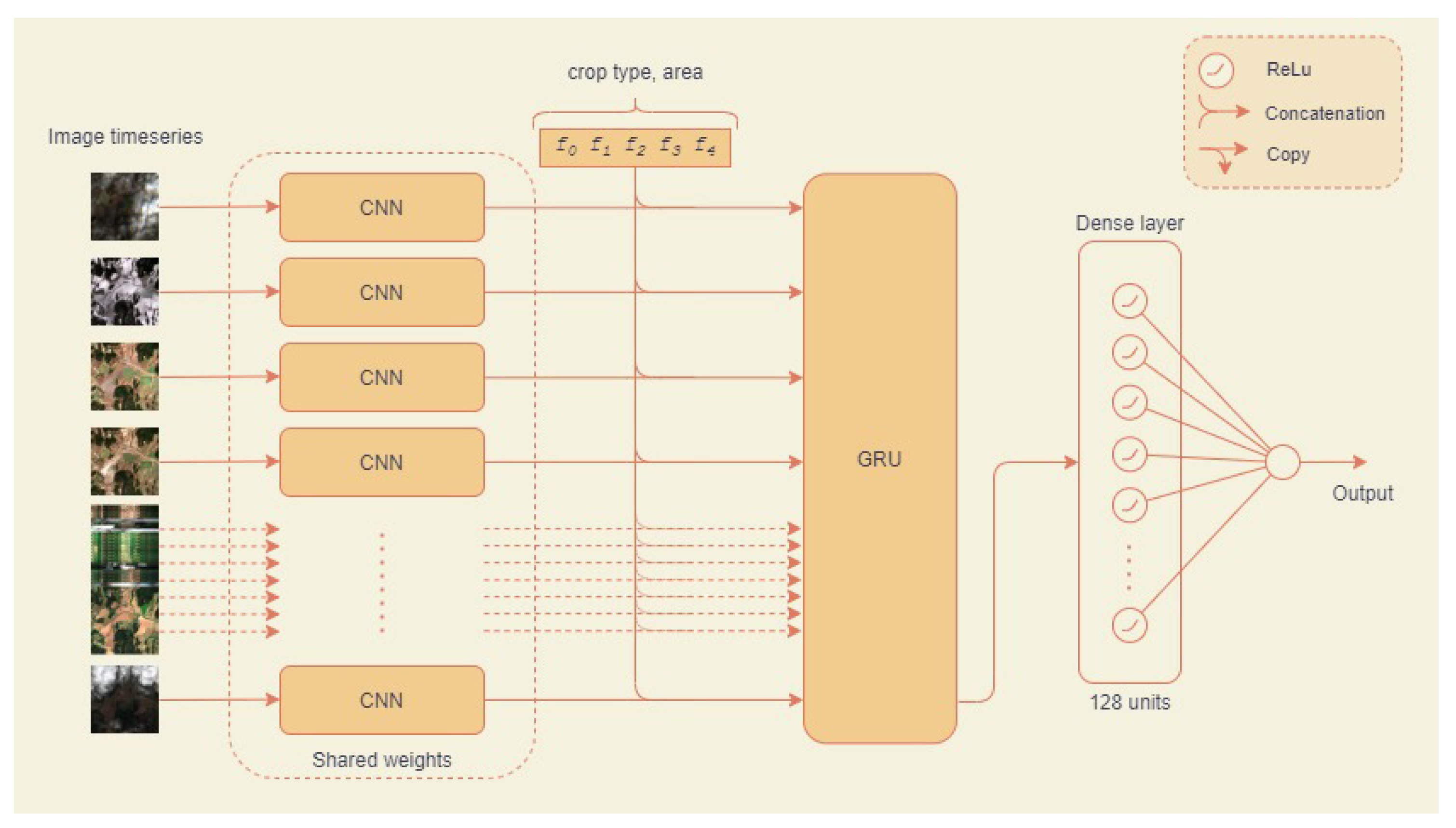
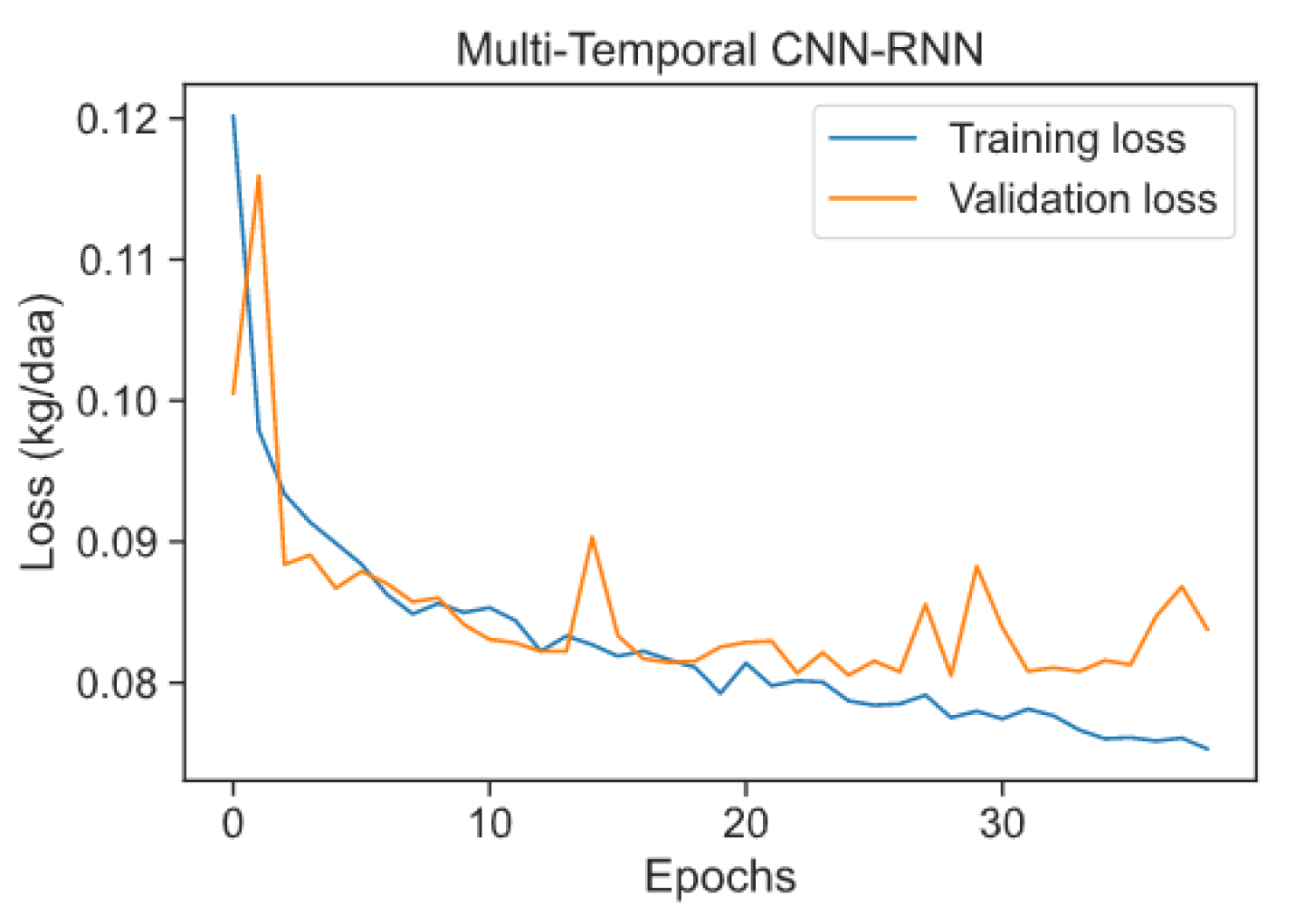
3.4.2. Initial Experiment 2: A Multi-Temporal CNN–RNN Model
3.5. Prediction Models Using Combined Satellite Images and Weather Data
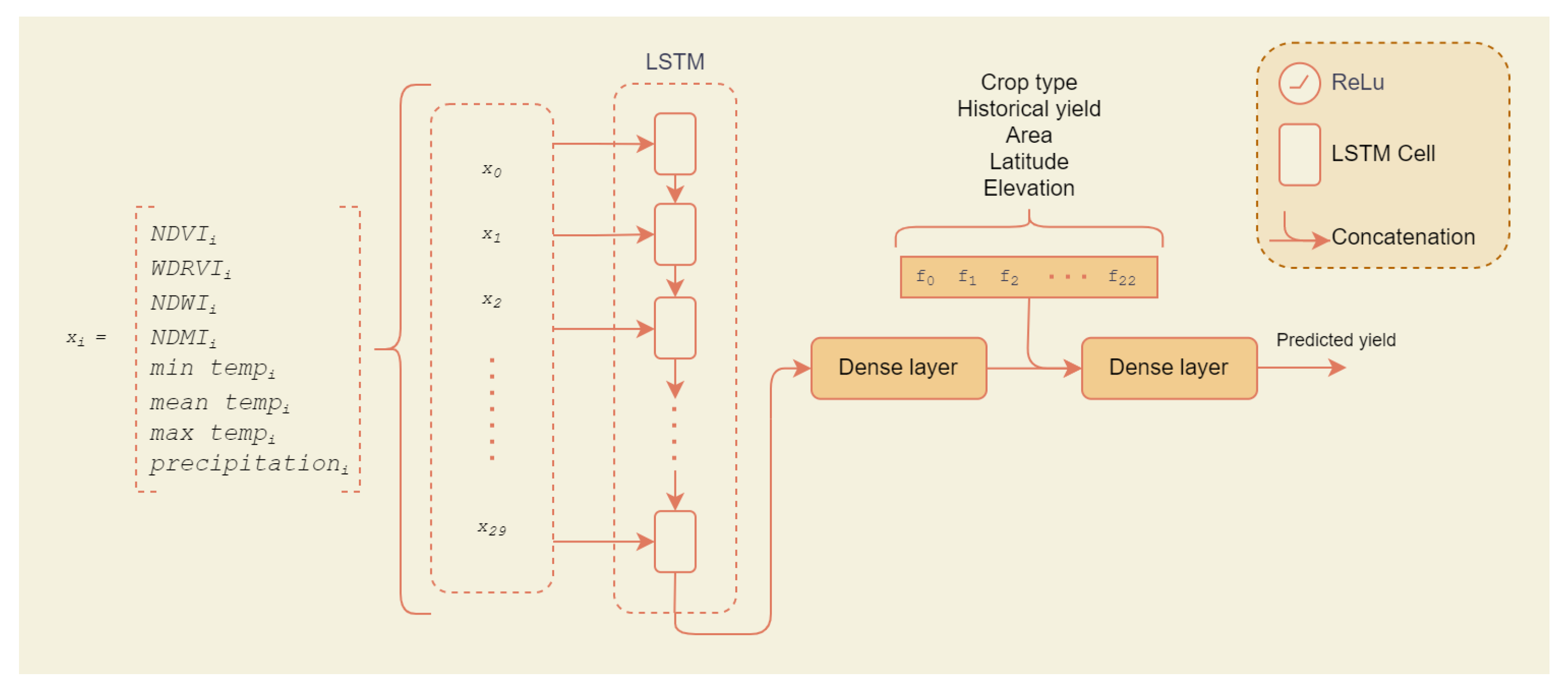
3.5.1. Initial Experiment: LSTM Model Using Handcrafted Features
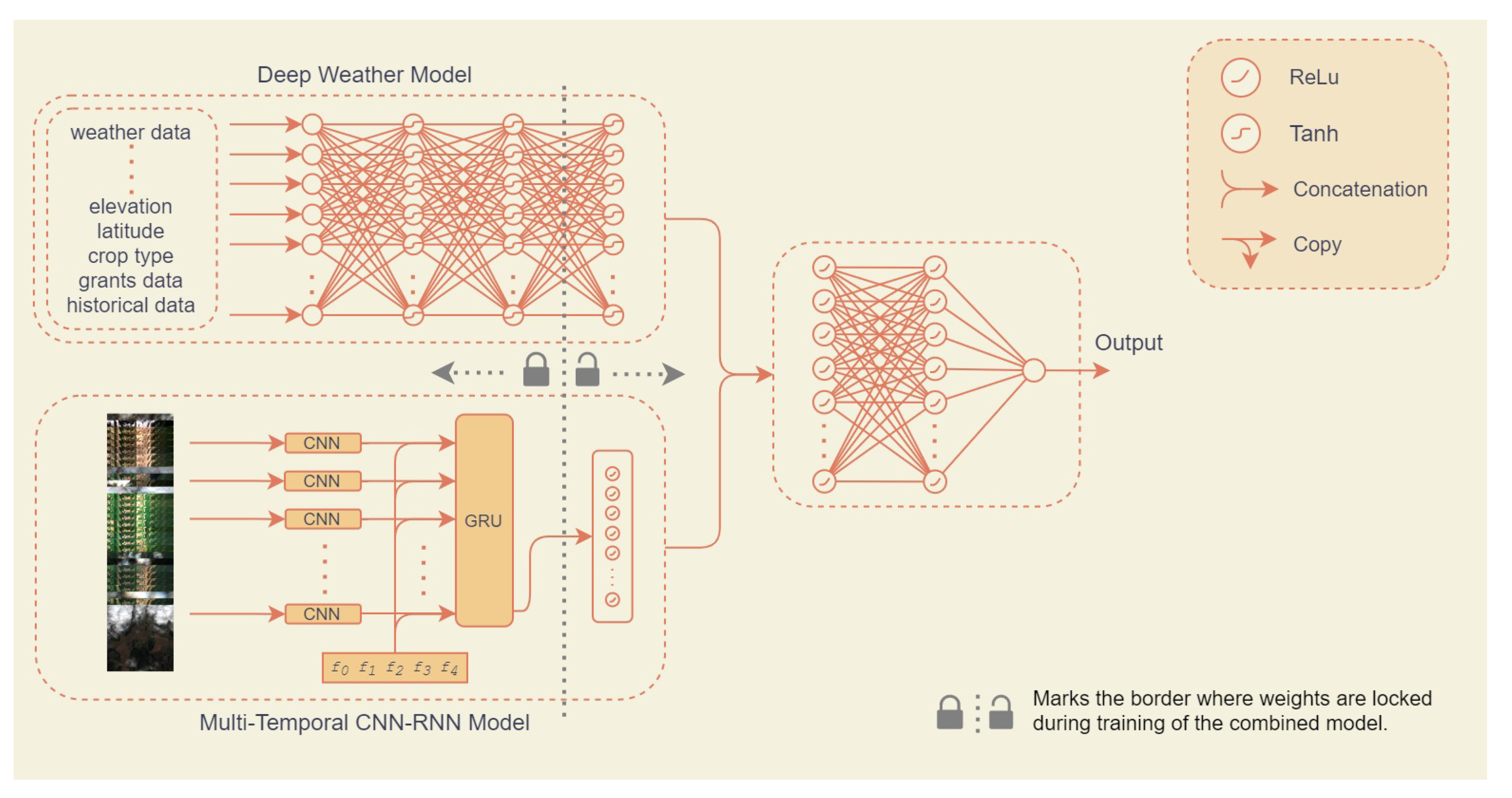
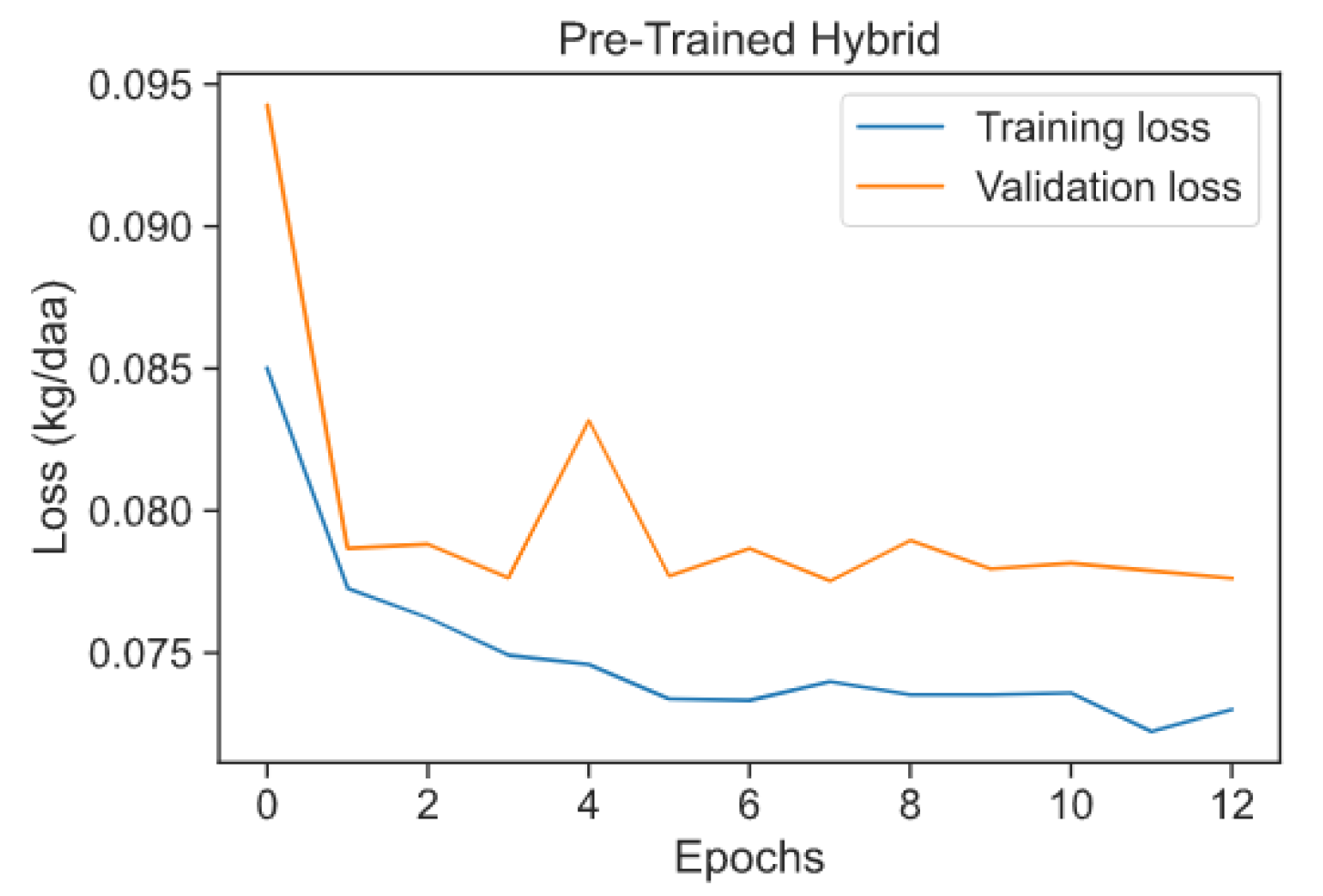
3.5.2. Novel Approach 1: Pre-Trained Hybrid Model
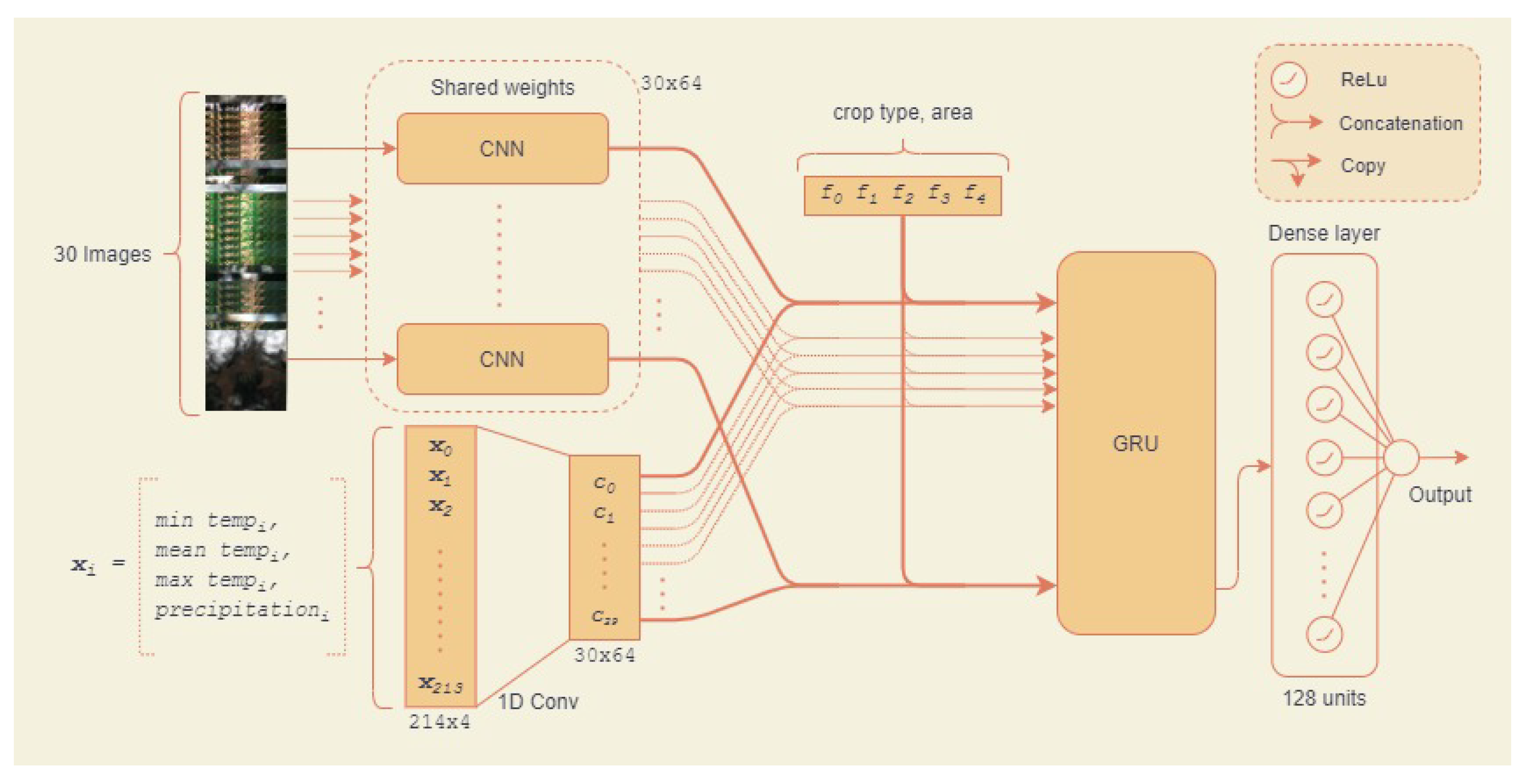
3.5.3. Novel Approach 2: Hybrid CNN Model
4. Results
4.1. Preliminary Experiments on Multispectral Images
4.1.1. Evaluating the Use of Multispectral Imagery for Crop Yield Prediction
4.1.2. Optimal Week to Predict Crop Yield
4.1.3. Effects of Data Augmentation
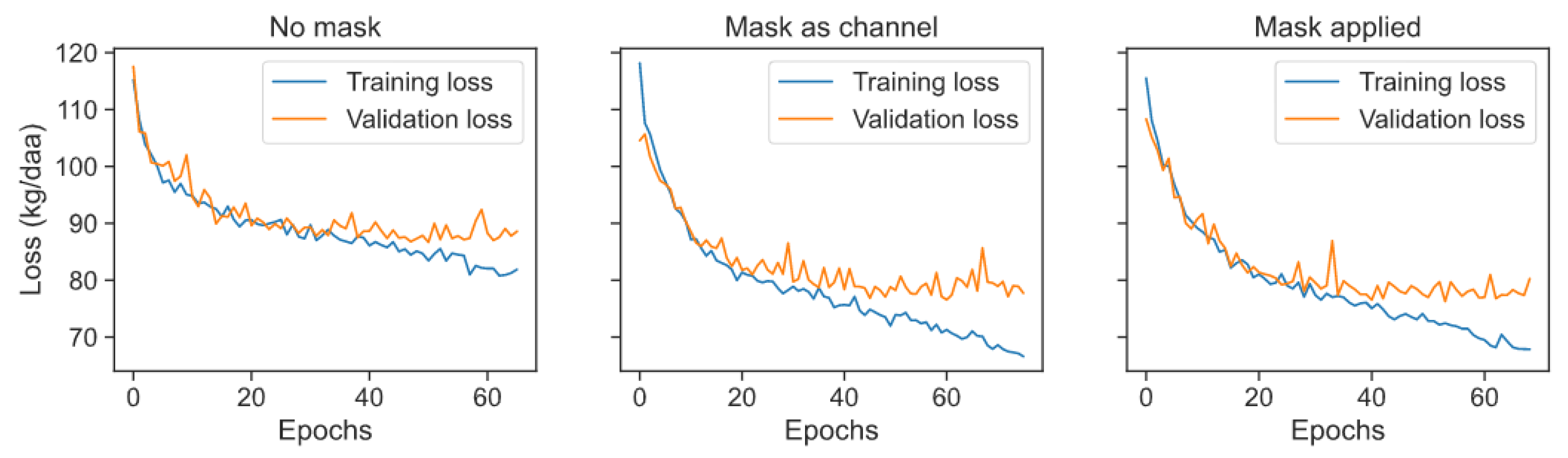
4.1.4. Effects of Image Masking
4.2. Comparison of Crop Yield Prediction Models
4.2.1. Baseline Approach: The Weather DNN Model
4.2.2. Initial Experiment 1: Multi-Temporal CNN–RNN
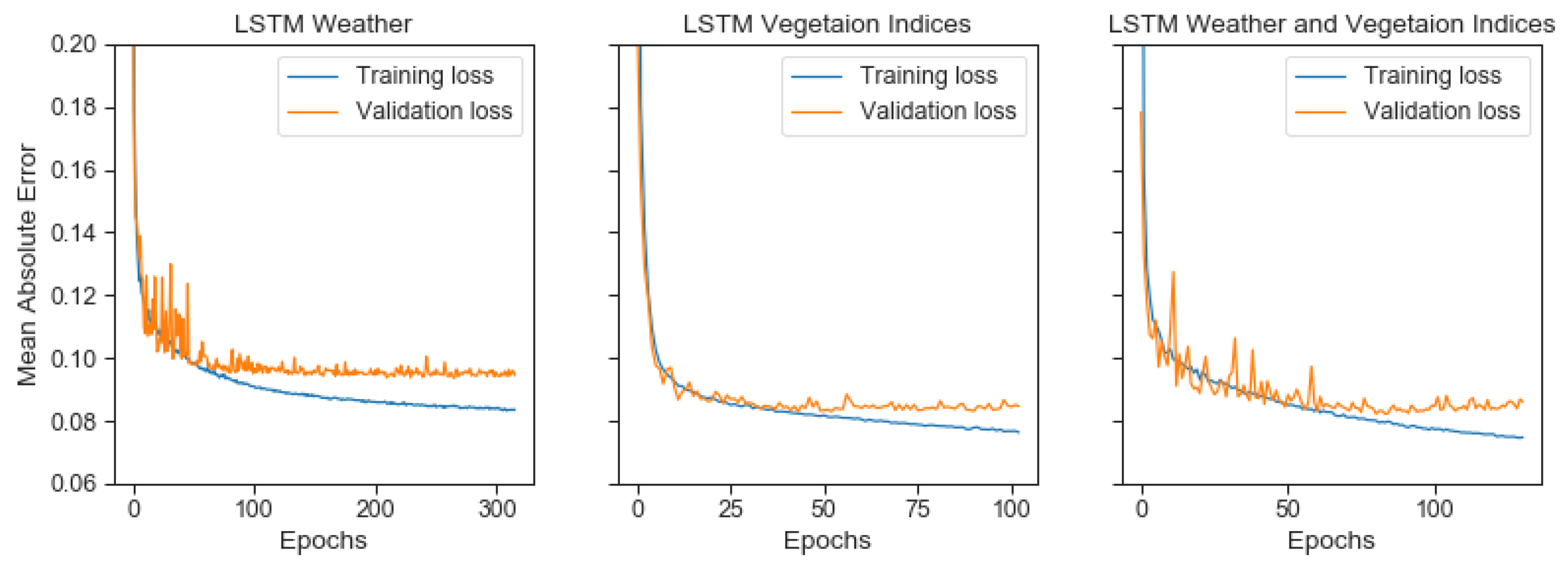
4.2.3. Initial Experiment 2: Handcrafted Features in LSTM
4.3. Novel Approach 1: Pre-Trained Hybrid Model
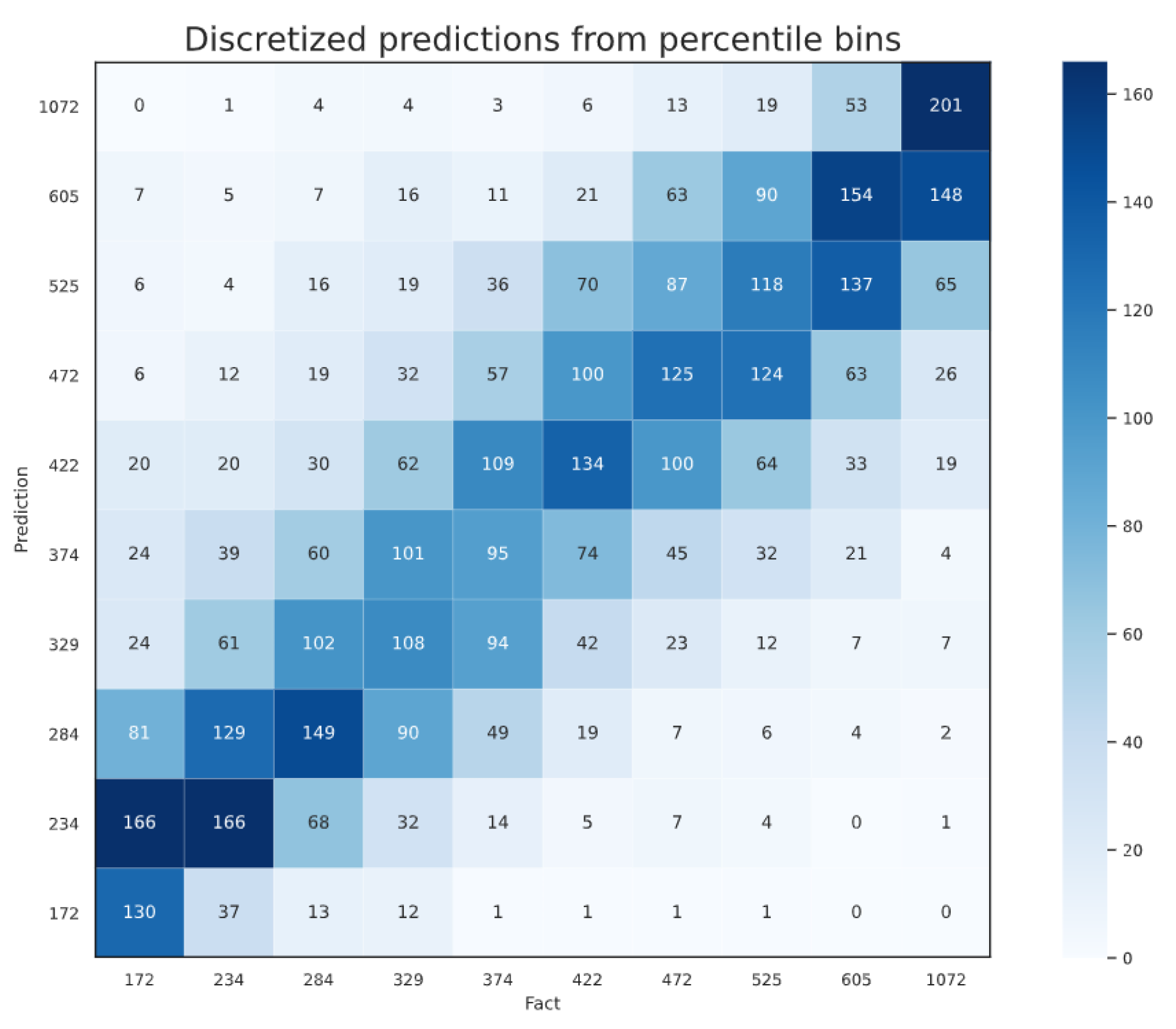
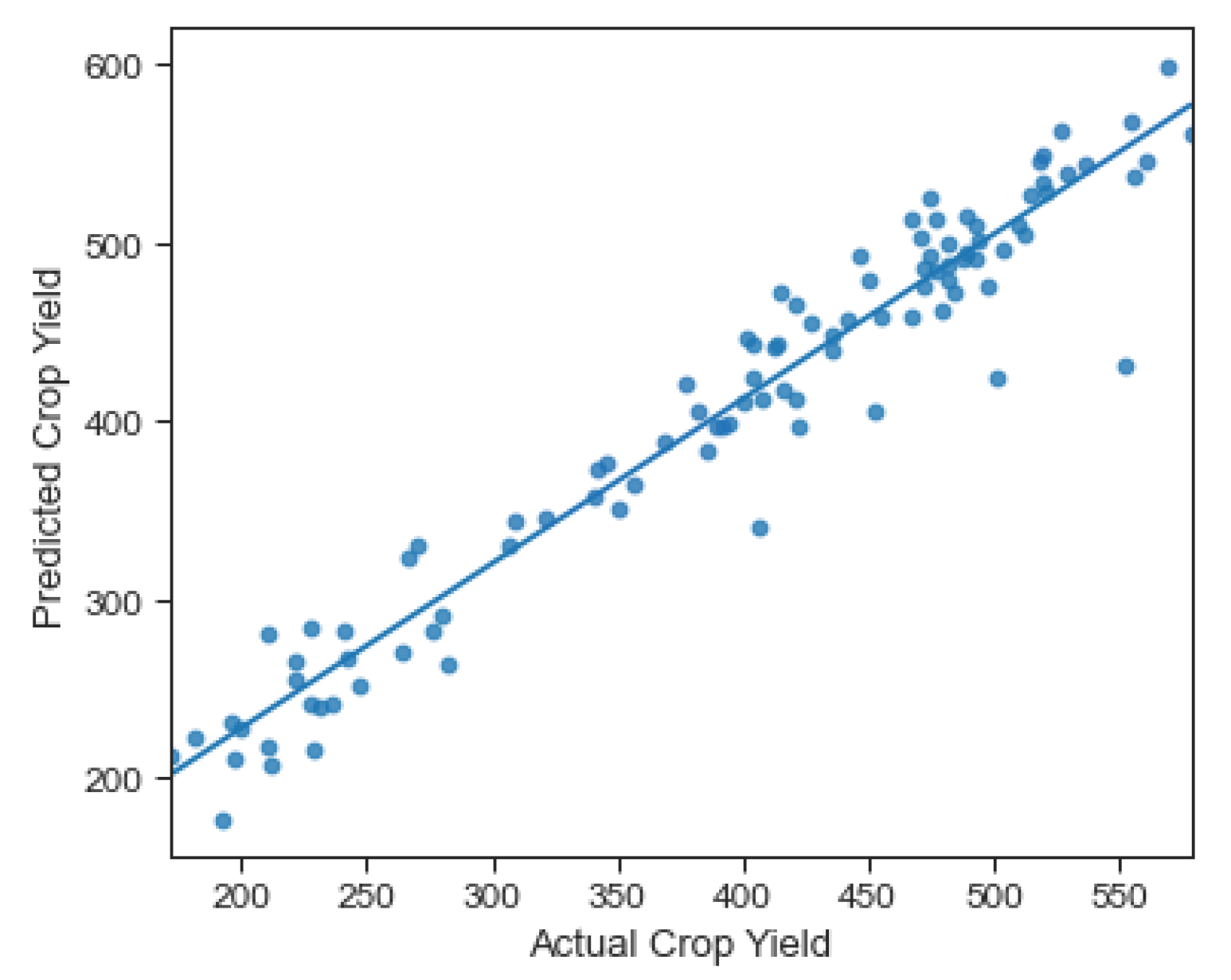
4.4. Novel Approach 2: Hybrid CNN Model
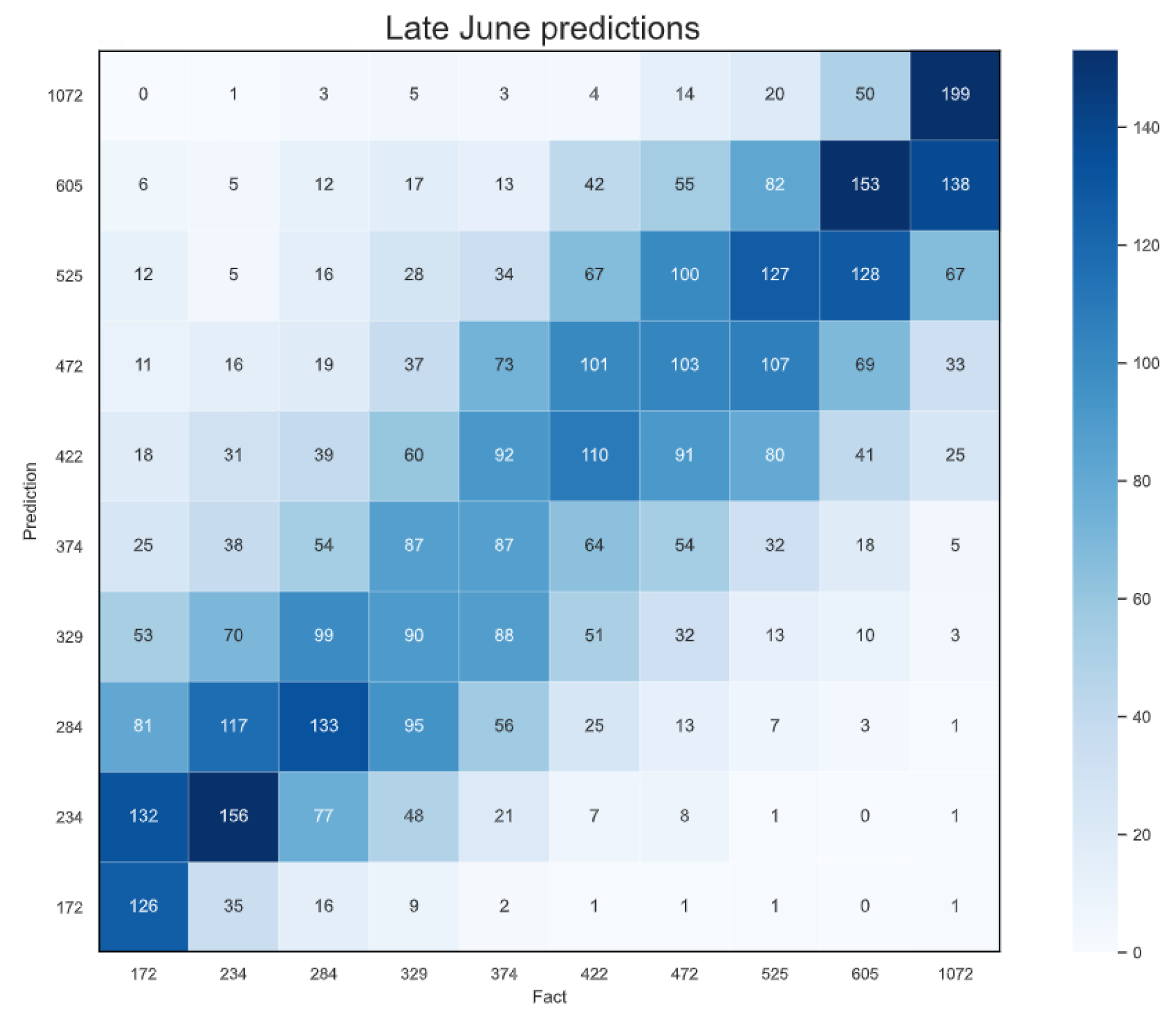
4.5. Early Predictions
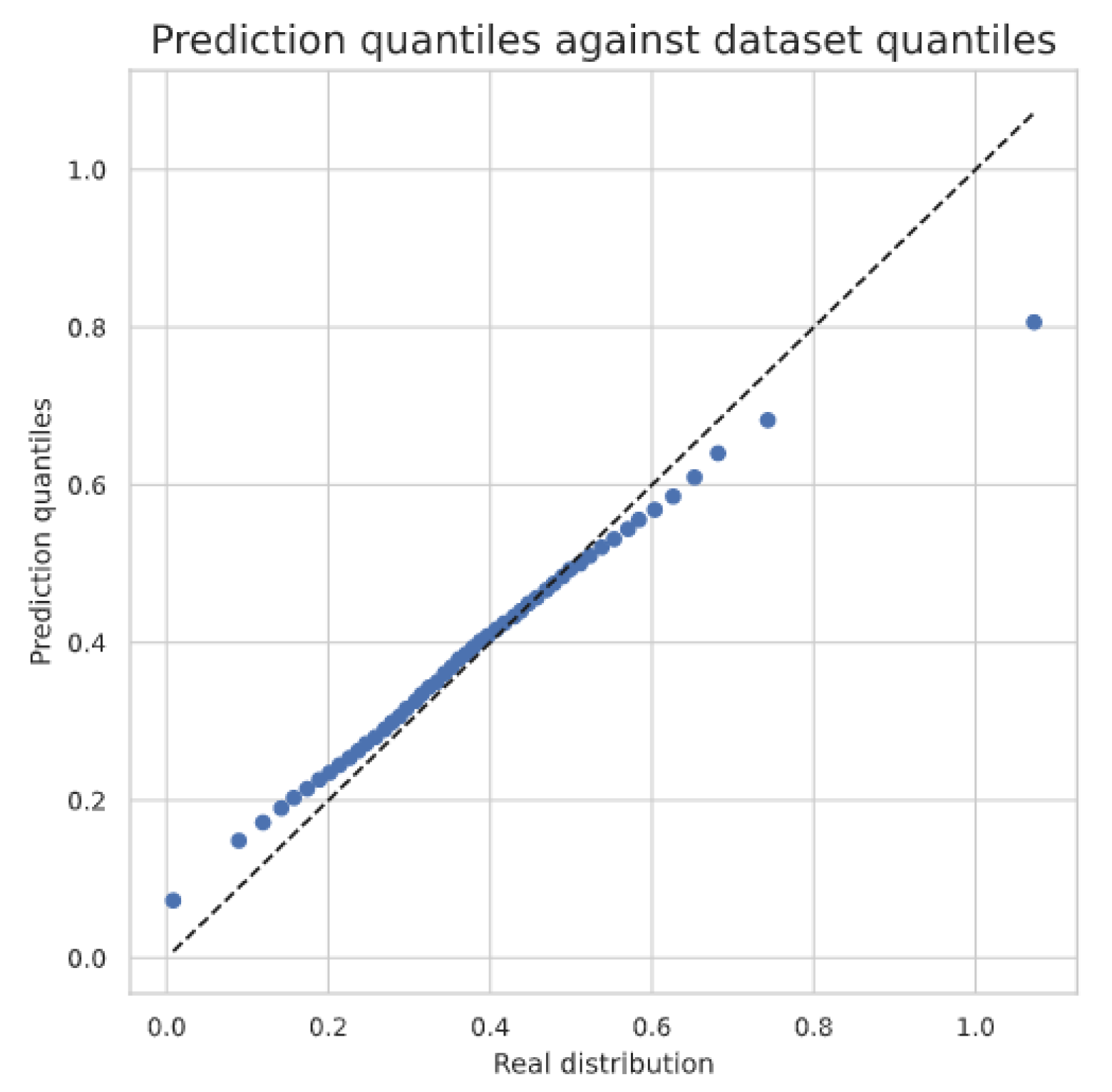
4.6. Predictions as Regional Analytics
5. Discussion
6. Conclusions and Future Work
- Improving generalisation: while our models show that accurate farm-scale crop yield predictions are possible with deep learning, the majority of models start to exhibit overfitting when training, even with the data augmenting methods used. This suggests that even higher accuracy might be possible given more data or using other known methods for reducing overfitting and increasing generalisation, such as batch normalisation.
- Remote sensed temperature: land surface temperatures derived from satellite sensors have successfully been used in US county-level predictions [14]. They provide temperature values that should be closer to the actual temperature at the farm compared to interpolations between sensors that are typically many kilometres away from the farm. Such values could replace temperature interpolation or be used to improve weather interpolation further.
- NIBIO field data: apply field data gathered by NIBIO to the models. Adding soil quality and water storage capacities could add meaningful information about crop yield potential in individual fields.
- Additional sources for satellite images: this study used Sentinel-2 as the source for the satellite images. It could be positive to introduce additional sources for satellite images to complement the Sentinel-2 dataset. Additional sources for satellite images could increase the frequency of the satellite images throughout the growing season and give higher resolution multispectral images. Some specific satellites of interest could be Landsat 8, WorldView-3, and PlantScope.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eltun, R.; Korsaeth, A.; Nordheim, O. A comparison of environmental, soil fertility, yield, and economical effects in six cropping systems based on an 8-year experiment in Norway. Agric. Ecosyst. Environ. 2002, 90, 155–168. [Google Scholar] [CrossRef]
- Klaus, G.G. Food quality and safety: Consumer perception and demand. Eur. Rev. Agric. Econ. 2005, 32, 369–391. [Google Scholar] [CrossRef]
- Klompenburg, T.V.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Shao, Y.; Ren, J.; Campbell, J.B. Multitemporal Remote Sensing Data Analysis for Agricultural Application. Compr. Remote Sens. 2018, 9, 29–38. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. Proceedings of 1ACM SIGCAS Conference on Computing and Sustainable Societies, San Jose, CA, USA, 20–22 June 2018. [Google Scholar]
- Lobell, D.; Thau, D.; Seifert, C.A.; Engle, E.; Little, B.B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Wart, J.; Bussel, L.; Wolf, J.; Licker, R.; Grassini, P.; Nelson, A.; Boogaard, H.; Gerber, J.; Mueller, N.; Claessens, L.; et al. Use of agro-climatic zones to upscale simulated crop yield potential. Field Crops Res. 2013, 143, 44–55. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.; Rai, S.; Krishnan, N.C. Wheat Crop Yield Prediction Using Deep LSTM Model. arXiv 2020, arXiv:2011.01498. [Google Scholar]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Landsat 1|Landsat Science. Available online: https://landsat.gsfc.nasa.gov/landsat-1-3/landsat-1 (accessed on 4 June 2021).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the 3rd Earth Resources Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973. [Google Scholar]
- Macdonald, R.B.; Hall, F.G.; Erb, R.B. The Use of LANDSAT Data in a Large Area Crop Inventory Experiment (LACIE). In Proceedings of the LARS Symposia, Purdue University, West Lafayette, Indiana, 3–5 June 1975. [Google Scholar]
- Wiegand, C.L.; Richardson, A.J.; Jackson, R.D.; Pinter, P.J.; Aase, J.K.; Smika, D.E.; Lautenschlager, L.F.; McMurtrey, J.E. Development of Agrometeorological Crop Model Inputs from Remotely Sensed Information. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 90–98. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Benedetti, R.; Rossini, P. On the use of NDVI profiles as a tool for agricultural statistics: The case study of wheat yield estimate and forecast in Emilia Romagna. Remote Sens. Environ. 1993, 45, 311–326. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, H.; Zhong, R.; Xu, J.; Xu, J.; Huang, J.; Wang, S.; Ying, Y.; Lin, T. A deep learning approach to conflating heterogeneous geospatial data for corn yield estimation: A case study of the US Corn Belt at the county level. Global change biology. Glob. Chang. Biol. 2019, 26, 1754–1766. [Google Scholar] [CrossRef]
- Walker, D.; Olesen, B.; Phillips, R. Reproduction and phenology in seagrasses. In Global Seagrass Research Methods; Frederick, T.S., Robert, G.C., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2001; pp. 59–78. [Google Scholar]
- Nejedlik, P.; Oger, R.; Sigvald, R. The Phenology of Crops and the Development of Pests and Diseases; Planteforsk. Available online: http://hdl.handle.net/11250/2507939 (accessed on 13 December 2021).
- Khaki, S.; Wang, L.; Archontoulis, S.V. A CNN–RNN Framework for Crop Yield Prediction. Front. Plant Sci. 2019, 10, 1750. [Google Scholar] [CrossRef] [PubMed]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous corn and soybean yield prediction from remote sensing data using deep transfer learning. Sci. Rep. 2021, 11, 11132. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Bhadra, S.; Maimaitiyiming, M.; Brown, D.R.; Sidike, P.; Fritschi, F.B. Field-scale crop yield prediction using multi-temporal WorldView-3 and PlanetScope satellite data and deep learning. Isprs J. Photogramm. Remote Sens. 2021, 174, 265–281. [Google Scholar] [CrossRef]
- Tine. Family Farming: The Key to Food Production in Norway. Available online: https://www.tine.no/english/about-tine/family-farming-the-key-to-food-production-in-norway (accessed on 23 November 2020).
- Bondelaget. Norwegian Agriculture—The Norwegian Model for Agriculture and Agricultural Policy. Available online: https://www.bondelaget.no/getfile.php/13894650-1550654949/MMA/BilderNB/Illustrasjoner/NorwegianAgricultureEN.pdf (accessed on 13 December 2021).
- Kildahl, K. Nine Facts about Norwegian Agriculture—Nibio. Available online: https://www.nibio.no/en/news/nine-facts-about-norwegian-agriculture (accessed on 17 December 2021).
- Norwegian Digital Learning Arena. Bygg. Available online: https://ndla.no/subjects/subject:41/topic:1:188696/topic:1:189185/resource:1:82133 (accessed on 1 December 2020).
- Holtekjølen, A.K.; Uhlen, A.; Holtet, E.K.; Hvete, E.A. Store Norske Leksikon. Available online: http://snl.no/hvete (accessed on 21 October 2019).
- Havre, A. Norwegian Digital Learning. Available online: https://ndla.no/subject:41/topic:1:188696/topic:1:189185/resource:1:82136 (accessed on 1 December 2020).
- Rug, A. Norwegian Digital Learning. Available online: https://ndla.no/nb/subject:41/topic:1:188696/topic:1:189185/resource:1:82142 (accessed on 1 December 2020).
- Encyclopaedia Britannica, Rye. Available online: https://www.britannica.com/plant/rye (accessed on 1 December 2020).
- Woodward, F.I. Climate and Plant Distribution; Cambridge University Press: Cambridge, UK, 1987; pp. 1–174. [Google Scholar]
- Oregon State University. Environmental Factors Affecting Plant Growth. Available online: https://extension.oregonstate.edu/gardening/techniques/environmental-factors-affecting-plant-growth (accessed on 7 December 2020).
- Åssveen, M.; Abrahamsen, U. Varmesum for sorter og arter av korn. Grønn Forsk. 1999, 2, 55–59. [Google Scholar]
- Wahid, A.; Gelani, S.; Ashraf, M.A.; Foolad, M.R. Heat tolerance in plants: An overview. Environ. Exp. Bot. 2007, 61, 199–223. [Google Scholar] [CrossRef]
- Soureshjani, H.K.; Dehkordi, A.G.; Bahador, M. Temperature effect on yield of winter and spring irrigated crops. Agric. For. Meteorol. 2019, 279, 107664. [Google Scholar] [CrossRef]
- Burns, R.G.; DeForest, J.L.; Marxsen, J.; Sinsabaugh, R.L.; Stromberger, M.E.; Wallenstein, M.D.; Weintraub, M.N.; Zoppini, A. Soil enzymes in a changing environment: Current knowledge and future directions. Soil Biol. Biochem. 2013, 58, 216–234. [Google Scholar] [CrossRef]
- Doerr, S.H.; Shakesby, R.A.; Walsh, R.P. Soil water repellency: Its causes, characteristics and hydro-geomorphological significance. Earth-Sci. Rev. 2000, 51, 33–65. [Google Scholar] [CrossRef]
- Farooq, M.; Wahid, A.; Kobayashi, N.; Fujita, D.; Basra, S.M. Plant drought stress: Effects, mechanisms and management. Agron. Sustain. Dev. 2011, 29, 185–212. [Google Scholar] [CrossRef] [Green Version]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Aggarwal, C. Neural Networks and Deep Learning: A Textbook, 1 ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–497. [Google Scholar]
- Fukushima, K.; Miyake, S. Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position. Pattern Recognit. 1982, 15, 455–469. [Google Scholar] [CrossRef]
- Venkatesan, R.; Li, B. Convolutional Neural Networks in Visual Computing: A Concise Guide; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–186. [Google Scholar]
- LeCun, Y.A.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Kolen, J.F.; Kremer, S.C. Gradient Flow in Recurrent Nets: The Difficulty of Learning LongTerm Dependencies; Wiley-IEEE Press: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Merrienboer, B.V.; Gülçehre, Ç.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Schott, J.R. Remote Sensing: The Image Chain Approach; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing, Models, and Methods for Image Processing; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- MSI Instrument-Sentinel-2 MSI Technical Guide-Sentinel Online-Sentinel. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/Sentinel-2-msi/msi-instrument (accessed on 15 April 2021).
- Pettorelli, N. The Normalized Difference Vegetation Index; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Sjølander, B.; Sandø, E.; Martin, M. Neural Network for Grain Yield Predictions in Norwegian Agriculture. 2020. Available online: https://uia.brage.unit.no/uia-xmlui/handle/11250/2823807 (accessed on 13 December 2021).
- Ngoune, L.T.; Shelton, C.M. Factors affecting yield of crops. In Agronomy-Climate Change & Food Security; IntechOpen: Rijeka, Croatia, 2020. [Google Scholar] [CrossRef]
- Kolberg, D.; Persson, T.; Mangerud, K.; Riley, H.C. Impact of projected climate change on workability, attainable yield, profitability and farm mechanization in Norwegian spring cereals. Soil Tillage Res. 2019, 185, 122–138. [Google Scholar] [CrossRef]
- Kukal, M.S.; Irmak, S. Climate-Driven Crop Yield and Yield Variability and Climate Change Impacts on the U.S. Great Plains Agricultural Production. Sci. Rep. 2018, 8, 3450. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chipanshi, A.; Daneshfar, B.; Koiter, L.; Champagne, C.; Davidson, A.; Reichert, G.; Bédard, F. Effect of using crop specific masks on earth observation based crop yield forecasting across Canada. Remote Sens. Appl. Soc. Environ. 2019, 13, 121–137. [Google Scholar] [CrossRef]
- Kastens, J.H.; Kastens, T.L.; Kastens, D.; Price, K.P.; Martinko, E.A.; Lee, R. Image masking for crop yield forecasting using AVHRR NDVI time series imagery. Remote Sens. Environ. 2005, 99, 341–356. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Hawkins, D.M. The Problem of Overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef]
- Basnyat, B.M.; Lafond, G.P.; Moulin, A.P.; Pelcat, Y. Optimal time for remote sensing to relate to crop grain yield on the Canadian prairies. Can. J. Plant Sci. 2004, 84, 97–103. [Google Scholar]





| Nearest Neighbour | Deep Neural Network | Change | |
|---|---|---|---|
| Precipitation error | 1.5 mm | 1.15 mm | −0.45 mm (−23%) |
| Temperature error | 1.6 C | 0.52 C | −1.08 C (−67%) |
| Feature | Lower | Upper |
|---|---|---|
| Crop yield (kg/1000 ) | 0 | 1000 |
| Temperature (C) | 30 | |
| Precipitation (mm) | 0 | 10 |
| Historical yield (kg) | 0 | 10,000 |
| Name | Abbr. | Formula | Description |
|---|---|---|---|
| Normalised Difference Vegetation Index | NDVI | Indicator of green leaf area, giving a measurement of healthy green vegetation in any given pixel. First used by Rouse et al. [11] | |
| Wide Dynamic Range Vegetation Index | WDRVI | Modification of the NDVI with an extra weighting coefficient parameter. Increased sensitivity when areas with moderate to high biomass are investigated [60]. | |
| Normalised Difference Water Index | NDWI | A measurement that is sensitive to changes in water content of vegetation [61]. | |
| Normalised Difference Moisture Index | NDMI | Indicator of the water content of vegetation. Effectively similar to that of NDWI, but calculated using other aspects of the spectrum [61]. |
| Augmentation | Validation Loss (Mean) | Improvement over Original (Percent) |
|---|---|---|
| Original (No augmentation) | 89.8 | |
| Salt-and-pepper noise | 86.8 | 3.34% |
| Rotating | 83.4 | 7.13% |
| Cropping | 83.3 | 7.24% |
| Model | Mean Absolute Error (kg/1000 m) |
|---|---|
| Weather DNN | 83.04 |
| Multi-temporal CNN–RNN | 80.52 |
| Handcrafted features in LSTM | 82.29 |
| Hybrid 1: pre-trained hybrid | 77.53 |
| Hybrid 2: hybrid CNN | 76.27 |
| Mask Type | Mean Absolute Error (kg/1000 m) |
|---|---|
| No mask | 86.69 |
| Mask as channel | 76.57 |
| Mask applied | 76.27 |
| Input | Description | Mean Absolute Error | Change |
|---|---|---|---|
| Weeks 10–39 | Full season | 76.27 kg/1000 | – |
| Weeks 10–26 | Late-June | 82.11 kg/1000 | +7.66% |
| Weeks 10–21 | Mid-May | 92.20 kg/1000 | +20.89% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Engen, M.; Sandø, E.; Sjølander, B.L.O.; Arenberg, S.; Gupta, R.; Goodwin, M. Farm-Scale Crop Yield Prediction from Multi-Temporal Data Using Deep Hybrid Neural Networks. Agronomy 2021, 11, 2576. https://doi.org/10.3390/agronomy11122576
Engen M, Sandø E, Sjølander BLO, Arenberg S, Gupta R, Goodwin M. Farm-Scale Crop Yield Prediction from Multi-Temporal Data Using Deep Hybrid Neural Networks. Agronomy. 2021; 11(12):2576. https://doi.org/10.3390/agronomy11122576
Chicago/Turabian StyleEngen, Martin, Erik Sandø, Benjamin Lucas Oscar Sjølander, Simon Arenberg, Rashmi Gupta, and Morten Goodwin. 2021. "Farm-Scale Crop Yield Prediction from Multi-Temporal Data Using Deep Hybrid Neural Networks" Agronomy 11, no. 12: 2576. https://doi.org/10.3390/agronomy11122576
APA StyleEngen, M., Sandø, E., Sjølander, B. L. O., Arenberg, S., Gupta, R., & Goodwin, M. (2021). Farm-Scale Crop Yield Prediction from Multi-Temporal Data Using Deep Hybrid Neural Networks. Agronomy, 11(12), 2576. https://doi.org/10.3390/agronomy11122576








