The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland
Abstract
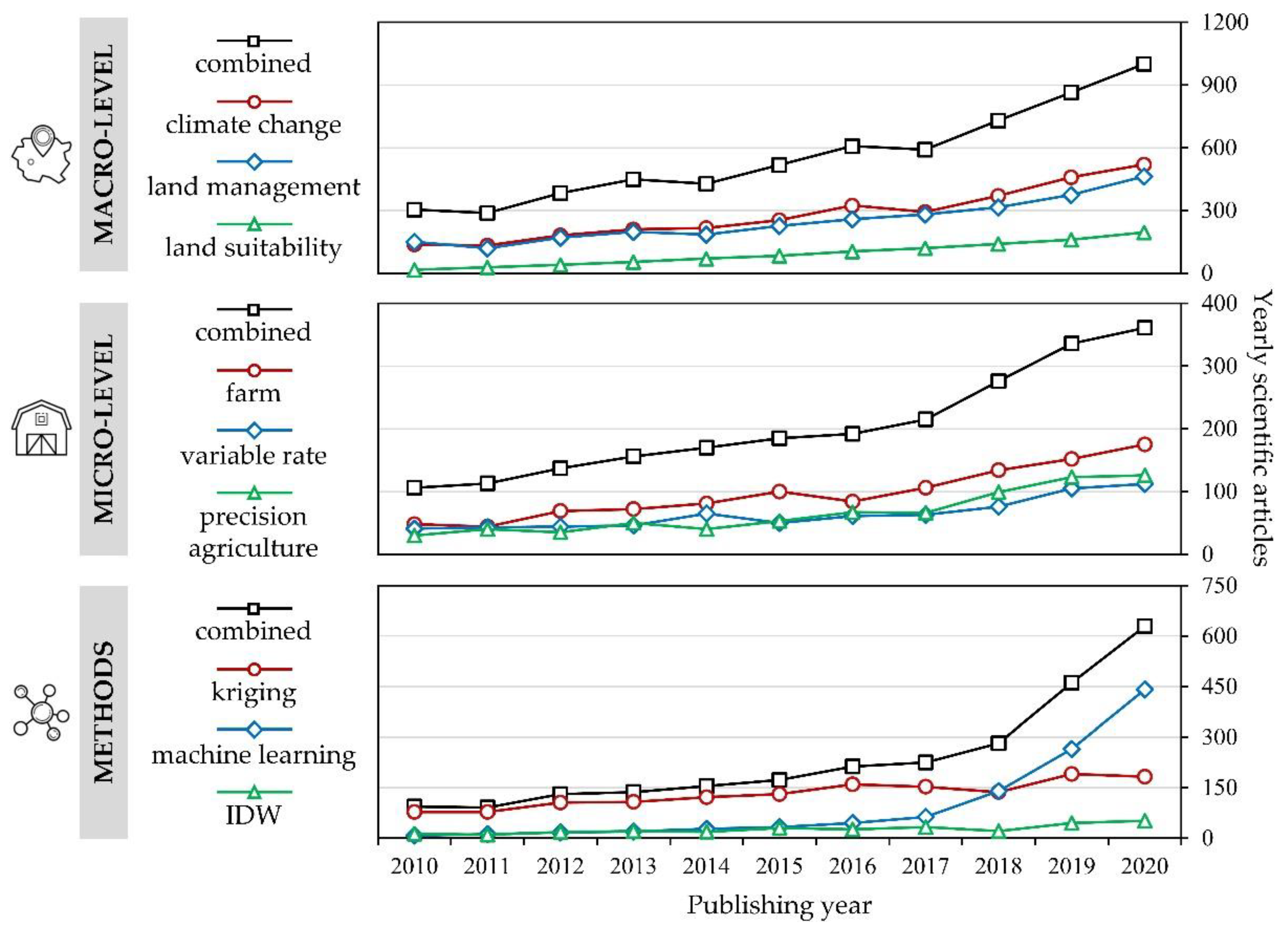
:1. Introduction
2. Materials and Methods
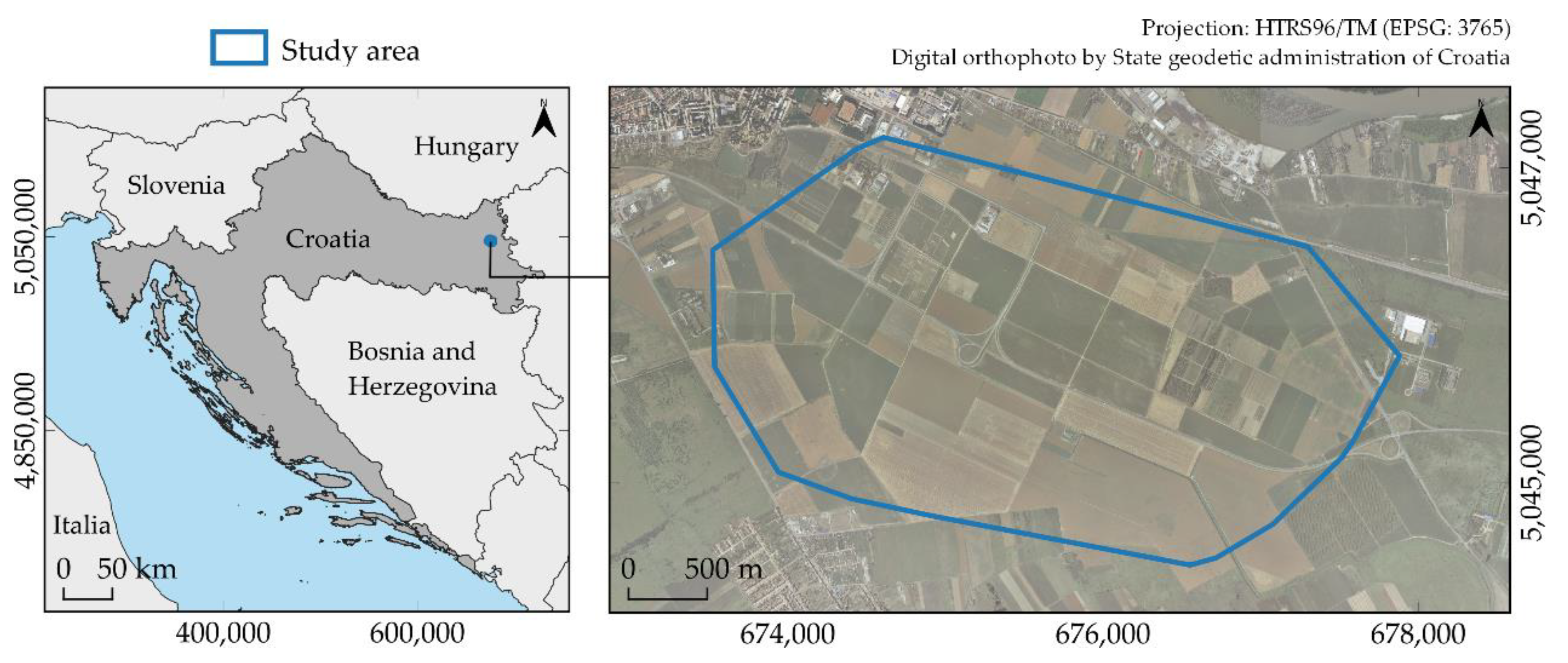
2.1. Study Area
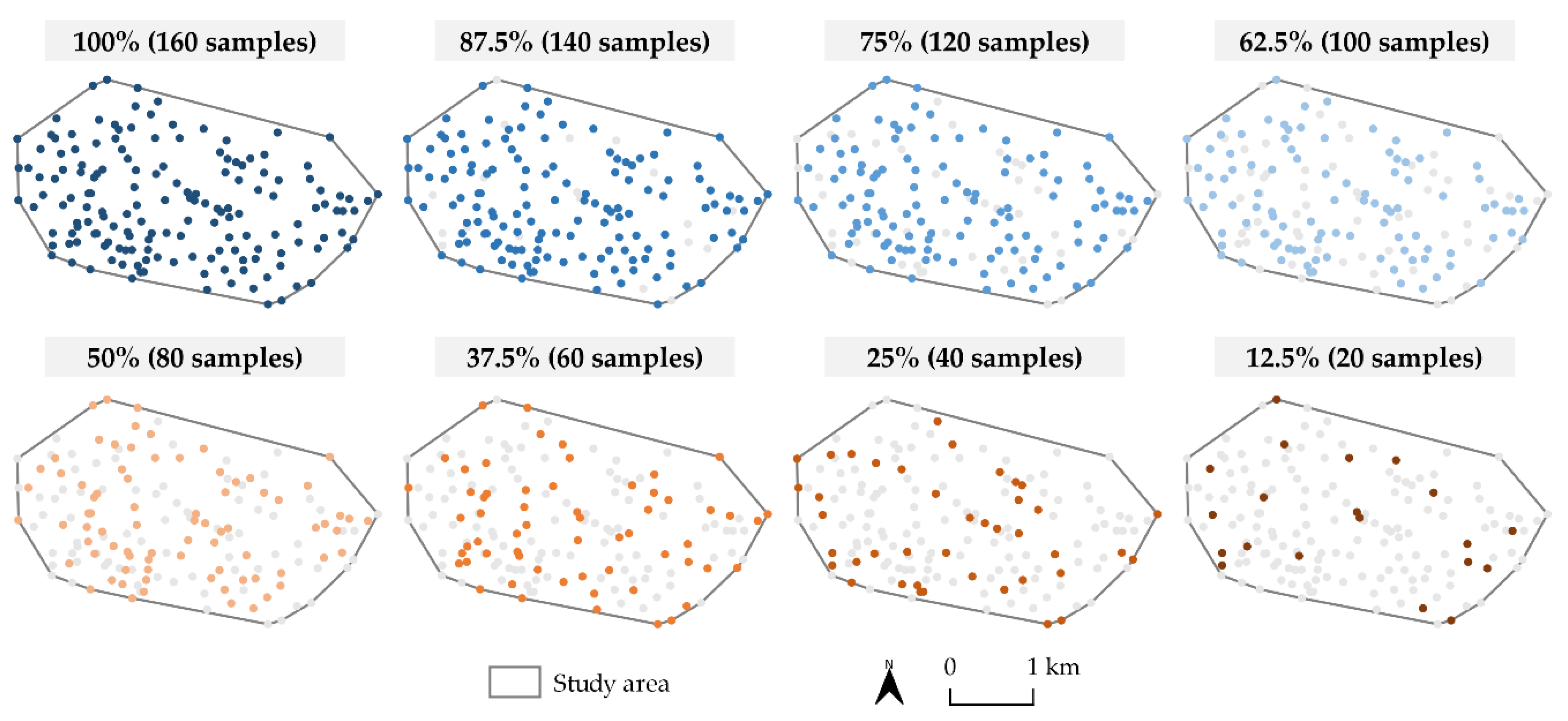
2.2. Soil Sampling Data
2.3. Spatial Interpolation Methods and Interpolation Parameters
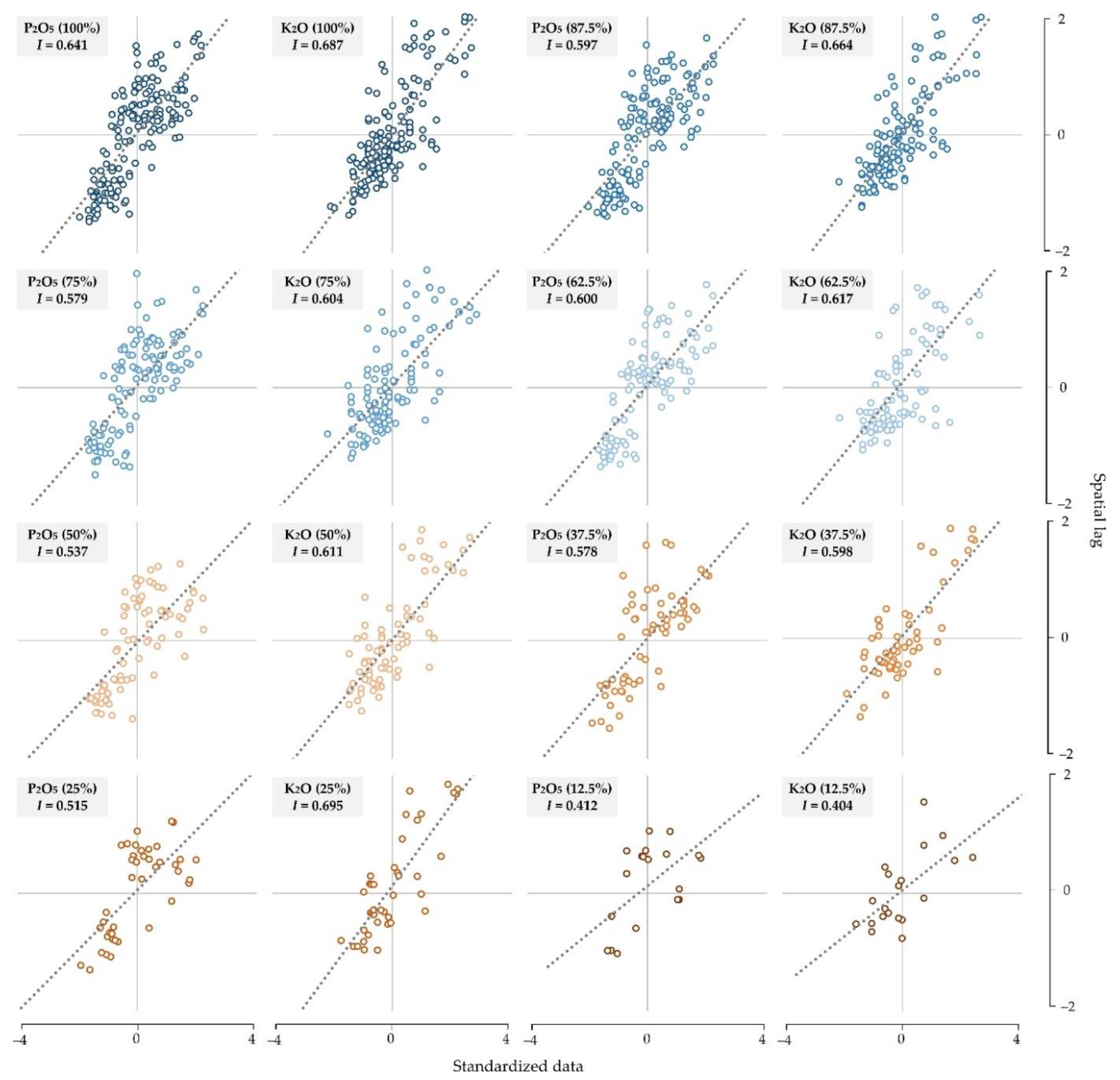
2.4. Interpolation Accuracy Assessment and Relationship with Sampling Density and Spatial Autocorrelation
3. Results
4. Discussion
5. Conclusions
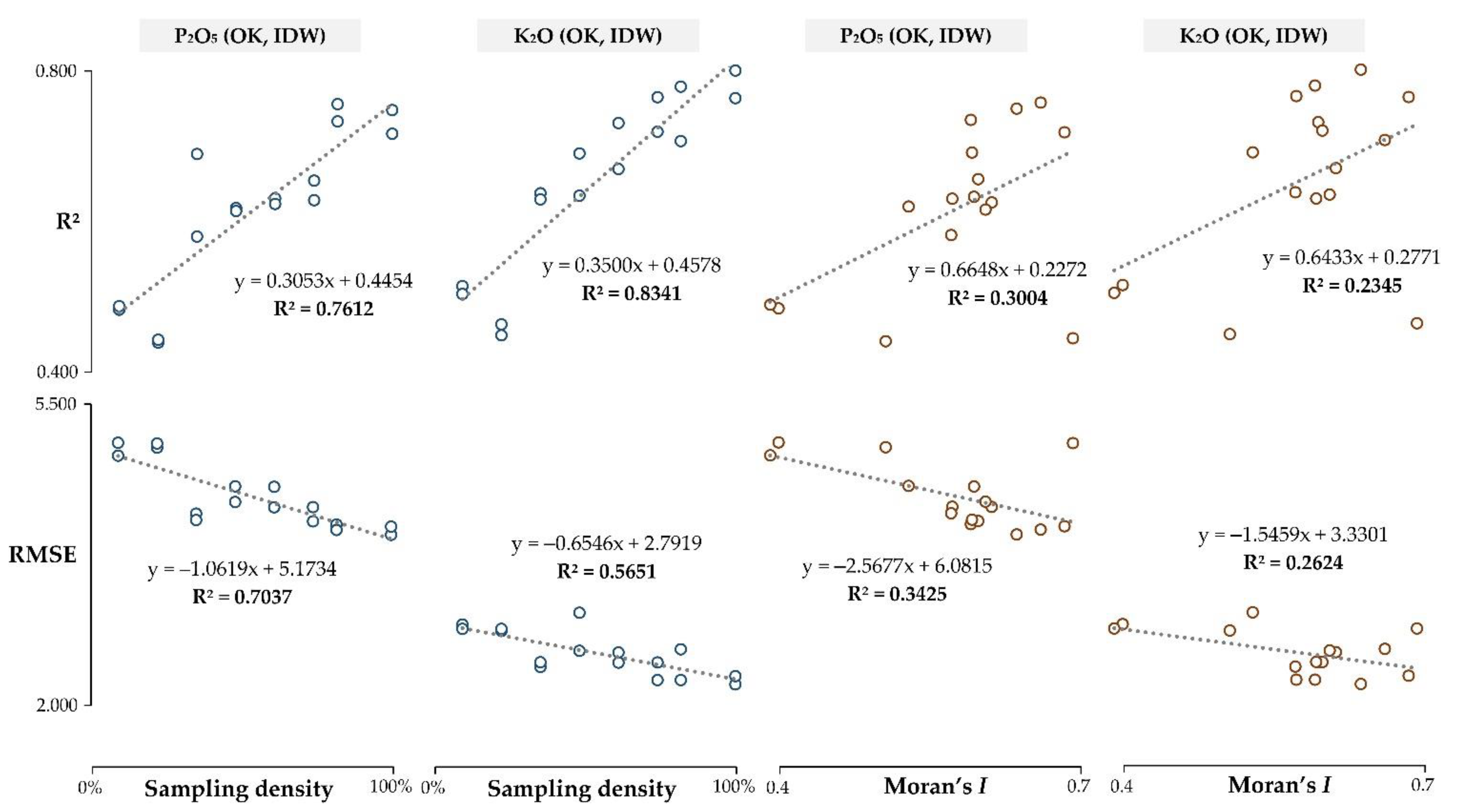
- Interpolation accuracy primarily increases with the sampling density, having R2 produced by linear regression in the range of 56.5–83.4%. Spatial autocorrelation indicated a lower impact on the interpolation accuracy but has potentially higher applicability in cases of lower spatial autocorrelation;
- Both soil sampling density and spatial autocorrelation limit the interpolation accuracy if the number of input values is not large enough to accurately fit the mathematical model with a variogram for OK. In this study, sampling density below 37.5% on input data of 160 samples caused a rapid decrease in interpolation accuracy;
- OK and IDW resulted in a similar interpolation accuracy for both soil P2O5 and K2O interpolation, while OK was more accurate in cases of lower CV and higher spatial autocorrelation. While deterministic interpolation methods, such as IDW, were inferior to OK in previous studies, they should be evaluated alongside geostatistical interpolation methods in similar studies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

| Soil Property | Percentage of Soil Samples | n | s | r (m) | R2v |
|---|---|---|---|---|---|
| P2O5 | 100% | 0.020 | 0.326 | 976 | 0.974 |
| 87.5% | 0.024 | 0.326 | 1020 | 0.981 | |
| 75% | 0.055 | 0.536 | 937 | 0.964 | |
| 62.5% | 0.089 | 0.475 | 1151 | 0.869 | |
| 50% | 0.032 | 0.488 | 985 | 0.943 | |
| 37.5% | 0.012 | 0.349 | 1068 | 0.862 | |
| 25% | 0.011 | 0.358 | 1501 | 0.908 | |
| 12.5% | 0.016 | 0.104 | 1630 | 0.761 | |
| K2O | 100% | 0.159 | 0.397 | 1490 | 0.993 |
| 87.5% | 0.017 | 0.242 | 1428 | 0.987 | |
| 75% | 0.020 | 0.238 | 1430 | 0.987 | |
| 62.5% | 0.006 | 0.235 | 1151 | 0.998 | |
| 50% | 0.058 | 0.461 | 985 | 0.951 | |
| 37.5% | 0.017 | 0.197 | 1068 | 0.747 | |
| 25% | 0.013 | 0.297 | 1651 | 0.745 | |
| 12.5% | 0.001 | 0.413 | 1585 | 0.759 |
References
- Shen, Q.; Wang, Y.; Wang, X.; Liu, X.; Zhang, X.; Zhang, S. Comparing Interpolation Methods to Predict Soil Total Phosphorus in the Mollisol Area of Northeast China. Catena 2019, 174, 59–72. [Google Scholar] [CrossRef]
- Sangani, M.F.; Khojasteh, D.N.; Owens, G. Dataset Characteristics Influence the Performance of Different Interpolation Methods for Soil Salinity Spatial Mapping. Environ. Monit. Assess. 2019, 191, 684. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Can the Spatial Prediction of Soil Organic Matter Contents at Various Sampling Scales Be Improved by Using Regression Kriging with Auxiliary Information? Geoderma 2010, 159, 63–75. [Google Scholar] [CrossRef]
- Reij, C.P.; Smaling, E.M.A. Analyzing Successes in Agriculture and Land Management in Sub-Saharan Africa: Is Macro-Level Gloom Obscuring Positive Micro-Level Change? Land Use Policy 2008, 25, 410–420. [Google Scholar] [CrossRef]
- Kostić, M.; Rajković, M.; Ljubičić, N.; Ivošević, B.; Radulović, M.; Blagojević, D.; Dedović, N. Georeferenced Tractor Wheel Slip Data for Prediction of Spatial Variability in Soil Physical Properties. Precis. Agric. 2021, 22, 1659–1684. [Google Scholar] [CrossRef]
- Franzen, D.; Mulla, D. A History of Precision Agriculture. In Precision Agriculture Technology for Crop Farming; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-0-429-15968-8. [Google Scholar]
- Long, J.; Liu, Y.; Xing, S.; Qiu, L.; Huang, Q.; Zhou, B.; Shen, J.; Zhang, L. Effects of Sampling Density on Interpolation Accuracy for Farmland Soil Organic Matter Concentration in a Large Region of Complex Topography. Ecol. Indic. 2018, 93, 562–571. [Google Scholar] [CrossRef]
- Hua, L.; Yang, X.; Liu, Y.; Tan, X.; Yang, Y. Spatial Distributions, Pollution Assessment, and Qualified Source Apportionment of Soil Heavy Metals in a Typical Mineral Mining City in China. Sustainability 2018, 10, 3115. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Xie, W.; Xia, J. Using Semivariogram and Moran’s I Techniques to Evaluate Spatial Distribution of Soil Micronutrients. Commun. Soil Sci. Plant Anal. 2013, 44, 1182–1192. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, D.; Shi, X.; Wang, N.; Zhang, G. Priority Selection Rating of Sampling Density and Interpolation Method for Detecting the Spatial Variability of Soil Organic Carbon in China. Environ. Earth Sci. 2015, 73, 2287–2297. [Google Scholar] [CrossRef]
- Kravchenko, A.N. Influence of Spatial Structure on Accuracy of Interpolation Methods. Soil Sci. Soc. Am. J. 2003, 67, 1564–1571. [Google Scholar] [CrossRef]
- Rodrigues, H.M.; Vasques, G.M.; Oliveira, R.P.; Tavares, S.R.L.; Ceddia, M.B.; Hernani, L.C. Finding Suitable Transect Spacing and Sampling Designs for Accurate Soil ECa Mapping from EM38-MK2. Soil Syst. 2020, 4, 56. [Google Scholar] [CrossRef]
- Liao, Y.; Li, D.; Zhang, N. Comparison of Interpolation Models for Estimating Heavy Metals in Soils under Various Spatial Characteristics and Sampling Methods. Trans. GIS 2018, 22, 409–434. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Wang, S.; Huang, X. Influence of Sampling Scale and Environmental Factors on the Spatial Heterogeneity of Soil Organic Carbon in a Small Karst Watershed. Fresenius Environ. Bull. 2018, 27, 1532–1544. [Google Scholar]
- Zhang, Z.; Sun, Y.; Yu, D.; Mao, P.; Xu, L. Influence of Sampling Point Discretization on the Regional Variability of Soil Organic Carbon in the Red Soil Region, China. Sustainability 2018, 10, 3603. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Zhao, Y.; Huang, B.; Shi, X.; Landon Darilek, J.; Yang, J.; Wang, Z.; Zhang, B. Effect of Sampling Density on Regional Soil Organic Carbon Estimation for Cultivated Soils. J. Plant Nutr. Soil Sci. 2012, 175, 671–680. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, X.; Tian, K.; Huang, B.; Hai, N. Comparison of Sampling Schemes for the Spatial Prediction of Soil Organic Matter in a Typical Black Soil Region in China. Environ. Earth Sci. 2015, 75, 4. [Google Scholar] [CrossRef]
- Ye, H.; Huang, W.; Huang, S.; Huang, Y.; Zhang, S.; Dong, Y.; Chen, P. Effects of Different Sampling Densities on Geographically Weighted Regression Kriging for Predicting Soil Organic Carbon. Spat. Stat. 2017, 20, 76–91. [Google Scholar] [CrossRef]
- Jurišić, M.; Radočaj, D.; Krčmar, S.; Plaščak, I.; Gašparović, M. Geostatistical Analysis of Soil C/N Deficiency and Its Effect on Agricultural Land Management of Major Crops in Eastern Croatia. Agronomy 2020, 10, 1996. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Antonić, O. Determination of Soil C:N Suitability Zones for Organic Farming Using an Unsupervised Classification in Eastern Croatia. Ecol. Indic. 2021, 123, 107382. [Google Scholar] [CrossRef]
- Croatian Bureau of Statistics Statistical Yearbook of the Republic of Croatia 2018. Available online: https://www.dzs.hr/Hrv_Eng/ljetopis/2018/sljh2018.pdf (accessed on 25 October 2021).
- Vukadinović, V. Plant Nutrition, 3rd ed.; Faculty of Agriculture Osijek: Osijek, Croatia, 2011. [Google Scholar]
- Zhao, R.; Li, J.; Wu, K.; Kang, L. Cultivated Land Use Zoning Based on Soil Function Evaluation from the Perspective of Black Soil Protection. Land 2021, 10, 605. [Google Scholar] [CrossRef]
- Bogunovic, I.; Filipovic, L.; Filipovic, V.; Pereira, P. Spatial Mapping of Soil Chemical Properties Using Multivariate Geostatistics. A Study from Cropland in Eastern Croatia. J. Cent. Eur. Agric. 2021, 22, 201–210. [Google Scholar] [CrossRef]
- Selmy, S.A.H.; Abd Al-Aziz, S.H.; Jiménez-Ballesta, R.; Jesús García-Navarro, F.; Fadl, M.E. Soil Quality Assessment Using Multivariate Approaches: A Case Study of the Dakhla Oasis Arid Lands. Land 2021, 10, 1074. [Google Scholar] [CrossRef]
- Yuan, W.; Sun, H.; Chen, Y.; Xia, X. Spatio-Temporal Evolution and Spatial Heterogeneity of Influencing Factors of SO2 Emissions in Chinese Cities: Fresh Evidence from MGWR. Sustainability 2021, 13, 12059. [Google Scholar] [CrossRef]
- Gazis, I.-Z.; Greinert, J. Importance of Spatial Autocorrelation in Machine Learning Modeling of Polymetallic Nodules, Model Uncertainty and Transferability at Local Scale. Minerals 2021, 11, 1172. [Google Scholar] [CrossRef]
- Hengl, T. Finding the Right Pixel Size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Robinson, T.P.; Metternicht, G. Testing the Performance of Spatial Interpolation Techniques for Mapping Soil Properties. Comput. Electron. Agric. 2006, 50, 97–108. [Google Scholar] [CrossRef]
- Negreiros, J.; Painho, M.; Aguilar, F.; Aguilar, M. Geographical Information Systems Principles of Ordinary Kriging Interpolator. J. Appl. Sci. 2010, 10, 852–867. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A Generic Framework for Spatial Prediction of Soil Variables Based on Regression-Kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Xu, Y.; Wang, X.; Bai, J.; Wang, D.; Wang, W.; Guan, Y. Estimating the Spatial Distribution of Soil Total Nitrogen and Available Potassium in Coastal Wetland Soils in the Yellow River Delta by Incorporating Multi-Source Data. Ecol. Indic. 2020, 111, 106002. [Google Scholar] [CrossRef]
- Huo, X.-N.; Li, H.; Sun, D.-F.; Zhou, L.-D.; Li, B.-G. Combining Geostatistics with Moran’s I Analysis for Mapping Soil Heavy Metals in Beijing, China. Int. J. Environ. Res. Public Health 2012, 9, 995–1017. [Google Scholar] [CrossRef] [Green Version]
- Lencsés, E.; Takács, I.; Takács-György, K. Farmers’ Perception of Precision Farming Technology among Hungarian Farmers. Sustainability 2014, 6, 8452–8465. [Google Scholar] [CrossRef] [Green Version]
- Bogunovic, I.; Pereira, P.; Brevik, E.C. Spatial Distribution of Soil Chemical Properties in an Organic Farm in Croatia. Sci. Total Environ. 2017, 584–585, 535–545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boubehziz, S.; Khanchoul, K.; Benslama, M.; Benslama, A.; Marchetti, A.; Francaviglia, R.; Piccini, C. Predictive Mapping of Soil Organic Carbon in Northeast Algeria. Catena 2020, 190, 104539. [Google Scholar] [CrossRef]
| Reference | Study Area | Total Sample Count | Average Area per Sample (ha) | Correlation of Interpolation Accuracy and Sampling Density |
|---|---|---|---|---|
| Rodrigues et al. [12] | 72 ha | 4306 | 0.02 | low |
| Kravchenko [11] | 20 ha | 529 | 0.04 | low |
| Zhang et al. [14] | 72 km2 | 2755 | 2.61 | moderate |
| Zhang et al. [10] | 40 km2 | 997 | 4.01 | high |
| Long et al. [7] | 10,636 km2 | 188,247 | 5.65 | high |
| Zhang et al. [15] | 40 km2 | 214 | 18.7 | high |
| Shen et al. [1] | 173 km2 | 700 | 24.7 | high |
| Li [3] | 400 km2 | 335 | 119 | low |
| Sun et al. [16] | 683 km2 | 394 | 173 | high |
| Zhao et al. [17] | 1450 km2 | 745 | 195 | moderate |
| Ye et al. [18] | 16,400 km2 | 1458 | 1125 | high |
| Liu et al. [9] | 620,000 km2 | 382 | 162,304 | low |
| Soil Property | Percentage of Soil Samples | Mean | CV | Min | Max | Shapiro–Wilk | Target Spatial Resolution (m) | |
|---|---|---|---|---|---|---|---|---|
| W | p | |||||||
| P2O5 | 100% | 21.59 | 0.32 | 8.3 | 36.5 | 0.971 | 0.002 | 18 |
| 87.5% | 21.59 | 0.31 | 8.3 | 36.5 | 0.973 | 0.007 | 19 | |
| 75% | 21.44 | 0.32 | 10.3 | 36.5 | 0.968 | 0.006 | 21 | |
| 62.5% | 21.55 | 0.32 | 10.5 | 36.5 | 0.967 | 0.012 | 23 | |
| 50% | 20.75 | 0.31 | 10.5 | 35.0 | 0.963 | 0.022 | 25 | |
| 37.5% | 21.65 | 0.33 | 8.3 | 36.5 | 0.972 | 0.180 | 29 | |
| 25% | 22.01 | 0.33 | 8.3 | 36.5 | 0.965 | 0.236 | 36 | |
| 12.5% | 21.55 | 0.39 | 10.5 | 36.5 | 0.936 | 0.198 | 51 | |
| K2O | 100% | 24.43 | 0.15 | 16.7 | 34.4 | 0.944 | >0.001 | 18 |
| 87.5% | 24.49 | 0.15 | 16.7 | 34.2 | 0.942 | >0.001 | 19 | |
| 75% | 24.36 | 0.15 | 16.7 | 34.4 | 0.952 | >0.001 | 21 | |
| 62.5% | 24.28 | 0.15 | 16.7 | 33.6 | 0.945 | >0.001 | 23 | |
| 50% | 24.82 | 0.15 | 19.5 | 34.4 | 0.938 | 0.001 | 25 | |
| 37.5% | 24.67 | 0.16 | 17.2 | 34.4 | 0.937 | 0.004 | 29 | |
| 25% | 24.62 | 0.18 | 17.2 | 34.2 | 0.923 | 0.008 | 36 | |
| 12.5% | 24.02 | 0.18 | 17.2 | 34.4 | 0.935 | 0.192 | 51 | |
| Soil Property | Percentage of Soil Samples | OK | IDW | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | R2 | RMSE | NRMSE | ||
| P2O5 | 100% | 0.743 | 4.157 | 0.193 | 0.713 | 4.249 | 0.197 |
| 87.5% | 0.729 | 4.272 | 0.198 | 0.751 | 4.211 | 0.195 | |
| 75% | 0.628 | 4.468 | 0.208 | 0.653 | 4.308 | 0.201 | |
| 62.5% | 0.630 | 4.696 | 0.218 | 0.623 | 4.466 | 0.207 | |
| 50% | 0.618 | 4.702 | 0.227 | 0.614 | 4.526 | 0.218 | |
| 37.5% | 0.581 | 4.394 | 0.203 | 0.687 | 4.323 | 0.202 | |
| 25% | 0.445 | 5.135 | 0.233 | 0.449 | 5.182 | 0.235 | |
| 12.5% | 0.487 | 5.190 | 0.241 | 0.492 | 5.044 | 0.234 | |
| K2O | 100% | 0.794 | 2.080 | 0.085 | 0.759 | 2.172 | 0.089 |
| 87.5% | 0.774 | 2.127 | 0.087 | 0.704 | 2.473 | 0.101 | |
| 75% | 0.760 | 2.127 | 0.087 | 0.716 | 2.325 | 0.095 | |
| 62.5% | 0.727 | 2.324 | 0.096 | 0.668 | 2.438 | 0.100 | |
| 50% | 0.688 | 2.884 | 0.116 | 0.634 | 2.457 | 0.099 | |
| 37.5% | 0.637 | 2.275 | 0.173 | 0.629 | 2.327 | 0.094 | |
| 25% | 0.455 | 2.678 | 0.109 | 0.469 | 2.702 | 0.110 | |
| 12.5% | 0.518 | 2.751 | 0.115 | 0.508 | 2.703 | 0.113 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radočaj, D.; Jug, I.; Vukadinović, V.; Jurišić, M.; Gašparović, M. The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland. Agronomy 2021, 11, 2430. https://doi.org/10.3390/agronomy11122430
Radočaj D, Jug I, Vukadinović V, Jurišić M, Gašparović M. The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland. Agronomy. 2021; 11(12):2430. https://doi.org/10.3390/agronomy11122430
Chicago/Turabian StyleRadočaj, Dorijan, Irena Jug, Vesna Vukadinović, Mladen Jurišić, and Mateo Gašparović. 2021. "The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland" Agronomy 11, no. 12: 2430. https://doi.org/10.3390/agronomy11122430
APA StyleRadočaj, D., Jug, I., Vukadinović, V., Jurišić, M., & Gašparović, M. (2021). The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland. Agronomy, 11(12), 2430. https://doi.org/10.3390/agronomy11122430










