Influential Points in Adaptability and Stability Methods Based on Regression Models in Cotton Genotypes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Statistical Analysis
2.3. Synthetic Data
2.4. Detecting Influential Points
2.5. Computational Features
3. Results
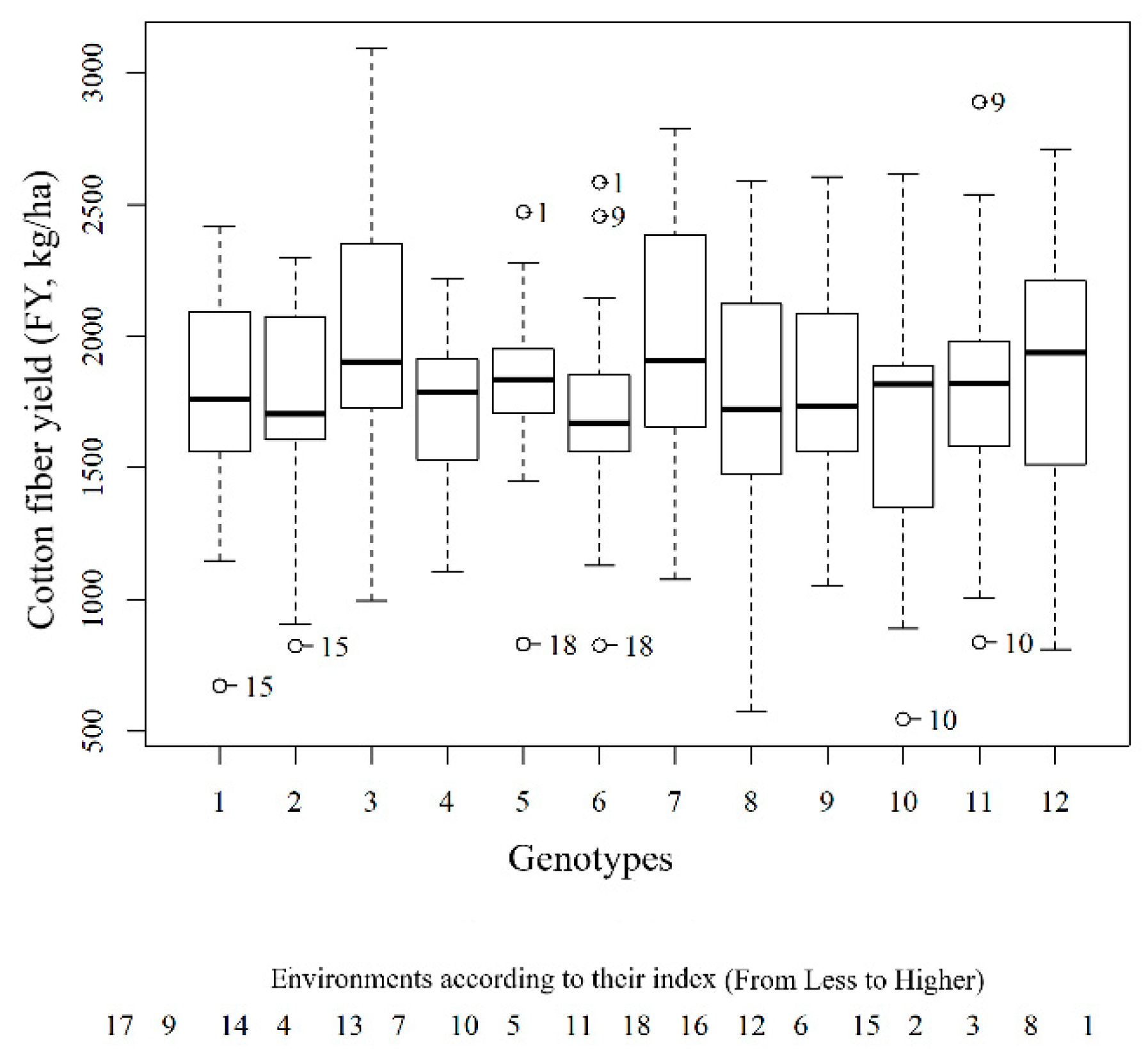
3.1. Analysis of Cotton Yields in Different Environments
3.2. Potential Influential Points on the Experimental Data
3.3. Yield Adaptability and Stability from Experimental Data
3.4. Potential Influential Points in the Synthetic Data
3.5. Yield Adaptability and Stability from Synthetic Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Cruz, C.D.; Regazzi, A.J.; Carneiro, P.C.S. Modelos Biométricos Aplicados ao Melhoramento Genético, 5th ed.; UFV—Universidade Federal de Viçosa: Viçosa, Brazil, 2012; ISBN 9788572694339. [Google Scholar]
- Van Eeuwijk, F.A.; Bustos-Korts, D.V.; Malosetti, M. What Should Students in Plant Breeding Know About the Statistical Aspects of Genotype × Environment Interactions? Crop Sci. 2016, 2140, 2119–2140. [Google Scholar] [CrossRef]
- Malosetti, M.; Ribaut, J.; Van Eeuwijk, F.A. The statistical analysis of multi-environment data: Modeling genotype-by-environment interaction and its genetic basis. Front. Physiol. 2013, 4, 1–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elias, A.A.; Robbins, K.R.; Doerge, R.W.; Tuinstra, M.R.; Elias, A.A.; Doerge, R.W.; Tuinstra, M.R. Half a Century of Studying Genotype × Environment Interactions in Plant Breeding Experiments. Crop Sci. 2016, 2105, 2090–2105. [Google Scholar] [CrossRef]
- Crossa, J.; Vargas, M.; Cossani, C.M.; Alvarado, G.; Burgueño, J.; Mathews, K.L.; Reynolds, M.P. Evaluation and interpretation of interactions. Agron. J. 2015, 107, 736–747. [Google Scholar] [CrossRef] [Green Version]
- Eberhart, S.A.; Russell, W.A. Stability Parameters for Comparing Varieties. Crop Sci. 1966, 28, 36–40. [Google Scholar] [CrossRef] [Green Version]
- Cruz, C.D.; de Torres, R.A.; Vencovsky, R. An alternative approach to the stability analysis proposed by Silva and Barreto. Revista Brasileira de Genética 1989, 12, 567–580. [Google Scholar]
- Mayara, L.; Barroso, A.; Nascimento, M.; Carolina, A.; Nascimento, C. Metodologia para análise de adaptabilidade e estabilidade por meio de regressão quantílica. Pesquisa Agropecuária Brasileira 2015, 50, 290–297. [Google Scholar] [CrossRef] [Green Version]
- Barroso, L.M.A.; Nascimento, M.; Barili, L.D.; Nascimento, A.C.C.; do Vale, N.M.; e Silva, F.F.; de Carneiro, J.E.S. Analysis of the adaptability of black bean cultivars by means of quantile regression. Ciência Rural 2019, 49, e20180045. [Google Scholar] [CrossRef]
- Lin, C.S.; Binns, M.R. A Superiority Measure of Cultivar Performance for Cultivar × Location Data. Can. J. Plant Sci. 1988, 68, 193–198. [Google Scholar] [CrossRef]
- Nascimento, M.; Ferreira, A.; Ferrão, R.G.; Campana, A.C.M.; Bhering, L.L.; Cruz, C.D.; Ferrão, M.A.G.; da Fonseca, A.F.A. Adaptabilidade e estabilidade via regressão não paramétrica em genótipos de café. Pesquisa Agropecuaria Brasileira 2010, 45, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, M.; Cruz, C.D.; Campana, A.C.M.; Tomaz, R.S.; Salgado, C.C.; de Paula Ferreira, R. Alteração no método centroide de avaliação da adaptabilidade genotípica. Pesquisa Agropecuaria Brasileira 2009, 44, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, M.; Ferreira, A.; Campana, A.C.M.; Salgado, C.C.; Cruz, C.D. Multiple centroid methodology to analyze genotype adaptability. Crop Breed. Appl. Biotechnol. 2009, 9, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Theil, H. A Rank Invariant Method of Linear and Polynomial Regression Analysis. Indag. Math. 1950, 23, 85–91. [Google Scholar]
- Children, N.; Kries, V.; Ness, A.R.; Ong, K.K.; Beyerlein, A. Genetic Markers of Obesity Risk: Stronger Associations with Body Composition in Overweight Compared to Normal-Weight Children. PLoS ONE 2011, 6, 4–7. [Google Scholar] [CrossRef] [Green Version]
- Barroso, L.M.A.; Nascimento, M.; Nascimento, A.C.C.; Silva, F.F.; Serão, N.V.L.; Cruz, C.D.; Resende, M.D.V. Regularized quantile regression for SNP marker estimation of pig growth curves. J. Anim. Sci. Biotechnol. 2017, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, A.C.C.; de Lima, J.E.; Braga, M.J.; Nascimento, M.; Gomes, A.P. Eficiência técnica da atividade leiteira em Minas Gerais: Uma aplicação de regressão quantílica. Rev. Bras. Zootec. 2012, 41, 783–789. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977; Volume 2. [Google Scholar]
- Chatterjee, S. Sensitivity Analysis in Linear Regression. Wiley Ser. Probab. Math. Stat. 1989, 38, 138. [Google Scholar] [CrossRef]
- Fox, J. Generalized Linear Models. Appl. Regres. Anal. Gen. Linear Model. 2008, 135, 379–424. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Komsta, L. mblm: Median-Based Linear Models. Available online: https://cran.r-project.org/web/packages/mblm/index.html (accessed on 10 January 2021).
- Koenker, R.; Portnoy, S.; Ng, P.T.; Zeileis, A.; Grosjean, P.; Ripley, B.D. quantreg: Quantile Regression. Available online: https://cran.r-project.org/web/packages/quantreg/index.html (accessed on 1 January 2021).
- Cruz, C.D. Acta Scientiarum GENES—A software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agron. 2013, 35, 271–276. [Google Scholar] [CrossRef]
- Draper, N.R.; John, J.A. Influential observations and outliers in regression. Technometrics 1981, 23, 21–26. [Google Scholar] [CrossRef]
- Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; Wiley: New York, NY, USA, 1980; ISBN 0471058564. [Google Scholar]
- Sprent, P.; Smeeton, N.C. Applied Nonparametric Statistical Methods, 4th ed.; CRC Press: Boca Raton, FL, USA, 2007; ISBN 13978-1-58488-701-0. [Google Scholar]
- John, O. Robustness of Quantile Regression to Outliers. Am. J. Appl. Math. Stat. 2015, 3, 86–88. [Google Scholar] [CrossRef]
| Environment State ‡ | Abbr. | Season | Alt. | Lat. | Long. | Prec. | Temp. |
|---|---|---|---|---|---|---|---|
| m | ° S | W | mm | °C | |||
| Trindade, MG | 1—TRI | 2013–2014 | 927 | 21.06 | 44.1 | 880 | 26.2 |
| Santa Helena de Goiás, GO | 2—SHE1 | 2013–2014 | 562 | 17.48 | 50.35 | 661 | 27.1 |
| 3—SHE2 | 2014–2015 | 642 | 26.8 | ||||
| Primavera do Leste, MT | 4—PVA1 | 2013–2014 | 465 | 15.33 | 54.17 | 601 | 27.5 |
| 5—PVA3 | 2014–2015 | 625 | 26.9 | ||||
| 6—PVA4 | 2014–2015 | 638 | 26.9 | ||||
| Campo Verde, MT | 7—CV1 | 2013–2014 | 736 | 15.32 | 55.1 | 864 | 25.8 |
| 8—CV2 | 2014–2015 | 879 | 25.4 | ||||
| Sinop, MT | 9—SIN | 2013–2014 | 345 | 11.51 | 55.3 | 409 | 30.9 |
| Pedra Preta, MT | 10—PPA1 | 2013–2014 | 248 | 16.37 | 54.28 | 849 | 26 |
| 11—PPA2 | 2014–2015 | 840 | 26.2 | ||||
| Luís Eduardo Magalhães, BA | 12—LEM | 2013–2014 | 769 | 12.5 | 45.47 | 802 | 25.4 |
| São Desidério, BA | 13—SDES | 2013–2014 | 497 | 12.21 | 44.58 | 658 | 27 |
| Magalhães de Almeida, MA | 14—MON | 2013–2014 | 821 | 17.26 | 51.1 | 455 | 30.1 |
| Montividiu, GO | 15—MAG | 2013–2014 | 36 | 3.23 | 42.12 | 817 | 26.8 |
| Teresina, PI | 16—TER | 2013–2014 | 72 | 5.05 | 42.48 | 810 | 26.8 |
| Chapadão do Sul, MS | 17—CHA | 2014–2015 | 800 | 18.47 | 52.37 | 898 | 26.7 |
| Sorriso, MT | 18—SOR | 2014–2015 | 365 | 12.32 | 55.42 | 436 | 31.2 |
| Source of Variation | Degree of Freedom | Mean Square |
|---|---|---|
| Environments (E) | 17 | 7,723,577.00 * |
| Blocks/environment | 54 | 44,347.00 |
| Genotypes (G) | 11 | 797,936.00 * |
| G × E | 187 | 201,748.00 * |
| Residual | 594 | 24,059.00 |
| General average | 1810.28 | |
| CV (%) | 13.29 |
| Genotype | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TMG 41 WS | 1763.61 | 1756.78 | 1770.10 | 0.93 | 0.94 | 0.87 * | 74.70 | 74.68 | 54.25 | 43,575.10 * |
| TMG 43 WS | 1732.82 | 1670.22 | 1690.16 | 0.80 * | 0.74 * | 0.95 | 65.81 | 65.52 | 41.29 | 50,291.91 * |
| IMA CV 690 | 2027.64 | 2007.15 | 2015.17 | 1.17 * | 1.14 * | 1.10 * | 85.80 | 85.75 | 58.66 | 32,384.43 * |
| IMA B2RF | 1737.20 | 1744.05 | 1732.98 | 0.62 * | 0.69 * | 0.60 * | 67.81 | 66.98 | 43.85 | 25,088.63 * |
| IMA 08 WS | 1818.91 | 1822.95 | 1832.94 | 0.61 * | 0.51 * | 0.67 * | 50.21 | 48.71 | 19.02 | 57,350.26 * |
| NUOPAL | 1698.35 | 1677.30 | 1693.74 | 0.97 | 0.98 | 1.04 | 84.44 | 84.42 | 61.66 | 23,602.33 * |
| DP 555 BGRR | 1978.41 | 1970.50 | 1961.59 | 1.22 * | 1.28 * | 1.15 * | 92.91 | 92.70 | 72.53 | 13,319.51 * |
| DELTA OPAL | 1710.32 | 1724.10 | 1712.43 | 1.21 * | 1.15 * | 1.11 * | 86.27 | 86.05 | 66.08 | 33,798.50 * |
| BRS 286 | 1801.36 | 1817.32 | 1806.78 | 0.98 | 0.97 | 0.90 * | 81.38 | 81.38 | 58.52 | 31,188.39 * |
| BRS 335 | 1743.39 | 1807.28 | 1802.79 | 1.15 * | 1.11 * | 1.10 * | 77.80 | 77.70 | 55.00 | 58,799.79 * |
| BRS 368 RF | 1827.35 | 1843.90 | 1833.29 | 1.14 * | 1.05 | 0.99 | 83.50 | 83.05 | 58.67 | 37,968.09 * |
| BRS 369 RF | 1883.99 | 1864.51 | 1862.17 | 1.22 * | 1.27 * | 1.26 * | 92.26 | 92.10 | 72.76 | 15,247.75 * |
| Genotype | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TMG 41 WS | 1842.15 | 1733.05 | 1733.05 | 0.57 * | 0.99 | 0.99 | 24.18 | 13.96 | 0.33 | 149,394.43 * |
| TMG 43 WS | 1732.82 | 1694.23 | 1688.77 | 0.84 * | 0.83 * | 0.95 | 64.64 | 64.55 | 0.41 | 52,273.67 * |
| IMA CV 690 | 2027.65 | 2049.11 | 2042.81 | 1.20 * | 1.17 * | 1.24 * | 81.67 | 81.42 | 0.56 | 43,647.29 * |
| IMA B2RF | 1737.20 | 1745.81 | 1760.93 | 0.68 * | 0.73 * | 0.65 * | 72.06 | 71.64 | 0.46 | 21,048.02 * |
| IMA 08 WS | 1818.91 | 1823.00 | 1833.22 | 0.63 * | 0.50 * | 0.68 * | 48.26 | 45.00 | 0.16 | 59,890.85 * |
| NUOPAL | 1747.64 | 1711.14 | 1697.45 | 1.04 | 1.08 | 1.21 * | 71.21 | 71.18 | 0.55 | 61,413.14 * |
| DP 555 BGRR | 1978.42 | 1989.74 | 1970.03 | 1.28 * | 1.33 * | 1.25 * | 92.28 | 92.03 | 0.76 | 15,099.32 * |
| DELTA OPAL | 1710.33 | 1706.01 | 1712.89 | 1.29 * | 1.27 * | 1.12 * | 88.24 | 88.14 | 0.64 | 28,150.74 * |
| BRS 286 | 1801.36 | 1819.52 | 1815.06 | 1.01 | 1.14 * | 1.06 | 78.62 | 78.42 | 0.58 | 36,778.73 * |
| BRS 335 | 1743.39 | 1768.41 | 1785.99 | 1.22 * | 1.18 * | 1.26 * | 77.77 | 77.67 | 0.53 | 58,952.44 * |
| BRS 368 RF | 1827.35 | 1833.40 | 1842.31 | 1.19 * | 1.16 * | 1.05 | 81.33 | 80.78 | 0.58 | 43,821.64 * |
| BRS 369 RF | 1805.58 | 1866.88 | 1862.69 | 1.03 | 1.28 * | 1.26 * | 50.79 | 46.73 | 0.51 | 151,289.81 * |
| Dataset | Genotype | Eberhart and Russell | Non-Parametric | Quantile |
|---|---|---|---|---|
| Synthetic | TMG 41 WS | Unfavorable | General | General |
| IMA 08 WS | Unfavorable | Unfavorable | Unfavorable | |
| BRS 369 RF | General | Favorable | Favorable | |
| Experimental | IMA 08 WS | Unfavorable | Unfavorable | Unfavorable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nascimento, M.; Teodoro, P.E.; Sant’Anna, I.d.C.; Barroso, L.M.A.; Nascimento, A.C.C.; Azevedo, C.F.; Teodoro, L.P.R.; Farias, F.J.C.; Almeida, H.C.; de Carvalho, L.P. Influential Points in Adaptability and Stability Methods Based on Regression Models in Cotton Genotypes. Agronomy 2021, 11, 2179. https://doi.org/10.3390/agronomy11112179
Nascimento M, Teodoro PE, Sant’Anna IdC, Barroso LMA, Nascimento ACC, Azevedo CF, Teodoro LPR, Farias FJC, Almeida HC, de Carvalho LP. Influential Points in Adaptability and Stability Methods Based on Regression Models in Cotton Genotypes. Agronomy. 2021; 11(11):2179. https://doi.org/10.3390/agronomy11112179
Chicago/Turabian StyleNascimento, Moysés, Paulo Eduardo Teodoro, Isabela de Castro Sant’Anna, Laís Mayara Azevedo Barroso, Ana Carolina Campana Nascimento, Camila Ferreira Azevedo, Larissa Pereira Ribeiro Teodoro, Francisco José Correia Farias, Helaine Claire Almeida, and Luiz Paulo de Carvalho. 2021. "Influential Points in Adaptability and Stability Methods Based on Regression Models in Cotton Genotypes" Agronomy 11, no. 11: 2179. https://doi.org/10.3390/agronomy11112179
APA StyleNascimento, M., Teodoro, P. E., Sant’Anna, I. d. C., Barroso, L. M. A., Nascimento, A. C. C., Azevedo, C. F., Teodoro, L. P. R., Farias, F. J. C., Almeida, H. C., & de Carvalho, L. P. (2021). Influential Points in Adaptability and Stability Methods Based on Regression Models in Cotton Genotypes. Agronomy, 11(11), 2179. https://doi.org/10.3390/agronomy11112179











