1. Introduction
Weeds are the main source of yield loss in crops, causing up to 34% loss across agricultural and horticultural crop production [
1,
2]. Farmers’ primary management target is maximising economic returns, which for many farmers involves the simultaneous handling of multiple objectives regarding weeds: reducing weed seedbank size, the eradication of competitive weeds, halting new invasions, and combatting herbicide resistance (HR). Many weed species generate populations with a heterogeneous density and distribution, which makes weed management difficult [
3,
4].
Site-specific management is already commonplace in many aspects of farming. Information-based management systems to adapt fertiliser distribution across the field were first introduced in the mid-1980s [
5], and since then, precision farming techniques, including GPS steering, soil mapping, and variable rate seeding are becoming increasingly popular. However, the uptake of site-specific weed management is lacking, largely due to the unavailability of accurate within-field weed species distribution maps. However, in recent years, developments in precision agriculture have led to an improved understanding of within-field spatial distributions of weeds, which is a key to improving the adoption rate of such management practices for weeds. Spatio-temporal models can predict the local development of weed populations, which may be useful in mapping pre-emergent herbicide use, although within-field distribution can be unpredictably variable [
6]. The accurate modelling of static within-field weed distributions can also be of benefit to farmers investigating herbicide resistance, checking for invasions of new weed species, and implementing biological control agents. The spatial heterogeneity within weed populations can be incorporated into temporal weed models, creating more realistic simulations, and improving differentiated weed management [
7]. Modelling within-field distributions in this way not only benefits farmers by supporting site-specific weed management, but such spatial models can also provide researchers with an improved understanding of the underlying processes determining weed spatial distributions, and open up new avenues for research and investigation to better understanding of the ecology and biology of agricultural weeds.
In this review, we outline the current state-of-the-art in both static and temporally dynamic weed spatial modelling. We highlight some of the strengths and weaknesses of current techniques and discuss the usefulness of current models. We also identify areas of emerging interest, where models of within-field weed spatial distributions could be instrumental in the development of novel weed management techniques.
2. Static Models of Within-Field Weed Distributions
Static within-field models of weed populations predict weed distribution and densities across fields. They are either based on real-time recording of the location of individual weeds or sampling at a number of discrete locations and interpolating the abundances at unsampled locations. Additional information about biotic and abiotic factors affecting within-field weed distributions can be included to improve the model predictions at unsampled locations.
2.1. Real-Time Weed Monitoring
Real-time approaches to weed management involve the assessment and treatment of weeds in the same operation, or mapping for imminent treatment. This is in combination with a decision algorithm, which allows an immediate decision to either treat, or not treat, individual parts of a field. Different real-time approaches are already feasible, but are not yet at the stage of widespread commercialization, and are continuously under development [
8]. One common type of real-time approach involves optical sensors mounted on sprayers, with real-time image analysis and decision making as the machinery passes over the field e.g., [
9,
10,
11]. Alternatively, cameras can be mounted on unmanned aerial vehicles for rapid mapping of whole fields, and machine learning techniques can be employed to rapidly produce spray maps for site-specific weed management [
12,
13]. The image processing methods deployed in these real-time approaches generally involve segmentation of the image to locate areas that are different from the crop. The sophistication of these algorithms is constantly being developed to achieve better classification of vegetation, as current methods are largely limited to identifying any vegetation growing prior to crop establishment, or outside the emerged crop rows [
14]. The detail of the maps produced by these real-time monitoring methods is unrivalled by other lower-tech mapping options, however, both the cost associated with the equipment required to produce such maps, and the dynamic nature of the research, are barriers to uptake for many farmers.
2.2. Manual Sampling of Within-Field Weed Distributions
In addition to real-time assessment, field-wide weed maps can also be created from manually collected data of weed distributions. However, manual collection is less often used in practice, as it is more time-consuming than real-time monitoring techniques. Rew and Cousens [
15] outlined three groups of methods for manual sampling of weeds: discrete area sampling, continuous area sampling, and co-ordinate mapping of individual plants. The three methods have pros and cons: discrete area sampling consists of point observations (usually weed counts in pre-selected quadrats) and is relatively cheap and fast to conduct, yet leaves a large part of the field unsampled; continuous area sampling takes observations across the whole fields assessing average densities across pre-defined grid cells, and requiring observer consistency in their assessment of weed densities; and co-ordinate mapping provides highly detailed maps, but requires very intensive sampling efforts.
2.3. Creating Maps
After sampling, interpolation is required to estimate weed densities in the spaces between sampling points. Several interpolation methods exist [
16], for creating smoothed maps of each weed species’ distribution, with Kriging proving a particularly popular method for producing unbiased estimates [
17]. The success of any interpolation method will depend on the quality of the data obtained. Maps based on observations at coarse resolutions will be poor in detail, yet sampling at fine resolution may highlight unnecessary details, and prevent the observation of any broader patterns [
18]. In contrast to a wide variety of smoothed maps, density maps maintain separated zones within previously defined boundaries [
16]. In density maps, individual samples are either kept separate (with one sample per zone) or combined locally. This creates maps with changes in density occurring abruptly, at the boundaries between zones [
19,
20].
Within-field weed distributions can be relatively stable between years [
21] making any map produced useful in future years, although annual weeds are more variable in distribution [
22]. Patch stability does, however, not necessarily imply stability in weed density [
23]. The greater the time between sampling and prediction, the less accurate the prediction becomes. Where the factors affecting patch stability are known, it is possible to apply buffer zones around mapped weed patches to account for potential spread [
15].
2.4. Improving Static Weed Distribution Models
In some cases, it is possible to improve the reliability of a static weed distribution model by incorporating supplementary data. The inclusion of environmental properties that have known associations with a particular weed species distribution can be a valuable addition to the development of static weed distribution models, particularly where sampling of weeds is sparse. Co-kriging is one method of interpolation that allows the use of maps of environmental properties, for example, soil type, to be used to supplement the weed data and create a more robust map of weed distribution [
24]. However, the strength of association between weeds and such environmental properties can be scale-dependent [
25], and should be considered in model development. The best mapping strategy will vary between different crops and weed management systems, influenced by the quality and quantity of the available data, as well as the purpose of the map.
3. Spatio-Temporal Models of Within-Field Weed Distributions
Spatio-temporal models not only aim to map the within-field distribution of weeds, but add predictions of weed development over time and space. Their parametrisation requires knowledge about initial weed distribution, as well as a detailed understanding of ecological, environmental, and management practices, in order to simulate the complete life cycle of the plant. These models are therefore more costly in terms of parameterisation than static weed models, but have the potential to be more valuable in terms of their wider use across a range of applications.
When building spatio-temporal models at the field scale, the size of the field and the number of weeds becomes important. Each square metre of a field can contain thousands of weed seeds resulting in millions of weed seeds in even the smallest fields [
26]. From each emerging weed plant, there are spheres of influence spreading out in terms of competition and dispersal, which, at the field scale, creates billions of interactions. The number of interactions is one of the main reasons that spatio-temporal modelling is infrequently used. Spatio-temporal models deal with these difficulties in different ways.
3.1. Cellular Automata (CA) Models
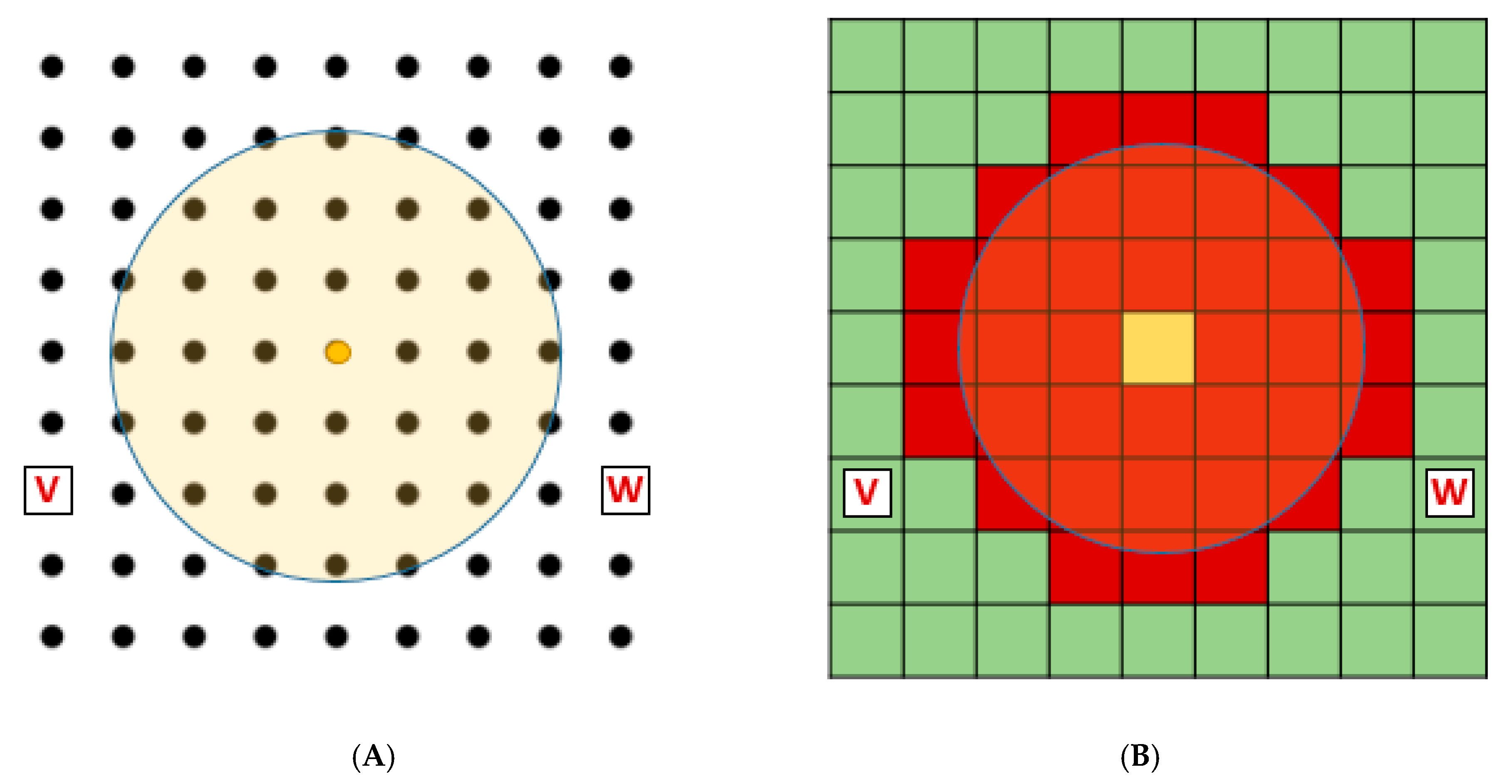
Typically, spatio-temporal models use a cellular automata (CA) approach. CA models utilise a lattice-based map of plant locations (examples shown in
Figure 1). These models either simulate single dynamic entities confined to one grid point of the lattice, sub-classified here as CA-E models (
Figure 1A), or utilise subpopulations within each cell of the lattice, sub-classified here as CA-P models (
Figure 1B). In a CA-E model, a maximum set number of entities is confined to the number of points within the lattice (81 in the case of
Figure 1) with competition and dispersal of pollen, seed, and other vegetative material assessed between nearby points in the lattice. In CA-E models information concerning vegetation and environment at each point can be quite complex, but any plants growing between the points are not specifically assessed. In CA-P models, inter- and intraspecific competition is confined within each subpopulation within a lattice cell, with the dispersal of reproductive material occurring primarily within and between nearby sub-populations. In CA-P models all plants within the lattice, of the species under consideration, are assessed.
3.1.1. CA Lattice
Lattice cells may be any shape which tessellates, although squares and hexagons are most common. The cell shape influences the type of dispersal algorithms used within the lattice. Squares simplify the incorporation and examination of anthropogenic dispersal, which is often along crop rows [
27,
28,
29], whereas hexagons simplify the parameterisation of natural dispersal, which is typically radial [
30]. Brix and Chadoeuf [
31] combined aspects of both CA-E and CA-P design with smaller cells placed within a framework of larger shapes, to simulate distribution and germination over one growing season.
Within CA-P models, cell size determines the size of each sub-population, imposing artificial constraints on the population. Competition is confined within cells and affects all plants within each cell, whereas both anthropogenic and natural dispersal occur between cells, relocating some percentage of seeds/pollen to each newly invaded cell. The dispersal of seeds typically declines rapidly with distance, meaning that species with limited dispersal are best replicated using smaller cell sizes, in order to achieve annual changes in distribution [
32]. However, larger cell sizes also have advantages: since competition is typically confined to within individual cells, they need to contain enough crop plants to capture the effect of each weed on crop growth; larger cells also allow a larger area to be simulated with the same number of sub-populations, which decreases the runtime of the model. Cell size choice may also need to consider anthropogenic processes, e.g., if combine harvester trails are simulated, cell width must be related to trail width [
27,
28]. Depending on the simulated situation, larger cells can be used without affecting the results, although some details on spatial differences within the weed population will be eliminated [
33]. The realistic spatial containment of competition and biological dispersal imposed by cell size are two of the main advantages of spatial modelling of within-field weed populations.
3.1.2. Edge of Lattice
Spatial models are highly variable in how they deal with the edge of the lattice, and how the chosen dispersal functions will receive and deposit biological material outside the lattice boundary. However, edge effects are less important when modelling spread from a central point [
33].
The simplest assumption is that the edges of the lattice neighbour an external area, which can be biologically different to the population within the lattice. This external area is typically uniform, and has been modelled as non-responsive [
34], or barren [
30]. However, in these studies, sub-populations near the edge of the lattice suffer a comparative genetic, or seed deficit, when compared to more centrally located sub-populations, which are both donating, and receiving, pollen and seed. Edge effects can be minimised by using more detailed lattices, [
30] or by using lattices covering a larger area [
27].
Edge effects can be accounted for by reflecting discarded seed and pollen from cells near the edges back into the cell it originated from, like placing a mirror along the edges of the lattice. Another method is to metaphysically wrap the edges of the lattice. When wrapping is used, weeds at one edge of the lattice (position ‘V’ in
Figure 1) are considered to neighbour weeds on the opposite side of the lattice (position ‘W’ in
Figure 1). Wrapping means that loss (and gain) from cells near the edge of the lattice is eliminated [
33,
35]. However, fields with directional movement, or spatial zones with gradients, may be unsuitable for wrapping.
3.1.3. Spatial Replication and Subpopulations
Early CA-E modelling using a lattice layout was conducted by Rees and Paynter [
35], who simulated weed growth and reproduction over a square lattice (of 5625 sites). Their simulation allowed for only a single weed plant (absent or present with a variety of growth stages) at each site position. More complex CA-E models have been used recently, with defined levels and types of weed flora possible at each CA-E point [
36,
37]. Richter, et al. [
38] presented an early CA-P model by using matrix population modelling within each sub-population. In contrast, most of the more recent work using CA-P modelling utilise sub-populations in the CA-P format, [
27,
32], with the added complexity of 3-D soil profiles in Metcalfe, et al. [
39]. The use of sub-populations in CA-P simulations means that every weed within the lattice is accounted for, each with its own genetic, germination, survival, and seed set probabilities. The multitude of calculations within CA-P models can be simplified by using matrix population models [
38], or by applying various probability theories within and between sub-population groups. In CA-E modelling, calculations do not involve individual plants, but instead examine changes in entity state. The use of states in CA-E models means less detail is included about genetics and individual plants, but that different species can be more easily included. In CA-E models, field surveys can be directly matched to the grid points, removing the need to interpolate weed maps for initial model parameterisation.
Seeds typically disperse over smaller distances than pollen, which can be simulated well in spatial models. However, the concept of cells limits the realism, by defining biological dispersal to a series of artificial ‘jumps’ between cells. This issue is more important for species with smaller seed distributions, and necessitates the use of smaller cells, however, results can still realistically mimic field data [
4]. These rigid boundaries between cells can be avoided with the use of either partial differential equations, or directional geometry in non-CA modelling [
40,
41]. In any case, the containment of seed dispersal possible in a spatial model means that weed population growth is realistically slower, due to localised intra-species competition. In comparison, in non-spatial weed models intra-species weed competition does not affect early population growth [
33,
34].
3.2. Non-CA Models
CA models are particularly useful for simulations in 2-D over a reasonably homogeneous environment such as a crop field. However, in some cases, the rigid nature of the CA lattice and the uniform nature of the utilised environment may be either unnecessary, or insufficient to provide optimal simulations. For example, Andujar et al. [
41] utilised both directional triangular geometry and directional rectangular geometry, to model a new invasive weed dispersing in individual GPS guided harvester trails.
Diverse landscapes can be divided into subdomains in non-CA spatial models, with dispersal between individual subdomains calculated in a similar way to dispersal between the points in a CA framework. However, the use of distinct sub-domains is more useful at the landscape level. By avoiding a CA lattice and instead working with sub-domains, it is possible to include separate calculations for each inter-subdomain pollen and seed exchange, with the inclusion of individual terms to account for agronomic and environmental conditions, which can be unique to each inter-subdomain exchange. Whereas this system could be used for within-field gradients of environmental variables, it is more commonly used in inter-field dispersal studies where larger and more predictable variation occurs [
40,
42].
Other non-CA models work at the level of individual plants, monitoring the location of each plant within the field and determining the zone of influence each plant has on its neighbours. Colbach et al. [
43] implemented such a model using 3D cylindrical shapes to represent individual plants.
4. Modelling Spatial Processes
Dispersal and competition processes affect weed distribution within a field, with the level of their influence varying in both space and time. Spatio-temporal modelling methods have been designed for dispersal and competition, both as independent spatial processes, and as components of spatio-temporal population models.
4.1. Dispersal
Seed dispersal is an important aspect of weed dispersal and of primary importance in spatial modelling, as seeds have a high capacity to colonise new areas [
44]. In addition, seed dispersal is one of the main causes of spatial heterogeneity in fields [
45]. Seed dispersal range determines the possibility of new site colonisation and depends on the weed species and seed characteristics, as well as external factors, such as wind speed and direction. Modelling the spread of weeds within fields is achieved by predicting the proportion of plant material (typically seeds), produced at one location, that moves to another location in a given time period, at the field scale.
Increasing wind speed can increase the number of seeds dispersed and the distance of dispersal [
46]. The most common distribution is a leptokurtic pattern with a maximum close to the seed producing plants. This implies that for many weed species natural seed dispersal occurs over short distances, making patch formation likely. Early maturing weed species will shed seeds prior to crop harvest [
47]. The distance of dispersal depends partly on the germination pattern and maximum height of the parent weed plants as well as physical properties of the seeds. Dispersal of seeds and pollen in the direction of crop rows can be due to natural dispersal in tall crops, where they move more freely in the row direction compared to movement across the crop rows [
23]. In shorter crops, where the weed flowers are above the crop canopy, natural dispersal is likely to extend further, and be more uniform [
29,
48]. In addition, vegetative material can be inadvertently dispersed by the farmer, whist conducting farm management activities. Soil tillage can displace seeds and vegetative material horizontally in space [
49] and redistribute them among soil layers, according to depth and type of cultivation [
50]. Seeds remaining on the weed plants at crop harvest are dispersed by the combine harvester. The proportion of seeds entering the harvester depends on the harvest height, phonological development of the species, harvesting date, and characteristics of the propagules [
51]. Dispersal parameters had more influence on the rate of spread than demographic parameters, and increased up to 16-fold when seeds were dispersed by the harvester [
23,
52,
53,
54].
In contrast to seed dispersal, pollen has been tracked over greater distances, although most plants are pollinated by close neighbours [
55]. Pollen movement disperses genetic material within and between populations, thereby decreasing genetic difference in the overall population. Pollen dispersal does not structurally relocate weeds, but only disperses genetic material within a population. The incorporation of pollen dispersal is therefore only necessary in spatio-temporal models, which study genetic change in terms of movement and mixing of plant genes. It has been used to simulate dispersal and mixing of GM genes, and herbicide resistant genes [
28,
56]. In contrast, in a non-spatial temporal model, all genes can mix freely from the first instance, making it impossible to accurately compare genetic changes within a field.
4.2. Competition
Competition is a major factor in weed population dynamics within a field, where plant densities affect both weed reproductive rates and crop yield. Competition modelling typically includes two-way interactions, influenced by both interspecific competition between the crop and weed and among weed species, and intra-specific competition within crop and weed species. The patchy nature of weed distributions will affect within-field competition modelling.
The modelling of intraspecific competition in monocultures has been described using a reciprocal function [
57,
58], but intraspecific competition is largely neglected in competition modelling [
59]. Interspecific competition has been modelled based on two underlying concepts: replacement series and additive design. In replacement series, the density is constant, and the composition of species are varied. In the additive design, both the density and the proportion of species changes. The value and application of these designs both have merits, depending on the situation to be modelled e.g., [
60,
61]. The hyperbolic yield loss function proposed by Cousens [
62] belongs to additive design, and has been extensively used and adjusted to a range of purposes. While the basic function models the effect of only one weed species on the crop yield, later versions include crop density, emergence time, and several weed species [
63,
64,
65]. The above models can be considered as descriptive or empirical models, contrary to mechanistic or explanatory modelling approaches. The latter often uses competition for light as the limiting resource, considering canopy structure and the space plants occupy. Four such models were compared by Deen et al. [
66].
The modelling of competition within spatio-temporal models typically utilises previously published competition parameters and equations to quantify competition. In spatio-temporal models, localised competition can capture weed patchiness, thereby improving accuracy compared with weaker field-wide competition in non-spatial temporal models. The extrapolation of localised competition equations to field-wide competition becomes less reliable when the calculated relationship between density and competition is not linear.
5. Environmental and Anthropogenic Processes
Many biotic, abiotic and anthropogenic processes have been incorporated into, and investigated with, various non-spatial weed models [
59,
67]. These processes can also be investigated with spatial models with the added advantage that all input parameters can be incorporated in ways which are non-uniform [
30], randomly dynamic, or even locally responsive [
37]. However, the use of spatial models for weed populations without spatial differentiation in either the weed distribution or genetics, or in the environmental or agronomic practices, may be of little advantage over using non-spatial models [
30]. Environmental and anthropogenic dispersal of reproductive material was discussed in
Section 4.1.
5.1. Environmental
Environmental factors including light, precipitation, temperature, soil type, pH, nutrients, and moisture can vary within fields, which may influence the location of weed patches [
68]. Seeds landing in unsuitable environments are unlikely to germinate, or to compete successfully. Spatial heterogeneity of weed populations can therefore be partially determined by the local distribution of sites with suitable abiotic conditions [
45]. Soil texture will influence seed burial [
69], and germination; for example
Galium aparine and
Alopecurus myosuroides are associated with a larger clay content, whereas
Senecio vulgaris thrives on lighter soil [
70,
71]. Other soil variables such as carbon, water, and macronutrient levels have also been linked to weed distributions [
70], although these are not well understood for many species [
72]. Metcalfe et al. [
39] developed a dynamic model of the within-field spatial distribution of
A. myosuroides, which incorporated within-field spatial variation in several environmental variables, including topography and soil. They demonstrated that incremental changes to the life cycle of the species due to these environmental properties, when combined in a spatio-temporal model, resulted in realistic simulations of within field weed distributions.
5.2. Anthropogenic
Weed distribution and dispersal are also influenced by annual activities in the cropping system. Any spatial variability in current agronomic practices within the field will influence the germination, growth, and survival of weeds [
73]. For example, fertiliser application, crop orientation, and crop establishment rate may vary across the field, and can affect weed composition and fitness [
70,
74,
75]. Herbicide application and efficiency may also vary within a field, due to drift, soil properties, or crop residues, which can influence weed spatial distribution within a field [
76,
77,
78]. In addition, weed detection and cross pollination can be affected by temporal differences in plant growth patterns. When suitable bare weed habitat is transient this can affect patch colonisation, particularly when seed dispersal is pulsed, rather than continuous [
79].
5.3. Field Edges
The field-edge is known to represent a distinct habitat within the field polygon: lower herbicide and fertiliser levels allow ruderal weed species to persist [
80,
81,
82], and decreased levels of ploughing, improve perennial weed survival [
80], and germination rates of several species [
83]. Field edges also have increased numbers of more competitive species due to spill over of species from neighbouring habitats [
84]. Additionally, field boundary hedges can trap, or redirect seed dispersal [
85,
86] and harbour animals, which are pollinators, consumers, or dispersers of weeds (reviewed in Petit, et al. [
87]. Some spatial models account for the importance of field edges, whilst others choose to negate this issue by focussing on the central part of the field.
5.4. Interactions
Currently, where models of within-field weed distributions consider external processes they frequently do so in isolation. However, whilst the factors discussed in this section each play a role in individually shaping the within-field distribution of weeds, they can also act in combination, both synergistically and antagonistically, which could be considered in spatial models. Several environmental variables may be correlated, making it difficult to disassociate one from another, for example, variation in weed distribution due to local topographic variations can be linked to multiple soil factors [
70]. Similarly, ecological factors may interact in spatially explicit ways, for example, predators affect weed distribution and density, just as weed distribution and density also influences predator population density [
88]. In addition, environmental and ecological drivers of spatial heterogeneity may interact, as not only are weeds affected by soil characteristics [
89], but they can themselves, in turn, affect the quality of the soil [
90,
91,
92]. Persistent weedy patches will influence both future weed invasions, and crop yields. Often, when a patch forms there will be a large seed return in following years, leading to patch longevity [
70]. In addition, patches can become self-regulating when the weeds produce secondary metabolites (allelochemicals), which influence the germination, growth, survival, and reproduction of other plant species [
93].
6. Sensitivity Analysis
6.1. Uncertainty
Sensitivity analysis determines how different variables contribute to the model’s overall uncertainty, where spatial models come with a unique set of considerations. For example, in CA models, both the scale and the size of the lattice may affect the simulation results [
33]. In addition, the optimum size for sub-populations in CA-P analyses can be influenced by many biotic factors, meaning that sensitivity analysis in relation to lattice planning is essential. Somerville et al. [
32] also demonstrated that decisions on cell size need to be species specific.
6.2. Error
Error in estimations of weed density and distribution in a weed model can be divided into two types: estimating that weeds are worse than they truly are (a type one error), and estimating weeds are not as bad as they are in reality (a type two error). Type one errors mean weed control measures will be implemented when they are not needed, wasting time and money. Type two errors mean that weeds will incorrectly not be controlled, possibly resulting in unexpected crop losses, and a larger weed seed bank [
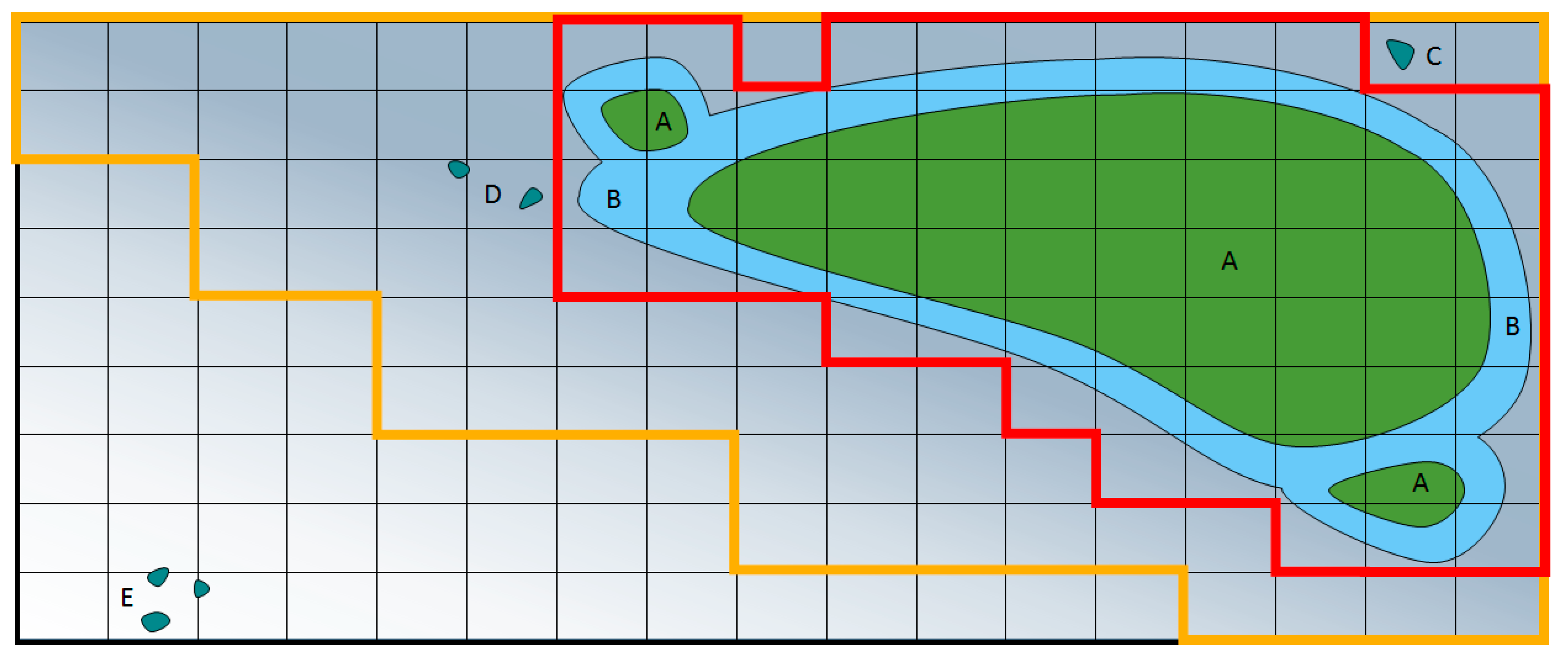
94]. Error can be reduced by increasing the frequency, size, and analysis of the weed images, or reducing the time between image capture and spraying. Changes in threshold calculations will affect the balance between type one and type two errors, for example in
Figure 2, when only the darker red area is sprayed this uses the least herbicide, whereas spraying the yellow area is a more conservative approach to weed control. The yellow area reduces type two errors (missed weeds), but increases type one errors (wasted spray). Both types of errors can occur within the same field, and may incur different levels of concern to the agronomist.
6.3. Stochasticity
Many of the factors affecting weed distribution are partly random in nature, making their full spatial assessment at least as difficult and time consuming as field-wide weed counts. To help account for this variability, stochastic processes are often used in simulations. However, the agroecosystem is a complex interaction of biological mechanisms, agricultural activities, and environmental variables.
Stochastic simulations are different from deterministic simulations, because they use probabilities to govern their biological processes. Stochastic parameterisations can be used in spatial, or non-spatial simulation models, but their incorporation into CA simulations means that a range of results will be found at the same time at different locations within the lattice, even when the starting population is uniform. Spatial variability in the starting population has been used in deterministic models to achieve reliable results in short run simulations [
95]. However, at densities of less than one weed per cell, the rounding in deterministic models will extinguish sub-populations earlier than in stochastic models.
7. Use-Cases and Future Directions
Models of within-field weed spatial distributions have been developed for several purposes, currently, the targeted application of herbicides is a predominant use. However, more varied uses also exist, with both farmers and scientists as the targeted end-user.
7.1. Targeted Weed Treatments
Integrated weed management (IWM) is promoted, both as a way to reduce the reliance on herbicides [
96], and as a method to slow herbicide resistance evolution [
97]. Spatial modelling can be useful in promoting IWM; targeted spraying of both current, and pre-emergent weeds is a growing area of research into lowering herbicide use. Improvements in static spatial modelling should help build better weed maps for spraying current and pre-emergent weeds, with additional advantages provided from using spatio-temporal models to predict weed numbers and crop yields in future years.
Both real time assessments and interpolated weed maps are useful for the design of within-field spray maps for herbicide applications, particularly when they incorporate buffer zones to account for potential patch spread. Spatio-temporal models can be used to predict “weed-vulnerable zones” and patch persistence [
39]. The resulting weed maps may be useful to generate predictive spray maps for use with pre-emergence herbicides, where it is not possible to spray based on observations of weed distributions alone (
Figure 2).
Each herbicide spray map needs to consider not only the flora, but also the capacity of the sprayer. The technology development in designing weed maps must be linked closely to the capacity of farmers to access appropriate sprayers. Sprayers with more nozzles across the boom, and graduated control of each nozzle, can implement more complex spray maps [
13], although large herbicide savings can still be achieved with limited sprayer refinement [
4]. In addition, sprayers may be developed with the capacity to apply multiple herbicides in a single operation, thereby further refining the weed modelling criteria.
7.2. Herbicide Resistance and Integrated Weed Management+
Outcrossing annual weed species producing high numbers of seeds are more susceptible to herbicide resistance, with high levels of herbicide resistance confined to a small number of species [
98]. However, changing climatic conditions [
99], new farming practices [
100,
101], legislative changes [
102], and higher levels of international trade [
103] will expose a new cohort of different weed species to different herbicide regimes. Herbicide resistance selection pressure is dynamic, and, in many instances, worsening [
102,
104].
Simulating spatial movement of HR genes was reviewed in Bagavathiannan and Norsworthy [
105], where they comment on the importance of within field spatial differences in both biology and environment. Knowledge of the location and movement of HR genes within fields is important, as diversity in the within-field management of weeds (integrated weed management) is the best method to reduce herbicide resistance [
97]. Typically, spatio-temporal models predict slower rates of HR evolution (see
Section 3.2), even for a single gene, when compared to (non-spatial) temporal models [
33,
34,
106]. In contrast, high concentrations of HR weeds develop in localised patches in CA simulations [
33].
Several HR genes are either partially, or fully recessive [
107], meaning that homozygous HR weeds have a greater chance of surviving herbicide applications. In addition, two genetically different, initially rare HR genes, causing multiple resistance (in the same weed plant), are unlikely to spontaneously occur near each other within a field [
28,
108]. CA models will, by definition, develop patches of weeds with the same form of HR (giving rise to more homozygous HR weeds) and simultaneously maintain some separation between different forms of HR genes, giving rise to less multiple HR weeds [
109]. Therefore, CA models examining either semi- or fully-recessive HR genes [
109,
110], or the development of a multiple HR population [
28], will give markedly different results to non-spatial simulations, which consider all weeds to be part of a freely interbreeding non-spatially defined, weed population.
Much of the earlier work on the spatial dispersal of herbicide resistance included a fitness cost within the HR weeds [
38,
109], and examined the effects of rotating herbicides or incorporating areas or times of reduced spraying. However, the coupling of HR and a fitness cost is evolutionarily selected against, and the permanence of any fitness cost is now questioned [
111]. The modelling of HR genes is useful in identifying the causes of HR, and best integrated weed management strategies. Modelling can help in the fight against present, and future outbreaks of herbicide resistance.
7.3. Cost-Benefit Analyses of Weed Management
Spatial models of weed populations can also be used to investigate the economic viability of different management practices. For example, Audsley [
112] used a spatially explicit model of
Avena fatua and
A. myosuroides to determine the weed density at which patch spraying becomes more cost effective than broadcast spraying. Similarly, González-Díaz et al. [
30] used a spatially explicit bio-economic model to determine that integrated weed management strategies are more cost effective than strategies with individual management tactics, such as herbicide application or crop rotation change, in controlling
Lolium rigidum populations. Bio-economic models can be of value in advisory services to visualise long-term consequences, which are not immediately evident for farmers.
7.4. Biocontrol, Invasive Species and Genetic Spread
Designing an invasive spread model to identify or track the spread of a new species, or the spread of new genetic material, is important in both farming and biosecurity. Spatio-temporal models of expansion from an initial site are simpler to model than whole fields of weeds, as the spread will typically be radially outwards from the initial source. This limited direction of spread means that both CA-E and non-CA models are suitable [
35,
41,
113], although CA-P models have also been used [
28].
Predictions of weed densities and distribution into the future are useful for maintaining biological weed control agents. The persistence of patches, as well as their density, size, and distribution, can all affect the persistence of biological weed control agents [
21,
88,
114]. In addition, interactions occur, with reductions in seed predator numbers, tillage [
115], and increased predation rates by weed patchiness [
21,
116,
117]. Herbivory can affect both weed seed production, and seed dispersal, adding further complexity to models of weeds under biocontrol [
118].
Simulated investigations into alternate strategies of biological control can investigate different biological control agents, release dates, and agent clumping strategies. However, the ideal choice can be dependent on whether spatial containment or population minimization is the aim of the control agent [
119], and whether type one or type two errors are of greater concern [
94].
7.5. Future Directions
In addition to the wide scope for using weed spatial and spatio-temporal models to answer emerging questions in weed ecology and management, we also see potential for the continuing improvement of the models themselves. Ongoing work in image analysis and machine learning is providing new means of real time weed detection, whilst novel geostatistical methods are enabling more reliable ways of producing accurate weed maps. In turn, these weed maps can provide improved inputs for CA models with the potential for multiple realisations of the same map, according to the uncertainty associated with it. In the area of model mechanics, there are increasing numbers of more detailed data sets available for parameterisation. Improvements in the understanding of weed species ecology and responses to management can also be incorporated into future models to allow more accurate predictions to be made. In addition, ongoing dynamics in the farming sector (
Section 7.2) will continue to provide impetus for future model developments.
8. Conclusions
Static spatial within-field weed models have many uses for growers, including tracking weeds, and targeting herbicide applications. The greatest range of development in weed modelling is currently observed for the spatio-temporal models. New models have focused on a wide range of problematic weed species and farming systems and, as such, parameterisation of the pertinent ecological processes has been widespread. Many modellers choose to use a CA approach (particularly CA-P) as this not only allows for simulation of spatially explicit processes, but maintains tractability of the model and provides output at a scale suitable for management decisions to be applied.
Traditionally, biological and ecological processes have formed the basis of spatio-temporal weed models with particular emphasis on processes such as dispersal and competition, which become particularly relevant when considering spatial distributions at the within-field scale. However, more recently, increased consideration has been given to external drivers of weed distribution, including the relationship between weeds and environmental properties, as well as anthropogenic drivers of weed distributions.
We identified a number of key areas, in
Section 7, for which the development of spatial weed models will be key to advancing the understanding of weed biology and ecology, and also in terms of allowing scientists to make recommendations about the best management practices to be implemented.
Author Contributions
Conceptualization, G.J.S.; methodology, investigation, resources, original draft preparation, review and editing, supervision and project administration by all authors; funding acquisition, S.K.M. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
H.M. and M.S. received funding from the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement No 727321. H.M. is partly supported by the Natural Environment Research Council (NERC) and the Biotechnology and Biological Sciences Research Council (BBSRC) research programme NE/N018125/1 LTS-M (ASSIST). G.J.S. and S.K.M. received funding from the Danish Innovation Fund through the project RoboWeedMaPS (project 6150-00027B).
Acknowledgments
Thank you to subsequent employers of G.J.S.: Some work on this manuscript was undertaken whilst she was employed, and under covid19 lockdown, at Rothamsted Research (UK), and later, at Lincoln University (NZ).
Conflicts of Interest
The authors declare no conflict of interest, the funders had no role in the design of the study; in the collection, analyses, or interpretation of resources; in the writing of the manuscript, or in the decision to publish.
References
- Oerke, E.-C. Crop losses to pests. J. Agric. Sci. 2005, 144, 31–43. [Google Scholar] [CrossRef]
- Llewellyn, R.S.; Ronning, D.; Ouzman, J.; Walker, S.; Mayfield, A.; Clarke, M. Impact of Weeds on Australian Grain Production: The Cost of Weeds to Australian Grain Growers and the Adoption of Weed Management and Tillage Practicess; GRDC, CSIRO: Kingston, ACT, Australia, 2016. [Google Scholar]
- Partel, V.; Kakarla, S.C.; Ampatzidis, Y. Development and evaluation of a low-cost and smart technology for precision weed management utilizing artificial intelligence. Comput. Electron. Agric. 2019, 157, 339–350. [Google Scholar] [CrossRef]
- Somerville, G.J.; Jørgensen, R.; Bojer, O.; Rydahl, P.; Dyrmann, M.; Andersen, P.; Jensen, N.-P.; Green, O. Utilise the potential herbicide savings using weed maps, when the sprayers have limited capabilities. In Precision Agriculture 19; Wageningen Academic Publishers: Wageningen, The Netherlands, 2019; pp. 231–237. [Google Scholar]
- Gebbers, R.; Adamchuk, V.I. Precision Agriculture and Food Security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef]
- Heijting, S.; Van Der Werf, W.; Stein, A.; Kropff, M. Are weed patches stable in location? Application of an explicitly two-dimensional methodology. Weed Res. 2007, 47, 381–395. [Google Scholar] [CrossRef]
- Emry, D.J.; Alexander, H.M.; Tourtellot, M.K. Modelling the local spread of invasive plants: Importance of including spatial distribution and detectability in management plans. J. Appl. Ecol. 2011, 48, 1391–1400. [Google Scholar] [CrossRef]
- Westwood, J.H.; Charudattan, R.; Duke, S.O.; Fennimore, S.A.; Marrone, P.; Slaughter, D.C.; Swanton, C.; Zollinger, R. Weed Management in 2050: Perspectives on the Future of Weed Science. Weed Sci. 2018, 66, 275–285. [Google Scholar] [CrossRef]
- Murdoch, A.J.; Pilgrim, R.A.; de la Warr, P. Proof of concept of automated mapping of weeds in arable fields. HGCA Project Report. 2010. [Google Scholar]
- Tian, L.F.; Steward, B.L.; Tang, L. Smart sprayer project: Sensor-based selective herbicide application system. In Proceedings of the Biological Quality and Precision Agriculture II, Boston, MA, USA, 6–8 November 2000; pp. 73–80. [Google Scholar]
- Viana, L.D.A.; Tomaz, D.C.; Martins, R.N.; Rosas, J.T.F.; Dos Santos, F.F.L.; Portes, M.F. Optical Sensors for Precision Agriculture: An Outlook. J. Exp. Agric. Int. 2019, 1–9. [Google Scholar] [CrossRef]
- Maes, W.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef]
- Castaldi, F.; Pelosi, F.; Pascucci, S.; Casa, R. Assessing the potential of images from unmanned aerial vehicles (UAV) to support herbicide patch spraying in maize. Precis. Agric. 2017, 18, 76–94. [Google Scholar] [CrossRef]
- Norris, W.R.; Patterson, A.E. Remote Sensing of Weeds in Field Crops via Image Processing: A Short Literature Collection; Technical report; University of Illinois: Champaign, IL, USA, 2019. [Google Scholar]
- Rew, L.J.; Cousens, R.D. Spatial distribution of weeds in arable crops: Are current sampling and analytical methods appropriate? Weed Res. 2001, 41, 1–18. [Google Scholar] [CrossRef]
- GIS. Types of Interpolation Methods. Available online: http://www.gisresources.com/types-interpolation-methods_3/ (accessed on 11 November 2019).
- Oliver, M.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Cousens, R.D.; Brown, R.W.; McBratney, A.B.; Whelan, B.; Moerkerk, M. Sampling strategy is important for producing weed maps: A case study using kriging. Weed Sci. 2002, 50, 542–546. [Google Scholar] [CrossRef]
- Gutjahr, C.; Sökefeld, M.; Gerhards, R. Evaluation of two patch spraying systems in winter wheat and maize. Weed Res. 2012, 52, 510–519. [Google Scholar] [CrossRef]
- Hamouz, P.; Hamouzova, K.; Holec, J.; Tyšer, L. Impact of site-specific weed management on herbicide savings and winter wheat yield. Plant Soil Environ. 2013, 59, 101–107. [Google Scholar] [CrossRef]
- Nunes, K.A.; Kotanen, P. Does local isolation allow an invasive thistle to escape enemy pressure? Oecologia 2018, 188, 139–147. [Google Scholar] [CrossRef]
- Blanco-Moreno, J.M.; Chamorro, L.; Sans, F.X. Spatial and temporal patterns of Lolium rigidum-Avena sterilis mixed populations in a cereal field. Weed Res. 2006, 46, 207–218. [Google Scholar] [CrossRef]
- Colbach, N.; Forcella, F.; Johnson, G.A. Spatial and temporal stability of weed populations over five years. Weed Sci. 2000, 48, 366–377. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: West Sussex, UK, 2007. [Google Scholar]
- Metcalfe, H.; Milne, A.E.; Webster, R.; Lark, R.M.; Murdoch, A.J.; Storkey, J. Designing a sampling scheme to reveal correlations between weeds and soil properties at multiple spatial scales. Weed Res. 2015, 56, 1–13. [Google Scholar] [CrossRef]
- Brenchley, W.E.; Warington, K. The Weed Seed Population of Arable Soil: I. Numerical Estimation of Viable Seeds and Observations on Their Natural Dormancy. J. Ecol. 1930, 18, 235–272. [Google Scholar] [CrossRef]
- Evans, J.A.; Williams, A.; Hager, A.G.; Mirsky, S.B.; Tranel, P.; Davis, A.S. Confronting herbicide resistance with cooperative management. Pest Manag. Sci. 2018, 74, 2424–2431. [Google Scholar] [CrossRef] [PubMed]
- Somerville, G.; Powles, S.B.; Walsh, M.J.; Renton, M. Modeling the Impact of Harvest Weed Seed Control on Herbicide-Resistance Evolution. Weed Sci. 2018, 66, 395–403. [Google Scholar] [CrossRef]
- Paice, M.E.R.; Day, W.; Rew, L.J.; Howard, A. A stochastic simulation model for evaluating the concept of patch spraying. Weed Res. 1998, 38, 373–388. [Google Scholar] [CrossRef]
- González-Díaz, L.; Blanco-Moreno, J.M.; Gonzalez-Andujar, J.L. Spatially explicit bioeconomic model for weed management in cereals: Validation and evaluation of management strategies. J. Appl. Ecol. 2015, 52, 240–249. [Google Scholar] [CrossRef]
- Brix, A.; Chadœuf, J. Spatio-temporal Modelling of Weeds by Shot-noiseG Cox processes. Biom. J. 2002, 44, 83–99. [Google Scholar] [CrossRef]
- Somerville, G.; Melander, B.; Kudsk, P.; Mathiassen, S.K. Modelling annual grass weed seed dispersal in winter wheat, when influenced by hedges and directional wind. Ecol. Model. 2019, 410, 108729. [Google Scholar] [CrossRef]
- Somerville, G.J.; Powles, S.; Walsh, M.J.; Renton, M. How do spatial heterogeneity and dispersal in weed population models affect predictions of herbicide resistance evolution? Ecol. Model. 2017, 362, 37–53. [Google Scholar] [CrossRef]
- Somerville, G.J.; Renton, M. Does adding a spatial component to a herbicide resistance population model improve understanding and predictions of the build-up of herbicide resistance over time? In Proceedings of the MODSIM2015, 21st International Congress on Modelling and Simulation. Modelling and Simulation Society of Australia and New Zealand, Gold Coast, Australia, 29 November–4 December 2015; pp. 476–482. [Google Scholar]
- Rees, M.; Paynter, Q. Biological Control of Scotch Broom: Modelling the Determinants of Abundance and the Potential Impact of Introduced Insect Herbivores. J. Appl. Ecol. 1997, 34, 1203–1221. [Google Scholar] [CrossRef]
- Cohen, Y.; Roei, I.; Blank, L.; Goldshtein, E.; Eizenberg, H. Spatial Spread of the Root Parasitic Weed Phelipanche aegyptiaca in Processing Tomatoes by Using Ecoinformatics and Spatial Analysis†. Front. Plant Sci. 2017, 8, 973. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-L.; Perry, G.L.W.; Brierley, G. A spatial simulation model to assess controls upon grassland degradation on the Qinghai-Tibet Plateau, China. Appl. Geogr. 2018, 98, 166–176. [Google Scholar] [CrossRef]
- Richter, O.; Zwerger, P.; Böttcher, U. Modelling spatio-temporal dynamics of herbicide resistance. Weed Res. 2002, 42, 52–64. [Google Scholar] [CrossRef]
- Metcalfe, H.; Milne, A.E.; Coleman, K.; Murdoch, A.; Storkey, J. Modelling the effect of spatially variable soil properties on the distribution of weeds. Ecol. Model. 2019, 396, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Richter, O. Modelling dispersal of populations and genetic information by finite element methods. Environ. Model. Softw. 2008, 23, 206–214. [Google Scholar] [CrossRef]
- Andujar, D.; Rodriguez-Lloveras, X.; Rueda-Ayala, V.; Martín, C.S.; Ribeiro, A.; Fernández-Quintanilla, C.; Dorado, J. A Geometrical Model to Predict the Spatial Expansion of Sorghum Halepense in Maize Fields. Gesunde Pflanz. 2017, 69, 73–81. [Google Scholar] [CrossRef]
- Lipsius, K.; Richter, O. Modelling dispersal of genetic information in structured agricultural landscapes with partial differential equations. In Proceedings of the COMSOL Conference, Hannover, Germany, 5 November 2005. [Google Scholar]
- Colbach, N.; Collard, A.; Guyot, S.H.; Mézière, D.; Munier-Jolain, N. Assessing innovative sowing patterns for integrated weed management with a 3D crop:weed competition model. Eur. J. Agron. 2014, 53, 74–89. [Google Scholar] [CrossRef]
- Maréchal, P.-Y.; Henriet, F.; Vancutsem, F.; Bodson, B. Ecological review of black-grass (Alopecurus myosuroides Huds.) propagation abilities in relationship with herbicide resistance. Biotechnol Agron. Soc. Environ. 2012, 16. [Google Scholar]
- Groenendael, J.M. Patchy distribution of weeds and some implications for modelling population dynamics: A short literature review. Weed Res. 1988, 28, 437–441. [Google Scholar] [CrossRef]
- Colbach, N.; Sache, I. Blackgrass (Alopecurus myosuroides Huds.) seed dispersal from a single plant and its consequences on weed infestation. Ecol. Model. 2001, 139, 201–219. [Google Scholar] [CrossRef]
- Bitarafan, Z.; Andreasen, C. Seed production and retention at maturity of blackgrass (Alopecurus myosuroides) and silky windgrass (Apera spica-venti) at wheat harvest. Weed Sci. 2020, 68, 151–156. [Google Scholar] [CrossRef]
- Rognli, O.A.; Nilsson, N.-O.; Nurminiemi, M. Effects of distance and pollen competition on gene flow in the wind-pollinated grass Festuca pratensis Huds. Heredity 2000, 85, 550–560. [Google Scholar] [CrossRef]
- Gonzalez-Andujar, J.L.; Perry, J.N.; Moss, S.R. Modeling effects of spatial patterns on the seed bank dynamics of Alopecurus myosuroides. Weed Sci. 1999, 47, 697–705. [Google Scholar] [CrossRef]
- Munier-Jolain, N.M.; Chavvel, B.; Gasquez, J. Long-term modelling of weed control strategies: Analysis of threshold-based options for weed species with contrasted competitive abilities. Weed Res. 2002, 42, 107–122. [Google Scholar] [CrossRef]
- Walsh, M.J.; Broster, J.C.; Aves, C.; Powles, S.B. Influence of annual ryegrass seed retention height on harvest weed seed control (HWSC) and harvest efficiency. In Proceedings of the 20th Australasian Weeds Conference, Perth, Western Australia, 11–15 September 2016; pp. 42–45. [Google Scholar]
- Woolcock, J.L.; Cousens, R. A mathematical analysis of factors affecting the rate of spread of patches of annual weeds in an arable field. Weed Sci. 2000, 48, 27–34. [Google Scholar] [CrossRef]
- Barroso, J.; Navarrete, L.; Del Arco, M.J.S.; Fernandez-Quintanilla, C.; Lutman, P.J.W.; Perry, N.H.; Hull, R.I. Dispersal of Avena fatua and Avena sterilis patches by natural dissemination, soil tillage and combine harvesters. Weed Res. 2006, 46, 118–128. [Google Scholar] [CrossRef]
- Blanco-Moreno, J.M.; Chamorro, L.; Masalles, R.M.; Recasens, J.; Sans, F.X. Spatial distribution of Lolium rigidum seedlings following seed dispersal by combine harvesters. Weed Res. 2004, 44, 375–387. [Google Scholar] [CrossRef]
- Busi, R.; Yu, Q.; Barrett-Lennard, R.; Powles, S. Long distance pollen-mediated flow of herbicide resistance genes in Lolium rigidum. Theor. Appl. Genet. 2008, 117, 1281–1290. [Google Scholar] [CrossRef]
- Richter, O.; Seppelt, R. Flow of genetic information through agricultural ecosystems: A generic modelling framework with application to pesticide-resistance weeds and genetically modified crops. Ecol. Model. 2004, 174, 55–66. [Google Scholar] [CrossRef]
- Bleasdale, J.K.A.; Nelder, J.A. Plant Population and Crop Yield. Nature 1960, 188, 342. [Google Scholar] [CrossRef]
- Watkinson, A. Density-dependence in single-species populations of plants. J. Theor. Boil. 1980, 83, 345–357. [Google Scholar] [CrossRef]
- Holst, N.; Rasmussen, I.; Bastiaans, L. Field weed population dynamics: A review of model approaches and applications. Weed Res. 2007, 47, 1–14. [Google Scholar] [CrossRef]
- Firbank, L.; Watkinson, A.R. On the Analysis of Competition within Two-Species Mixtures of Plants. J. Appl. Ecol. 1985, 22, 503–517. [Google Scholar] [CrossRef]
- Park, S.; Benjamin, L.; Watkinson, A.R. The Theory and Application of Plant Competition Models: An Agronomic Perspective. Ann. Bot. 2003, 92, 741–748. [Google Scholar] [CrossRef]
- Cousens, R. A simple model relating yield loss to weed density. Ann. Appl. Boil. 1985, 107, 239–252. [Google Scholar] [CrossRef]
- Cousens, R.D.; Moss, S.; Cussans, G.; Wilson, B. Modeling weed populations in cereals. In Reviews of Weed Science (USA); Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Cousens, R. An empirical model relating crop yield to weed and crop density and a statistical comparison with other models. J. Agric. Sci. 1985, 105, 513–521. [Google Scholar] [CrossRef]
- Holst, N. Recursive density equivalents: An improved method for forecasting yield loss caused by mixed weed populations. J. Agric. Sci. 2005, 143, 293–298. [Google Scholar] [CrossRef]
- Deen, W.; Cousens, R.; Warringa, J.; Bastiaans, L.; Carberry, P.; Rebel, K.; Riha, S.; Murphy, C.; Benjamin, L.; Cloughley, C.; et al. An evaluation of four crop: Weed competition models using a common data set. Weed Res. 2003, 43, 116–129. [Google Scholar] [CrossRef]
- Renton, M.; Busi, R.; Neve, P.; Thornby, D.; Vila-Aiub, M. Herbicide resistance modelling: Past, present and future. Pest Manag. Sci. 2014, 70, 1394–1404. [Google Scholar] [CrossRef]
- Robertson, G.P.; Gross, K.L. Assessing the Heterogeneity of Belowground Resources: Quantifying Pattern and Scale. In Exploitation of Environmental Heterogeneity by Plants: Ecophysiological Processes above-and Belowground; Academic Press: San Diego, CA, USA, 1994; pp. 237–253. [Google Scholar]
- Benvenuti, S. Weed seed movement and dispersal strategies in the agricultural environment. Weed Boil. Manag. 2007, 7, 141–157. [Google Scholar] [CrossRef]
- Lutman, P.; Perry, N.; Hull, R.; Miller, P.; Wheeler, H.; Hale, R. Developing a Weed Patch Spraying System for Use in Arable Crops; Home Grown Cereals Authority: London, UK, 2002. [Google Scholar]
- Finch-Savage, W.E.; Leubner-Metzger, G. Seed dormancy and the control of germination. New Phytol. 2006, 171, 501–523. [Google Scholar] [CrossRef]
- Dieleman, J.A.; Mortensen, D.A.; Buhler, D.D.; Cambardella, C.A.; Moorman, T.B. Identifying associations among site properties and weed species abundance. I. Multivariate analysis. Weed Sci. 2000, 48, 567–575. [Google Scholar] [CrossRef]
- Wiles, L.J. Sampling to make maps for site-specific weed management. Weed Sci. 2005, 53, 228–235. [Google Scholar] [CrossRef]
- Borger, C.P.D.; Hashem, A.; Powles, S. Manipulating crop row orientation and crop density to suppress Lolium rigidum. Weed Res. 2015, 56, 22–30. [Google Scholar] [CrossRef]
- Tsiouris, S.; Marshall, E. Observations on patterns of granular fertiliser deposition beside hedges and its likely effects on the botanical composition of field margins. Ann. Appl. Boil. 1998, 132, 115–127. [Google Scholar] [CrossRef]
- Khalil, Y.; Flower, K.; Kadambot, H.M.S.; Ward, P. Effect of crop residue and rainfall on the availability of pre-emergnet herbicides in the soil. Grain Res. Dev. Corp. 2017, 2017, 68–69. [Google Scholar]
- Ii, M.M.W.; Mortensen, D.A.; Martin, A.R.; Marx, D.B. Within-field soil heterogeneity effects on herbicide-mediated crop injury and weed biomass. Weed Sci. 2001, 49, 798–805. [Google Scholar] [CrossRef]
- Metcalfe, H.; Milne, A.E.; Hull, R.; Murdoch, A.J.; Storkey, J. The implications of spatially variable pre-emergence herbicide efficacy for weed management. Pest Manag. Sci. 2017, 74, 755–765. [Google Scholar] [CrossRef]
- Reigada, C.; Schreiber, S.J.; Altermatt, F.; Holyoak, M. Metapopulation Dynamics on Ephemeral Patches. Am. Nat. 2015, 185, 183–195. [Google Scholar] [CrossRef]
- Fried, G.; Petit, S.; Dessaint, F.; Reboud, X. Arable weed decline in Northern France: Crop edges as refugia for weed conservation? Boil. Conserv. 2009, 142, 238–243. [Google Scholar] [CrossRef]
- Kleijn, D.; Van Der Voort, L.A. Conservation headlands for rare arable weeds: The effects of fertilizer application and light penetration on plant growth. Boil. Conserv. 1997, 81, 57–67. [Google Scholar] [CrossRef]
- Wagner, M.; Bullock, J.M.; Hulmes, L.; Hulmes, S.; Pywell, R. Cereal density and N-fertiliser effects on the flora and biodiversity value of arable headlands. Biodivers. Conserv. 2017, 26, 85–102. [Google Scholar] [CrossRef]
- Scherner, A.; Melander, B.; Jensen, P.K.; Kudsk, P.; Avila, L. Reducing tillage intensity affects the cumulative emergence dynamics of annual grass weeds in winter cereals. Weed Res. 2017, 57, 314–322. [Google Scholar] [CrossRef]
- Metcalfe, H.; Hassall, K.L.; Boinot, S.; Storkey, J. The contribution of spatial mass effects to plant diversity in arable fields. J. Appl. Ecol. 2019, 56, 1560–1574. [Google Scholar] [CrossRef]
- Christensen, S. Vegetation Spread from Hedgerows and Copses into Open Farmland; Danish Agricultural Research, Departent of Plant Protection: Slagelse, Danmark, Unpublished; 2000; pp. 40–43. (In Danish)
- Bullock, J.M.; Moy, I.L. Plants as seed traps: Inter-specific interference with dispersal. Acta Oecol. 2004, 25, 35–41. [Google Scholar] [CrossRef]
- Petit, S.; Alignier, A.; Colbach, N.; Joannon, A.; Le Cœur, D.; Thenail, C. Weed dispersal by farming at various spatial scales. A review. Agron. Sustain. Dev. 2012, 33, 205–217. [Google Scholar] [CrossRef]
- Biedermann, R. Incidence and population dynamics of the leaf beetle Gonioctena olivacea in dynamic habitats. Ecography 2005, 28, 673–681. [Google Scholar] [CrossRef]
- Metcalfe, H.; Milne, A.E.; Webster, R.; Lark, R.M.; Murdoch, A.J.; Kanelo, L.; Storkey, J. Defining the habitat niche of Alopecurus myosuroides at the field scale. Weed Res. 2018, 58, 165–176. [Google Scholar] [CrossRef]
- Patriquin, D.G. Biological Husbandry and the “Nitrogen Problem”. Boil. Agric. Hortic. 1986, 3, 167–189. [Google Scholar] [CrossRef]
- Swamy, P.S.; Ramakrishnan, P.S. Ecological implications of traditional weeding and other imposed weeding regimes under slash-and-burn agriculture (jhum) in northeastern India. Weed Res. 1988, 28, 127–136. [Google Scholar] [CrossRef]
- Ziska, L.H.; Dukes, J.S. Weed Biology and Climate Change; John Wiley & Sons: Ames, IA, USA, 2011. [Google Scholar]
- Qasem, J.R.; Foy, C.L. Weed Allelopathy, Its Ecological Impacts and Future Prospects. J. Crop. Prod. 2001, 4, 43–119. [Google Scholar] [CrossRef]
- Berge, T.; Fykse, H.; Aastveit, A.H. Patch spraying of weeds in spring cereals: Simulated influences of threshold level and spraying resolution on spraying errors and potential herbicide reduction. Acta Agric. Scand. Sect. B Soil Plant Sci. 2007, 57, 212–221. [Google Scholar] [CrossRef]
- Dicke, D.; Gerhards, R.; Kuhbauch, W. Predicting Dynamics of Chenopodium Album in a Four Year Crop Rotation Using Site-Specific Weed Control. In Precision Agriculture 05; Wageningen Academic Publishers: Wageningen, The Netherlands, 2005; pp. 779–786. [Google Scholar]
- European Parliament: Council of the European Union. Directive 2009/128/EC of the European Parliament and of the Council of 21 October 2009 Establishing a Framework for Community Action to Achieve the Sustainable Use of Pesticides (Text with EEA Relevance); Office for Official Publications of the European Communities: Luxembourg, 2009; pp. 71–86. [Google Scholar]
- Norsworthy, J.K.; Ward, S.M.; Shaw, D.R.; Llewellyn, R.S.; Nichols, R.L.; Webster, T.; Bradley, K.; Frisvold, G.; Powles, S.; Burgos, N.R.; et al. Reducing the Risks of Herbicide Resistance: Best Management Practices and Recommendations. Weed Sci. 2012, 60, 31–62. [Google Scholar] [CrossRef]
- Heap, I. International Survey of Herbicide-resistant Weeds. Available online: http://www.weedscience.org (accessed on 12 September 2019).
- Peters, K.; Breitsameter, L.; Gerowitt, B. Impact of climate change on weeds in agriculture: A review. Agron. Sustain. Dev. 2014, 34, 707–721. [Google Scholar] [CrossRef]
- Smith, C.S.; Van Klinken, R.D.; Seabrook, L.; McAlpine, C. Estimating the influence of land management change on weed invasion potential using expert knowledge. Divers. Distrib. 2011, 18, 818–831. [Google Scholar] [CrossRef]
- Tuesca, D.; Puricelli, E.; Papa, J.C. A long-term study of weed flora shifts in different tillage systems. Weed Res. 2001, 41, 369–382. [Google Scholar] [CrossRef]
- Kudsk, P.; Mathiassen, S.K. Pesticide regulation in the European Union and the glyphosate controversy. Weed Sci. 2020, 68, 214–222. [Google Scholar] [CrossRef]
- Dafni, A.; Heller, D. The threat posed by alien weeds in Israel. Weed Res. 1980, 20, 277–283. [Google Scholar] [CrossRef]
- Owen, M.D.; Zelaya, I.A. Herbicide-resistant crops and weed resistance to herbicides. Pest Manag. Sci. 2005, 61, 301–311. [Google Scholar] [CrossRef] [PubMed]
- Bagavathiannan, M.V.; Norsworthy, J.K. Modeling the evolution of herbicide resistance in weeds: Current knowledge and future directions. Indian J. Weed Sci. 2016, 48, 122–127. [Google Scholar] [CrossRef]
- Roux, F.; Reboud, X. Herbicide resistance dynamics in a spatially heterogeneous environment. Crop. Prot. 2007, 26, 335–341. [Google Scholar] [CrossRef]
- Powles, S.; Yu, Q. Evolution in Action: Plants Resistant to Herbicides. Annu. Rev. Plant Boil. 2010, 61, 317–347. [Google Scholar] [CrossRef]
- Preston, C.; Powles, S. Evolution of herbicide resistance in weeds: Initial frequency of target site-based resistance to acetolactate synthase-inhibiting herbicides in Lolium rigidum. Heredity 2002, 88, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Roux, F.; Paris, M.; Reboud, X. Delaying weed adaptation to herbicide by environmental heterogeneity: A simulation approach. Pest Manag. Sci. 2007, 64, 16–29. [Google Scholar] [CrossRef]
- Evans, F.H.; Diggle, A.; Renton, M. Modelling the effects of farm management on the spread of herbicide resistance. In Proceedings of the 21st Asian Pacific Weed Science Society (APWSS) Conference, Colombo, Sri Lanka, 2–6 October 2007; pp. 88–93. [Google Scholar]
- Chen, J.; Yu, Q.; Owen, M.; Han, H.; Powles, S. Dinitroaniline herbicide resistance in a multiple-resistant Lolium rigidum population. Pest Manag. Sci. 2018, 74, 925–932. [Google Scholar] [CrossRef]
- Audsley, E. Operational research analysis of patch spraying. Crop. Prot. 1993, 12, 111–119. [Google Scholar] [CrossRef]
- Buckley, Y.M.; Rees, M.; Paynter, Q.; Lonsdale, M. Modelling integrated weed management of an invasive shrub in tropical Australia. J. Appl. Ecol. 2004, 41, 547–560. [Google Scholar] [CrossRef]
- Mills, N.; Heimpel, G.E. Could increased understanding of foraging behavior help to predict the success of biological control? Curr. Opin. Insect Sci. 2018, 27, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Brust, G.E.; House, G.J. Weed seed destruction by arthropods and rodents in low-input soybean agroecosystems. Am. J. Altern. Agric. 1988, 3, 19–25. [Google Scholar] [CrossRef]
- Torra, J.; Atanackovic, V.; Blanco-Moreno, J.M.; Royo-Esnal, A.; Westerman, P.R. Effect of patch size on seed removal by harvester ants. Weed Res. 2016, 56, 14–21. [Google Scholar] [CrossRef]
- Pannwitt, H.; Westerman, P.R.; De Mol, F.; Selig, C.; Gerowitt, B. Biological control of weed patches by seed predators; responses to seed density and exposure time. Boil. Control. 2017, 108, 1–8. [Google Scholar] [CrossRef]
- Marchetto, K.; Shea, K.; Kelly, D.; Groenteman, R.; Sezen, Z.; Jongejans, E. Unrecognized impact of a biocontrol agent on the spread rate of an invasive thistle. Ecol. Appl. 2014, 24, 1178–1187. [Google Scholar] [CrossRef] [PubMed]
- Shea, K. Models for Improving the Targeting and Implementation of Biological Control of Weeds1. Weed Technol. 2004, 18, 1578–1581. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).