Mechanical Devices for Mass Distribution Adjustment: Are They Really Convenient?
Abstract
1. Introduction
2. Materials and Methods
2.1. Interpolation of Data Obtained from Experiments
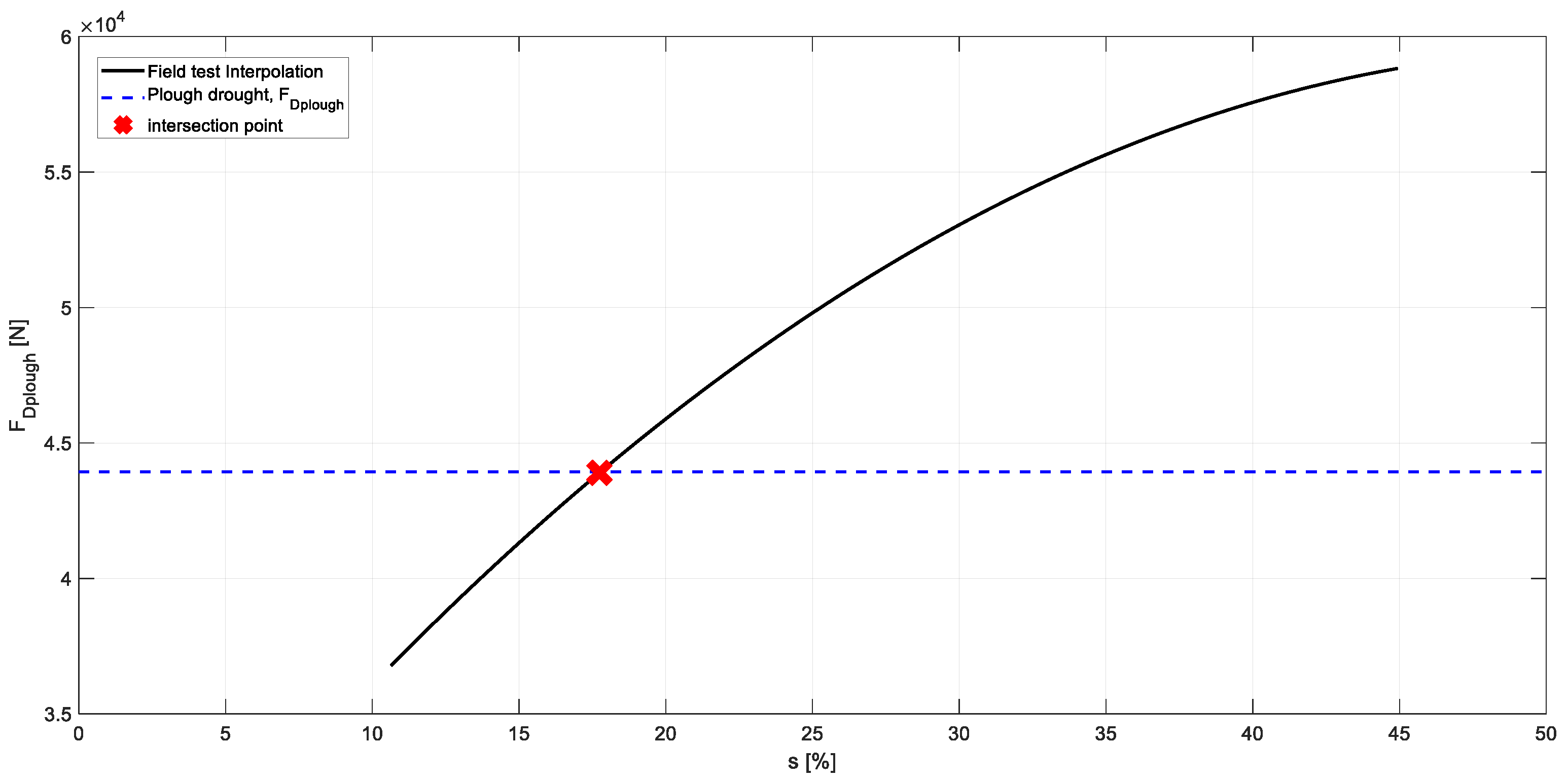
2.2. Field Productivity and Fuel Consumption Prediction
3. Results
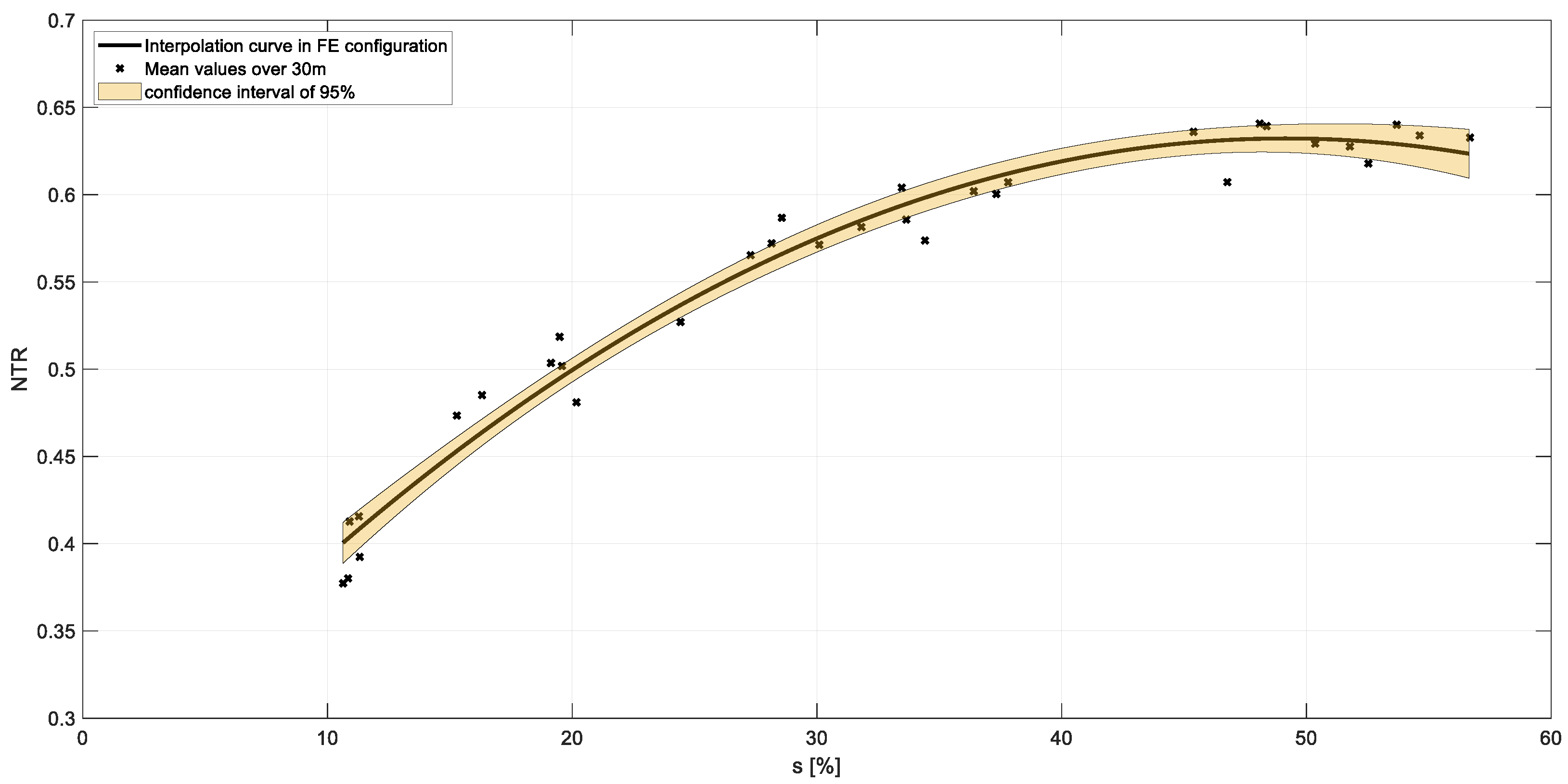
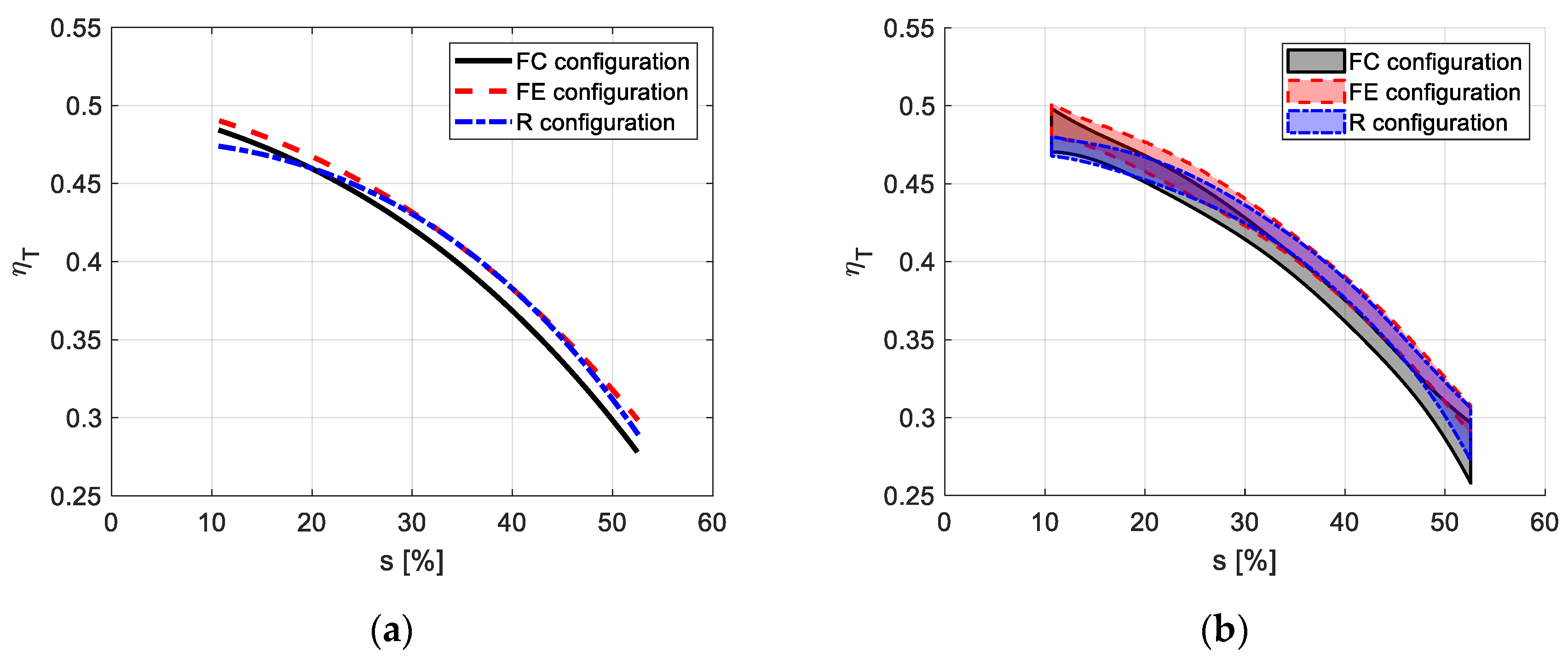
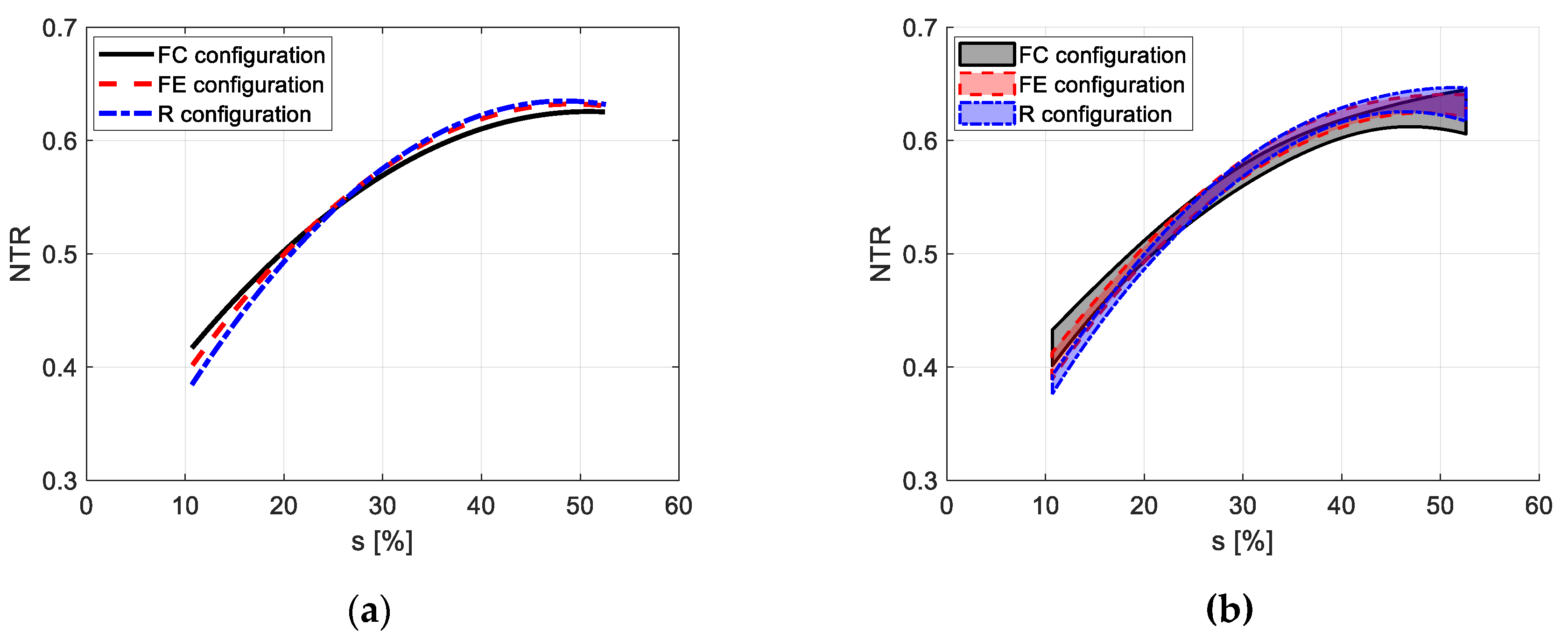
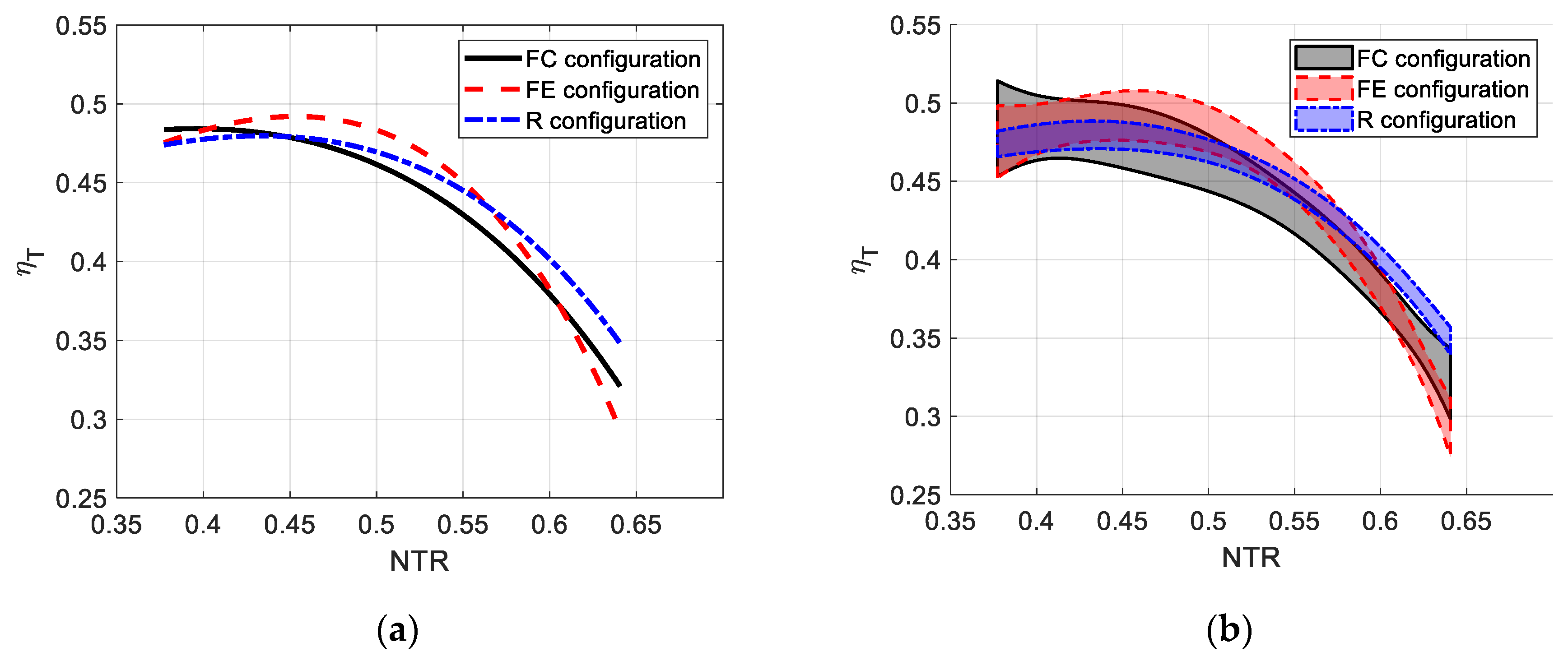
3.1. Tractive Performance
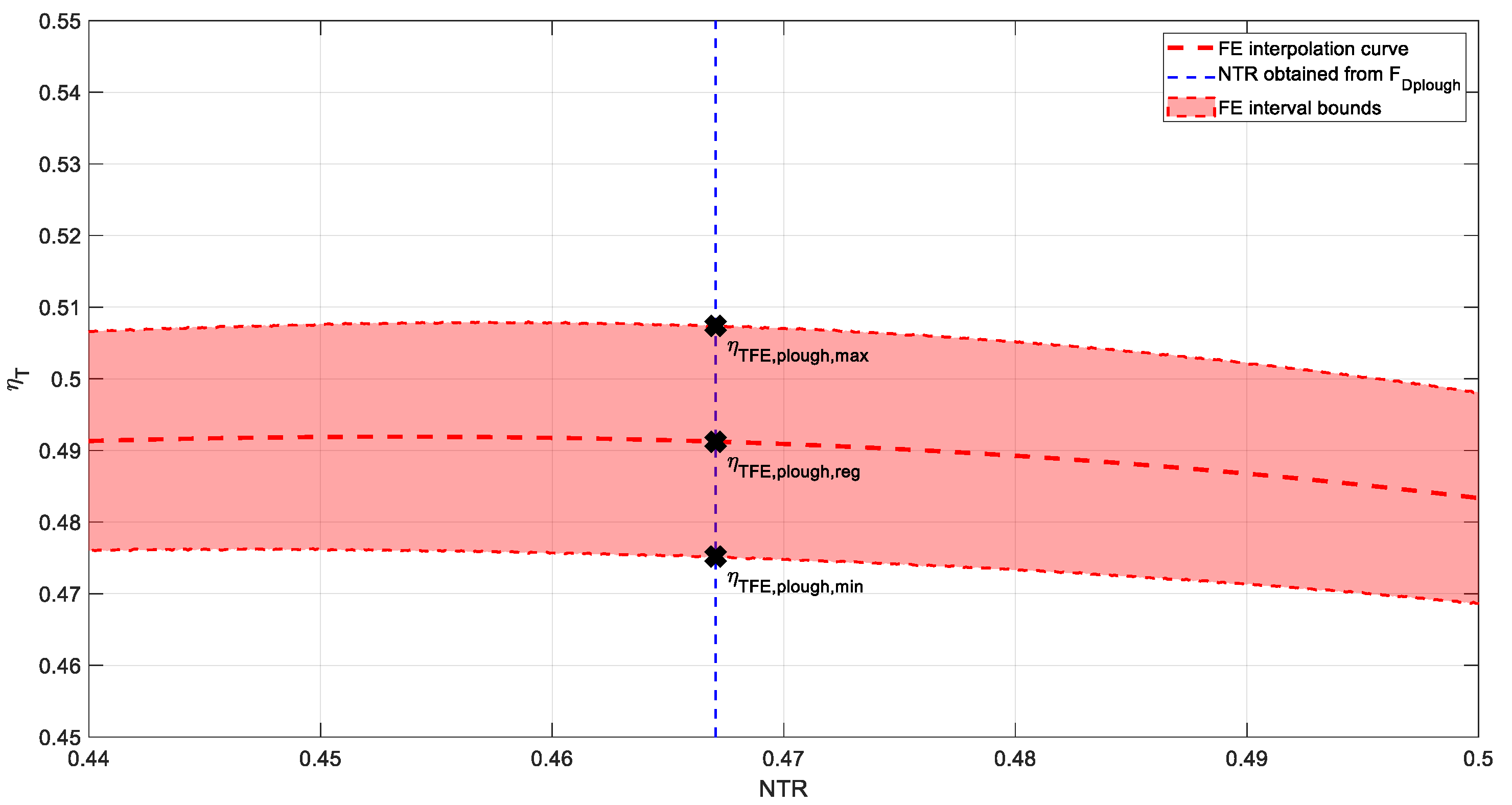
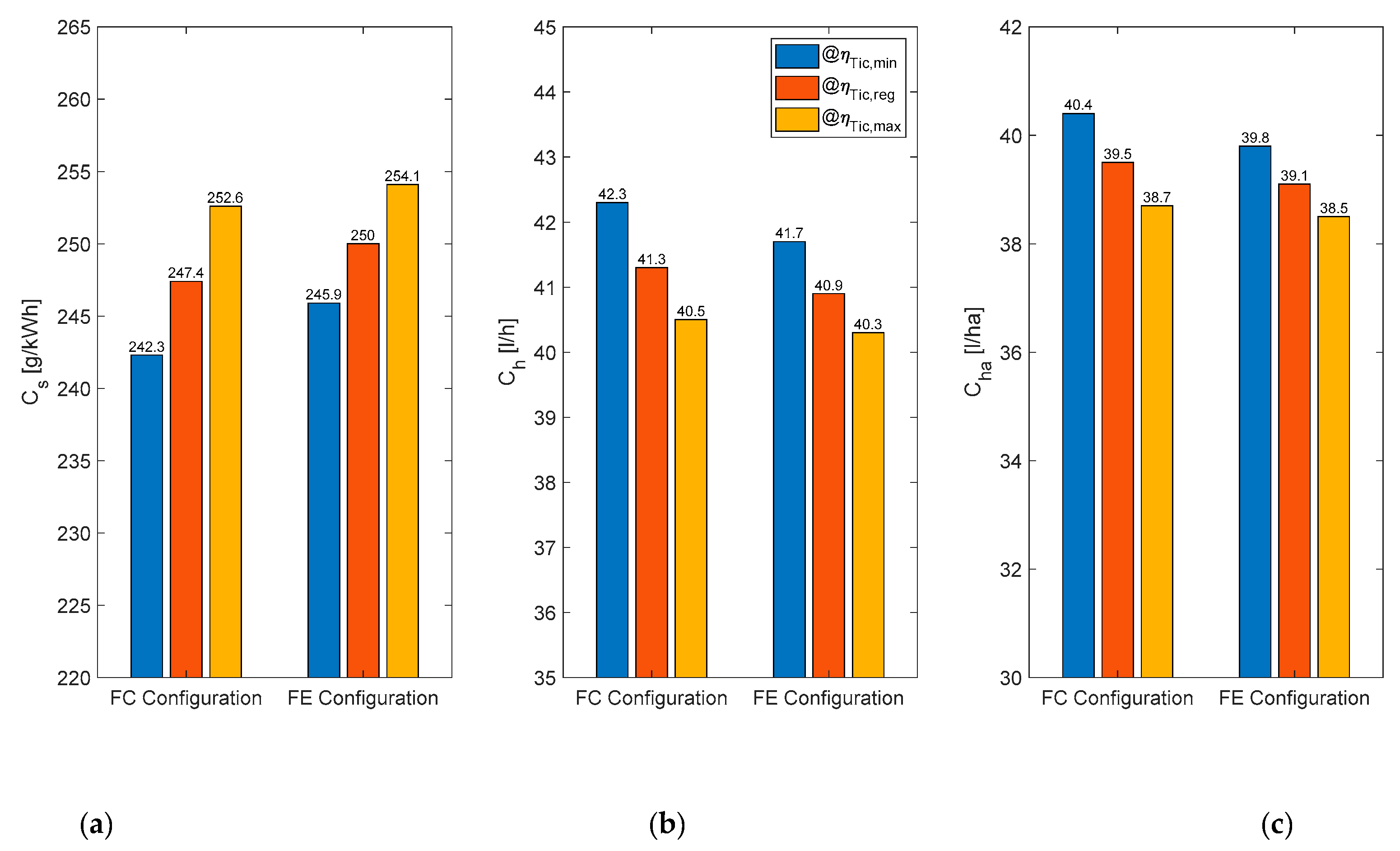
3.2. Cost-Effectiveness Analysis in FE and FC Configurations
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A



| Parameter | Value (mm) |
|---|---|
| Wheelbase (WB) | 2884 |
| Longitudinal distance of the front hitch from the front wheel hubs (xfh) | 1665 |
| Height above ground of the front hitch (hfh) | 850 |
| Longitudinal distance of the rear hitch from the rear wheel hubs (xrh) | 1200 |
| Height above ground of the rear hitch (hrh) | 655 |
| Longitudinal length of the ballast over the rear hitch (xrb) | 400 |
| Longitudinal length (hitch to hitch) of the MC (MCl) | 690 in FC 1690 in FE |
| Longitudinal length of the ballast over the MC hitch (Bl) | 280 |
| Vertical distance between tractor front lower hitch and MC lower hitch (MChl) | 120 |
| Vertical distance between tractor front upper hitch and MC lower hitch (MChh) | 480 |
Appendix B
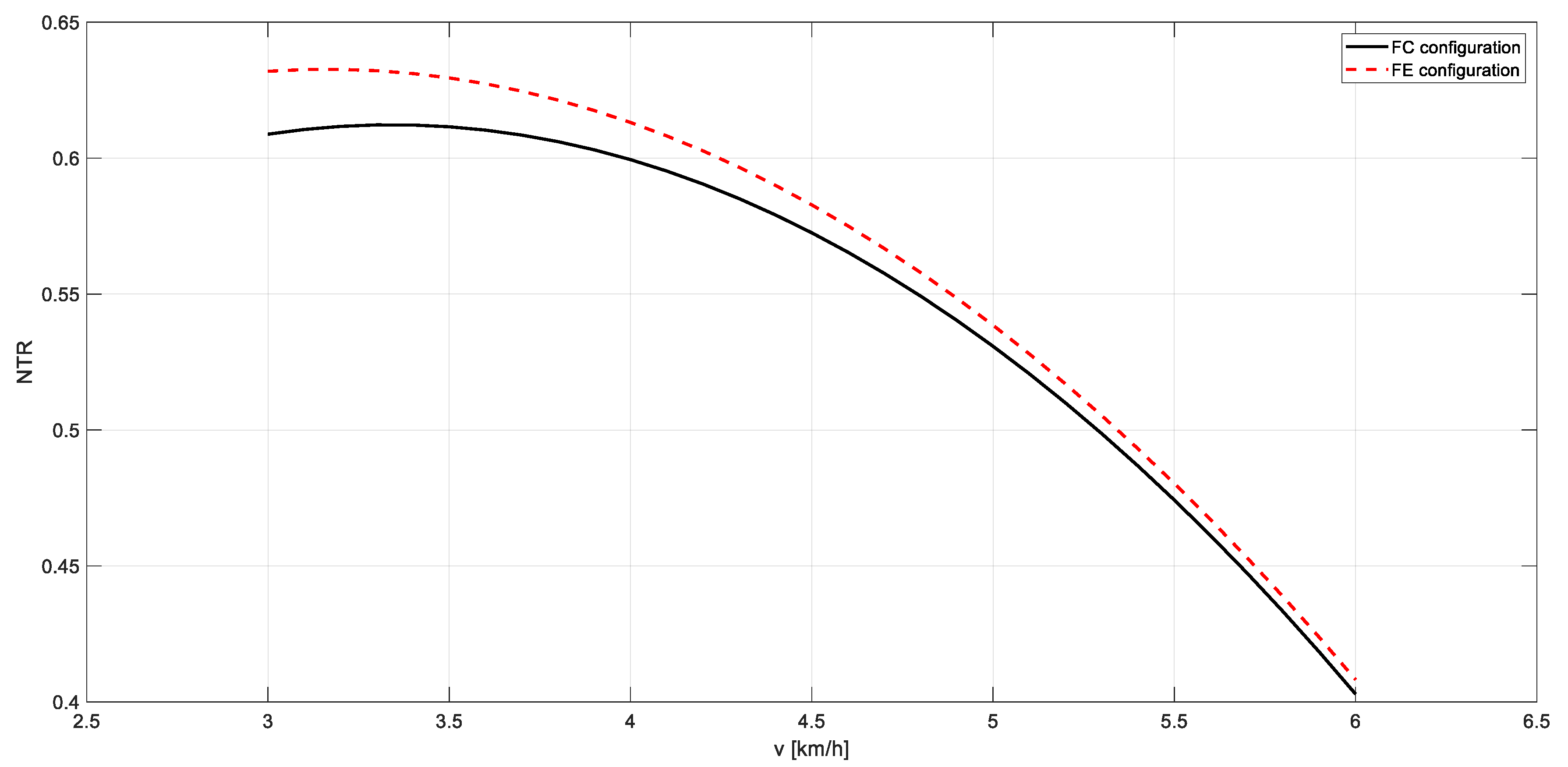
| Regression Parameters | FC | FE |
|---|---|---|
| Coefficient p1 (with 95% confidence bounds) | −2789 (−3955, −1623) | −2624 (−3838, −1410) |
| Coefficient p2 (with 95% confidence bounds) | 1.864 × 104 (7424, 2.986 × 104) | 1.660 × 104 (5432, 2.776 × 104) |
| Coefficient p3 (with 95% confidence bounds) | 2.645 × 104 (40.67, 5.285 × 104) | 3.328 × 104 (9004, 5.755 × 104) |
| R^2 | 0.97 | 0.97 |
Appendix C
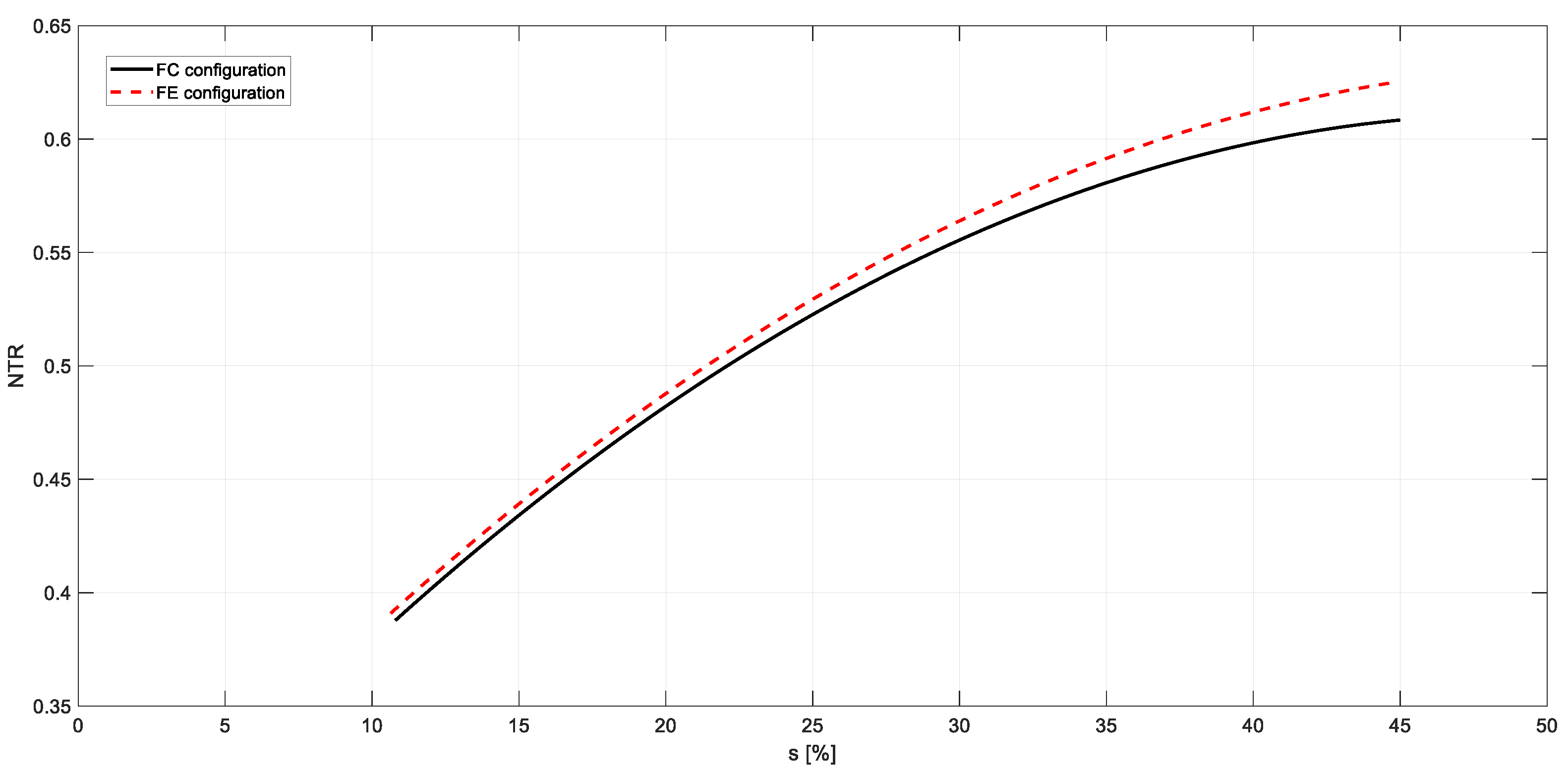
| Regression Parameters | FC | FE |
|---|---|---|
| Coefficient p1 (with 95% confidence bounds) | −14.31 (−20.65, −7.972) | −13.24 (−19.63, −6.842) |
| Coefficient p2 (with 95% confidence bounds) | 1405 (1032, 1779) | 1378 (961.8, 1795) |
| Coefficient p3 (with 95% confidence bounds) | 2.298 × 104 (1.797 × 104, 2.799 × 104) | 2.361 × 104 (1.822 × 104, 2.900 × 104) |
| R^2 | 0.97 | 0.97 |
References
- Rosenzweig, C.; Hillel, D. Soils and global climate change: Challenges and opportunities. Soil Sci. 2000, 165, 47–56. [Google Scholar] [CrossRef]
- Olesen, J.; Bindi, M. Consequences of climate change for European agricultural productivity, land use and policy. Eur. J. Agron. 2002, 16, 239–262. [Google Scholar] [CrossRef]
- Kutzbach, H.D. Trends in Power and Machinery. J. Agric. Eng. Res. 2000, 76, 237–247. [Google Scholar] [CrossRef]
- Gu, Y.; Kushwaha, R. Dynamic load distribution and tractive performance of a model tractor. J. Terramechanics 1994, 31, 21–39. [Google Scholar] [CrossRef]
- Bashford, L.L.; Woerman, G.R.; Shropshire, G.J. Front Wheel Assist Tractor Performance in Two and Four-Wheel Drive Modes. Trans. ASAE 1985, 28, 23–29. [Google Scholar] [CrossRef]
- Botta, G.F.; Jorajuria, D.; Draghi, L. Influence of the axle load, tyre size and configuration on the compaction of a freshly tilled clayey soil. J. Terramechanics 2002, 39, 47–54. [Google Scholar] [CrossRef]
- Battiato, A.; Diserens, E. Tractor traction performance simulation on differently textured soils and validation: A basic study to make traction and energy requirements accessible to the practice. Soil Tillage Res. 2017, 166, 18–32. [Google Scholar] [CrossRef]
- Burt, E.C.; Lyne, P.W.L.; Meiring, P.; Keen, J.F. Ballast and Inflation Effects on Tire Efficiency. Trans. ASAE 1983, 26, 1352–1354. [Google Scholar] [CrossRef]
- Serrano, J.M.; Peça, J.O.; Silva, J.R.; Márquez, L. The effect of liquid ballast and tyre inflation pressure on tractor performance. Biosyst. Eng. 2009, 102, 51–62. [Google Scholar] [CrossRef]
- Khalid, M.; Smith, J. Axle torque distribution in 4WD tractors. J. Terramechanics 1981, 18, 157–167. [Google Scholar] [CrossRef]
- Jadhav, P.P.; Sharma, A.K.; Wandkar, S.V.; Gholap, B.S. Study of tractive efficiency as an effect of ballast and tire inflation pressure in sandy loam soil. Agric. Eng. Int. CIGR J. 2013, 15, 60–67. [Google Scholar]
- Özarslan, C.; Erdogän, D. Optimization of tractor plowing performance. AMA Agric. Mech. Asia Afr. Lat. Am. 1996, 27, 9–12. [Google Scholar]
- Burt, E.C.; Bailey, A.C.; Patterson, R.M.; Taylor, J.H. Combined Effects of Dynamic Load and Travel Reduction on Tire Performance. Trans. ASAE 1979, 22, 40–45. [Google Scholar] [CrossRef]
- Bloome, P.D.; Summers, J.D.; Khalilian, A.; Batchelder, D.G. Ballasting Recommendations for Two-Wheel and Four-Wheel Drive Tractors [Tractor Performance], Microfiche Collection. 1983. Available online: http://agris.fao.org/agris-search/search.do?recordID=US8528799 (accessed on 4 April 2018).
- Wismer, R.D.; Luth, H.J. Off-Road Traction Prediction for Wheeled Vehicles. Trans. ASAE 1974, 17, 8–10. [Google Scholar] [CrossRef]
- Brixius, W.W. Traction Prediction Equations for Bias Ply Tires, American Society of Agricultural Engineers (Microfiche Collection) (USA). 1987. Available online: http://agris.fao.org/agris-search/search.do?recordID=US8843391 (accessed on 4 April 2018).
- Wong, J.Y.; McLaughlin, N.B.; Knezevic, Z.; Burtt, S. Optimization of the tractive performance of four-wheel-drive tractors: Theoretical analysis and experimental substantiation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1998, 212, 285–297. [Google Scholar] [CrossRef]
- Zoz, F.M. Predicting Tractor Field Performance (Updated), American Society of Agricultural Engineers (Microfiche Collection) (USA). 1987. Available online: http://agris.fao.org/agris-search/search.do?recordID=US8843392 (accessed on 6 April 2018).
- Regazzi, N.; Maraldi, M.; Molari, G. A theoretical study of the parameters affecting the power delivery efficiency of an agricultural tractor. Biosyst. Eng. 2019, 186, 214–227. [Google Scholar] [CrossRef]
- Stoilov, S.; Kostadinov, G.D. Effect of weight distribution on the slip efficiency of a four-wheel-drive skidder. Biosyst. Eng. 2009, 104, 486–492. [Google Scholar] [CrossRef]
- Osinenko, P.V.; Geissler, M.; Herlitzius, T. A method of optimal traction control for farm tractors with feedback of drive torque. Biosyst. Eng. 2015, 129, 20–33. [Google Scholar] [CrossRef]
- Damanauskas, V.; Janulevičius, A. Differences in tractor performance parameters between single-wheel 4WD and dual-wheel 2WD driving systems. J. Terramechanics 2015, 60, 63–73. [Google Scholar] [CrossRef]
- Janulevičius, A.; Giedra, K. Tractor ballasting in field work. Mechanika 2008, 73, 27–34. [Google Scholar]
- Giedra, K.; Janulevičius, A. Tractor ballasting in field transport work. Transport 2005, 20, 146–153. [Google Scholar] [CrossRef]
- Pranav, P.; Pandey, K. Computer simulation of ballast management for agricultural tractors. J. Terramechanics 2008, 45, 185–192. [Google Scholar] [CrossRef]
- Gee-Clough, D.; Pearson, G.; McAllister, M. Ballasting wheeled tractors to achieve maximum power output in frictional-cohesive soils. J. Agric. Eng. Res. 1982, 27, 1–19. [Google Scholar] [CrossRef]
- Zhang, N.; Chancellor, W. Automatic Ballast Position Control for Tractors. Trans. ASAE 1989, 32, 1159–1164. [Google Scholar] [CrossRef]
- Molari, G.; Mattetti, M.; Perozzi, D.; Sereni, E. Monitoring of the tractor working parameters from the CAN-Bus. J. Agric. Eng. 2013, 44. [Google Scholar] [CrossRef]
- USDA. Soil Mechanichs Level I; National Employee Develoment Staff, Soil Conservation Service, United State Department o Agriculture: Washington, DC, USA, 1987.
- ASTM. D7263-09—Standard Test Method for Bulk Density (Unit Weight) and Voids in Aggregate; ASTM International: West Conshohocken, PA, USA, 2009. [Google Scholar]
- ASTM. Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Upadhyaya, S.; Chancellor, W.; Wulfsohn, D. Sources of variability in traction data. J. Terramechanics 1988, 25, 249–272. [Google Scholar] [CrossRef]
- Mattetti, M.; Varani, M.; Maraldi, M.; Paolini, F.; Fiorati, S.; Molari, G. Tractive performance of Trelleborg PneuTrac tyres. J. Agric. Eng. 2020, 51, 100–106. [Google Scholar] [CrossRef]
- Swiler, L.P.; Sullivan, S.P.; Stucky-Mack, N.J.; Roberts, R.M.; Vugrin, K.W. Confidence Region Estimation Techniques for Nonlinear Regression: Three Case Studies; U.S. Department of Commerce National Technical Information Service: Springfield, VA, USA, 2005.
- ASAE. D497.7 Agricultural Machinery Management Data; ASAE: St. Joseph, MI, USA, 2015. [Google Scholar]
- Zoz, F.; Grisso, R. Traction and Tractor Performance; ASAE: St. Joseph, MI, USA, 2012; Volume 27. [Google Scholar]
- Clark, R.L.; Dahua, Z. A Theoretical Ballast and Traction Model for a Wide Span Tractor. Trans. ASAE 1995, 38, 1613–1620. [Google Scholar] [CrossRef]
- Self, K.P. Dynamic Load and Wheel Speed Ratio Effects on Four Wheel Drive Tractive Performance, May 1990. Available online: https://shareok.org/handle/11244/20877 (accessed on 3 November 2018).
- Wong, J.Y.; Zhao, Z.; Li, J.; McLaughlin, N.; Burtt, S.D. Optimization of the Tractive Performance of Four-Wheel-Drive Tractors—Correlation between Analytical Predictions and Experimental Data. SAE Tech. Paper Ser. 2000. [Google Scholar] [CrossRef]
- Jenane, C.; Bashford, L.; Monroe, G. Reduction of Fuel Consumption through Improved Tractive Performance. J. Agric. Eng. Res. 1996, 64, 131–138. [Google Scholar] [CrossRef]
- Spagnolo, R.T.; Volpato, C.E.S.; Barbosa, J.A.; Palma, M.A.Z.; De Barros, M.M. Fuel consumption of a tractor in function of wear, of ballasting and tire inflation pressure. Eng. Agrícola 2012, 32, 131–139. [Google Scholar] [CrossRef][Green Version]
- Senatore, C.; Sandu, C. Torque distribution influence on tractive efficiency and mobility of off-road wheeled vehicles. J. Terramechanics 2011, 48, 372–383. [Google Scholar] [CrossRef]
- Janulevičius, A.; Pupinis, G.; Lukštas, J.; Damanauskas, V.; Kurkauskas, V. Dependencies of the lead of front driving wheels on different tire deformations for a MFWD tractor. Transport 2015, 32, 23–31. [Google Scholar] [CrossRef][Green Version]
- Charles, S.M. Effects of ballast and inflation pressure on tractor tire performance. Agric. Eng. 1984, 65, 11–13. [Google Scholar]



| Specification | Value/Description |
|---|---|
| Engine speed at the maximum engine power (nrated) (rpm) | 2000 |
| Max engine power @ nrated (kW) | 191 |
| Max torque (Tmax) @1500 rpm (Nm) | 1100 |
| Torque @ nrated (Nm) | 912 |
| Unballasted mass (kg) | 8590 |
| Transmission | Full Powershift (gears: 19 forward, 6 reverse) |
| Front tires | Michelin MACHXBIB 600/65 R28 (50 kPa) speed radius index rf = 0.700 m |
| Rear tires | Michelin MACHXBIB 710/70 R38 (50 kPa) speed radius index rr = 0.925 m |
| Tractor Configuration | Total Tractor Mass (M) (kg) | Mass on the Front Axle (%) | Mass on the Rear Axle (%) |
|---|---|---|---|
| MC Fully Extended (FE) | 9590 | 59 | 41 |
| MC Fully Closed (FC) | 9590 | 56 | 44 |
| Standard ballast on the rear three-point linkage (R) | 9590 | 32 | 68 |
| Gear | Gear Ratio |
|---|---|
| 7th | 7.475 × 10−3 |
| 8th | 8.932 × 10−3 |
| 9th | 1.074 × 10−2 |
| Curves | Fitting Method | Model Equation |
|---|---|---|
| ηT as a function of s (R1) | Non-linear least squares | ηT = a(b s) + c(d s) |
| NTR as a function of s (R2) | Linear least squares | NTR = p1 s2 + p2 s + p3 |
| ηT as a function of NTR (R3) | Non-linear least squares | ηT = a(b NTR) + c(d NTR) |
| Curves | Fitting Method | Model Equation |
|---|---|---|
| NTR as a function of v (E1) regression curve and parameters are reported in Appendix B | Linear least squares | NTR = p1 v2 + p2 v + p3 |
| Curves | Fitting Method | Model Equation |
|---|---|---|
| FDplough as a function of s (E2) regression curve and parameters are reported in Appendix C | Linear least squares | FDplough = p1 s2 + p2 s + p3 |
| Regression Parameters | FE | FC | R |
|---|---|---|---|
| Coefficient a (with 95% confidence bounds) | 2943 (−1.907 × 1012, 1.907 × 1012) | 37.56 (−4.421 × 106, 4.421 × 106) | −2199 (−6.029 × 1011, 6.029 × 1011) |
| Coefficient b (with 95% confidence bounds) | 1.036 × 10−2 (−699.3, 699.3) | 1.060 × 10−2 (−10.33, 10.36) | 1.366 × 10−2 (−399.5, 399.5) |
| Coefficient c (with 95% confidence bounds) | −2942 (−1.907 × 1012, 1.907 × 1012) | −37.06 (−4.421 × 106, 4.421 × 106) | 2200 (−6.029 × 1011, 6.029 × 1011) |
| Coefficient d (with 95% confidence bounds) | 1.036 × 10−2 (−699.4, 699.4) | 1.077 × 10−2 (−10.42, 10.44) | 1.366 × 10−2 (−399.4, 399.5) |
| R^2 | 0.97 | 0.96 | 0.94 |
| Regression Parameters | FE | FC | R |
|---|---|---|---|
| Coefficient p1 (with 95% confidence bounds) | −1.561 × 10−4 (−1.839 × 10−4, −1.284 × 10−4) | −1.290 × 10−4 (−1.716 × 10−4, −8.637 × 10−5) | −1.761 × 10−4 (−2.033 × 10−4, −1.488 × 10−4) |
| Coefficient p2 (with 95% confidence bounds) | 1.535 × 10−2 (1.350 × 10−2, 1.720 × 10−2) | 1.313 × 10−2 (1.053 × 10−2, 1.573 × 10−2) | 1.704 × 10−2 (1.555 × 10−2, 1.860 × 10−2) |
| Coefficient p3 (with 95% confidence bounds) | 0.254 (0.228, 0.282) | 0.291 (0.255, 0.327) | 0.223 (0.203, 0.242) |
| R^2 | 0.97 | 0.94 | 0.97 |
| Regression Parameters | FE | FC | R |
|---|---|---|---|
| Coefficient a (with 95% confidence bounds) | −505.1 (−1.103 × 1011, 1.103 × 1011) | −7.706 (−3.584 × 105, 3.584 × 105) | 173.9 (−1.000 × 109, 1.000 × 109) |
| Coefficient b (with 95% confidence bounds) | 3.769 (−7.257 × 104, 7.258 × 104) | 2.710 (−1302, 1307) | 2.909 (−6541, 6547) |
| Coefficient c (with 95% confidence bounds) | 505.3 (−1.103 × 1011, 1.103 × 1011) | 8.050 (−3.584 × 105, 3.584 × 105) | −173.6 (−1.000 × 109, 1.000 × 109) |
| Coefficient d (with 95% confidence bounds) | 3.769 (−7.256 × 104, 7.257 × 104) | 2.660 (−1284, 1289) | 2.912 (−6545, 6551) |
| R^2 | 0.92 | 0.84 | 0.90 |
| MC Configuration | FDplough (kN) | NTRplough | v (km/h) | s (%) | Π (ha/h) | ηT | Pe (kW) |
|---|---|---|---|---|---|---|---|
| FC | 43.4 | 0.46 | 5.6 | 17.7 | 1.05 | ηT FC,min = 0.45 ηT FC,reg = 0.48 ηT FC,max = 0.50 | 148@ ηT FC,min 142@ ηT FC,reg 136@ ηT FC,max |
| FE | 43.9 | 0.47 | 5.6 | 17.7 | 1.05 | ηT FE,min = 0.47 ηT FE,reg = 0.49 ηT FE,max = 0.51 | 144@ ηT FE,min 139@ ηT FE,reg 135@ ηT FE,max |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varani, M.; Mattetti, M.; Maraldi, M.; Molari, G. Mechanical Devices for Mass Distribution Adjustment: Are They Really Convenient? Agronomy 2020, 10, 1820. https://doi.org/10.3390/agronomy10111820
Varani M, Mattetti M, Maraldi M, Molari G. Mechanical Devices for Mass Distribution Adjustment: Are They Really Convenient? Agronomy. 2020; 10(11):1820. https://doi.org/10.3390/agronomy10111820
Chicago/Turabian StyleVarani, Massimiliano, Michele Mattetti, Mirko Maraldi, and Giovanni Molari. 2020. "Mechanical Devices for Mass Distribution Adjustment: Are They Really Convenient?" Agronomy 10, no. 11: 1820. https://doi.org/10.3390/agronomy10111820
APA StyleVarani, M., Mattetti, M., Maraldi, M., & Molari, G. (2020). Mechanical Devices for Mass Distribution Adjustment: Are They Really Convenient? Agronomy, 10(11), 1820. https://doi.org/10.3390/agronomy10111820







