Abstract
Standardization of crop yield estimation methods at various levels of farming helps to obtain accurate agricultural statistics as well as assessing the suitability of agricultural practices under various production conditions. The current paper reviews various maize yield estimation methods, taking into account available yield parameters, and it also analyses the yield gap between maize potential and attainable yield. The easiest and more reliable methods of yield estimation are based on yield parameters collected from the field. However, farmer estimation methods are cheaper and faster compared to any other method of yield estimation from farmers’ fields. This paper also elaborates on the importance of the use of more complex methods for yield estimation, such as remote sensing and crop modelling. These complex methods are more accurate and can predict yield before field harvest with less deviation from the exact harvest yield. However, they are very expensive and not efficient for small plots of land (less than 1 ha). Factors that contribute to the gap between potential and actual yield include poor implementation of agricultural policies, strict regulation of fertilizer inputs, vulnerability of smallholder cropping systems to adverse climatic conditions, occurrence of biotic and abiotic constraints, as well as unavailability of seeds and labor.
1. Introduction
Maize (Zea mays L.) is one of the most important annual cereal crops in the world, providing a staple food, and being used as source of income for many populations in developing countries. The way maize is processed and consumed greatly varies from country to country, with maize flour and meal being the most popular products [1,2]. It is an important source of carbohydrate for human diets in developing countries and for animal feed in the developed world [3].
Evans and Fisher [4] defined yield as being the mass of product at final harvest, with specified dry matter content. Crop yield is broadly defined as the amount of harvest product in a specific area (amount of harvest products/crop area) [5]. The grain yield of maize depends on the genetic potential of the genotype used, the characteristics of the soil, the field management practices, and agro-climatic factors [6,7]. Potential yield refers to the maximum yield that can be attained by a crop in a given environment [4]. Potential yield is largely determined by a specific combination of factors, such as solar radiation, soil type, temperature, plant density, genetic potential of a given genotype, biotic and abiotic constraints [8,9,10]. However, realized yield, also known as attainable yield, obtained by a farmer is more frequently influenced by poor agricultural practices [9]. Maize yields can be estimated for different purposes, including marketing, estimation of storage requirements, organizing harvest equipment, making decisions about pests and diseases, and for crop improvement. Maize yield estimates are also used to forecast production, and thus contribute to the estimation of food security status at district, provincial, and national levels.
Different methods can be used for estimating maize yields depending on the purpose for which the crop was produced. The estimation of yield can be calculated using kernel weight at harvest, plot area harvested, plant density, and moisture content of grain at harvest. For instance, to get the full expression of maize yield potential, the plants must be at optimum density. In some circumstances, the maize planted area may be bigger than the plot area harvested because of poor germination, pest and disease damage, animal grazing, floods, lack of labor for harvesting, and lack of adequate markets for the product [11]. The methods used to estimate crop yields are crop cuts (on-station, on-farm trials), statistical techniques, farmer estimates, whole plot harvest methods, the sampling of harvest units, expert assessments, and yield prediction through simulation models (such as crop modelling and remote sensing) [11].
This paper reviews various maize yield estimation methods, taking into account statistical techniques, farmer estimation, crop modelling, and remote sensing technologies. It provides the rationale of each of the named methods, as well as their limits. It also reviews the yield gap between maize potential yield and yield attained by farmers.
2. Components of Maize Yield Estimates
In each agro-climatic environment, yields of maize plants are influenced by several components linked to agronomic practices that are used. These are plant population density (determines number of cobs and kernels harvested in a given area), the shelling percentage, and the amount of water in the harvested grains. The magnitude of yield components is a function of the physiological response of a crop to the growth environment, which is of great importance to maize physiologists, modelers, and breeders.
2.1. Plant Density and Kernel Number
Plant density refers to the total number of plants grown in a given area, and it is an important factor in yield estimation. Maize density is calculated based on row spacing, row length, number of plants per planting station, and the distance between two consecutive planting stations. Ali et al. [12] estimated maize plant density per plot at physiological maturity by counting the total plants in the plot and dividing by soil area. Maize density has been widely investigated worldwide. An increase in plant density results in relatively higher yield increments if the appropriate fertilization rates and agronomic practices are adopted [13]. Huang et al. [14] found a 5% yield increase of diamond plants at high density (90,000 plants ha−1) resulted in increased kernel numbers per ear in the top and middle canopy layers. Moreover, they reported that the optimum distribution of light in the canopy delayed leaf senescence, especially for plants with a triangle shape. In a dense population, canopy architecture becomes an important factor determining yield because of interplant competition for light distribution and absorption [15].
Maize grain yield is normally highly and positively correlated with kernel numbers. The number of kernels per plant depends on the number of ears per plant and the number of mature kernels per ear [16]. To produce more grain per unit area, the genetic potential of most recent hybrids takes advantage of their capacity to withstand higher densities [17]. Qian et al. [18] reported that spring maize hybrids attained an average increase of 17.9 g per plant per decade, which corresponds to an increase of 936 kg/ha per decade over the period from 1970 to 2010 in Northeast China. The yield gain was attributed to an increase of yield per plant, resulting from an increase in number of kernels per ear and an increased 1000 kernel weight under appropriate agronomic practices.
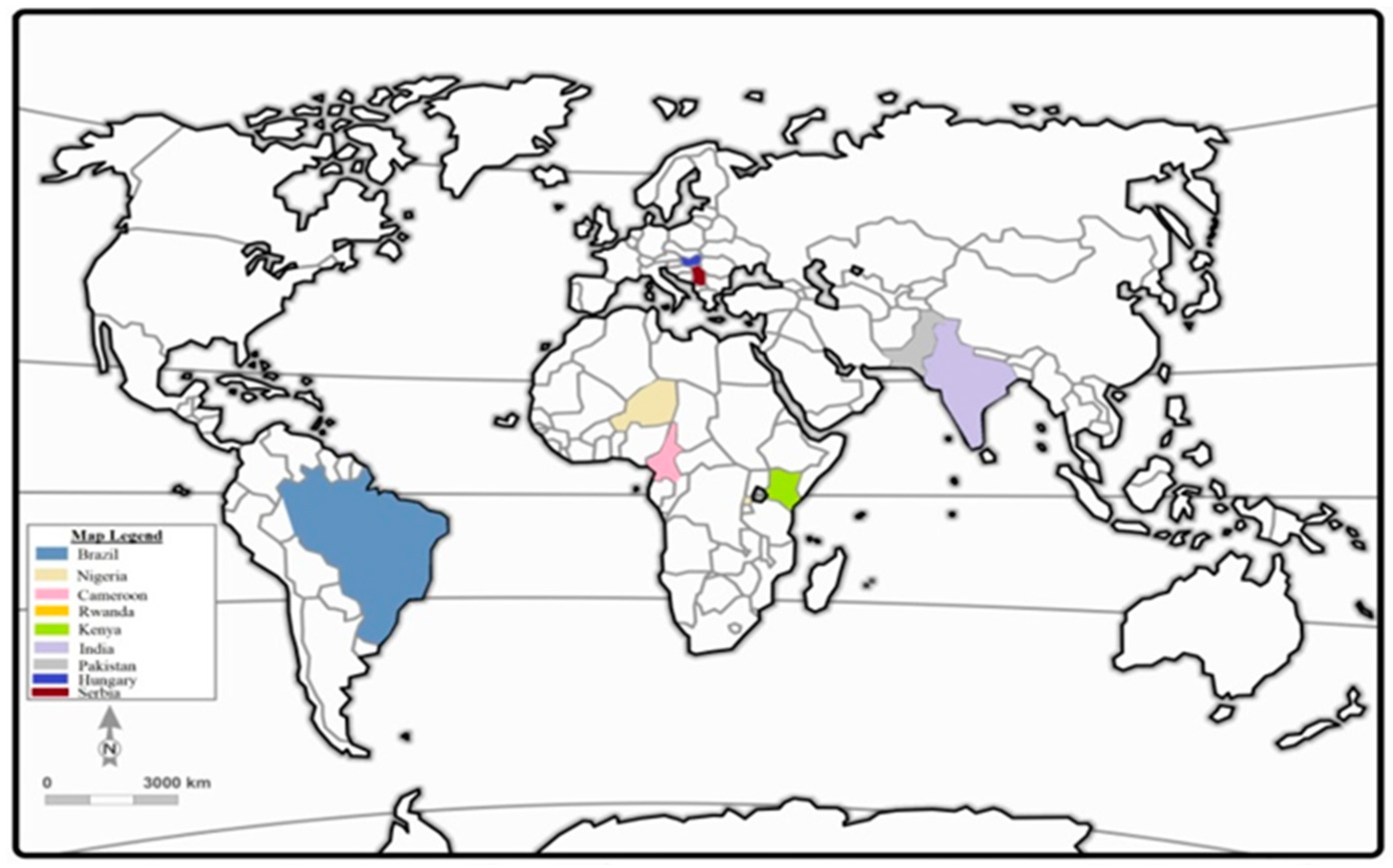
Several spacings have been recommended, given a required number of plants per unit area in various regions in the world, as indicated in the map (Table 1). The various distances between rows and hills in a row have been estimated for a resultant density of 53,000 plants per hectare. Plant spacing impacts the number of individual plants grown on a given area and will therefore influence the number of ears harvested and the resultant yield. Plant spacing is usually based on the agro-climatic conditions, the plant material used, and the cropping system (monoculture or mixed culture). Therefore, spacing varied from region to region and sometimes from one country to another. Large distances between rows facilitate use of mixed cropping systems. The number of plants can be increased by either reducing the spacing between hills in a row or reducing the distance between rows. When the distance between two consecutive hills is very small, the number of plants per hill tends to be one.

Table 1.
Some plant densities and spacings used in various agro-ecological environments for maize production.
An increase in maize density significantly increased plant height, ear height, and yield. However, some yield parameters such as ear length, number of grains per row, number of grains per ear, grain weight per ear, cob weight, and 1000 grain weight were decreased by increase in maize density [19]. This is because of the competition among plants for nutrients uptake from the soil and for light absorbance as well. Some individuals would tend to grow taller and some failed to bear ears, resulting in significant decreases in overall yield. Short maize varieties could be grown at higher plant populations than the taller varieties, which may be susceptible to lodging under high population density. The environmental conditions and genetic potential of some maize genotypes allow them to tolerate high plant density. Mandić et al. [19] reported that a crop density of 71,429 plants ha−1 was optimal for growing Dijamant 6 hybrid maize in the Srem region of Serbia, because at that density, the cited hybrid efficiently used available resources to achieve higher grain yield (grain yields increased by about 0.72 to 1.51 t/ha with the increase of plant density). The newly developed maize hybrids by Tokatlidis and Koutrubas [20] resulted in a yield increase at optimum plant density. This could be attributed to their genetic potential to perform well in high plant density.
The factors facilitating modern maize genotypes to produce maximum yield in high plant density include orientation, size, and distribution of leaf area which determines light interception and overall photosynthesis in a crop canopy. Therefore, optimum architecture allows modern maize genotypes to be more productive with improved tolerance to high plant density. It is also expected that maize tolerates high plant density when grown at high altitude because of light availability, less daytime heat stress, and low night temperature. In general, plant density is closely related to grain yield estimates. Additionally, high density is appropriate for early-planted crops under high rainfall or irrigated conditions with good management standards.
2.2. Moisture Content
Moisture content can be defined as the ratio of mass of water to the mass of solids in a given sample [37]. The moisture content of maize grains represents the amount of water present in the grains. Moisture content of maize grain recorded at the time of harvest should be representative of the entire plot planted, taking into account the total number of genotypes.
The moisture content can either be determined using a moisture meter or it can be calculated. To estimate the moisture content of grain in a given plot, ten ears should be sampled randomly. Then, the shelled grains from two central kernel rows should be mixed to determine the moisture percentage using portable moisture testers [38]. Estimation of grain moisture content is important because kernel density decreases as moisture content of the grain increases [39]. Bello et al. [30] calculated the moisture content by selecting three hundred grain samples from each of their plots at harvest, weighed and recorded the initial weight. They dried the grains to a constant weight in the oven at 80 °C for 48 h in the laboratory and collected the final weight. The difference between the two weights was recorded as grain moisture content at harvest.
Moisture content also affects grain properties and ease of storage. When the weight of the grain is stable, the grains can be kept for many years. The moisture content of the maize cob can change when dried to less than 15% in storage into an inadequate atmospheric condition [40]. Heisey et al. [41] reported that ear moisture was negatively correlated with grain yield and they suggested that harvesting before physiological maturity of the plant limits grain yield. The moisture content should be standardized to appropriate moisture percentage (ranges from 10 to 15%) when computing grain yield.
2.3. Maize Harvest and Shelling Percentage
Maize harvest is recommended to be delayed until a relatively low grain moisture content has been attained (15–25%) to facilitate shelling and increase the accuracy of moisture meters during data collection [37]. However, a long delay in maize harvesting may cause quantitative and qualitative losses to the grain yield, due to physiological and morphological factors such as development of ear rots, plant lodging, or animal attacks [42,43]. High grain yield and good seed quality are obtained when the harvest is carried out after physiological maturity of the plants [43,44,45,46]. Gaile [47] reported the dry moisture content of maize (min 25%, optimum 28–30%) as the main criterion for determination of proper harvesting time.
The ear weight (in kilograms) of a particular genotype should be recorded after harvesting a plot. Maize shelling is known as the removal of kernels from the cob. The shelling percentage is one of the yield quality measurements that should be estimated. Masuka et al. [48] hand-harvested all the evaluated plants, then measured shelled grain weight and estimated grain yield using 80% shelling percentage. Maize having moisture content of 12% is likely to express the best shelling performance as it will be very easy to remove grains from the cob without damaging them. Horrocks and Zuber [49] reported that different row spacings (50.8, 76.2, and 101.6 cm) resulted in a slight increase in shelling percentage varying from 82.2, 82.6, and 82.8%, respectively. The average shelling percentage of maize ears is usually about 80% when plants are harvested with 20 to 25% moisture content, though this may depend on the agro-ecological zone. The shelling percentage can be determined from ten plants randomly sampled after harvest using the following formula [3,50]:
Shelling percentage = (seed weight/cob weight) × 100%
The shelling percentage is strongly influenced by several factors, such as the method of its determination, years, locations, genotypes, agro-climatic conditions, cultural practices, and kernel moisture content [49].
2.4. Harvest Area
The use of global positioning system (GPS) technology provides an affordable and more reliable alternative method for measurement of plot area harvested in large scale production. Ngie and Ahmed [51] used combine harvesters that recorded the grain weight per hectare within 20 m × 20 m ranges (in kg/ha), associated with a GPS system which recorded the coordinates of the plots against the dry weight of the harvested grain. However, the easiest way of estimating the harvest area for small plots of land consists of multiplying row length by the space between two consecutive rows, and factoring in the number of rows in the plot using the following formula:
where harvest area is in m2, row length is in m, and intra–row distance is in m.
Harvest area = row length × intra − row distance × number of rows
3. Grain Yield Estimates
Crop yield represents a culmination of the efficiency of the plant population to use available environmental resources for its growth [52]. Also, it can be defined as the amount of harvest product per crop production area. Crop yield is expressed in kilograms (kg) or metric tons (t) of product per hectare (ha) [53]. Crop productivity per unit area is one of the essential indicators for agricultural development. The estimation of crop yield involves estimation of crop area and quantity of harvested products [11]. In maize production, it has been shown that yield can increase consistently with density up to 90,000 plants ha−1 and decrease for any higher density [13]. Nowadays, maize breeding leads to the development of genotypes with high potential yield under high plant density. In many circumstances, grain yield determination brings a lot of errors and biases, and the measurement taken is time consuming. Different types of yields are considered in maize production (Figure 1). After evaluating maize genotypes for tolerance or resistance to biotic and abiotic stresses across several environments, the potential yield of the desired and selected genotypes is determined, as well as the production practices. Most often, farmers do not follow the recommended agronomic practices and end up having less yields than expected. After harvest, the losses faced in storage negatively impacts on the quantity and quality of the final product to be sold, which represents the economic yield.

Figure 1.
Different types of yields from maize production.
3.1. Yield Estimation from Experimental Plots
According to Cassman [54], yield potential (Yp) is defined as the biophysical yield obtained with adequate water to avoid deficits, appropriate temperature regime determining the length of the growing season, and the optimum amount of solar radiation during the growing season. The yield potential cannot be obtained in the natural environment, where all biotic and abiotic constraints are not always under control. However, potential yield (Yw) is obtained from non-irrigated crops or rain-fed crops, which are exposed to water-limited conditions depending on the quantity, the timing of rainfall, and the capacity of soil to store water. The potential yield is obtained from a well-managed crop in a given set of conditions. The easiest and more reliable methods are the estimation of yield based on yield parameters collected. Maize yield can be calculated based on cob weight or kernel weight. The determination of yield based on grain weight can be adjusted to a required percentage of moisture content (varies from 10 to 15%) using the following formula [38]:
where grain weight is in kg, moisture content (MC) is in percentage (%), and plot area is in m2. In the current formula, the shelling percentage is not taken into account since the yield is determined from the total kernel weight. If grain yield is to be calculated using the ear fresh weight, and the adjusted MC percentage (from 10 to 15%), the following formula is recommended:
GY (t/ha) = [Grain Weight × 10 × (100 − MC)/(100 − Adjusted MC)/(Plot Area)]
Grain yield (t/ha) = [Fresh ear weight (kg/plot) × 10 × (100 − MC) × 0.8)/((100 − adjusted MC) × Plot Area]
In this case, fresh ear weight is in kg, moisture content (MC) of grains and adjusted MC in percentage (%), 0.8 is the shelling coefficient, and the harvested plot area is in m2. The shelling percentage can vary from one environment to another. The above formula has been widely used in research studies [32,55,56,57,58]. The determination of grain yield requires knowledge of the harvest area, the weight of the ears or the weight of the total kernels per plot, the moisture content, and the appropriate percentage of yield adjustment depending on moisture content in the given environment. Chen et al. [59] estimated maize grain yield from three plots of 14.4 m2 selected randomly and adjusted the yield to 15.5% moisture content. Pixley and Bänziger [60], Vivek et al. [61], and Bello et al. [30] estimated grain yield (t/ha) after adjustment to 12.5% moisture content at harvest. Parentoni et al. [62] adjusted grain yield to standard grain moisture of 15%.
When a genotype is grown in monoculture, the entire plot can be randomly harvested, and the yield estimation will be based on the total ear or cob weight in a harvest area. The current method is employed during on farm trials and in demonstration plots [63]. The total harvest is dried, and then weighed to calculate the harvested yield. This method is known as the absolute standard for crop yield estimation [64]. The method is free of bias, suitable for small-scale investigations of a case-study nature [11,65,66]. However, it is time and labor consuming, requires large volume of work, making it unsuitable for moderate-to-large sample sizes of the crop [11].
3.2. Yield Estimation from Farmers’ Fields
The harvest yield from farmers’ fields is known as actual or realized yield. Most often, in smallholder farms, maize planting does not follow any rule making the estimation of plant density difficult as well as the estimation of the harvest yield. The estimation of crop yield can be complicated by heterogeneous performance of a given crop within a plot, continuous planting, and use of mixed cropping systems. Farmers use much higher seed rates than recommended [67] due to use of the broadcast planting methods [41]. It is recommended for maize to be planted in rows to maximize the yield per harvest area.
Diverse methods can be applied for yield estimation at the farmer level. Estimating crop production through farmer interviews involves farmer recall from previous harvests (quantify the yield of the previous harvest) and farmer prediction (estimate the current yield based on the previous harvest) [53]. Most often, farmers predict their yield based on the previous harvest. Singh [68] reported that yield estimation at farmer level using survey methods should be considered at maximum crop growth stage. However, farmer estimation methods are very cheap and provide rapid results compared to any other method of yield estimation at farmer level. These methods of yield estimation are less accurate and sometimes bring more biases. Therefore, the use of simple mathematical models could be recommended. Farmers sometimes roughly estimate their yield production at harvest based on the number of bags (25, 50, or 100 kg) harvested in a given area. This estimation is applied either for fresh or dried maize harvested in a specified plot size.
The estimation of crop yield using test weight technique is one of the easiest and quickest pre-estimation methods under farm conditions. This method is based on the sampling frame and can be applied in any farm. The number of ears per planting station is counted in one meter square area, repeated at least 5 to 7 times within the entire plot, where yield is to be determined and the average number is taken. Similarly, the number of kernel rows per ear is counted in 20 to 25 ears randomly selected and the average is used. 1000 kernels are sampled randomly from the ear and weighed. The yield of the crop is then calculated using the following formula modified from Sapkota et al. [69]:
Yield (kg/ha) = [(number of kernel rows per ear × number of ears per m2/100) × (weight of 1000 − kernel (g)/1000) × 10,000]
The result obtained from the above formula can be multiplied by 1000 to express it in t/ha. Sampathkumar et al. [70] reported that the average weight of 1000 kernels ranged from 237 to 268 g. Most often, the current method of estimating yields can overestimate or underestimate the harvested products since it does not take into account the moisture content of the grains, the total number of plants harvested, the shelling percentage, the cob filling percentage, and the total weight of grains per cobs harvested. However, the method provides a broad idea on maize yield production in farmers’ fields. The current yield estimation method can lead to trade-off analysis on crop yield and appropriate decision-making without compromising smallholder farmers’ productivity [71].
3.3. Complex Models Used in Yield Estimation
Crop simulation methods can be used to estimate crop growth, yield, and improve agricultural management systems by allowing farmers to be prepared for climatic conditions of the forthcoming season [9,72,73,74,75]. Crop modelling and remote sensing are two methods that enable government agencies, private industry, and researchers to estimate yield before harvest. Numerous studies have been conducted to predict crop yield at regional scales using remote sensing approaches, yield modelling, and a combination of the two methods. There are numerous crop simulation models that take into account the interactions of a crop with climatic conditions, soil properties, and agronomic management practices.
4. Yield Simulation
Crop simulation models are mathematical representations of complex real-world systems [76], which can mimic crop growth and estimate crop yield on the basis of weather (precipitation, temperature and solar radiation), soil, and crop management conditions [77,78,79,80,81]. Numerous simulation models have been developed over the years for a range of crops and are useful in understanding cropping system [80,81,82,83]. Early crop yield forecasts provide a warning to farmers as they prepare for an upcoming season. When the season is forecasted to be poor, farmers could probably change the planting date, cultivar type, as well as management and monitoring activities such as adjustment in fertilizer application rates and irrigation cycles, in line with the expected conditions [84]. Yield simulation can reduce the risks associated with seasonal variation, thus allowing famers to make appropriate decisions and take advantage of good seasons.
Model ensembles have become a relevant tool of forecasting over the last few years [85]. Multi-model forecasts have been reported to be more skillful than single-model forecasts [86]. A crop simulation model called CORN-CROPS was used to simulate the interactions of management practices and weather on maize yields from 1970 to 1983 in East Central Illinois. The results showed a strong agreement between simulated yields and actual yields obtained during that period [87]. Le Roux [88] compared two global circulation models (conformal cubic atmospheric model (CCAM) and ECHAM4.5 model) in CERES-Maize simulation system to estimate maize yields from 1979 to 2003 in South Africa. They found that CERES-Maize model simulation using CCAM was closely related to the target skill, whereas CERES-ECHAM4.5 simulation system provided poor skill. Schulthess et al. [89] used hybrid maize crop simulation model to estimate potential yields for maize grown during winter in the North-western region of Bangladesh. The model predicted mean potential yield of 12.87 Mg/ha while farmers achieved the highest yield of 12 Mg/ha. Cheng et al. [90] used the World Food Studies (WOFOST) model to simulate the growing of spring maize. They found that the proposed method reliably improved the estimation of spring maize yield in terms of spatial heterogeneity, simulation ability, and prediction accuracy without reducing the simulation efficiency.
Field crop yield prediction is important for relevant design of grain storage facilities, agricultural field management, as well as national agricultural decision-making. However, complex models are not always appropriate and do not provide reliable information in all situations because they may require inputs that cannot practically be obtained in field situations [79]. Table 2 summarizes some models that were previously used at various stages of maize production.

Table 2.
Some simulation models applied in maize production.
5. Remote Sensing
Remote sensing is a technique to observe the earth’s surface, the atmosphere from space using satellites (space borne), or from the air using aircrafts (airborne). In other words, it refers to the activities of recording/observing/ perceiving (sensing) objects or events from faraway (remote) places [91]. Remote sensing is a dynamic monitoring yield estimation technique used in diverse types of crops which can estimate crop yields on a large scale and provide relevant results. It is an important tool for generating agricultural statistics because of the synoptic view and online information provided in a short period of time which can be used to predict yield before harvesting [11,51].
Remote sensing can be integrated with geographic information system (GIS) technologies and/or with satellite method. The estimation method relates the vegetation indices with the final yield at a specific growth stage of the plant (vegetative and reproductive stages) during the growing season [92,93,94,95]. Vegetation indices refer to spectral transformation of two or more bands designed to enhance the contribution of vegetation properties and allows reliable spatial and temporal inter-comparisons of terrestrial photosynthetic activity and canopy structural variations. These vegetation indices are derived from remotely sensed data. Remote sensing can also relate the final yield with the cumulative values of vegetation indices obtained during the whole growing season or during a specific plant growth period (vegetative or reproductive stages) depending on the model used (normalized difference vegetation index, NDVI) [96,97,98].
Remote sensing forms a base for estimating parameters of spatial variability through a very large area frame sample design. It provides an efficient and low-cost stratification based on crop proportion derived from visual interpretation or digital classification of remote sensing data. Remote sensing makes the estimates based on ground surveys near-real time monitoring of crops, very easy derivation of vegetation (covers hilly terrain as well) and reduces the amount of field data to be collected [11,99]. Several studies have been successfully conducted using remote sensing approaches. Jovanović et al. [99] estimated crop yields in Vojvodina province of Serbia two months before harvest using moderate resolution imaging spectroradiometer (MODIS), normalized difference vegetation index (NDVI), as an indicator of specific crop condition, and land surface temperature (LST) as an indicator of crop moisture. Doraiswamy et al. [100] found their results of maize and soybean prediction within 20% standard deviation of the official estimates using the MODIS sensor. Fernandez–Ordoñez and Soria–Ruiz [95] estimated maize yields at flowering stage and total volume of production in Mexico using Spot-5 satellite images and empirical models. They found a prediction value of 5.96 t/ha and 5.04 t/ha for the models Y = f (LAI) and Y = f (NDVI), respectively.
When predicting yield using remote sensing, the leaf area index (LAI) is an important variable contributing to determination of the reflectance values of a crop in an image, and as NDVI, which is related to crop vigor and biomass. Guindin–Garcia [101] reported that the estimates of LAI obtained during the mid-grain filling period of a maize plant can be efficiently (RMSE < 900 kg/ha) used to rapidly detect variability of grain yield at country level using MODIS 250 m products. Ngie and Ahmed [51] utilized canopy reflectance from a multispectral sensor to develop vegetation indices that serve as input variables into an empirical pre-harvest maize yield prediction model in the North Eastern section of the Free State province in South Africa. They obtained successful estimates of maize grain yields from the March images through the random forest algorithm predictive models. Despite the satisfactory yield prediction results provided by the remote sensing technique, the method remains very expensive and not accurate for small plots of land (less than one hectare). When the remote sensing facilities are available in the region, the profitability could be appreciated after few years. Tenkorang and Lowenberg–Doboer [102] reported that in agriculture, remote sensing has the potential to improve average on-farm profit by about $31.74/ha at standardized budget assumptions. The localization of maize experimental site at CIMMYT Mexico on fungicide and non-fungicide treatments was reported using remote sensing techniques (Figure 2a) [103], crop acreage estimate at the peak of crop growth during growing season using SPOT-5 satellite (Figure 2b), and monthly SPOT NDVI crop phenology behavior in a rainfed area of Punjab (Figure 2c) [104].

Figure 2.
Images of remote sensing in crop production: Localization of Agua Fria experimental station trial in the state of Puebla Mexico (a) A, color-infrared image (550, 660, 790 nm) of maize hybrids in the experimental trials for phenotyping of Tar Spot Complex Resistance under fungicide treatment (a) A1 and non-fungicide treatment (a) A2, image data extracted from two polygons of two central rows in each plot (a) B, SPOT-5 satellite for crops acreage estimate during peak growth of crops (b), and monthly SPOT NDVI crop phenology behavior in a rainfed area of Punjab (c).
Yield Gap Between Potential and Actual Yields
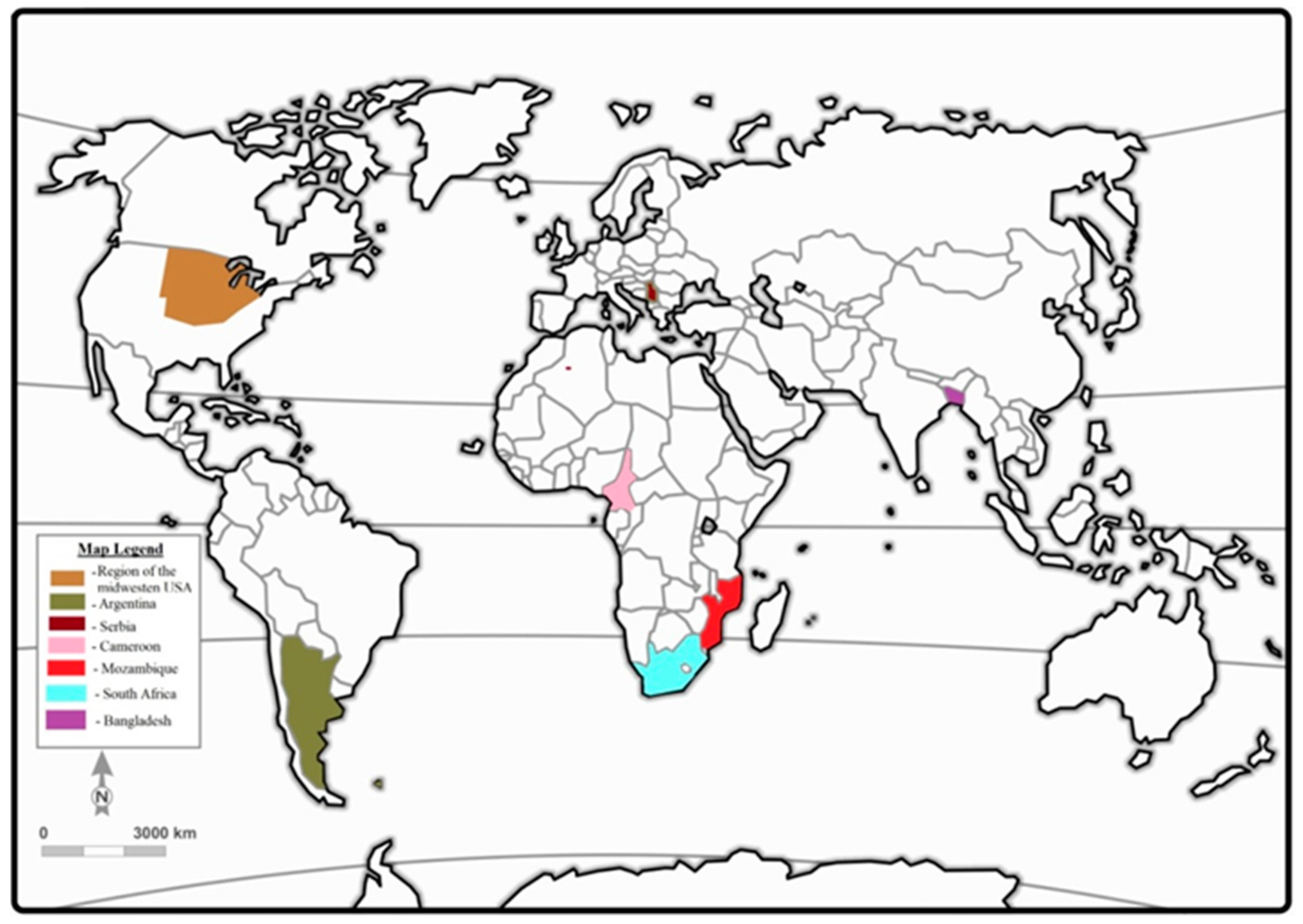
In farmers’ fields, yields obtained from maize crops (actual or attainable yield) are usually lower than the expected yield (potential yield). A multitude of factors contribute to such yield decreases, and they include poor agricultural policies that restrict affordability and access to production inputs. Other constraints contributing to yield losses in farmers’ fields are inadequate or incorrect fertilizer application rates, biotic and abiotic constraints, unavailability of improved seeds, and high cost of labor [54]. Urassa [105] found that farmers in the Southern highlands of Tanzania failed to increase maize yields because of inaccessibility to new seeds, fertilizers, and extension services. In addition, farmers try to maximize profits instead of looking for maximum yield per unit area of production. In the Eastern Cape Province of South Africa, as in most African countries, emerging farmers experienced poor economic yield due to lack of transport for their harvested products from the farm to the nearest market, poor market infrastructure, poor roads, lack of good marketing skills and information, high cost of transaction, lack of agricultural implements for better production, poor management skills leading to low productivity, lack of local point sales in rural areas, labor shortage, and low educational skills [106,107]. The difference between potential yield of maize and attainable yield at farmer level in some countries worldwide, as indicated on the map, is summarized in Table 3. In the USA and Bangladesh, the gap between attainable yield and potential yield is very low. This could be attributed the high adoption rate of improved technologies in agriculture.

Table 3.
Attainable and potential yield of maize in some countries.
6. Conclusions
Yield estimation is critical in any crop production system. The estimation of potential yields takes into account production area, plant density, kernel moisture content, and sometimes shelling percentage. In smallholder farms, the estimation of yield is challenging because of continuous planting and use of mixed intercropping systems. Nevertheless, maize yield production can be broadly estimated under such conditions. Crop yield simulation models and remote sensing provide government agencies, private industry, and researchers the option to estimate yield before harvest and can help farmers to be well prepared for the forthcoming growing season. These methods of yield estimation are expensive and not accurate for small plot sizes. Farmer estimation techniques remain the cheapest and are faster compared to any other method of yield estimation at farmer level.
Author Contributions
L.N.T. had conceptualized the idea of this review topic and wrote the first draft. C.S.M. contributed to the overall preparation of the manuscript and provided technical guidance and editing support. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We appreciate the funding provided by the Govan Mbeki Research and Development Centre (GMRDC) at the University of Fort Hare and by the National Research Foundation (NRF) in South Africa.
Conflicts of Interest
The authors declare no conflict of interest.
References
- USAID. Micronutrient Programs and DSM Nutritional Products. Fortification Basics. Maize flour/Meal; 2002. Available online: https://www.dsm.com/en_US/nip/public/home/downloads/Corn.pdf (accessed on 22 December 2013).
- Ranum, P.; Peña-Rosas, J.P.; Garcia-Casal, M.N. Global maize production, utilization, and consumption. Ann. N. Y. Acad. Sci. 2014, 1312, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Undie, U.L.; Uwah, D.F.; Attoe, E.E. Effect of intercropping and crop arrangement of yield and productivity of late season maize/soybean mixtures in the humid environment of South Southern Nigeria. J. Agric. Sci. 2012, 4, 37–50. [Google Scholar] [CrossRef]
- Evans, L.T.; Fischer, R.A. Yield potential: Its definition, measurement and significance. Crop Sci. 1999, 39, 1544–1551. [Google Scholar] [CrossRef]
- Benson, T.; Fermont, A. Estimating yield of food crops grown by smallholder farmers: A review in the Uganda context. In International Food Policy Research Institute; IFPRI Discussion Paper 01097; Development Strategy and Governance Division: Washington, DC, USA, 2011; p. 69. [Google Scholar]
- Jocković, Đ.; Stojaković, M.; Ivanović, M.; Bekavac, G.; Popov, R.; Đalović, I. NS maize hybrids—Today and tomorrow. Ratar. Povrt. 2010, 47, 325–333. [Google Scholar]
- Đalović, I. More Important Morphological Traits and the Content of Mineral Elements in Maize at the Different Levels of Fertilization (In Serbian). Ph.D. Thesis, University of Novi Sad, Faculty of Agriculture, Novi Sad, Serbi, 2014. [Google Scholar]
- Van Ittersum, M.K.; Rabbinge, R. Concepts in production ecology for analysis and quantification of agricultural input-output combinations. Field Crops Res. 1997, 52, 197–208. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Lin, X.; Hubbard, K.G.; Lv, S.; Wang, J. Narrowing the agronomic yield gaps of maize by improved soil, cultivar, and agricultural management practices in different climate zones of Northeast China. Earth Interact. 2016, 20, 1–18. [Google Scholar] [CrossRef]
- Ndhleve, S.; Nakin, M.D.V.; Longo-Mbenza, B. Impact of supplemental irrigation as a climate change adaptation strategy for maize production: A case of the Eastern Cape Province of South Africa. Water SA 2017, 43, 222–228. [Google Scholar] [CrossRef]
- Sud, U.C.; Ahmad, T.; Gupta, V.K.; Chandra, H.; Sahoo, P.M.; Aditya, K.; Singh, M.; Biswas, A. Global Strategy. In Synthesis of Literature and Framework—Research on Improving Methods for Estimating Crop Area, Yield and Production under Mixed, Repeated and Continuous Cropping; ICAR-Indian Agricultural Statistics Research Institute: New Delhi, India, 2016; p. 127. [Google Scholar]
- Fermont, A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers: A Review in the Uganda Context; International Food Policy Research Institute/CGIAR: Washington, DC, USA, 2011; p. 68. [Google Scholar]
- Ali, F.; Ahsan, M.; Ali, Q.; Kanwal, N. Phenotypic stability of Zea mays grain yield and its attributing traits under drought stress. Front. Plant. Sci. 2017, 8, 1397. [Google Scholar] [CrossRef]
- Muranui, E. Effect of plant density and row spacing on maize (Zea mays L.) grain yield in different crop year. J. Agric. Environ. Sci. 2015, 2, 57–63. [Google Scholar] [CrossRef]
- Huang, S.; Gao, Y.; Li, Y.; Xu, L.; Tao, H.; Wang, P. Influence of plant architecture on maize physiology and yield in the Heilonggang River Valley. Crop J. 2017, 5, 52–62. [Google Scholar] [CrossRef]
- Vazin, F.; Hassanzadeh, M.; Madani, A.; Nassiri-Mahallati, M.; Nasri, M. Modeling light interception and distribution in mixed canopy of common cocklebur (Xanthium stramarium) in competition with corn. Planta Daninha 2010, 28, 455–462. [Google Scholar] [CrossRef]
- Andrade, F.H.; Vega, C.; Uhart, S.; Cirilo, A.; Cantarero, M.; Valentinuz, O. Kernel number determination in maize. Crop Sci. 1999, 39, 453–459. [Google Scholar] [CrossRef]
- Russell, W.A. Genetic improvement of maize yields. Adv. Agron. 1991, 46, 245–298. [Google Scholar] [CrossRef]
- Qian, C.; Yu, Y.; Gong, X.; Jiang, Y.; Zhao, Y.; Yang, Z.; Hao, Y.; Li, L.; Song, Z.; Zhang, W. Response of grain yield to plant density and nitrogen rate in spring maize hybrids released from 1970 to 2010 in Northeast China. Crop J. 2016, 4, 459–467. [Google Scholar] [CrossRef]
- Mandić, V.; Bijelić, Z.; Krnjaja, V.; Tomić, Z.; Stanojković-Sebić, A.; Stanojković, A.; CaroPetrović, V. The effect of crop density on maize grain yield. Biotechnol. Anim. Husb. 2016, 32, 83–90. [Google Scholar] [CrossRef]
- Tokatlidis, I.S.; Koutroubas, S.D. A review study of the maize hybrids’ dependence on high plant populations and its implications on crop yield stability. Field Crops Res. 2004, 88, 103–114. [Google Scholar] [CrossRef]
- Berzsenyi, Z.; Lap, D.Q. Responses of maize (Zea mays L.) hybrids to sowing date, N fertiliser and plant density in different years. Acta Agron. Hung. 2005, 53, 119–131. [Google Scholar] [CrossRef]
- Shiluli, M.C.; Macharia, C.N.; Kamau, A.W. Economic analysis of maize yield response to nitrogen and phosphorus in the sub-humid zones of Western Kenya. Afr. Crop Sci. J. 2003, 11, 181–187. [Google Scholar] [CrossRef][Green Version]
- Gakunga, J.; Mugo, S.; Njoroge, K.; Olubayo, F. Combining ability of maize lines resistant to Chilo partellus (Swinhoe) in the mid-altitude environment of Kenya. J. Plant Breed. Crop Sci. 2012, 4, 161–168. [Google Scholar] [CrossRef]
- Mrkovacki, N.; Dalovic, I.; Josic, D.; Bjelic, D.; Jokanovic, M.B. The effect of PGPR Strains on microbial abundance in maize rhizosphere in field conditions. Ratar. Povrt. 2016, 53, 15–19. [Google Scholar] [CrossRef]
- Ngaboyisonga, C. On-farm adaptability of four maize varieties under recommended cultural practices in the highlands of Rwanda. In Proceedings of the Seventh Eastern Southern Africa Regional Maize Conference, Nairobi, Kenya, 11–15 February 2001; pp. 72–76. [Google Scholar]
- Rafique, M.; Hussain, A.; Mahmood, T.; Alvi, A.W.; Alvi, M.B. Heritability and interrelationships among grain yield and yield components in maize (Zea mays L.). Int. J. Agric. Biol. 2005, 6, 1113–1114. [Google Scholar]
- Rafiq, C.M.; Rafique, M.; Hussain, A.; Altaf, M. Studies on heritability, correlation and path analysis in maize (Zea mays L.). J. Agric. Res. 2010, 48, 35–38. [Google Scholar]
- Nagarajan, D.; Nallathambi, G. Correlation studies for grain yield attributes in maize (Zea mays L.). Bull. Environ. Pharmacol. Life Sci. 2017, 6, 65–68. [Google Scholar]
- Tagne, A.; Feujio, T.P.; Sonna, C. Essential oil and plant extracts as potential substitutes to synthetic fungicides in the control of fungi. In Proceedings of the International Conference, Diversifying Crop Protection. ENDURE, La Grande Mott, France, 12–15 October 2008. [Google Scholar]
- Bello, O.B.; Ige, S.A.; Azeez, M.A.; Afolabi, M.S.; Abdulmaliq, S.Y.; Mahamood, J. Heritability and genetic advance for grain yield and its component characters in maize (Zea mays L.). Int. J. Plant. Res. 2012, 2, 138–145. [Google Scholar] [CrossRef]
- Tandzi, L.N.; Ngonkeu, E.M.; Youmbi, E.; Nartey, E.; Yeboah, M.; Gracen, V.; Ngeve, J.; Mafouasson, H.A. Agronomic performance of maize hybrids under acid and control soil conditions. Int. J. Agron. Agric. Res. 2015, 6, 275–291. [Google Scholar]
- Petmi, C.L.; Ngonkeu, E.L.M.; Tandzi, N.L.; Ambang, Z.; Boyomo, O.; Bell, J.M.; Tekeu, H.; Mafouasson, H.; Malaa, D.; Noé, W. Screening of maize (Zea mays L.) genotypes for adaptation on contrasting acid soils in the humid forest zone of Cameroon. J. Exp. Agric. Int. 2016, 14, 1–15. [Google Scholar] [CrossRef]
- Mafouasson, H.N.A.; Gracen, V.; Yeboah, M.A.; Ntsomboh-Ntsefong, G.; Tandzi, N.L.; Mutengwa, C. Genotype-by-environment interaction and yield stability of maize single cross hybrids developed from tropical inbred lines. Agronomy 2018, 8, 62. [Google Scholar] [CrossRef]
- Shehu, B.M.; Merckx, R.; Jibrin, J.M.; Kamara, A.Y.; Ruinda, J. Quantifying variability in maize yield response to nutrient applications in the Northern Nigerian Savanna. Agronomy 2018, 8, 18. [Google Scholar] [CrossRef]
- Szareski, V.J.; Carvalho, R.I.; Kehl, K.; de Junior Pelegrin, A.; Nardino, M.; Demari, H.G.; Barbosa, H.M.; Lautenchleger, F.; Smaniotto, D.; Aumonde, T.Z.; et al. Interrelations of characters and multivariate analysis in corn. J. Agric. Sci. 2018, 10, 187–194. [Google Scholar] [CrossRef]
- Blank World Map to Print 2018–2019. Available online: http://plageiledyeu.club/carte-vierge-a-imprimer/planisphere-vierge-a-imprimer-argandor-a-carte-vierge-a-imprimer/ (accessed on 5 January 2019).
- ASTM. Annual Book of ASTM Standards. In American Society for Testing and Materials, 100 Barr Harbor Drive; ASTM: West Conshohocken, PA, USA, 2001. [Google Scholar]
- CIMMYT. Managing Trials and Reporting Data for CIMMYT’s International Maize Testing Program; CIMMYT: México City, México, 1985; p. 23. [Google Scholar]
- Dorsey-Redding, C.; Hurburgh, R.C.; Johnson, L.A.; Fox, S.R. Adjustment of maize quality data for moisture content. Cereal Chem. 1990, 67, 292–295. [Google Scholar]
- Miles, S.R.; Remenga, E.E. Relation of kernel, cob, and ear moisture in dent corn. Purdue Agr. Exp. Sta. Res. Bul. 1953, 599, 42. [Google Scholar]
- Heisey, P.; Ahmad, M.; Stevens, E.J.; Khan, K.; Zeb, J.; Javed, H.I. Diagnosing Research Priorities for Higher-Altitude Maize-Based Farming Systems in Swat; Agricultural Economics Research Unit (PARC)/CIMMYT collaborative Program: Islamabad, Pakistan, 1990; p. 62. [Google Scholar]
- Gomes, L.S.; Brandão, A.M.; Brito, C.H.; Moraes, D.F.; Lopes, M.T.G. Resistance to plant lodging and stem breaking in tropical maize. Pesquisa Agropecuária Brasileira 2010, 45, 140–145. [Google Scholar] [CrossRef][Green Version]
- Panison, F.; Sangoi, L.; Kolling, D.F.; Coelho, C.M.M.; Durli, M.M. Harvest time and agronomic performance of maize hybrids with contrasting growth cycles. Acta Sci. 2016, 38, 219–226. [Google Scholar] [CrossRef][Green Version]
- Araujo, E.F.; Araujo, R.F.; Sofiatti, V.; Silva, R.F. Physiological quality of maize seeds harvested in different times. Bragantia 2006, 65, 687–692. [Google Scholar] [CrossRef][Green Version]
- Marques, O.J.; Dalpasquale, V.A.; Vidigal Filho, P.S.; Scapim, C.A.; Reche, D.L. Grain mechanical damage of maize commercial hybrids as affected by moisture content at harvest. Semin Ciências Agrárias 2011, 32, 565–576. [Google Scholar] [CrossRef]
- Galvão, J.C.C.; Conceição, P.M.; Araújo, E.F.; Karstein, J.; Finger, F.L. Physiological and enzymatic alterations in maize seeds submitted to different harvest times and shelling methods. Revista Brasileira de Milho e Sorgo 2014, 13, 14–23. [Google Scholar] [CrossRef]
- Gaile, Z. Harvest time effect on yield and quality of maize (Zea mays L.) grown for silage. Latv. J. Agron. 2008, 10, 104–111. [Google Scholar]
- Masuka, B.; Atlin, G.N.; Olsen, M.; Magorokosho, C.; Labuschagne, M.; Crossa, J.; Bänziger, M.; Pixley, K.V.; Vivek, B.S.; von Biljon, A.; et al. Grains in genetic improvement in Eastern and Southern Africa: I. CIMMYT hybrid breeding pipeline. Crop Sci. 2017, 57, 168–179. [Google Scholar] [CrossRef]
- Horrocks, R.D.; Zuber, M.S. Corn shelling percentage studies. University of Missouri-Columbia, College of Agriculture, Agricultural Experiment Station. Res. Bull. 1970, 976, 1–35. [Google Scholar]
- Thakur, S.K. Gen etic Analysis of Yield and Its Components in Maize (Zea mays L.) Inbred Lines Using Line X Tester Analysis. Master’s Thesis, Indira Gandhi Krishi Vishwavidyalaya, Raipur, India, 2016; p. 128. [Google Scholar]
- Ngie, A.; Hmed, F. Estimation of maize yield using multispectral satellite data sets (SPOT 5) and the random forest algorithm. S. Afr. J. Geomat. 2018, 7, 11–30. [Google Scholar] [CrossRef]
- Onat, B.; Bakal, H.; Gulluoglu, L.; Arioglu, H. The effects of row spacing and plant density on yield and yield components of peanut grown as a double crop in Mediterranean environment in Turkey. Turk. J. Field Crops 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Cassman, K.G. Long-term trajectories: Crop yields, farmland, and irrigated agriculture. Econ. Rev. Spec. Issue 2016, 1–26. Available online: http://www.KansasCityFed.org (Accessed on 15 July 2018).
- The, C.; Tandzi, N.L.; Zonkeng, C.; Ngonkeu, E.L.M.; Meka, S.; Leon, C.; Horst, W.J. Contribution of introduced inbred lines to maize varietal improvement for acid soil tolerance. In Demand-Driven Technologies for Sustainable Maize Production in West and Central Africa; Badu-Apraku, B., Fakorede, M.A.B., Lum, A.F., Menkir, A., Ouedraogo, M., Eds.; International Institute of Tropical Agriculture (IITA): Cotonou, Bénin, 2005. [Google Scholar]
- Ifie, B.E. Genetic Analysis of Striga Resistance and Low Soil Nitrogen Tolerance in Early Maturing Maize (Zea mays L.) Inbred lines. Ph.D. Thesis, University of Ghana, Ghana, Accra, 2013; p. 191. [Google Scholar]
- The, C.; Mafouasson, H.; Calba, H.; Mbouemboue, P.; Zonkeng, C. Identification de groupes hétérotiques pour la tolérance du maïs (Zea mays L.) aux sols acides des tropiques. Cah. Agric. 2006, 15, 337–346. [Google Scholar]
- Mafouasson, A.H.N.; Kenga, R.; Gracen, V.; Yeboah, A.M.; Mahamane, N.L.; Tandzi, N.L.; Ntsomboh-Ntsefong, G. Combining ability and gene action of Tropical Maize (Zea mays L.) inbred lines under low and high nitrogen conditions. J. Agric. Sci. 2016, 9, 222–235. [Google Scholar] [CrossRef]
- Chen, G.; Cao, H.; Liang, J.; Ma, W.; Guo, L.; Zhang, S.; Jiang, R.; Zhang, H.; Goulding, K.W.T.; Zhang, F. Factors affecting nitrogen use efficiency and grain yield of Summer Maize on smallholder farms in the North China Plain. Sustainability 2017, 10, 363. [Google Scholar] [CrossRef]
- Pixley, K.; Bänziger, M. Open-pollinated maize varieties: A backward step or valuable option for farmers? In Proceedings of the Seventh Eastern and Southern Africa Regional Maize Conference, Nairobi, Kenya, 11–15 February 2001; pp. 22–28. [Google Scholar]
- Vivek, B.; Bänziger, M.; Pixley, K.V. Characterization of Maize Germplasm Grown in Eastern and Southern Africa: Results of the 2000 Regional Trials Coordinated by CIMMYT; CIMMYT: Harare, Zimbabwe, 2001. [Google Scholar]
- Parentoni, S.N.; de Souza, C.L., Jr.; de Carvalho Alves, V.M.; Gama, E.E.G.; Coelho, A.M.; Oliveira, A.C.; Guimaraes, P.E.O.; Guimaraes, C.T.; Vasconcelos, M.J.V.; Pacheco, P.C.A.; et al. Inheritance and breeding strategies for phosphorus efficiency in Tropical Maize (Zea mays L.). Maydica 2010, 55, 1–15. [Google Scholar]
- Norman, D.W.; Worman, F.D.; Siebert, J.D.; Modiakgotla, E. The Farming Systems Approach to Development and Appropriate Technology Generation; FAO Farm System Management Series 10; Food and Agriculture Organization of the United Nations: Rome, Italy, 1995. [Google Scholar]
- Casley, D.J.; Kumar, K. The Collection, Analysis and Use of Monitoring and Evaluation Data; Johns Hopkins University Press for the World Bank: Baltimore, MD, USA, 1988. [Google Scholar]
- Poate, C.D. A Review of Methods for Measuring Crop Production from Smallholder Producers. Exp. Agric. 1988, 24, 1–14. [Google Scholar] [CrossRef]
- Murphy, J.; Casley, D.J.; Curry, J.J. Farmers’ Estimations as a Source of Production Data; World Bank: Washington, DC, USA, 1991; p. 132. [Google Scholar]
- Byerlee, D.; Hussain, S.S. Maize Production in NWFP: A Review of Technological Issues in Relation to Farmers’ Circumstances; PARC/CIMMYT: Islamabad, Pakistan, 1986. [Google Scholar]
- Singh, R. Use of satellite data and farmers eye estimate for crop yield modelling. J. Indian Soc. Agric. Stat. 2013, 56, 166–176. [Google Scholar]
- Sapkota, T.B.; Jat, M.L.; Jat, R.K.; Kapoor, P.; Stirling, C. Yield estimation of food and non-food crops in smallholder production systems, Chapter 8. In Methods for Measuring Greenhouse Gas Balances and Evaluating Mitigation Option in Smallholder Agriculture; Rosenstock, T.S., Ed.; Springer Open: Cham, Switzerland, 2016; pp. 163–174. [Google Scholar] [CrossRef]
- Sampathkumar, T.; Pandian, B.J.; Rangaswamy, M.V.; Manickasundaram, P.; Jeyakumar, P. Influence of deficit irrigation on growth, yield and yield parametersof cooton-maize cropping sequence. Agric. Water Manag. 2013, 130, 90–102. [Google Scholar] [CrossRef]
- Rosenstock, T.S.; Rufino, M.C.; Butterbach-Bahl, K.; Wollenberg, E. Toward a protocol for quantifying the greenhouse gas balance and identifying mitigation options in smallholder farming systems. Environ. Res. Lett. 2013, 8, 021003. [Google Scholar] [CrossRef]
- Rockström, J.; Falkenmark, M. Semiarid crop production from a hydrological perspective: Gap between potential and actual yields. Crit. Rev. Plant. Sci. 2000, 19, 319–346. [Google Scholar] [CrossRef]
- van Ittersum, M.K.; Leffelaar, P.A.; van Keulen, H.; Kropff, M.J.; Bastiaans, L.; Goudriaan, J. On approaches and applications of the Wageningen crop models. Eur. J. Agron. 2003, 18, 201–234. [Google Scholar] [CrossRef]
- Nelson, G.C.; Rosegrant, M.W.; Palazzo, A.; Gray, I.; Ingersoll, C.; Tokgoz, S.; Zhu, T.; Sulser, T.B.; Ringler, C.; Msangi, S.; et al. Food Security, Farming, and Climate Change to 2050: Scenarios, Results, Policy Options; International Food Policy Research Institute: Washington, DC, USA, 2010; p. 131. [Google Scholar] [CrossRef]
- Liu, X.; Andresen, J.; Yang, H.; Niyogi, D. Calibration and validation of the hybrid-maize crop model for regional analysis and application over the U.S. Corn Belt. Earth Interact. 2015, 19, 1–16. [Google Scholar] [CrossRef]
- Fodor, N.; Kovacs, G.J. Sensitivity of 4M maize model to the inaccuracy of weather and soil input data. Appl. Ecol. Environ. Res. 2003, 1, 75–85. [Google Scholar] [CrossRef]
- Egli, D.B.; Bruening, W. Planting date and soybean yield: Evaluation of environmental effect with a crop simulation model: SOYGRO. Agric. For. Meteorol. 1992, 62, 19–29. [Google Scholar] [CrossRef]
- Boote, K.J.; Jones, J.W.; Pickering, N.B. Potential uses and limitations of crop models. Agron. J. 1996, 88, 704–716. [Google Scholar] [CrossRef]
- Hoogenboom, G. Contribution of agrometeorology to the simulation pf crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Matthews, R. Where to now with crop modelling? In Crop-Soil Simulation Models, Applications in Developing Countries; Matthews, R., Stephens, W., Eds.; CABI publishing: Wallingford, UK; New York, NY, USA, 2002; pp. 209–229. [Google Scholar]
- Palmer, T.N.; Alessandri, A.; Andersen, U.; Cantelaube, P.; Davey, M.; Delecluse, P.; Deque, M.; Diez, E.; Doblas-Reyes, F.J.; Feddersen, H.; et al. Development of a European Multi-Model Ensemle System for Seasonal to Inter-Annual Prediction (DEMETER). Am. Meteorol. Soc. 2004, 85, 853–872. [Google Scholar] [CrossRef]
- Ritchie, J.T. Classification of crop models. In Crop Modelling and Related Environmental Data; Uhlir, P.F., Carter, G.C., Eds.; CODATA: Paris, France, 1994; pp. 3–14. [Google Scholar]
- Bannayan, M.; Crout, N.M.J. A stochastic modelling approach for real-time forecasting of winter wheat yield. Field Crops Res. 1999, 62, 85–95. [Google Scholar] [CrossRef]
- Martin, R.V.; Washington, R.; Downing, T.E. Seasonal maize forecasting for South Africa and Zimbabwe derived from an agro climatological model. J. Appl. Meteor. 2000, 39, 1473–1479. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kishtawal, C.M.; LaRow, T.E.; Bachiochi, D.R.; Zhang, Z.; Willford, C.E.; Gadgil, S.; Surendran, S. Climate forecasts from multimodel superensemble. Science 1999, 285, 1548–1550. [Google Scholar] [CrossRef]
- Reason, C.J.C.; Engelbrecht, F.; Landman, W.A.; Lutjeharms, J.R.E.; Piketh, S.; de Rautenbach, C.J.W.; Hewitson, B.C. A review of South African research in atmospheric science and physical oceanography during 2000-2005. S. Afr. J. Sci. 2006, 102, 35–45. [Google Scholar]
- Hollinger, S.E. Modeling the effects of weather and management practices on maize yield. Agric. For. Meteorol. 1988, 44, 81–97. [Google Scholar] [CrossRef]
- Le Roux, N. Seasonal Maize Simulations for South Africa Using a Multi-Model Ensemble System. Master’s Thesis, University of Pretoria, Pretoria, South Africa, 2009; p. 170. [Google Scholar]
- Schulthess, U.; Timsina, J.; Herrera, J.M.; McDonald, A. Mapping field—Scale yield gaps for maize: An example from Bangladesh. Field Crops Res. 2013, 143, 151–156. [Google Scholar] [CrossRef]
- Cheng, Z.; Meng, J.; Wang, Y. Improving spring maize yield estimation at field scale by assimilating time-series HJ-1 CCD data into WOFOST model using a new method with fast algorithms. Remote Sens. 2016, 8, 303. [Google Scholar] [CrossRef]
- Weng, Q. Introduction to Remote Sensing Systems, Data, and Applications; Taylor and Francis/CRC Press: Boca Raton, FL, USA, 2016; p. 19. [Google Scholar]
- Shanahan, J.F.; Schepers, J.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ. 2002, 94, 205–220. [Google Scholar] [CrossRef]
- Martin, K.L.; Girma, K.; Freeman, K.W.; Teal, R.K.; Tubana, B.; Amall, D.B.; Chung, B.; Walsh, O.; Solie, J.B.; Stone, M.L.; et al. Expression of variability in corn as influence by growth stage using optical sensor measurements. Agron. J. 2007, 99, 384–389. [Google Scholar] [CrossRef]
- Fernandez-Ordoñez, Y.M.; Soria-Ruiz, J. Maize crop yield estimation with remote sensing and empirical models. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3035–3038. [Google Scholar] [CrossRef]
- Labus, M.P.; Nielsen, G.A.; Lawrence, R.L.; Engel, R.; Long, D.S. Wheat yield estimates using multi-temporal NDVI satellite imagery. Int. J. Remote Sens. 2002, 23, 4169–4180. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Mkhabela, M.S.; Mashinini, N.N. Early maize yield forescating in four agro-ecological regions of Swaziland using NDVI data derived from NOAA’s-AVHRR. Agric. For. Meteorol. 2005, 129, 1–9. [Google Scholar] [CrossRef]
- Wall, L.; Larocque, D.; Léger, P.M. The early explanatory power of NDVI in crop yield modelling. Int. J. Remote Sens. 2008, 29, 2211–2225. [Google Scholar] [CrossRef]
- Jovanović, D.; Sabo, F.; Govedarica, M.; Marinković, B. Crop yield estimation in 2014 for Vojvodina using methods of remote sensing. Ratar. Povrt. 2014, 51, 145–153. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Akhmedov, B.; Beard, L.; Stern, A.; Mueller, R. Operational prediction of crop yields using modis data and products. In Proceedings of the Remote Sensing Support to Crop Yield Forecast and Area Estimates; 2007. ISPRS Archives XXXVI-8/W48. [Google Scholar]
- Guindin-Garcia, N. Estimating Maize Yield from Crop Biophysical Parameters Using Remote Sensing. Ph.D. Thesis, University of Nebraska, Lincoln, NE, USA, 2010; p. 121. [Google Scholar]
- Tenkorang, F.; Lowenberg-Doboer, J. On-farmm profitability of remote sensing in agriculture. J. Terr. Obs. 2008, 1, 50–59. [Google Scholar]
- Loladze, A.; Rodrigues, F.A., Jr.; Toledo, F.; Vicente, F.S.; Gérard, B.; Boddupalli, M.P. Application of remote sensing for phenotyping Tar Spot Complex resistance in Maize. Front. Plant Sci. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Ghafoor, A.; Bhatti, M.I.; Akhtar Ibrar-ul, H.; Ibrahim, M. Obaid-ur-Rehman. Satellite remote sensing and GIS-based crops forecasting & estimation system in Pakistan. In Proceedings of the Expert Meeting on Crop Monitoring for Improved Food Security, Vientiane, Laos, 17 February 2014; Srivastava, M.K., Ed.; pp. 1–16. [Google Scholar]
- Urassa, J.K. Factors influencing maize crop production at household levels: A case of Rukwa Region in the Southern Highlands of Tanzania. Afr. J. Agric. Res. 2015, 10, 1097–1106. [Google Scholar] [CrossRef]
- Manyevere, A.; Muchaonyerwa, P.; Laker, M.C.; Mnkeni, P.N.S. Farmers’ perspectives with regards to crop production: An analysis of Nkonkobe Municipality, South Africa. J. Agric. Rural Dev. Trop. Subtrop. 2014, 115, 41–53. [Google Scholar]
- Khapayi, M.; Celliers, P.R. Factors limiting and preventing emerging farmers to progress to commercial agricultural farming in the King Williams’s Town area of the Eastern Cape Province, South Africa. S. Afr. J. Agric. Ext. 2016, 44, 25–41. [Google Scholar] [CrossRef]
- Ngoko, Z.; Cardwell, K.F.; Marasas, W.F.O.; Wingfield, M.J.; Ndemah, R. Biological and physical constraints on maize production in the humid forest and western highlands of Cameroon. Eur. J. Plant Pathol. 2002, 108, 893–902. [Google Scholar] [CrossRef]
- Tandzi, N.L.; Mutengwa, C.S.; Ngonkeu, E.L.M.; Gracen, V. Breeding maize for tolerance to acidic soils: A review. Agronomy 2018, 8, 84. [Google Scholar] [CrossRef]
- Grassini, P.; Yang, H.; Irmak, S.; Thorburn, J.; Burr, C.; Cassman, K.G. High-yield irrigated maize in the Western, U.S. Corn Belt: II. Irrigation management and crop water productivity. Field Crops Res. 2010, 120, 133–141. [Google Scholar] [CrossRef]
- Grassini, P.; Thorburn, J.; Burr, C.; Cassman, K.G. High-yield irrigated maize in the Western, U.S. Corn Belt: I. On-farm yield, yield potential, and impact of agronomic practices. Field Crops Res. 2011, 120, 142–150. [Google Scholar] [CrossRef]
- Harrison, L.; Michaelsen, J.; Funk, C.; Husak, G. Effects of temperature changes on maize production in Mozambique. Clim. Res. 2011, 46, 211–222. [Google Scholar] [CrossRef]
- Mngqawa, P.; Mangena-Netshikweta, L.M.; Katerere, D.R. Grain production by rural susbsistance farmers in selected districts of Limpopo and Mpumalanga Provinces South Africa. Botsw. J. Afr. Stud. 2016, 30, 49–63. [Google Scholar]
- DAFF (Department of Agriculture Forestry and Fisheries). Trends in the Agricultural Sector. 2017; p. 79. Available online: http: www.daff.gov.za (accessed on 7 July 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).