Programming of One- and Two-Step Stress Recovery in a Poly(ester urethane)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
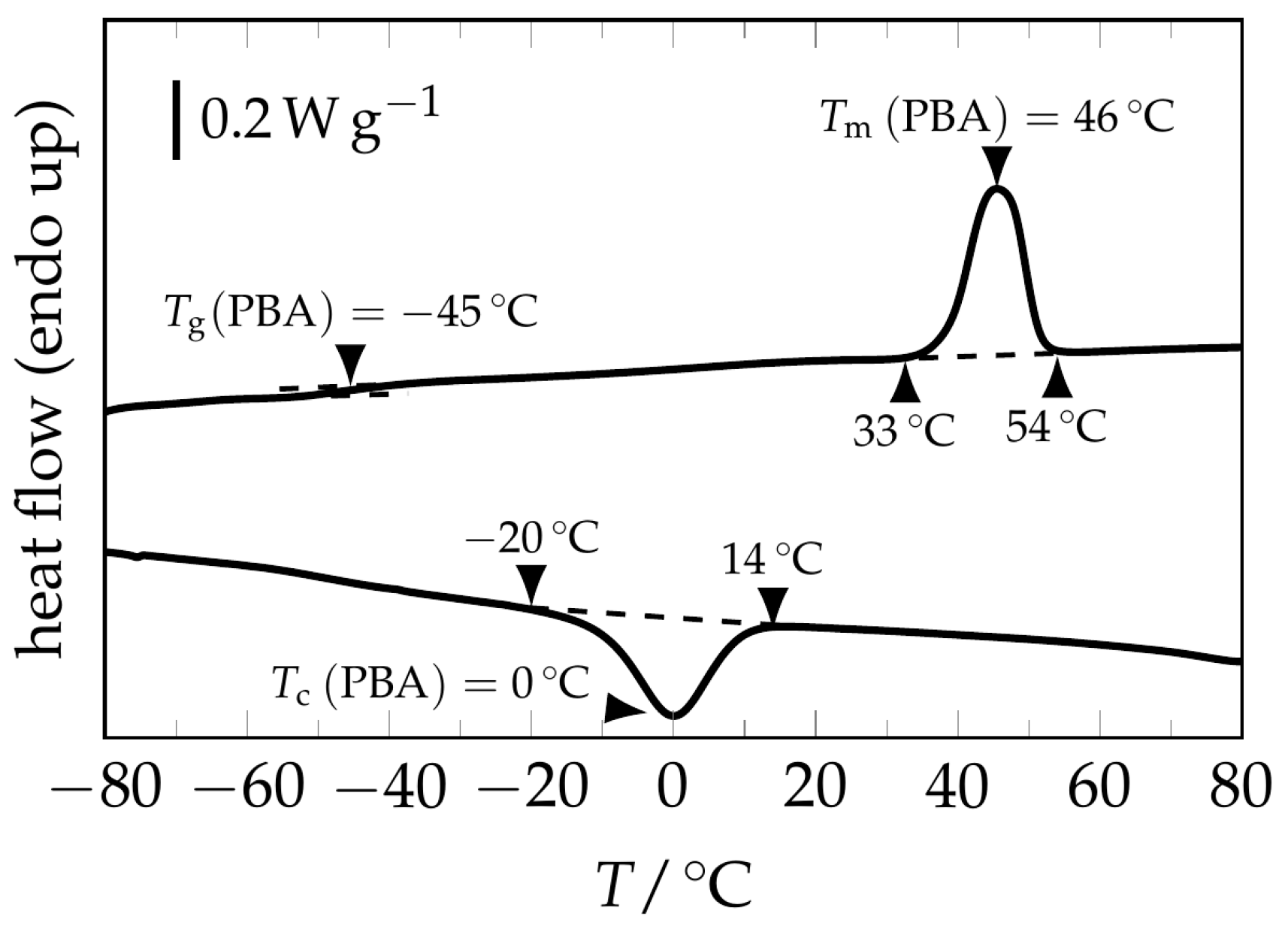
2.2. Characterization Methods
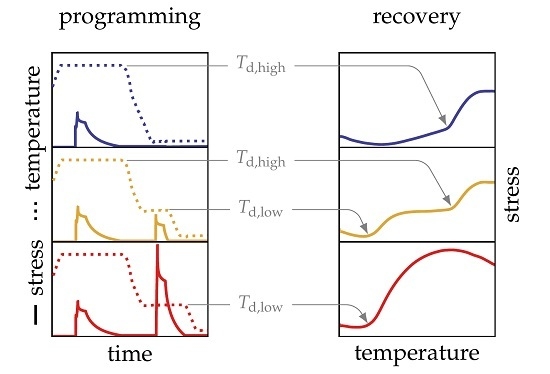
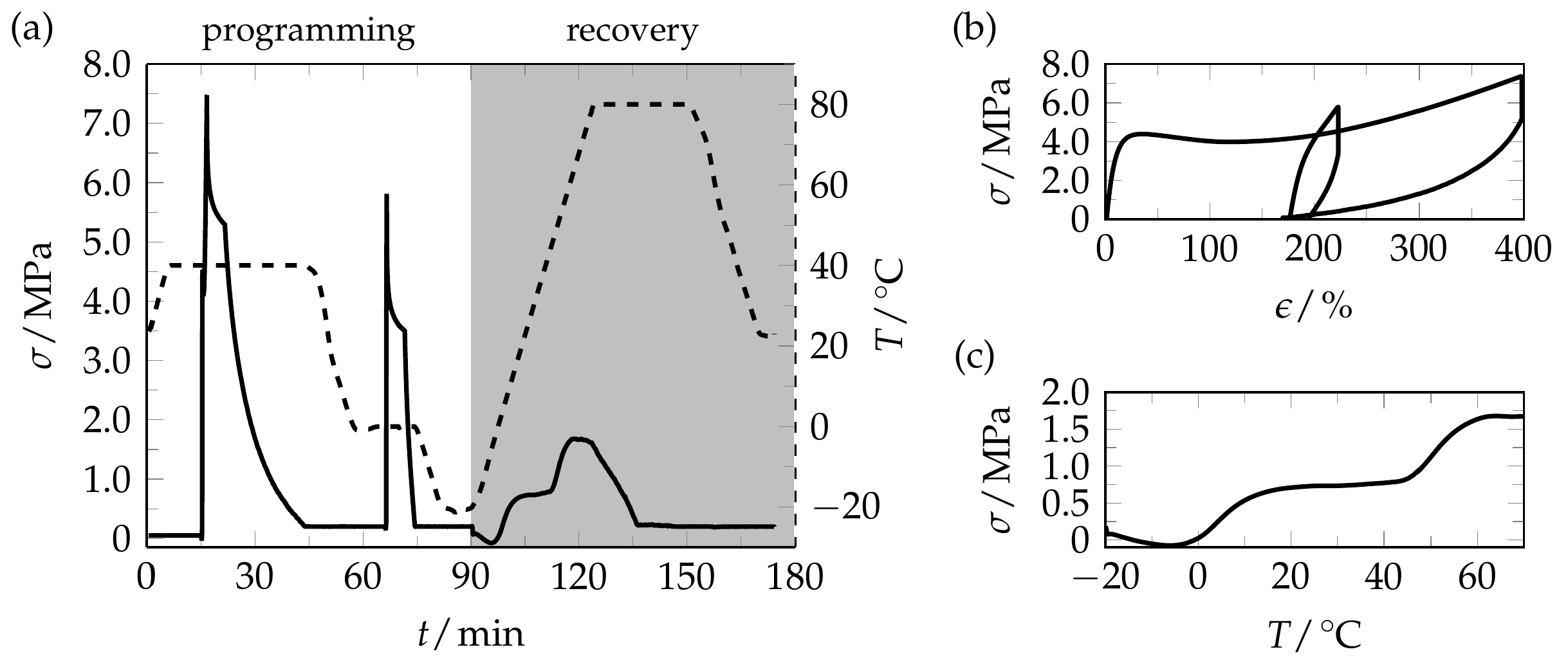
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-responsive shape memory materials: A review. Mater. Des. 2012, 33, 577–640. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Barbarino, S.; Saavedra Flores, E.I.; Ajaj, R.M.; Dayyani, I.; Friswell, M.I. A review on shape memory alloys with applications to morphing aircraft. Smart Mater. Struct. 2014, 23, 063001. [Google Scholar] [CrossRef]
- Mohd, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Pretsch, T. Review on the functional determinants and durability of shape memory polymers. Polymers 2010, 2, 120–158. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Wang, C.C.; Ding, Z.; Zhao, Y.; Tang, C.; Gao, X.Y. Polymeric shape memory materials and actuators. Liq. Cryst. 2013, 41, 277–289. [Google Scholar] [CrossRef]
- Zhao, Q.; Qi, H.J.; Xie, T. Recent progress in shape memory polymer: New behavior, enabling materials, and mechanistic understanding. Prog. Polym. Sci. 2015, 49, 79–120. [Google Scholar] [CrossRef]
- Hasan, S.M.; Nash, L.D.; Maitland, D.J. Porous shape memory polymers: Design and applications. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1300–1318. [Google Scholar] [CrossRef]
- Li, G.; Wang, A. Cold, warm, and hot programming of shape memory polymers. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1319–1339. [Google Scholar] [CrossRef]
- Bothe, M.; Pretsch, T. Bidirectional actuation of a thermoplastic polyurethane elastomer. J. Mater. Chem. A 2013, 1, 14491–14497. [Google Scholar] [CrossRef]
- Zhou, J.; Turner, S.A.; Brosnan, S.M.; Li, Q.; Carrillo, J.-M.Y.; Nykypanchuk, D.; Gang, O.; Ashby, V.S.; Dobrynin, A.V.; Sheiko, S.S. Shapeshifting: Reversible shape memory in semicrystalline elastomers. Macromolecules 2014, 47, 1768–1776. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, J.; Vatankhah-Varnoosfaderani, M.; Nykypanchuk, D.; Gang, O.; Sheiko, S.S. Advancing reversible shape memory by tuning the polymer network architecture. Macromolecules 2016, 49, 1383–1391. [Google Scholar] [CrossRef]
- Sokolowski, W.M.; Tan, S.C. Advanced self-deployable structures for space applications. J. Spacecr. Rockets 2007, 44, 750–754. [Google Scholar] [CrossRef]
- Lan, X.; Liu, Y.; Lv, H.; Wang, X.; Leng, J.; Du, S. Fiber reinforced shape-memory polymer composite and its application in a deployable hinge. Smart Mater. Struct. 2009, 18, 24–32. [Google Scholar] [CrossRef]
- Purnawali, H.; Xu, W.W.; Zhao, Y.; Ding, Z.; Wang, C.C.; Huang, W.M.; Fan, H. Poly(methyl methacrylate) for active disassembly. Smart Mater. Struct. 2012, 21, 075006. [Google Scholar] [CrossRef]
- Liu, Y.; Du, H.; Liu, L.; Leng, J. Shape memory polymers and their composites in aerospace applications: A review. Smart Mater. Struct. 2014, 23, 023001. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, K.; Isakov, M.S.; Wu, J.; Dunn, M.L.; Jerry, H. Sequential Self-Folding Structures by 3D Printed Digital Shape Memory Polymers. Sci. Rep. 2015, 5, 13616. [Google Scholar] [CrossRef] [PubMed]
- Kunzelman, J.; Chung, T.; Mather, P.T.; Weder, C. Shape memory polymers with built-in threshold temperature sensors. J. Mater. Chem. 2008, 18, 1082–1086. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Leo, C.D.; Floerkemeier, C.; Sarma, S.; Anand, L. RFID tag antenna based temperature sensing using shape memory polymer actuation. IEEE Sens. Conf. Proc. 2010, 1, 2363–2368. [Google Scholar]
- Lu, H.; Yu, K.; Liu, Y.; Leng, J. Sensing and actuating capabilities of a shape memory polymer composite integrated with hybrid filler. Smart Mater. Struct. 2010, 19, 065014. [Google Scholar] [CrossRef]
- DiOrio, A.M.; Luo, X.; Lee, K.M.; Mather, P.T. A functionally graded shape memory polymer. Soft Matter 2011, 7, 68–74. [Google Scholar] [CrossRef]
- Fritzsche, N.; Pretsch, T. Programming of temperature-memory onsets in a semicrystalline polyurethane elastomer. Macromolecules 2014, 47, 5952–5959. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Yi, G.; Wang, Y.; Zu, X.; Wang, H.; Huang, H.; Liang, Z. Temperature sensing of conductive shape memory polymer composites. Mater. Lett. 2015, 140, 71–74. [Google Scholar] [CrossRef]
- Pretsch, T.; Ecker, M.; Schildhauer, M.; Maskos, M. Switchable information carriers based on shape memory polymer. J. Mater. Chem. 2012, 22, 7757–7766. [Google Scholar] [CrossRef]
- Fritzsche, N.; Pretsch, T. Miniaturization of QR code carriers based on shape memory polymer. ASME Conf. Smart Mater. 2012, 1, 81–88. [Google Scholar]
- Ecker, M.; Pretsch, T. Durability of switchable QR code carriers under hydrolytic and photolytic conditions. Smart Mater. Struct. 2013, 22, 094005. [Google Scholar] [CrossRef]
- Ecker, M.; Pretsch, T. Multifunctional poly(ester urethane) laminates with encoded information. RSC Adv. 2014, 4, 286–292. [Google Scholar] [CrossRef]
- Ecker, M.; Pretsch, T. Novel design approaches for multifunctional information carriers. RSC Adv. 2014, 4, 46680–46688. [Google Scholar] [CrossRef]
- Pretsch, T.; Jakob, I.; Müller, W. Hydrolytic degradation and functional stability of a segmented shape memory poly(ester urethane). Polym. Degrad. Stab. 2009, 94, 61–73. [Google Scholar] [CrossRef]
- Ji, F.L.; Hu, J.L.; Chui, S.S.-Y. Influences of phase composition and thermomechanical conditions on shape memory properties of segmented polyurethanes with amorphous reversible phase. Polym. Eng. Sci. 2012, 52, 1015–1026. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Y.; Xiong, Z.; Liu, X.; Na, H.; Zhang, R.; Zhu, J. Highly recoverable rosin-based shape memory polyurethanes. J. Mater. Chem. A 2013, 1, 3263–3267. [Google Scholar] [CrossRef]
- Kim, B.K.; Lee, S.Y.; Xu, M. Polyurethanes having shape memory effects. Polymer 1996, 37, 5781–5793. [Google Scholar] [CrossRef]
- Xie, T.; Rousseau, I.A. Facile tailoring of thermal transition temperatures of epoxy shape memory polymers. Polymer 2009, 50, 1852–1856. [Google Scholar] [CrossRef]
- Gu, X.; Mather, P.T. Entanglement-based shape memory polyurethanes: Synthesis and characterization. Polymer 2012, 53, 5924–5934. [Google Scholar] [CrossRef]
- Miaudet, P.; Derré, A.; Maugey, M.; Zakri, C.; Piccione, P.M.; Inoubli, R.; Poulin, P. Shape and temperature memory of nanocomposites with broadened glass transition. Science 2007, 318, 1294–1296. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Li, G. Investigation into stress recovery behavior of shape memory polyurethane fiber. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 1429–1440. [Google Scholar] [CrossRef]
- Hashmi, S.A.R.; Prasad, H.C.; Abishera, R.; Bhargaw, H.N.; Naik, A. Improved recovery stress in multi-walled-carbon-nanotubes reinforced polyurethane. Mater. Des. 2015, 67, 492–500. [Google Scholar] [CrossRef]
- Hu, J.; Kumar, B.; Narayana, H. Stress memory polymers. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 893–898. [Google Scholar] [CrossRef]
- Wang, A.; Li, G. Stress memory of a thermoset shape memory polymer. J. Appl. Polym. Sci. 2015, 132, 42112. [Google Scholar] [CrossRef]
- Momtaz, M.; Razavi-Nouri, M.; Barikani, M. Effect of block ratio and strain amplitude on thermal, structural, and shape memory properties of segmented polycaprolactone-based polyurethanes. J. Mater. Sci. 2014, 49, 7575–7584. [Google Scholar] [CrossRef]
- Voit, W.; Ware, T.; Dasari, R.R.; Smith, P.; Danz, L.; Simon, D.; Barlow, S.; Marder, S.R.; Gall, K. High-strain shape-memory polymers. Adv. Funct. Mater. 2010, 20, 162–171. [Google Scholar] [CrossRef]
- Xie, T.; Page, K.A.; Eastman, S.A. Strain-based temperature memory effect for nafion and its molecular origins. Adv. Funct. Mater. 2011, 21, 2057–2066. [Google Scholar] [CrossRef]
- Koerner, H.; Price, G.; Pearce, N.A.; Alexander, M.; Vaia, R.A. Remotely actuated polymer nanocomposites—Stress-recovery of carbon-nanotube-filled thermoplastic elastomers. Nat. Mater. 2004, 3, 115–120. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Jana, S.C. Nanoclay-tethered shape memory polyurethane nanocomposites. Polymer 2007, 48, 3790–3800. [Google Scholar] [CrossRef]
- Ponyrko, S.; Donato, R.K.; Matějka, L. Tailored high performance shape memory epoxy-silica nanocomposites: Structure design. Polym. Chem. 2016, 7, 560–572. [Google Scholar] [CrossRef]
- Gall, K.; Dunn, M.L.; Liu, Y.; Stefanic, G.; Balzar, D. Internal stress storage in shape memory polymer nanocomposites. Appl. Phys. Lett. 2004, 85, 290–292. [Google Scholar] [CrossRef]
- Atli, B.; Gandhi, F.; Karst, G. Thermomechanical characterization of shape memory polymers. J. Intell. Mater. Syst. Struct. 2008, 20, 87–95. [Google Scholar] [CrossRef]
- Cui, J.; Kratz, K.; Lendlein, A. Adjusting shape-memory properties of amorphous polyether urethanes and radio-opaque composites thereof by variation of physical parameters during programming. Smart Mater. Struct. 2010, 19, 065019. [Google Scholar] [CrossRef]
- Mirtschin, N.; Pretsch, T. Designing temperature-memory effects in semicrystalline polyurethane. RSC Adv. 2015, 5, 46307–46315. [Google Scholar] [CrossRef]
- Ping, P.; Wang, W.; Chen, X.; Jing, X. Poly(ε-caprolactone) polyurethane and its shape-memory property. Biomacromolecules 2005, 6, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ping, P.; Chen, X.; Jing, X. Polylactide-based polyurethane and its shape-memory behavior. Eur. Polym. J. 2006, 42, 1240–1249. [Google Scholar] [CrossRef]
- Grillard, F.; Zakri, C.; Gaillard, P.; Korzhenko, A.; Néri, W.; Poulin, P. How polymers lose memory with age. Soft Matter 2014, 10, 8985–8991. [Google Scholar] [CrossRef] [PubMed]
- Kratz, K.; Madbouly, S.A.; Wagermaier, W.; Lendlein, A. Temperature-memory polymer networks with crystallizable controlling units. Adv. Mater. 2011, 23, 4058–4062. [Google Scholar] [CrossRef] [PubMed]
- Langer, R.S.; Lendlein, A. Shape Memory Polymers. U.S. Patent 6,388,043, 14 May 2002. [Google Scholar]
- Li, J.; Xie, T. Significant impact of thermo-mechanical conditions on polymer triple-shape memory effect. Macromolecules 2011, 44, 175–180. [Google Scholar] [CrossRef]
- Ware, T.; Hearon, K.; Lonnecker, A.; Wooley, K.L.; Maitland, D.J.; Voit, W. Triple-shape memory polymers based on self-complementary hydrogen bonding. Macromolecules 2012, 45, 1062–1069. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Zhang, X.; Wang, Q.; Wang, T. A tough shape memory polymer with triple-shape memory and two-way shape memory properties. J. Mater. Chem. A 2014, 2, 4771–4778. [Google Scholar] [CrossRef]
- Kolesov, I.S.; Radusch, H.-J. Multiple shape-memory behavior and thermal-mechanical properties of peroxide cross-linked blends of linear and short-chain branched polyethylenes. Express Polym. Lett. 2008, 2, 461–473. [Google Scholar] [CrossRef]
- Pretsch, T. Triple-shape properties of a thermoresponsive poly(ester urethane). Smart Mater. Struct. 2010, 19, 015006. [Google Scholar] [CrossRef]
- Bothe, M.; Mya, K.Y.; Jie Lin, E.M.; Yeo, C.C.; Lu, X.; He, C.; Pretsch, T. Triple-shape properties of star-shaped POSS-polycaprolactone polyurethane networks. Soft Matter 2012, 8, 965–972. [Google Scholar] [CrossRef]
- Xie, T. Tunable polymer multi-shape memory effect. Nature 2010, 464, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, T.; Xia, S.; Pan, Y.; Zheng, Z.; Ding, X.; Peng, Y. A versatile approach to achieve quintuple-shape memory effect by semi-interpenetrating polymer networks containing broadened glass transition and crystalline segments. J. Mater. Chem. 2011, 21, 12213–12217. [Google Scholar] [CrossRef]
- Radusch, H.J.; Kolesov, I.; Gohs, U.; Heinrich, G. Multiple shape-memory behavior of polyethylene/polycyclooctene blends cross-linked by electron irradiation. Macromol. Mater. Eng. 2012, 297, 1225–1234. [Google Scholar] [CrossRef]
- Hoeher, R.; Raidt, T.; Krumm, C.; Meuris, M.; Katzenberg, F.; Tiller, J.C. Tunable multiple-shape memory polyethylene blends. Macromol. Chem. Phys. 2013, 214, 2725–2732. [Google Scholar] [CrossRef]
- Bellin, I.; Kelch, S.; Langer, R.; Lendlein, A. Polymeric triple-shape materials. Proc. Natl. Acad. Sci. USA 2006, 103, 18043–18047. [Google Scholar] [CrossRef] [PubMed]
- Tobushi, H.; Hara, H.; Yamada, E.; Hayashi, S. Thermomechanical properties in a thin film of shape memory polymer of polyurethane series. Smart Mater. Struct. 1996, 5, 483–491. [Google Scholar] [CrossRef]
- Sperling, L.H. Introduction to Physical Polymer Science, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 356. [Google Scholar]
- Bothe, M.; Emmerling, F.; Pretsch, T. Poly(ester urethane) with varying polyester chain length: Polymorphism and shape-memory behavior. Macromol. Chem. Phys. 2013, 214, 2683–2693. [Google Scholar] [CrossRef]
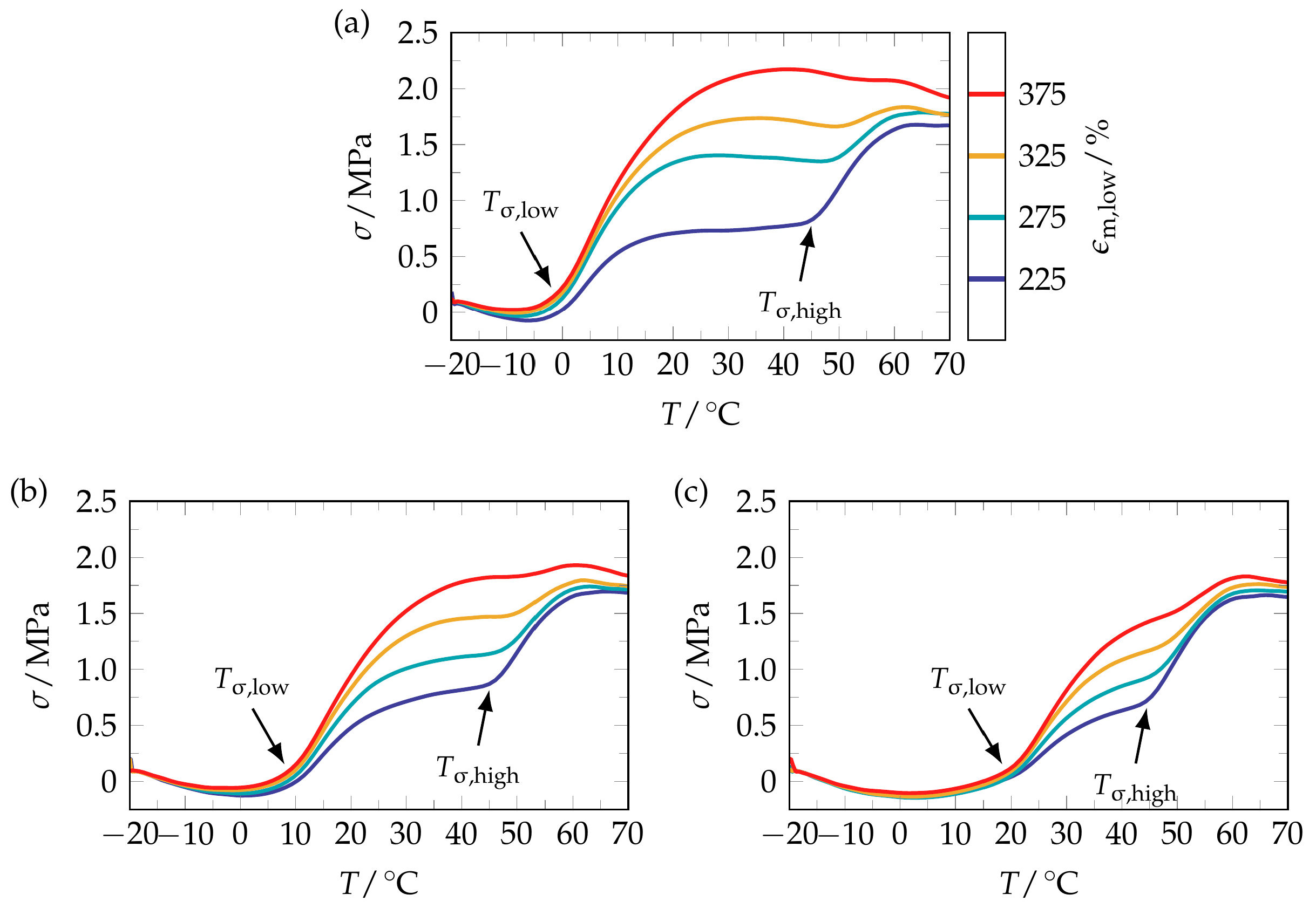

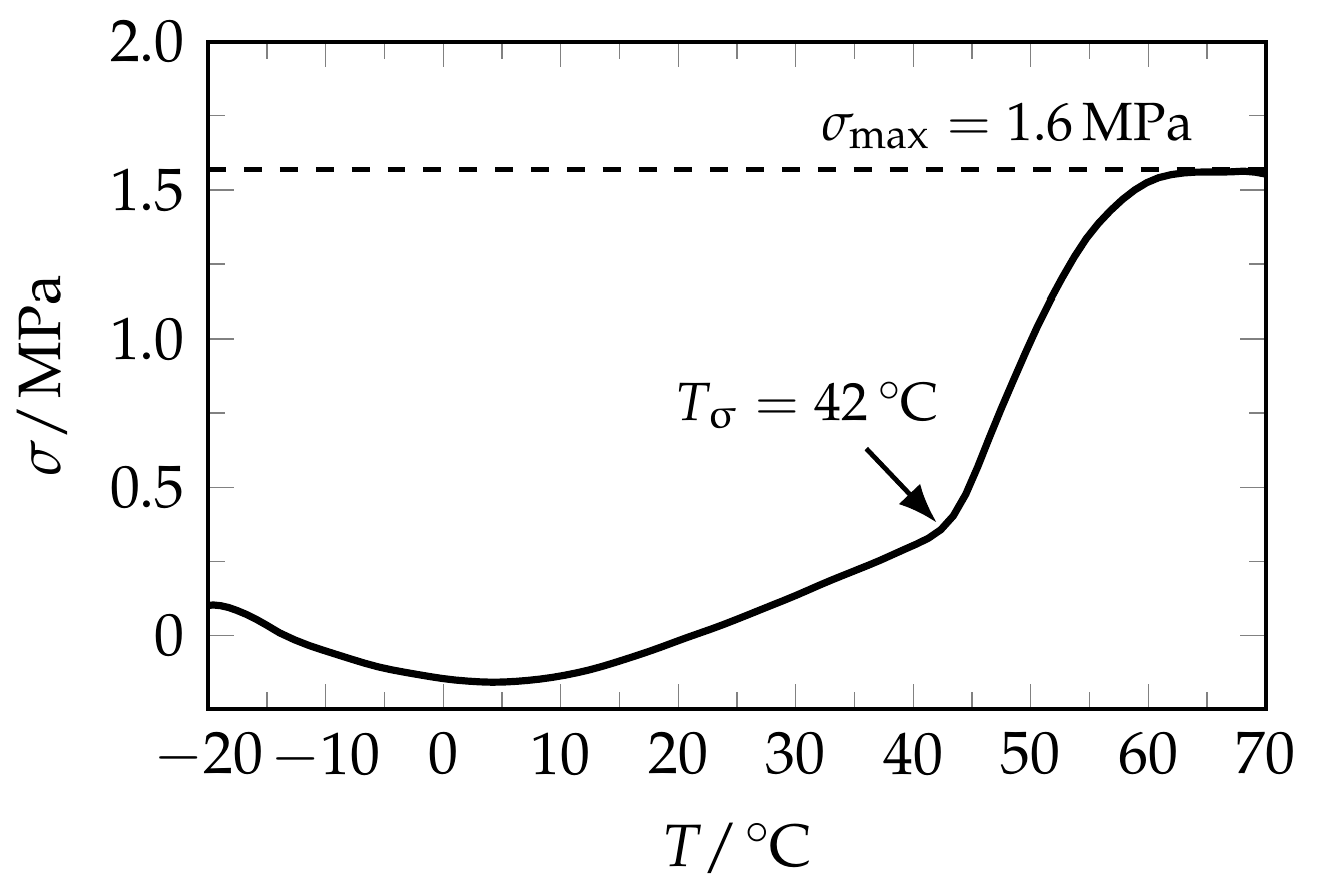
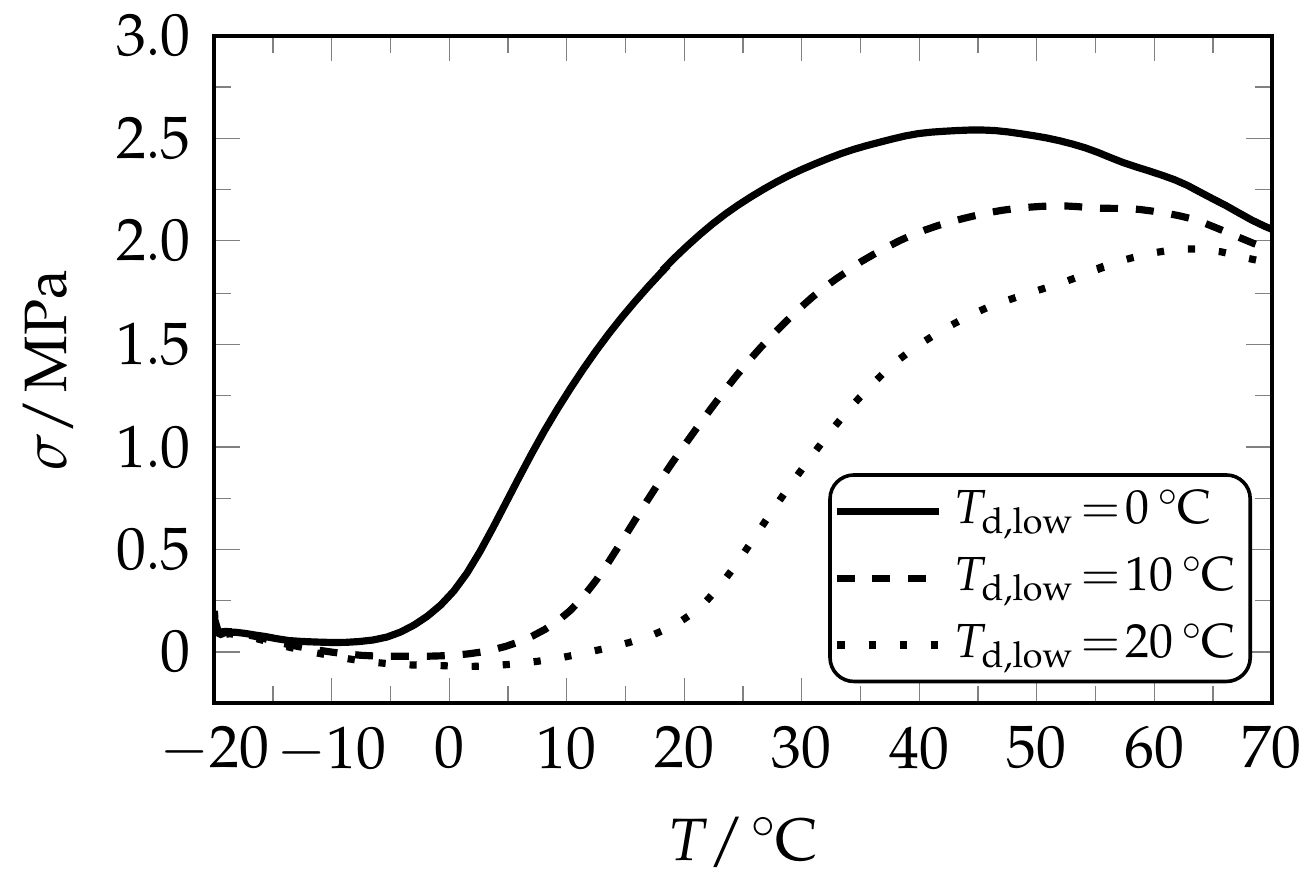
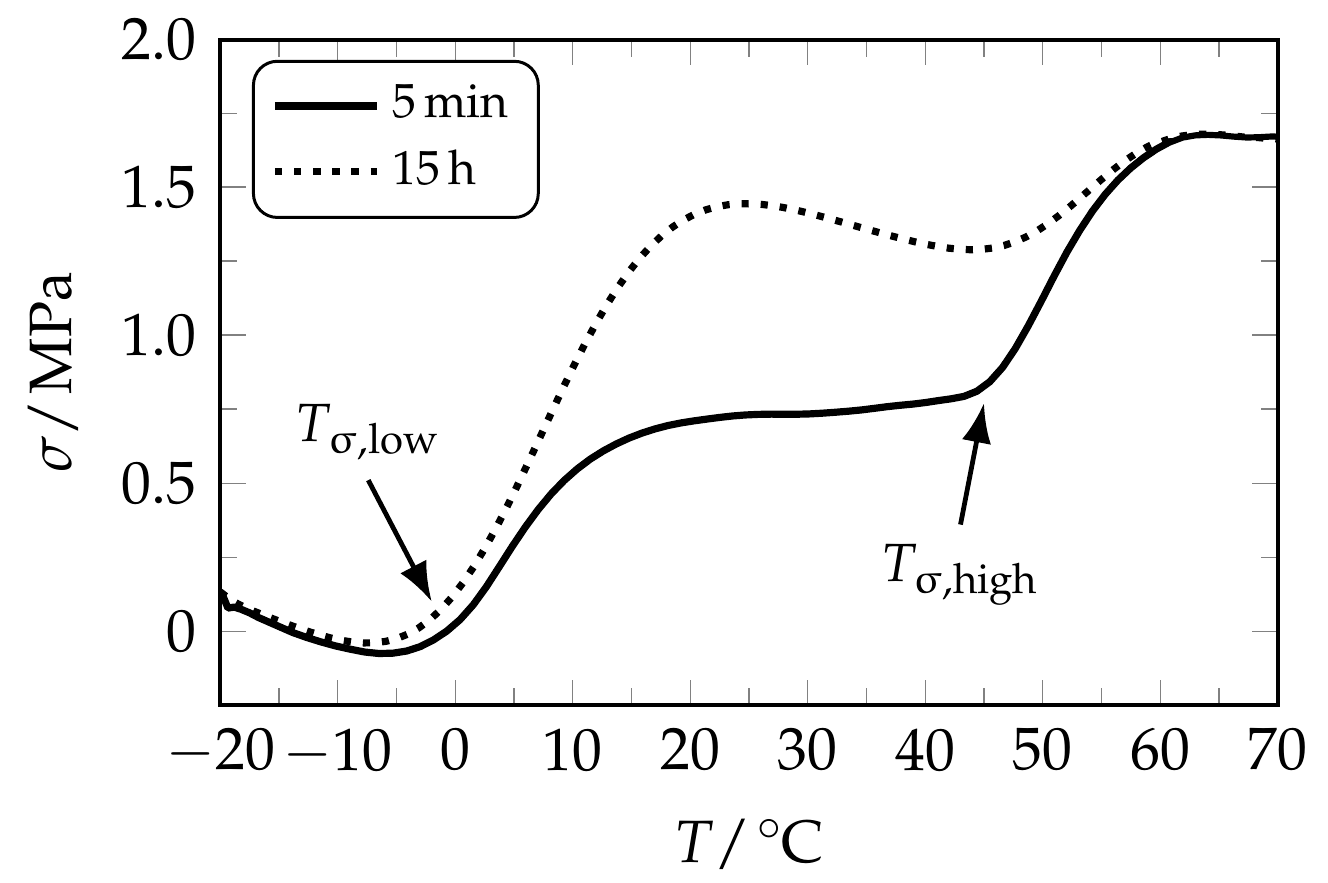
| Td,low | εm,low | Tσ,low | Tσ,max,low | σmax,low | Tσ,high | Tσ,max,high | σmax,high |
|---|---|---|---|---|---|---|---|
| (°C) | (%) | (°C) | (°C) | (MPa) | (°C) | (°C) | (MPa) |
| 0 | 225 | −1 ± 2 | 27 ± 2 | 0.7 ± 0.2 | 45 ± 2 | 64 ± 2 | 1.7 ± 0.2 |
| 0 | 275 | −1 ± 2 | 28 ± 2 | 1.4 ± 0.2 | 49 ± 2 | 65 ± 2 | 1.8 ± 0.2 |
| 0 | 325 | −2 ± 2 | 36 ± 2 | 1.7 ± 0.2 | 51 ± 2 | 62 ± 2 | 1.8 ± 0.2 |
| 0 | 375 | −1 ± 2 | 40 ± 2 | 2.2 ± 0.2 | 53 ± 2 | 59 ± 2 | 2.1 ± 0.2 |
| 10 | 225 | 9 ± 2 | 39 ± 2 | 0.8 ± 0.2 | 46 ± 2 | 66 ± 2 | 1.7 ± 0.2 |
| 10 | 275 | 8 ± 2 | 41 ± 2 | 1.1 ± 0.2 | 47 ± 2 | 63 ± 2 | 1.8 ± 0.2 |
| 10 | 325 | 8 ± 2 | 45 ± 2 | 1.5 ± 0.2 | 49 ± 2 | 62 ± 2 | 1.8 ± 0.2 |
| 10 | 375 | 8 ± 2 | 47 ± 2 | 1.8 ± 0.2 | 51 ± 2 | 60 ± 2 | 1.9 ± 0.2 |
| 20 | 225 | 18 ± 2 | 40 ± 2 | 0.6 ± 0.2 | 45 ± 2 | 66 ± 2 | 1.7 ± 0.2 |
| 20 | 275 | 19 ± 2 | 42 ±2 | 0.9 ± 0.2 | 46 ± 2 | 65 ± 2 | 1.7 ± 0.2 |
| 20 | 325 | 19 ± 2 | 44 ± 2 | 1.2 ± 0.2 | 48 ± 2 | 64 ± 2 | 1.8 ± 0.2 |
| 20 | 375 | 18 ± 2 | 46 ± 2 | 1.5 ± 0.2 | 50 ± 2 | 62 ± 2 | 1.8 ± 0.2 |
| Td,low = 0 °C | Td,low = 10 °C | Td,low = 20 °C | ||||
|---|---|---|---|---|---|---|
| εm,low (%) | σm,low (MPa) | εu,low (%) | σm,low (MPa) | εu,low (%) | σm,low (MPa) | εu,low (%) |
| 225 | 5.8 ± 0.2 | 198 ± 5 | 4.7 ± 0.2 | 187 ± 5 | 3.4 ± 0.2 | 186 ± 5 |
| 275 | 9.3 ± 0.2 | 215 ± 5 | 6.8 ± 0.2 | 212 ± 5 | 5.4 ± 0.2 | 202 ± 5 |
| 325 | 11.8 ± 0.2 | 245 ± 5 | 9.3 ± 0.2 | 235 ± 5 | 7.6 ± 0.2 | 221 ± 5 |
| 375 | 15.9 ± 0.2 | 269 ± 5 | 12.4 ± 0.2 | 256 ± 5 | 10.1 ± 0.2 | 241 ± 5 |
| Td,low (°C) | σm,low (MPa) | εu,low (%) | Tσ,on (°C) | Tσ,max (°C) | σmax (MPa) |
|---|---|---|---|---|---|
| 0 | 19.5 ± 0.2 | 300 ± 5 | −2 ± 2 | 45 ± 2 | 2.5 ± 0.2 |
| 10 | 15.4 ± 0.2 | 285 ± 5 | 8 ± 2 | 51 ± 2 | 2.2 ± 0.2 |
| 20 | 12.9 ± 0.2 | 266 ± 5 | 18 ± 2 | 63 ± 2 | 2.0 ± 0.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirtschin, N.; Pretsch, T. Programming of One- and Two-Step Stress Recovery in a Poly(ester urethane). Polymers 2017, 9, 98. https://doi.org/10.3390/polym9030098
Mirtschin N, Pretsch T. Programming of One- and Two-Step Stress Recovery in a Poly(ester urethane). Polymers. 2017; 9(3):98. https://doi.org/10.3390/polym9030098
Chicago/Turabian StyleMirtschin, Nikolaus, and Thorsten Pretsch. 2017. "Programming of One- and Two-Step Stress Recovery in a Poly(ester urethane)" Polymers 9, no. 3: 98. https://doi.org/10.3390/polym9030098
APA StyleMirtschin, N., & Pretsch, T. (2017). Programming of One- and Two-Step Stress Recovery in a Poly(ester urethane). Polymers, 9(3), 98. https://doi.org/10.3390/polym9030098