Dynamics of Dual Scale-Free Polymer Networks
Abstract
:1. Introduction
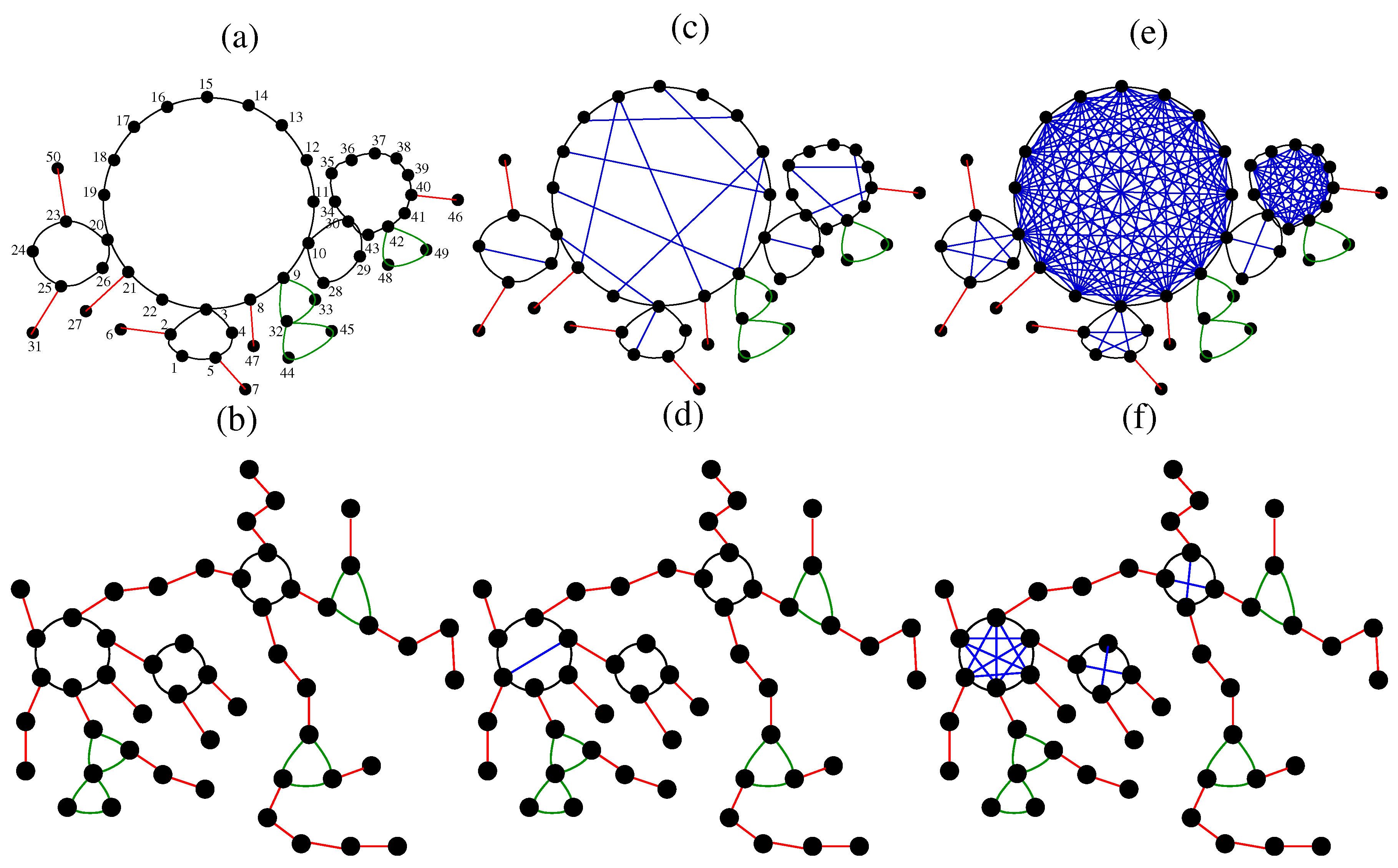
2. Sequentially Growing Dual Scale-Free Networks
3. Theoretical Model
4. Results
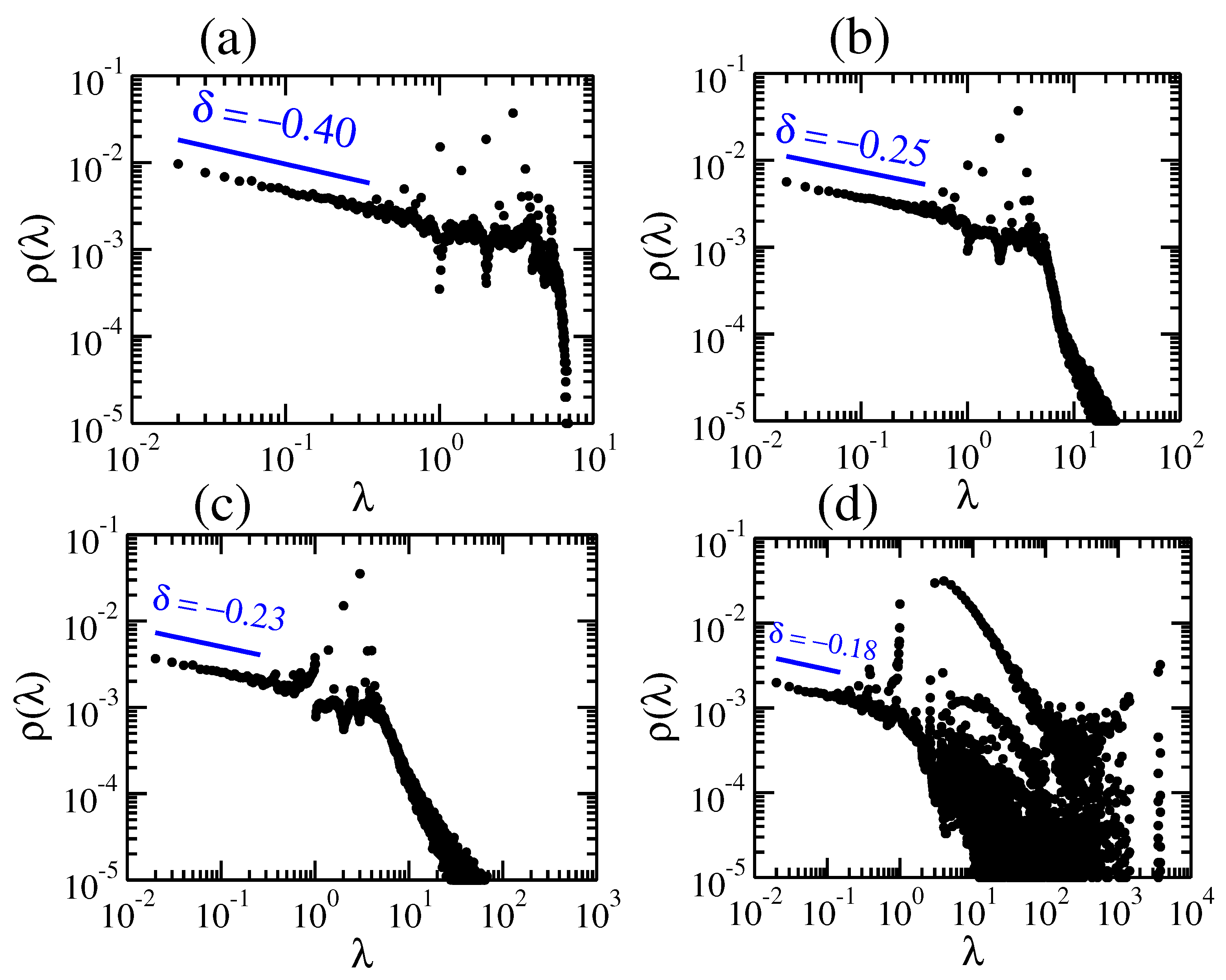
4.1. Eigenvalues Spectrum
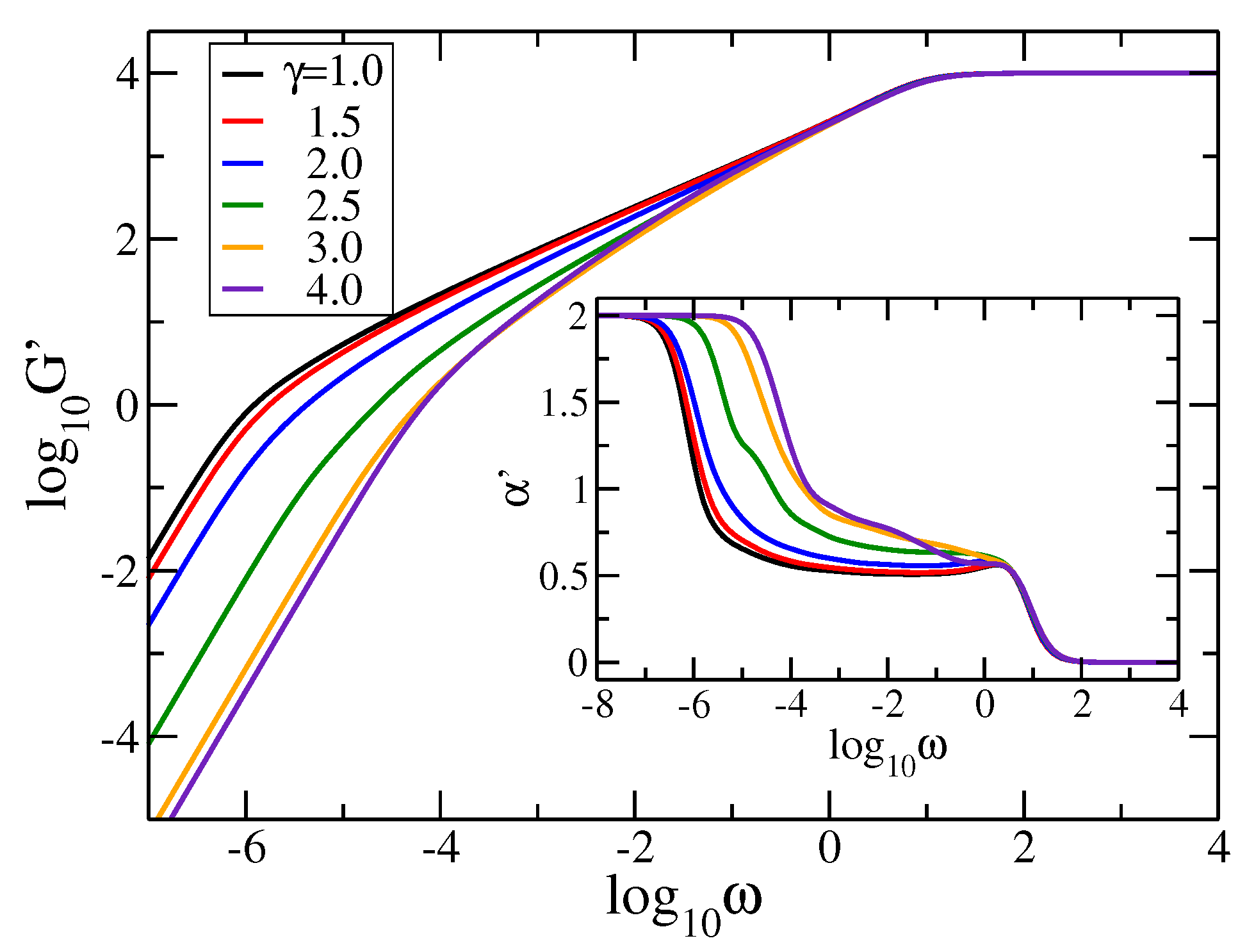
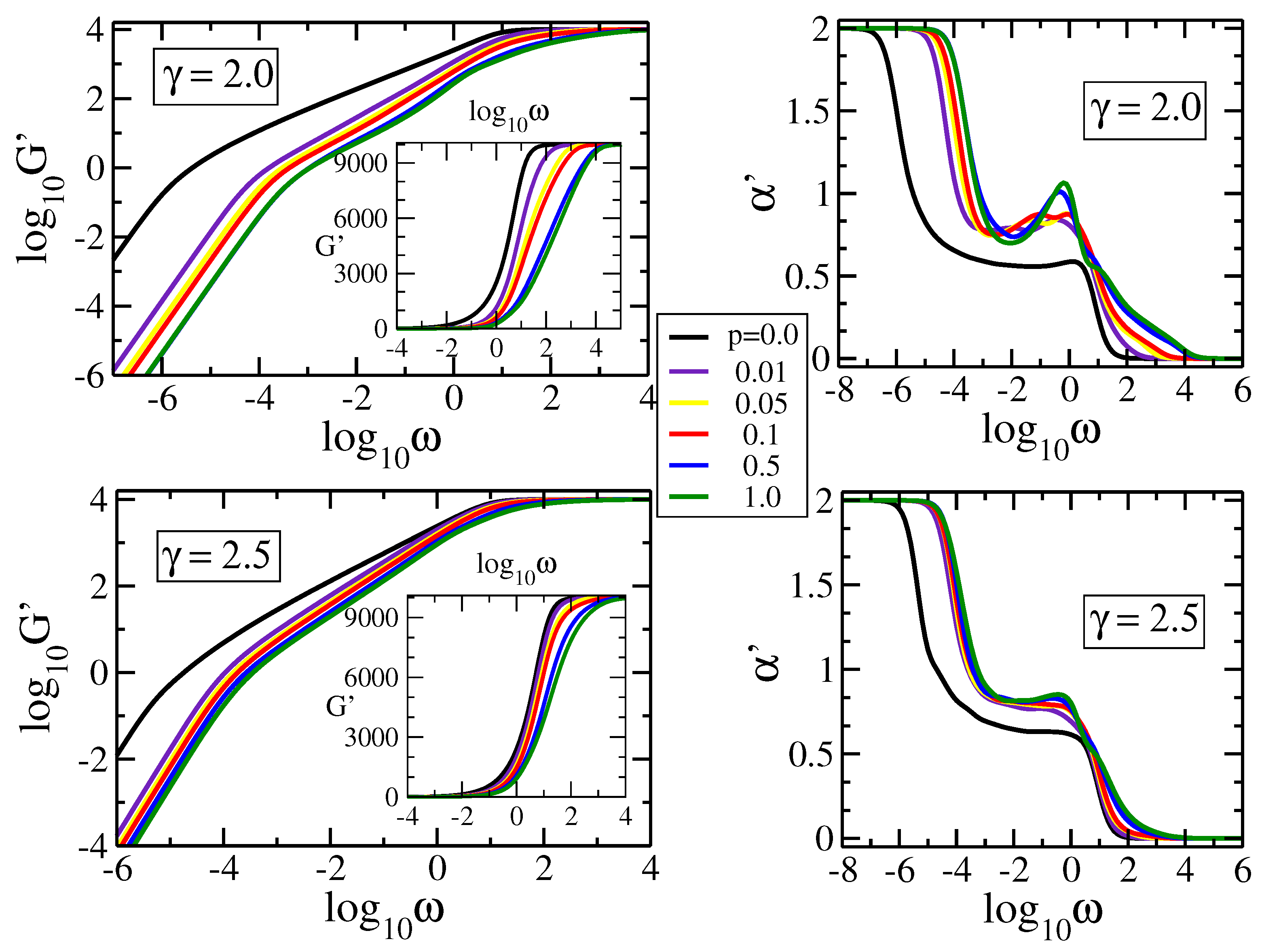
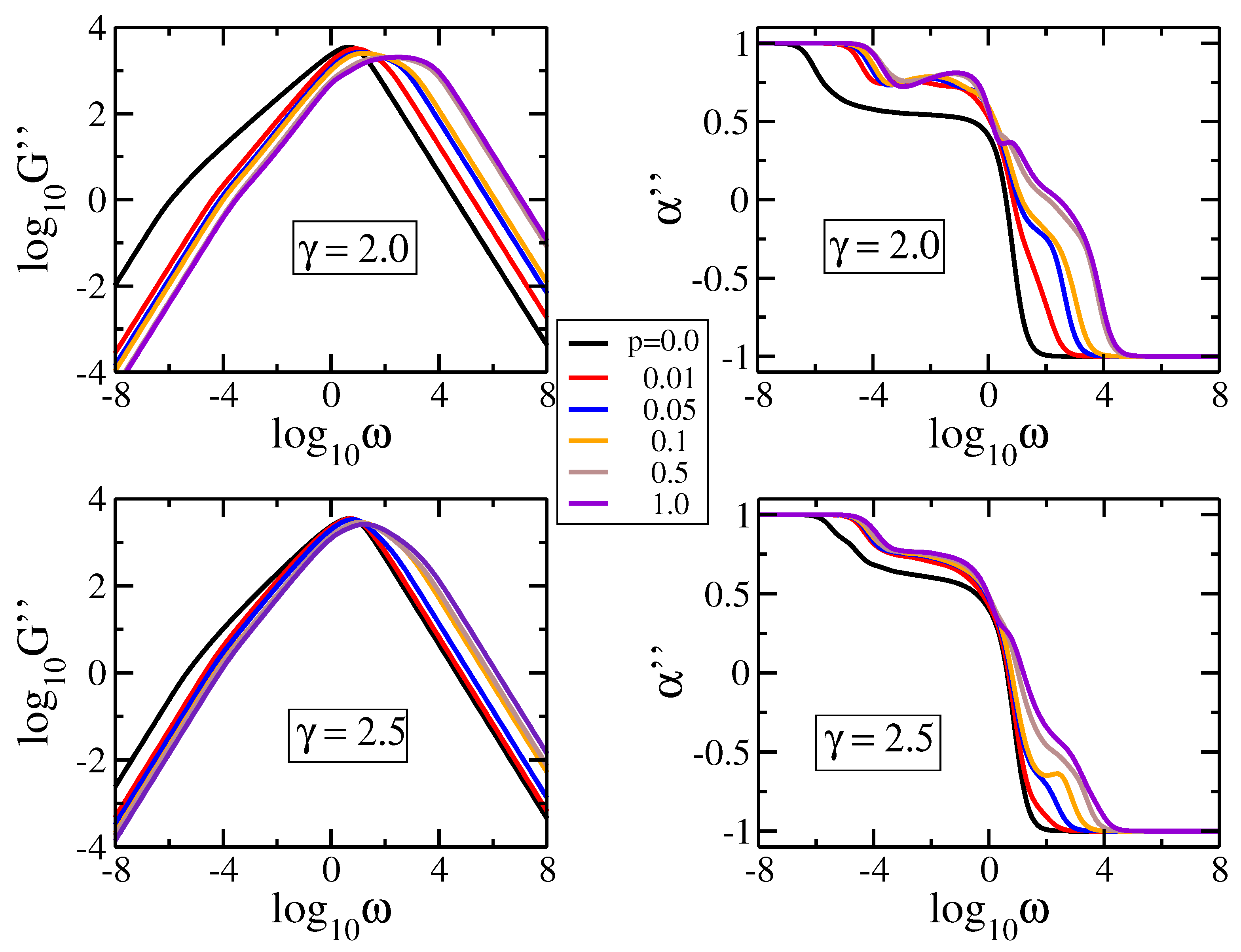
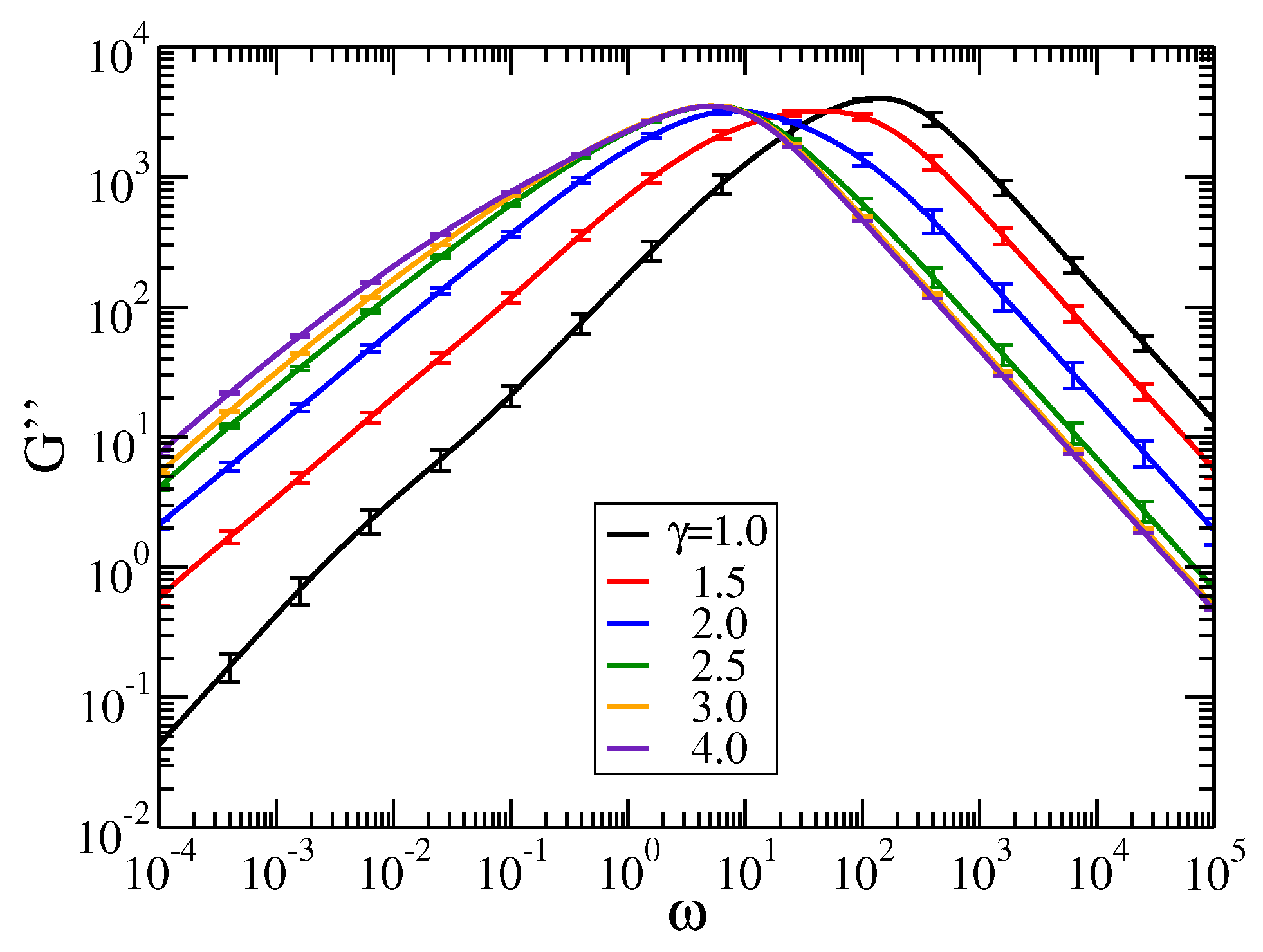
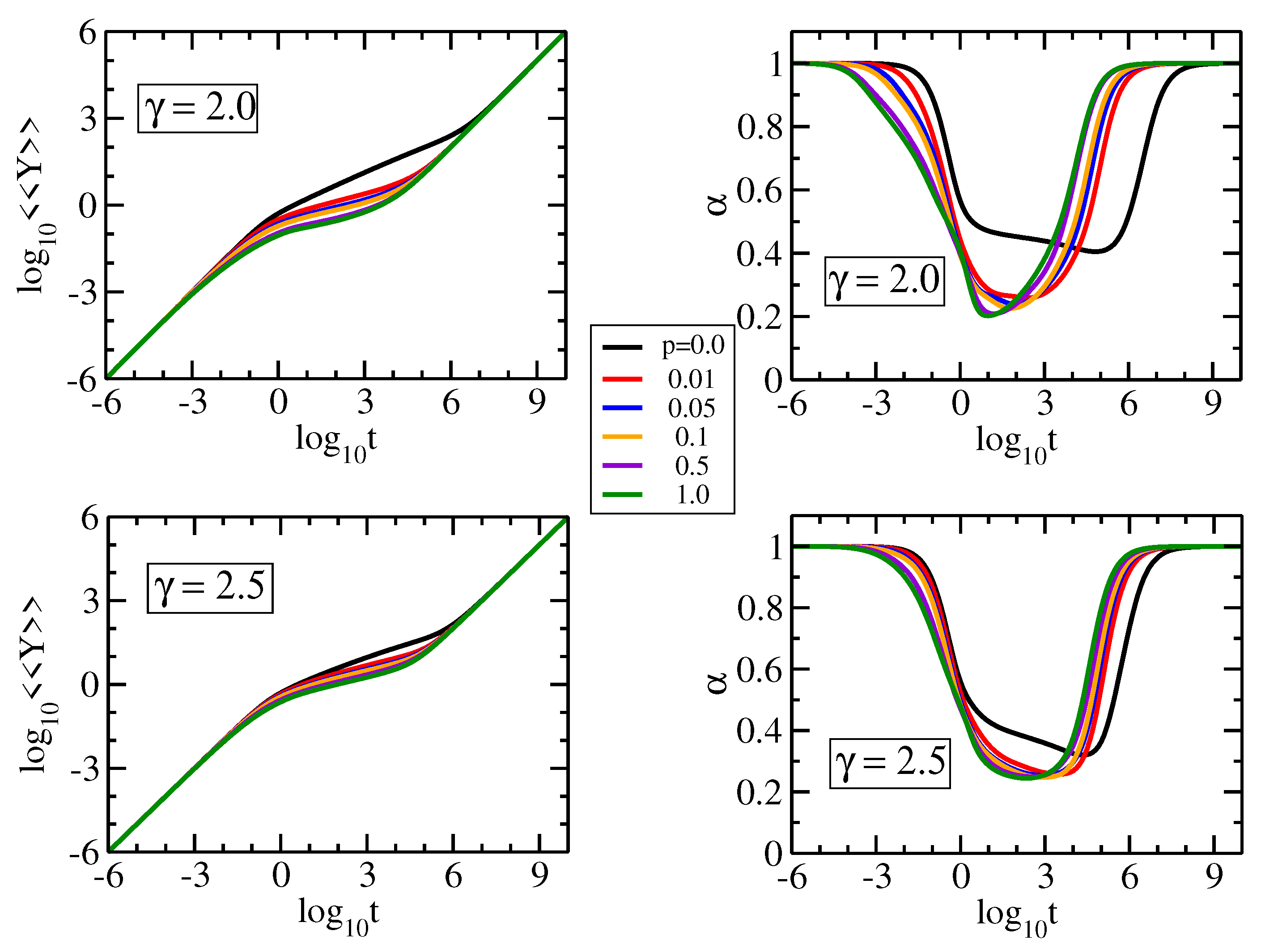
4.2. Relaxation Dynamics
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GGS | generalised Gaussian structures |
| rDSFNs | ring-based dual scale-free networks |
| cDSFNs | complete-graph based dual scale-free networks |
| pDSFNs | sequentially growing partially dual scale-free networks |
References
- Albert, R.; Jeong, H.; Barabási, A.-L. Internet: Diameter of the World-Wide Web. Nature 1999, 401, 130–131. [Google Scholar]
- Hubermann, B.A.; Adamic, L.A. Internet: Growth dynamics of the World-Wide Web. Nature 2000, 401, 131. [Google Scholar]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvani, Z.N.; Barabási, A.-L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [PubMed]
- Gallos, L.K. Random walk and trapping processes on scale-free networks. Phys. Rev. E 2004, 70, 046116. [Google Scholar] [CrossRef] [PubMed]
- Onnela, J.-P.; Kaki, K.; Kertész, J. Clustering and information in correlation based financial networks. Eur. Phys. J. B 2004, 38, 353–362. [Google Scholar] [CrossRef]
- Von Ferber, C.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Network harness: Metropolis public transport. Physica A 2007, 380, 585–591. [Google Scholar] [CrossRef]
- Guimerá, R.; Mossa, S.; Turtschi, A.; Amaral, L.A.N. The worldwide air transportation network: Anomalous centrality, community structure, and cities’ global roles. Proc. Natl. Acad. Sci. USA 2005, 102, 7794–7799. [Google Scholar] [CrossRef] [PubMed]
- Jasch, F.; von Ferber, C.; Blumen, A. Dynamical scaling behavior of percolation clusters in scale-free networks. Phys. Rev. E 2004, 70, 016112. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M. Relaxation dynamics of scale-free polymer networks. Phys. Rev. E 2012, 86, 041803. [Google Scholar] [CrossRef] [PubMed]
- Migulin, D.; Tatarinova, E.; Meshkov, I.; Cherkaev, G.; Vasilenko, N.; Buzin, M.; Muzafarov, A. Synthesis of the first hyperbranched polyorganoethoxysilsesquioxanes and their chemical transformations to functional core–shell nanogel systems. Polym. Int. 2016, 65, 72–83. [Google Scholar] [CrossRef]
- Dolynchuk, O.; Kolesov, I.; Jehnichen, D.; Reuter, U.; Radusch, H.J.; Sommer, J.-U. Reversible Shape-Memory Effect in Cross-Linked Linear Poly (ε-caprolactone) under Stress and Stress-Free Conditions. Macromolecules 2017, 50, 3841–3854. [Google Scholar] [CrossRef]
- Ivaneiko, I.; Toshchevikov, V.; Saphiannikova, M.; Stöckelhuber, K.W.; Petry, F.; Westermann, S.; Heinrich, G. Modeling of dynamic-mechanical behavior of reinforced elastomers using a multiscale approach. Polymer 2016, 82, 356–365. [Google Scholar] [CrossRef]
- Shi, X.; Xiao, H.; Lackner, K.S.; Chen, X. Capture CO2 from Ambient Air Using Nanoconfined Ion Hydration. Angew. Chem. 2016, 128, 4094–4097. [Google Scholar] [CrossRef]
- Shi, X.; Li, Q.; Wang, T.; Lackner, K.S. Kinetic analysis of an anion exchange absorbent for CO2 capture from ambient air. PLoS ONE 2017, 12, e0179828. [Google Scholar] [CrossRef] [PubMed]
- Mülken, O.; Dolgushev, M.; Galiceanu, M. Complex Quantum Networks: From Universal Breakdown to Optimal Transport. Phys. Rev. E 2016, 93, 022304. [Google Scholar] [CrossRef] [PubMed]
- Harary, F. Graph Theory; Perseus: Cambridge, MA, USA, 1969. [Google Scholar]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Dorogovtsev, S.N.; Mendes, J.F.F. Evolution of networks with aging of sites. Phys. Rev. E 2000, 62, 1842. [Google Scholar] [CrossRef]
- Sommer, J.-U.; Blumen, A. On the statistics of generalized Gaussian structures: Collapse and random external fields. J. Phys. A 1995, 28, 6669–6674. [Google Scholar] [CrossRef]
- Gurtovenko, A.; Blumen, A. Generalized Gaussian Structures: Models for polymer systems with complex topologies. Adv. Polym. Sci. 2005, 182, 171–282. [Google Scholar]
- Galiceanu, M. Relaxation of polymers modeled by generalized Husimi cacti. J. Phys. A Math. Theor. 2010, 43, 305002. [Google Scholar] [CrossRef]
- Liu, H.X.; Zhang, Z.Z. Laplacian Spectra of Recursive Treelike Small-World Polymer Networks: Analytical Solutions and Applications. J. Chem. Phys. 2013, 138, 114904. [Google Scholar] [CrossRef] [PubMed]
- Jespersen, S.; Sokolov, I.M.; Blumen, A. Small-world Rouse networks as models of cross-linked polymers. J. Chem. Phys. 2000, 113, 7652–7655. [Google Scholar] [CrossRef]
- Galiceanu, M.; Jurjiu, A. Relaxation dynamics of multilayer triangular Husimi cacti. J. Chem. Phys. 2016, 145, 104901. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Biter, T.-L.; Turcu, F. Dynamics of a Polymer Network Based on Dual Sierpinski Gasket and Dendrimer: A Theoretical Approach. Polymers 2017, 9, 245. [Google Scholar] [CrossRef]
- Agliari, E.; Tavani, F. The exact Laplacian spectrum for the Dyson hierarchical network. Sci. Rep. 2017, 7, 39962. [Google Scholar] [CrossRef] [PubMed]
- Schiessel, H. Unfold dynamics of generalized Gaussian structures. Phys. Rev. E 1998, 57, 5775–5781. [Google Scholar] [CrossRef]
- Newman, M.E.J. Scientific collaboration networks. I. Network construction and fundamental results. Phys. Rev. E 2001, 64, 016131. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Monasson, R. Diffusion, localization and dispersion relations on “small-world” lattices. Eur. Phys. J. B 1999, 12, 555–567. [Google Scholar] [CrossRef]
- Biswas, P.; Kant, R.; Blumen, A. Polymer dynamics and topology: Extension of stars and dendrimers in external fields. Macromol. Theory Simul. 2000, 9, 56–67. [Google Scholar] [CrossRef]
- Jurjiu, A.; Koslowski, T.; Blumen, A. Dynamics of deterministic fractal polymer networks: Hydrodynamic interactions and the absence of scaling. J. Chem. Phys. 2003, 118, 2398–2404. [Google Scholar] [CrossRef]
- Rouse, P.E. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Dolgushev, M.; Guérin, T.; Blumen, A.; Bénichou, O.; Voituriez, R. Gaussian semiflexible rings under angular and dihedral restrictions. J. Chem. Phys. 2014, 141, 014901. [Google Scholar] [CrossRef] [PubMed]
- Mehta, A.D.; Reif, M.; Spudich, J.A.; Smith, D.A.; Simmons, R.M. Single-molecule biomechanics with optical methods. Science 1999, 283, 1689–1695. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Cooke, I.R.; Williams, D.R.M. Stretching polymers in poor and bad solvents: Pullout peaks and an unraveling transition. Europhys. Lett. 2003, 64, 267–273. [Google Scholar] [CrossRef]
- Quake, S.R.; Babcock, H.; Chu, S. The dynamics of partially extended single molecules of DNA. Nature 1997, 388, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.T.; Weeks, E.R.; Crocker, J.C.; Islam, M.F.; Verma, R.; Gruber, J.; Levine, A.J.; Lubensky, T.C.; Yodh, A.G. Rheological Microscopy: Local Mechanical Properties from Microrheology. Phys. Rev. Lett. 2003, 90, 108301. [Google Scholar] [CrossRef] [PubMed]
- Katyal, D.; Kant, R. Dynamics of generalized Gaussian polymeric structures in random layered flows. Phys. Rev. E 2015, 91, 042602. [Google Scholar] [CrossRef] [PubMed]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon: Oxford, UK, 1986. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Strobl, G. The Physics of Polymers; Springer: Berlin, Germany, 1997. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; Sorensen, D. LAPACK Users’ Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Galiceanu, M.; Oliveira, E.S.; Dolgushev, M. Relaxation dynamics of small-world degree-distributed treelike polymer networks. Physica A 2016, 462, 376–385. [Google Scholar] [CrossRef]
- Alexander, S.; Orbach, R. Density of states on fractals: “Fractons”. J. Phys. Lett. 1982, 43, 625–631. [Google Scholar] [CrossRef]
- Blumen, A.; von Ferber, C.; Jurjiu, A.; Koslowski, T. Generalized Vicsek Fractals: Regular Hyperbranched Polymers. Macromolecules 2004, 37, 638–650. [Google Scholar] [CrossRef]
- Jurjiu, A.; Koslowski, T.; von Ferber, C.; Blumen, A. Dynamics and scaling of polymer networks: Vicsek fractals and hydrodynamic interactions. Chem. Phys. 2003, 294, 187–199. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.-J.; Harris, F.E. Mathematical Methods for Physicists: A Comprehensive Guide; Academic Press: Oxford, UK, 2012. [Google Scholar]
- Rössler, E.A.; Stapf, S.; Fatkullin, N. Recent NMR investigations on molecular dynamics of polymer melts in bulk and in confinement. Curr. Opin. Colloid Interface Sci. 2013, 18, 173–182. [Google Scholar] [CrossRef]
- Markelov, D.A.; Dolgushev, M.; Lähderanta, E. NMR Relaxation in Dendrimers. Annu. Rep. NMR Spectrosc. 2017, 91, 1–66. [Google Scholar]
- Dolgushev, M.; Markelov, D.A.; Fürstenberg, F.; Guérin, T. Local orientational mobility in regular hyperbranched polymers. Phys. Rev. E 2016, 94, 012502. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galiceanu, M.; Tota de Carvalho, L.; Mülken, O.; Dolgushev, M. Dynamics of Dual Scale-Free Polymer Networks. Polymers 2017, 9, 577. https://doi.org/10.3390/polym9110577
Galiceanu M, Tota de Carvalho L, Mülken O, Dolgushev M. Dynamics of Dual Scale-Free Polymer Networks. Polymers. 2017; 9(11):577. https://doi.org/10.3390/polym9110577
Chicago/Turabian StyleGaliceanu, Mircea, Luan Tota de Carvalho, Oliver Mülken, and Maxim Dolgushev. 2017. "Dynamics of Dual Scale-Free Polymer Networks" Polymers 9, no. 11: 577. https://doi.org/10.3390/polym9110577
APA StyleGaliceanu, M., Tota de Carvalho, L., Mülken, O., & Dolgushev, M. (2017). Dynamics of Dual Scale-Free Polymer Networks. Polymers, 9(11), 577. https://doi.org/10.3390/polym9110577





