Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
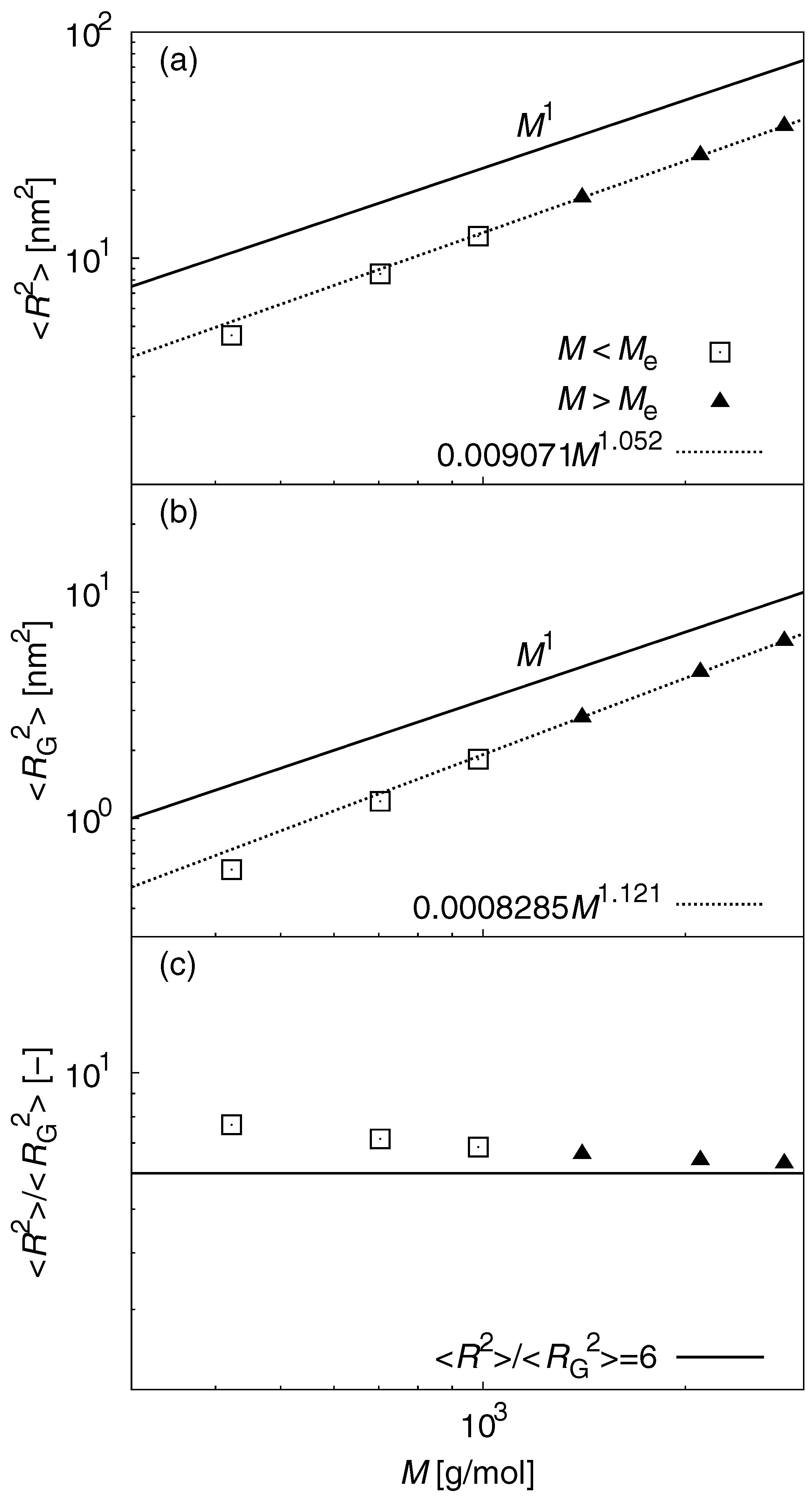
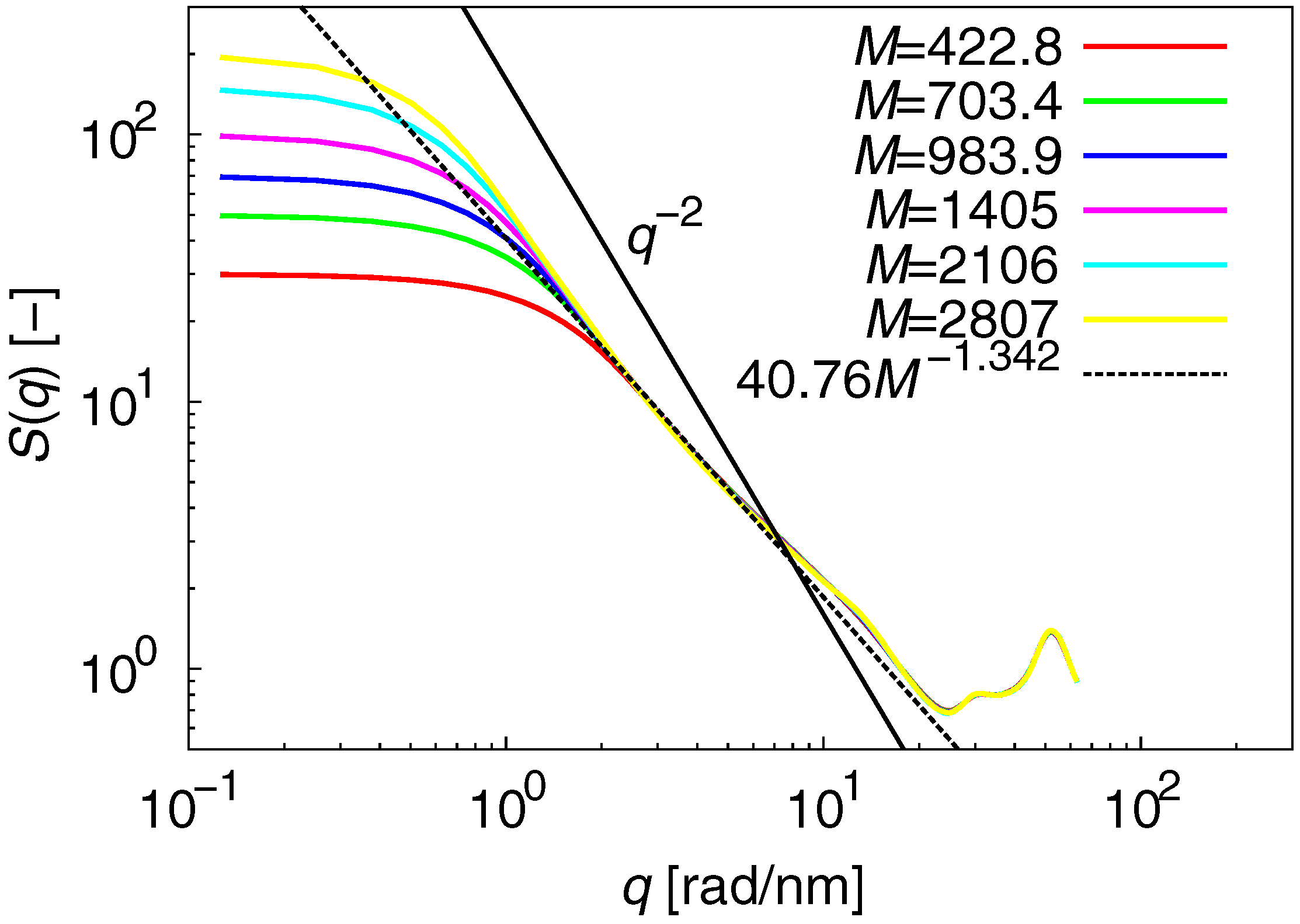
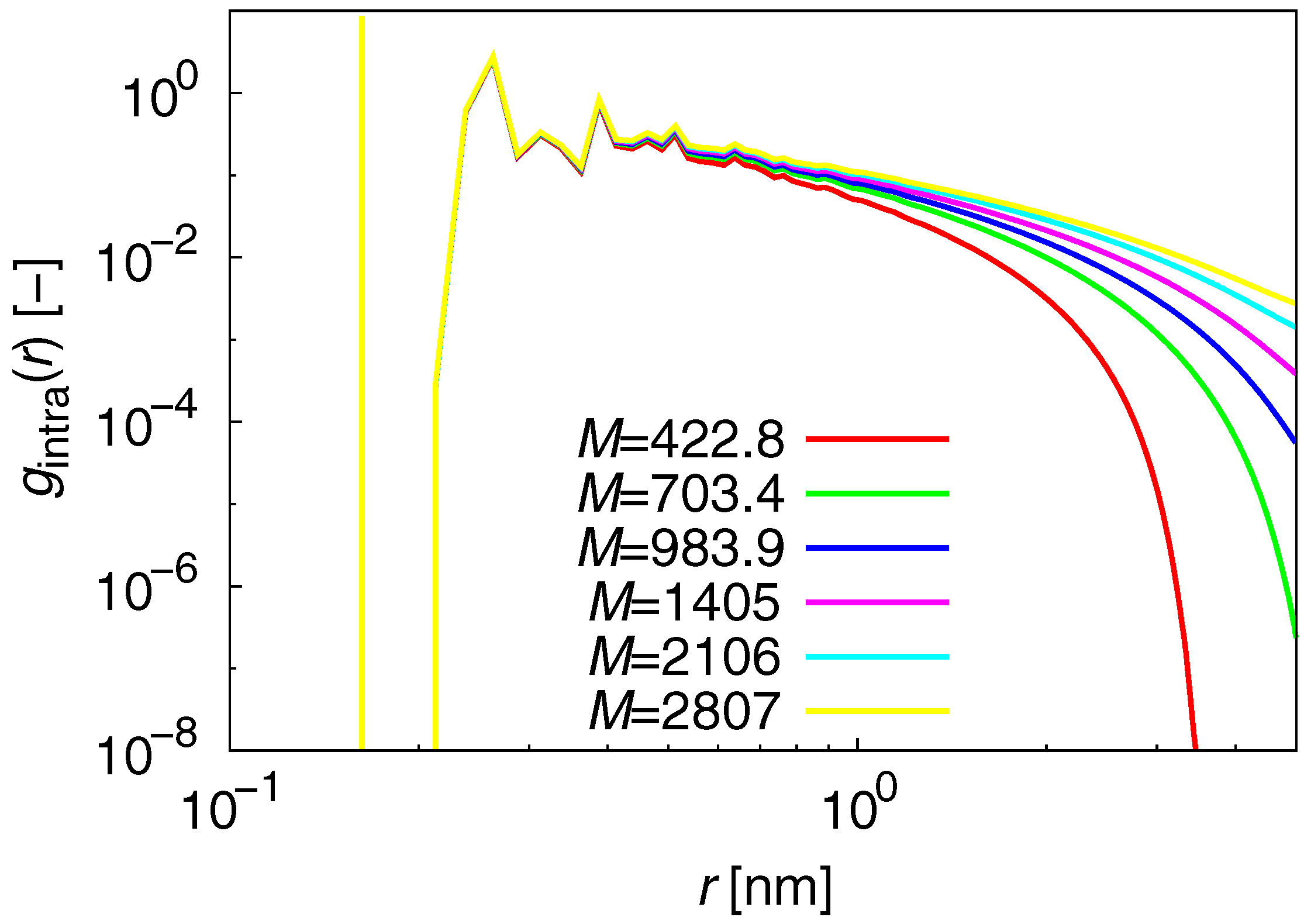
3.1. Static Properties
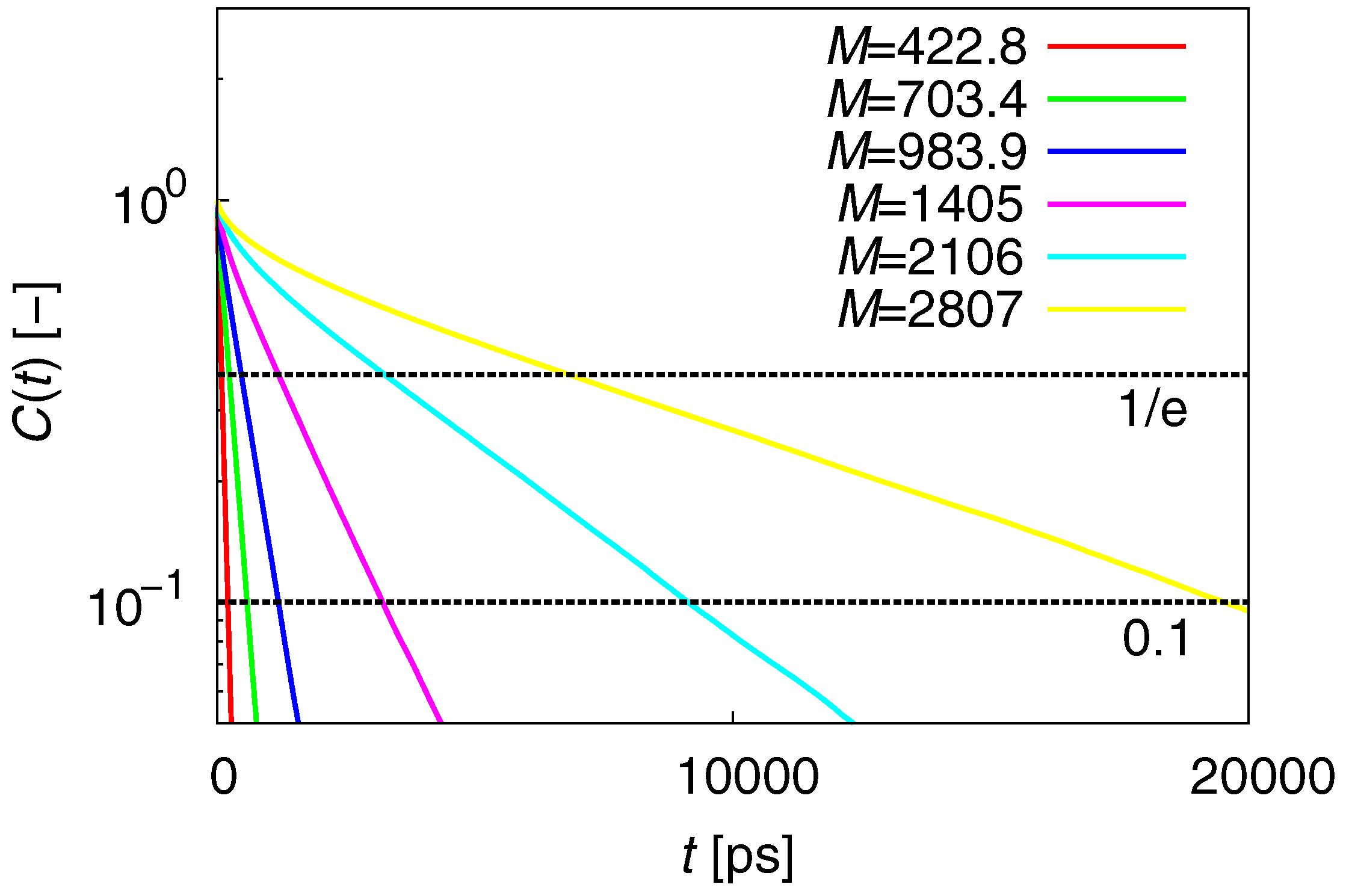
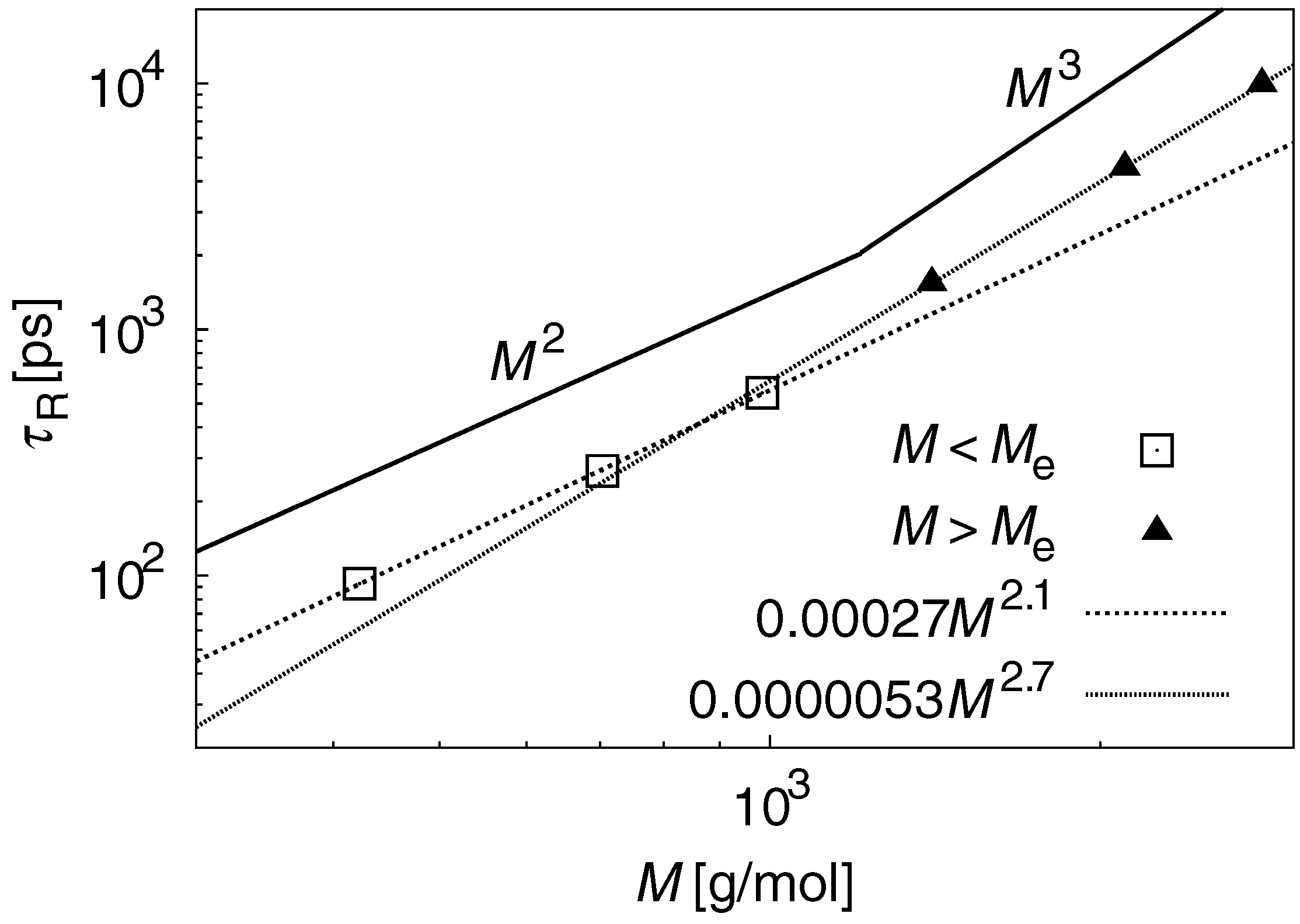
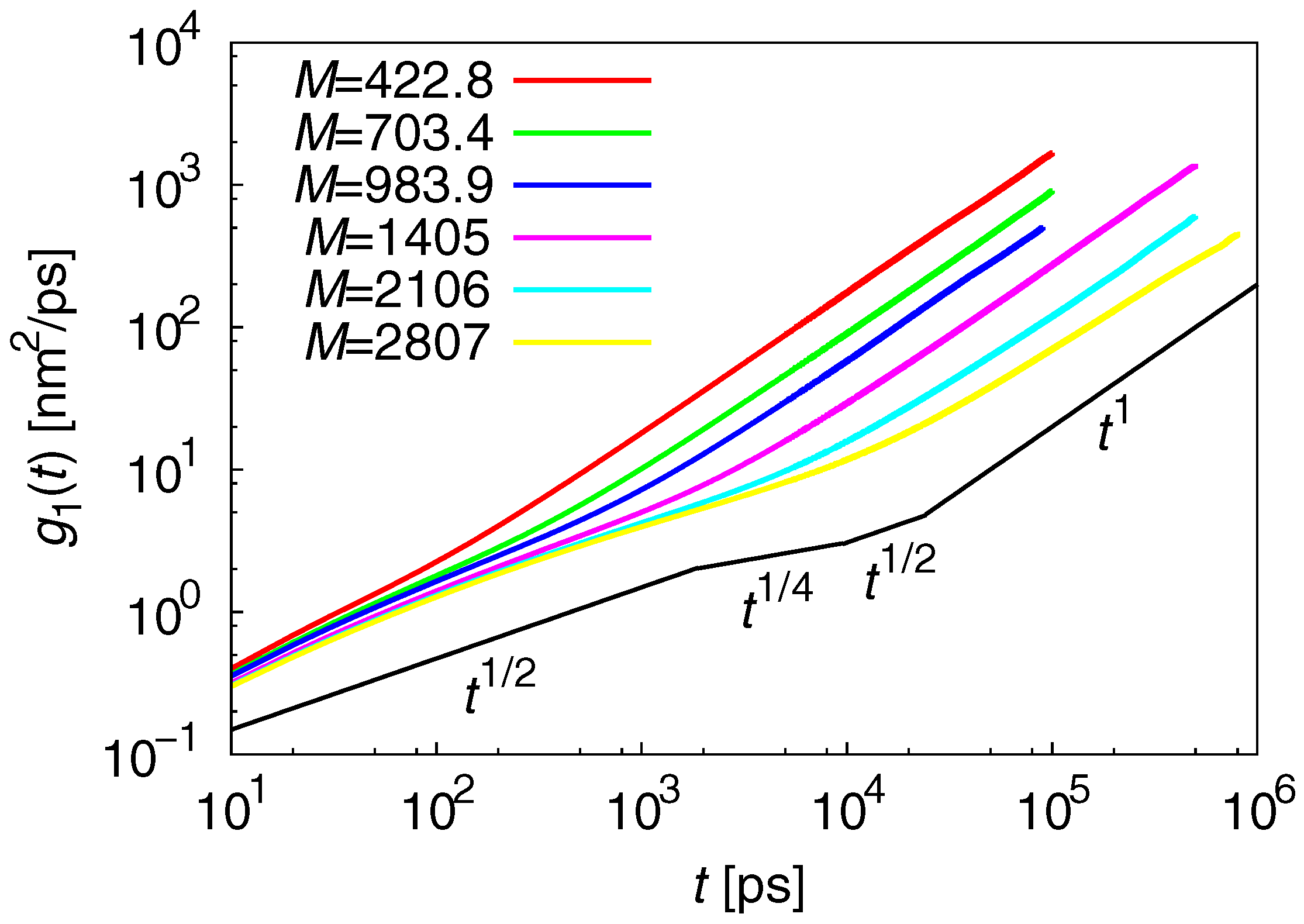
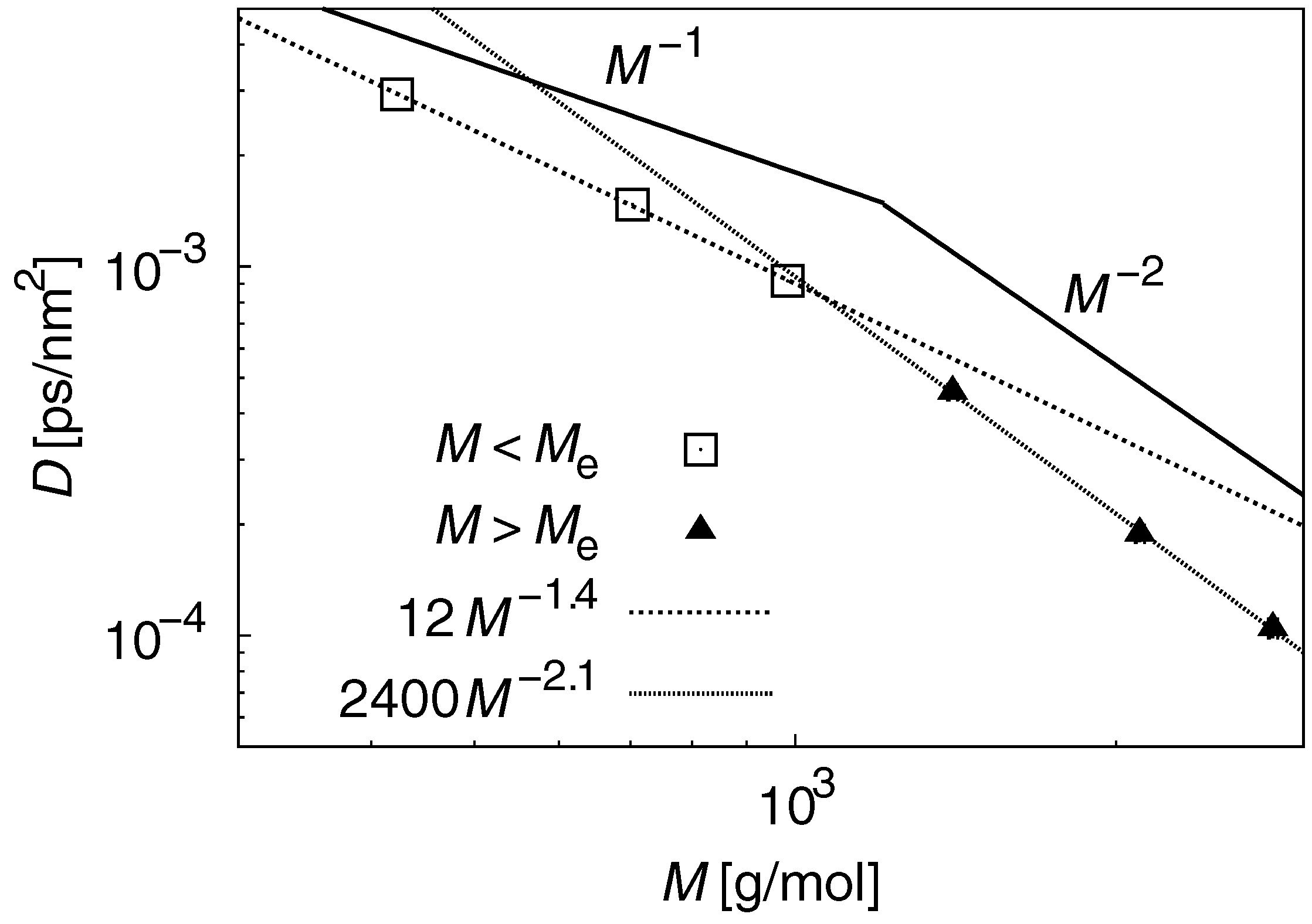
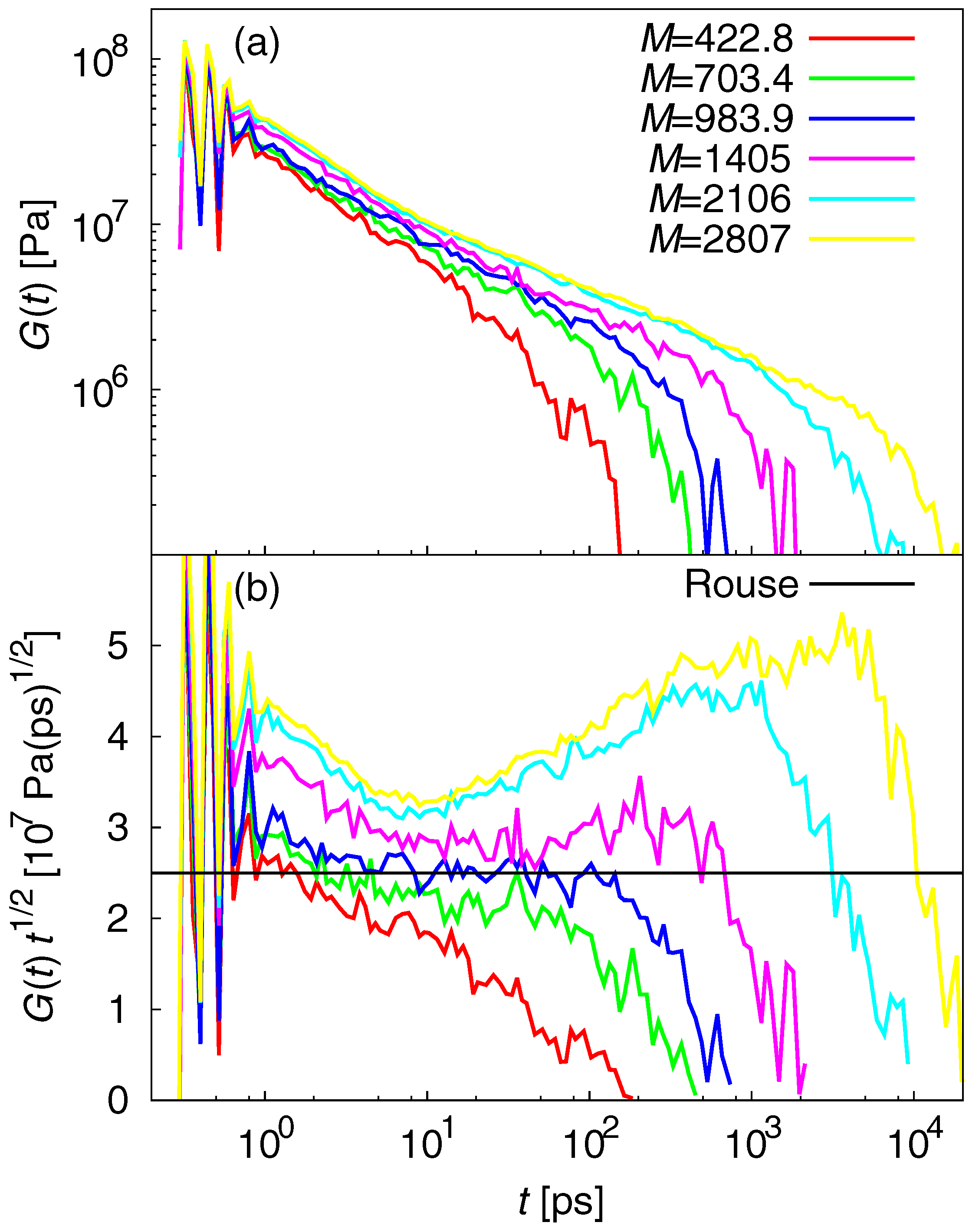
3.2. Dynamic Properties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Masubuchi, Y. Simulating the flow of entangled polymers. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 11–33. [Google Scholar] [CrossRef] [PubMed]
- Baaden, M.; Marrink, S.J. Coarse-grain modelling of protein–protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 878–886. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodríguez-Ropero, F.; van der Vegt, N.F. Systematic coarse-graining methods for soft matter simulations—A review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Gay, J.; Berne, B. Modification of the overlap potential to mimic a linear site–site potential. J. Chem. Phys. 1981, 74, 3316–3319. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423. [Google Scholar] [CrossRef]
- Jury, S.; Bladon, P.; Cates, M.; Krishna, S.; Hagen, M.; Ruddock, N.; Warren, P. Simulation of amphiphilic mesophases using dissipative particle dynamics. Phys. Chem. Chem. Phys. 1999, 1, 2051–2056. [Google Scholar] [CrossRef]
- Karimi-Varzaneh, H.A.; van der Vegt, N.F.; Müller-Plathe, F.; Carbone, P. How good are coarse-grained polymer models? A comparison for atactic polystyrene. ChemPhysChem 2012, 13, 3428–3439. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Riniker, S.; Allison, J.R.; van Gunsteren, W.F. On developing coarse-grained models for biomolecular simulation: A review. Phys. Chem. Chem. Phys. 2012, 14, 12423–12430. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wiley Interdiscip. Rev. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Baumgärtner, A.; Binder, K.; Hansen, J.P.; Kalos, M.; Kehr, K.; Landau, D.; Levesque, D.; Müller-Krumbhaar, H.; Rebbi, C.; Saito, Y.; et al. Applications of the Monte Carlo Method in Statistical Physics; Springer Science & Business Media: Berlin, Germany, 2013; Volume 36. [Google Scholar]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Baig, C.; Mavrantzas, V.G.; Kröger, M. Flow effects on melt structure and entanglement network of linear polymers: Results from a nonequilibrium molecular dynamics simulation study of a polyethylene melt in steady shear. Macromolecules 2010, 43, 6886–6902. [Google Scholar]
- Barrat, J.L.; Baschnagel, J.; Lyulin, A. Molecular dynamics simulations of glassy polymers. Soft Matter 2010, 6, 3430–3446. [Google Scholar] [CrossRef]
- Chung, H.S.; Piana-Agostinetti, S.; Shaw, D.E.; Eaton, W.A. Structural origin of slow diffusion in protein folding. Science 2015, 349, 1504–1510. [Google Scholar] [CrossRef] [PubMed]
- Do, C.; Lunkenheimer, P.; Diddens, D.; Götz, M.; Weiß, M.; Loidl, A.; Sun, X.G.; Allgaier, J.; Ohl, M. Li+ transport in poly (ethylene oxide) based electrolytes: Neutron scattering, dielectric spectroscopy, and molecular dynamics simulations. Phys. Rev. Lett. 2013, 111, 018301. [Google Scholar] [CrossRef] [PubMed]
- Hossain, D.; Tschopp, M.; Ward, D.; Bouvard, J.; Wang, P.; Horstemeyer, M. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Hur, K.; Jeong, C.; Winkler, R.G.; Lacevic, N.; Gee, R.H.; Yoon, D.Y. Chain dynamics of ring and linear polyethylene melts from molecular dynamics simulations. Macromolecules 2011, 44, 2311–2315. [Google Scholar] [CrossRef]
- Mitchell, J.S.; Harris, S.A. Thermodynamics of writhe in DNA minicircles from molecular dynamics simulations. Phys. Rev. Lett. 2013, 110, 148105. [Google Scholar] [CrossRef]
- Ndoro, T.V.; Voyiatzis, E.; Ghanbari, A.; Theodorou, D.N.; Böhm, M.C.; Müller-Plathe, F. Interface of grafted and ungrafted silica nanoparticles with a polystyrene matrix: Atomistic molecular dynamics simulations. Macromolecules 2011, 44, 2316–2327. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Tsolou, G.; Mavrantzas, V.G.; Kröger, M. Quantifying chain reptation in entangled polymer melts: Topological and dynamical mapping of atomistic simulation results onto the tube model. J. Chem. Phys. 2010, 132, 124904. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene melts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Pant, P.K.; Han, J.; Smith, G.D.; Boyd, R.H. A molecular dynamics simulation of polyethylene. J. Chem. Phys. 1993, 99, 597–604. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Boyd, R.H.; Gee, R.H.; Han, J.; Jin, Y. Conformational dynamics in bulk polyethylene: A molecular dynamics simulation study. J. Chem. Phys. 1994, 101, 788–797. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic molecular dynamics simulation of polydisperse linear polyethylene melts. Macromolecules 1998, 31, 7934–7943. [Google Scholar] [CrossRef]
- Jin, Y.; Boyd, R.H. Subglass chain dynamics and relaxation in polyethylene: A molecular dynamics simulation study. J. Chem. Phys. 1998, 108, 9912–9923. [Google Scholar] [CrossRef]
- Kavassalis, T.; Sundararajan, P. A molecular-dynamics study of polyethylene crystallization. Macromolecules 1993, 26, 4144–4150. [Google Scholar] [CrossRef]
- Moore, J.; Cui, S.; Cochran, H.; Cummings, P. A molecular dynamics study of a short-chain polyethylene melt.: I. steady-state shear. J. Non-Newton. Fluid Mech. 2000, 93, 83–99. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.; Yoon, D.Y.; Farago, B.; Rathgeber, S.; Zirkel, A.; Willner, L.; Richter, D. Chain motion in an unentangled polyethylene melt: A critical test of the rouse model by molecular dynamics simulations and neutron spin echo spectroscopy. Phys. Rev. Lett. 1998, 80, 2346. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Theodorou, D.N.; Martinez-Salazar, J. Entanglement relaxation time in polyethylene: Simulation versus experimental data. Macromolecules 2008, 41, 2959–2962. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Power, A.J.; Harmandaris, V. Structural and dynamical properties of polyethylene/graphene nanocomposites through molecular dynamics simulations. Polymers 2015, 7, 390–417. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X.; Muthu, J.; Mabrouki, T.; Fontaine, M.; Gong, Y.; Rabczuk, T. Load transfer of graphene/carbon nanotube/polyethylene hybrid nanocomposite by molecular dynamics simulation. Compos. Part B Eng. 2014, 63, 27–33. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Daoulas, K.C.; Mavrantzas, V.G. Molecular dynamics simulation of a polymer melt/solid interface: Local dynamics and chain mobility in a thin film of polyethylene melt adsorbed on graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Hu, M.; Keblinski, P.; Schelling, P.K. Kapitza conductance of silicon–amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 2009, 79, 104305. [Google Scholar] [CrossRef]
- Taylor, D.; Strawhecker, K.; Shanholtz, E.; Sorescu, D.; Sausa, R. Investigations of the intermolecular forces between RDX and polyethylene by force—Distance spectroscopy and molecular dynamics simulations. J. Phys. Chem. A 2014, 118, 5083–5097. [Google Scholar] [CrossRef] [PubMed]
- Hur, K.; Winkler, R.G.; Yoon, D.Y. Comparison of ring and linear polyethylene from molecular dynamics simulations. Macromolecules 2006, 39, 3975–3977. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular dynamics simulation of homogeneous crystal nucleation in polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Henry, A.; Chen, G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations. Phys. Rev. Lett. 2008, 101, 235502. [Google Scholar] [CrossRef] [PubMed]
- Henry, A.; Chen, G. Anomalous heat conduction in polyethylene chains: Theory and molecular dynamics simulations. Phys. Rev. B 2009, 79, 144305. [Google Scholar] [CrossRef]
- Kim, J.M.; Locker, R.; Rutledge, G.C. Plastic deformation of semicrystalline polyethylene under extension, compression, and shear using molecular dynamics simulation. Macromolecules 2014, 47, 2515–2528. [Google Scholar] [CrossRef]
- Lavine, M.S.; Waheed, N.; Rutledge, G.C. Molecular dynamics simulation of orientation and crystallization of polyethylene during uniaxial extension. Polymer 2003, 44, 1771–1779. [Google Scholar] [CrossRef]
- Yeh, I.C.; Andzelm, J.W.; Rutledge, G.C. Mechanical and structural characterization of semicrystalline polyethylene under tensile deformation by molecular dynamics simulations. Macromolecules 2015, 48, 4228–4239. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Keitel, H.; Zhao, J.; Zhuang, X.; Rabczuk, T. Stochastic predictions of bulk properties of amorphous polyethylene based on molecular dynamics simulations. Mech. Mater. 2014, 68, 70–84. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hockney, R.W. The potential calculation and some applications. Methods Comput. Phys. 1970, 9, 135–211. [Google Scholar]
- Flory, P.J. The configuration of real polymer chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two-and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Sukumaran, S.K.; Ramirez, J. Linear viscoelasticity from molecular dynamics simulation of entangled polymers. Macromolecules 2007, 40, 6748–6757. [Google Scholar] [CrossRef]
| M (g/mol) | No. of chains | Simulation time (ns) | No. of initial structures |
|---|---|---|---|
| 422.8 | 1000 | 100 | 3 |
| 703.4 | 600 | 100 | 3 |
| 983.9 | 428 | 100 | 3 |
| 1405 | 300 | 500 | 6 |
| 2106 | 200 | 500 | 6 |
| 2807 | 150 | 800 | 6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, K.Z.; Nishimura, R.; Yasuoka, K.; Masubuchi, Y. Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts. Polymers 2017, 9, 24. https://doi.org/10.3390/polym9010024
Takahashi KZ, Nishimura R, Yasuoka K, Masubuchi Y. Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts. Polymers. 2017; 9(1):24. https://doi.org/10.3390/polym9010024
Chicago/Turabian StyleTakahashi, Kazuaki Z., Ryuto Nishimura, Kenji Yasuoka, and Yuichi Masubuchi. 2017. "Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts" Polymers 9, no. 1: 24. https://doi.org/10.3390/polym9010024
APA StyleTakahashi, K. Z., Nishimura, R., Yasuoka, K., & Masubuchi, Y. (2017). Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts. Polymers, 9(1), 24. https://doi.org/10.3390/polym9010024







