Relaxation Dynamics of Semiflexible Fractal Macromolecules
Abstract
:1. Introduction
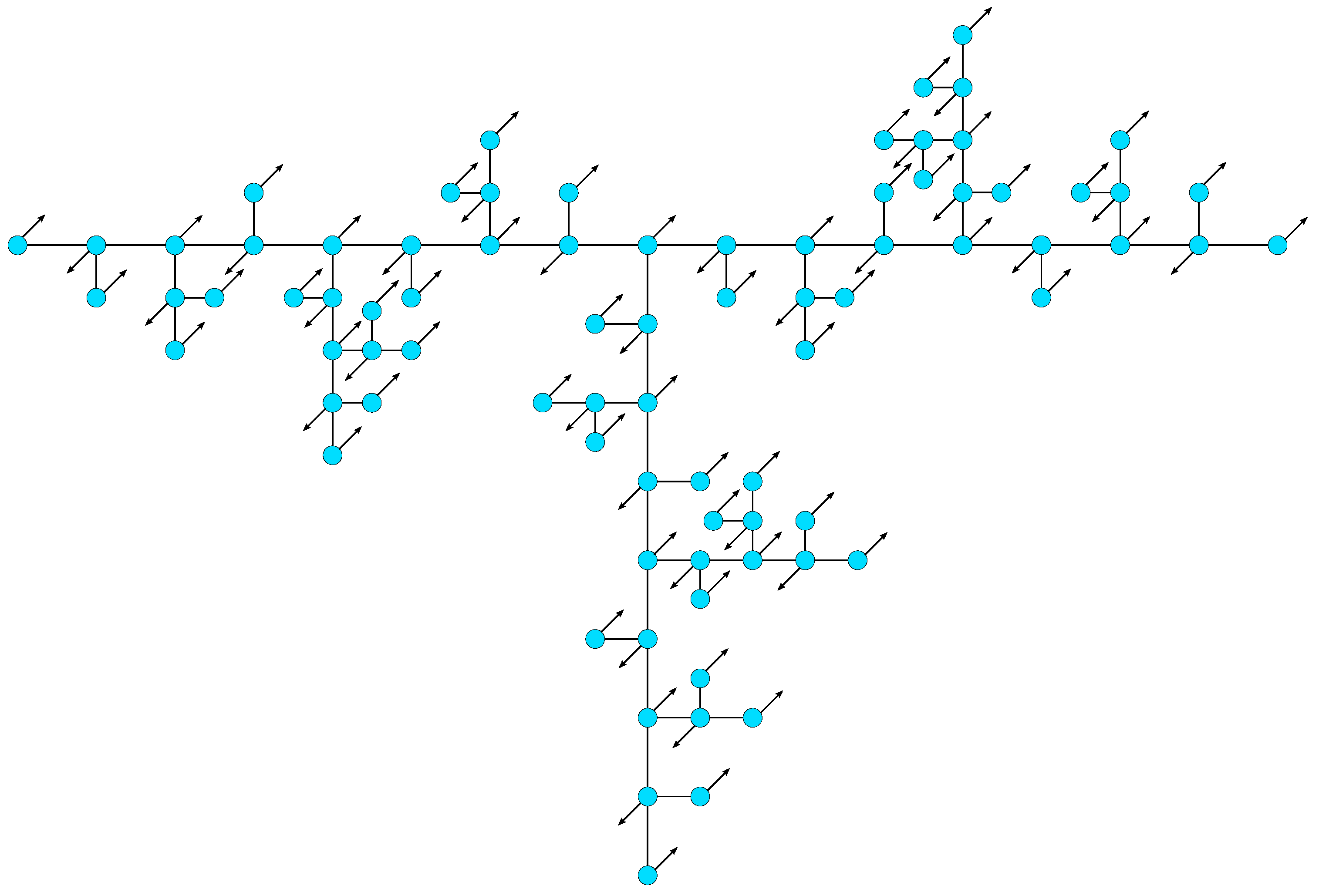
2. Methods
- The mean squared length of the bonds is fixed .
- For adjacent bonds a and b, directly connected over a bead i, holds. The sign is determined by the relative orientation of the bonds. The positive sign describes the case of head-to-tail orientation of a and b; otherwise, the minus sign is obtained. The common stiffness parameter related to a and b is denoted by .
- Due to the freely-rotating condition imposed on non-adjacent bonds a and c (connected over the unique path ), one obtains . For linear chains, this restriction under the continuous chain limit and leads to the definition of the persistence length ; see Equation (3.15) of [44]. However, for branched structures, no smooth curve description due to the branching points is possible.
3. Results and Discussion
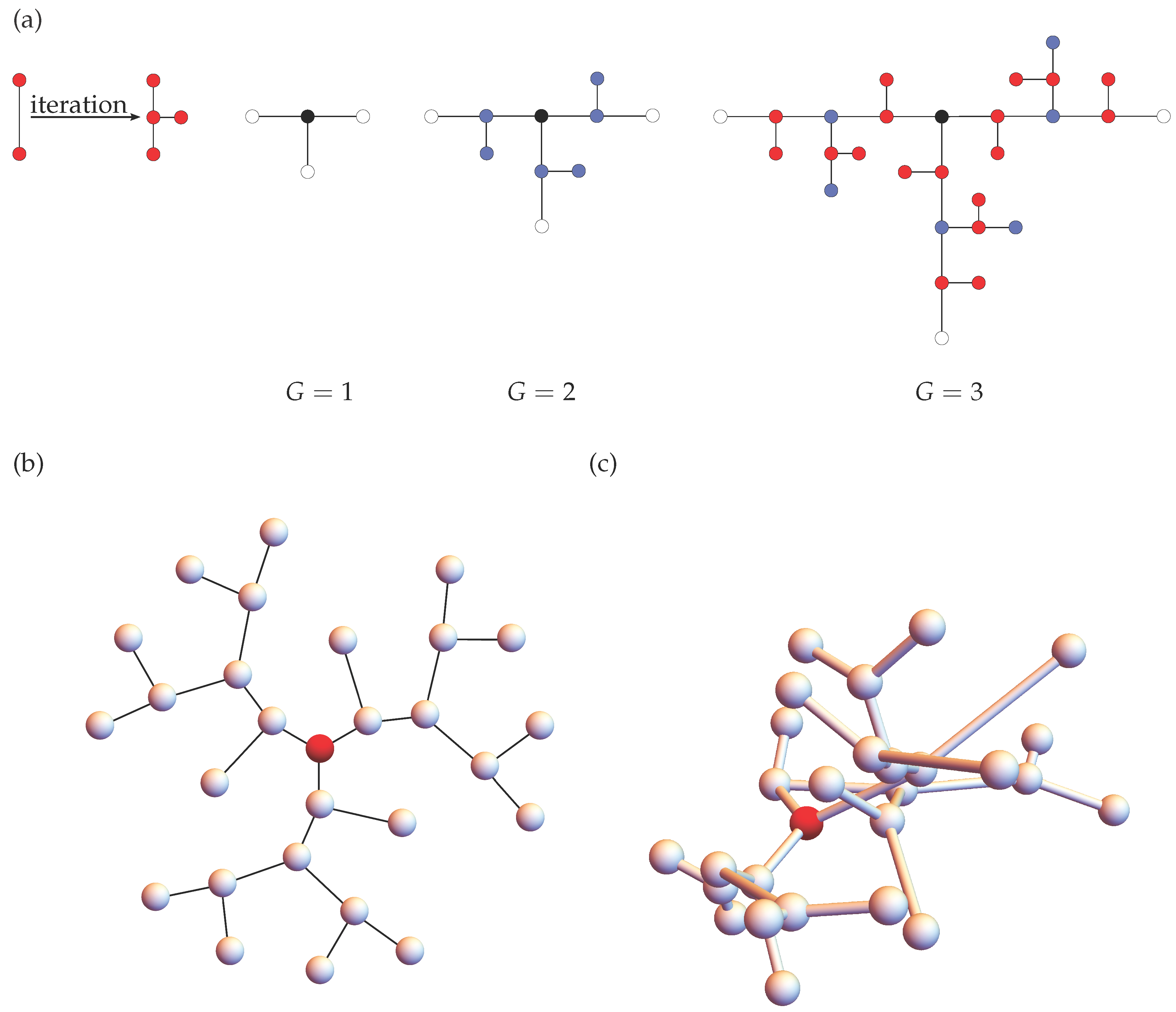
3.1. Dynamical Matrix of T-fractals
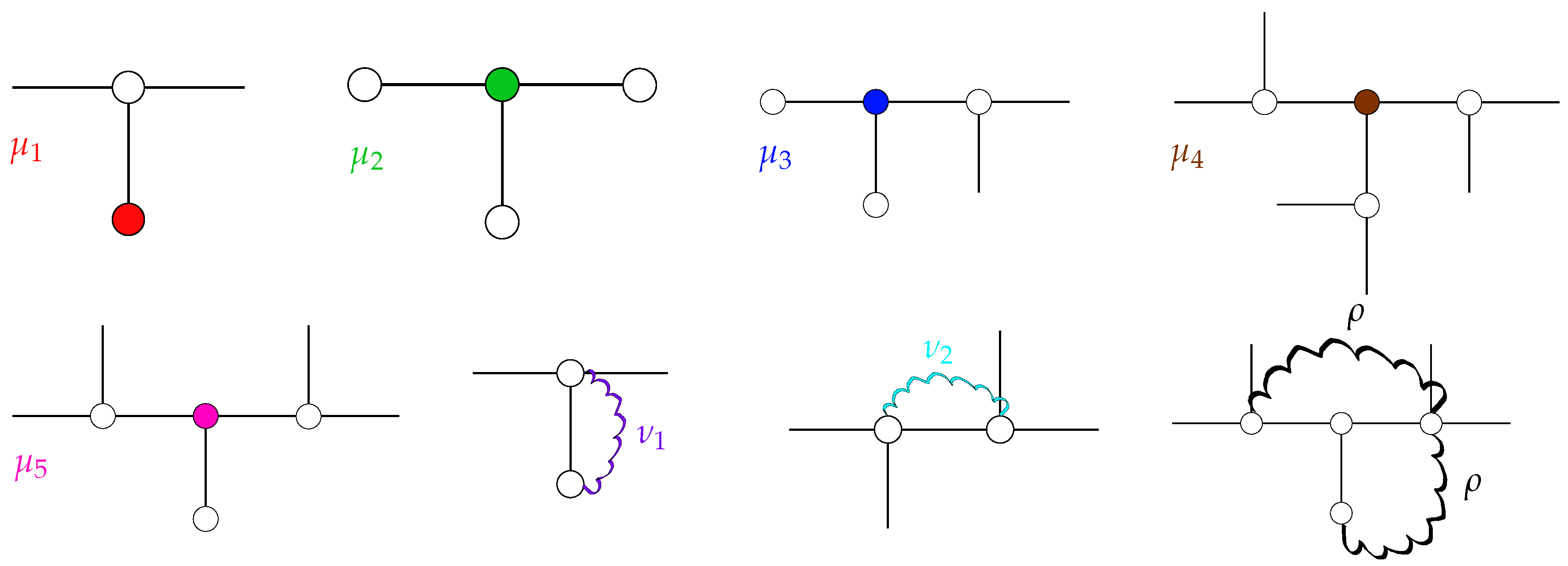
- Terminal beads with functionality (i.e., number of NN) have exactly one internal NN with . Hence, one obtains the matrix element:
- For T-fractals of generation , the single internal bead is directly connected to three terminal beads. The corresponding matrix element is given by:
- An internal bead with two terminal and one internal NN is described by the diagonal element:
- The diagonal element corresponds to internal beads with three internal NN:
- If an internal bead has two internal and one terminal NN, it is described by the diagonal element:
- If one of the two considered beads is a terminal bead, we obtain the NN element:
- Otherwise, two internal beads in NN position result in the matrix element:
3.2. Hierarchical Eigenmodes of T-fractals
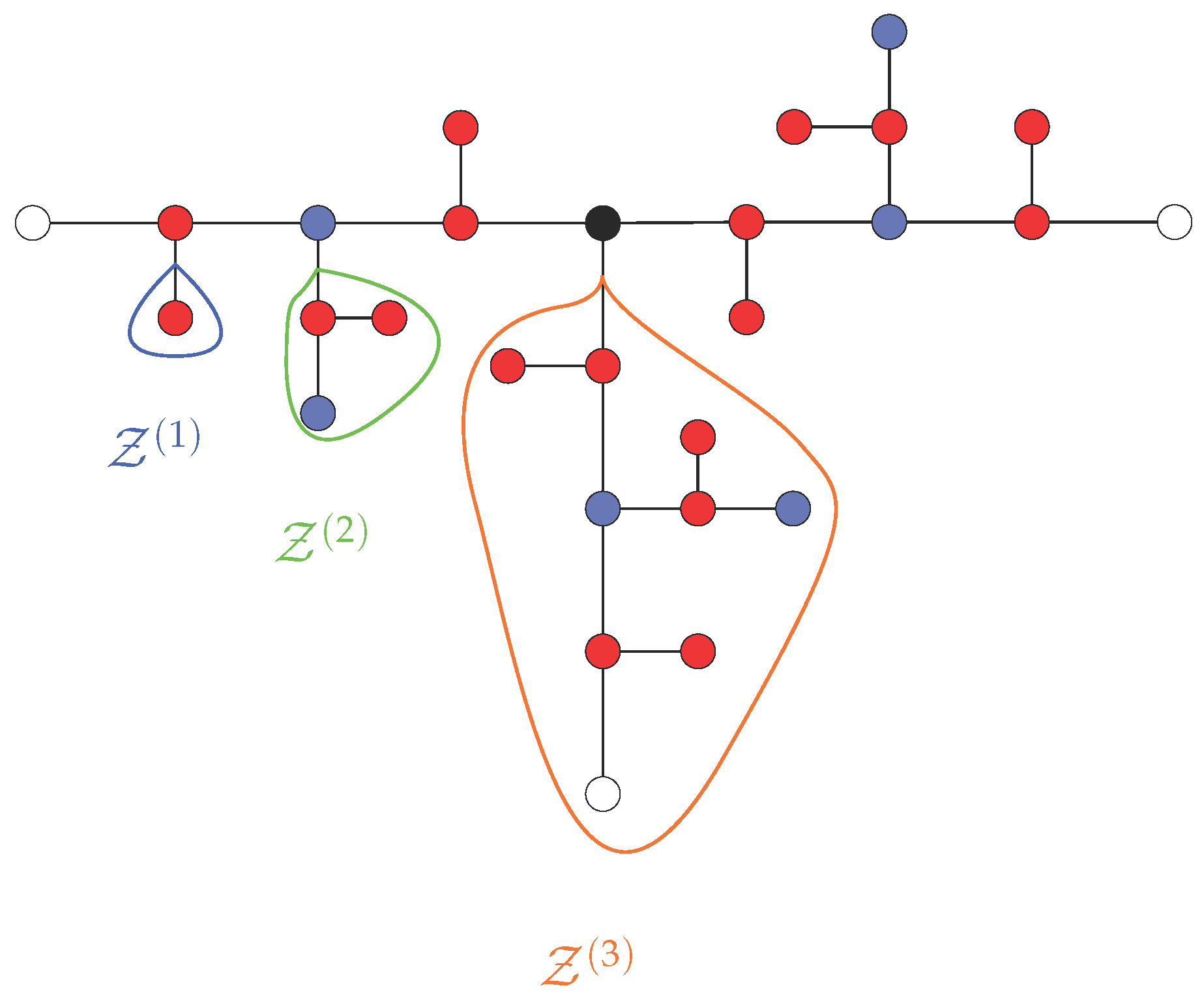
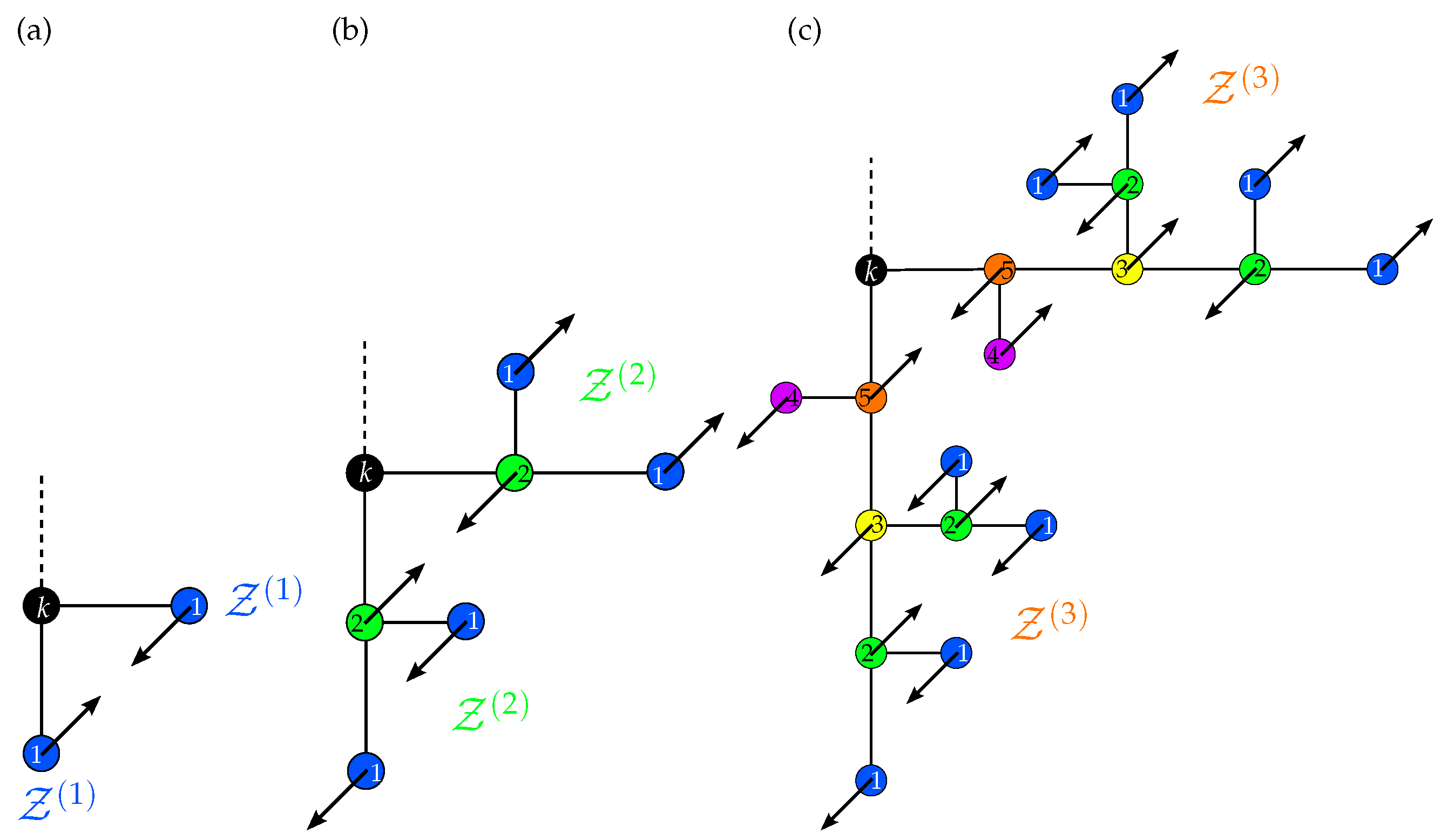
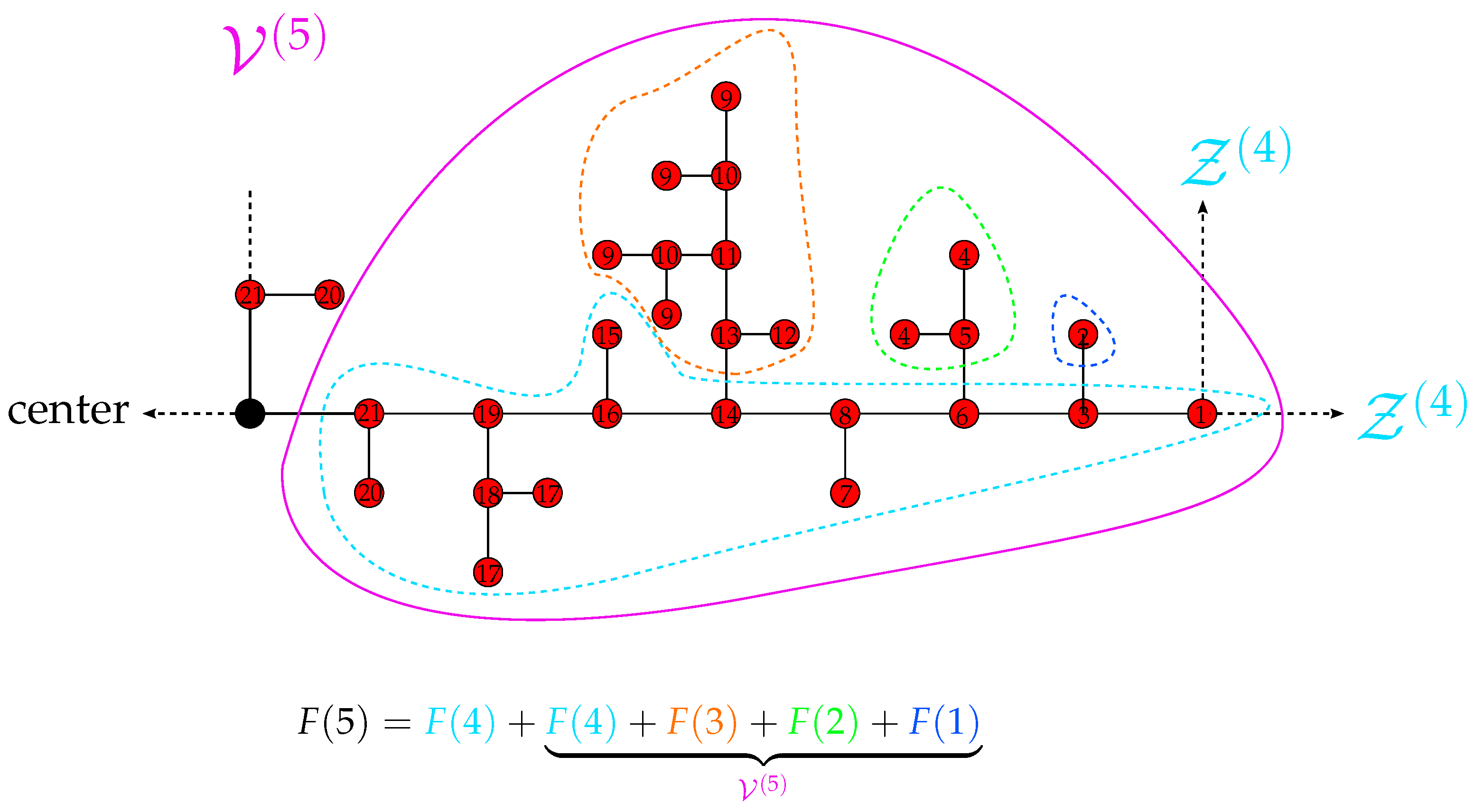
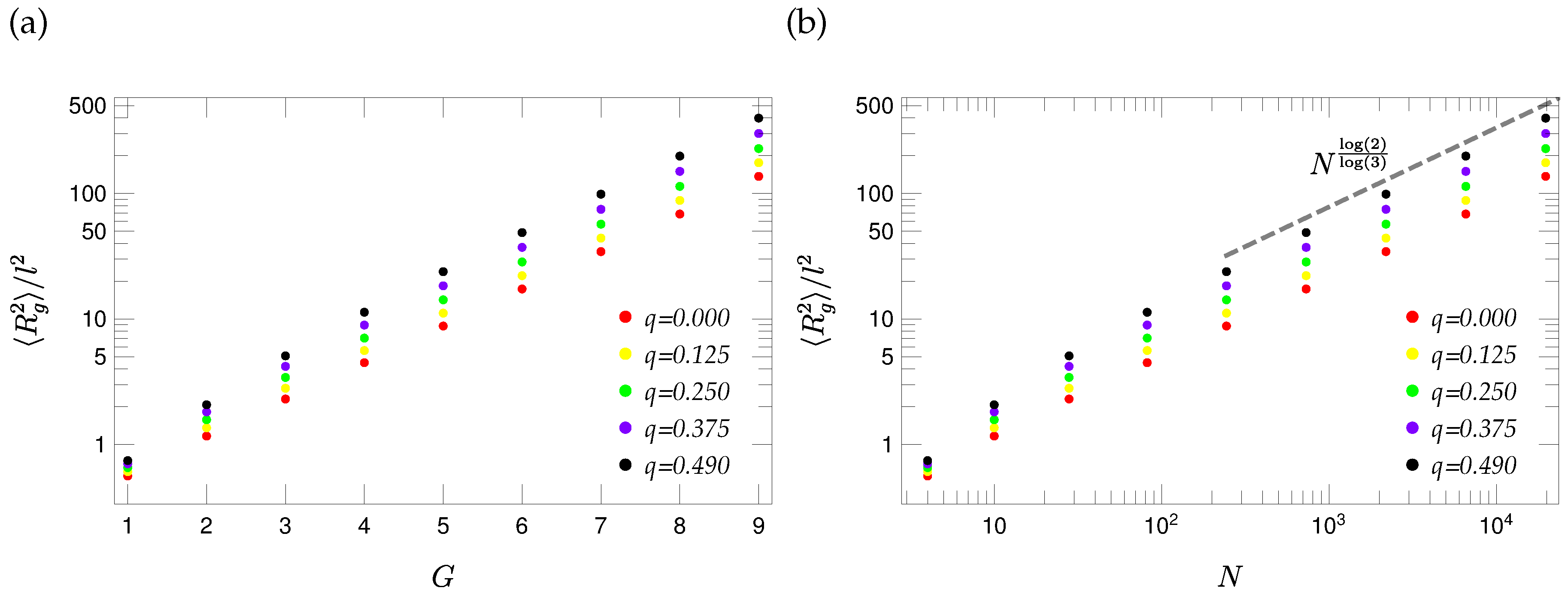
3.3. Reduced Matrices
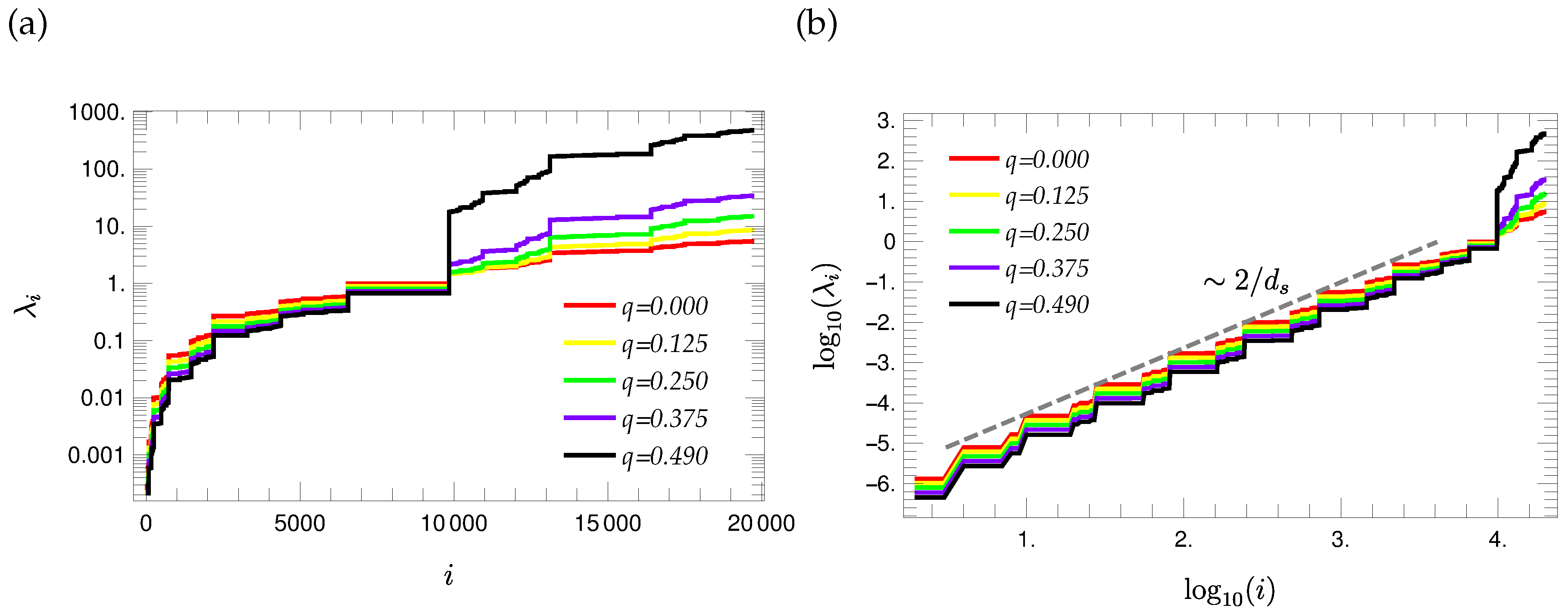
3.4. Eigenvalue Spectra of
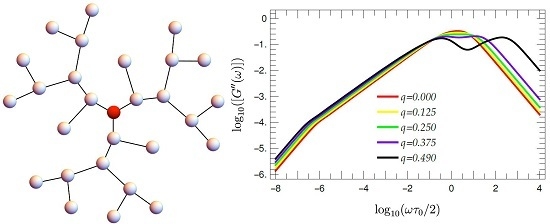
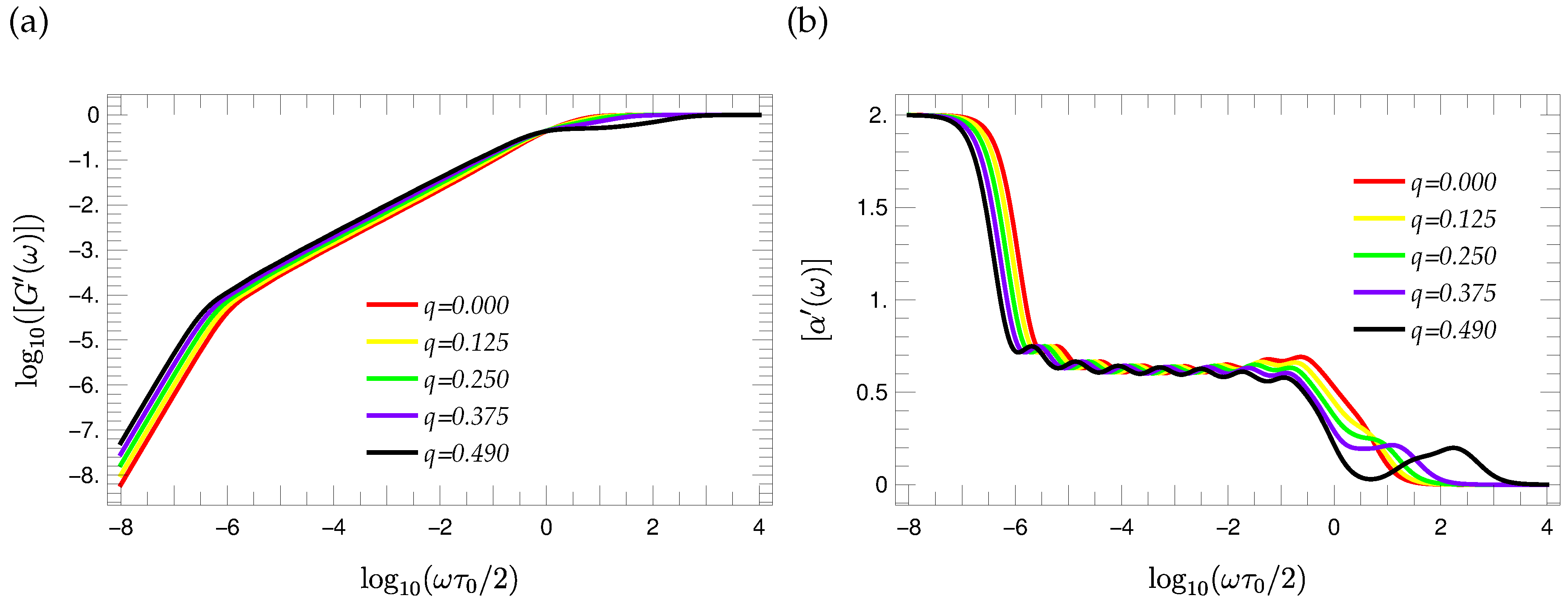
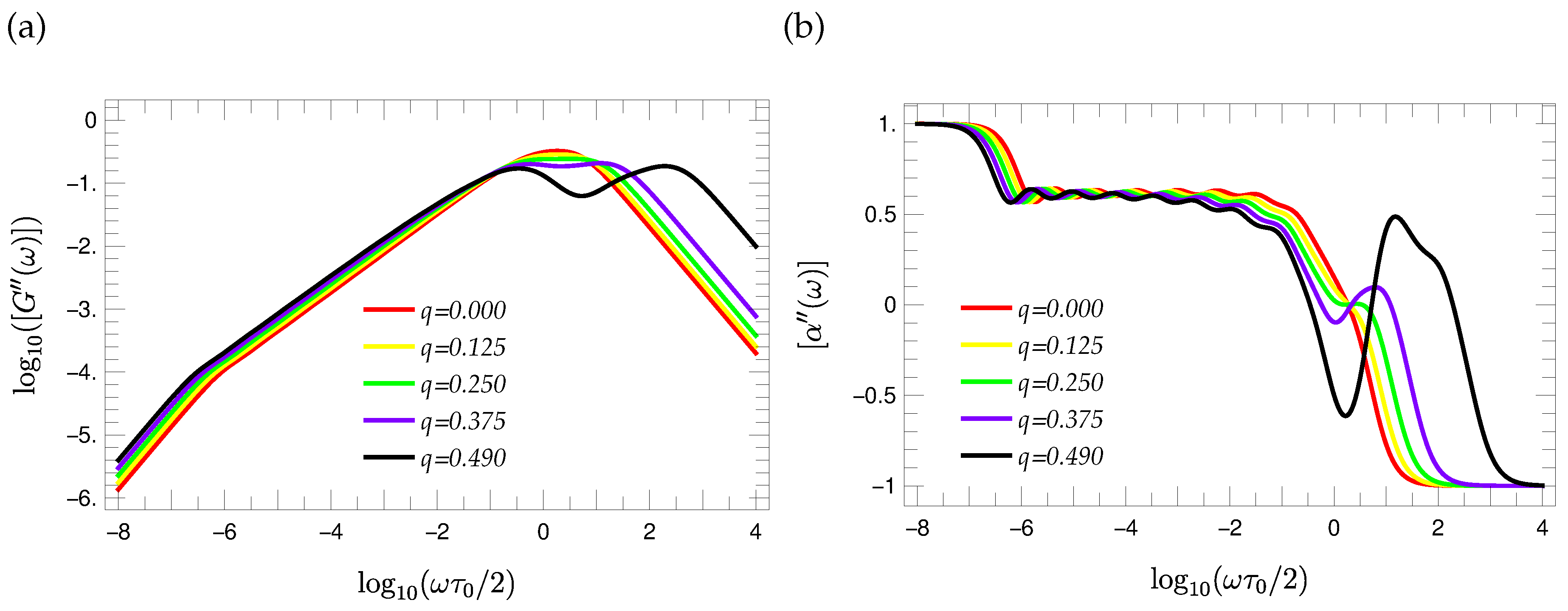
3.5. Mechanical Relaxation
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GGS | generalized Gaussian structures |
| STP | semiflexible treelike polymers |
| NN | nearest neighbor |
| NNN | next-nearest neighbor |
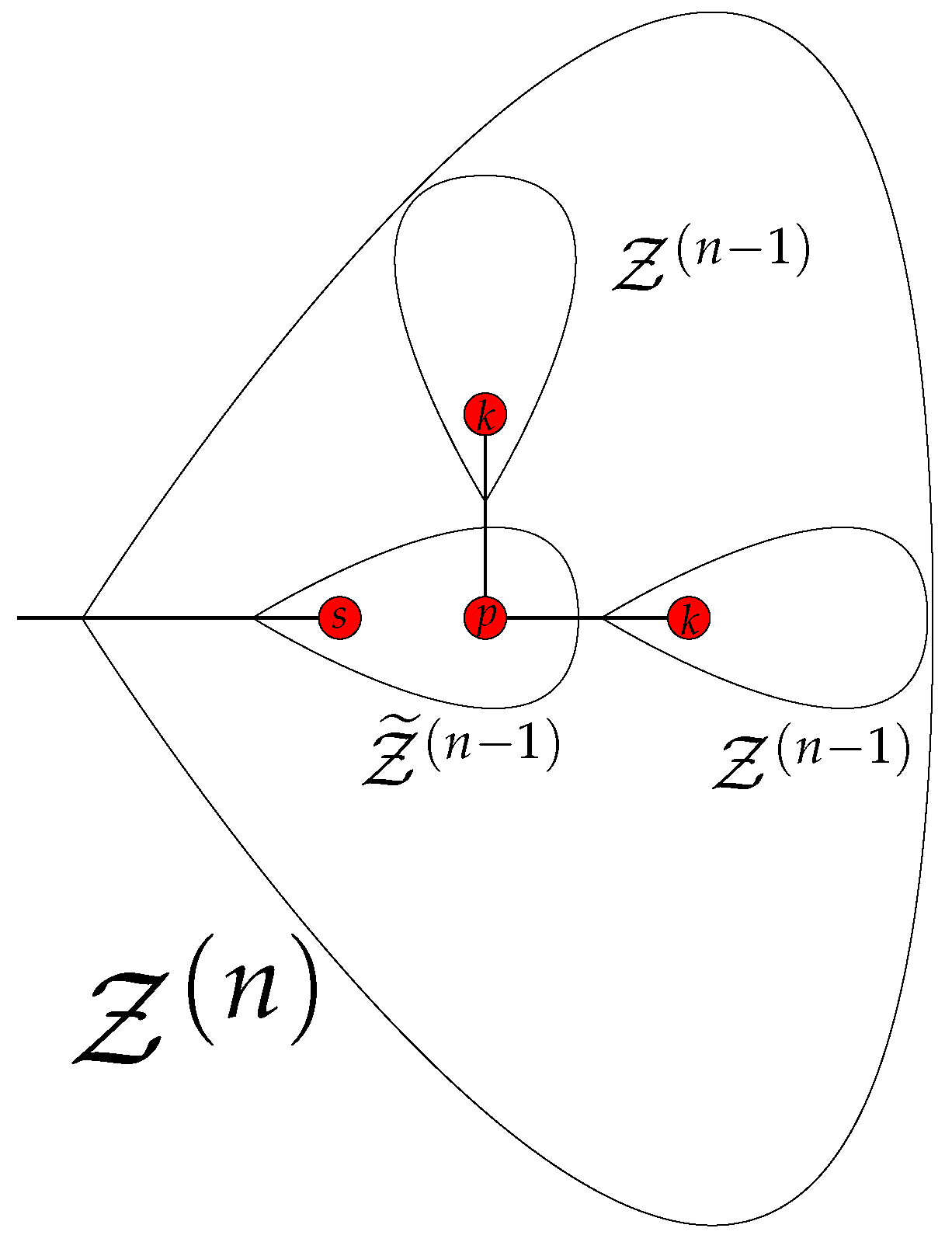
Appendix A. Iterative Procedure for the Calculation of the Matrix An+1 from An
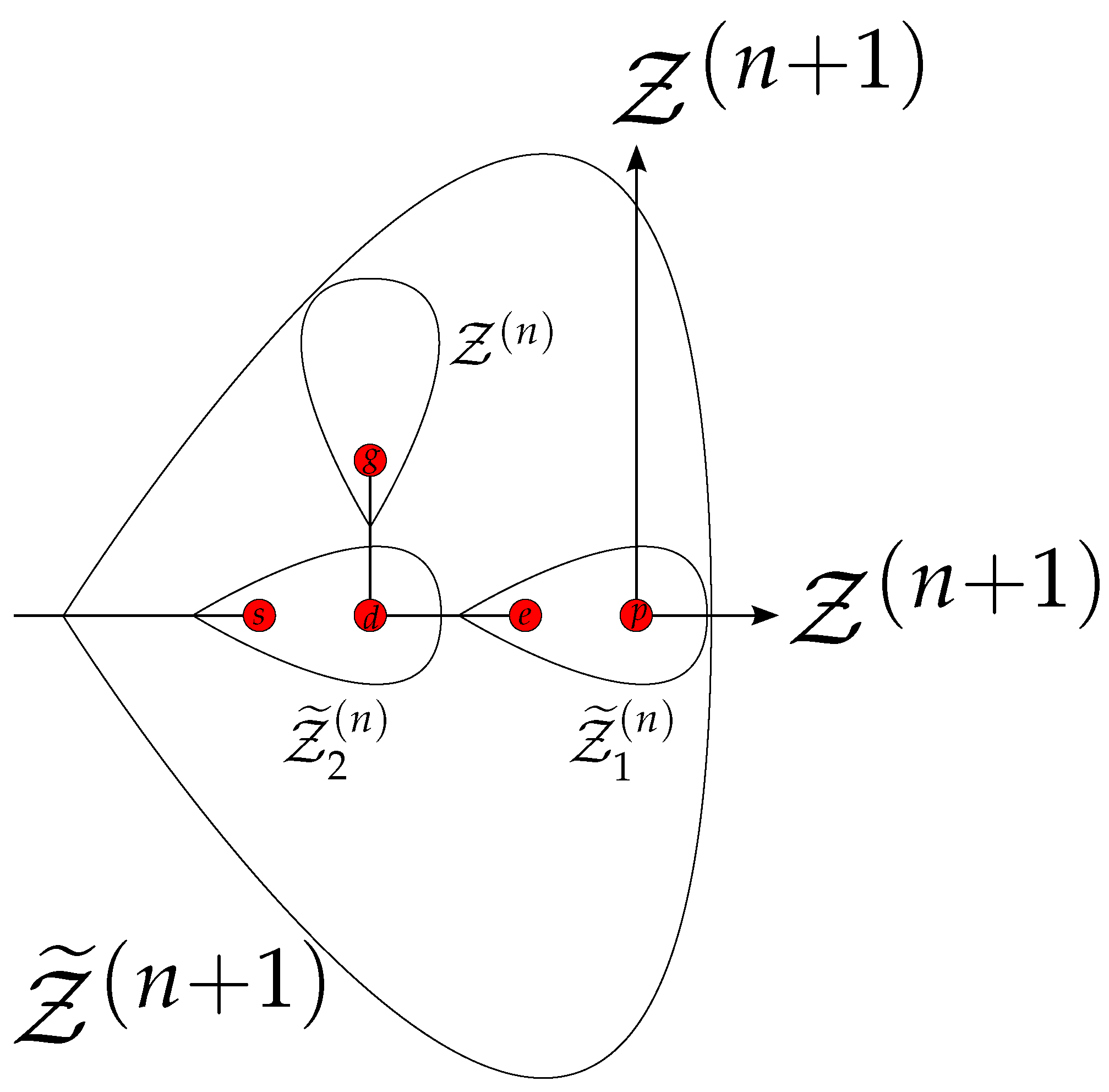
References
- Gao, C.; Yan, D. Hyperbranched polymers: From synthesis to applications. Prog. Polym. Sci. 2004, 29, 183–275. [Google Scholar] [CrossRef]
- Voit, B.I.; Lederer, A. Hyperbranched and highly branched polymer architectures: Synthetic strategies and major characterization aspects. Chem. Rev. 2009, 109, 5924–5973. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Gao, C.; Frey, H. Hyperbranched Polymers: Synthesis, Properties, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 8. [Google Scholar]
- Lederer, A.; Burchard, W. Hyperbranched Polymers: Macromolecules in between Deterministic Linear Chains and Dendrimer Structures; Royal Society of Chemistry: Cambridge, UK, 2015; Volume 16. [Google Scholar]
- Fischer, M.; Vögtle, F. Dendrimers: From design to application—A progress report. Angew. Chem. Int. Ed. 1999, 38, 884–905. [Google Scholar] [CrossRef]
- Ballauff, M.; Likos, C.N. Dendrimers in solution: Insight from theory and simulation. Angew. Chem. Int. Ed. 2004, 43, 2998–3020. [Google Scholar] [CrossRef] [PubMed]
- Sowinska, M.; Urbanczyk-Lipkowska, Z. Advances in the chemistry of dendrimers. New J. Chem. 2014, 38, 2147–2708. [Google Scholar] [CrossRef]
- Lederer, A.; Burchard, W.; Khalyavina, A.; Lindner, P.; Schweins, R. Is the universal law valid for branched polymers? Angew. Chem. Int. Ed. 2013, 52, 4659–4663. [Google Scholar] [CrossRef] [PubMed]
- Hölter, D.; Burgath, A.; Frey, H. Degree of branching in hyperbranched polymers. Acta Polym. 1997, 48, 30–35. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Adolf, D.B.; Davies, G.R. Computer simulations of hyperbranched polymers in shear flows. Macromolecules 2001, 34, 3783–3789. [Google Scholar] [CrossRef]
- Sheridan, P.F.; Adolf, D.B.; Lyulin, A.V.; Neelov, I.; Davies, G.R. Computer simulations of hyperbranched polymers: The influence of the Wiener index on the intrinsic viscosity and radius of gyration. J. Chem. Phys. 2002, 117, 7802–7812. [Google Scholar] [CrossRef]
- Polińska, P.; Gillig, C.; Wittmer, J.P.; Baschnagel, J. Hyperbranched polymer stars with Gaussian chain statistics revisited. Eur. Phys. J. E 2014, 37, 12. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Dockhorn, R.; Mironova, O.; Sommer, J.U. Two universality classes for random hyperbranched polymers. Soft Matter 2014, 10, 4935–4946. [Google Scholar] [CrossRef] [PubMed]
- Wawrzyńska, E.; Sikorski, A.; Zifferer, G. Monte Carlo simulation studies of regular and irregular dendritic polymers. Macromol. Theory Simul. 2015, 24, 477–489. [Google Scholar] [CrossRef]
- Lederer, A.; Burchard, W.; Hartmann, T.; Haataja, J.S.; Houbenov, N.; Janke, A.; Friedel, P.; Schweins, R.; Lindner, P. Dendronized hyperbranched macromolecules: Soft matter with a novel type of segmental distribution. Angew. Chem. Int. Ed. 2015, 54, 12578–12583. [Google Scholar] [CrossRef] [PubMed]
- Kahng, B.; Redner, S. Scaling of the first-passage time and the survival probability on exact and quasi-exact self-similar structures. J. Phys. A Math. Gen. 1989, 22, 887. [Google Scholar] [CrossRef]
- Matan, O.; Havlin, S. Mean first-passage time on loopless aggregates. Phys. Rev. A 1989, 40, 6573. [Google Scholar] [CrossRef]
- Maritan, A.; Sartoni, G.; Stella, A.L. Singular dynamical renormalization group and biased diffusion on fractals. Phys. Rev. Lett. 1993, 71, 1027. [Google Scholar] [CrossRef] [PubMed]
- Burioni, R.; Cassi, D.; Regina, S. Cutting-decimation renormalization for diffusive and vibrational dynamics on fractals. Phys. A 1999, 265, 323–332. [Google Scholar] [CrossRef]
- Burioni, R.; Cassi, D.; Corberi, F.; Vezzani, A. Phase-ordering kinetics on graphs. Phys. Rev. E 2007, 75, 011113. [Google Scholar] [CrossRef] [PubMed]
- Agliari, E. Exact mean first-passage time on the T-graph. Phys. Rev. E 2008, 77, 011128. [Google Scholar] [CrossRef] [PubMed]
- Haynes, C.P.; Roberts, A.P. Global first-passage times of fractal lattices. Phys. Rev. E 2008, 78, 041111. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Lin, Y.; Zhou, S.; Wu, B.; Guan, J. Mean first-passage time for random walks on the T-graph. New J. Phys. 2009, 11, 103043. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, B.; Zhang, Z. Determining mean first-passage time on a class of treelike regular fractals. Phys. Rev. E 2010, 82, 031140. [Google Scholar] [CrossRef] [PubMed]
- Agliari, E.; Blumen, A.; Mülken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 2010, 82, 012305. [Google Scholar] [CrossRef]
- Dolgushev, M.; Guérin, T.; Blumen, A.; Bénichou, O.; Voituriez, R. Contact kinetics in fractal macromolecules. Phys. Rev. Lett. 2015, 115, 208301. [Google Scholar] [CrossRef] [PubMed]
- Gurtovenko, A.; Blumen, A. Generalized Gaussian Structures: Models for polymer systems with complex topologies. In Polymer Analysis Polymer Theory; Springer Berlin Heidelberg: Berlin, Germany, 2005; Volume 182, pp. 171–282. [Google Scholar]
- Rouse, P.E. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Markelov, D.A.; Dolgushev, M.; Gotlib, Y.Y.; Blumen, A. NMR relaxation of the orientation of single segments in semiflexible dendrimers. J. Chem. Phys. 2014, 140, 244904. [Google Scholar] [CrossRef] [PubMed]
- Markelov, D.A.; Falkovich, S.G.; Neelov, I.M.; Ilyash, M.Y.; Matveev, V.V.; Lähderanta, E.; Ingman, P.; Darinskii, A.A. Molecular dynamics simulation of spin–lattice NMR relaxation in poly-l-lysine dendrimers: Manifestation of the semiflexibility effect. Phys. Chem. Chem. Phys. 2015, 17, 3214–3226. [Google Scholar] [CrossRef] [PubMed]
- Bixon, M.; Zwanzig, R. Optimized Rouse–Zimm theory for stiff polymers. J.Chem. Phys. 1978, 68, 1896–1902. [Google Scholar] [CrossRef]
- Guenza, M.; Perico, A. A reduced description of the local dynamics of star polymers. Macromolecules 1992, 25, 5942–5949. [Google Scholar] [CrossRef]
- La Ferla, R. Conformations and dynamics of dendrimers and cascade macromolecules. J. Chem. Phys. 1997, 106, 688–700. [Google Scholar] [CrossRef]
- Von Ferber, C.; Blumen, A. Dynamics of dendrimers and of randomly built branched polymers. J. Chem. Phys. 2002, 116, 8616–8624. [Google Scholar] [CrossRef]
- Dolgushev, M.; Blumen, A. Dynamics of semiflexible treelike polymeric networks. J. Chem. Phys. 2009, 131, 044905. [Google Scholar] [CrossRef] [PubMed]
- Dolgushev, M.; Blumen, A. Dynamics of semiflexible chains, stars, and dendrimers. Macromolecules 2009, 42, 5378–5387. [Google Scholar] [CrossRef]
- Kumar, A.; Biswas, P. Dynamics of semiflexible dendrimers in dilute solutions. Macromolecules 2010, 43, 7378–7385. [Google Scholar] [CrossRef]
- Kumar, A.; Rai, G.J.; Biswas, P. Conformation and intramolecular relaxation dynamics of semiflexible randomly hyperbranched polymers. J. Chem. Phys. 2013, 138, 104902. [Google Scholar] [CrossRef] [PubMed]
- Fürstenberg, F.; Dolgushev, M.; Blumen, A. Analytical model for the dynamics of semiflexible dendritic polymers. J. Chem. Phys. 2012, 136, 154904. [Google Scholar] [CrossRef] [PubMed]
- Fürstenberg, F.; Dolgushev, M.; Blumen, A. Dynamics of semiflexible regular hyperbranched polymers. J. Chem. Phys. 2013, 138, 034904. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Dolgushev, M.; Zhang, Z. Dynamics of semiflexible recursive small-world polymer networks. Sci. Rep. 2014, 4, 7576. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M.; Reis, A.S.; Dolgushev, M. Dynamics of semiflexible scale-free polymer networks. J. Chem. Phys. 2014, 141, 144902. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Chen, Z.Y. Rouse dynamics of a dendrimer Model in the ϑ Condition. Macromolecules 1997, 30, 5104–5117. [Google Scholar] [CrossRef]
- Winkler, R.G.; Reineker, P.; Harnau, L. Models and equilibrium properties of stiff molecular chains. J. Chem. Phys. 1994, 101, 8119–8129. [Google Scholar] [CrossRef]
- Mansfield, M.L.; Stockmayer, W.H. Unperturbed dimensions of wormlike stars. Macromolecules 1980, 13, 1713–1715. [Google Scholar] [CrossRef]
- Doi, M. Introduction to Polymer Physics; Oxford university press: Qxford, UK, 1996. [Google Scholar]
- Gurtovenko, A.A.; Gotlib, Y.Y.; Blumen, A. Rouse dynamics of polymer networks bearing dendritic wedges. Macromolecules 2002, 35, 7481–7491. [Google Scholar] [CrossRef]
- Gurtovenko, A.A.; Markelov, D.A.; Gotlib, Y.Y.; Blumen, A. Dynamics of dendrimer-based polymer networks. J. Chem. Phys. 2003, 119, 7579–7590. [Google Scholar] [CrossRef]
- Koda, S. Equivalence between a generalized dendritic network and a set of one-dimensional networks as a ground of linear dynamics. J. Chem. Phys. 2015, 142, 204112. [Google Scholar] [CrossRef] [PubMed]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Alexander, S.; Orbach, R. Density of states on fractals: «fractons». J. Phys. Lett. 1982, 43, 625–631. [Google Scholar] [CrossRef]
- Dolgushev, M.; Berezovska, G.; Blumen, A. Cospectral polymers: Differentiation via semiflexibility. J. Chem. Phys. 2010, 133, 154905. [Google Scholar] [CrossRef] [PubMed]
- Sommer, J.-U.; Blumen, A. On the statistics of generalized Gaussian structures: Collapse and random external fields. J. Phys. A 1995, 28, 6669–6674. [Google Scholar] [CrossRef]
- Friedrich, C. Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 1991, 30, 151–158. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A. Mesoscopic pictures of the sol-gel transition: Ladder models and fractal networks. Macromolecules 1995, 28, 4013–4019. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
| G | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| N | 4 | 10 | 28 | 82 | 244 | 730 | 2188 | 6562 | 19,684 | 59,050 |
| 2 | 3 | 6 | 14 | 35 | 90 | 234 | 611 | 1598 | 4182 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mielke, J.; Dolgushev, M. Relaxation Dynamics of Semiflexible Fractal Macromolecules. Polymers 2016, 8, 263. https://doi.org/10.3390/polym8070263
Mielke J, Dolgushev M. Relaxation Dynamics of Semiflexible Fractal Macromolecules. Polymers. 2016; 8(7):263. https://doi.org/10.3390/polym8070263
Chicago/Turabian StyleMielke, Jonas, and Maxim Dolgushev. 2016. "Relaxation Dynamics of Semiflexible Fractal Macromolecules" Polymers 8, no. 7: 263. https://doi.org/10.3390/polym8070263
APA StyleMielke, J., & Dolgushev, M. (2016). Relaxation Dynamics of Semiflexible Fractal Macromolecules. Polymers, 8(7), 263. https://doi.org/10.3390/polym8070263