Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study
Abstract
:1. Introduction
2. Model
2.1. Connectivity
2.2. Excluded Volume
2.3. Temperature, Deformation and Wall
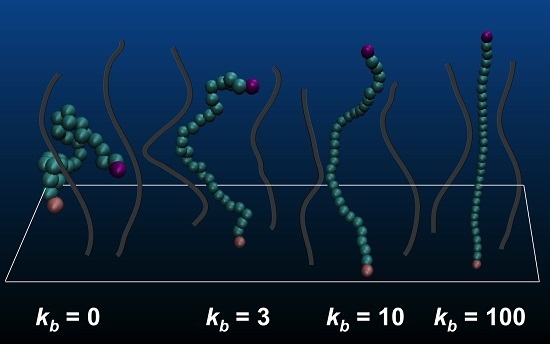
2.4. Semiflexibility
2.5. Simulation Details
3. Results and Discussion
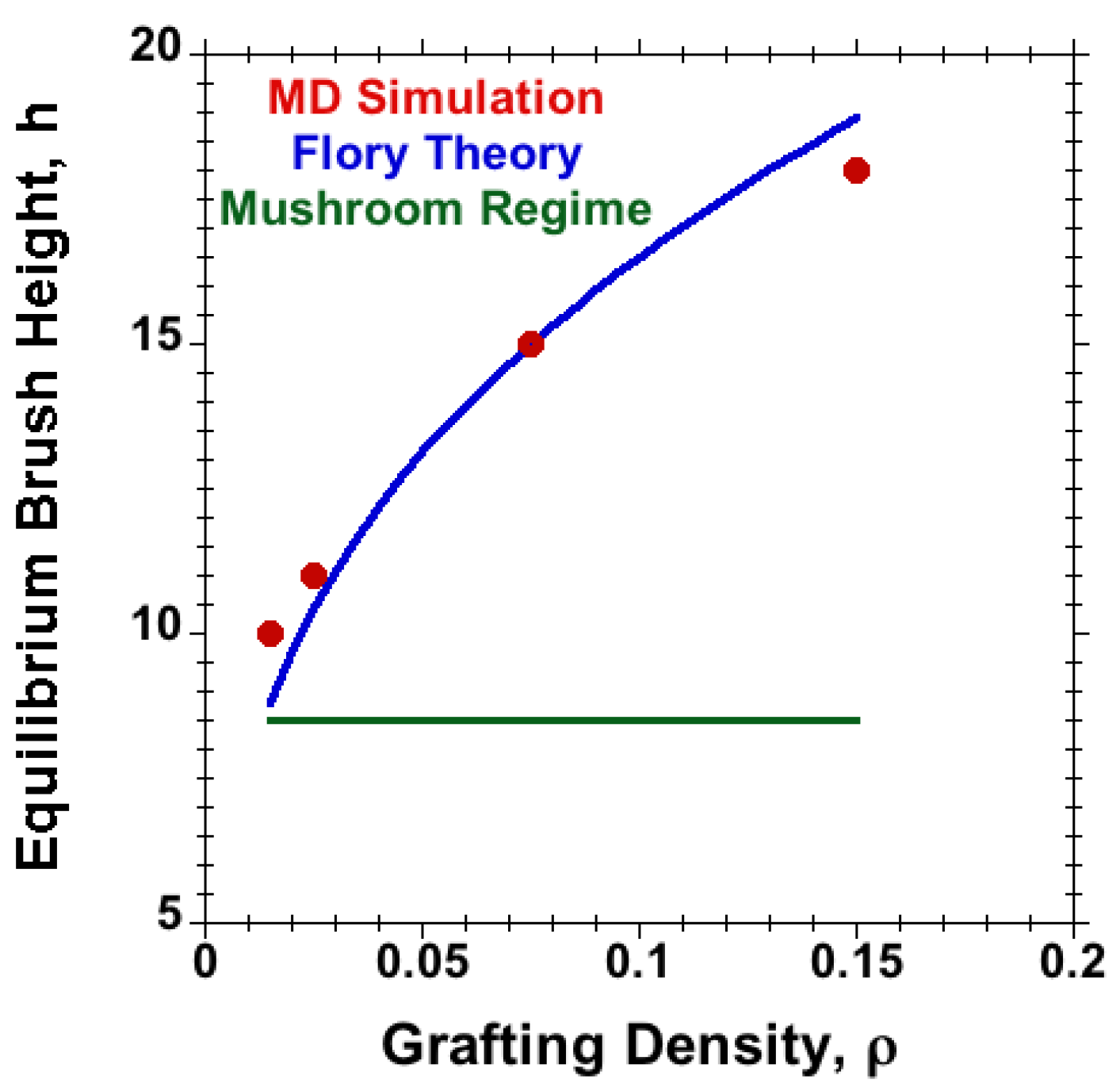
3.1. Equilibrium
3.2. Sheared Brushes Made of Flexible Chains
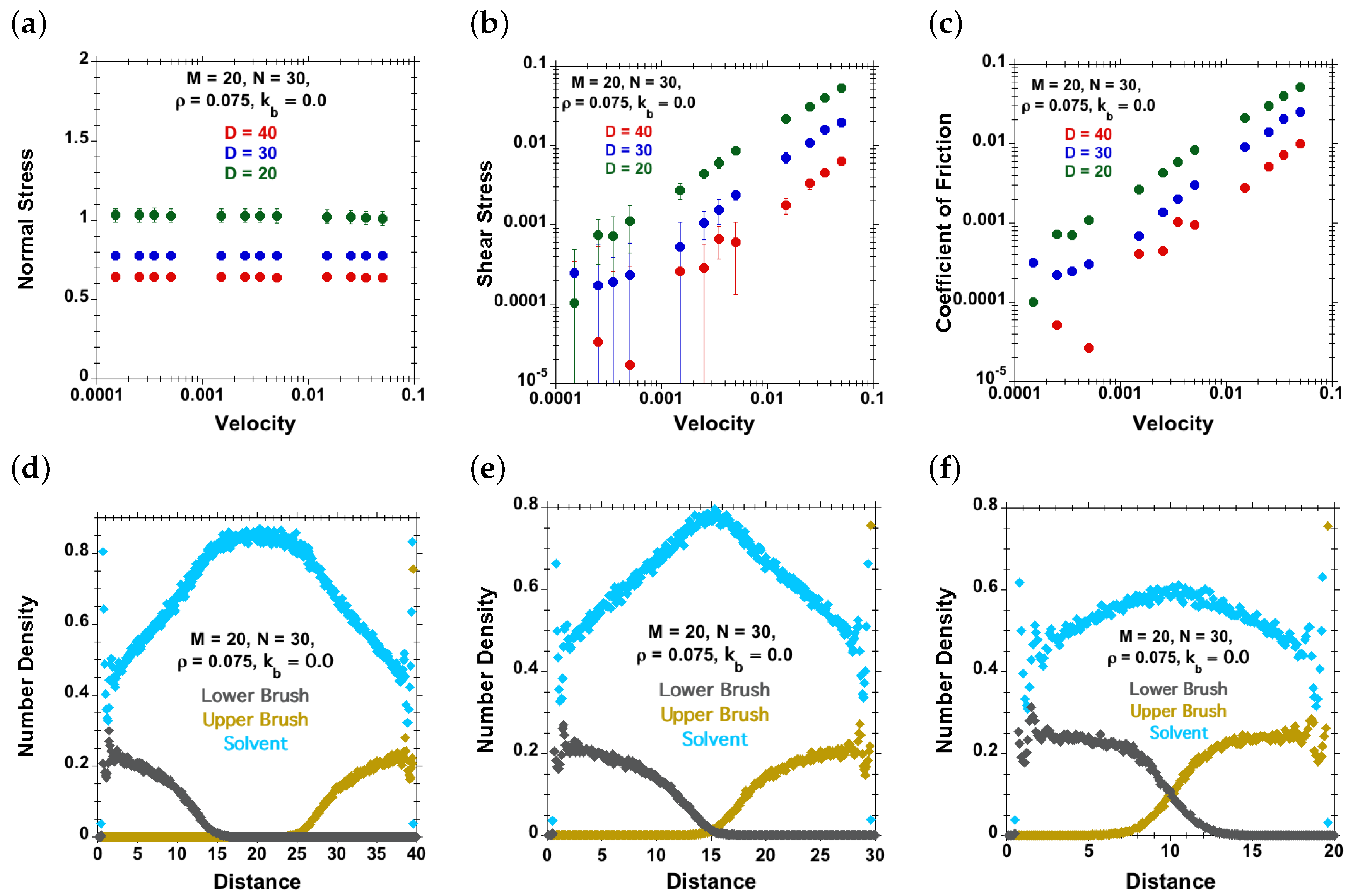
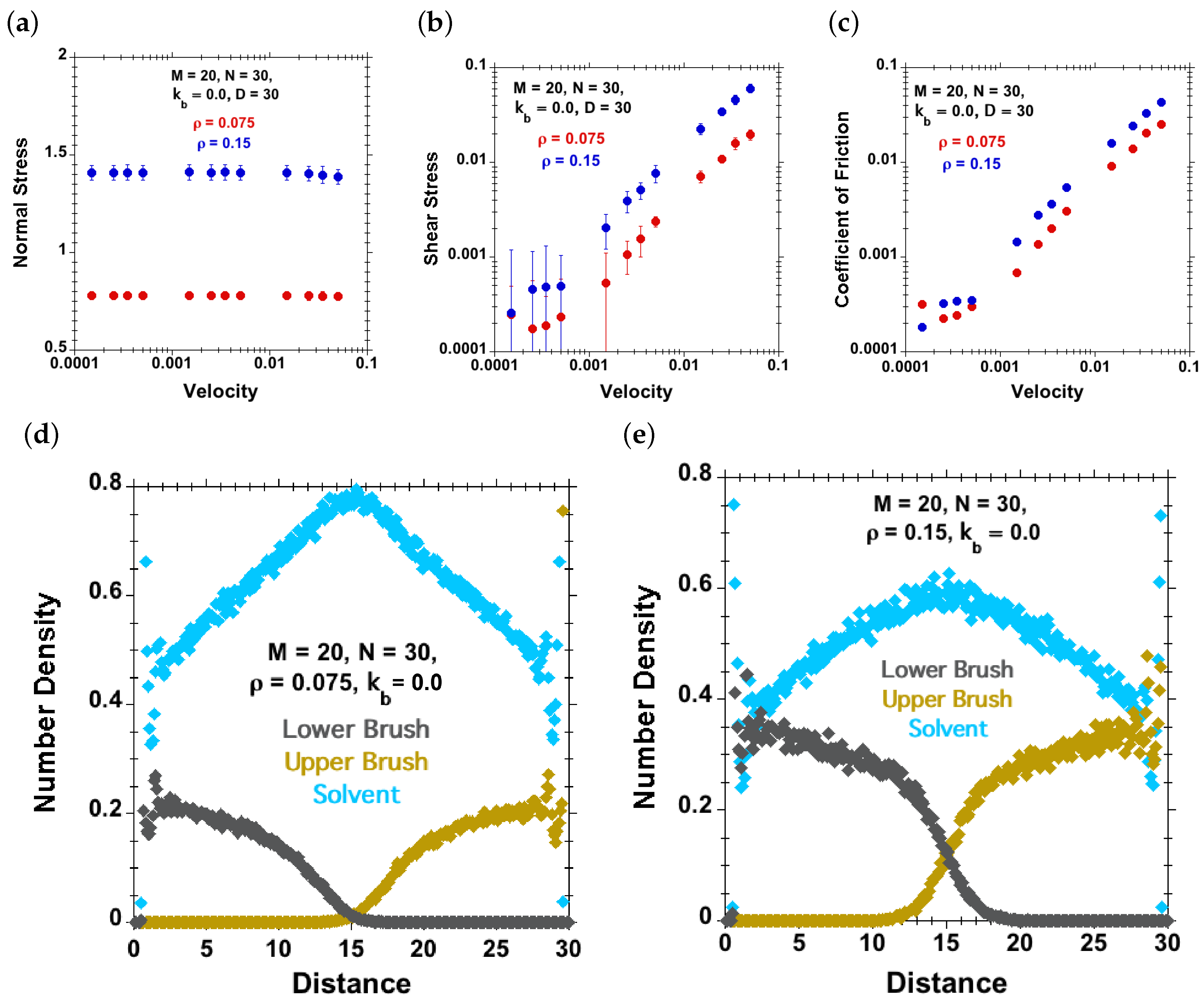
3.2.1. Effect of Shear Velocity at Various Separations, but Fixed Tethering Density
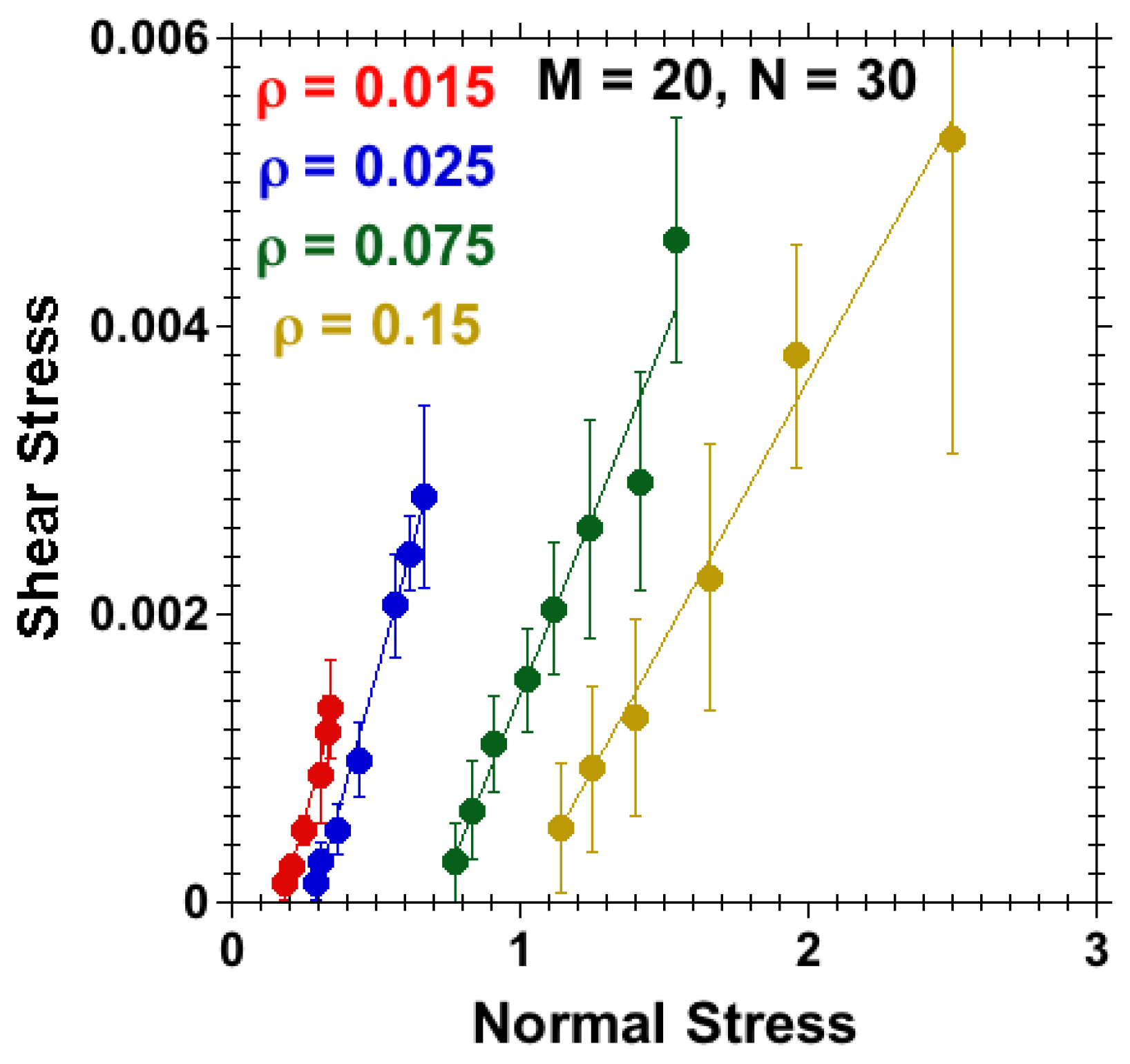
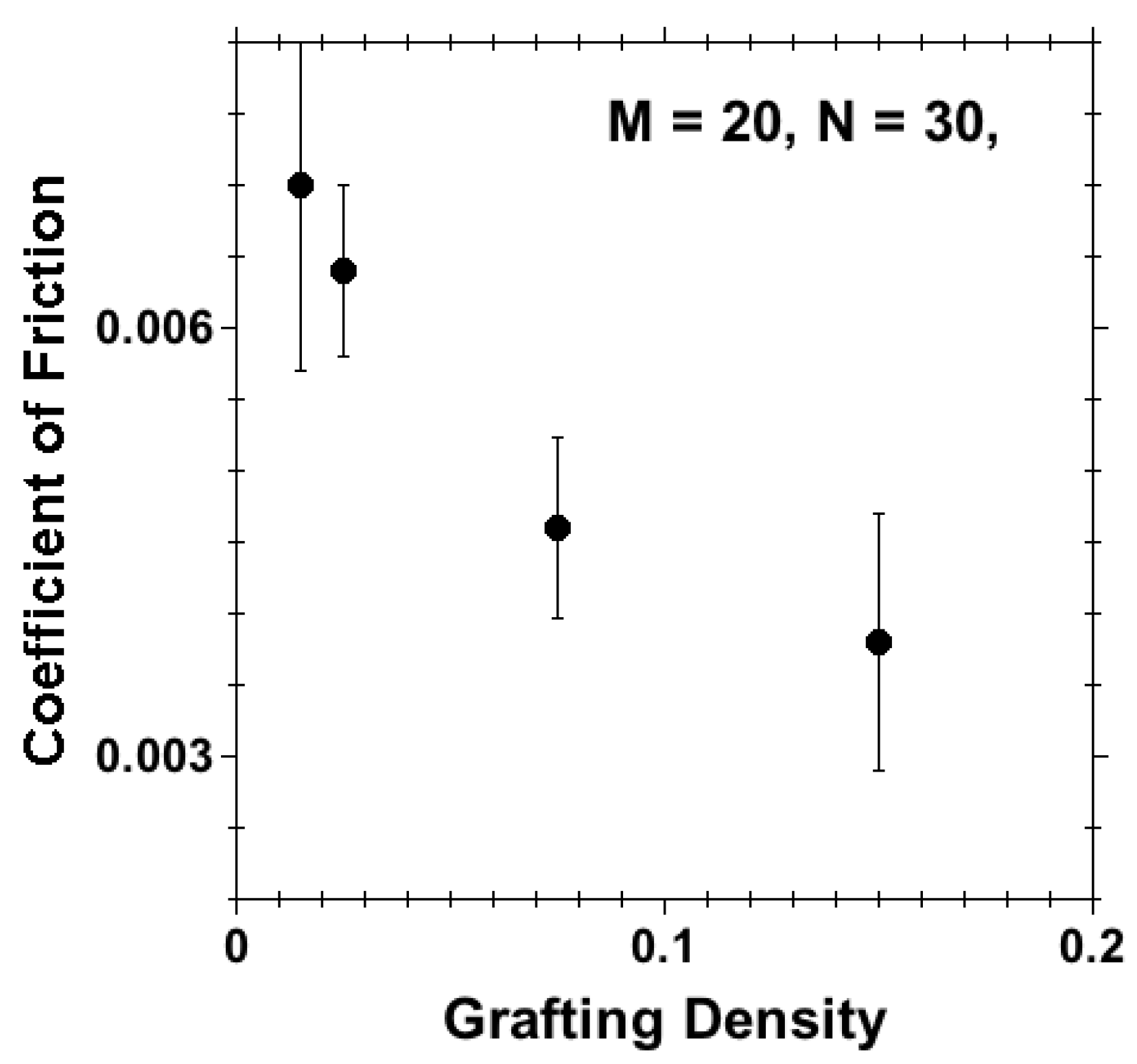
3.2.2. Effect of Grafting Density and Separation at Fixed Velocity
3.2.3. Effect of Shear Velocity for Two Grafting Densities at Fixed Separation
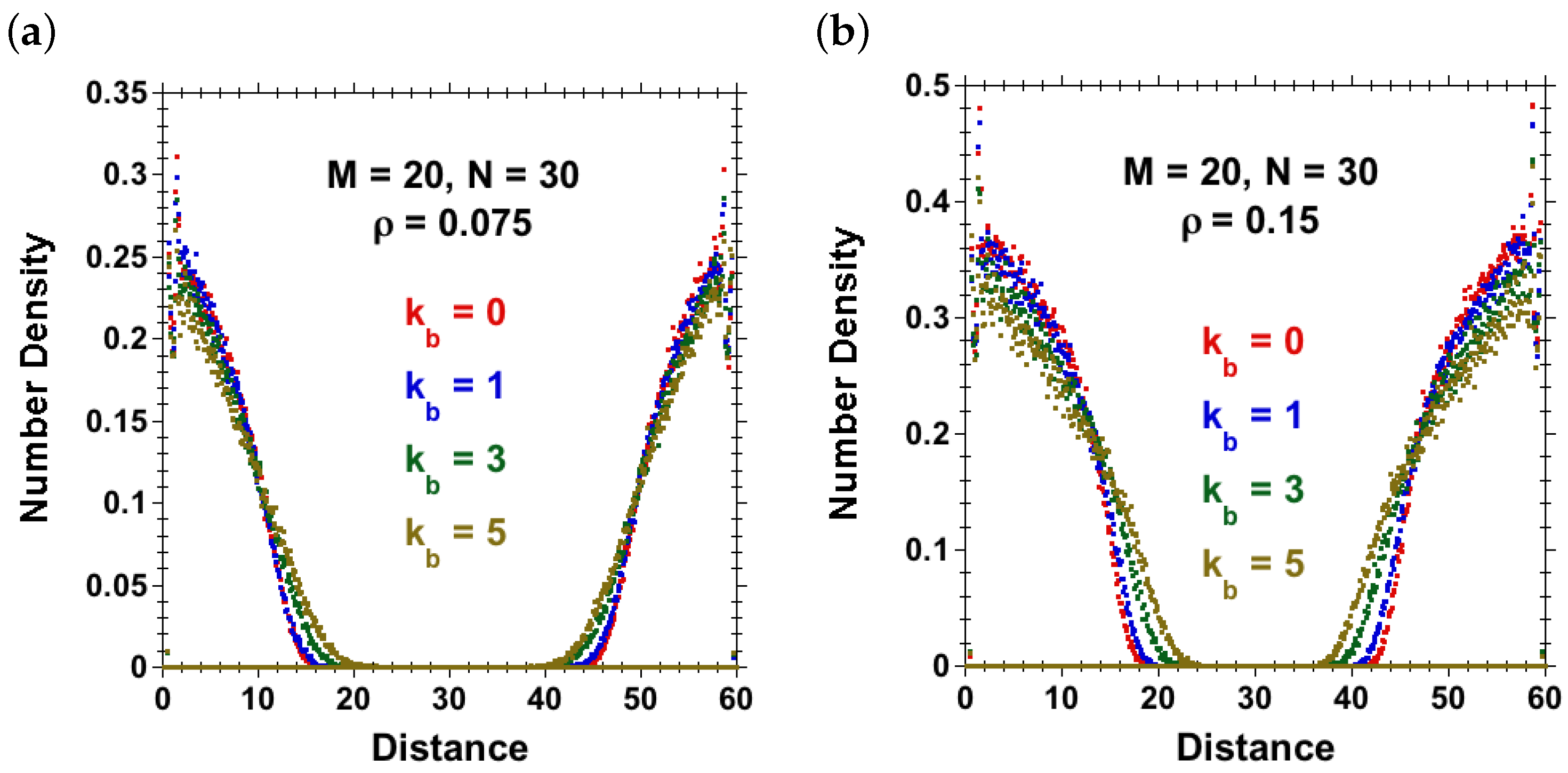
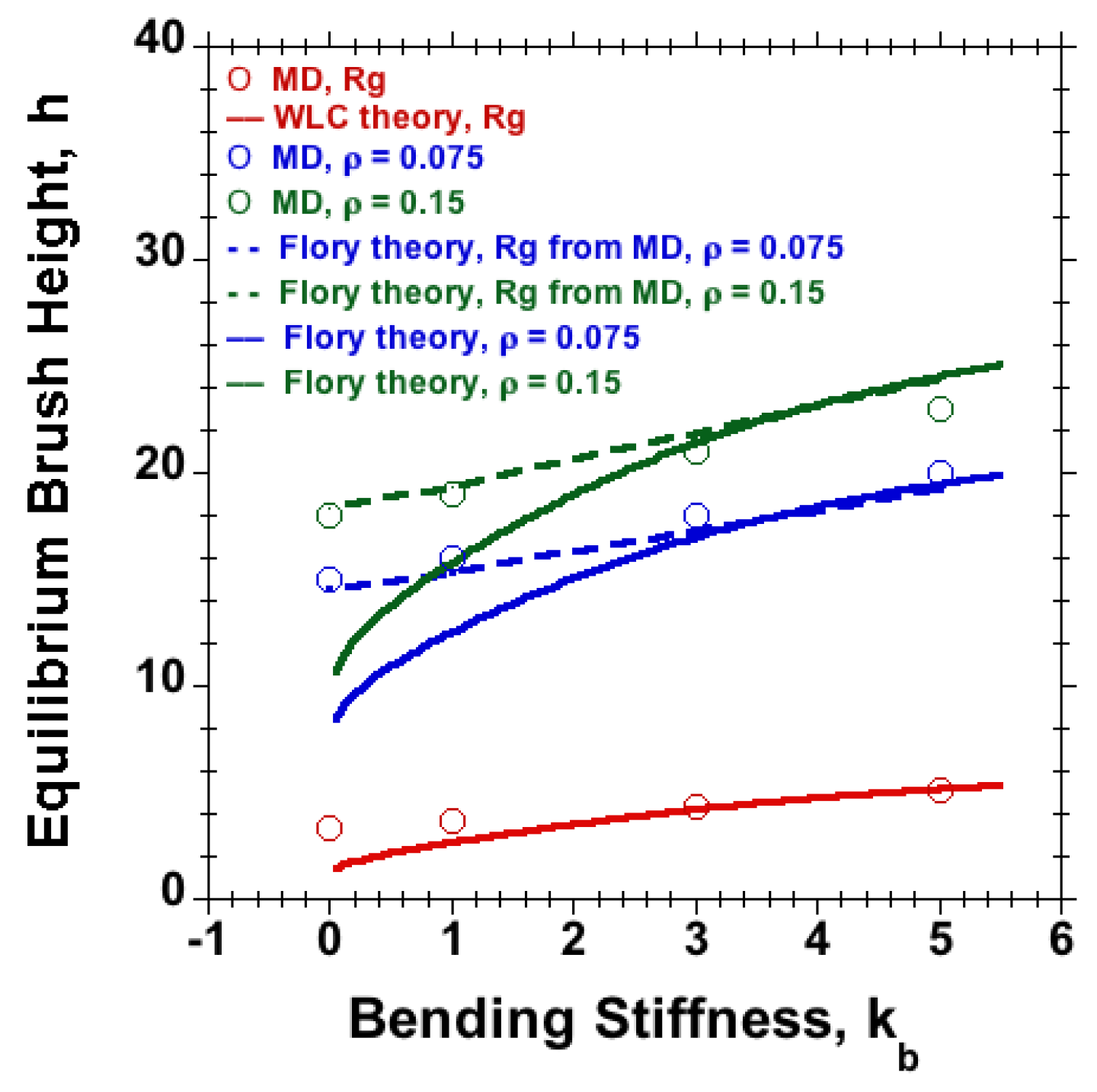
3.3. Sheared Brushes Made of Semiflexible Chains
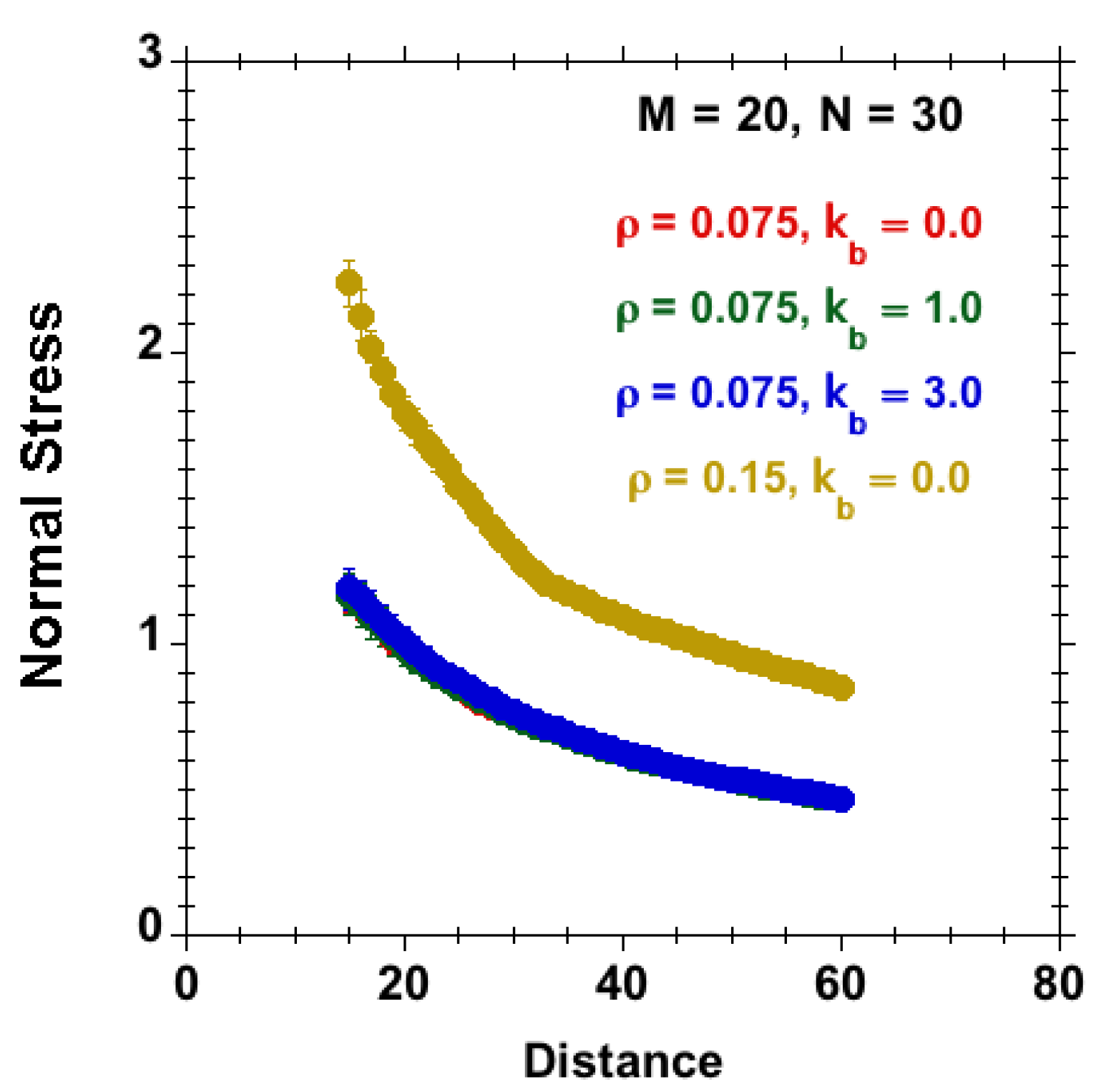
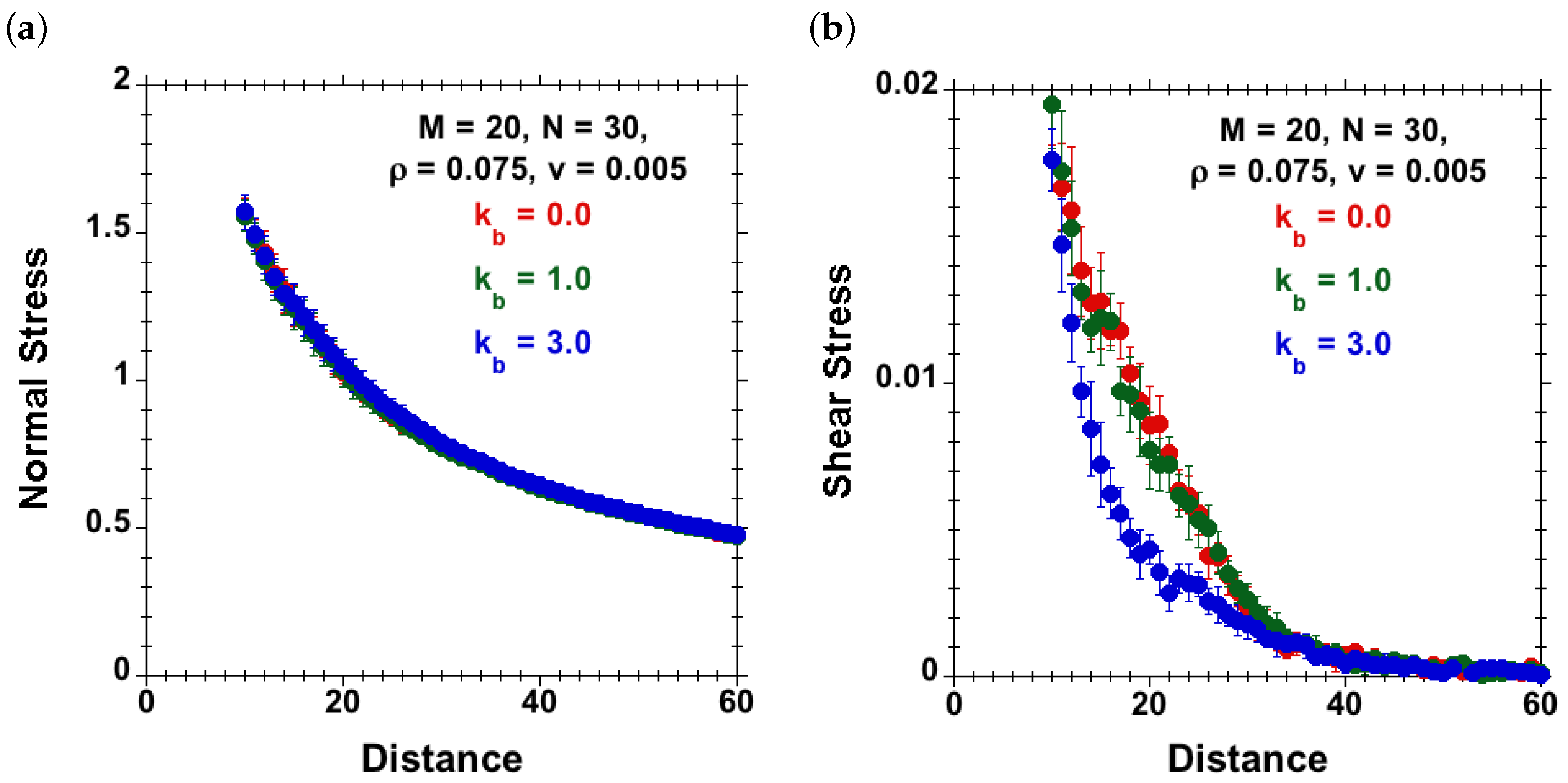
3.3.1. Effect of Chain Stiffness and Separation at Fixed Velocity and Surface Density
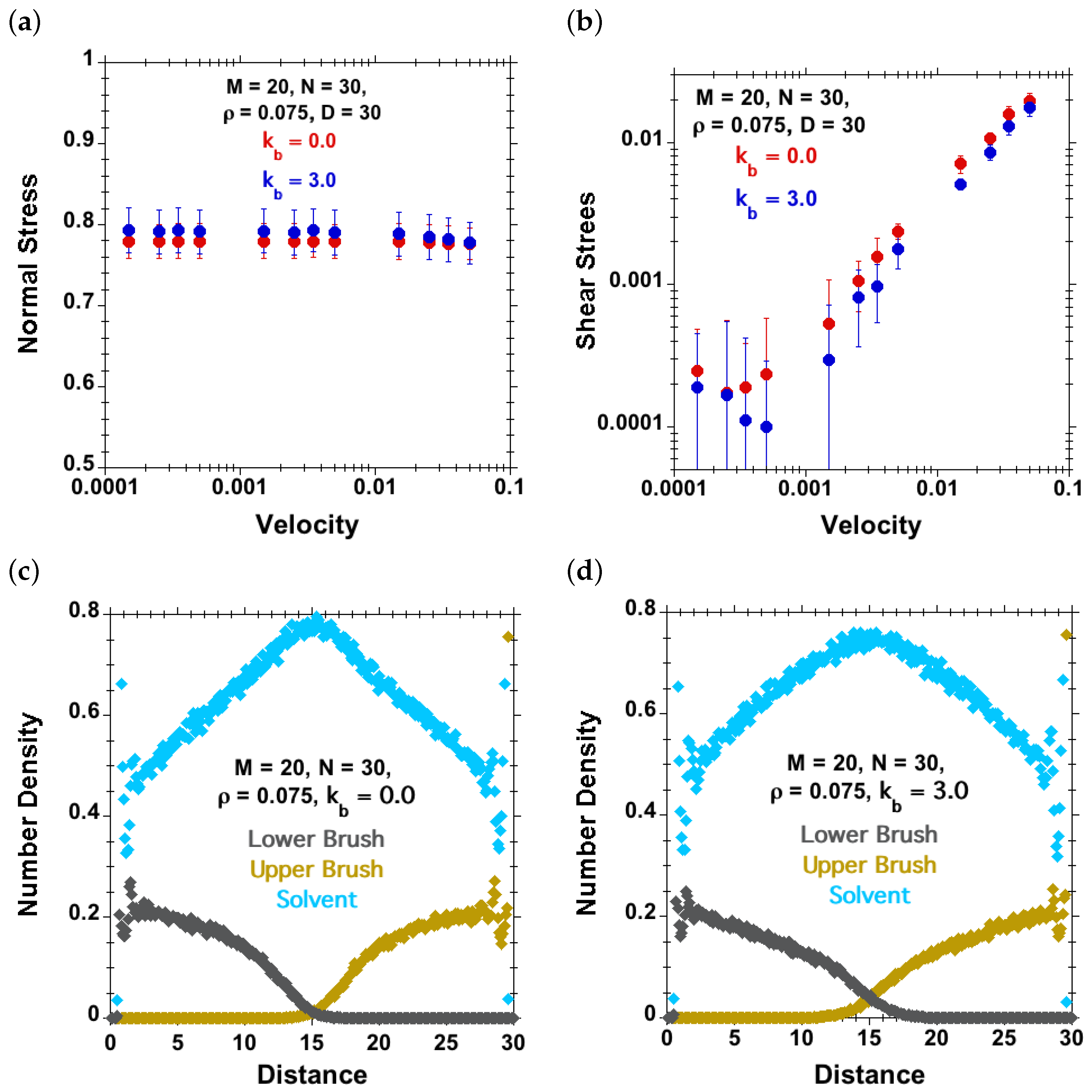
3.3.2. Effect of Velocity and Chain Stiffness at Fixed Separation and Surface Density
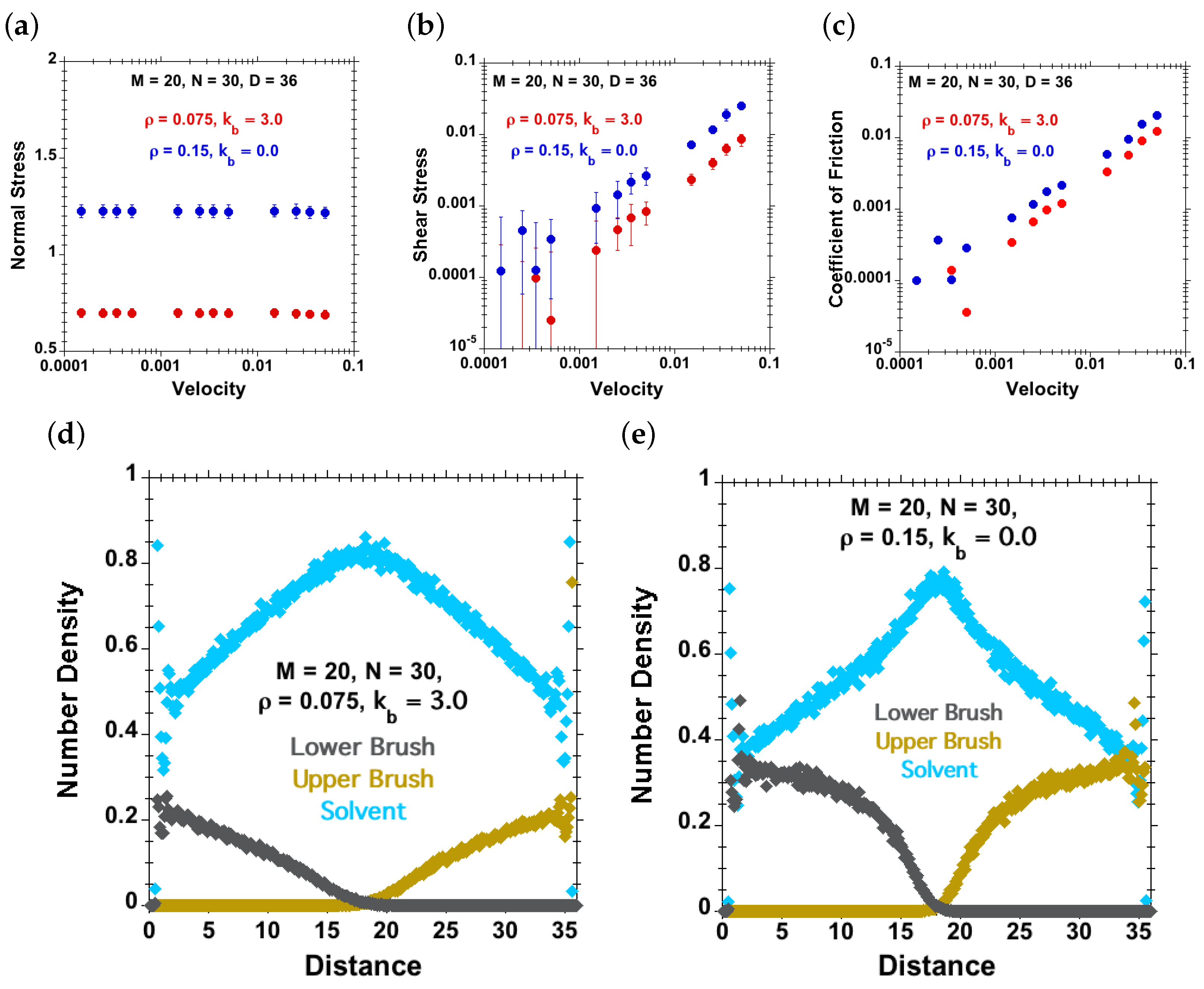
3.4. Comparing Flexible and Semiflexible Brushes of Identical Height
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Napper, D.H. Polymeric Stabilization of Colloidal Dispersions; Academic Press: London, UK, 1983. [Google Scholar]
- Hucknall, A.; Simnick, A.J.; Hill, R.T.; Chilkoti, A.; Garcia, A.; Johannes, M.S.; Clark, R.L.; Zauscher, S.; Ratner, B.D. Versatile synthesis and micropatterning of nonfouling polymer brushes on the wafer scale. Biointerphases 2009, 4, FA50–FA57. [Google Scholar] [CrossRef] [PubMed]
- Auroy, P.; Auvray, L.; Leger, L. Characterization of the brush regime for grafted polymer layers at the solid-liquid interface. Phys. Rev. Lett. 1991, 66, 719–722. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Spencer, N.D. Achieving ultralow friction by aqueous, brush-assisted lubrication. In Superlubricity; Erdemir, A., Martin, J.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 365–396. [Google Scholar]
- Li, A. Structure-Property Relationships of Surface-Grafted Polymeric Architectures: From Ultra-Thin Films to Quasi-3D Polymer Assemblies. Ph.D. Thesis, ETH Zurich, Switzerland, 2013. [Google Scholar]
- Raviv, U.; Klein, J. Adhesion, friction, and lubrication between polymer-bearing surfaces. In Polymer Science: A Comprehensive Reference; Matya, K., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 607–628. [Google Scholar]
- Klein, J.; Perahia, D.; Warburg, S. Forces between polymer-bearing surfaces undergoing shear. Nature 1991, 352, 143–145. [Google Scholar] [CrossRef]
- Klein, J.; Kumacheva, E.; Perahia, D.; Mahalu, D.; Warburg, S. Interfacial sliding of polymer-bearing surfaces. Faraday Discuss. 1994, 98, 173. [Google Scholar] [CrossRef]
- Klein, J.; Kumacheva, E.; Mahaiu, D.; Perahia, D.; Fetters, L.J. Reduction of frictional forces between solid surfaces bearing polymer brushes. Nature 1994, 370, 634–636. [Google Scholar] [CrossRef]
- Nalam, P.C.; Ramakrishna, S.N.; Espinosa-Marzal, R.M.; Spencer, N.D. Exploring lubrication regimes at the nanoscale: Nanotribological characterization of silica and polymer brushes in viscous solvents. Langmuir 2013, 29, 10149–10158. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Spencer, N.D. Sweet, hairy, soft, and slippery. Science 2008, 319, 575–576. [Google Scholar] [CrossRef] [PubMed]
- Grest, G.S. Computer simulations of shear and friction between polymer brushes. Curr. Opin. Colloid Interf. Sci. 1997, 2, 271–277. [Google Scholar] [CrossRef]
- Hoy, R.S.; Grest, G.S. Entanglements of an end-grafted polymer brush in a polymeric matrix. Macromolecules 2007, 40, 8389–8395. [Google Scholar] [CrossRef]
- Grest, G.S. Grafted polymer brushes: A constant surface pressure molecular dynamics simulation. Macromolecules 1994, 27, 418–426. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Grest, G. Interfacial sliding of polymer brushes: A molecular dynamics simulation. Phys. Rev. Lett. 1996, 76, 4979–4982. [Google Scholar] [CrossRef] [PubMed]
- Murat, M.; Grest, G.S. Molecular dynamics simulations of the force between a polymer brush and an AFM tip. Macromolecules 1996, 29, 8282–8284. [Google Scholar] [CrossRef]
- Grest, G.S. Normal and shear forces between polymer brushes. Adv. Polym. Sci. 1999, 138, 149–183. [Google Scholar]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Kröger, M.; Spencer, N.D. Polymer brushes under shear: Molecular dynamics simulations compared to experiments. Langmuir 2015, 31, 4798–4805. [Google Scholar] [CrossRef] [PubMed]
- Galuschko, A.; Spirin, L.; Kreer, T.; Johner, A.; Pastorino, C.; Wittmer, J.; Baschnagel, J. Frictional forces between strongly compressed, nonentangled polymer brushes: Molecular dynamics simulations and scaling theory. Langmuir 2010, 26, 6418–6429. [Google Scholar] [CrossRef] [PubMed]
- De Beer, S.; Müser, M.H. Alternative dissipation mechanisms and the effect of the solvent in friction between polymer brushes on rough surfaces. Soft Matter 2013, 9, 7234–7241. [Google Scholar] [CrossRef]
- De Beer, S.; Kutnyanszky, E.; Schön, P.M.; Vancso, G.J.; Müser, M.H. Solvent-induced immiscibility of polymer brushes eliminates dissipation channels. Nat. Commun. 2014, 5, 3781. [Google Scholar] [CrossRef] [PubMed]
- Nalam, P.C. Polymer Brushes in Aqueous Solvent Mixtures: Impact of Polymer Conformation on Tribological Properties. Ph.D. Thesis, ETH Zurich, Switzerland, 2012. [Google Scholar]
- Tsujii, Y.; Nomura, A.; Okayasu, K.; Gao, W.; Ohno, K.; Fukuda, T. AFM studies on microtribology of concentrated polymer brushes in solvents. J. Phys. Conf. Ser. 2009, 184, 012031. [Google Scholar] [CrossRef]
- Nomura, A.; Okayasu, K.; Ohno, K.; Fukuda, T.; Tsujii, Y. Lubrication mechanism of concentrated polymer brushes in solvents: Effect of solvent quality and thereby swelling state. Macromolecules 2011, 44, 5013–5019. [Google Scholar] [CrossRef]
- Rosenberg, K.J.; Goren, T.; Crockett, R.; Spencer, N.D. Load-induced transitions in the lubricity of adsorbed poly(L-lysine)—G-dextran as a function of polysaccharide chain density. ACS Appl. Mater. Interf. 2011, 3, 3020–3025. [Google Scholar] [CrossRef] [PubMed]
- Drobek, T.; Spencer, N.D. Nanotribology of surface-grafted PEG layers in an aqueous environemnt. Langmuir 2008, 24, 1484–1488. [Google Scholar] [CrossRef] [PubMed]
- Alexander, S. Adsorption of chain molecules with a polar head a scaling description. J. Phys. France 1977, 38, 983–987. [Google Scholar] [CrossRef]
- De Gennes, P.G. Conformations of polymers attached to an interference. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Semenov, A.N. Contribution to the theory of microphase layering in block-copolymer melts. Sov. Phys. JETP 1985, 61, 733–742. [Google Scholar]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Zhulina, Y.B.; Pryamitsyn, V.A.; Borisov, O.V. Structure and conformational transitions in grafted polymer chain layers. A new theory. Polym. Sci. USSR 1989, 31, 205–216. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479–3501. [Google Scholar] [CrossRef] [PubMed]
- Binder, K.; Müller, M. Monte Carlo simulation of block copolymers. Curr. Opin. Colloid Interf. Sci. 2000, 5, 315–323. [Google Scholar] [CrossRef]
- Hsu, H.P.; Paul, W. A fast Monte Carlo algorithm for studying bottle-brush polymers. Comput. Phys. Commun. 2011, 182, 2115–2121. [Google Scholar] [CrossRef]
- Binder, K.; Müller, M.; Schmid, M.; Werner, F. Interfaces in partly compatible polymer mixtures: A Monte-Carlo simulation approach. Physica A 1998, 249, 293–300. [Google Scholar] [CrossRef]
- Doyle, P.S.; Shaqfeh, E.; Gast, A.P. Rheology of polymer brushes: A Brownian dynamics study. Macromolecules 1998, 31, 5474–5486. [Google Scholar] [CrossRef]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. The kinetic friction coefficient of neutral and charged polymer brushes. Soft Matter 2013, 9, 2966. [Google Scholar] [CrossRef]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Kröger, M.; Spencer, N.D. Effect of crosslinking on the microtribological behavior of model polymer brushes. Tribol. Lett. 2016, 63, 17. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K. Polymer brushes in solvents of variable quality: Molecular dynamics simulations using explicit solvent. J. Chem. Phys. 2007, 127, 084905. [Google Scholar] [CrossRef] [PubMed]
- Erbas, A.; Paturej, J. Friction between ring polymer brushes. Soft Matter 2015, 11, 3139–3148. [Google Scholar] [CrossRef] [PubMed]
- Carrillo, J.M.Y.; Russano, D.; Dobrynin, A.V. Friction between brush layers of charged and neutral bottle-brush macromolecules. Molecular dynamics simulations. Langmuir 2011, 27, 14599–14608. [Google Scholar] [CrossRef] [PubMed]
- Carrillo, J.M.Y.; Brown, W.M.; Dobrynin, A.V. Explicit solvent simulations of friction between brush layers of charged and neutral bottle-brush macromolecules. Macromolecules 2012, 45, 8880–8891. [Google Scholar] [CrossRef]
- Speyer, K.; Pastorino, C. Brushes of semiflexible polymers in equilibrium and under flow in a super-hydrophobic regim. Soft Matter 2015, 11, 5473–5484. [Google Scholar] [CrossRef] [PubMed]
- Doig, M.; Warrens, C.P.; Camp, P.J. Structure and friction of stearic acid and oleic acid films adsorbed on iron oxide surfaces in squalane. Langmuir 2014, 30, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.P.; Gattoni, C.; Morgan, N.; Spikes, H.A.; Dini, D. Nonequilibrium molecular dynamics simulations of organic friction modifiers adsorbed on iron oxide surfaces. Langmuir 2016, 32, 4450–4463. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, C.D.; Webb, E.B.; Stevens, M.J.; Chandross, M.; Grest, G.S. Frictional dynamics of perfluorinated self-assembled monolayers on amorphous SiO2. Tribo. Lett. 2005, 19, 93–99. [Google Scholar] [CrossRef]
- Soddemann, T. Non–Equilibrium Molecular Dynamics Study of an Amphiphilic Model System. Ph.D. Thesis, University Mainz, Mainz, Germany, 2001. [Google Scholar]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Hess, S.; Kröger, M.; Voigt, H. Thermo-mechanical properties of the WCA-Lennard-Jones model system in its fluid and solid states. Physica A 1998, 250, 58–82. [Google Scholar] [CrossRef]
- Kozuch, D.J.; Zhang, W.; Milner, S.T. Predicting the Flory-Huggins χ parameter for polymers with stiffness mismatch from molecular dynamics simulations. Polymers 2016, 8, 241. [Google Scholar] [CrossRef]
- Kröger, M.; Loose, W.; Hess, S. Rheology and structural changes of polymer melts via nonequilibrium molecular dynamics. J. Rheol. 1993, 37, 1057–1079. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, MI, USA, 1987. [Google Scholar]
- Bernardi, S.; Todd, B.D.; Searles, D.J. Thermostating highly confined fluids. J. Chem. Phys. 2010, 132, 244706. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Semiflexible chains. Basics, facts, theory and simulation. A review. Polymers 2016. in preparation. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Kröger, M. Models for Polymeric and Anisotropic Liquids; Springer: Berlin, Germany, 2005. [Google Scholar]
- Galuschko, A. Molecular Dynamics Simulations of Sheared Polymer Brushes. Ph.D. Thesis, Strasbourg University, Strasbourg, France, 2010. [Google Scholar]
- Hess, S.; Kröger, M. Elastic and plastic behavior of model solids. Tech. Mech. 2002, 22, 79–88. [Google Scholar]
- Gattinoni, C.; Mackowiak, S.; Heyes, D.M.; Branka, A.C.; Dini, D. Boundary-controlled barostats for slab geometries in molecular dynamics simulations. Phys. Rev. E 2014, 90, 043302. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.K. Simulation and Experimental Studies of Polymer Brushes Under Shear. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2016. [Google Scholar]
- Espinosa-Marzal, R.M.; Nalam, P.C.; Bolisetty, S.; Spencer, N.D. Impact of solvation on equilibrium conformation of polymer brushes in solvent mixtures. Soft Matter 2013, 9, 4045–4057. [Google Scholar] [CrossRef]
- Kröger, M.; Peleg, O.; Halperin, A. From dendrimers to dendronized polymers and forests: Scaling theory and its limitations. Macromolecules 2010, 43, 6213–6224. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN 77; Cambridge University Press: Cambridge, UK, 1992; Volume 1. [Google Scholar]

| Grafting density | Velocity range | Separation | Relaxation time | Weissenberg numbers |
|---|---|---|---|---|
| ρ | v | D | Wi | |
| 0.015 | 0.001 | 12–24 | 325–262 | 0.054–0.022 |
| 0.025 | 0.001 | 13–26 | 371–299 | 0.056–0.024 |
| 0.075 | 0.001 | 15–30 | 499–403 | 0.066–0.026 |
| 0.15 | 0.001 | 18–36 | 585–472 | 0.066–0.026 |
| Grafting density | Velocity range | Separation | Relaxation time | Weissenberg numbers |
|---|---|---|---|---|
| ρ | v | D | Wi | |
| 0.075 | 0.00015–0.05 | 20 | 457 | 0.00686–2.28 |
| 0.075 | 0.00015–0.05 | 30 | 403 | 0.004–1.34 |
| 0.075 | 0.00015–0.05 | 40 | 368 | 0.0028–0.92 |
| 0.15 | 0.00015–0.05 | 30 | 499 | 0.005–1.66 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Spencer, N.D.; Kröger, M. Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study. Polymers 2016, 8, 254. https://doi.org/10.3390/polym8070254
Singh MK, Ilg P, Espinosa-Marzal RM, Spencer ND, Kröger M. Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study. Polymers. 2016; 8(7):254. https://doi.org/10.3390/polym8070254
Chicago/Turabian StyleSingh, Manjesh K., Patrick Ilg, Rosa M. Espinosa-Marzal, Nicholas D. Spencer, and Martin Kröger. 2016. "Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study" Polymers 8, no. 7: 254. https://doi.org/10.3390/polym8070254
APA StyleSingh, M. K., Ilg, P., Espinosa-Marzal, R. M., Spencer, N. D., & Kröger, M. (2016). Influence of Chain Stiffness, Grafting Density and Normal Load on the Tribological and Structural Behavior of Polymer Brushes: A Nonequilibrium-Molecular-Dynamics Study. Polymers, 8(7), 254. https://doi.org/10.3390/polym8070254