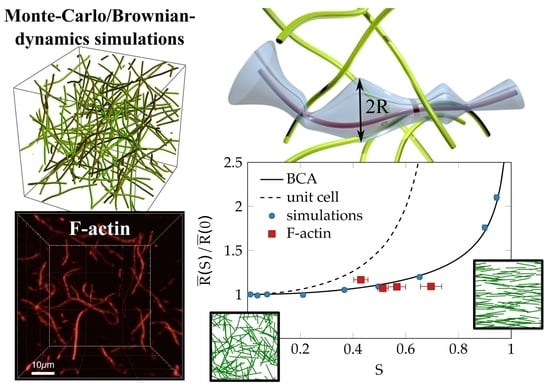
Microstructure of Sheared Entangled Solutions of Semiflexible Polymers
Abstract
:1. Introduction
2. Results and Discussion
2.1. Tube Alignment
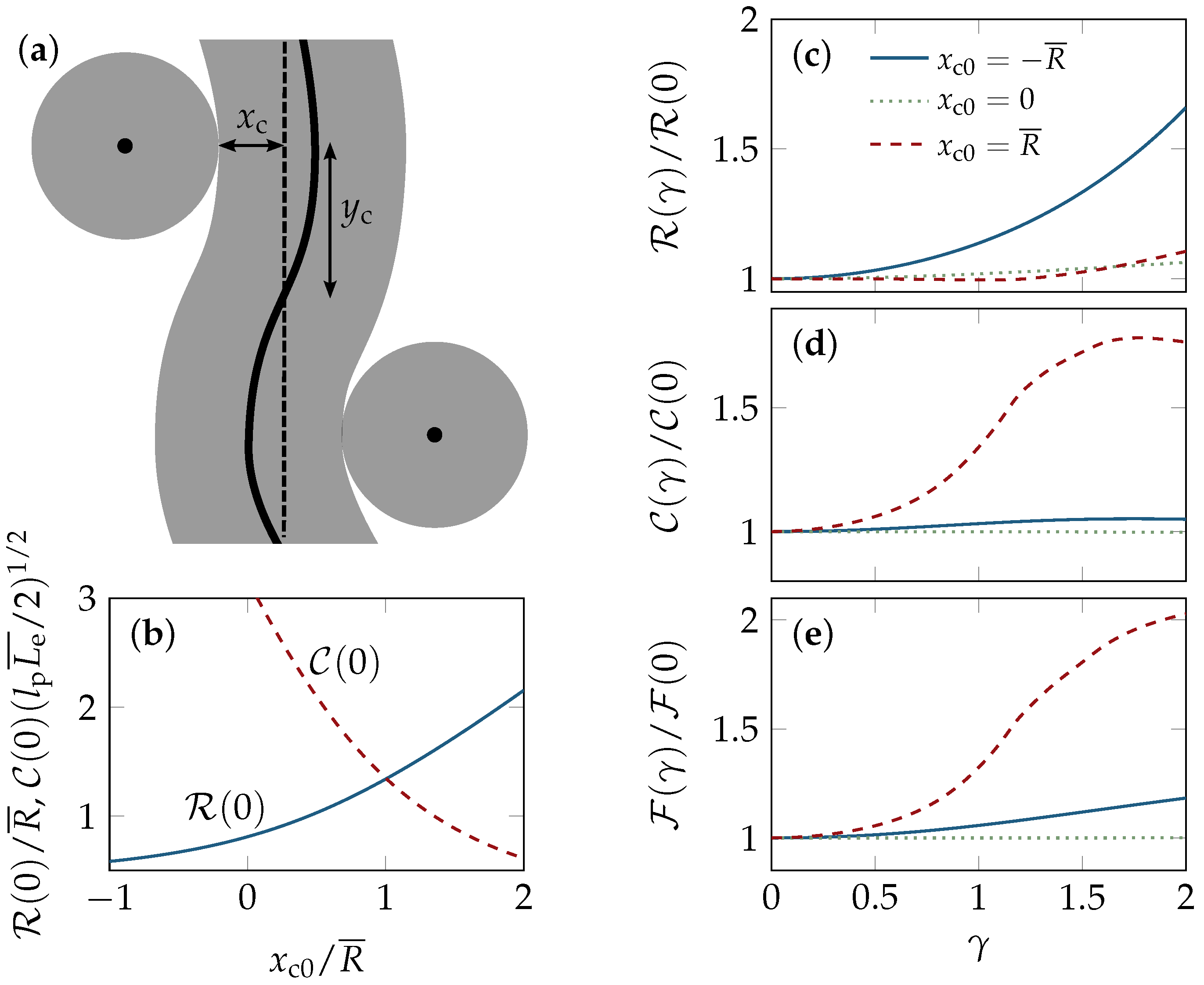
2.2. Tube Deformation
2.3. Experiments and Simulations
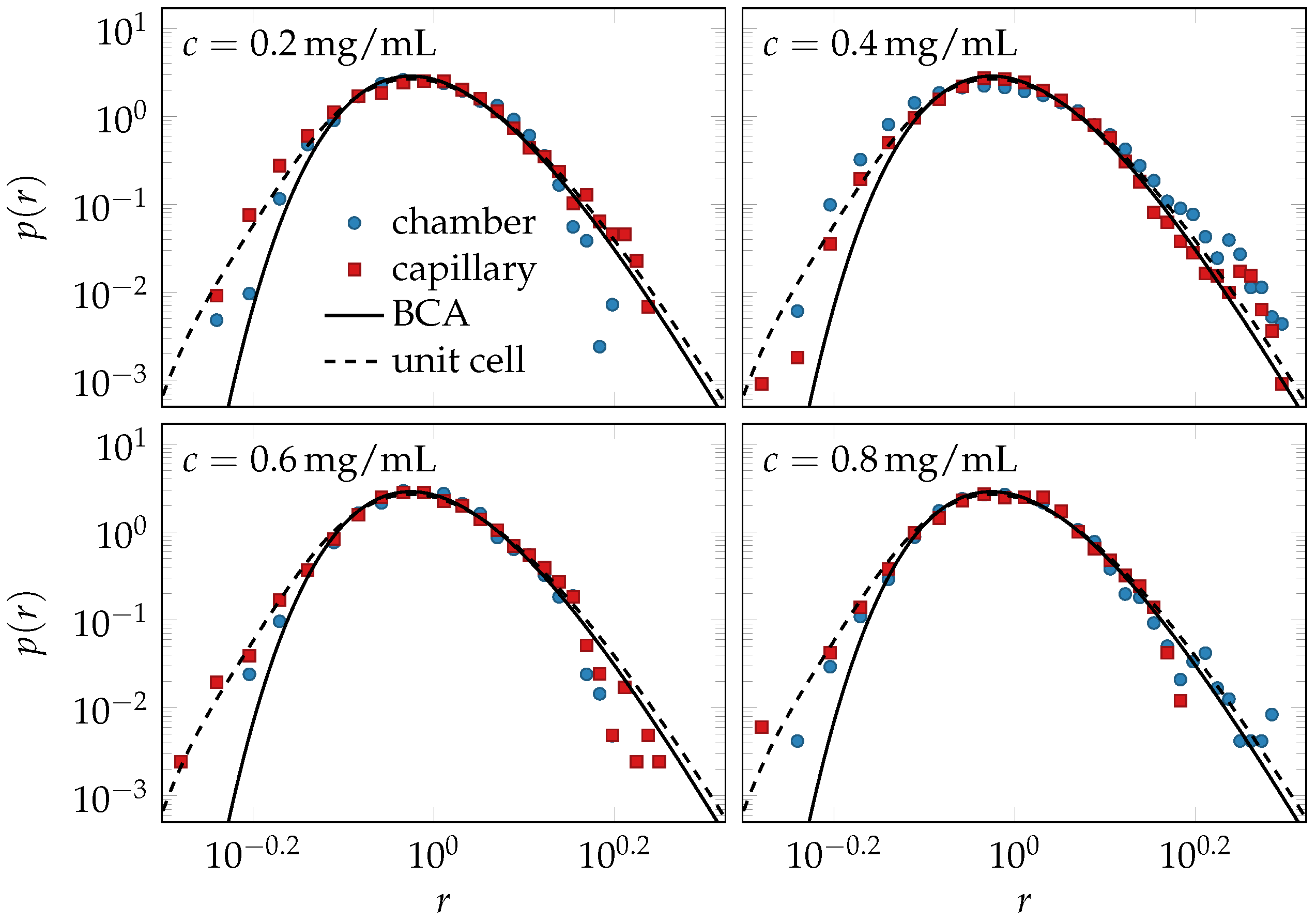
2.4. Comparison of Theory and Data
3. Conclusions
4. Materials and Methods
4.1. Experiments
4.2. Simulations
4.3. Binary Collision Approximation (BCA)
4.4. Affine Strain Alignment
4.4.1. Two-Dimensional Solution
4.4.2. Three-Dimensional Solution
4.5. Unit-Cell Approach
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WLC | Wormlike chain |
| BCA | Binary collision approximation |
| MC/BD | Monte Carlo/Brownian dynamics |
References
- Kollmannsberger, P.; Fabry, B. Linear and nonlinear rheology of living cells. Annu. Rev. Mater. Res. 2011, 41, 75–97. [Google Scholar] [CrossRef]
- Pritchard, R.H.; Shery Huang, Y.Y.; Terentjev, E.M. Mechanics of biological networks: From the cell cytoskeleton to connective tissue. Soft Matter 2014, 10, 1864–1884. [Google Scholar] [CrossRef] [PubMed]
- Bausch, A.R.; Kroy, K. A bottom-up approach to cell mechanics. Nat. Phys. 2006, 2, 231–238. [Google Scholar] [CrossRef]
- Storm, C.; Pastore, J.J.; MacKintosh, F.C.; Lubensky, T.C.; Janmey, P.A. Nonlinear elasticity in biological gels. Nature 2005, 435, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Janmey, P.A.; McCulloch, C.A. Cell mechanics: Integrating cell responses to mechanical stimuli. Annu. Rev. Biomed. Eng. 2007, 9, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Kasza, K.E.; Rowat, A.C.; Liu, J.; Angelini, T.E.; Brangwynne, C.P.; Koenderink, G.H.; Weitz, D.A. The cell as a material. Curr. Opin. Cell Biol. 2007, 19, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.H.; Gardel, M.L.; Mahadevan, L.; Matsudaira, P.; Weitz, D.A. Relating microstructure to rheology of a bundled and cross-linked F-actin network in vitro. Proc. Natl. Acad. Sci. USA 2004, 101, 9636–9641. [Google Scholar] [CrossRef] [PubMed]
- Lieleg, O.; Claessens, M.M.A.E.; Bausch, A.R. Structure and dynamics of cross-linked actin networks. Soft Matter 2010, 6, 218–225. [Google Scholar] [CrossRef]
- Kurniawan, N.A.; Enemark, S.; Rajagopalan, R. The role of structure in the nonlinear mechanics of cross-linked semiflexible polymer networks. J. Chem. Phys. 2012, 136, 065101. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University: New York, NY, USA, 1988; Volume 73. [Google Scholar]
- Pearson, D.; Herbolzheimer, E.; Grizzuti, N.; Marrucci, G. Transient behavior of entangled polymers at high shear rates. J. Polym. Sci. B Polym. Phys. 1991, 29, 1589–1597. [Google Scholar] [CrossRef]
- Mhetar, V.; Archer, L. Nonlinear viscoelasticity of entangled polymeric liquids. J. Nonnewton. Fluid. Mech. 1999, 81, 71–81. [Google Scholar] [CrossRef]
- Marrucci, G. Dynamics of entanglements: A nonlinear model consistent with the Cox-Merz rule. J. Nonnewton. Fluid Mech. 1996, 62, 279–289. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Kunita, I.; Sato, K.; Tanaka, Y.; Takikawa, Y.; Orihara, H.; Nakagaki, T. Shear banding in an F-Actin solution. Phys. Rev. Lett. 2012, 109, 248303. [Google Scholar] [CrossRef] [PubMed]
- Kirchenbuechler, I.; Guu, D.; Kurniawan, N.A.; Koenderink, G.H.; Lettinga, M.P. Direct visualization of flow-induced conformational transitions of single actin filaments in entangled solutions. Nat. Commun. 2014, 5, 5060. [Google Scholar] [CrossRef] [PubMed]
- Falzone, T.T.; Blair, S.; Robertson-Anderson, R.M. Entangled F-actin displays a unique crossover to microscale nonlinearity dominated by entanglement segment dynamics. Soft Matter 2015, 11, 4418–4423. [Google Scholar] [CrossRef] [PubMed]
- Gurmessa, B.; Fitzpatrick, R.; Falzone, T.T.; Robertson-Anderson, R.M. Entanglement density tunes microscale nonlinear response of entangled Actin. Macromolecules 2016, 49, 3948–3955. [Google Scholar] [CrossRef]
- Morse, D.C. Viscoelasticity of Concentrated Isotropic Solutions of Semiflexible Polymers. 3. Nonlinear Rheology. Macromolecules 1999, 32, 5934–5943. [Google Scholar] [CrossRef]
- Fernandez, P.; Grosser, S.; Kroy, K. A unit-cell approach to the nonlinear rheology of biopolymer solutions. Soft Matter 2009, 5, 2047–2056. [Google Scholar] [CrossRef]
- Morse, D.C. Viscoelasticity of tightly entangled solutions of semiflexible polymers. Phys. Rev. E 1998, 58, R1237–R1240. [Google Scholar] [CrossRef]
- Semmrich, C.; Storz, T.; Glaser, J.; Merkel, R.; Bausch, A.R.; Kroy, K. Glass transition and rheological redundancy in F-actin solutions. Proc. Natl. Acad. Sci. USA 2007, 104, 20199–20203. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Tseng, Y.; Wirtz, D. Strain hardening of actin filament networks: Regulation by the dynamic cross-linking protein α-actinin. J. Biol. Chem. 2000, 275, 35886–35892. [Google Scholar] [CrossRef] [PubMed]
- Semmrich, C.; Larsen, R.J.; Bausch, A.R. Nonlinear mechanics of entangled F-actin solutions. Soft Matter 2008, 4, 1675–1680. [Google Scholar] [CrossRef]
- Broedersz, C.P.; MacKintosh, F.C. Modeling semiflexible polymer networks. Rev. Mod. Phys. 2014, 86, 995–1036. [Google Scholar] [CrossRef]
- Thorpe, M. Continuous deformations in random networks. J. Non-Cryst. Solids 1983, 57, 355–370. [Google Scholar] [CrossRef]
- Heussinger, C.; Frey, E. Floppy modes and nonaffine deformations in random fiber networks. Phys. Rev. Lett. 2006, 97, 105501. [Google Scholar] [CrossRef] [PubMed]
- Wyart, M.; Liang, H.; Kabla, A.; Mahadevan, L. Elasticity of floppy and stiff random networks. Phys. Rev. Lett. 2008, 101, 215501. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Licup, A.J.; Jansen, K.A.; Rens, R.; Sheinman, M.; Koenderink, G.H.; MacKintosh, F.C. Strain-controlled criticality governs the nonlinear mechanics of fibre networks. Nat. Phys. 2016, 12, 584–587. [Google Scholar] [CrossRef]
- Huisman, E.M.; Storm, C.; Barkema, G.T. Frequency-dependent stiffening of semiflexible networks: A dynamical nonaffine to affine transition. Phys. Rev. E 2010, 82, 061902. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Wen, Q.; Janmey, P.A.; Tang, J.X.; Conti, E.; MacKintosh, F.C. Nonlinear elasticity of stiff filament networks: Strain stiffening, negative normal stress, and filament alignment in fibrin gels. J. Phys. Chem. B 2009, 113, 3799–3805. [Google Scholar] [CrossRef] [PubMed]
- Vader, D.; Kabla, A.; Weitz, D.; Mahadevan, L. Strain-induced aalignment in collagen gels. PLoS ONE 2009, 4, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Harasim, M.; Wunderlich, B.; Peleg, O.; Kröger, M.; Bausch, A.R. Direct observation of the dynamics of semiflexible polymers in shear Flow. Phys. Rev. Lett. 2013, 110, 108302. [Google Scholar] [CrossRef] [PubMed]
- Huber, B.; Harasim, M.; Wunderlich, B.; Kröger, M.; Bausch, A.R. Microscopic origin of the non-newtonian viscosity of Semiflexible polymer solutions in the semidilute regime. ACS Macro Lett. 2014, 3, 136–140. [Google Scholar] [CrossRef]
- Sussman, D.M.; Schweizer, K.S. Microscopic theory of topologically entangled fluids of rigid macromolecules. Phys. Rev. E 2011, 83, 061501. [Google Scholar] [CrossRef] [PubMed]
- Lang, P.S.; Obermayer, B.; Frey, E. Dynamics of a semiflexible polymer or polymer ring in shear flow. Phys. Rev. E 2014, 89, 022606. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Levine, H.; Mao, X.; Sander, L.M. Alignment and nonlinear elasticity in biopolymer gels. Phys. Rev. E 2015, 91, 042710. [Google Scholar] [CrossRef] [PubMed]
- Foucard, L.C.; Price, J.K.; Klug, W.S.; Levine, A.J. Cooperative buckling and the nonlinear mechanics of nematic semiflexible networks. Nonlinearity 2015, 28, R89. [Google Scholar] [CrossRef]
- Alvarado, J.; Mulder, B.M.; Koenderink, G.H. Alignment of nematic and bundled semiflexible polymers in cell-sized confinement. Soft Matter 2014, 10, 2354–2364. [Google Scholar] [CrossRef] [PubMed]
- Münster, S.; Jawerth, L.M.; Leslie, B.A.; Weitz, J.I.; Fabry, B.; Weitz, D.A. Strain history dependence of the nonlinear stress response of fibrin and collagen networks. Proc. Natl. Acad. Sci. USA 2013, 110, 12197–12202. [Google Scholar] [CrossRef] [PubMed]
- Morse, D.C. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 1. Model and stress tensor. Macromolecules 1998, 31, 7030–7043. [Google Scholar] [CrossRef]
- Morse, D.C. Tube diameter in tightly entangled solutions of semiflexible polymers. Phys. Rev. E 2001, 63, 031502. [Google Scholar] [CrossRef] [PubMed]
- Glaser, J.; Kroy, K. Tube-width fluctuations of entangled stiff polymers. Phys. Rev. E 2011, 84, 051801. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Sussman, D.; Schweizer, K. Microscopic theory of the tube confinement potential for liquids of topologically entangled rigid macromolecules. Phys. Rev. Lett. 2011, 107, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Szamel, G. Reptation as a dynamic mean-field theory: Study of a simple model of rodlike polymers. Phys. Rev. Lett. 1993, 70, 3744–3747. [Google Scholar] [CrossRef] [PubMed]
- Glaser, J.; Chakraborty, D.; Kroy, K.; Lauter, I.; Degawa, M.; Kirchgeßner, N.; Hoffmann, B.; Merkel, R.; Giesen, M. Tube width fluctuations in F-Actin solutions. Phys. Rev. Lett. 2010, 105, 037801. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1344. [Google Scholar] [CrossRef]
- Schöbl, S.; Sturm, S.; Janke, W.; Kroy, K. Persistence-length renormalization of polymers in a crowded environment of hard disks. Phys. Rev. Lett. 2014, 113, 238302. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, S. Study of Dynamics and Viscoelasticity in Entangled Solutions of Semiflexible Polymers by Brownian Dynamics Simulations. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2006. [Google Scholar]
- Ramanathan, S.; Morse, D.C. Simulations of dynamics and viscoelasticity in highly entangled solutions of semiflexible rods. Phys. Rev. E 2007, 76, 010501. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, S.; Morse, D.C. Brownian dynamics algorithm for entangled wormlike threads. J. Chem. Phys. 2007, 126, 094906. [Google Scholar] [CrossRef] [PubMed]
- Romanowska, M.; Hinsch, H.; Kirchgeßner, N.; Giesen, M.; Degawa, M.; Hoffmann, B.; Frey, E.; Merkel, R. Direct observation of the tube model in F-actin solutions: Tube dimensions and curvatures. Europhys. Lett. 2009, 86, 26003. [Google Scholar] [CrossRef]
- Doi, M.; Kuzuu, N.Y. Nonlinear elasticity of rodlike macromolecules in condensed state. J. Polym. Sci. B Polym. Phys. 1980, 18, 409–419. [Google Scholar] [CrossRef]
- Larson, R.; Desai, P.S. Modeling the rheology of polymer melts and solutions. Annu. Rev. Fluid Mech. 2015, 47, 47–65. [Google Scholar] [CrossRef]
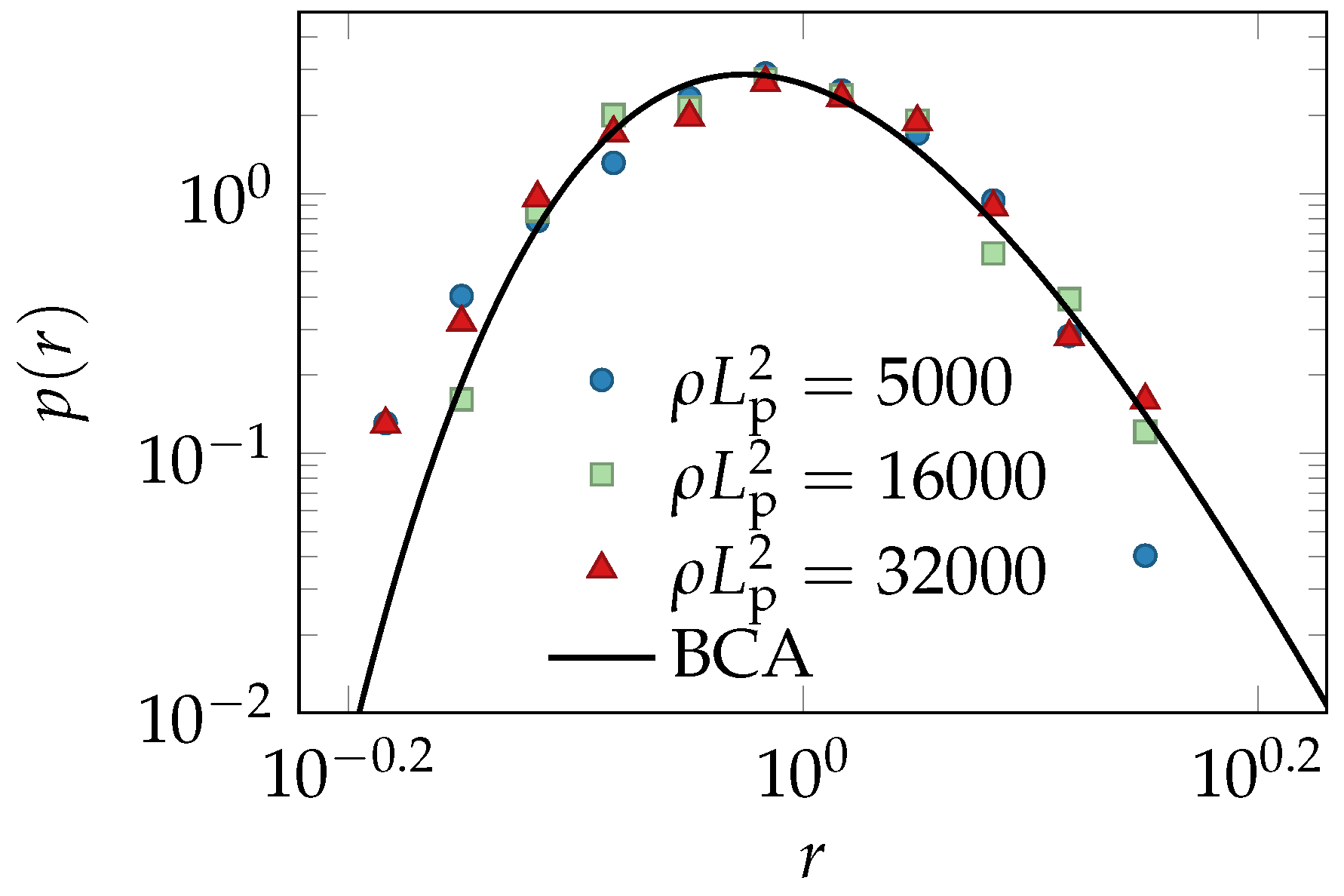
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lämmel, M.; Jaschinski, E.; Merkel, R.; Kroy, K. Microstructure of Sheared Entangled Solutions of Semiflexible Polymers. Polymers 2016, 8, 353. https://doi.org/10.3390/polym8100353
Lämmel M, Jaschinski E, Merkel R, Kroy K. Microstructure of Sheared Entangled Solutions of Semiflexible Polymers. Polymers. 2016; 8(10):353. https://doi.org/10.3390/polym8100353
Chicago/Turabian StyleLämmel, Marc, Evelin Jaschinski, Rudolf Merkel, and Klaus Kroy. 2016. "Microstructure of Sheared Entangled Solutions of Semiflexible Polymers" Polymers 8, no. 10: 353. https://doi.org/10.3390/polym8100353
APA StyleLämmel, M., Jaschinski, E., Merkel, R., & Kroy, K. (2016). Microstructure of Sheared Entangled Solutions of Semiflexible Polymers. Polymers, 8(10), 353. https://doi.org/10.3390/polym8100353