Role of Bending Energy and Knot Chirality in Knot Distribution and Their Effective Interaction along Stretched Semiflexible Polymers
Abstract
:1. Introduction
2. Materials and Methods
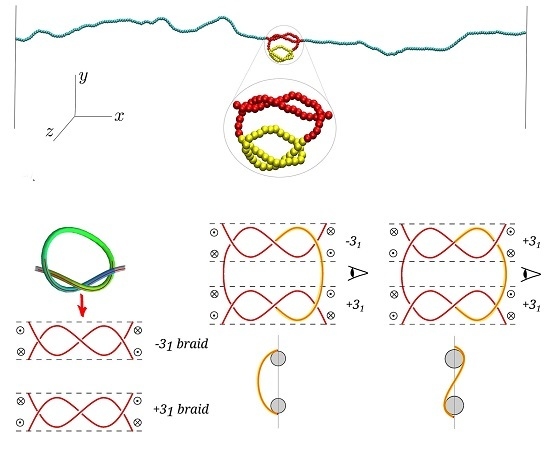
Model and Simulation Methodology
3. Results
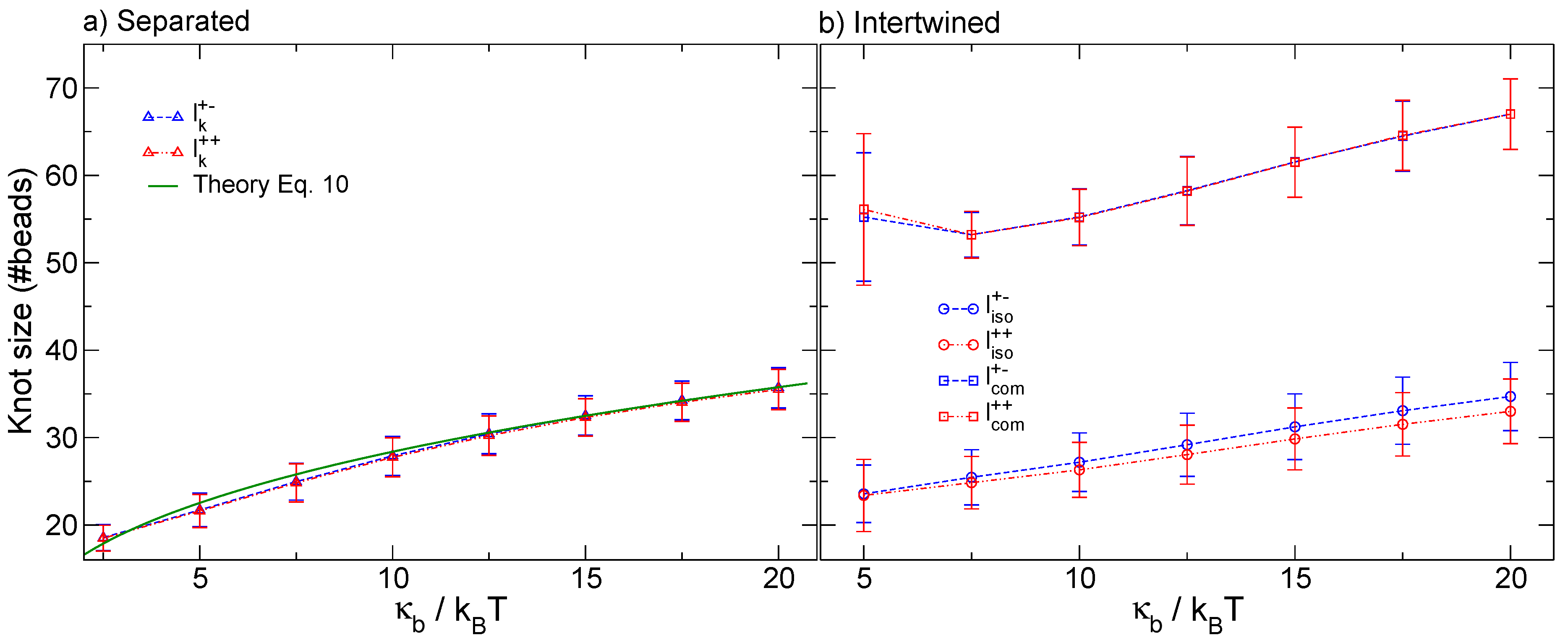
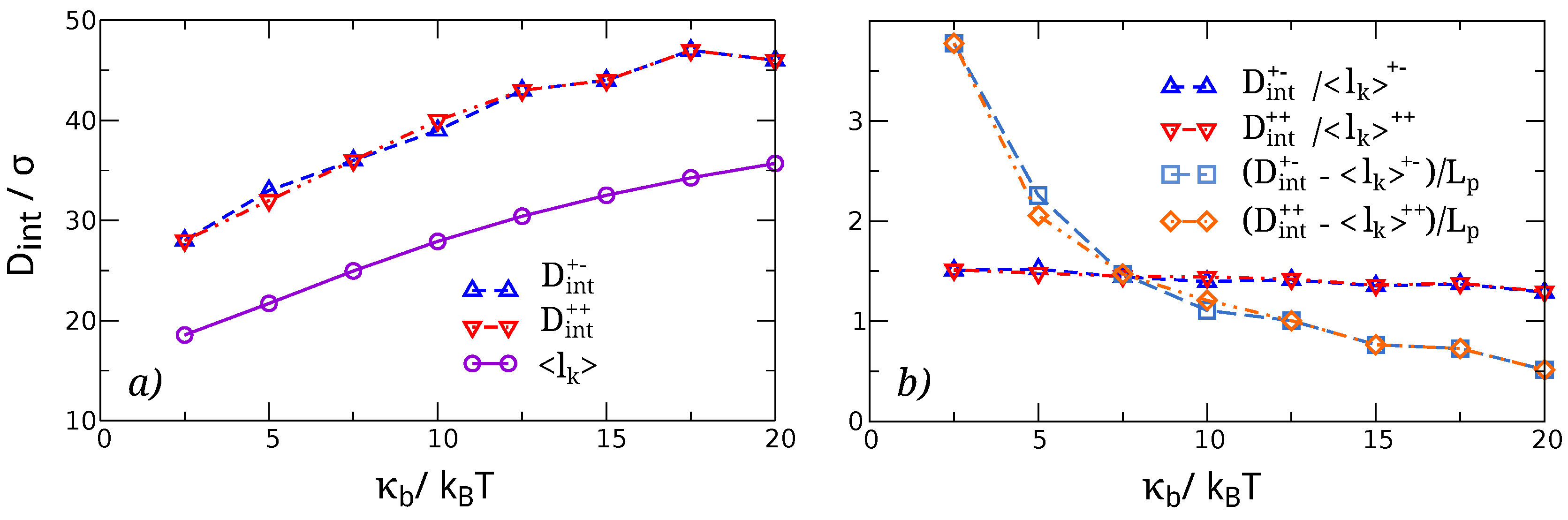
3.1. Knots Sizes
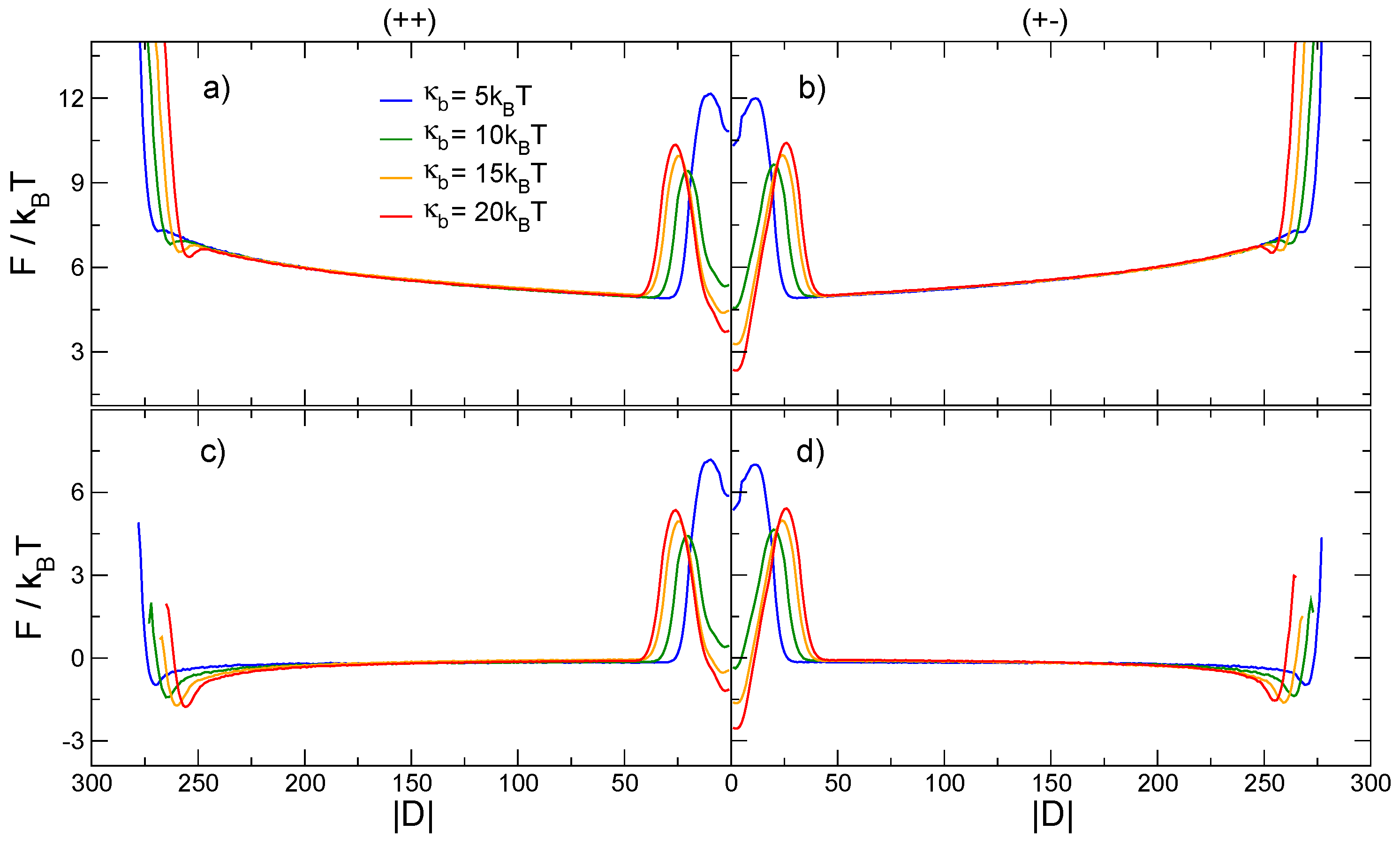
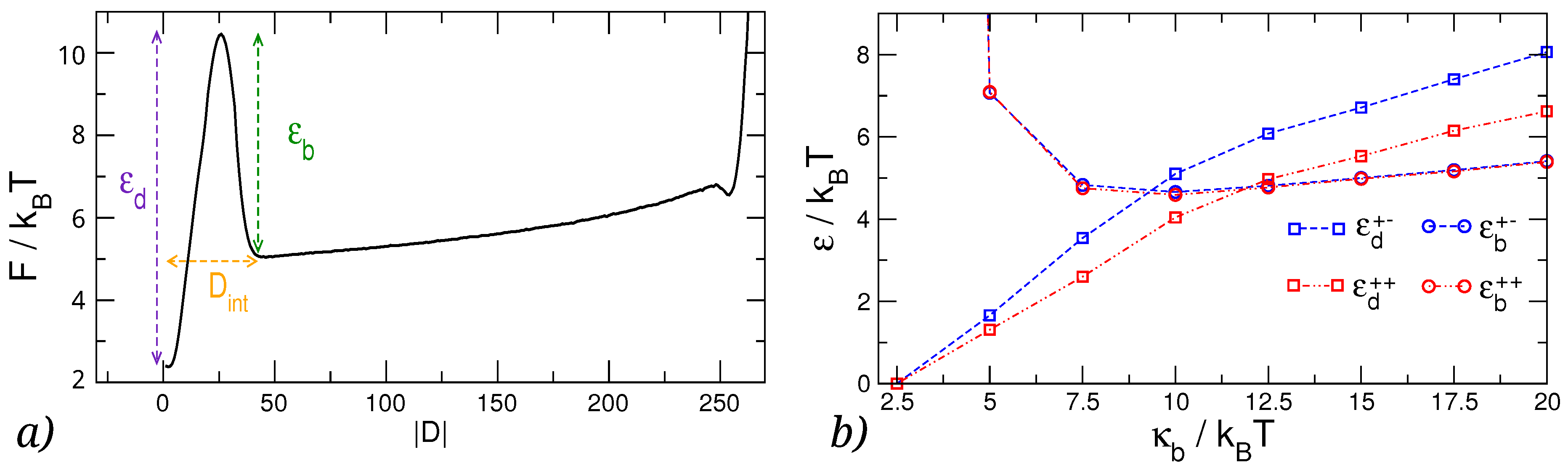
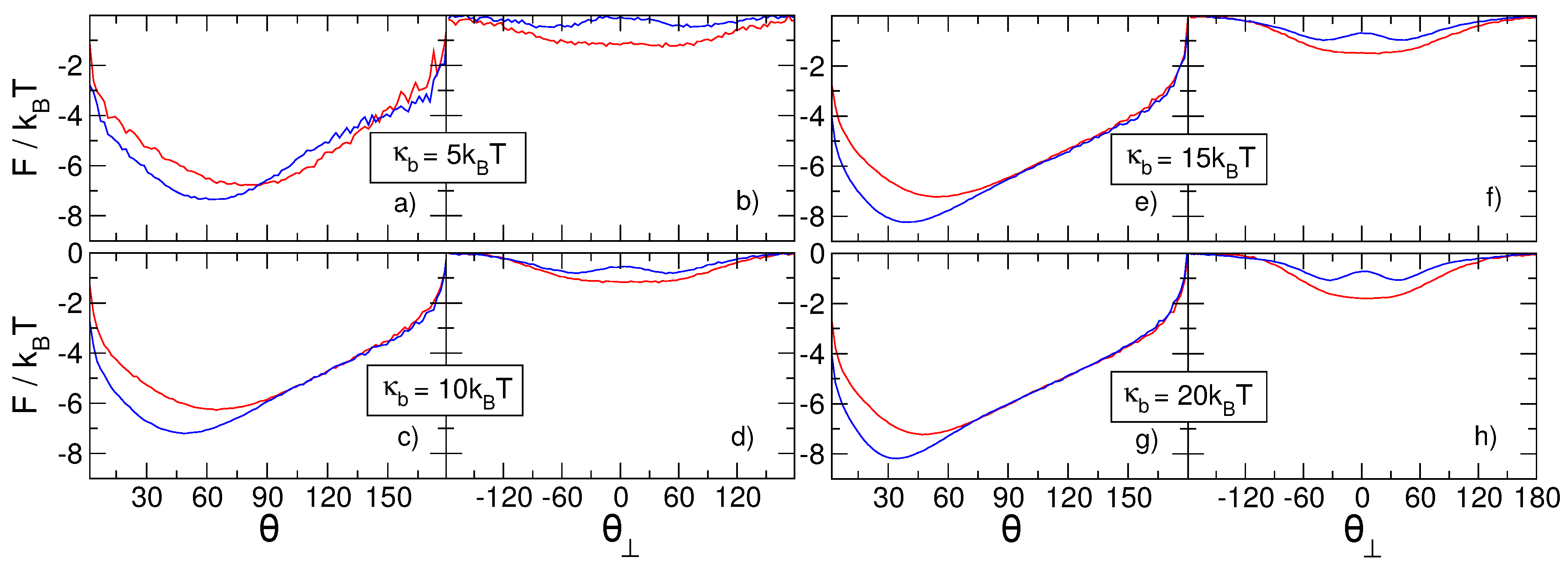
3.2. Knots Free Energy
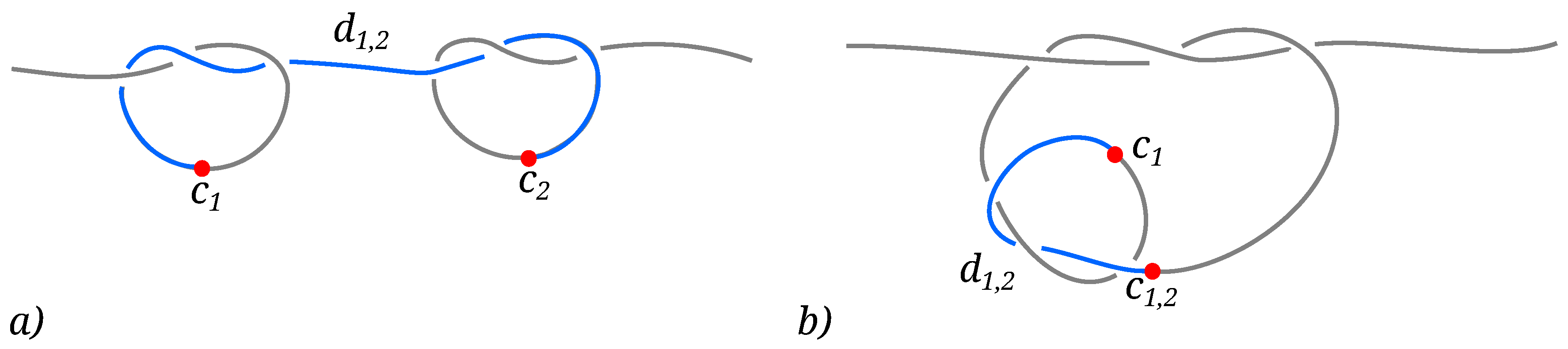
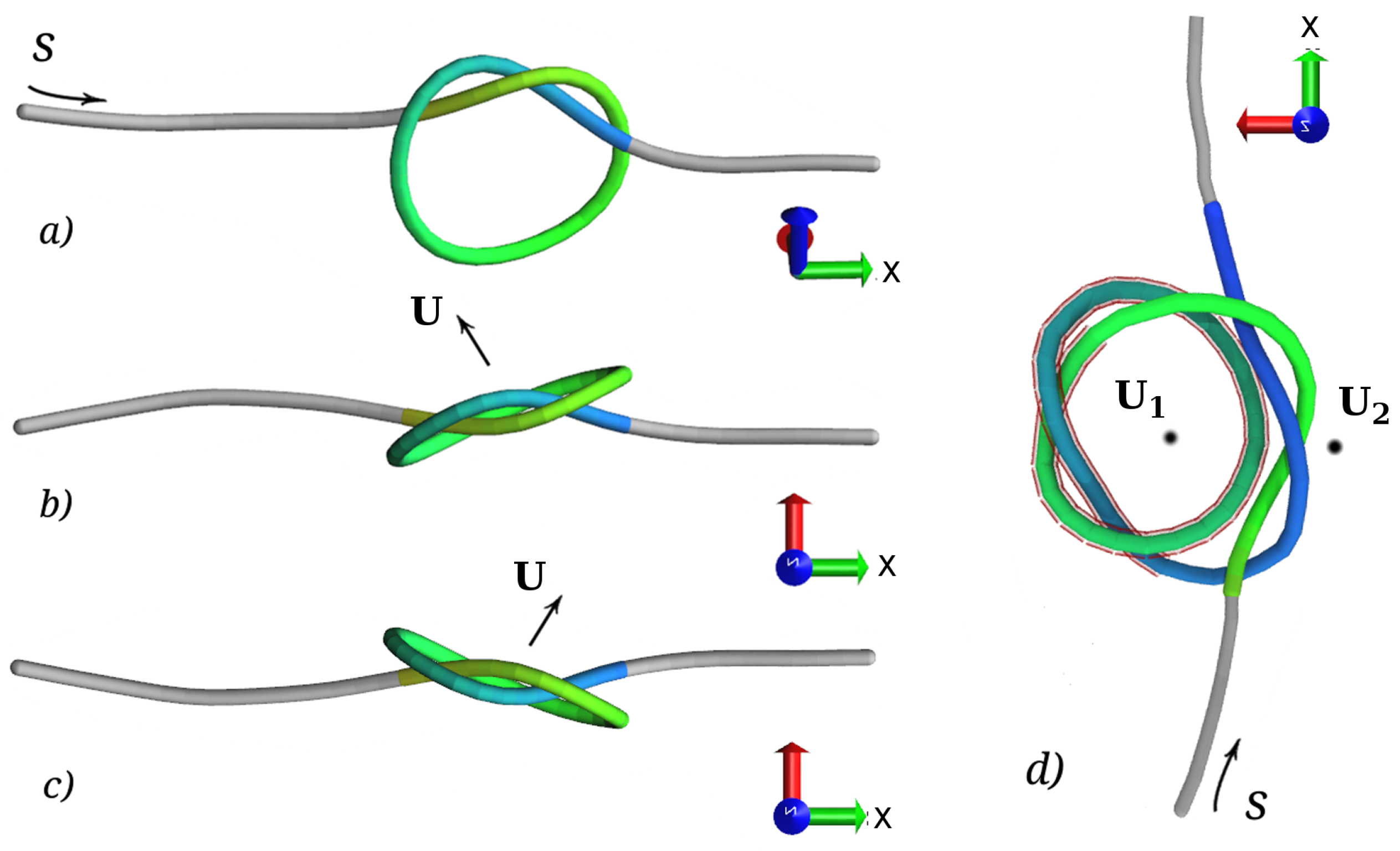
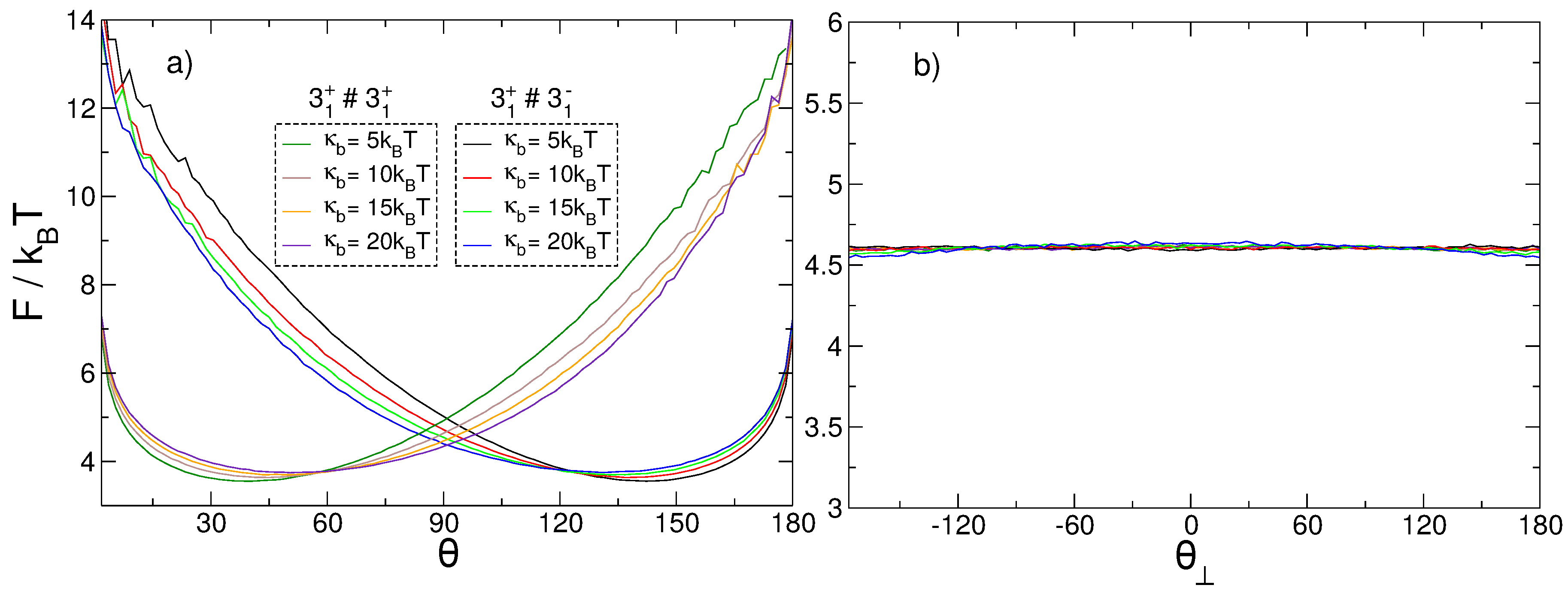
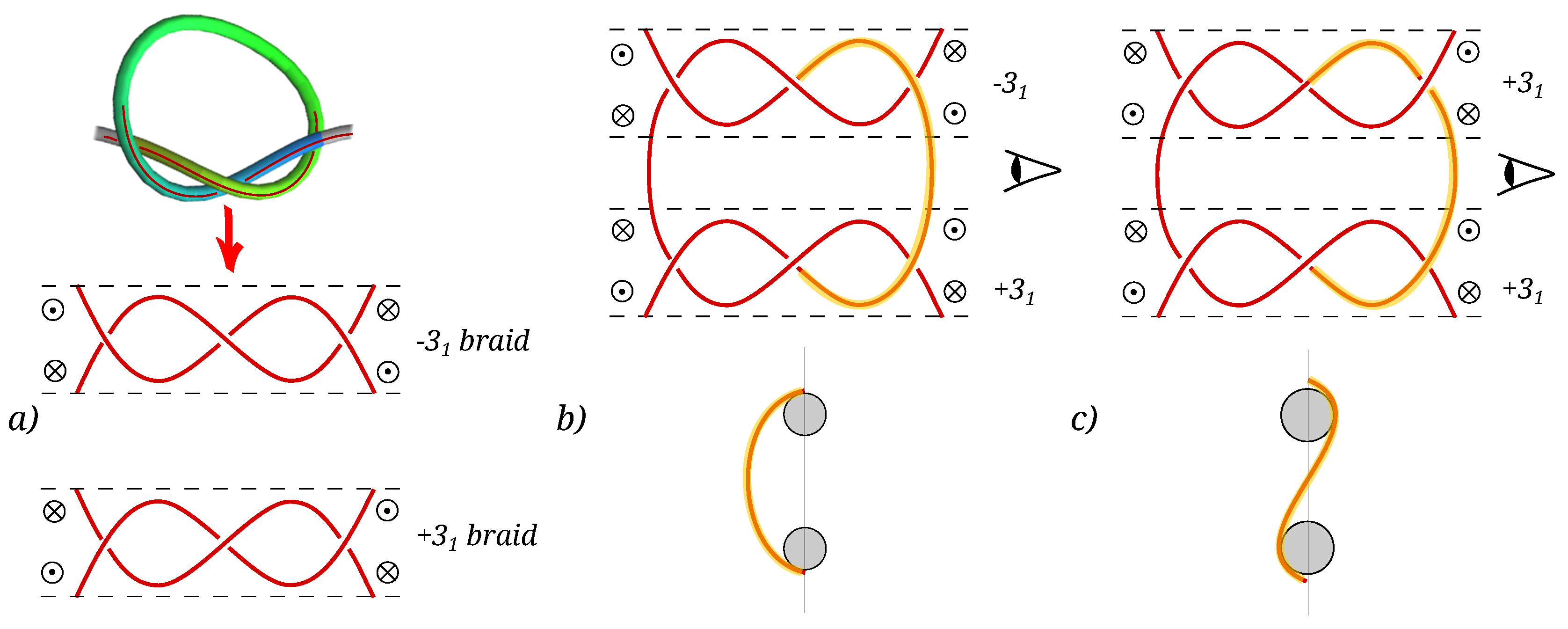
3.3. Relative Orientation of the Knots
4. Discussion
- When the knots along the chain are clearly separated and sufficiently far from the hard walls, the free energy is dominated by an entropic interaction between the knots, dependent on the absolute linear distance between them as well as the length of the knots.
- As the knots get closer to one another, but can still be considered as two simple separate knots, a repulsive interaction starts to dominate the free energy, stemming primarily from the steric hindrance of the proximal loops of the knots.
- Finally, as the knots become intertwined at yet smaller effective separations, the absolute magnitude of the free energy—And consequently, the stability of the knotted chain configuration—Is dependent both on the bending stiffness of the polymer chain as well as on the relative chirality of the two knots.
4.1. Elastic Energy Model for the Size of Two Separate, Non-Interacting Knots
4.2. Elastic Energy Model for Chirality Effects in Knot–Knot Interaction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Phillips, R.B.; Kondev, J.; Theriot, J. Physical Biology of the Cell, 2nd ed.; Garland Science: New York, NY, USA, 2012. [Google Scholar]
- Marko, J.; Cocco, S. The micromechanics of DNA. Phys. World 2003, 16, 37–41. [Google Scholar] [CrossRef]
- Brown, P.O.; Cozzarelli, N.R. A sign inversion mechanism for enzymatic supercoiling of DNA. Science 1979, 206, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Meluzzi, D.; Smith, D.; Arya, G. Biophysics of knotting. Annu. Rev. Biophys. 2010, 39, 349–366. [Google Scholar] [CrossRef] [PubMed]
- Olavarrieta, L.; Martínez-Robles, M.L.; Hernández, P.; Krimer, D.B.; Schvartzman, J.B. Knotting dynamics during DNA replication. Mol. Microbiol. 2002, 46, 699–707. [Google Scholar] [CrossRef] [PubMed]
- Bates, A.; Maxwell, A. DNA Topology; Oxford Bioscience: Boston, MA, USA, 2005. [Google Scholar]
- Arsuaga, J.; Vazquez, M.; Trigueros, S.; Sumners, D.W.; Roca, J. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. USA 2002, 99, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Orlandini, E.; Stasiak, A.; Sumners, D.W.; Tubiana, L.; Micheletti, C. DNA–DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. USA 2009, 106, 22269–22274. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E.; Sumners, D.W. Topological friction strongly affects viral DNA ejection. Proc. Natl. Acad. Sci. USA 2013, 110, 20081–20086. [Google Scholar] [CrossRef] [PubMed]
- Delbrück, M. Knotting problems in biology. In Mathematical Problems in Biological Sciences; Bellman, R.E., Ed.; SIAM: Philadelphia, PA, USA, 1962; Volume 14, p. 55. [Google Scholar]
- Frisch, H.L.; Wasserman, E. Chemical Topology 1. J. Am. Chem. Soc. 1961, 83, 3789–3795. [Google Scholar] [CrossRef]
- Arai, Y.; Yasuda, R.; Akashi, K.; Harada, Y.; Miyata, H.; Kinosita, T.; Itoh, H. Tying a molecular knot with optical tweezers. Nature 1999, 399, 446–448. [Google Scholar] [PubMed]
- Bao, X.; Lee, H.; Quake, S. Behavior of complex knots in single DNA molecules. Phys. Rev. Lett. 2003, 91, 265506. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, E.; Daya, Z.A.; Vorobieff, P.; Ecke, R.E. Knots and Random Walks in Vibrated Granular Chains. Phys. Rev. Lett. 2001, 86, 1414–1417. [Google Scholar] [CrossRef] [PubMed]
- Farago, O.; Kantor, Y.; Kardar, M. Pulling knotted polymers. Europhys. Lett. 2002, 60, 53–59. [Google Scholar] [CrossRef]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in Globule and Coil Phases of a Model Polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef] [PubMed]
- Vologodskii, A. Brownian Dynamics Simulation of Knot Diffusion along a Stretched DNA Molecule. Biophys. J. 2006, 90, 1594. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Makarov, D.E. Langevin Dynamics Simulations of the Diffusion of Molecular Knots in Tensioned Polymer Chains. J. Phys. Chem. A 2007, 111, 10338–10344. [Google Scholar] [CrossRef] [PubMed]
- Matthews, R.; Louis, A.; Yeomans, J. Effect of topology on dynamics of knots in polymers under tension. Europhys. Lett. 2010, 89, 20001. [Google Scholar] [CrossRef]
- Tubiana, L.; Rosa, A.; Fragiacomo, F.; Micheletti, C. Spontaneous Knotting and Unknotting of Flexible Linear Polymers: Equilibrium and Kinetic Aspects. Macromolecules 2013, 46, 3669–3678. [Google Scholar] [CrossRef]
- Poier, P.; Likos, C.N.; Matthews, R. Influence of Rigidity and Knot Complexity on the Knotting of Confined Polymers. Macromolecules 2014, 47, 3394–3400. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Rabin, Y. Metastable Tight Knots in a Wormlike Polymer. Phys. Rev. Lett. 2007, 99, 217801. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Renner, C.B.; Doyle, P.S. Metastable Tight Knots in Semiflexible Chains. Macromolecules 2014, 47, 6135–6140. [Google Scholar] [CrossRef]
- Dai, L.; Renner, C.B.; Doyle, P.S. Origin of Metastable Knots in Single Flexible Chains. Phys. Rev. Lett. 2015, 114, 037801. [Google Scholar] [CrossRef] [PubMed]
- Caraglio, M.; Micheletti, C.; Orlandini, E. Stretching Response of Knotted and Unknotted Polymer Chains. Phys. Rev. Lett. 2015, 115, 188301. [Google Scholar] [CrossRef] [PubMed]
- Sumners, D.; Whittington, S. Knots in self-avoiding walks. J. Phys. A Math. Gen. 1988, 21, 1689. [Google Scholar] [CrossRef]
- Ercolini, E.; Valle, F.; Adamcik, J.; Witz, G.; Metzler, R.; De Los Rios, P.; Roca, J.; Dietler, G. Fractal Dimension and Localization of DNA Knots. Phys. Rev. Lett. 2007, 98, 058102. [Google Scholar] [CrossRef] [PubMed]
- Baiesi, M.; Orlandini, E.; Stella, A.L. The entropic cost to tie a knot. J. Stat. Mech. Theory Exp. 2010, 2010, P06012. [Google Scholar] [CrossRef]
- Tsurusaki, K.; Deguchi, T. Fractions of Particular Knots in Gaussian Random Polygons. J. Phys. Soc. Jpn. 1995, 64, 1506. [Google Scholar] [CrossRef]
- Tubiana, L. Computational study on the progressive factorization of composite polymer knots into separated prime components. Phys. Rev. E 2014, 89, 052602. [Google Scholar] [CrossRef] [PubMed]
- Trefz, B.; Siebert, J.; Virnau, P. How molecular knots can pass through each other. Proc. Natl. Acad. Sci. USA 2014, 111, 7948–7951. [Google Scholar] [CrossRef] [PubMed]
- Dommersnes, P.G.; Kantor, Y.; Kardar, M. Knots in charged polymers. Phys. Rev. E 2002, 66, 031802. [Google Scholar] [CrossRef] [PubMed]
- Najafi, S.; Tubiana, L.; Podgornik, R.; Potestio, R. Chirality modifies the interaction between knots. Europhys. Lett. 2016, 114, 50007. [Google Scholar] [CrossRef]
- Bustamante, C.; Smith, S.B.; Liphardt, J.; Smith, D. Single-molecule studies of DNA mechanics. Curr. Opin. Struct. Biol. 2000, 10, 279–285. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628–3631. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. [Google Scholar] [CrossRef]
- Kauffman, L.H. An invariant of regular isotopy. Trans. Am. Math. Soc. 1990, 318, 417–471. [Google Scholar] [CrossRef]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Probing the Entanglement and Locating Knots in Ring Polymers: A Comparative Study of Different Arc Closure Schemes. Prog. Theor. Phys. Suppl. 2011, 191, 192–204. [Google Scholar] [CrossRef]
- Audoly, B.; Clauvelin, N.; Neukirch, S. Elastic knots. Phys. Rev. Lett. 2007, 99, 164301. [Google Scholar] [CrossRef] [PubMed]
- Jawed, M.; Dieleman, P.; Audoly, B.; Reis, P. Untangling the Mechanics and Topology in the Frictional Response of Long Overhand Elastic Knots. Phys. Rev. Lett. 2015, 115, 118302. [Google Scholar] [CrossRef] [PubMed]
- Dean, D.; Hammant, T.; Horgan, R.; Naji, A.; Podgornik, R. Wrapping transition and wrapping-mediated interactions for discrete binding along an elastic filament: An exact solution. J. Chem. Phys. 2012, 137, 144904. [Google Scholar] [CrossRef] [PubMed]
- Zandi, R.; Kantor, Y.; Kardar, M. Entropic competition between knots and slip-links. ARI Bull. ITU 2003, 53, 6–15. [Google Scholar]

© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi, S.; Podgornik, R.; Potestio, R.; Tubiana, L. Role of Bending Energy and Knot Chirality in Knot Distribution and Their Effective Interaction along Stretched Semiflexible Polymers. Polymers 2016, 8, 347. https://doi.org/10.3390/polym8100347
Najafi S, Podgornik R, Potestio R, Tubiana L. Role of Bending Energy and Knot Chirality in Knot Distribution and Their Effective Interaction along Stretched Semiflexible Polymers. Polymers. 2016; 8(10):347. https://doi.org/10.3390/polym8100347
Chicago/Turabian StyleNajafi, Saeed, Rudolf Podgornik, Raffaello Potestio, and Luca Tubiana. 2016. "Role of Bending Energy and Knot Chirality in Knot Distribution and Their Effective Interaction along Stretched Semiflexible Polymers" Polymers 8, no. 10: 347. https://doi.org/10.3390/polym8100347
APA StyleNajafi, S., Podgornik, R., Potestio, R., & Tubiana, L. (2016). Role of Bending Energy and Knot Chirality in Knot Distribution and Their Effective Interaction along Stretched Semiflexible Polymers. Polymers, 8(10), 347. https://doi.org/10.3390/polym8100347