Polymeric Shape-Memory Micro-Patterned Surface for Switching Wettability with Temperature
Abstract
:1. Introduction

2. Experimental Section
2.1. Materials
2.2. Preparation of Samples
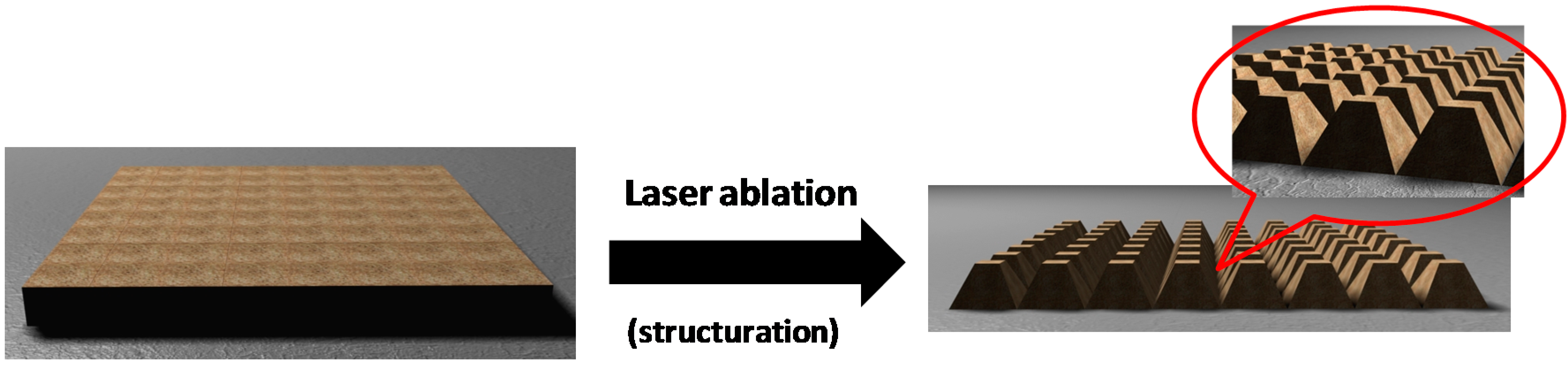
2.3. Experimental Methods
2.3.1. Dynamic Mechanical Thermal Analysis
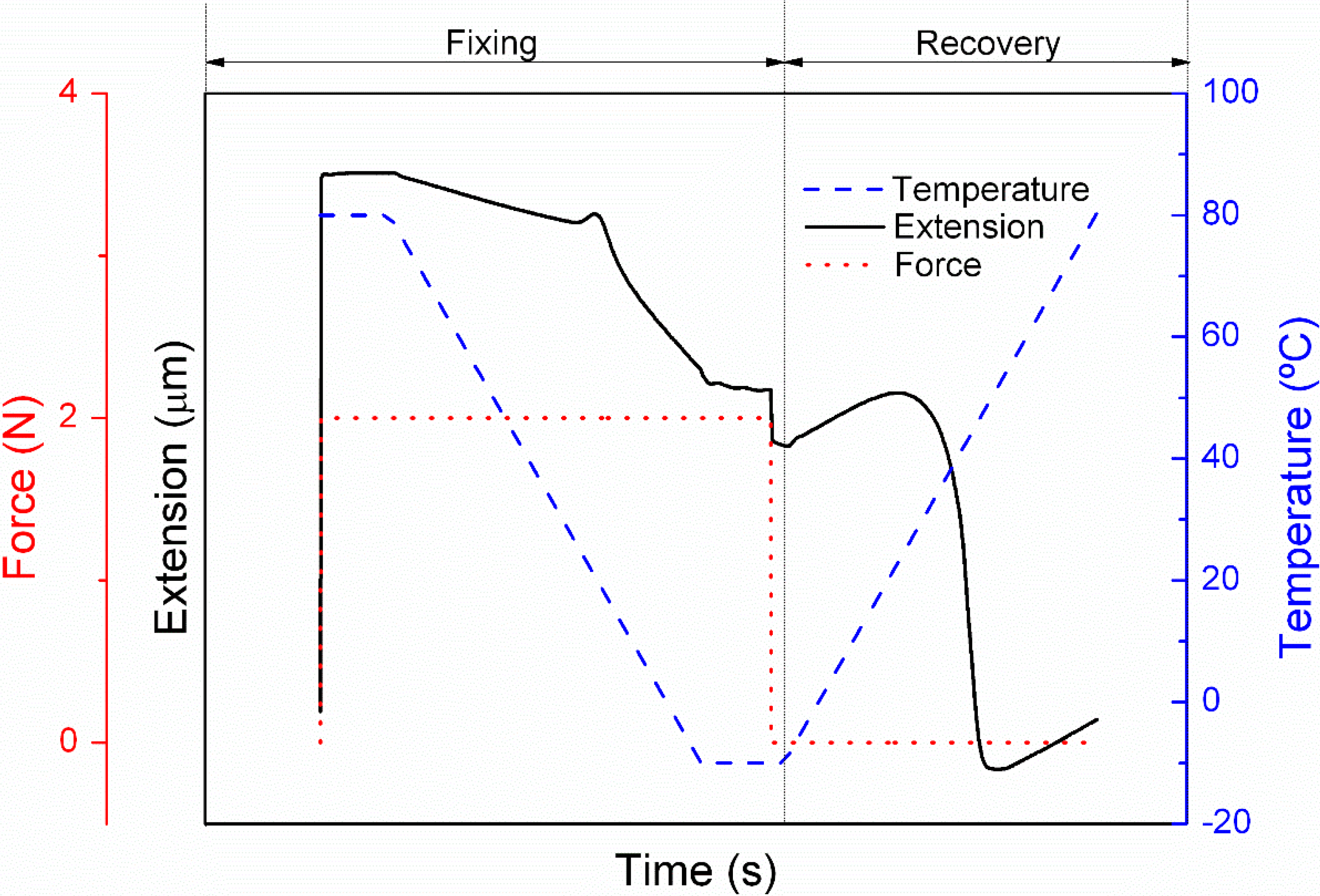
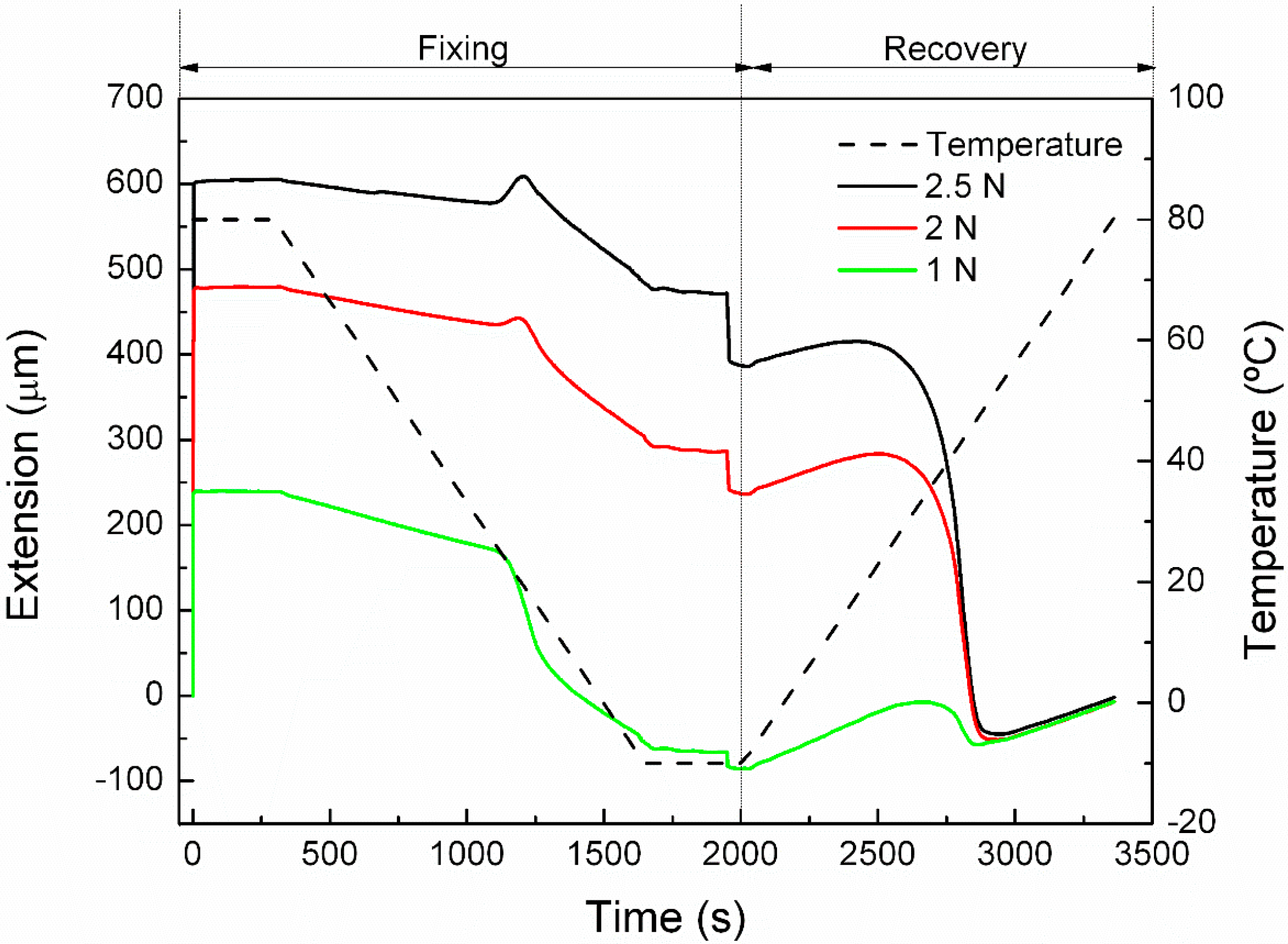
2.3.2. Cyclic Thermomechanical Shape Memory Properties
| Experiment | Force (N) | Cooling rate (°C min−1) | Heating rate (°C min−1) |
|---|---|---|---|
| 1 | 1 | 4 | 4 |
| 2 | 2 | 4 | 4 |
| 3 | 2.5 | 4 | 4 |
| 4 | 2.5 | 20 | 4 |
2.3.3. Shape Memory Micropillars
| Measured parameters | Initial | Cycle 1 | Cycle 2 | ||
|---|---|---|---|---|---|
| Deformed | Recovered | Deformed * | Recovered | ||
| Height (µm) | 15.9 ± 0.4 | 13.1 ± 0.2 | 15.8 ± 0.4 | 12.0 ± 0.5 | 16.2 ± 0.5 |
| Contact angle (°) | 136 ± 1.2 | 124 ± 1.2 | 135 ± 0.5 | 120 ± 1.0 | 136 ± 1.5 |
3. Results and Discussion
3.1. Dynamic Mechanical Thermal Analysis

3.2. Cyclic Thermomechanical Shape Memory Properties
| Experiment | Rf (%) | Rr (%) |
|---|---|---|
| 1 | - | 100 |
| 2 | 65.0 | 100 |
| 3 | 65.0 | 100 |
| 4 | 71.2 | 100 |
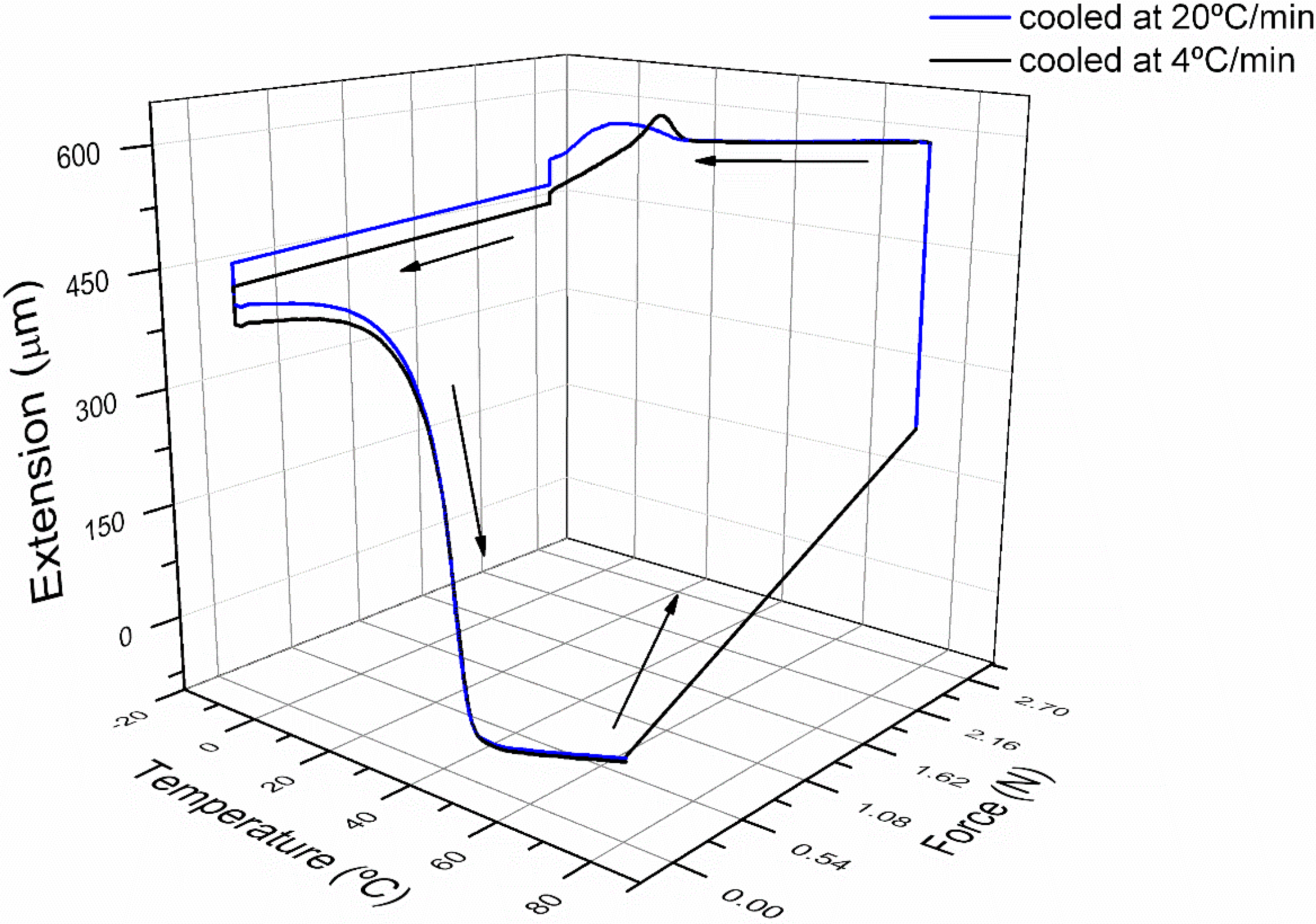
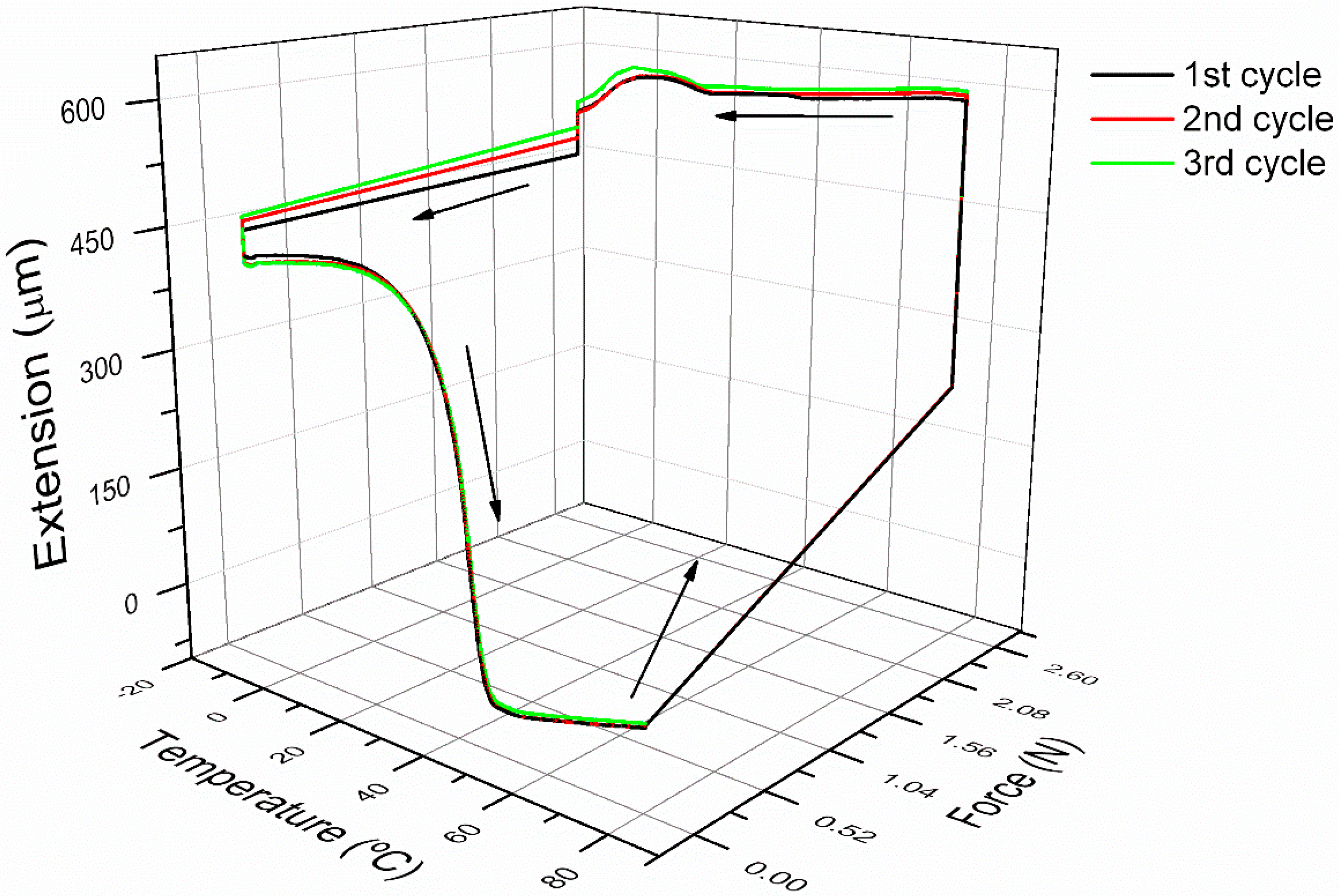
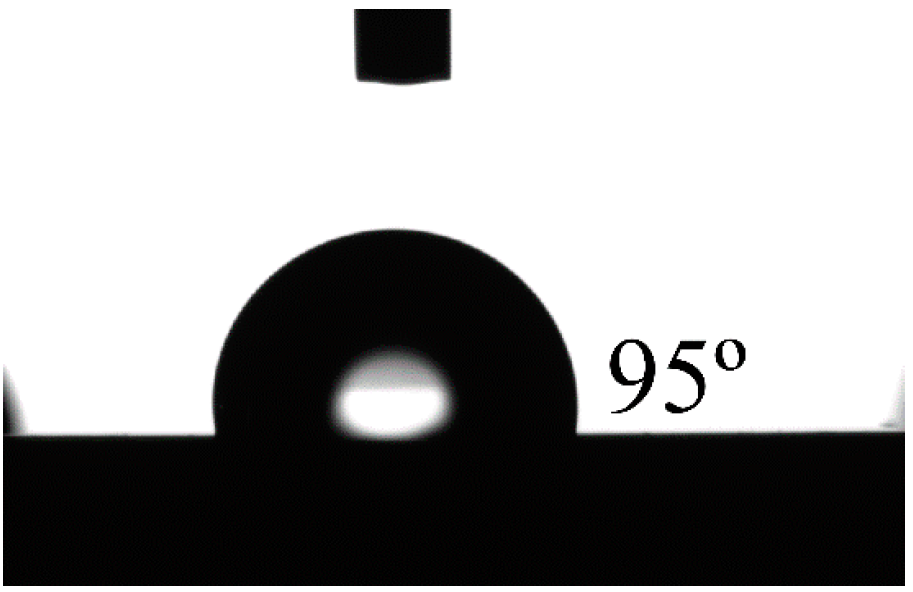
3.3. Shape Memory Micropillars
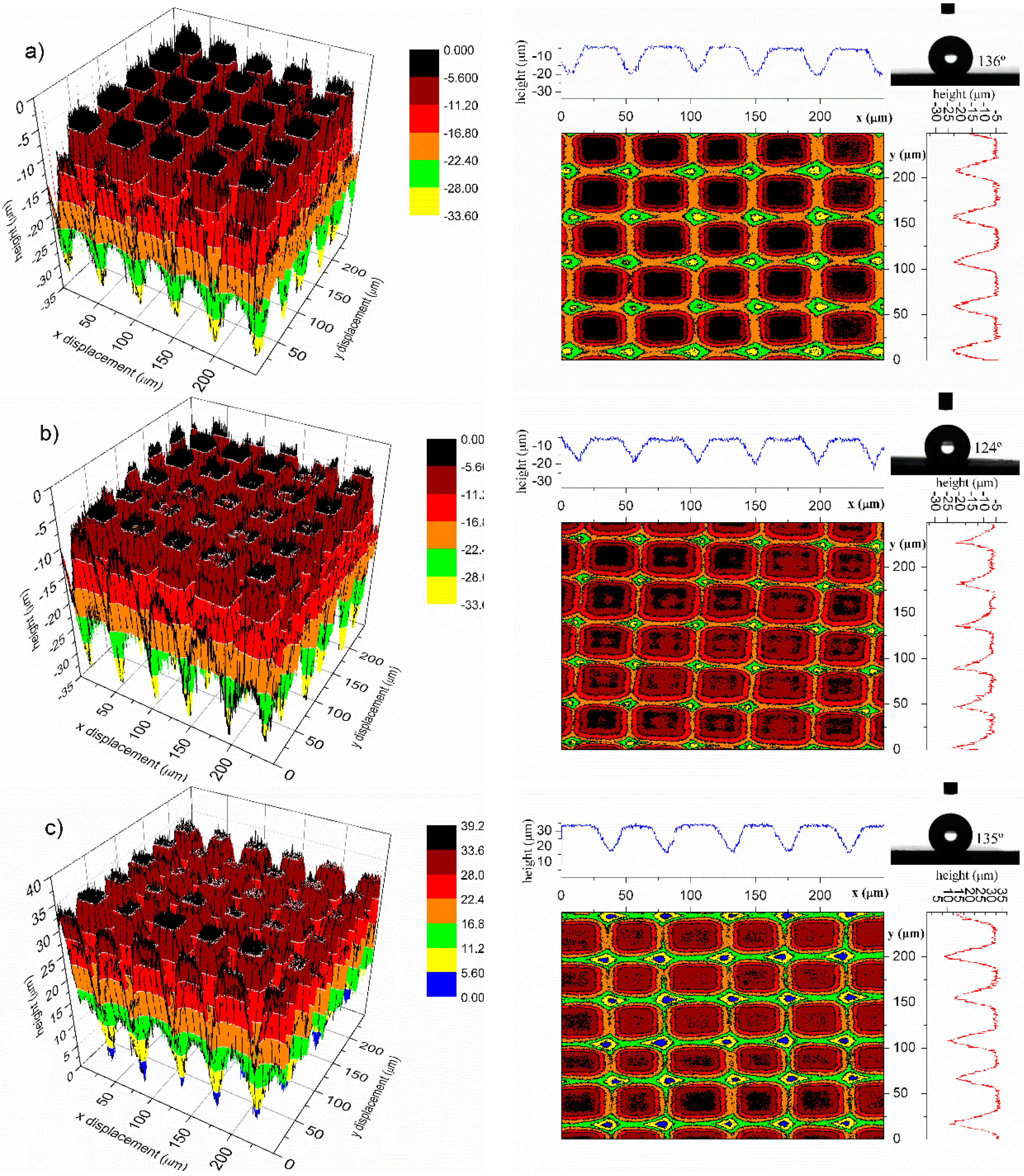
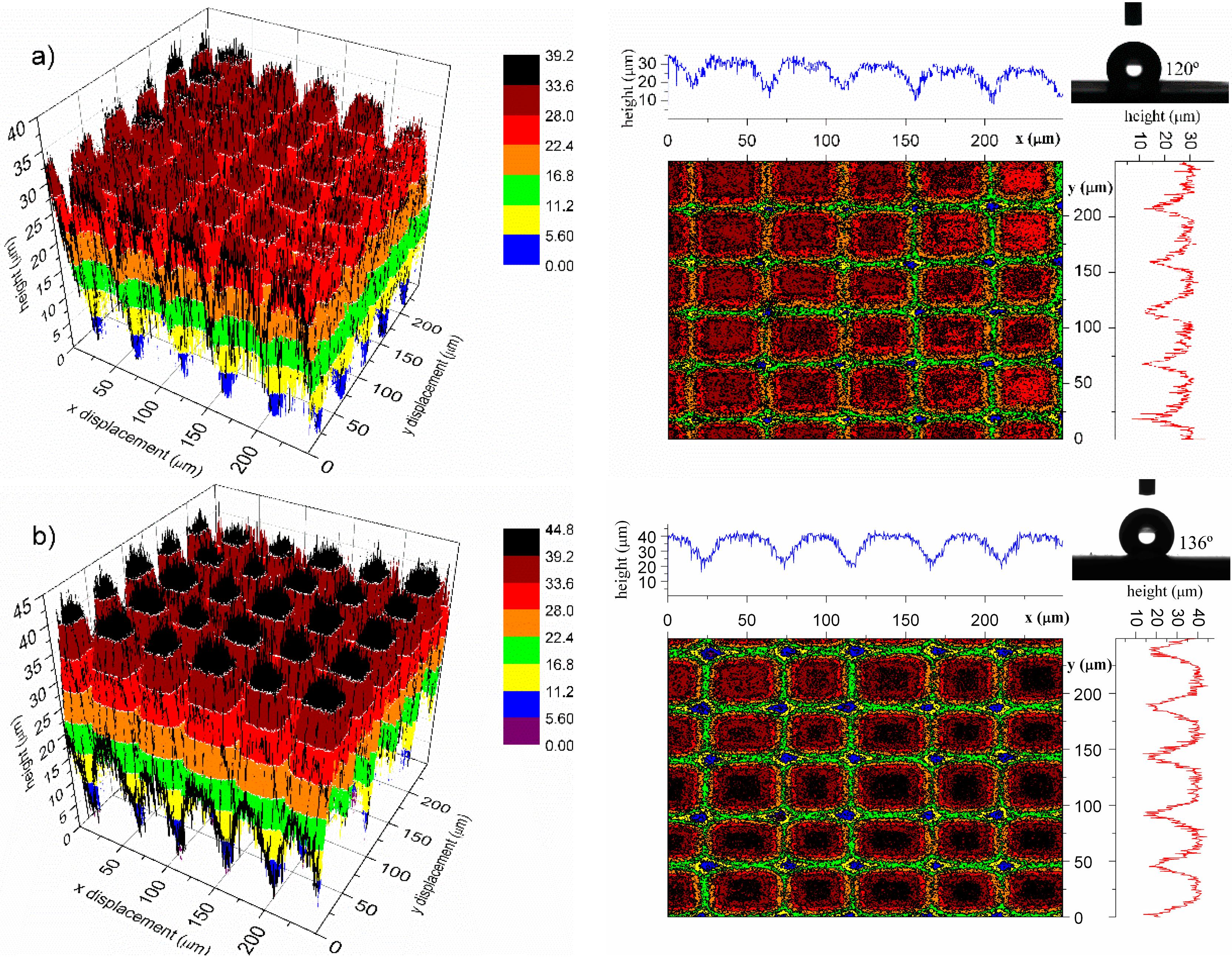
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marmur, A. Wetting on hydrophobic rough surfaces: To be heterogeneous or not to be? Langmuir 2003, 19, 8343–8348. [Google Scholar] [CrossRef]
- Patankar, N.A. On the modeling of hydrophobic contact angles on rough surfaces. Langmuir 2003, 19, 1249–1253. [Google Scholar] [CrossRef]
- Takeshita, N.; Paradis, L.A.; Öner, D.; McCarthy, T.J.; Chen, W. Simultaneous tailoring of surface topography and chemical structure for controlled wettability. Langmuir 2004, 20, 8131–8136. [Google Scholar] [CrossRef] [PubMed]
- Forward, K.M.; Moster, A.L.; Schwartz, D.K.; Lacks, D.J. Contact angles of submillimeter particles: Connecting wettability to nanoscale surface topography. Langmuir 2007, 23, 5255–5258. [Google Scholar] [CrossRef] [PubMed]
- Jabbarzadeh, A. Effect of nano-patterning on oleophobic properties of a surface. Soft Matter 2013, 9, 11598–11608. [Google Scholar] [CrossRef]
- Jo, H.B.; Choi, J.; Byeon, K.J.; Choi, H.J.; Lee, H. Superhydrophobic and superoleophobic surfaces using ZnO nano-in-micro hierarchical structures. Microelectron. Eng. 2014, 116, 51–57. [Google Scholar] [CrossRef]
- Drelich, J.; Chibowski, E. Superhydrophilic and superwetting surfaces: Definition and mechanisms of control. Langmuir 2010, 26, 18621–18623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Wang, S.; Wang, S.; Jiang, L. Superwetting surfaces under different media: Effects of surface topography on wettability. Small 2015, 11, 1939–1946. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shi, F.; Niu, J.; Jiang, Y.; Wang, Z. Superhydrophobic surfaces: From structural control to functional application. J. Mater. Chem. 2008, 18, 621–633. [Google Scholar] [CrossRef]
- Oh, S.-K.; Nakagawa, M.; Ichimura, K. Photocontrol of liquid motion on an azobenzene monolayer. J. Mater. Chem. 2002, 12, 2262–2269. [Google Scholar] [CrossRef]
- Delorme, N.; Bardeau, J.F.; Bulou, A.; Poncin-Epaillard, F. Azobenzene-containing monolayer with photoswitchable wettability. Langmuir 2005, 21, 12278–12282. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Wang, G.; He, Y.; Wang, X.; An, Y.; Song, Y.; Jiang, L. Photo-switched wettability on an electrostatic self-assembly azobenzene monolayer. Chem. Commun. 2005, 3550–3552. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Yu, C.; Wang, S.; Malyarchuk, V.; Xie, T.; Rogers, J.A. Deformable, programmable, and shape-memorizing micro-optics. Adv. Funct. Mater. 2013, 23, 3299–3306. [Google Scholar] [CrossRef]
- Chen, C.-M.; Chiang, C.-L.; Lai, C.-L.; Xie, T.; Yang, S. Buckling-based strong dry adhesives via interlocking. Adv. Funct. Mater. 2013, 23, 3813–3823. [Google Scholar] [CrossRef]
- Reddy, S.; Arzt, E.; del Campo, A. Bioinspired surfaces with switchable adhesion. Adv. Mater. 2007, 19, 3833–3837. [Google Scholar] [CrossRef]
- Li, W.; Gong, T.; Chen, H.; Wang, L.; Li, J.; Zhou, S. Tuning surface micropattern features using a shape memory functional polymer. RSC Adv. 2013, 3, 9865–9874. [Google Scholar] [CrossRef]
- Chen, C.M.; Yang, S. Directed water shedding on high-aspect-ratio shape memory polymer micropillar arrays. Adv. Mater. 2014, 26, 1283–1288. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Li, J.; Lee, E.; Yang, S. Light-induced shape recovery of deformed shape memory polymer micropillar arrays with gold nanorods. RSC Adv. 2015, 5, 30495–30499. [Google Scholar] [CrossRef]
- Turner, S.A.; Zhou, J.; Sheiko, S.S.; Ashby, V.S. Switchable micropatterned surface topographies mediated by reversible shape memory. ACS Appl. Mater. Interfaces 2014, 6, 8017–8021. [Google Scholar] [CrossRef] [PubMed]
- Lendlein, A.; Kelch, S. Shape-memory polymers. Angew. Chem. Int. Ed. 2002, 41, 2034–2057. [Google Scholar] [CrossRef]
- Meng, Q.; Hu, J. A review of shape memory polymer composites and blends. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1661–1672. [Google Scholar] [CrossRef]
- Behl, M.; Lendlein, A. Shape-memory polymers. Mater. Today 2007, 10, 20–28. [Google Scholar] [CrossRef]
- Liu, C.; Chun, S.B.; Mather, P.T.; Zheng, L.; Haley, E.H.; Coughlin, E.B. Chemically cross-linked polycyclooctene: Synthesis, characterization, and shape memory behavior. Macromolecules 2002, 35, 9868–9874. [Google Scholar] [CrossRef]
- Cuevas, J.M.; Alonso, J.; German, L.; Iturrondobeitia, M.; Laza, J.M.; Vilas, J.L.; León, L.M. Magneto-active shape memory composites by incorporating ferromagnetic microparticles in a thermo-responsive polyalkenamer. Smart Mater. Struct. 2009, 18. [Google Scholar] [CrossRef]
- Cuevas, J.M.; Laza, J.M.; Rubio, R.; German, L.; Vilas, J.L.; León, L.M. Development and characterization of semi-crystalline polyalkenamer based shape memory polymers. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- García-Huete, N.; Laza, J.M.; Cuevas, J.M.; Gonzalo, B.; Vilas, J.L.; León, L.M. Shape memory effect for recovering surface damages on polymer substrates. J. Polym. Res. 2014, 21, 481. [Google Scholar] [CrossRef]
- Huang, H.; Zheng, H.Y.; Lim, G.C. Femtosecond laser machining characteristics of Nitinol. Appl. Surf. Sci. 2004, 228, 201–206. [Google Scholar] [CrossRef]
- García-Huete, N.; Laza, J.M.; Cuevas, J.M.; Vilas, J.L.; Bilbao, E.; León, L.M. Study of the effect of gamma irradiation on a commercial polycyclooctene I. Thermal and mechanical properties. Radiat. Phys. Chem. 2014, 102, 108–116. [Google Scholar] [CrossRef]
- Garle, A.; Kong, S.; Ojha, U.; Budhlall, B.M. Thermoresponsive semicrystalline poly(ε-caprolactone) networks: Exploiting cross-linking with cinnamoyl moieties to design polymers with tunable shape memory. ACS Appl. Mater. Interfaces 2012, 4, 645–657. [Google Scholar] [CrossRef] [PubMed]
- Axpe, E.; García-Huete, N.; Cuevas, J.M.; Ribeiro, C.; Mérida, D.; Laza, J.M.; García, J.Á.; Vilas, J.L.; Lanceros-Méndez, S.; Plazaola, F.; et al. Connecting free volume with shape memory properties in noncytotoxic gamma-irradiated polycyclooctene. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 1080–1088. [Google Scholar] [CrossRef]
- De Gennes, P.-G.; Brochard-Wyart, F.; Quere, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, WA, USA, 2004. [Google Scholar]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Shastry, A.; Case, M.J.; Bohringer, K.F. Engineering surface roughness to manipulate droplets in microfluidic systems. Micro Electro Mech. Syst. 2005, 694–697. [Google Scholar]
- Cuevas, J.M.; Rubio, R.; German, L.; Laza, J.M.; Vilas, J.L.; Rodriguez, M.; Leon, L.M. Triple-shape memory effect of covalently crosslinked polyalkenamer based semicrystalline polymer blends. Soft Matter 2012, 8, 4928–4935. [Google Scholar] [CrossRef]
- Xie, T. Tunable polymer multi-shape memory effect. Nature 2010, 464, 267–270. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Huete, N.; Cuevas, J.M.; Laza, J.M.; Vilas, J.L.; León, L.M. Polymeric Shape-Memory Micro-Patterned Surface for Switching Wettability with Temperature. Polymers 2015, 7, 1674-1688. https://doi.org/10.3390/polym7091477
García-Huete N, Cuevas JM, Laza JM, Vilas JL, León LM. Polymeric Shape-Memory Micro-Patterned Surface for Switching Wettability with Temperature. Polymers. 2015; 7(9):1674-1688. https://doi.org/10.3390/polym7091477
Chicago/Turabian StyleGarcía-Huete, Nuria, José María Cuevas, José Manuel Laza, José Luis Vilas, and Luis Manuel León. 2015. "Polymeric Shape-Memory Micro-Patterned Surface for Switching Wettability with Temperature" Polymers 7, no. 9: 1674-1688. https://doi.org/10.3390/polym7091477
APA StyleGarcía-Huete, N., Cuevas, J. M., Laza, J. M., Vilas, J. L., & León, L. M. (2015). Polymeric Shape-Memory Micro-Patterned Surface for Switching Wettability with Temperature. Polymers, 7(9), 1674-1688. https://doi.org/10.3390/polym7091477






