Consolidation of Inorganic Precipitated Silica Gel

Abstract

Colloidal gels are possible intermediates in the generation of highly porous particle systems. In the production process the gels are fragmented after their formation. These gel fragments compact to particles whose application-technological properties are determined by their size and porosity. In the case of precipitated silica gels, this consolidation process depends on temperature and pH, among other parameters. It is shown that these dependencies can be characterized by oedometer measurements. Originally, the oedometer test (one-dimensional compression test) stemmed from soil mechanics. It has proven to be an interesting novel examination method for gels. Quantitative data of the time-dependent shrinkage of gel samples can be obtained. The consolidation of the gels shows a characteristic dependence on the above parameters.

1. Introduction

Silica gel consists of nanoscale particles of amorphous SiO₂ (see Figure 1).

Silica gels were first mentioned in 1640 [1] and remained a curiosity until their adsorption properties were found to be useful. Dried silica gel is used, for example, as a desiccant because of its highly hygroscopic properties. The manufacturing is carried out by mixing water glass (Na₂SiO₃·xH₂O) with acid. This work pursues the goal to quantify the consolidation of silica gels and gel fragments.

The phenomenon of syneresis occurs during the aging of gel samples. Syneresis is a consolidation of the nano-particulate gel network resulting in the expulsion of liquid [2]. In the following it is shown that the oedometer test is applicable to silica gel. This measuring method originally stems from soil mechanics and has not been used in colloid science so far. In principle the oedometer test is a one-dimensional compression test. A load is applied to a gel sample. While the sample is shrinking, liquid passes through the pore network and leaves the sample at its top and at its bottom. The consolidation is measured as a function of time [3]. The oedometer test is regarded as an appropriate experiment for the investigation of consolidation of gel samples. It is a faster testing method than aging, and the effect of the process parameters, such as pH value, ionic strength, temperature, and solids content, can be identified more rapidly. Experimental results of the consolidation of gel samples as a function of time measured with the oedometer test are given. Furthermore, the semi-empirical method of Terzaghi is used to describe the experimental curves.

2. Experimental

2.1. State of the Art

Syneresis is believed to be driven by van der Waals forces [4]. Shrinkage is ultimately stopped by the remaining repulsive force [2]. Syneresis is irreversible in most inorganic gels, and swelling of the gel is not observed. Syneresis in these systems is generally attributed to the formation of new bonds through condensation reactions of two silanol groups (–Si-OH) or hydrogen bonds [2].

The most thorough studies of syneresis have been performed by Vysotskii et al. [5,6] using silica gel made by the neutralization of sodium silicate with acid. Shrinkage of the gel was observed with a cathetometer. Vertical changes in position can be measured with a cathetometer. A cathetometer consists of a telescope that can be moved up and down along a stand. The kinetics of shrinkage is shown in Figure 2. There is an initial period during which no shrinkage occurs; then the shrinkage rate rises rapidly and eventually decreases again [2]. The total extent of shrinkage is about 15 vol%.

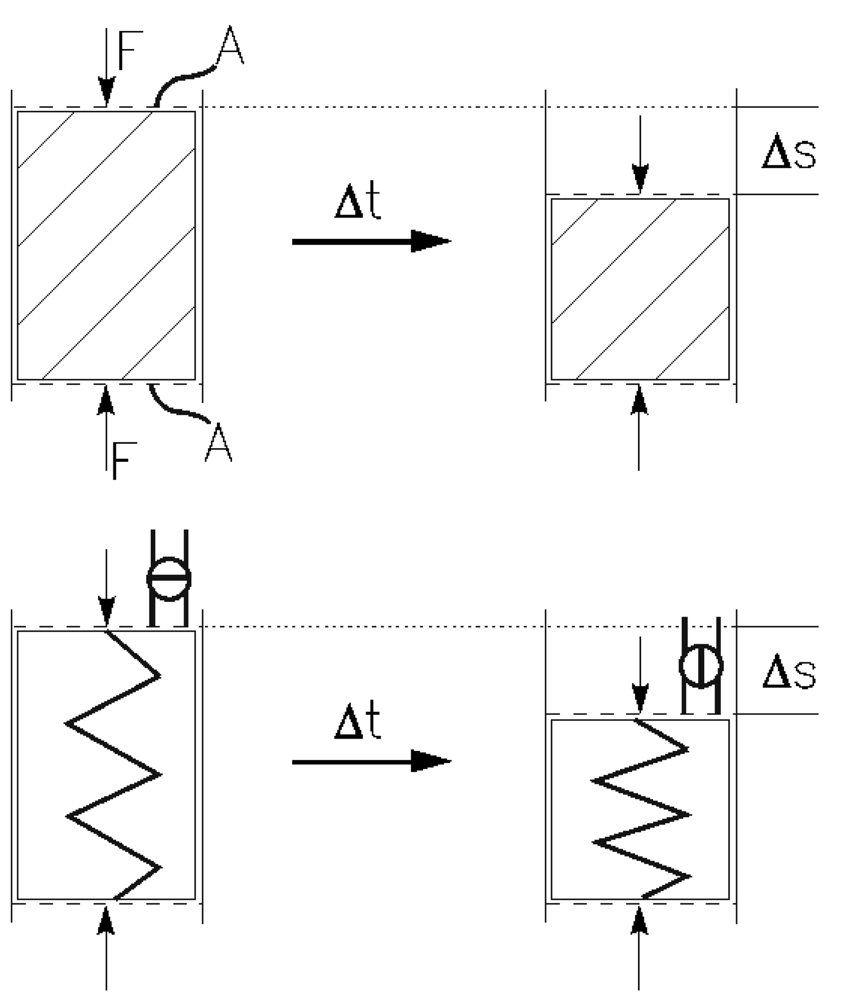
Since gel aging is a relatively slow test, it is desirable to have a faster and more quantitative testing method, e.g., the above mentioned oedometer test. Figure 3 (top) shows a schematic illustration of the consolidation of a gel sample during an oedometer test.

The consolidation curves measured (consolidation Δs vs. time t) are described by semi-empirical models. The most important physical description is the piston-spring analogy according to Terzaghi (1925) [7]: The filter cake (here: gel body) that is to be squeezed is represented as a spring which is immersed in a liquid [8]. Pressure is applied by a frictionless piston (see Figure 3, bottom). The piston cannot move down because the tap on the piston is shut and the pressure is entirely supported by the liquid. When the tap is opened the piston moves down and liquid flows out. The descent of the piston is slowed by the stiffness of the spring until equilibrium is reached, where liquid no longer flows and the pressure is fully supported by the compressed spring [8]. Shirato [9] succeeded in proposing an equation based on the piston-spring analogy that is valid for filter cakes with a sinusoidal initial distribution of the hydraulic pressure [8,9]:

$$U=1-exp\left\{-\frac{{\pi }^2{T}_c}{4}\right\}$$

(1)

with the consolidation ratio

$$U=\frac{\Delta \text{s}}{\Delta {\text{s}}_{\infty }}$$

(2)

and the reduced consolidation time

$$T_c=\frac{i^2{C}_{e}t}{A^2}$$

(3)

where i is the number of dewatering surfaces (i = 2 for oedometer testing), A is the cross-sectional area of filtration and C_e is a material specific parameter.

2.2. Experimental Setup

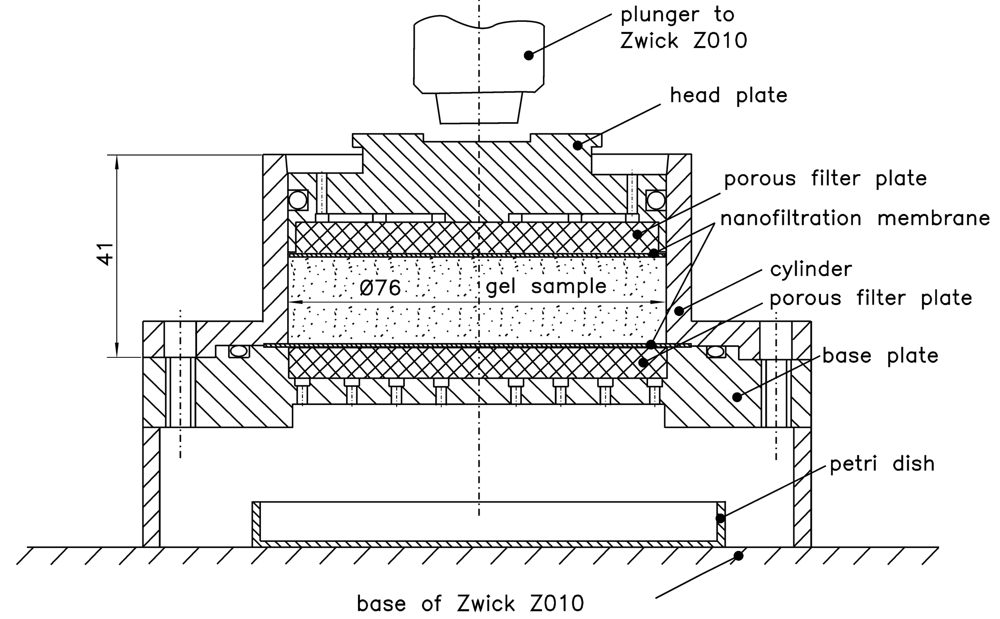
The setup of the used oedometer measuring cell is illustrated in Figure 4. The head plate, the cylinder and the base plate are made of stainless steel, and so are the highly porous, sintered filter plates (Tridelta Siperm^® R with a pore size of 100 μm). The nanofiltration membranes (Dow FILMTEC NF 270 and NF 90) are necessary for the retention of small gel fragments in the order of micrometers or nanometers. It was observed that the loss of solid through the membrane was higher for the NF 270 membrane than for the NF 90 membrane. Therefore, the latter was used for the further tests. The load was put on the gel sample for the experiments via a universal testing machine (Zwick Z010—load up to 10 kN).

It is possible with this experimental setup to investigate gel samples at different pressure differences. The set-up was immersed in a thermostated water bath for the investigation of gel samples at different temperatures.

The silica gels were generated by rapidly mixing alkaline water glass (sodium silicate solution Na₂O·3.3SiO₂) and sulfuric acid in a Y-mixing nozzle [10-13]. Acidic and alkaline gels can be formed depending on the mixing ratio. Gels with a short gelation time (∼12 min) were chosen as acidic and alkaline model gels: The acidic gel is produced by mixing sulfuric acid (50 %w/w) with sodium silicate solution (40 %w/w) in a ratio of 1:1 and has pH −0.97. The alkaline gel is produced by mixing sulfuric acid (3.2 %w/w) with sodium silicate solution (40 %w/w) in a ratio of 1:1 and has ∼pH 9.

2.3. Data Evaluation

The consolidation measured Δs is plotted against the consolidation time t. The course of a series of measurement is shown in Figure 5.

The square-root-of-time fitting method of consolidation courses is described in [14]. Shirato mentions the equations [9]

$$U=\frac{\overline{\text{AC}}}{\overline{\text{AB}}}=1.08\text{and}{C}_e=\frac{0.933A^2}{i^2{t}_{90}}$$

for a sinusoidal initial distribution of the hydraulic pressure. These relations are valid if U = 0.90. Hence, point C belongs to a consolidation ratio of U = 0.90 [8,14]. The consolidation time t₉₀ in Equation 4 where U = 0.9 is determined using the fitting method. It follows that

$$U=1-exp\left\{-\frac{{\pi }^2}{4}\frac{0.933}{t_{90}}t\right\}$$

(4)

2.4. Results and Discussion

In Figure 6 the consolidation ratio U is shown as a function of the square root of time (√t) for the alkaline and the acidic SiO₂ model gel at constant pressure but at variable temperature. In 1 s, 10 s and 100 s almost no consolidation takes place, but it can be observed after longer times. In the scale of seconds, the gel resists and bears the load, but in the scale of hours consolidation of the gel occurs until an extent of about 90% of its original volume. The gel skeleton gives way to the outer pressure (∼15 bar) more rapidly with increasing temperature. Shrinkage of 50% is achieved for the alkaline gel at 80 °C after a shorter time (factor ∼ 4) than for the gel at 20 °C. This shrinkage is achieved after an even shorter time (factor ∼ 5) for the acidic gel.

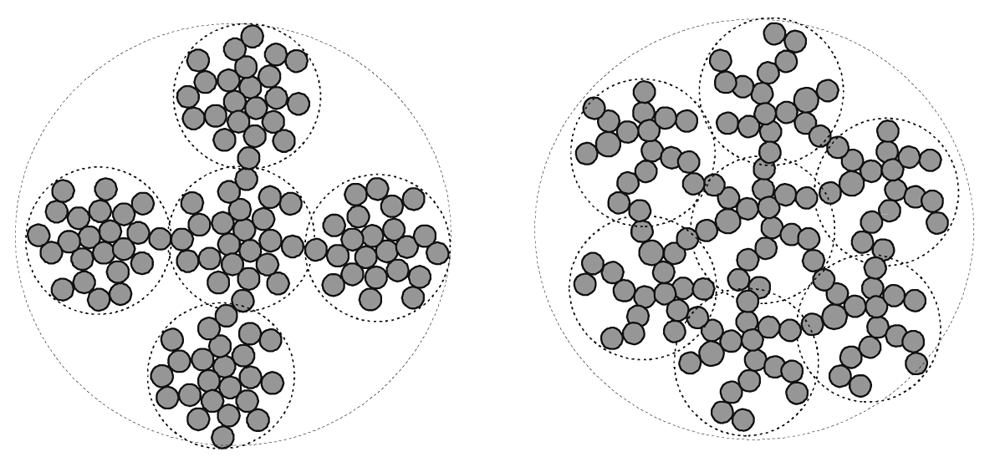
In general, the shrinkage is faster for the acidic gel than for the alkaline gel. Quarch et al. (2010) have found that the primary particles of acidic gels are smaller than the primary particles of alkaline gels. The structure of the acidic gel is compact in the nanoscale, but is open structured in the microscale. This structure is vice versa for the alkaline gel, see Figure 7 [15].

We assume that the microscale structure of the gel is firstly destroyed during oedometer testing. Since the acidic gel is open-structured in the microscale, it can be more easily compressed than the dense structure of the alkaline gel in the microscale. This might be the reason for the faster shrinkage of the acidic gels. These findings indicate that it is possible to investigate the consolidation behavior of gel samples and their dependence on temperature and pH more rapidly than with gel aging.

The analytical course of the consolidation ratio U according to Terzaghi-Shirato's Equation 4 is also given in Figure 6. The compliance of this semi-empirical approach to the experimental data is quite good except for the acidic gel at 20 °C. The model parameter t₉₀ is given in

Table 1. Model parameter t₉₀.

t90	20 °C	80 °C
alkaline (∼pH 9)	40,401 s	11,236 s
acidic (pH −0.97)	31,506 s	5,625 s

.

Leclerc et al. [8] investigated non-flocculated kaolin and measured S-shaped compression curves in the U-√t plot. They succeeded in describing the experimental data with the analytical expression for the pressing of filter cakes with a sinusoidal initial hydraulic pressure distribution within the cake (Equation 1). They showed that Terzaghi's model is limited to the initial phase of primary consolidation. They used the Voigt model, which includes a damping pot in the equivalent network, for a better description of the secondary consolidation which occurs at high consolidation times. With this combined Terzaghi-Voigt model they found an even better agreement with the experimental data for high consolidation times. Finally, they mentioned simplified models—industrial equations— developed by Shirato. However, they found that the simplified equation for filter cakes brings less simplification [8]. Contrary to kaolin, investigated by Leclerc et al., the silica gels investigated here deviate from Terzaghi's analytical expression in the primary consolidation phase. This means that the sole assumption of a spring cannot satisfactorily describe the data measured. The theoretical curves run below the experimental curves in this phase, except for the 80 °C acidic curve, where the agreement with the theoretical curve is very good. A new equivalent network including a damping pot in the primary consolidation phase probably has to be added in order to describe the experimental data in a better way.

There are also deviations from the theoretical Terzaghi curves in the phase of secondary consolidation. The reason why the Terzaghi curve for an 80 °C acidic gel assumes values of U > 1 is an overestimated value of Δs_∞. Δs_∞ can be estimated with Equation 2. There are deviations for high consolidation times because this estimated value is different from the real value of Δs_∞.

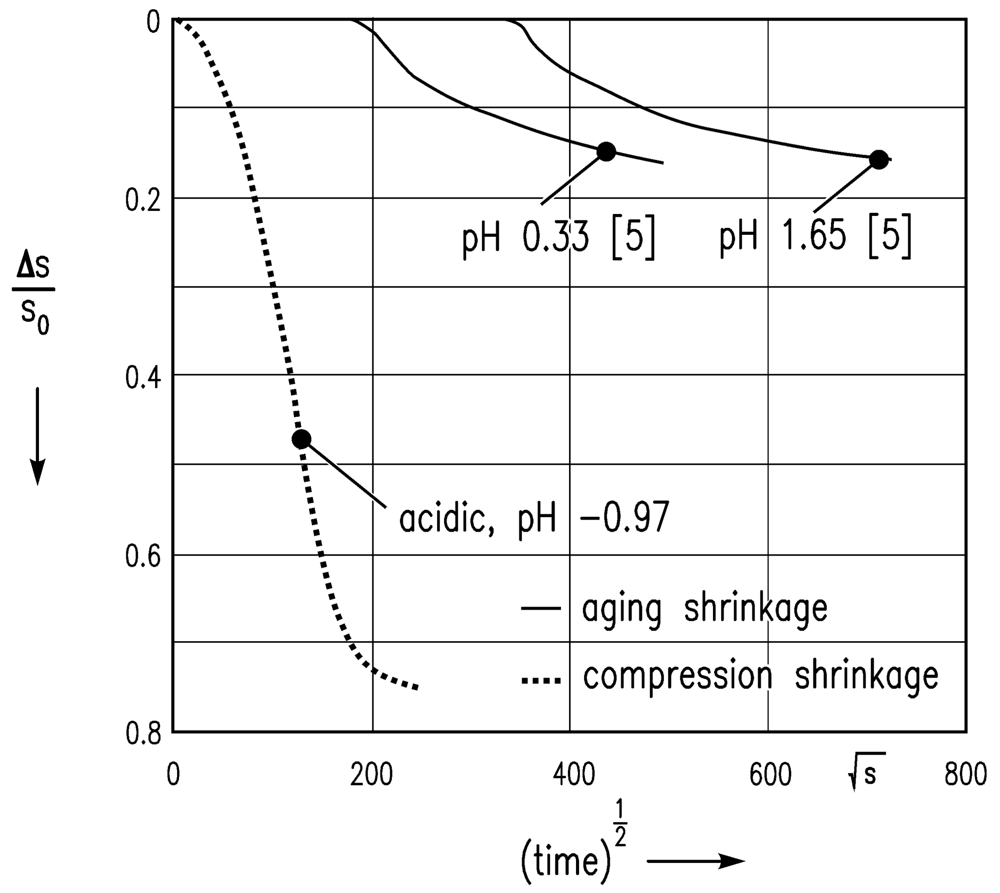
In the following a qualitative comparison between “aging shrinkage” (syneresis) and “compression shrinkage” (consolidation in oedometer testing) is given. The kinetics of syneresis for two exemplary acidic experiments (pH 0.33 and pH 1.65) from [5] and the consolidation in oedometer testing of an exemplary acidic experiment (pH −0.97) are shown in Figure 8.

In Figure 7, the ratio

$$\frac{\Delta \text{s}}{{\text{s}}_0}=\frac{\Delta \text{s}\cdot \text{A}}{{\text{s}}_0\cdot \text{A}}=\frac{\Delta \text{V}}{{\text{V}}_0}$$

(5)

is given as a function of time. Δs is the consolidation, s₀ is the height of the original gel sample, A is the cross-sectional area of the gel sample, ΔV is the change in volume and V₀ is the volume of the original gel sample. The extent of syneresis is about 15% of the original gel volume for the acidic gels (pH 0.33 and pH 1.65) while the time for this shrinkage is between 70 to 150 h. In the exemplary oedometer experiment (acidic, pH −0.97) the extent of the consolidation of the gel is about 75% while the time for this shrinkage is about 20 h.

3. Conclusions

The experimental findings can be summarized as follows: The process of reorganization of the gel fragments (syneresis) that occurs after fragmentation, depends on the process parameters, pH value and temperature. Hence, the rate at which syneresis occurs can be influenced in wide ranges by the choice of temperature. The oedometer test is suitable for the characterization of these dependencies. The mathematical description of the semi-empirical models shows deficiencies which may be attributed to the simplicity of these models.