Path-Based Discrete Modeling and Process Simulation for Thermoplastic Fused Deposition Modeling Technology
Abstract
1. Introduction
2. Methodology
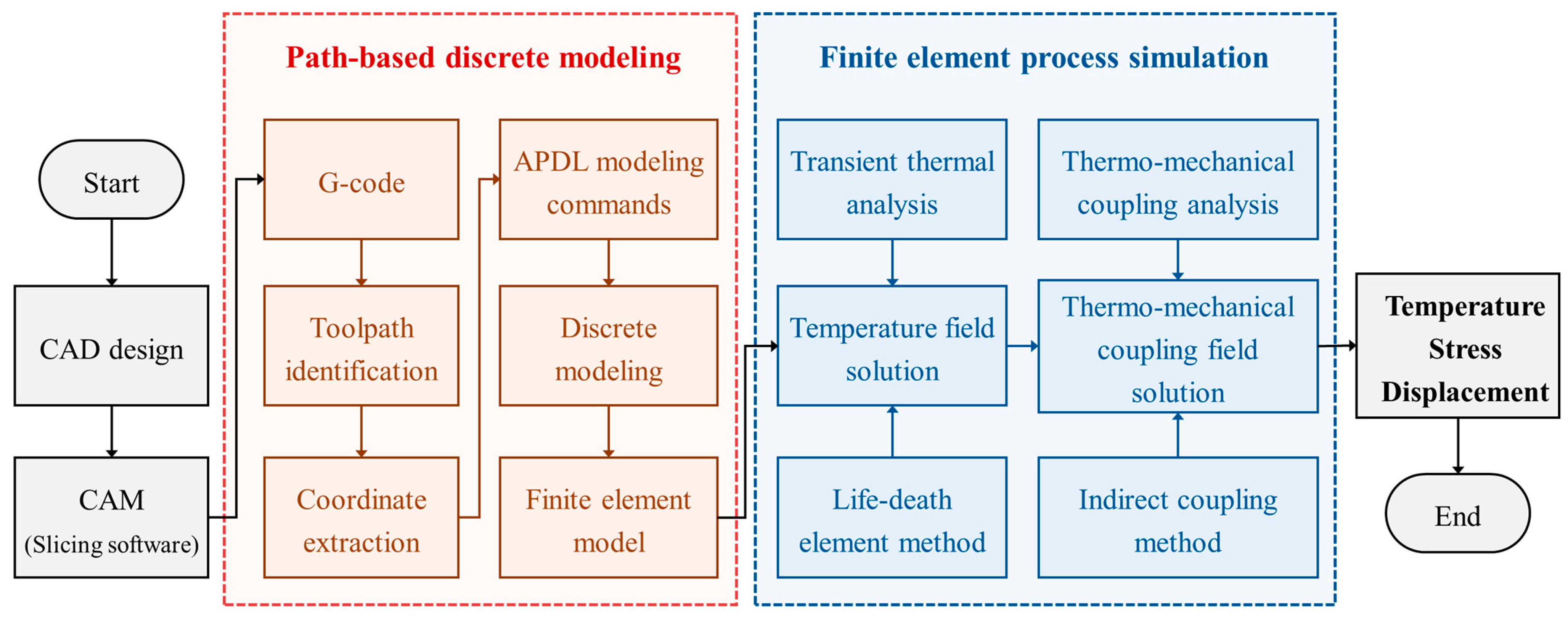
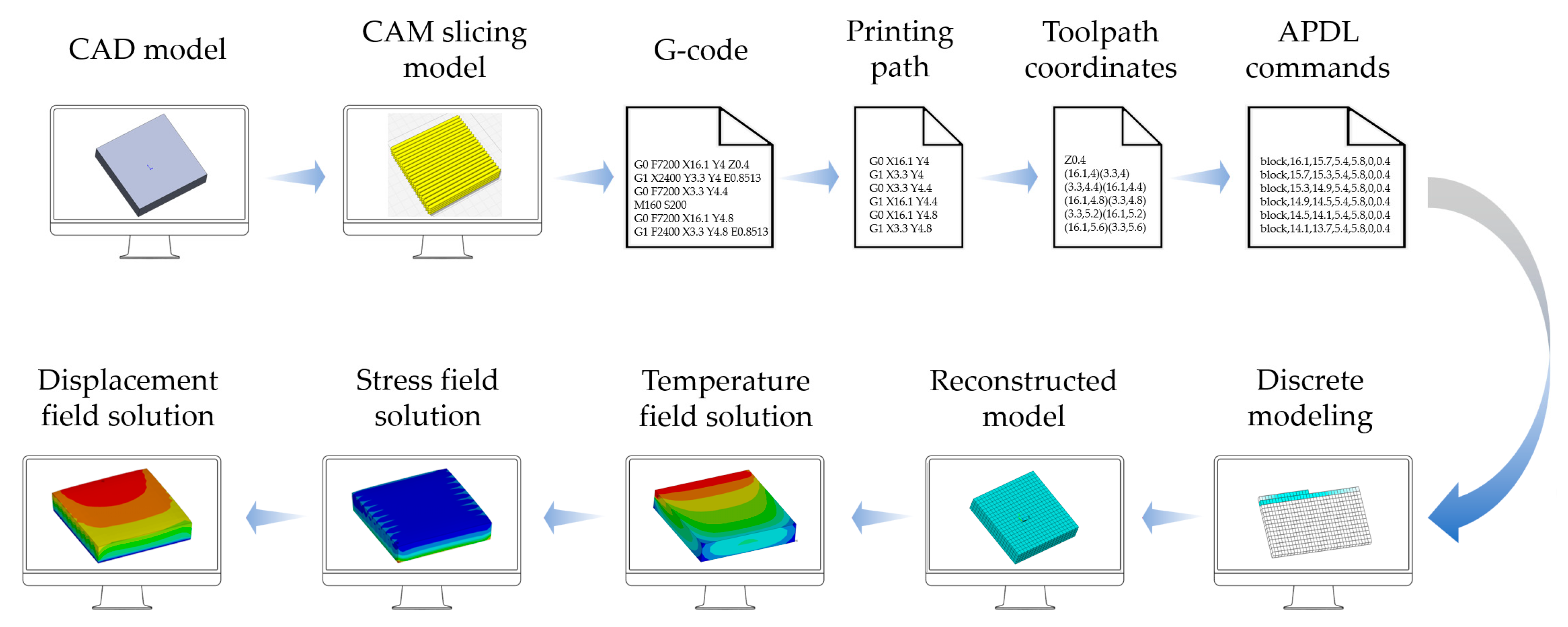
2.1. Framework of Path-Based Discrete Modeling and Process Simulation Method
2.2. Path-Based Discrete Modeling Method
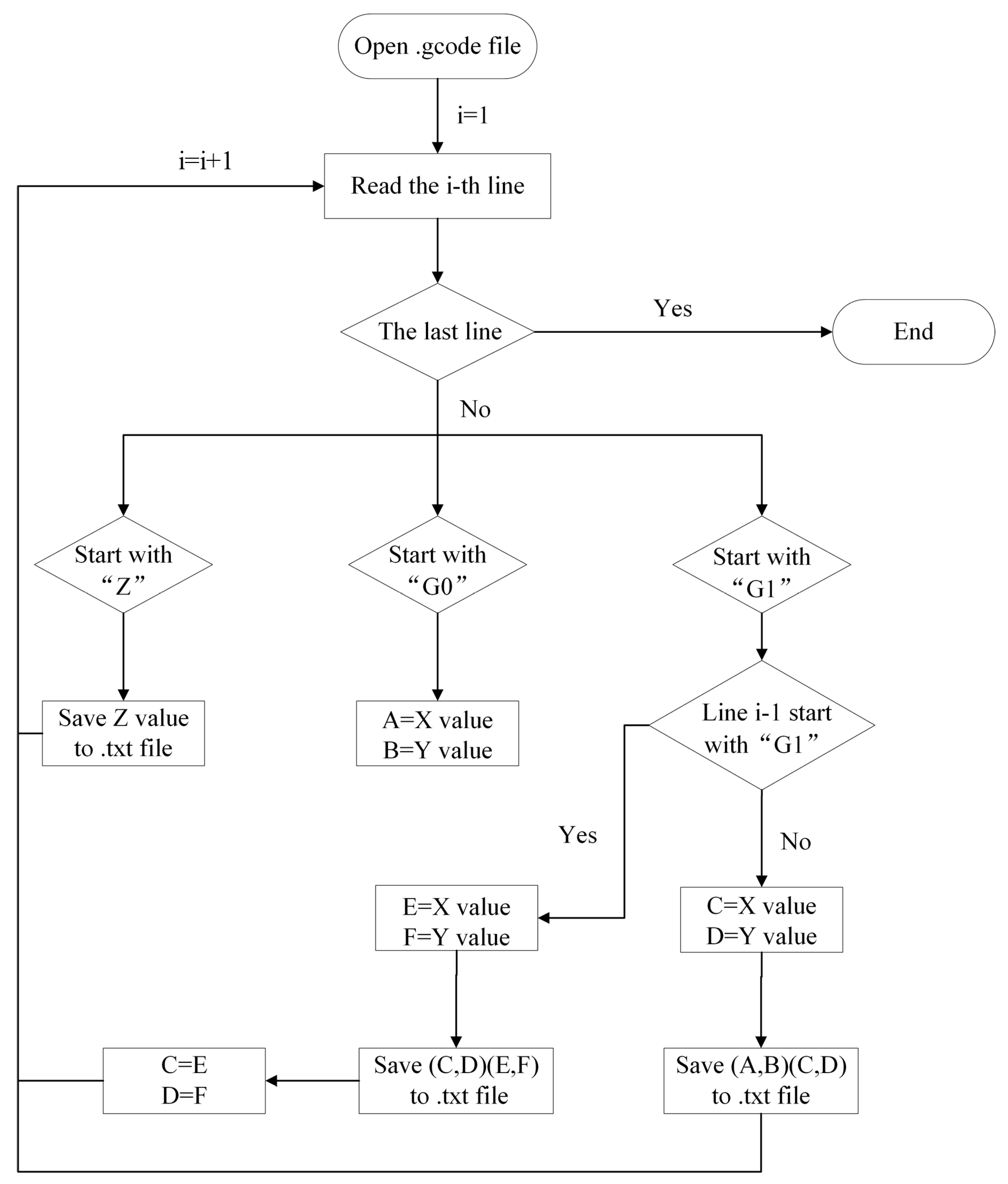
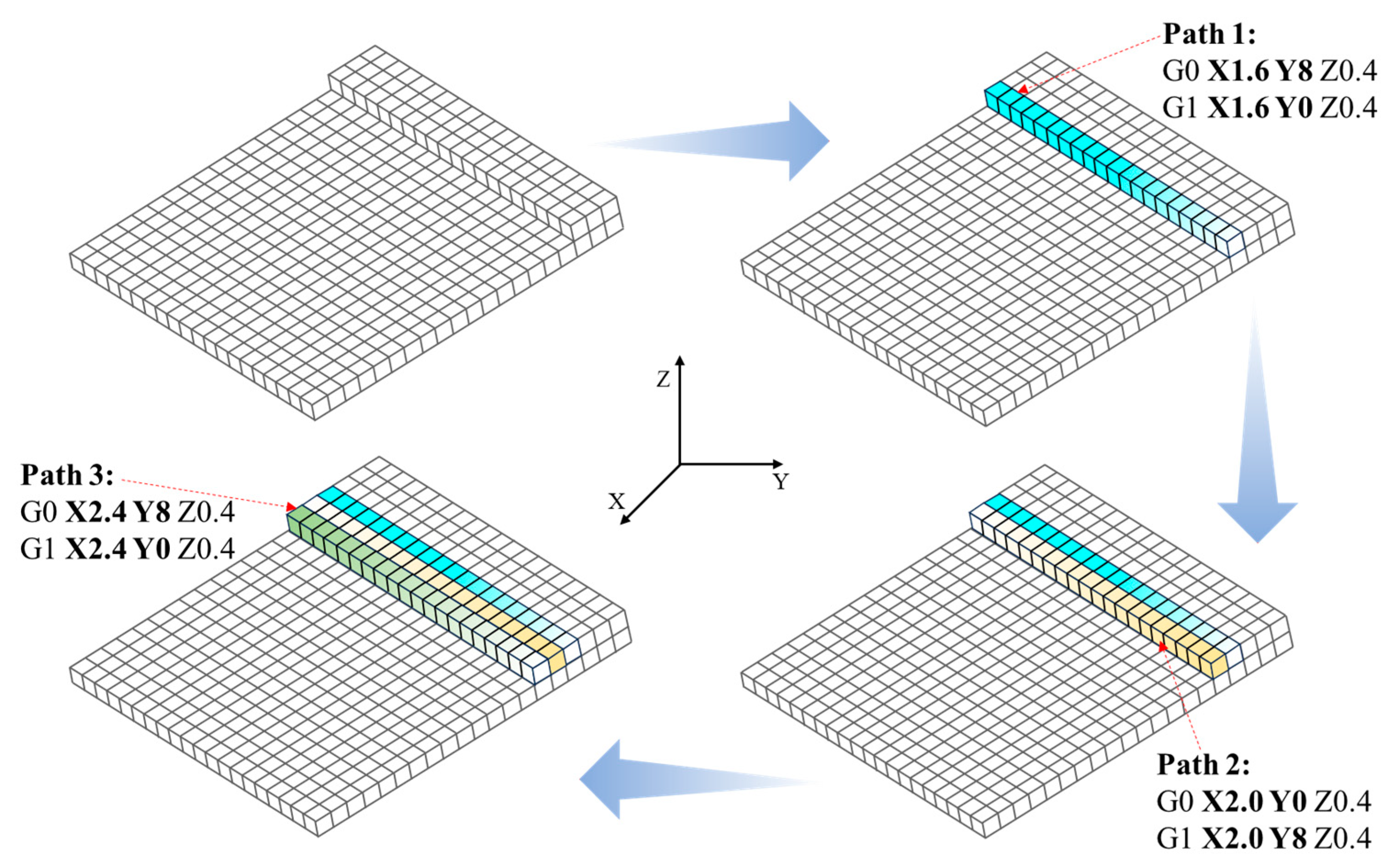
2.2.1. Extraction of Toolpath Coordinates
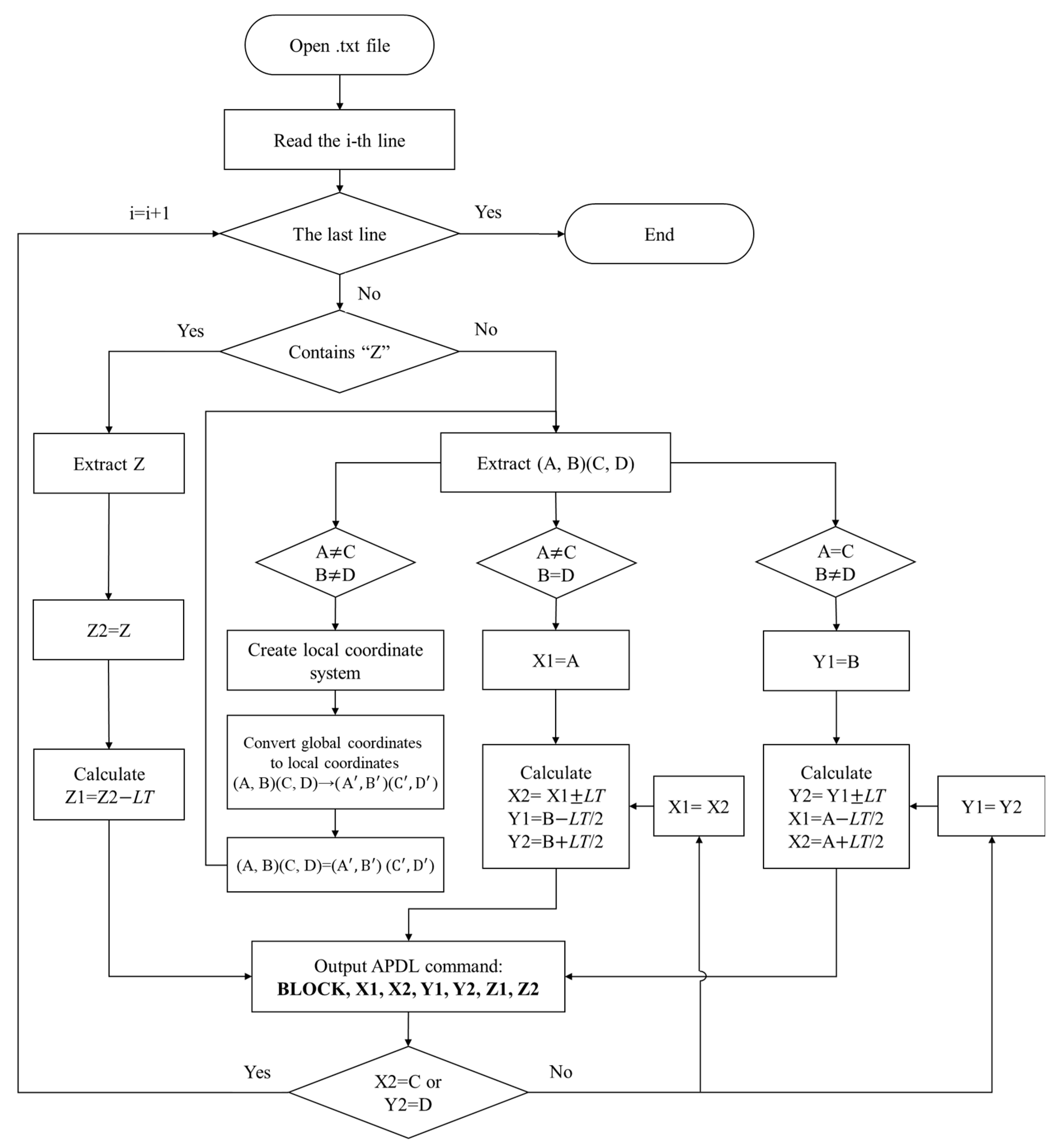
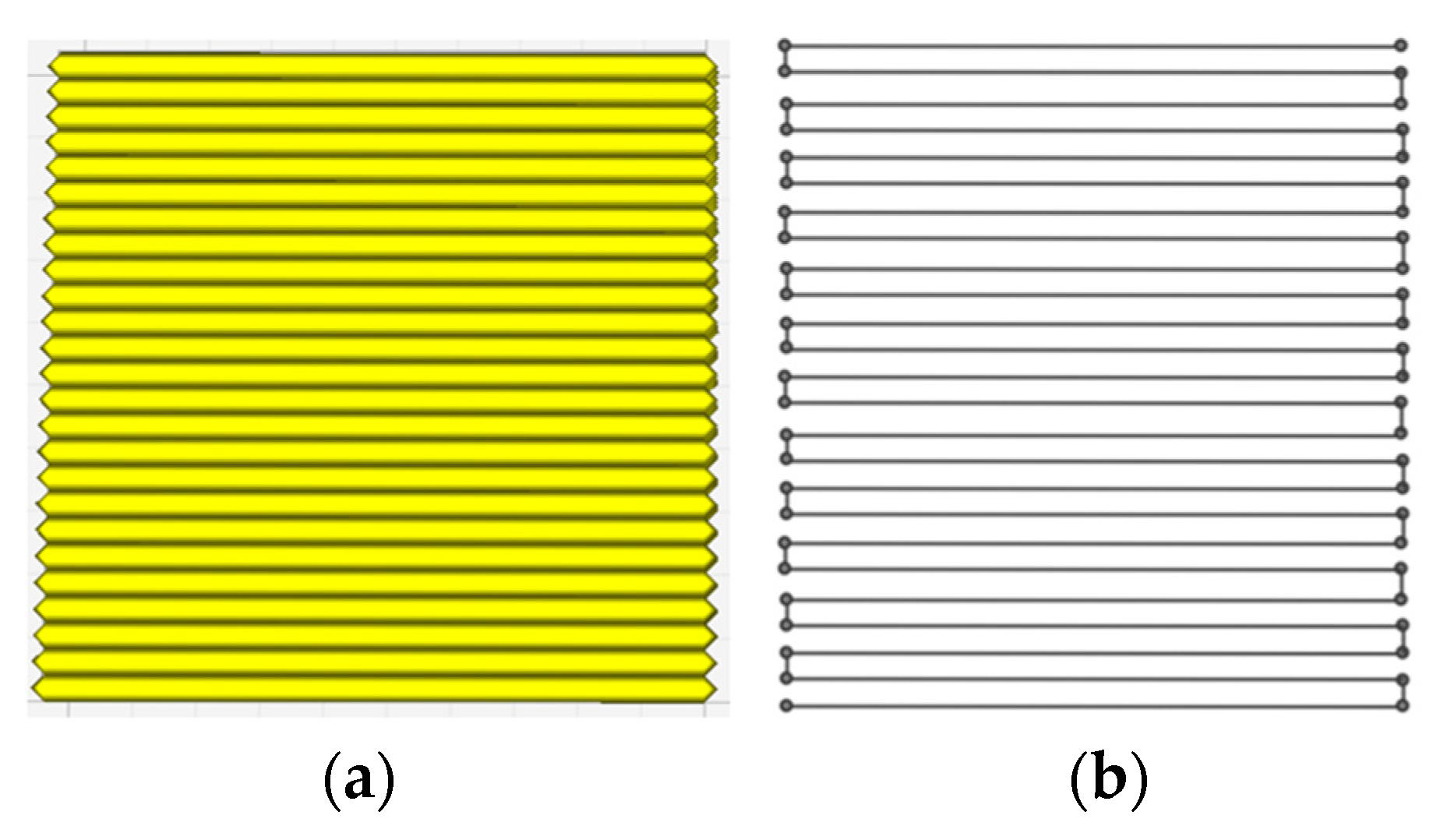
2.2.2. Path-Based Discrete Modeling
2.3. Finite Element Process Simulation Method
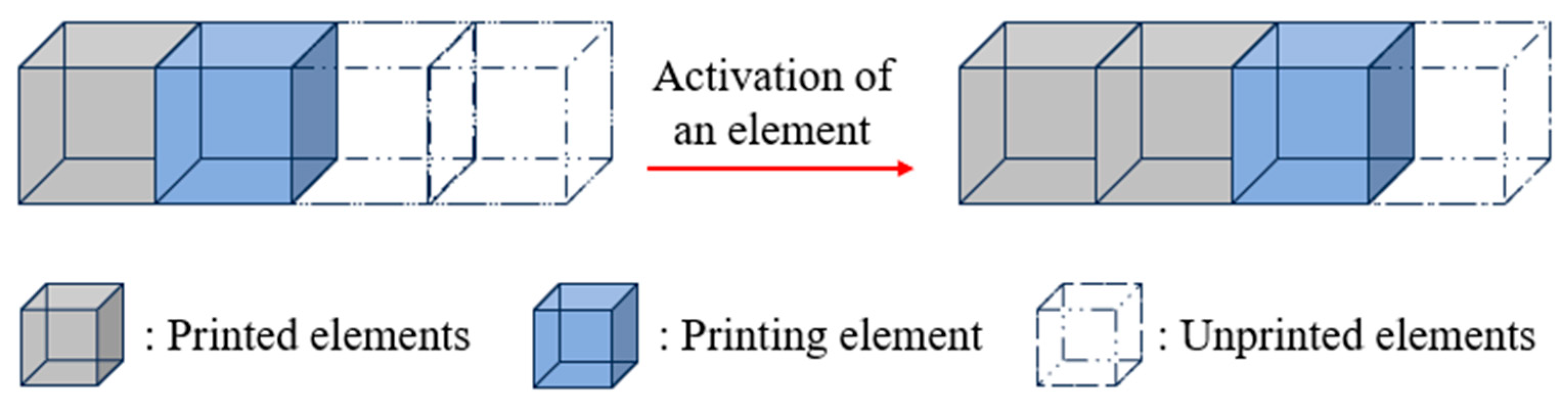
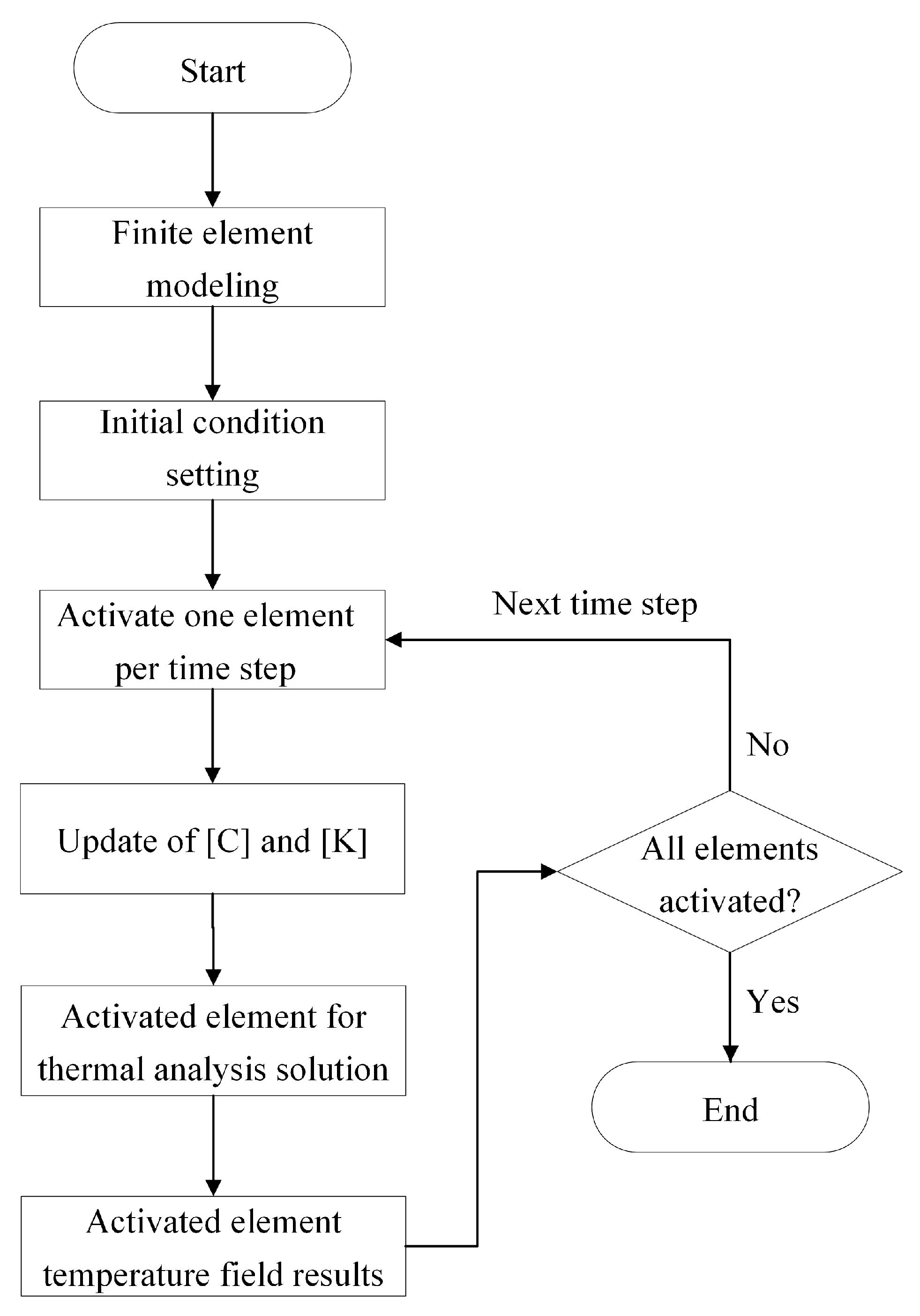
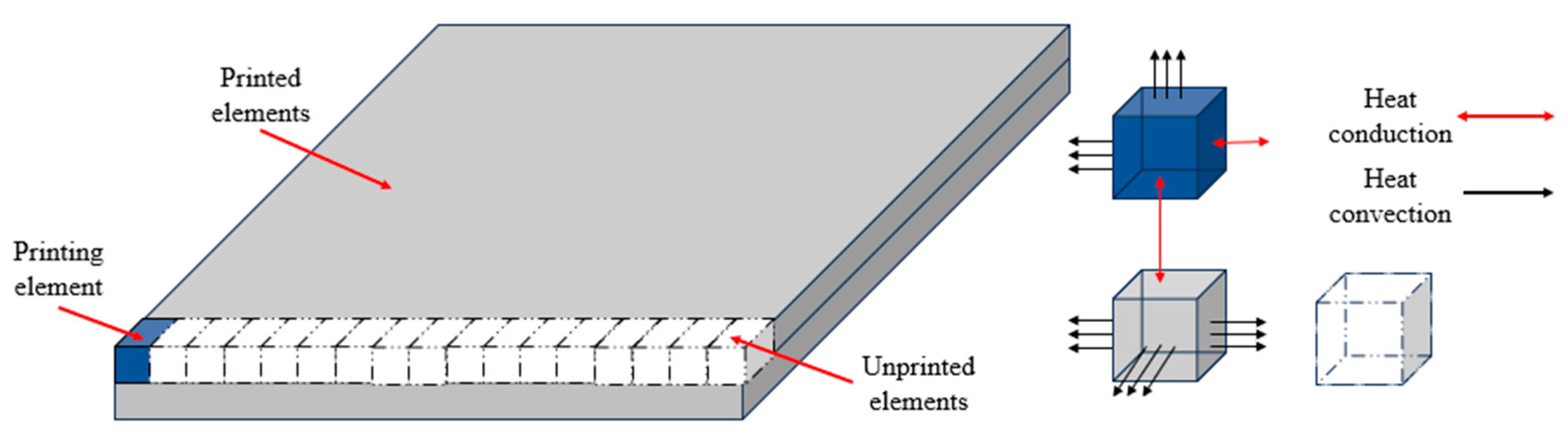
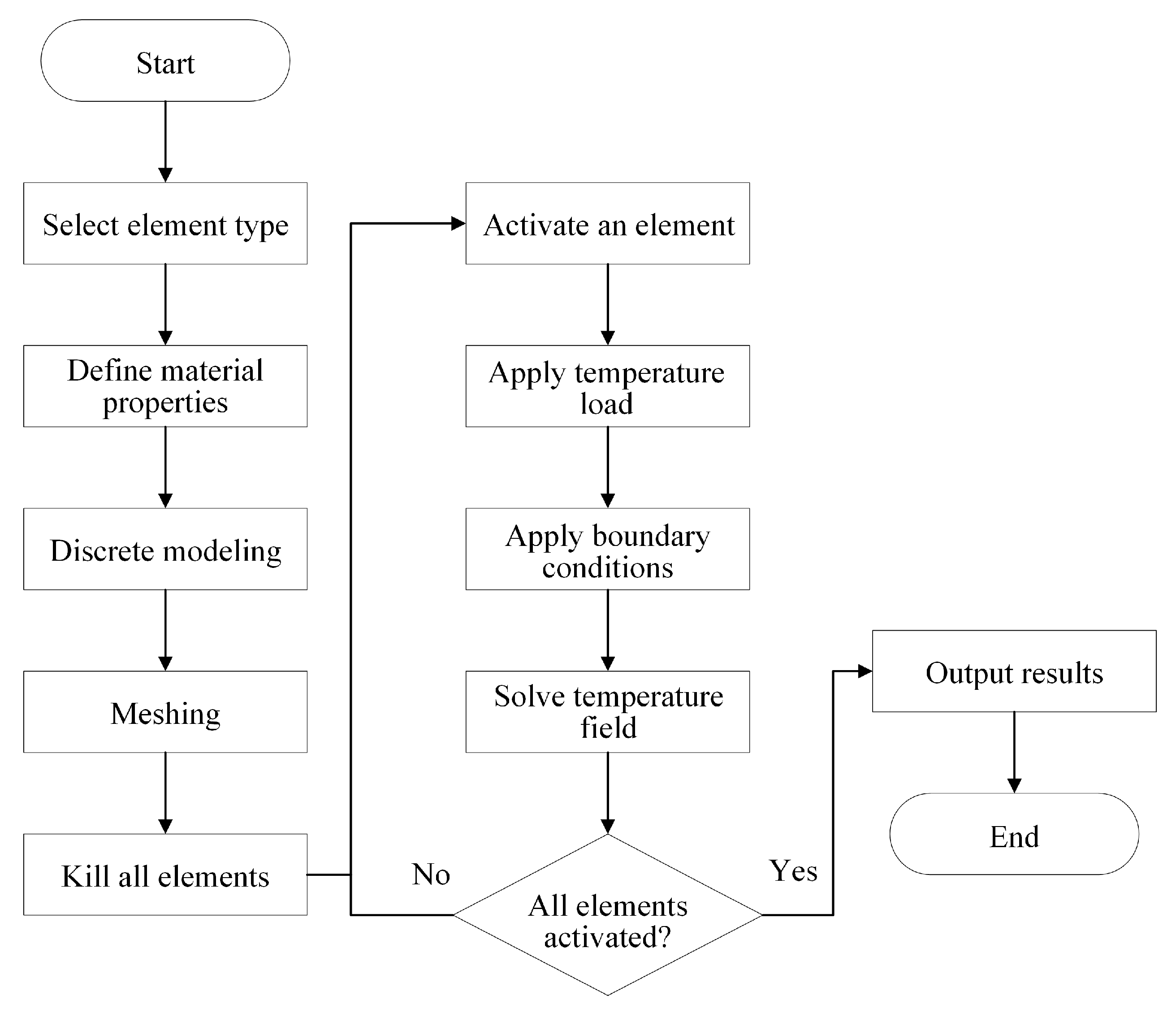
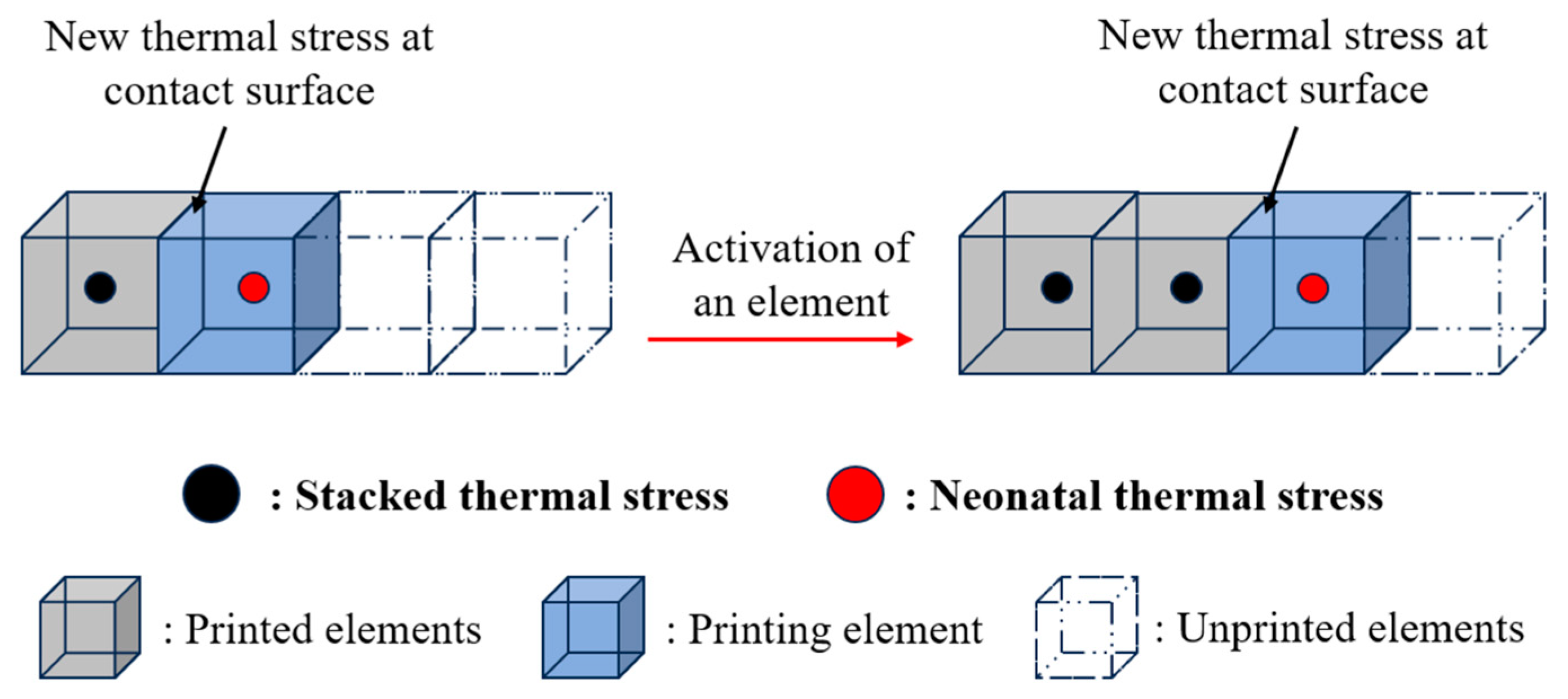
2.3.1. Birth–Death Element Method
2.3.2. Theory of Thermal Analysis
- Heat conduction: the temperature distribution at the boundary of the printed part:where denotes the time-varying temperature of activated elements that have been previously solved. The subscript denotes the boundary of the printed part.
- Heat convection: the convective heat transfer between the printed part and air medium in contact:where , , denote the thermal conductivity in X, Y, Z directions, respectively; , , denote the directional cosines of the boundary normal; h denotes the convective heat transfer coefficient; and T denotes the surface temperature of the printed part. The meaning of depends on the thermal convection conditions. Under natural convection conditions, denotes the ambient or medium temperature; under forced convection conditions, denotes the wall temperature of the boundary layer.
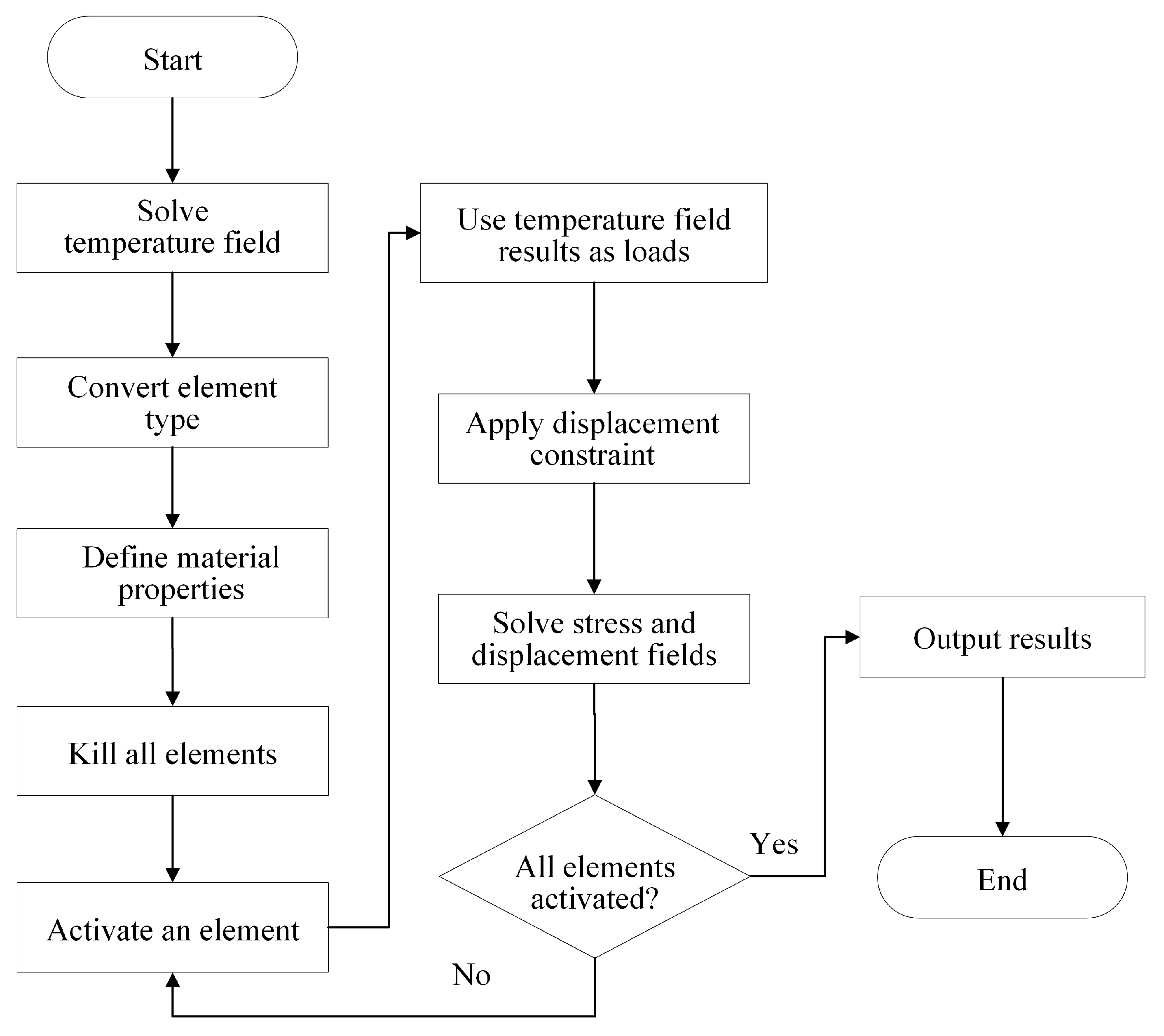
2.3.3. Theory of Thermo-Mechanical Coupling Analysis
3. Results and Discussions
3.1. Finite Element Simulation and Experimental Setup
3.2. Application Indication
3.3. Numercial Examples
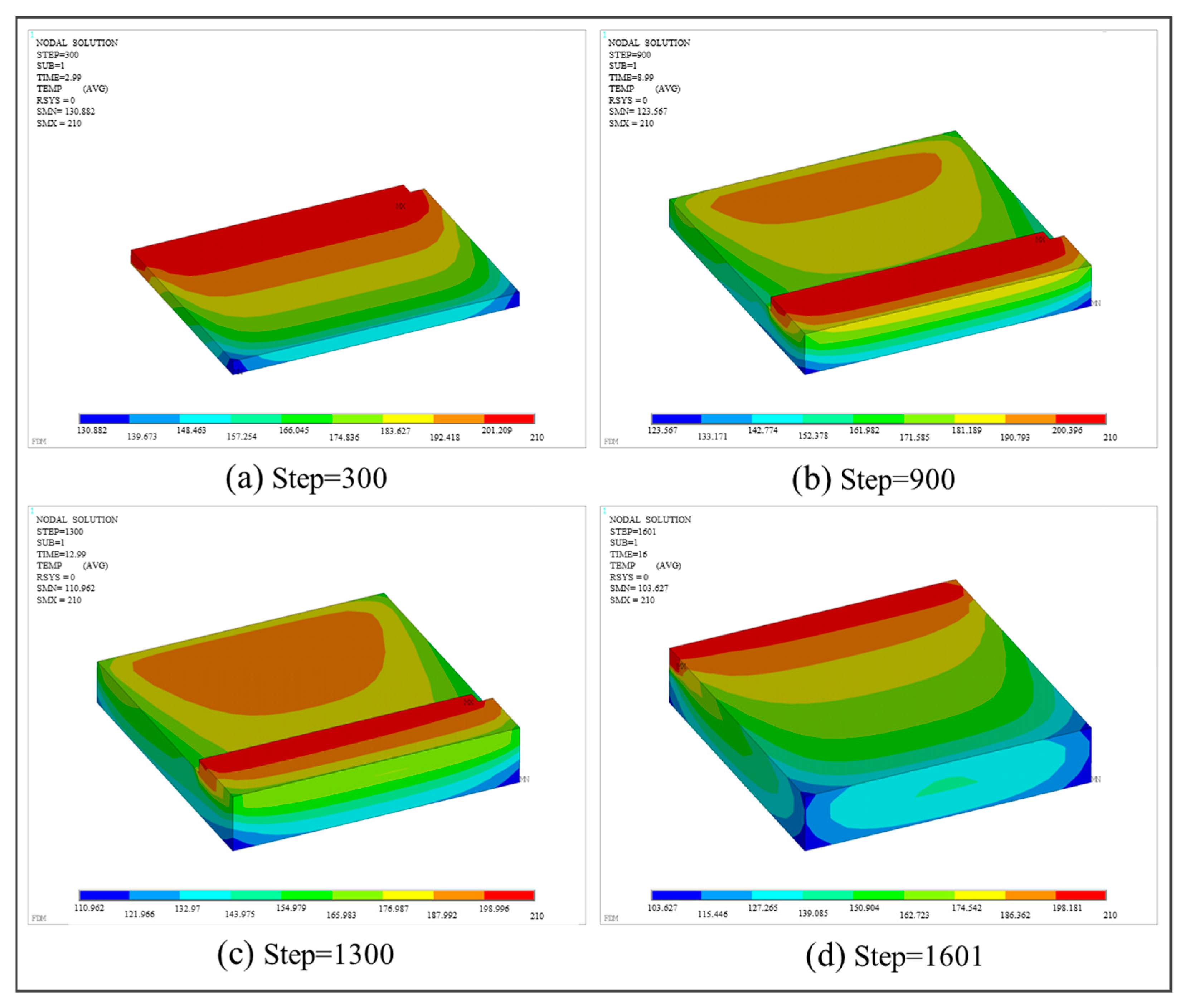
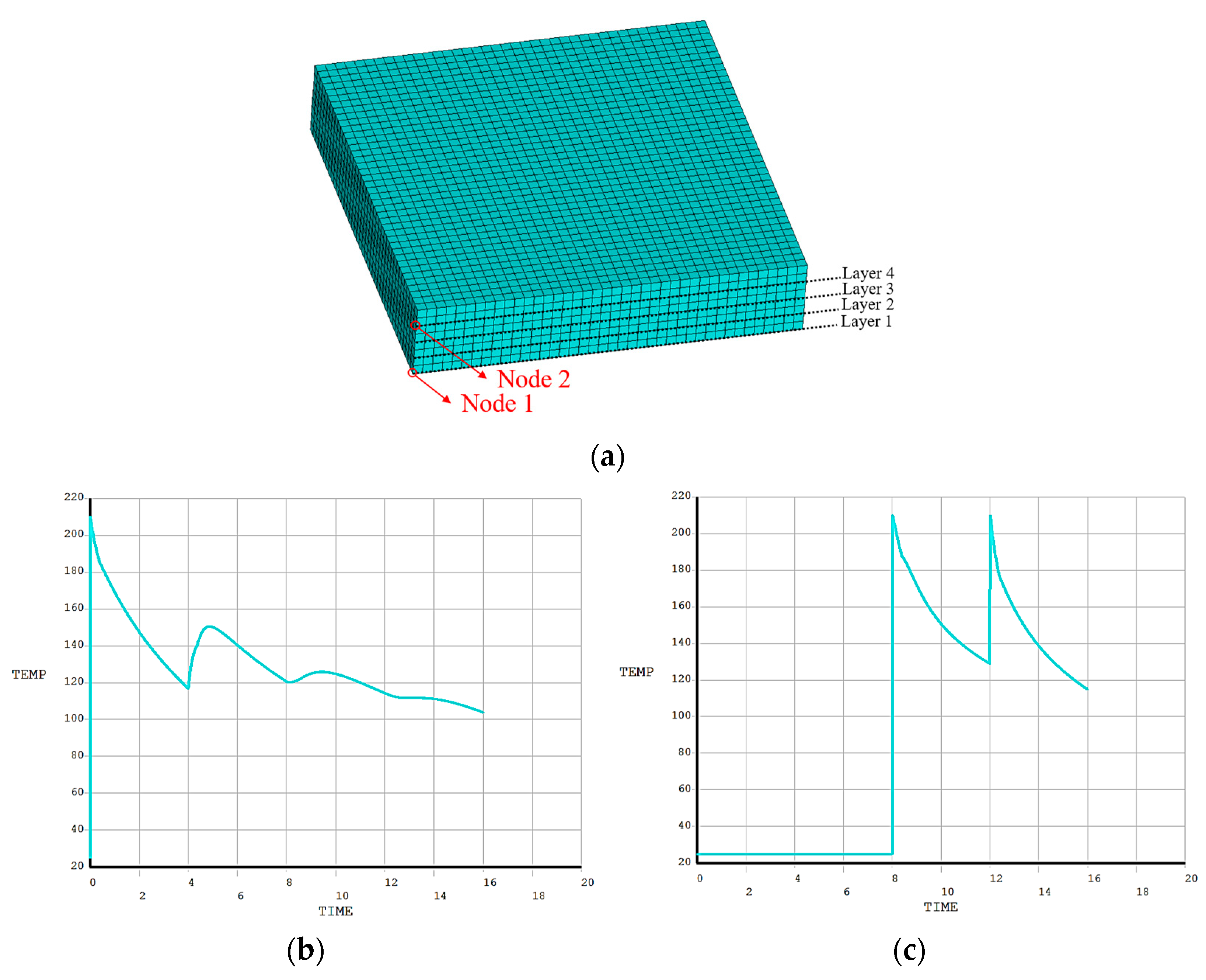
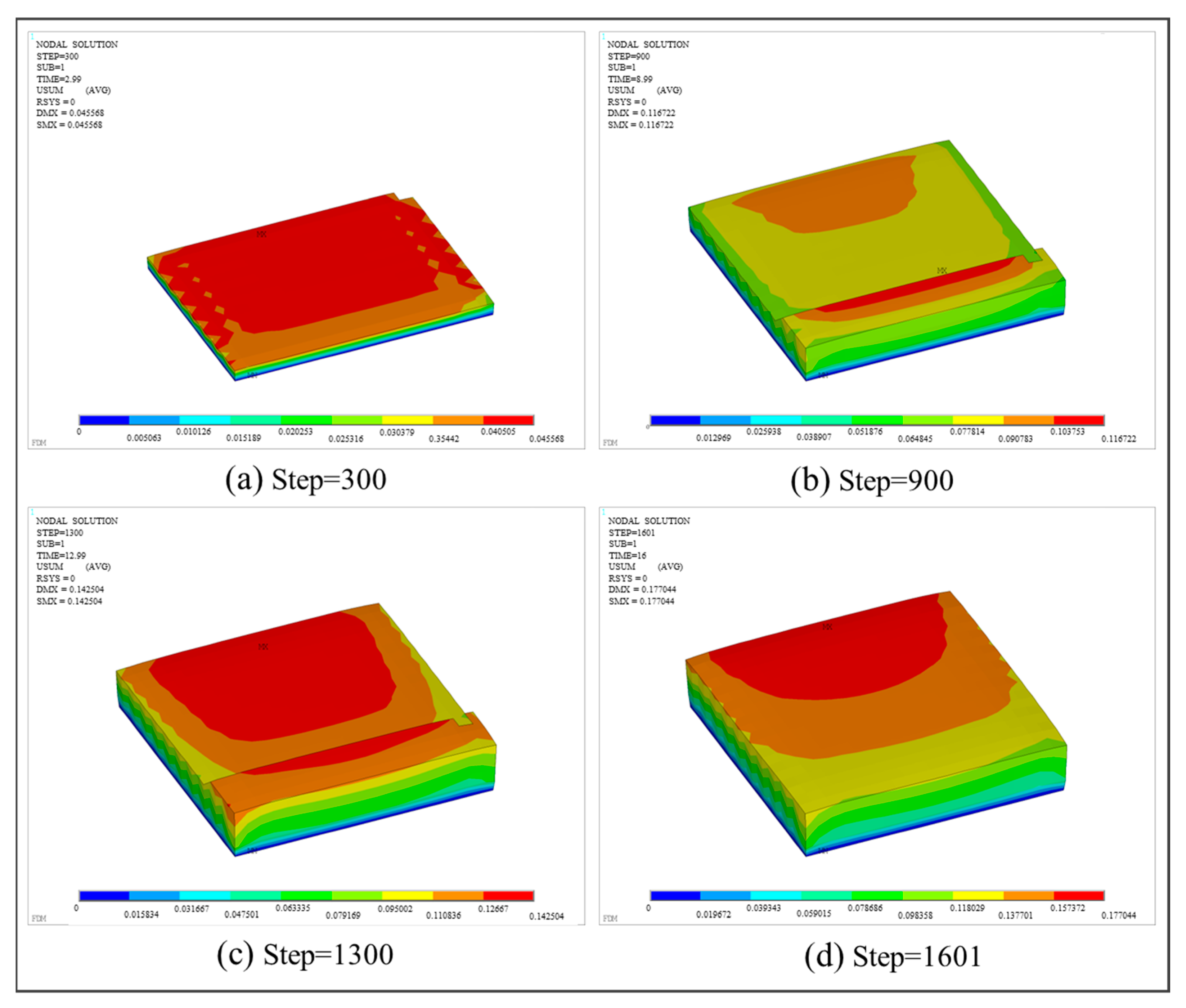
3.3.1. Square Plate Structure
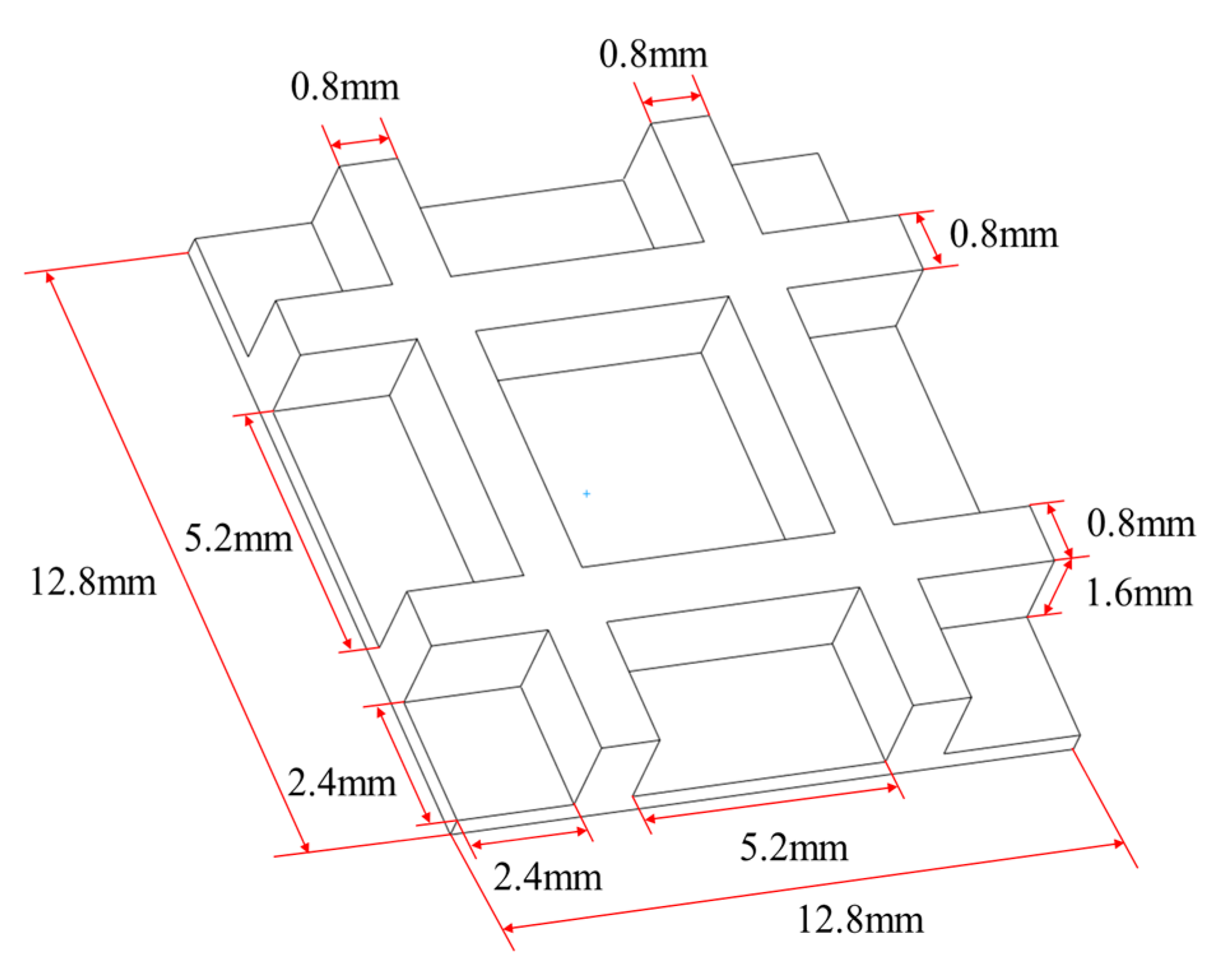
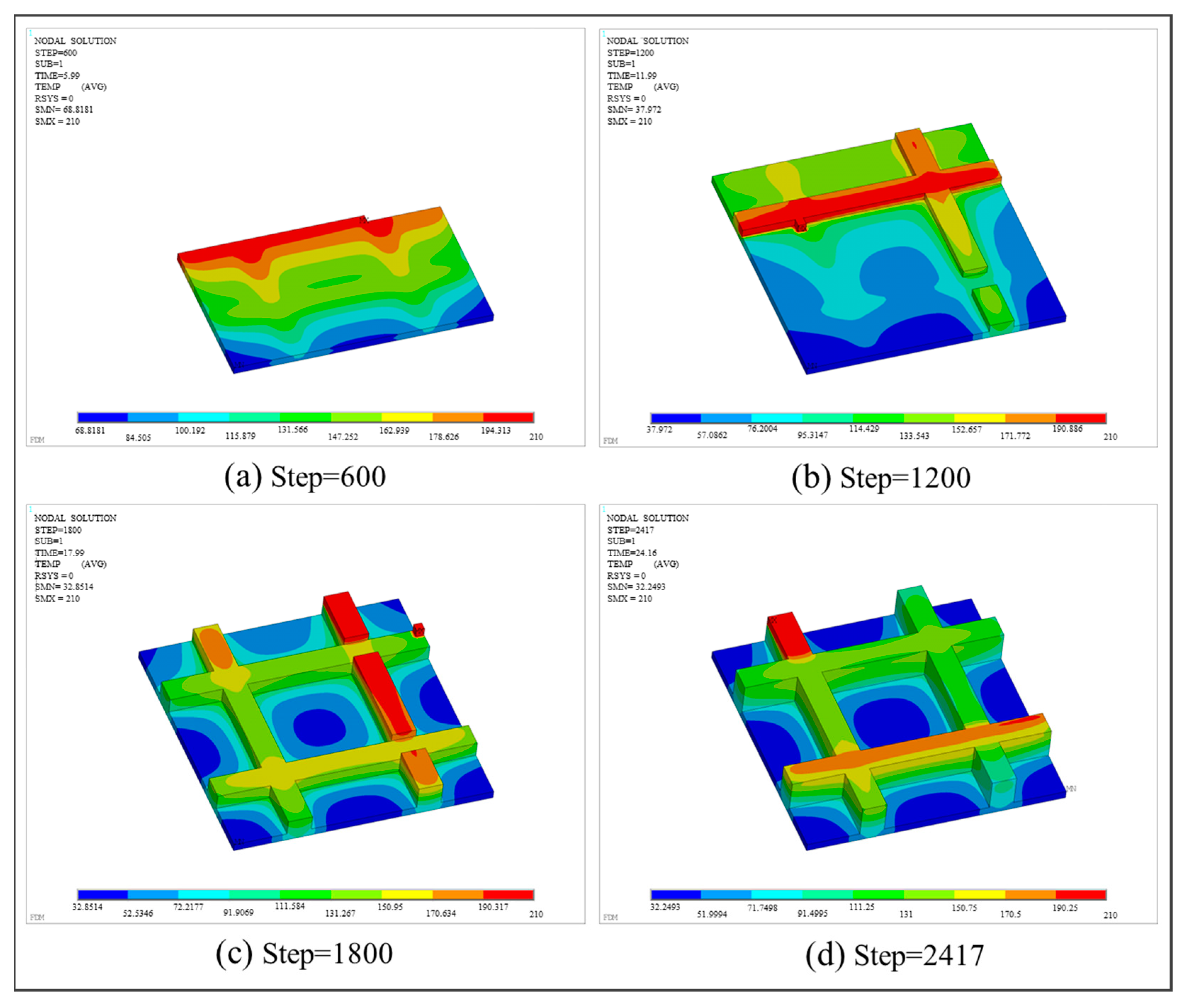
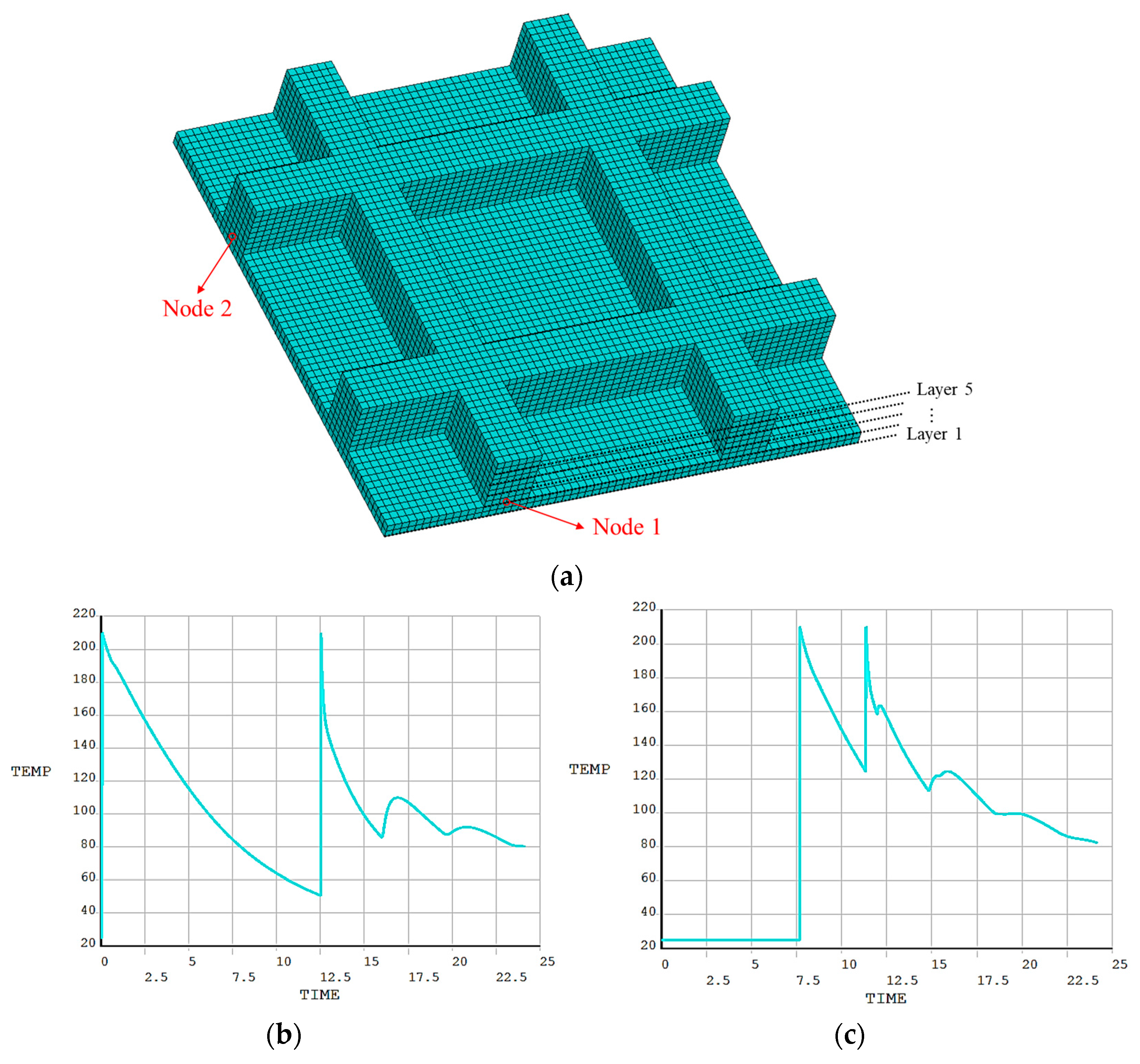
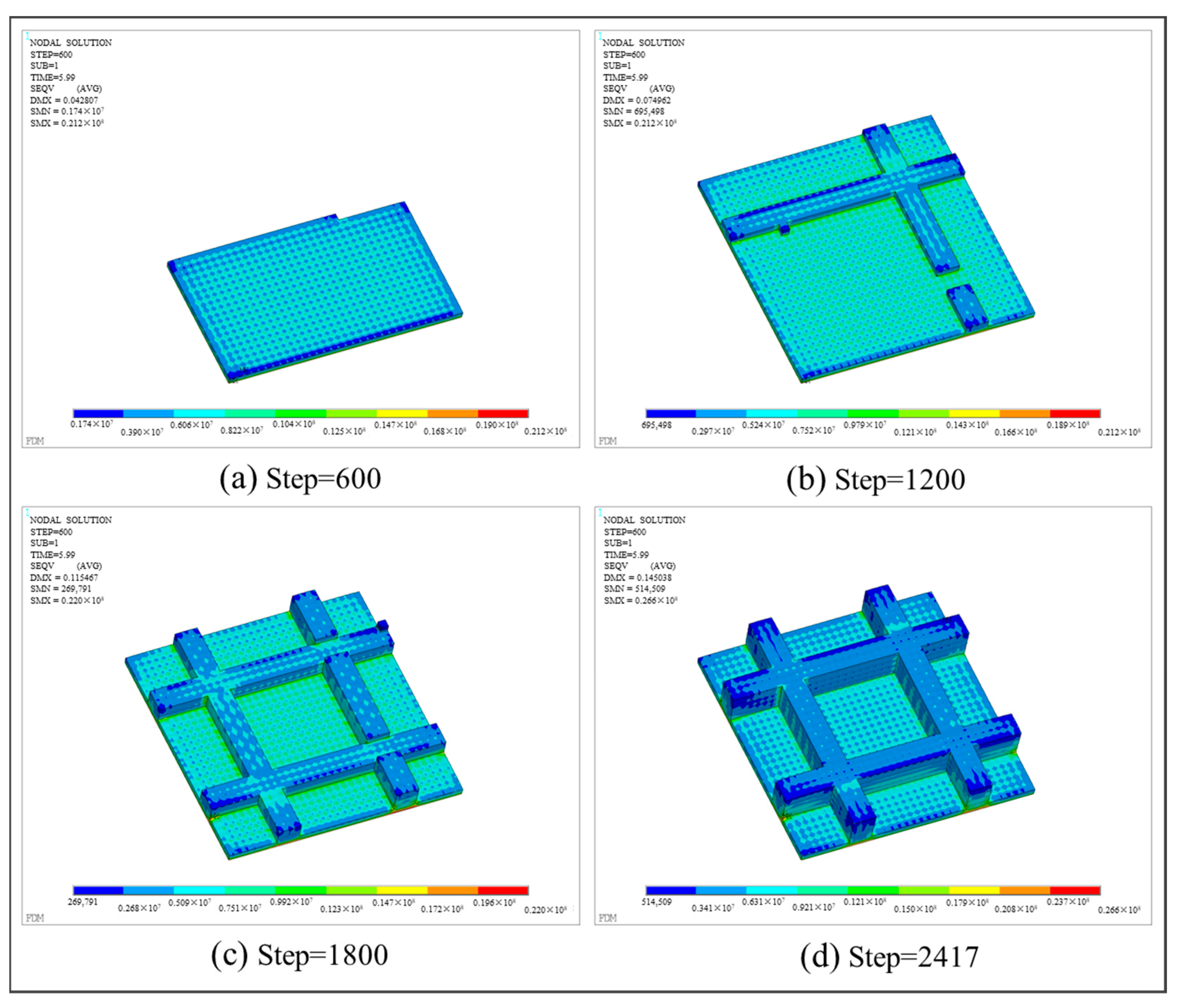
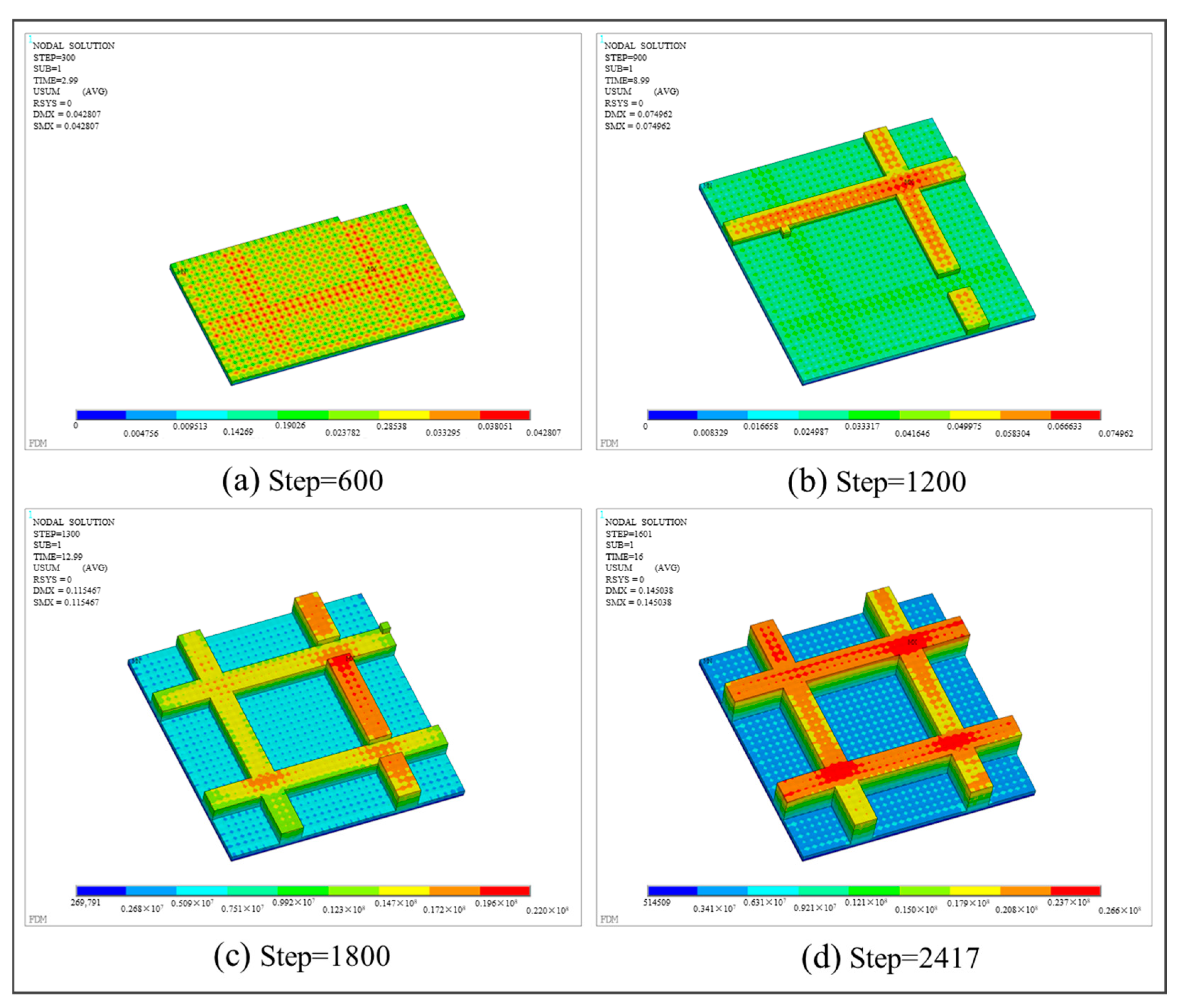
3.3.2. Grid Plate Structure
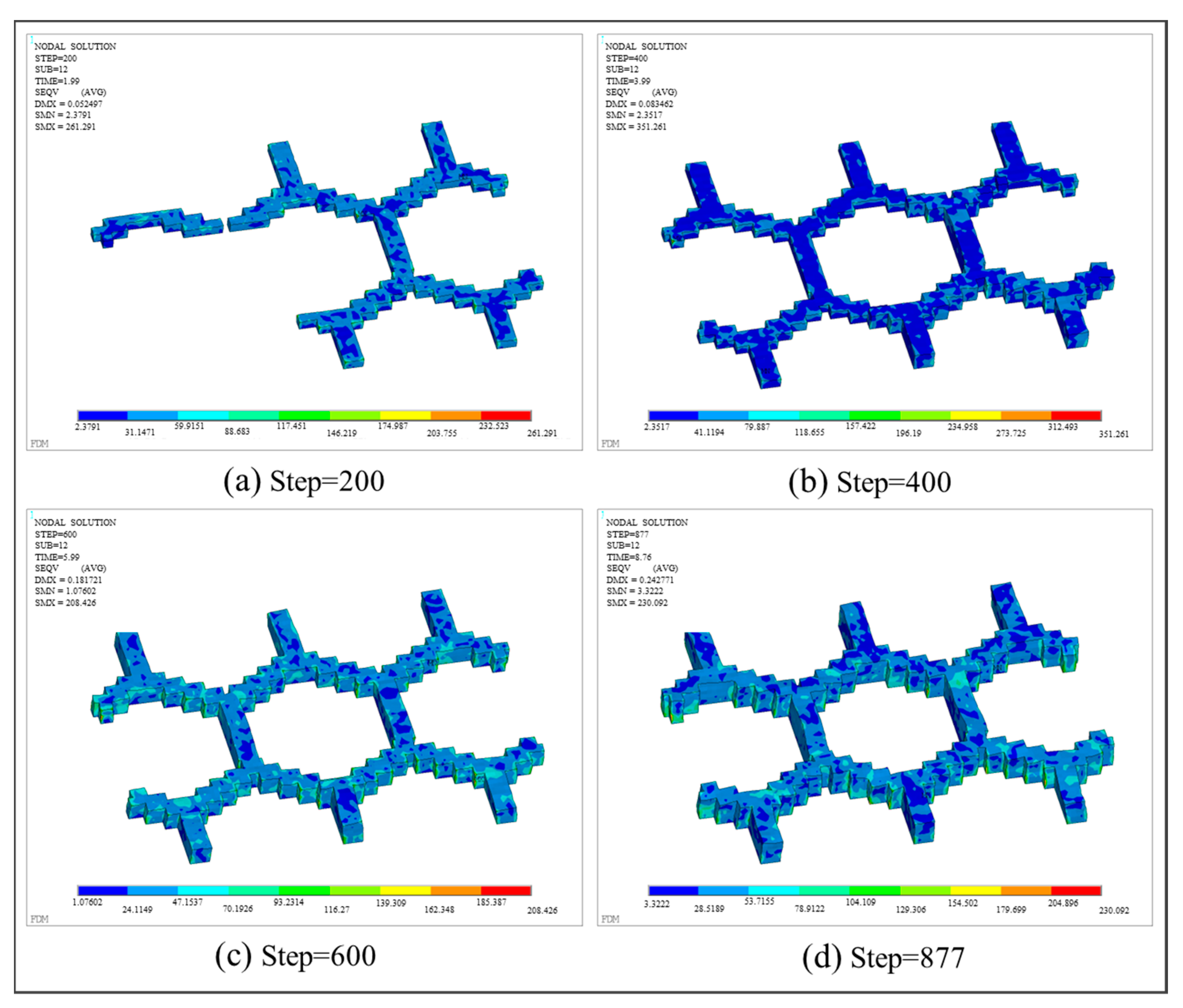
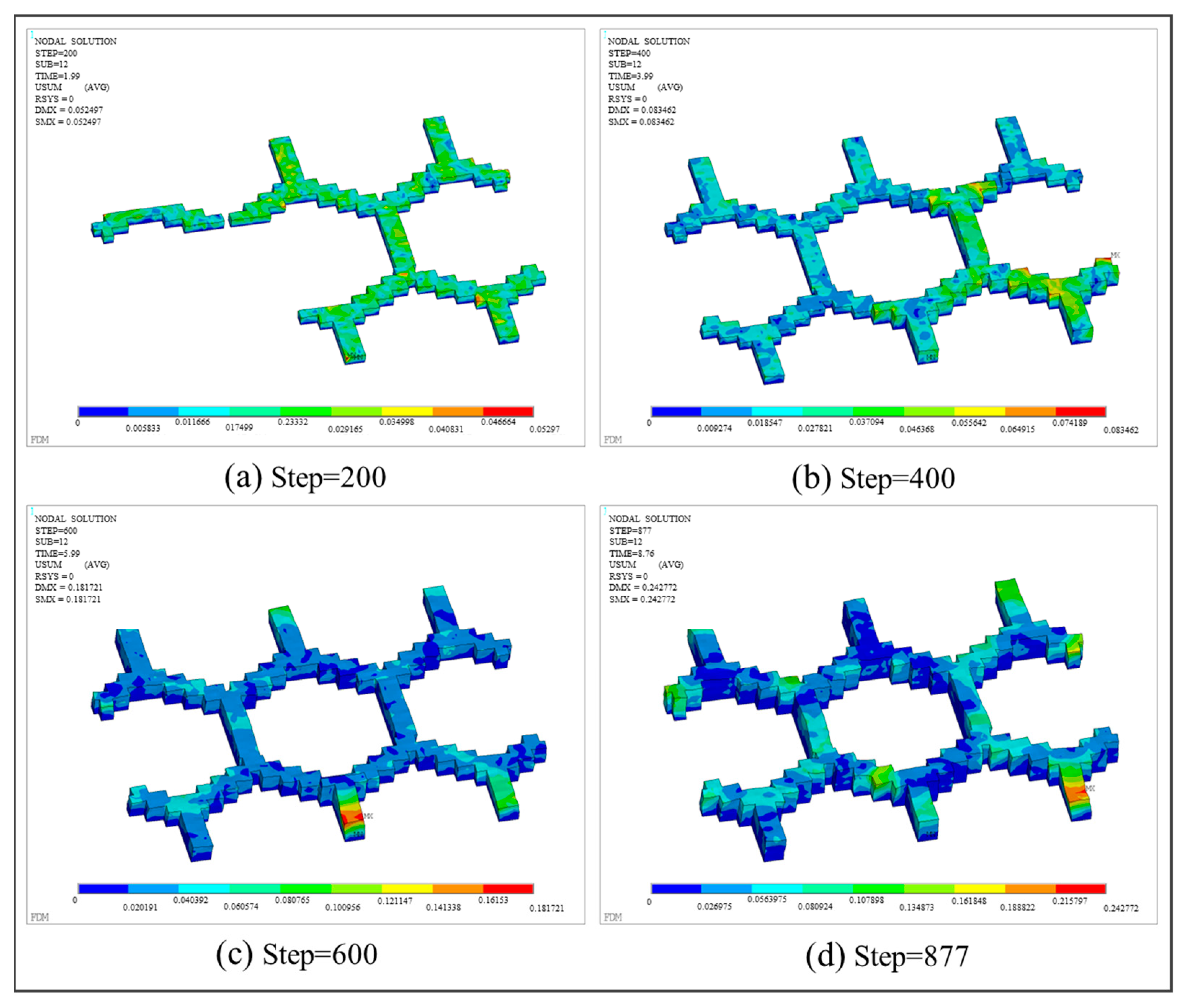
3.3.3. Honeycomb Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, N.Z.; Parthasarathy, M.; Patil, S.; Coates, D.; Myers, K.; Zhu, H.Y.; Li, W. Direct additive manufacturing of metal parts for automotive applications. J. Manuf. Syst. 2023, 68, 368–375. [Google Scholar] [CrossRef]
- Pierre, J.; Iervolino, F.; Farahani, R.D.; Piccirelli, N.; Lévesque, M.; Therriault, D. Material extrusion additive manufacturing of multifunctional sandwich panels with load-bearing and acoustic capabilities for aerospace applications. Addit. Manuf. 2022, 61, 103344. [Google Scholar] [CrossRef]
- Tamez, M.B.A.; Taha, I. A review of additive manufacturing technologies and markets for thermosetting resins and their potential for carbon fiber integration. Addit. Manuf. 2021, 37, 101748. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Li, S.X.; Rao, Y.N.; Le Duigou, A.; Wang, K.; Ahzi, S. 3D printed continuous fiber reinforced composite lightweight structures: A review and outlook. Compos. Part. B-Eng. 2023, 250, 110450. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Panghal, D.; Kumar, S. Fused deposition modeling: A review. Rapid. Prototyping. J. 2020, 26, 176–201. [Google Scholar] [CrossRef]
- Li, M.Y.; Xu, Y.A.; Fang, J.G. Orthotropic mechanical properties of PLA materials fabricated by fused deposition modeling. Thin. Wall. Struct. 2024, 199, 111800. [Google Scholar] [CrossRef]
- Zaki, R.M.; Strutynski, C.; Kaser, S.; Bernard, D.; Hauss, G.; Faessel, M.; Sabatier, J.; Canioni, L.; Messaddeq, Y.; Danto, S.; et al. Direct 3D-printing of phosphate glass by fused deposition modeling. Mater. Design. 2020, 194, 108957. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, X.; Kong, L.B.; Dong, G.X.; Remani, A.; Leach, R. Defect inspection technologies for additive manufacturing. Int. J. Extreme. Manuf. 2021, 3, 022002. [Google Scholar] [CrossRef]
- Xu, L.Y.; Zhang, X.X.; Ma, F.; Chang, G.Y.; Zhang, C.; Li, J.M.; Wang, S.X.; Huang, Y.Y. Detecting defects in fused deposition modeling based on improved YOLO v4. Mater. Res. Express. 2023, 10, 095304. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Bozic, Z.; Zolfagharian, A.; Reinicke, T. Failure analysis of 3D-printed PLA components: Impact of manufacturing defects and thermal ageing. Eng. Fail. Anal. 2022, 136, 106214. [Google Scholar] [CrossRef]
- Mohd, N.A.; Abdul, R.M. Analysis on Dimensional Accuracy of 3D Printed Parts by Taguchi Approach; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2021; pp. 219–231. [Google Scholar]
- Hariri-Ardebili, M.A.; Furgani, L.; Salamon, J.; Rezakhani, R.; Xu, J. Numerical simulation of large-scale structural systems. Adv. Mech. Eng. 2019, 11, 1–5. [Google Scholar] [CrossRef]
- Ojeda-López, A.; Botana-Galvín, M.; González-Rovira, L.; Botana, F.J. Numerical Simulation as a Tool for the Study, Development, and Optimization of Rolling Processes: A Review. Metals 2024, 14, 737. [Google Scholar] [CrossRef]
- Paul, S. FE analysis in fused deposition modeling research: A literature review. Measurement 2021, 178, 109320. [Google Scholar] [CrossRef]
- Al Rashid, A.; Koc, M. Fused Filament Fabrication Process: A Review of Numerical Simulation Techniques. Polymers 2021, 13, 3534. [Google Scholar] [CrossRef]
- Zouaoui, M.; Gardan, J.; Lafon, P.; Makke, A.; Labergere, C.; Recho, N. A FE Method to Predict the Mechanical Behavior of a Pre-Structured Material Manufactured by Fused Filament Fabrication in 3D Printing. Appl. Sci. 2021, 11, 5075. [Google Scholar] [CrossRef]
- Hachimi, T.; Majid, F.; Zekriti, N.; Rhanim, R.; Rhanim, H. Improvement of 3D printing polymer simulations considering converting G-code to Abaqus. Int. J. Adv. Manuf. Technol. 2024, 131, 5193–5208. [Google Scholar] [CrossRef]
- Antonio, B.; Francesco, F.; Enrico, T.; Raffaella, D.S.; Alfredo, L. Geometry reconstruction for additive manufacturing: From G-CODE to 3D CAD model. Mater. Today Proc. 2022, 75, 16–22. [Google Scholar]
- Gleadall, A. FullControl GCode Designer: Open-source software for unconstrained design in additive manufacturing. Addit. Manuf. 2021, 46, 102109. [Google Scholar] [CrossRef]
- Gahbiche, M.A.; Boudhaouia, S.; Giraud, E.; Ayed, Y.; Santo, P.D.; Salem, W.B. A FE simulation of the incremental sheet forming process: A new method for G-code implementation. Int. J. Mater. Prod. Tec. 2020, 61, 68–86. [Google Scholar] [CrossRef]
- Zeradam, Y.; Arkanti, K. Extraction of Coordinate Points for the Numerical Simulation of Single Point Incremental Forming Using Microsoft Excel. ICETE 2020, 2, 577–586. [Google Scholar]
- Zeradam, Y.; Arkanti, K. Spiral Toolpath Definition and G-code Generation for Single Point Incremental Forming. J. Mech. Eng. 2020, 17, 91–102. [Google Scholar]
- Zhang, Y.; Sang, S.; Bei, Y. Image to G-Code Conversion using JavaScript for CNC Machine Control. Acade. J. Sci. Technol. 2023, 6, 2771–3032. [Google Scholar] [CrossRef]
- Tawfik, S.M.; Nasr, M.N.A.; El Gamal, H.A. FE modeling for part distortion calculation in selective laser melting. Alex. Eng. J. 2019, 58, 67–74. [Google Scholar] [CrossRef]
- Mashhood, M.; Peters, B.; Zilian, A.; Baroli, D.; Wyart, E. Developing the AM G-code based thermomechanical FE platform for the analysis of thermal deformation and stress in metal additive manufacturing process. J. Mech. Sci. Technol. 2023, 37, 1103–1112. [Google Scholar] [CrossRef]
- Yue, M.K.; Li, M.E.; An, N.; Yang, K.; Wang, J.; Zhou, J.X. Modeling SEBM process of tantalum lattices. Rapid. Prototyping. J. 2023, 29, 232–245. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Li, H.; Feng, H. Simulation of Temperature Field in FDM Process. IOP. Conf. Ser. Mater. Sci. Eng. 2019, 677, 032080. [Google Scholar] [CrossRef]
- Akbar, I.; Hadrouz, M.E.; Mansori, M.E.; Lagoudas, D. Continuum and subcontinuum simulation of FDM process for 4D printed shape memory polymers. J. Manuf. Process. 2022, 76, 335–348. [Google Scholar] [CrossRef]
- Syrlybayev, D.; Zharylkassyn, B.; Seisekulova, A.; Perveen, A.; Talamona, D. Optimization of the Warpage of Fused Deposition Modeling Parts Using FE Method. Polymers 2021, 13, 3849. [Google Scholar] [CrossRef]
- Samy, A.A.; Golbang, A.; Harkin-Jones, E.; Archer, E.; McIlhagger, A. Prediction of part distortion in Fused Deposition Modeling (FDM) of semi-crystalline polymers via COMSOL: Effect of printing conditions. CIRP J. Manuf. Sci. Tec. 2021, 33, 443–453. [Google Scholar] [CrossRef]
- Schmidt, A.M.; Kyosev, Y. Particle based simulation of the polymer penetration into porous structures during the fused deposition modeling. J. Manuf. Process. 2023, 101, 1205–1213. [Google Scholar] [CrossRef]
- Lei, M.J.; Wei, Q.H.; Li, M.Y.; Zhang, J.; Yang, R.B.; Wang, Y.N. Numerical Simulation and Experimental Study the Effects of Process Parameters on Filament Morphology and Mechanical Properties of FDM 3D Printed PLA/GNPs Nanocomposite. Polymers 2022, 14, 3081. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.M.; Ying, L. Hybrid modelling method for the prediction and experimental validation of 3D printing resource consumption. J. Manuf. Process. 2023, 101, 1275–1300. [Google Scholar] [CrossRef]
- Liu, B.S.; Dong, B.X.; Li, H.M.; Lou, R.S.; Chen, Y. 3D printing finite element analysis of continuous fiber reinforced composite materials considering printing pressure. Compos. Part. B-Eng. 2024, 227, 111397. [Google Scholar] [CrossRef]
- Jiang, H.; Man, Z.Z.; Guo, Z.F.; Feng, W.W.; Yang, Z.Y.; Lei, Z.K.; Bai, R.X.; Yan, S.T.; Cheng, B. Determination of residual stress field in laser cladding using finite element updating method driven by contour deformation. Opt. Laser. Technol. 2024, 179, 111371. [Google Scholar] [CrossRef]
- Chen, G.G.; Wang, D.S.; Hua, W.J.; Wu, W.B.; Zhou, W.Y.; Jin, Y.F.; Zheng, W.X. Simulating and Predicting the Part Warping in Fused Deposition Modeling by Thermal–Structural Coupling Analysis. 3D Print. Addit. Manuf. 2021, 10, 70–82. [Google Scholar] [CrossRef]









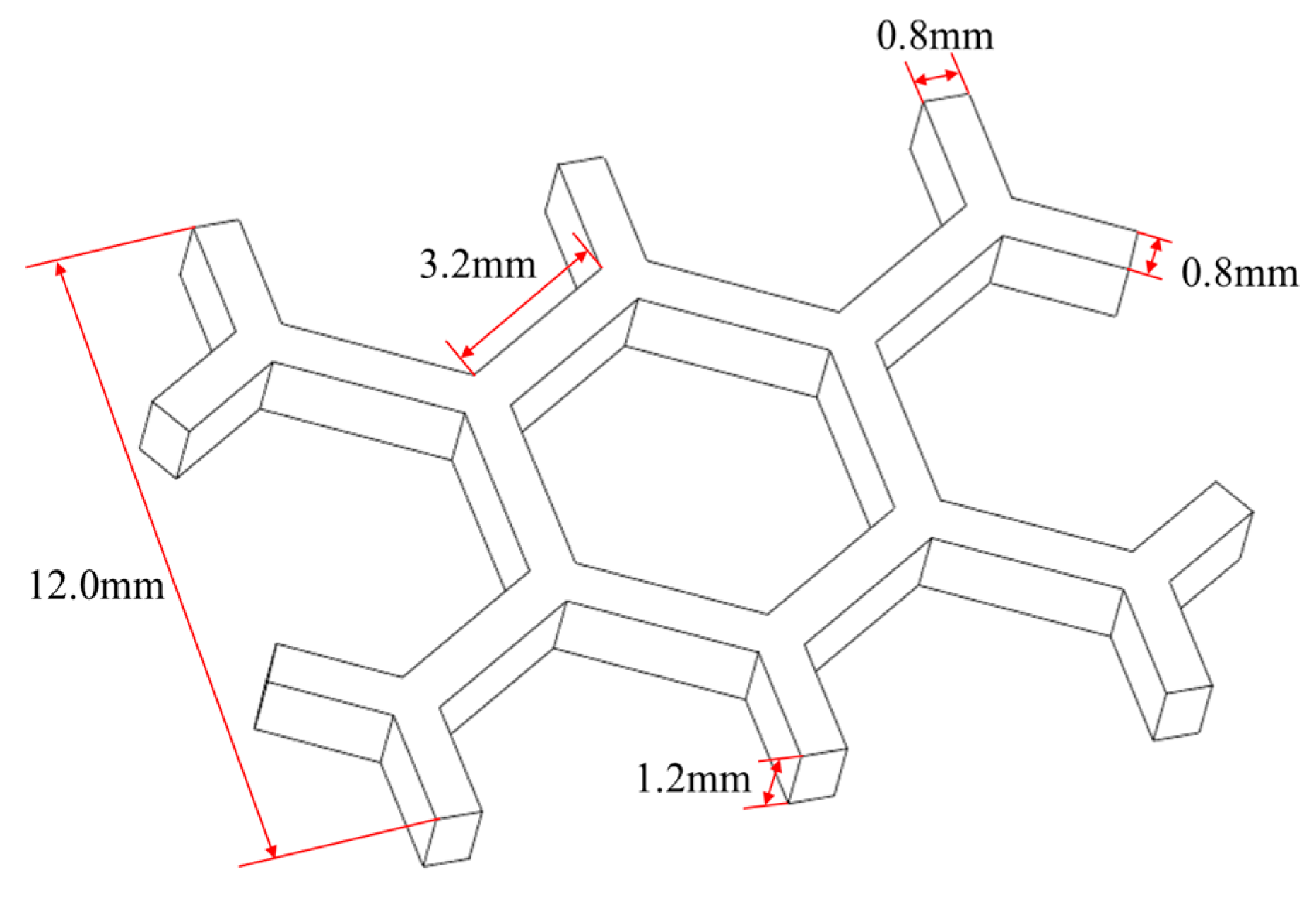
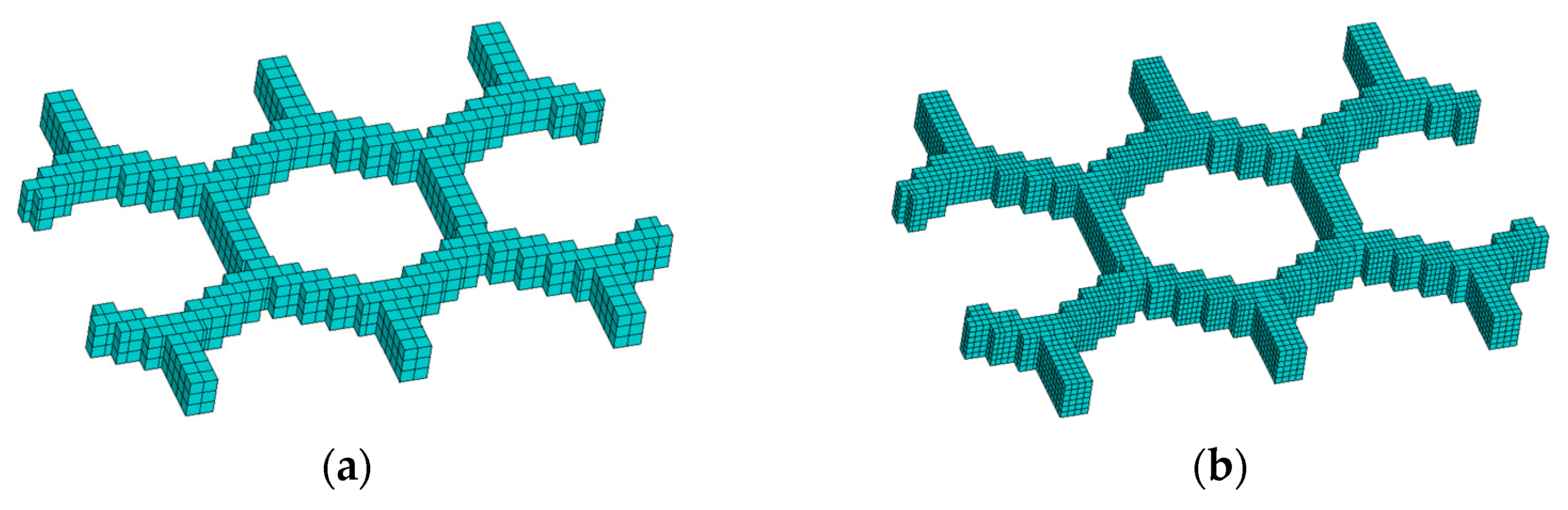
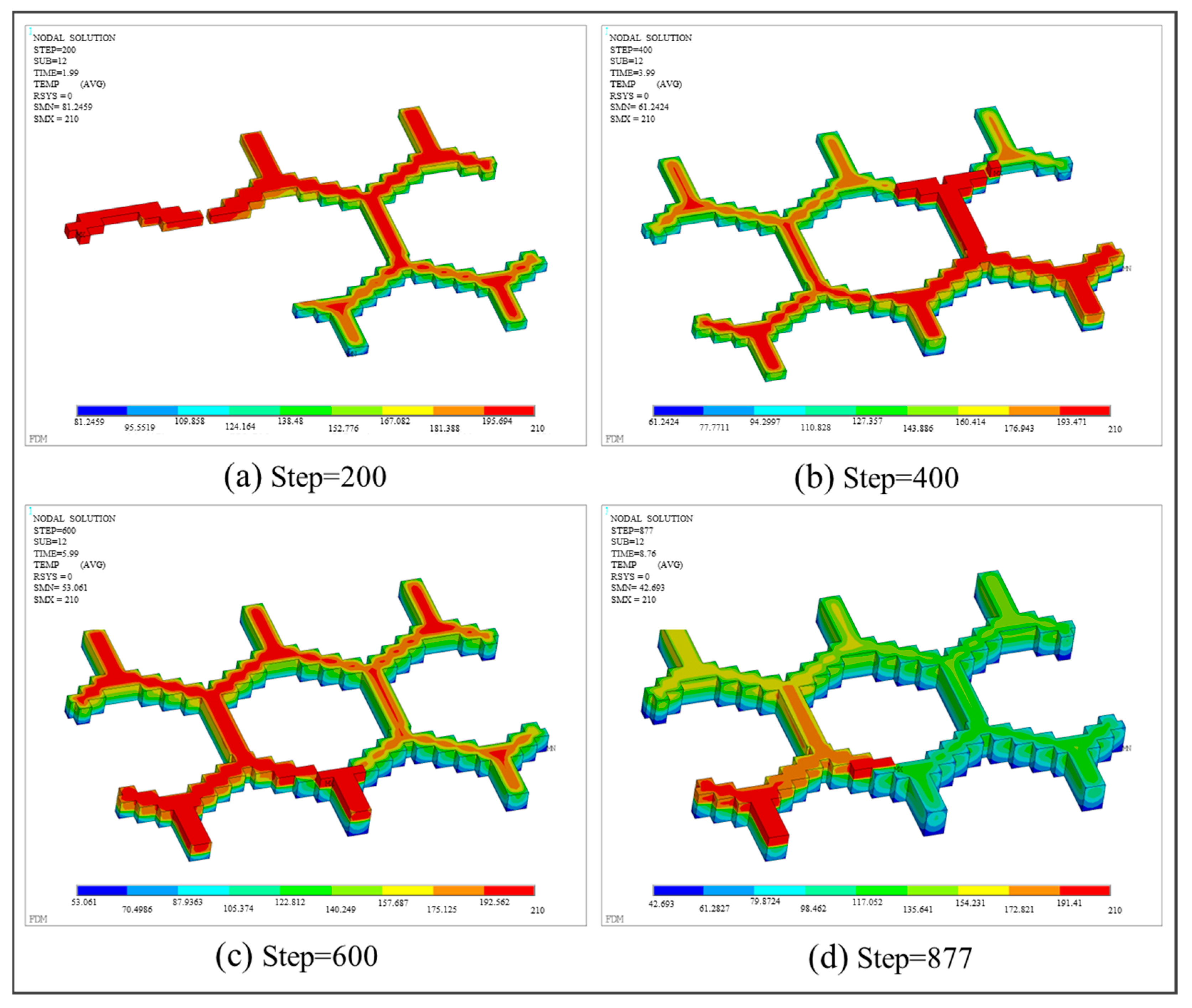

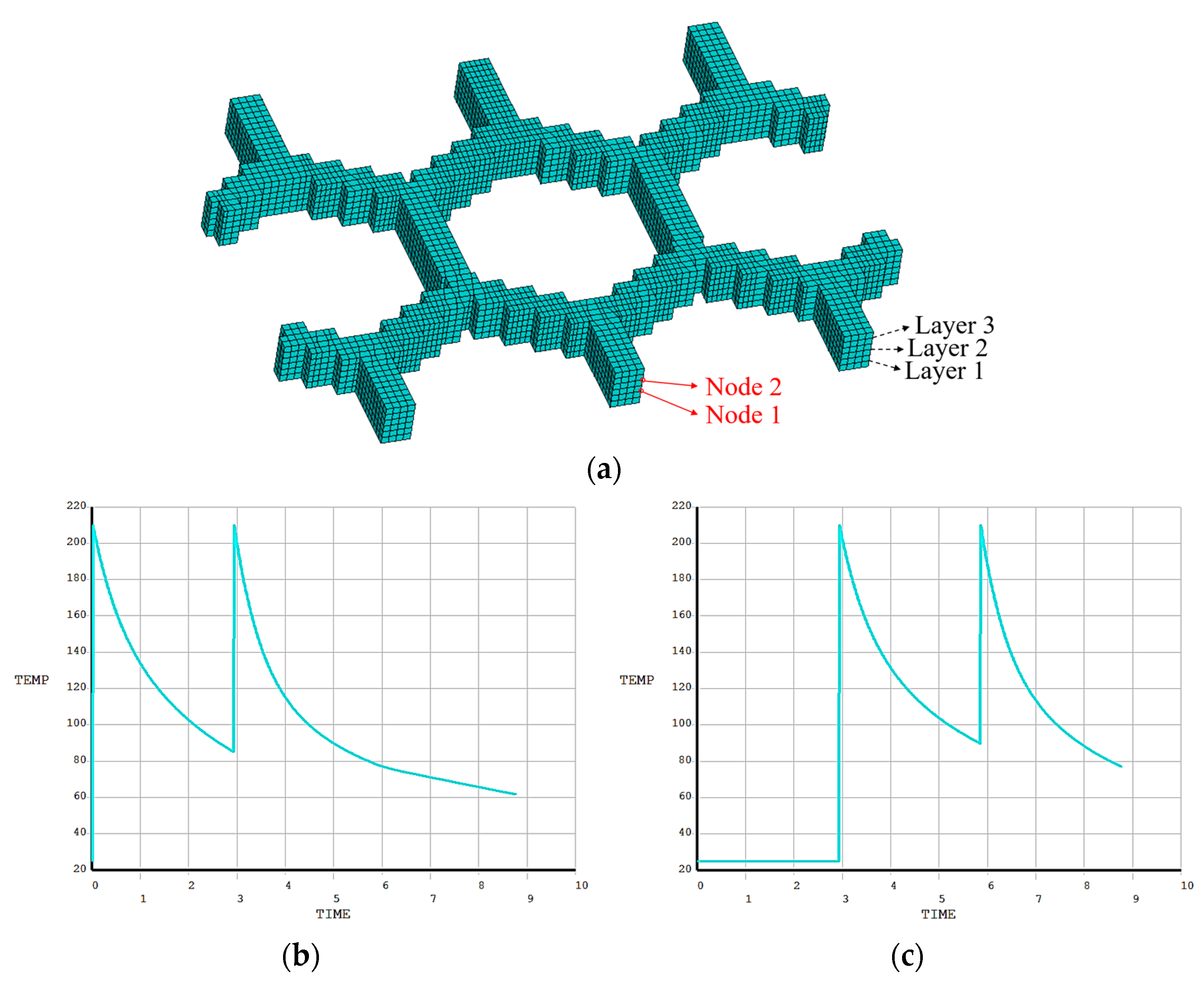

| Machine Operations | G-Code Commands | Meanings | Parameters | Meanings |
|---|---|---|---|---|
| Linear nozzle movement | G0 | Linear movement without material extrusion | F | Material feeding rate (mm/min) |
| G1 | Linear movement with material extrusion | X | Target coordinate on the X-axis | |
| Nozzle heating | M104 | Start heating the nozzle to the target temperature | Y | Target coordinate on the Y-axis |
| M109 | Wait for the nozzle to heat to the target temperature | Z | Target coordinate on Z-axis | |
| Hot bed heating | M140 | Start the hot bed heating to the target temperature | E | Length of material extrusion per toolpath (mm) |
| M190 | Wait for the hot bed heating to reach the target temperature | S | Target temperature (°C) |
| Software/Hardware | Configurations |
|---|---|
| Slicing software | Ultimaker Cura 5.2.1 |
| FE analysis software | Mechanical APDL Product Launcher 2022 R1 |
| Programming software | Microsoft Visual Studio 2008 (language: C++) |
| FDM material | Acrylonitrile-butadiene-styrene (ABS) |
| FDM machine | Bambu Lab X1-Carbon model 3D printer |
| Nozzle diameter | 0.4 mm |
| Temperature (°C) | Thermal Conductivity | Specific Heat Capacity (J) | Young’s Modulus | Poisson’s Ratio | Density (Kg/m3) | Coefficient of Thermal Expansion |
|---|---|---|---|---|---|---|
| 50 | 0.03 | 1470 | 3.50 × 105 | 0.38 | 1150 | 8.51 × 10−5 |
| 100 | 0.028 | 1490 | 2.48 × 109 | 0.39 | 1150 | 8.42 × 10−5 |
| 150 | 0.029 | 1710 | 1.68 × 109 | 0.40 | 1150 | 8.40 × 10−5 |
| 250 | 0.033 | 2020 | 0.50 × 109 | 0.41 | 1150 | 8.38 × 10−5 |
| Process Parameters | Values | Units |
|---|---|---|
| Nozzle temperature | 210 | °C |
| Hot bed temperature | 50 | °C |
| Printing speed | 40 | mm/s |
| Layer thickness | 0.4 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, F.; Dun, Y.; Li, D. Path-Based Discrete Modeling and Process Simulation for Thermoplastic Fused Deposition Modeling Technology. Polymers 2025, 17, 1026. https://doi.org/10.3390/polym17081026
Yang Z, Wang F, Dun Y, Li D. Path-Based Discrete Modeling and Process Simulation for Thermoplastic Fused Deposition Modeling Technology. Polymers. 2025; 17(8):1026. https://doi.org/10.3390/polym17081026
Chicago/Turabian StyleYang, Zhuoran, Feibo Wang, Yiheng Dun, and Dinghe Li. 2025. "Path-Based Discrete Modeling and Process Simulation for Thermoplastic Fused Deposition Modeling Technology" Polymers 17, no. 8: 1026. https://doi.org/10.3390/polym17081026
APA StyleYang, Z., Wang, F., Dun, Y., & Li, D. (2025). Path-Based Discrete Modeling and Process Simulation for Thermoplastic Fused Deposition Modeling Technology. Polymers, 17(8), 1026. https://doi.org/10.3390/polym17081026






