Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data
Abstract
1. Introduction
2. Computational Methods Used in Materials Science
3. Materials and Methods
3.1. Materials and Their Properties
3.2. Experimental Materials Design
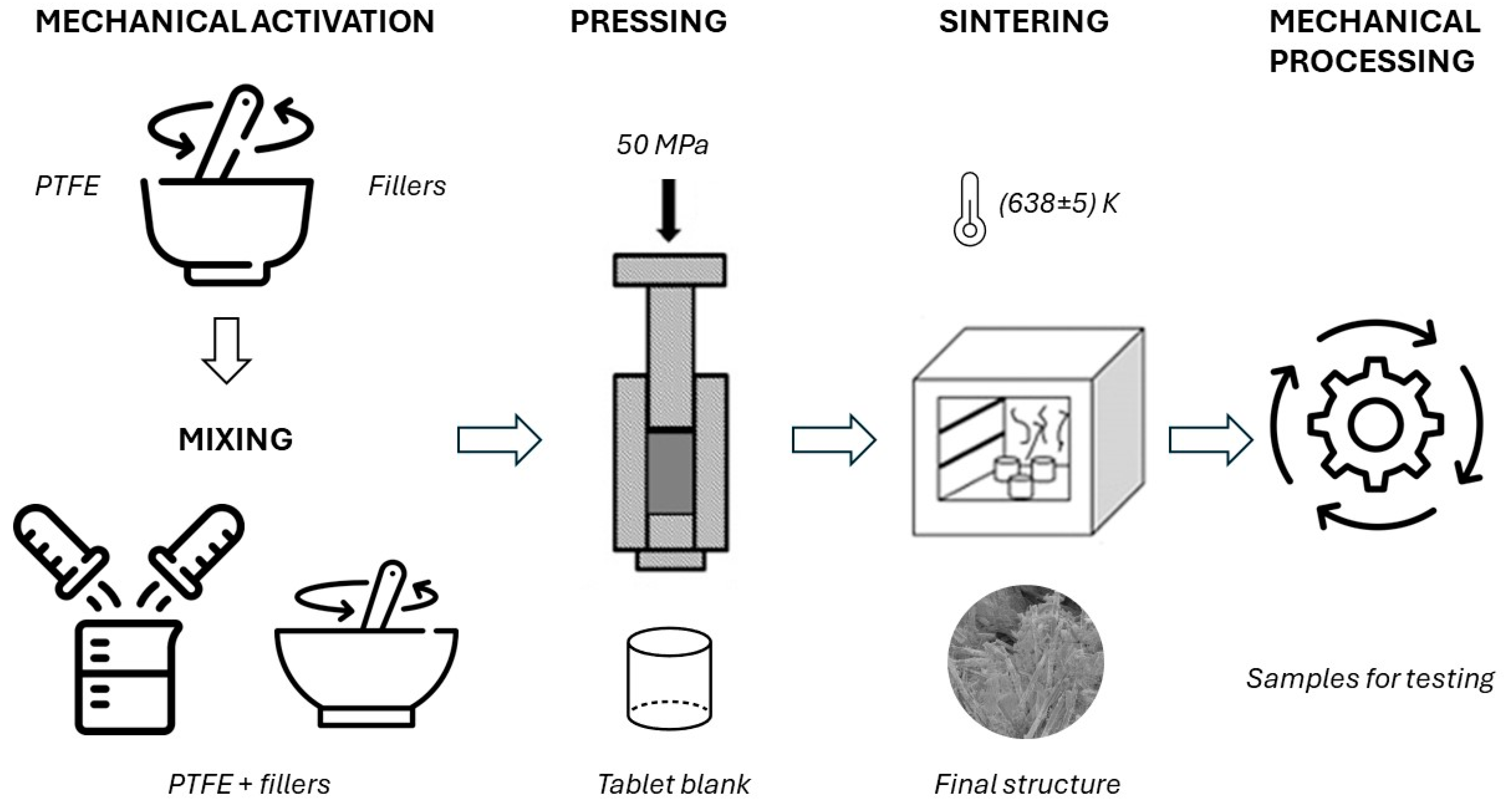
3.3. Production of Test Samples
3.4. Materials Testing
3.5. Machine Learning Approach
- Linearity (the relationship between the dependent variable and the independent variables is linear);
- Independence (observations are independent of each other);
- Homoscedasticity (constant variance of the errors);
- Normality of the errors (errors are normally distributed for statistical tests).
4. Experimental Results
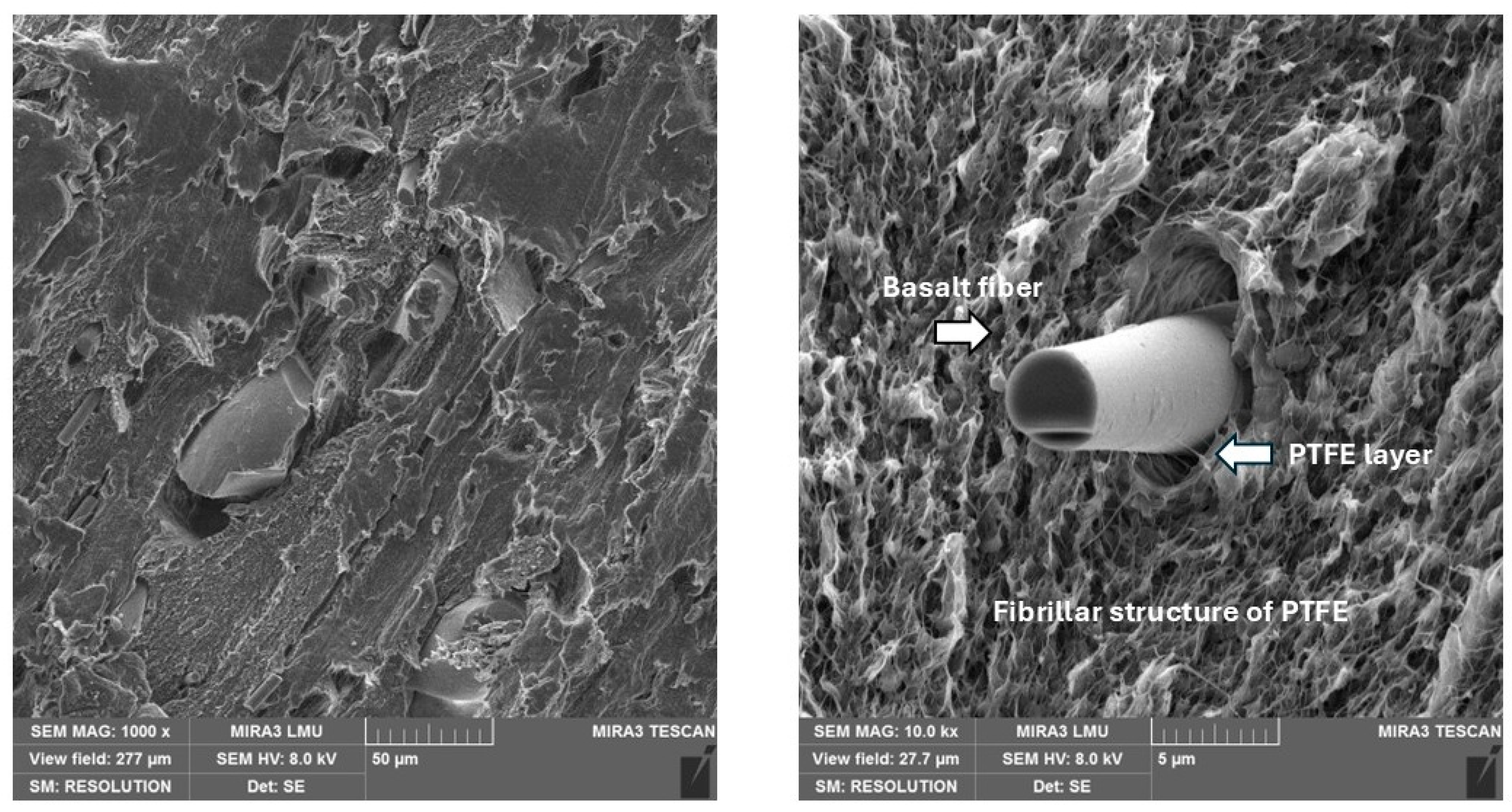
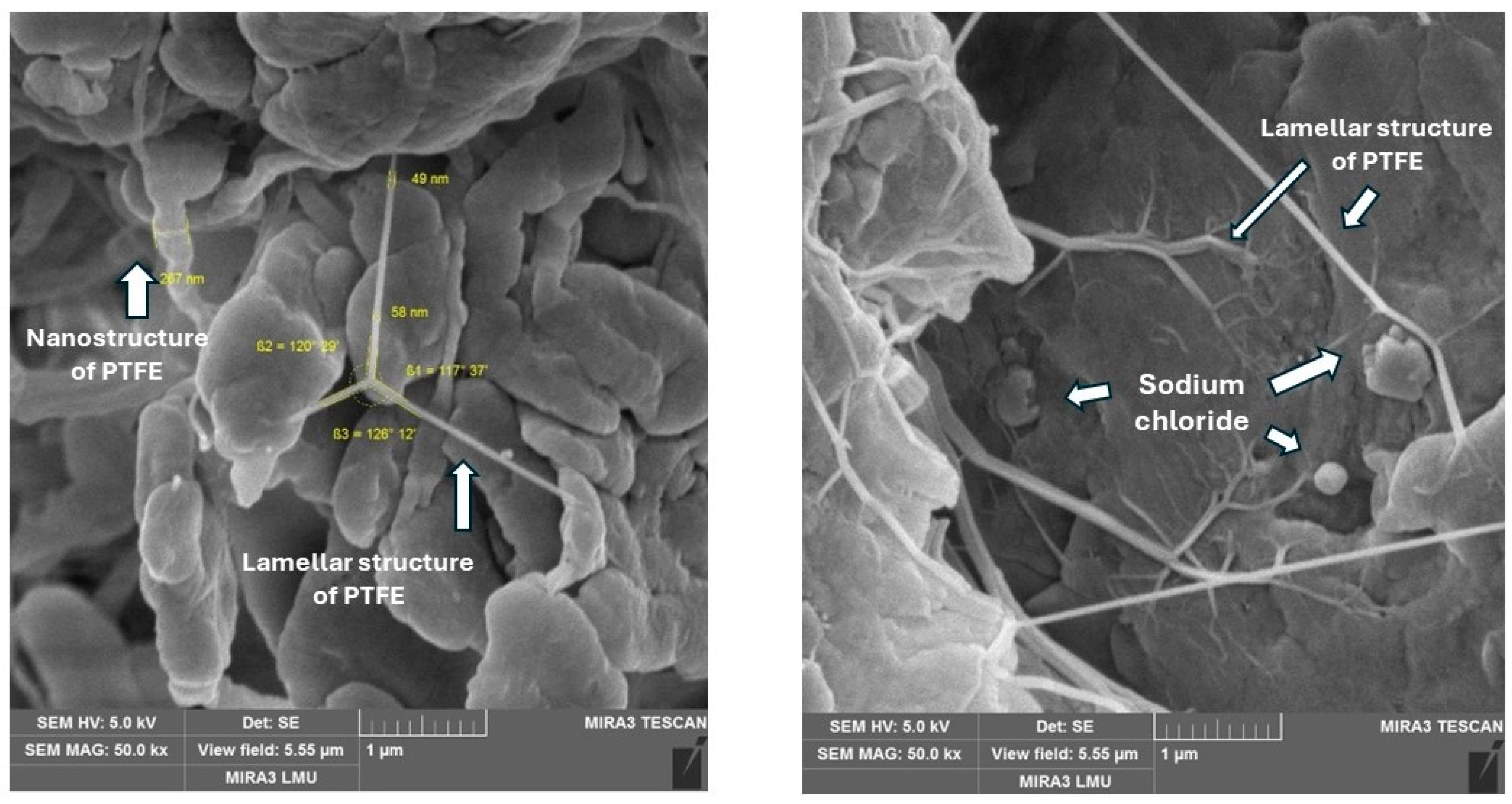
4.1. Microstructure Analysis
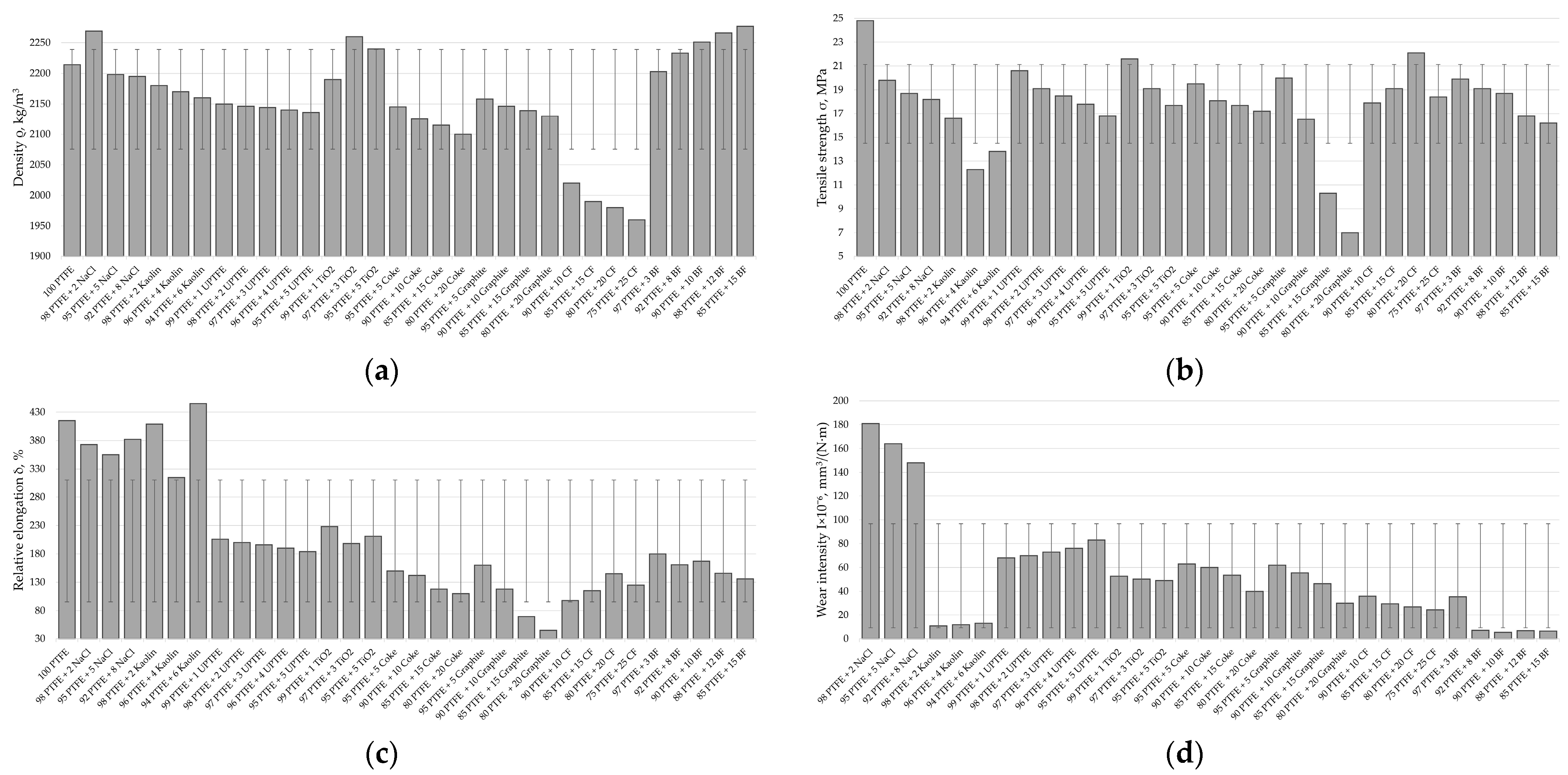
4.2. Testing Analysis
5. Prediction Results Analysis and Discussion
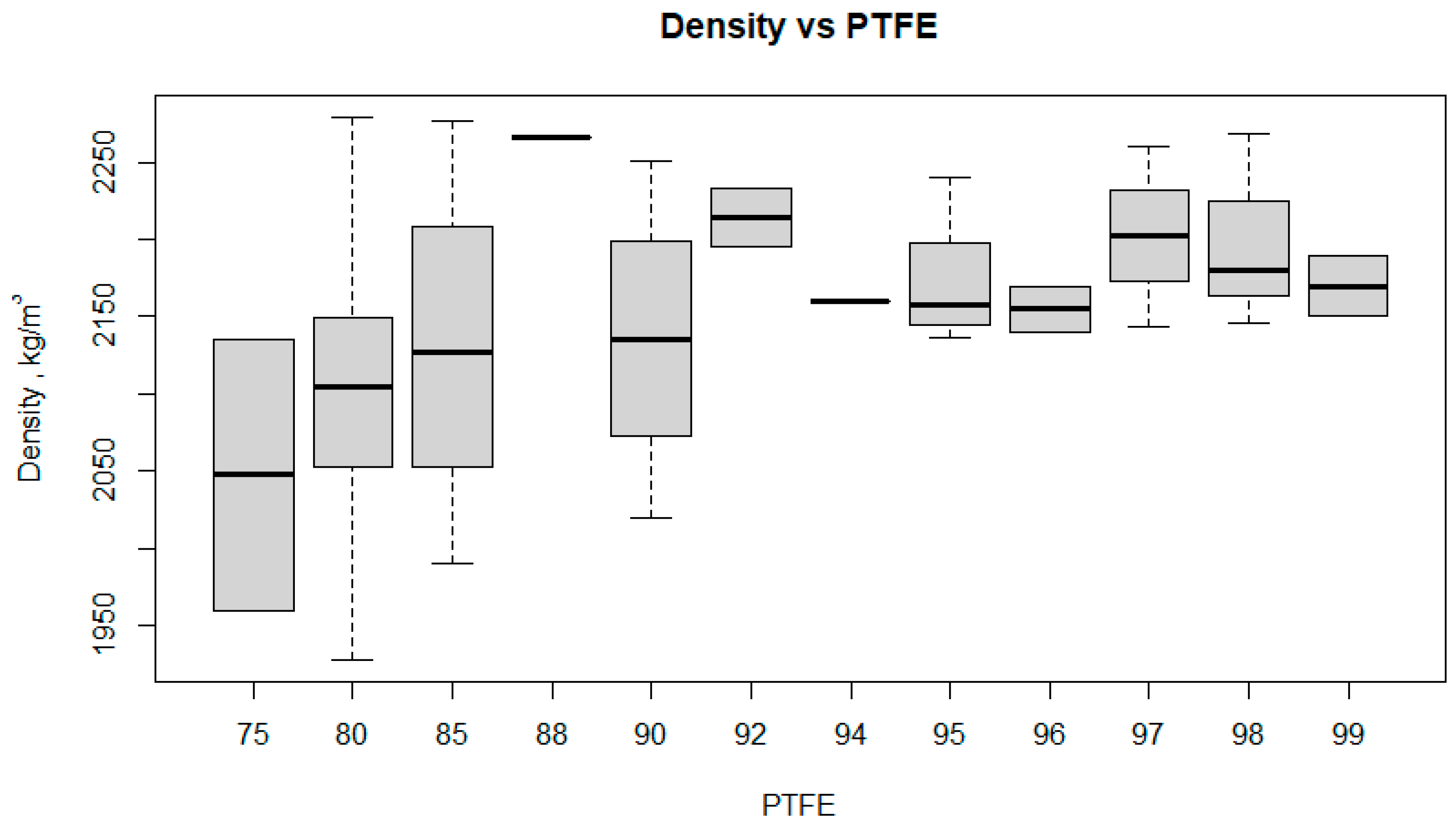
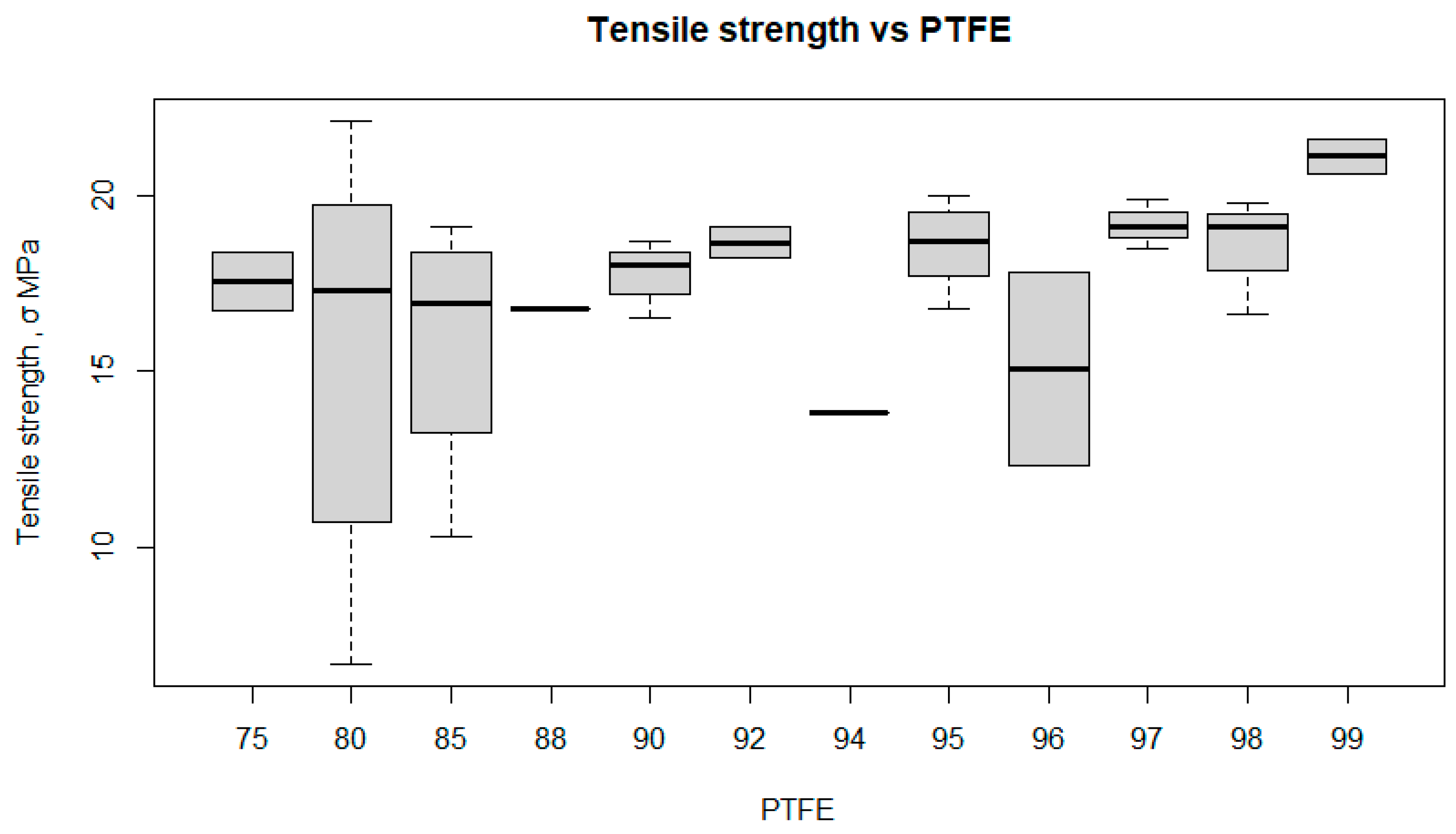
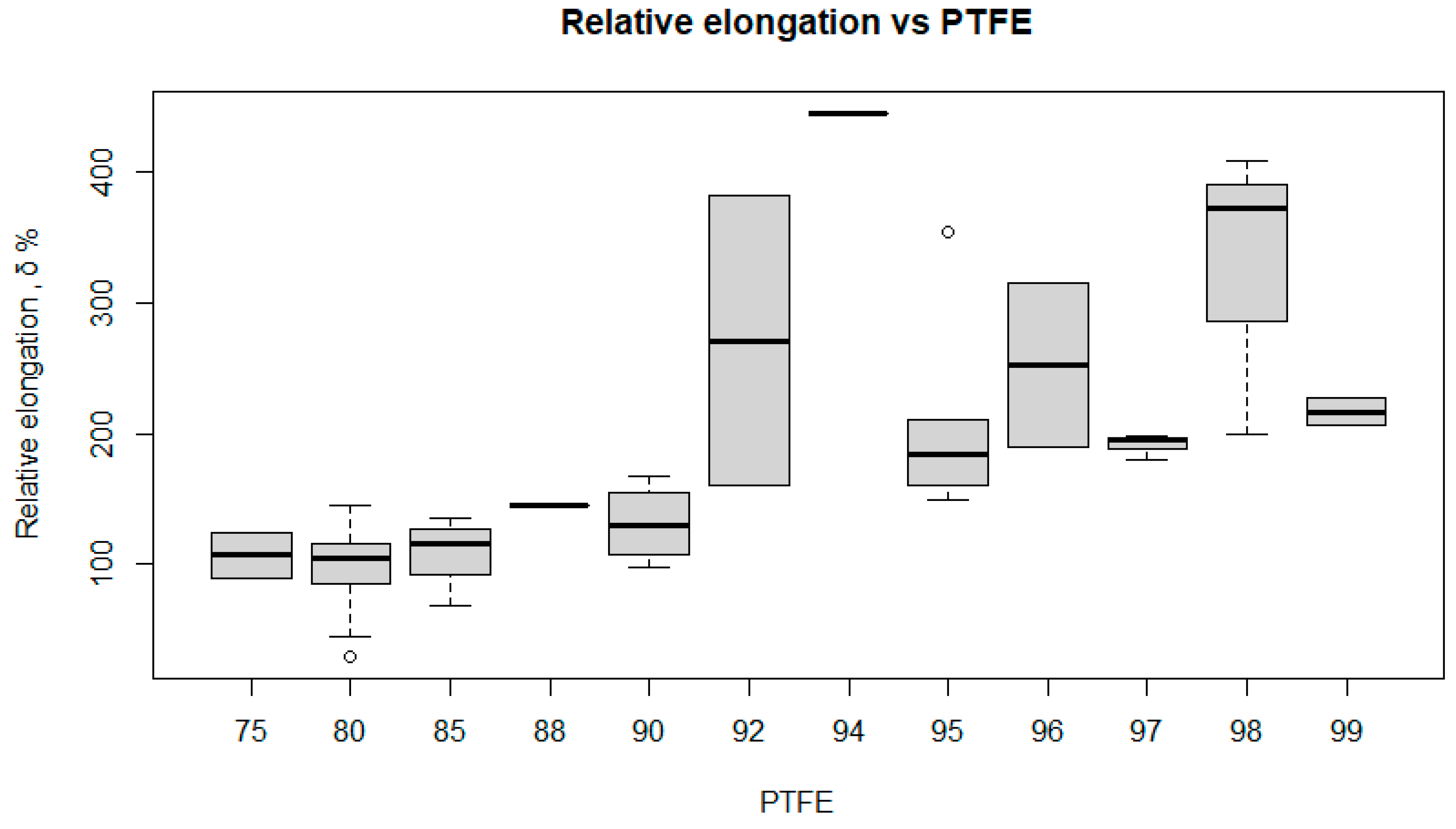
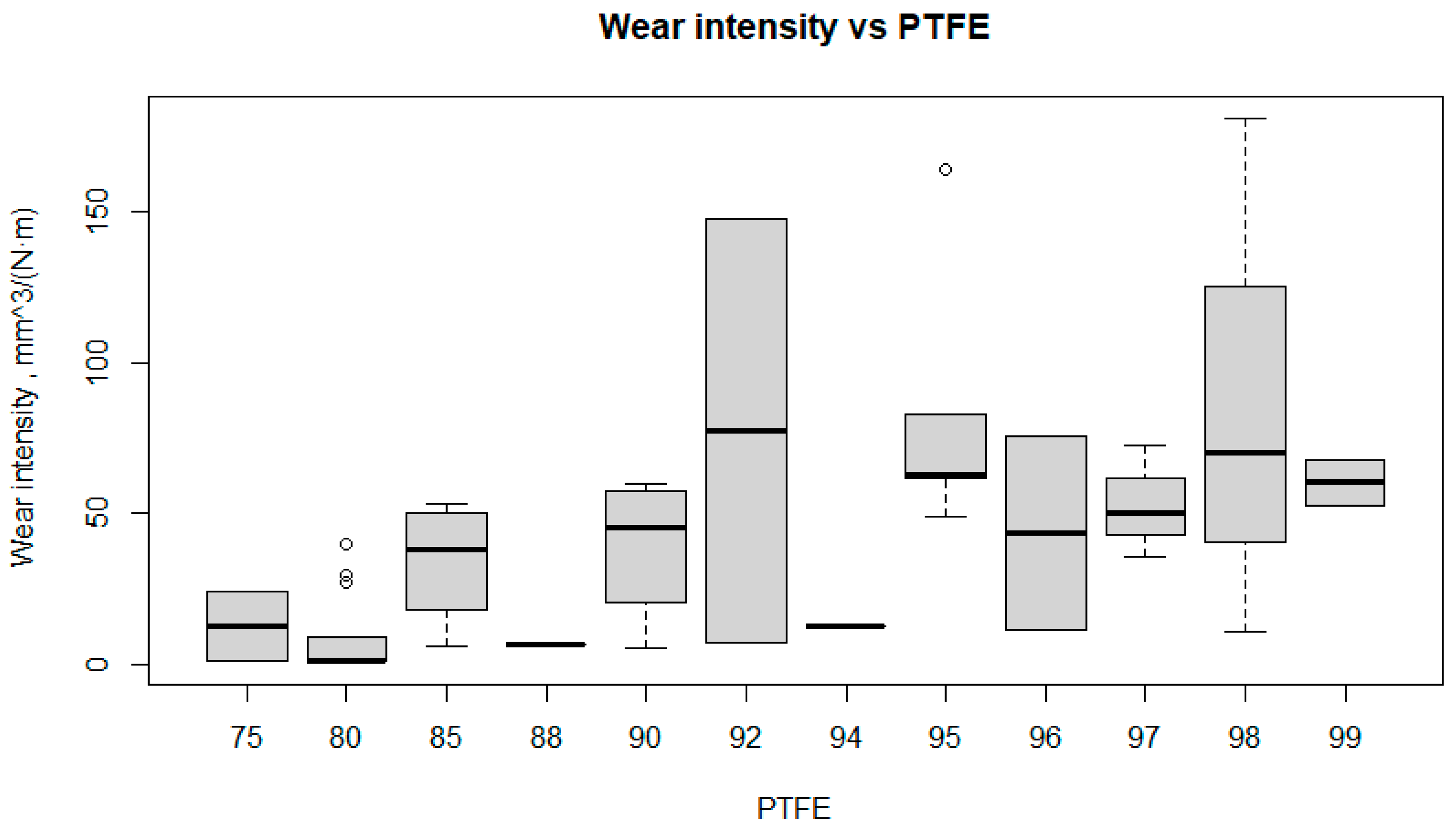
5.1. Effect of PTFE Content on Composite Properties
5.2. Effect of Filler Content on Composite Properties
- PTFE is significant for relative elongation, wear intensity and density, but not for tensile strength.
- Kaolin has a significant effect on relative elongation and tensile strength, is close to significance for wear intensity, and is not significant for density.
- Sodium chloride is significant for relative elongation and wear intensity but not for density and tensile strength.
- Graphite is significant for density, wear intensity, and tensile strength, but not for relative elongation.
- Carbon fiber is significant for wear intensity and density but not for relative elongation and tensile strength.
- Titanium dioxide is not significant in any of the models.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Ince, J.C.; Peerzada, M.; Mathews, L.D.; Pai, A.R.; Al-Qatatsheh, A.; Abbasi, S.; Yin, Y.; Hameed, N.; Duffy, A.R.; Lau, A.K.; et al. Overview of emerging hybrid and composite materials for space applications. Adv. Compos. Hybrid Mater. 2023, 6, 130. [Google Scholar] [CrossRef]
- Chatziparaskeva, G.; Papamichael, I.; Voukkali, I.; Loizia, P.; Sourkouni, G.; Argirusis, C.; Zorpas, A.A. End-of-Life of Composite Materials in the Framework of the Circular Economy. Microplastics 2022, 1, 377–392. [Google Scholar] [CrossRef]
- Pulidindi, K.; Prakash, A. Advanced Polymer Composites Market—By Product (Resin, Fiber, Others), By Application (Resin, Fiber, Others) & Forecast, 2022–2030. Available online: https://www.gminsights.com/industry-analysis/advanced-polymer-composites-market (accessed on 2 February 2025).
- Kolosov, A.E.; Sivetskii, V.I.; Kolosova, E.P.; Vanin, V.V.; Gondlyakh, A.V.; Sidorov, D.E.; Ivitskiy, I.I. Creation of Structural Polymer Composite Materials for Functional Application Using Physicochemical Modification. Adv. Polym. Technol. 2019, 2019, 3501456. [Google Scholar] [CrossRef]
- Kamarudin, S.H.; Mohd Basri, M.S.; Rayung, M.; Abu, F.; Ahmad, S.; Norizan, M.N.; Osman, S.; Sarifuddin, N.; Desa, M.S.Z.M.; Abdullah, U.H.; et al. A Review on Natural Fiber Reinforced Polymer Composites (NFRPC) for Sustainable Industrial Applications. Polymers 2022, 14, 3698. [Google Scholar] [CrossRef] [PubMed]
- Krusenbaum, A.; Grätz, S.; Tigineh, G.T.; Borchardt, L.; Kim, L.G. The mechanochemical synthesis of polymers. Chem. Soc. Rev. 2022, 51, 2873–2905. [Google Scholar] [CrossRef] [PubMed]
- Oladele, I.O.; Omotosho, T.F.; Adediran, A.A. Polymer-Based Composites: An Indispensable Material for Present and Future Applications. Int. J. Polym. Sci. 2020, 2020, 8834518. [Google Scholar] [CrossRef]
- Sajan, S.; Selvaraj, D.P. A review on polymer matrix composite materials and their applications. Mater. Today Proc. 2021, 47, 5493–5498. [Google Scholar] [CrossRef]
- Kangishwar, S.; Radhika, N.; Sheik, A.A.; Chavali, A.; Hariharan, S. A comprehensive review on polymer matrix composites: Material selection, fabrication, and application. Polym. Bull. 2023, 80, 47–87. [Google Scholar] [CrossRef]
- Ramesh, M.; Rajeshkumar, L.N.; Srinivasan, N.; Kumar, D.V.; Balaji, D. Influence of filler material on properties of fiber-reinforced polymer composites: A review. e-Polymers 2022, 22, 898–916. [Google Scholar] [CrossRef]
- Kiran, M.D.; Govindaraju, H.K.; Jayaraju, T.; Kumar, N. Review-Effect of Fillers on Mechanical Properties of Polymer Matrix Composites. Mater. Today Proc. 2018, 5, 22421–22424. [Google Scholar] [CrossRef]
- Yang, G.; Park, M.; Park, S.-J. Recent progresses of fabrication and characterization of fibers-reinforced composites: A review. Compos. Commun. 2019, 14, 34–42. [Google Scholar] [CrossRef]
- DeArmitt, C.; Rothon, R. Particulate Fillers, Selection, and Use in Polymer Composites. In Polymers and Polymeric Composites: A Reference Series; Palsule, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–26. [Google Scholar]
- Wu, J.; Li, C.; Hailatihan, B.; Mi, L.; Baheti, Y.; Yan, Y. Effect of the Addition of Thermoplastic Resin and Composite on Mechanical and Thermal Properties of Epoxy Resin. Polymers 2022, 14, 1087. [Google Scholar] [CrossRef]
- Tian, J.; Qi, X.; Li, C.; Xian, G. Friction behaviors and wear mechanisms of multi-filler reinforced epoxy composites under dry and wet conditions: Effects of loads, sliding speeds, temperatures, water lubrication. Tribol. Int. 2023, 179, 108148. [Google Scholar] [CrossRef]
- Yadav, V.; Pal, D.; Poonia, A.K. Nanofillers as a potential key for shaping the future of the industries. Hybrid Adv. 2024, 7, 100340. [Google Scholar] [CrossRef]
- Motloung, M.P.; Mofokeng, T.G.; Ojijo, V.; Ray, S.S. A review on the processing–morphology–property relationship in biodegradable polymer composites containing carbon nanotubes and nanofibers. Polym. Eng. Sci. 2021, 61, 2719. [Google Scholar] [CrossRef]
- Almushaikeh, A.M.; Alaswad, S.O.; Alsuhybani, M.S.; AlOtaibi, B.M.; Alarifi, I.M.; Alqahtani, N.B.; Aldosari, S.M.; Alsaleh, S.S.; Haidyrah, A.S.; Alolyan, A.A.; et al. Manufacturing of carbon fiber reinforced thermoplastics and its recovery of carbon fiber: A review. Polym. Test. 2023, 122, 108029. [Google Scholar] [CrossRef]
- Sharma, H.; Kumar, A.; Rana, S.; Sahoo, N.G.; Jamil, M.; Kumar, R.; Sharma, S.; Li, C.; Kumar, A.; Eldin, S.M.; et al. Critical review on advancements on the fiber-reinforced composites: Role of fiber/matrix modification on the performance of the fibrous composites. J. Mater. Res. Technol. 2023, 26, 2975–3002. [Google Scholar] [CrossRef]
- Maiti, S.; Islam, M.R.; Uddin, M.A.; Afroj, S.; Eichhorn, S.J.; Karim, N. Sustainable Fiber-Reinforced Composites: A Review. Adv. Sustain. Syst. 2022, 6, 2200258. [Google Scholar] [CrossRef]
- He, R.; Chang, Q.; Huang, X.; Bo, J. Improved mechanical properties of carbon fiber reinforced PTFE composites by growing graphene oxide on carbon fiber surface. Compos. Interfaces 2018, 25, 995–1004. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, J.; Zhu, Y.; Wang, X.; Jin, Y. Microstructure and Properties of Polytetrafluoroethylene Composites Modified by Carbon Materials and Aramid Fibers. Coatings 2020, 10, 1103. [Google Scholar] [CrossRef]
- Zhang, J. The reinforcing effect of basalt fiber and polyamide-6 on the mechanical properties of polytetrafluoroethylene composite. J. Thermoplast. Compos. Mater. 2015, 28, 287–294. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Y.; Liu, Y.; Zhang, M.; Li, L.; Ma, L.; Sun, Y.; Wang, W. A Review on Basalt Fiber Composites and Their Applications in Clean Energy Sector and Power Grids. Polymers 2022, 14, 2376. [Google Scholar] [CrossRef] [PubMed]
- Dhand, V.; Mittal, G.; Rhee, K.Y.; Park, S.-J.; Hui, D. A short review on basalt fiber reinforced polymer composites. Compos. Part B Eng. 2015, 73, 166–180. [Google Scholar] [CrossRef]
- Arul Jeya Kumar, A.; Prakash, M.; Lakshmankumar, A.; Haswanth, K. Wear characterization of basalt fiber reinforced polypropylene/polylactic acid hybrid polymer composite. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 250–258. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Ma, H.; Xu, X. Properties and Applications of Basalt Fiber and Its Composites. IOP Conf. Ser. Earth Environ. Sci. 2018, 186, 012052. [Google Scholar] [CrossRef]
- Ouyang, J.-H.; Li, Y.-F.; Zhang, Y.-Z.; Wang, Y.-M.; Wang, Y.-J. High-Temperature Solid Lubricants and Self-Lubricating Composites: A Critical Review. Lubricants 2022, 10, 177. [Google Scholar] [CrossRef]
- Sujuan, Y.; Xingrong, Z. Tribological Properties of PTFE and PTFE Composites at Different Temperatures. Tribol. Trans. 2014, 57, 382–386. [Google Scholar] [CrossRef]
- Mazur, K.; Gądek-Moszczak, A.; Liber-Kneć, A.; Kuciel, S. Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition. Materials 2021, 14, 1712. [Google Scholar] [CrossRef]
- Zarichnyak, Y.P.; Ivanov, V.A. The Dependence of the Thermophysical Properties of Filled Fluoroplastics on the Temperature and Concentration of Fillers. Int. Polym. Sci. Technol. 2015, 42, 31–34. [Google Scholar] [CrossRef]
- Dykha, A.; Svidersky, V.; Danilenko, I.; Bilichenko, V.; Kukurudzyak, Y.; Kirichenko, L. Design and Study of Nanomodified Composite Fluoropolymer Materials for Tribotechnical Purposes. East. Eur. J. Enterp. Technol. 2020, 5, 38–48. [Google Scholar] [CrossRef]
- Xiang, D.; Gu, C. A study on the friction and wear behavior of PTFE filled with ultra-fine kaolin particulates. Mater. Lett. 2006, 60, 689–692. [Google Scholar] [CrossRef]
- Jang, K.-S. Mineral filler effect on the mechanics and flame retardancy of polycarbonate composites: Talc and kaolin. e-Polymers 2016, 16, 379–386. [Google Scholar] [CrossRef]
- Sudeepan, J.; Kumar, K.; Barman, T.K.; Sahoo, P. Study of Friction and Wear Properties of ABS/Kaolin Polymer Composites Using Grey Relational Technique. Procedia Technol. 2014, 14, 196–203. [Google Scholar] [CrossRef]
- Shelestova, V.A.; Grakovich, P.N.; Zhandarov, S.F. A Fluoropolymer Coating on Carbon Fibers Improves Their Adhesive Interaction with PTFE Matrix. Compos. Interfaces 2011, 18, 419–440. [Google Scholar] [CrossRef]
- Antonov, A.; Avdeychik, S.; Sarokin, V.; Struk, V.; Vorontsov, A.; Mikhailova, L. Nanocomposite materials based on thermoplastic blends for the technological equipment with a long service life. Mater. Sci. Non-Equilib. Phase Transform. 2017, 3, 92–94. [Google Scholar]
- Bouznik, V.M.; Ignatieva, L.N.; Kuryavyi, V.G.; Tsvetnikov, A.K. Synthesis of Ultradispersed Powders from Products of Polytetrafluoroethylene Pyrolisis. KONA Powder Part. J. 2008, 26, 3–12. [Google Scholar] [CrossRef]
- Budnik, A.F.; Rudenko, P.V.; Berladir, K.V.; Budnik, O.A. Structured Nanoobjects of Polytetrafluoroethylene Composites. J. Nano Electron. Phys. 2015, 7, 02022. [Google Scholar]
- Cazan, C.; Enesca, A.; Andronic, L. Synergic Effect of TiO2 Filler on the Mechanical Properties of Polymer Nanocomposites. Polymers 2021, 13, 2017. [Google Scholar] [CrossRef]
- Gopal, K.V.; Kumar, K.R.V.; Suresh, G.; Rajasekharan, V.; Nagarajan, P.K.; Meenakshi, C.M. Investigation of TiO2 Nano Filler in Mechanical, Thermal Behaviour of Sisal/Jute Fiber Reinforced Interpenetrating Polymer Network (IPN) Composites. Mater. Res. 2022, 25, e20220406. [Google Scholar] [CrossRef]
- Nawaz, H.; Umar, M.; Maryam, R.; Nawaz, I.; Razzaq, H.; Malik, T.; Liu, X. Polymer Nanocomposites Based on TiO2 as a Reinforcing Agent: An Overview. Adv. Eng. Mater. 2022, 23, 2200844. [Google Scholar] [CrossRef]
- Awang, M.; Wan Mohd, W.R. Comparative studies of Titanium Dioxide and Zinc Oxide as a potential filler in Polypropylene reinforced rice husk composite. IOP Conf. Ser. Mater. Sci. Eng. 2018, 342, 012046. [Google Scholar] [CrossRef]
- Singh, V.; Patra, S.; Murugan, N.A.; Toncu, D.-C.; Tiwari, A. Recent trends in computational tools and data-driven modeling for advanced materials. Mater. Adv. 2022, 3, 4069–4087. [Google Scholar] [CrossRef]
- Marzari, N.; Ferretti, A.; Wolverton, C. Electronic-structure methods for materials design. Nat. Mater. 2021, 20, 736–749. [Google Scholar] [CrossRef]
- Barhoumi, M. The Density Functional Theory and Beyond: Example and Applications; IntechOpen: London, UK, 2022. [Google Scholar]
- Ciccotti, G.; Dellago, C.; Ferrario, M.; Hernández, E.R.; Tuckerman, M.E. Molecular simulations: Past, present, and future (a Topical Issue in EPJB). Eur. Phys. J. B 2022, 95, 3. [Google Scholar] [CrossRef]
- Tafrishia, H.; Sadegh Sadeghzadeh, S.; Ahmadi, R. Molecular dynamics simulations of phase change materials for thermal energy storage: A review. RSC Adv. 2022, 12, 14776–14807. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Liu, R.; Liu, B.; Shao, Y.; Liu, M. Molecular Dynamics Simulation Studies of Properties, Preparation, and Performance of Silicon Carbide Materials: A Review. Energies 2023, 16, 1176. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Zhan, M. A review on the modeling and simulations of solid-state diffusional phase transformations in metals and alloys. Manuf. Rev. 2018, 5, 10. [Google Scholar] [CrossRef]
- Guo, W.; Errington, J.R. Monte Carlo Simulation Strategies to Compute the Interfacial Properties of a Model Octane–Water–Silica System. J. Phys. Chem. C 2018, 122, 17309–17318. [Google Scholar] [CrossRef]
- Nukala, S.G.; Kong, I.; Kakarla, A.B.; Patel, V.I.; Abuel-Naga, H. Simulation of Wood Polymer Composites with Finite Element Analysis. Polymers 2023, 15, 1977. [Google Scholar] [CrossRef]
- Di Pietro, N.; Ceddia, M.; Romasco, T.; De Bortoli Junior, N.; Mello, B.F.; Tumedei, M.; Specchiulli, A.; Piattelli, A.; Trentadue, B. Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally. Appl. Sci. 2023, 13, 8147. [Google Scholar] [CrossRef]
- Zhyhylii, D.; Pozovnyi, O.; Chai, E.Y.; Dvurecenska, K.; Christian, W.J. Quantified assessment of modelled impacts on asymmetric composite laminates. J. Compos. Mater. 2025, 00219983251319085. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, X.; Wang, H. A comparative study of finite element analysis of single-particle impact on mild steel with and without strain rate considered. Int. J. Impact Eng. 2022, 159, 104029. [Google Scholar] [CrossRef]
- Krmela, J.; Krmelová, V. Computational Simulation of Biaxial Loading of Polymer Composites in ANSYS. In Engineering Design Applications VI. Advanced Structured Materials; Öchsner, A., Altenbach, H., Eds.; Springer: Cham, Switzerland, 2024; Volume 209, pp. 65–81. [Google Scholar]
- Chew, P.Y.; Reinhardt, A. Phase diagrams—Why they matter and how to predict them. J. Chem. Phys. 2023, 158, 030902. [Google Scholar] [CrossRef]
- Kroupa, A. Modelling of phase diagrams and thermodynamic properties using Calphad method—Development of thermodynamic databases. Comput. Mater. Sci. 2013, 66, 3–13. [Google Scholar] [CrossRef]
- Arnold, J.E.; Day, G.M. Crystal Structure Prediction of Energetic Materials. Cryst. Growth Des. 2023, 23, 6149–6160. [Google Scholar] [CrossRef]
- Yin, X.; Gounaris, C.E. Search methods for inorganic materials crystal structure prediction. Curr. Opin. Chem. Eng. 2022, 35, 100726. [Google Scholar] [CrossRef]
- Soltani, M.; Raahemifar, K.; Nokhosteen, A.; Kashkooli, F.M.; Zoudani, E.L. Numerical Methods in Studies of Liquid Crystal Elastomers. Polymers 2021, 13, 1650. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, C.; Guerrini, M.; Krumland, J.; Nguyen, N.T.; Valencia, A.M. Modeling the electronic structure of organic materials: A solid-state physicist’s perspective. J. Phys. Mater. 2023, 6, 012001. [Google Scholar] [CrossRef]
- Qian, W.; Zhang, C. Review of the phonon calculations for energetic crystals and their applications. Energetic Mater. Front. 2021, 2, 154–164. [Google Scholar] [CrossRef]
- Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, Z.; Hu, H.; He, X.; Fu, H.; Xie, J. A rapid and effective method for alloy materials design via sample data transfer machine learning. npj Comput. Mat. 2023, 9, 26. [Google Scholar] [CrossRef]
- Kozinsky, B.; Singh, D.J. Thermoelectrics by Computational Design: Progress and Opportunities. Annu. Rev. Mater. Res. 2021, 51, 565–590. [Google Scholar] [CrossRef]
- Xu, B.; Yin, H.; Jiang, X.; Zhang, C.; Zhang, R.; Wang, Y.; Qu, X. Computational materials design: Composition optimization to develop novel Ni-based single crystal superalloys. Comput. Mater. Sci. 2022, 202, 111021. [Google Scholar] [CrossRef]
- Sivan, D.; Satheesh Kumar, K.; Abdullah, A.; Raj, V.; Misnon, I.I.; Ramakrishna, S.; Jose, R. Advances in materials informatics: A review. J. Mater. Sci. 2024, 59, 2602–2643. [Google Scholar] [CrossRef]
- Wieczorowski, M.; Trojanowska, J.; Sokolov, O. Digital and Information Technologies in Metrology 4.0. In Advances in Design, Simulation and Manufacturing VI. DSMIE 2023. Lecture Notes in Mechanical Engineering; Ivanov, V., Trojanowska, J., Pavlenko, I., Rauch, E., Piteľ, J., Eds.; Springer: Cham, Switzerland, 2023; pp. 81–90. [Google Scholar]
- Li, C.; Zheng, K. Methods, progresses, and opportunities of materials informatics. InfoMat 2023, 5, e12425. [Google Scholar] [CrossRef]
- Jain, A. Machine learning in materials research: Developments over the last decade and challenges for the future. Curr. Opin. Solid State Mater. Sci. 2024, 33, 101189. [Google Scholar] [CrossRef]
- Fiedler, L.; Modine, N.A.; Schmerler, S.; Vogel, D.J.; Popoola, G.A.; Thompson, A.P.; Rajamanickam, S.; Cangi, A. Predicting electronic structures at any length scale with machine learning. npj Comput. Mat. 2023, 9, 115. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Mimona, M.A.; Islam, M.A.; Hossain, N.; Zohura, F.T.; Imtiaz, I.; Rimon, M.I.H. Scope of machine learning in materials research—A review. Appl. Surf. Sci. Adv. 2023, 18, 100523. [Google Scholar] [CrossRef]
- Rodrigues, J.F.; Florea, L.; de Oliveira, M.C.F.; Diamond, D.; Oliveira, O.N. Big data and machine learning for materials science. Discov. Mater. 2021, 1, 12. [Google Scholar] [CrossRef]
- Chong, S.S.; Ng, Y.S.; Wang, H.-Q.; Zheng, J.-C. Advances of machine learning in materials science: Ideas and techniques. Front. Phys. 2024, 19, 13501. [Google Scholar] [CrossRef]
- Yasniy, O.; Mytnyk, M.; Maruschak, P.; Mykytyshyn, A.; Didych, I. Machine learning methods as applied to modelling thermal conductivity of epoxy-based composites with different fillers for aircraft. Aviation 2024, 28, 64–71. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, X. Artificial Intelligence-Powered Materials Science. Nano-Micro Lett. 2025, 17, 135. [Google Scholar] [CrossRef]
- Yadav, D.K.; Kaushik, A.; Yadav, N. Predicting machine failures using machine learning and deep learning algorithms. Sustain. Manuf. Serv. Econ. 2024, 3, 100029. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Olawumi, M.A.; Omigbodun, F.T. Machine Learning for Optimising Renewable Energy and Grid Efficiency. Atmosphere 2024, 15, 1250. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Wang, Z.; Dong, H.; Wang, J.; Tang, S. Using Deep Learning to Detect Defects in Manufacturing: A Comprehensive Survey and Current Challenges. Materials 2020, 13, 5755. [Google Scholar] [CrossRef]
- Zribi, M.; Pagliuca, P.; Pitolli, F. A Computer Vision-Based Quality Assessment Technique for the automatic control of consumables for analytical laboratories. Expert Syst. Appl. 2024, 256, 124892. [Google Scholar] [CrossRef]
- Khedr, A.M.; Rani, S.S. Enhancing supply chain management with deep learning and machine learning techniques: A review. J. Open Innov. Technol. Mark. Complex. 2024, 10, 100379. [Google Scholar] [CrossRef]
- Chen, W.; Men, Y.; Fuster, N.; Osorio, C.; Juan, A.A. Artificial Intelligence in Logistics Optimization with Sustainable Criteria: A Review. Sustainability 2024, 16, 9145. [Google Scholar] [CrossRef]
- ISO 13000-1:2021; Plastics—Polytetrafluoroethylene (PTFE) Semi-Finished Products. Part 1: Requirements and Designation. ISO: Geneva, Switzerland, 2021.
- Jiang, L.; Zhou, Y.; Jin, F.; Hou, Z. Influence of Polymer Matrices on the Tensile and Impact Properties of Long Fiber-Reinforced Thermoplastic Composites. Polymers 2023, 15, 408. [Google Scholar] [CrossRef]
- Berladir, K.V.; Hovorun, T.P.; Sviderskiy, V.A.; Rudenko, P.V.; Vyshehorodtseva, M.E. Nanostructural modification of polytetrafluoroethylene and its composition by energy influence. J. Nano Electron. Phys. 2016, 8, 01033-1–01033-5. [Google Scholar] [CrossRef] [PubMed]
- Budnik, O.A.; Budnik, A.F.; Rudenko, P.V.; Sviderskiy, V.A.; Berladir, K.V. Influence of mechanical activation polytetrafluoroethylene matrix of tribotechnical composites at its structural and phase transformations and properties. Funct. Mater. 2015, 22, 499–506. [Google Scholar] [CrossRef]
- Deshwal, D.; Belgamwar, S.U.; Bekinal, S.I.; Doddamani, M. Role of reinforcement on the tribological properties of polytetrafluoroethylene composites: A comprehensive review. Polym. Compos. 2024, 24, 14475–14497. [Google Scholar] [CrossRef]










| Parameter | Value |
|---|---|
| Average particle size, μm | 50–500 |
| Density, kg/m3 | 2200 |
| Tensile strength, MPa | 23 |
| Relative elongation at break, % | 350 |
| C | H | O | B | P |
|---|---|---|---|---|
| 60–65 | 1.1–4.5 | 3.5–4.5 | 3.0–3.6 | 3.0–3.6 |
| SiO2 | Al2O3 | FeO | Fe2O3 | CaO | MgO | MnO | Na2O | TiO2 |
|---|---|---|---|---|---|---|---|---|
| 51.56 | 15.49 | 10.43 | 4.42 | 8.5 | 5.22 | 0.2 | 2.1 | 2.08 |
| SiO2 | TiO2 | Al2O3 | Fe2O3 | FeO | MgO | CaO | Na2O | K2O | H2O |
|---|---|---|---|---|---|---|---|---|---|
| 45.81 | 0.72 | 39.24 | 0.13 | – | 0.31 | 0.52 | – | – | 0.13 |
| Filler | Chemical Nature | Shape | Size, μm | Density, kg/m3 |
|---|---|---|---|---|
| Fibrous | ||||
| Carbon fibers (CF) | synthetic inorganic | fibrous (cylindrical) | ø =10–12 l = 100–150 | 1510 |
| Basalt fibers (BF) | synthetic inorganic | fibrous (cylindrical) | ø =2 l = 50–200 | 30–125 |
| Dispersed | ||||
| Coke | natural organic | irregular | 10–50 | 1730 |
| Graphite | natural inorganic | lamellar (scaly) | 15–30 | 1600 |
| Kaolin | natural inorganic | lamellar (scaly) | up to 5 | 2580 |
| Sodium chloride (NaCl) | synthetic inorganic | irregular | up to 600 | 2165 |
| Nano | ||||
| Ultra PTFE (UPTFE) | synthetic organic | spherical | 0.5–0.6 | 1900–2000 |
| Titanium dioxide (TiO2) | synthetic inorganic | spherical | up to 0.4 | 3900–4250 |
| No | PTFE | Carbon Fiber | Basalt Fiber | Coke | Graphite | Kaolin | Sodium Chloride | Ultra PTFE | Titanium Dioxide |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 90 | 10 | − | − | − | − | − | − | − |
| 2 | 85 | 15 | − | − | − | − | − | − | − |
| 3 | 80 | 20 | − | − | − | − | − | − | − |
| 4 | 75 | 25 | − | − | − | − | − | − | − |
| 5 | 97 | − | 3 | − | − | − | − | − | − |
| 6 | 92 | − | 8 | − | − | − | − | − | − |
| 7 | 90 | − | 10 | − | − | − | − | − | − |
| 8 | 88 | − | 12 | − | − | − | − | − | − |
| 9 | 85 | − | 15 | − | − | − | − | − | − |
| 10 | 95 | − | − | 5 | − | − | − | − | − |
| 11 | 90 | − | − | 10 | − | − | − | − | − |
| 12 | 85 | − | − | 15 | − | − | − | − | − |
| 13 | 80 | − | − | 20 | − | − | − | − | − |
| 14 | 95 | − | − | − | 5 | − | − | − | − |
| 15 | 90 | − | − | − | 10 | − | − | − | − |
| 16 | 85 | − | − | − | 15 | − | − | − | − |
| 17 | 80 | − | − | − | 20 | − | − | − | − |
| 18 | 98 | − | − | − | − | 2 | − | − | − |
| 19 | 96 | − | − | − | − | 4 | − | − | − |
| 20 | 94 | − | − | − | − | 6 | − | − | − |
| 21 | 98 | − | − | − | − | − | 2 | − | − |
| 22 | 95 | − | − | − | − | − | 5 | − | − |
| 23 | 92 | − | − | − | − | − | 8 | − | − |
| 24 | 99 | − | − | − | − | − | − | 1 | − |
| 25 | 98 | − | − | − | − | − | − | 2 | − |
| 26 | 97 | − | − | − | − | − | − | 3 | − |
| 26 | 96 | − | − | − | − | − | − | 4 | − |
| 27 | 95 | − | − | − | − | − | − | 5 | − |
| 28 | 99 | − | − | − | − | − | − | − | 1 |
| 29 | 97 | − | − | − | − | − | − | − | 3 |
| 30 | 95 | − | − | − | − | − | − | − | 5 |
| No | PTFE | Carbon Fiber | Basalt Fiber | Coke | Graphite | Kaolin |
|---|---|---|---|---|---|---|
| 31 | 80 | 5 | 15 | − | − | − |
| 32 | 80 | 10 | 10 | − | − | − |
| 33 | 80 | 15 | 5 | − | − | − |
| 34 | 75 | 20 | 5 | − | − | − |
| 35 | 80 | 18 | − | − | − | 2 |
| 36 | 80 | 16 | − | − | − | 4 |
| 37 | 80 | 14 | − | − | − | 6 |
| 38 | 80 | 15 | − | 5 | − | − |
| 39 | 80 | 10 | − | 10 | − | − |
| 40 | 80 | 5 | − | 15 | − | − |
| 41 | 80 | 15 | − | − | 5 | − |
| 42 | 80 | 10 | − | − | 10 | − |
| 43 | 80 | 5 | − | − | 15 | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berladir, K.; Antosz, K.; Ivanov, V.; Mitaľová, Z. Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data. Polymers 2025, 17, 694. https://doi.org/10.3390/polym17050694
Berladir K, Antosz K, Ivanov V, Mitaľová Z. Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data. Polymers. 2025; 17(5):694. https://doi.org/10.3390/polym17050694
Chicago/Turabian StyleBerladir, Khrystyna, Katarzyna Antosz, Vitalii Ivanov, and Zuzana Mitaľová. 2025. "Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data" Polymers 17, no. 5: 694. https://doi.org/10.3390/polym17050694
APA StyleBerladir, K., Antosz, K., Ivanov, V., & Mitaľová, Z. (2025). Machine Learning-Driven Prediction of Composite Materials Properties Based on Experimental Testing Data. Polymers, 17(5), 694. https://doi.org/10.3390/polym17050694








