Electrically Driven Liquid Crystal Elastomer Self-Oscillators via Rheostat Feedback Mechanism
Abstract
1. Introduction
2. Theoretical Model and Formulation
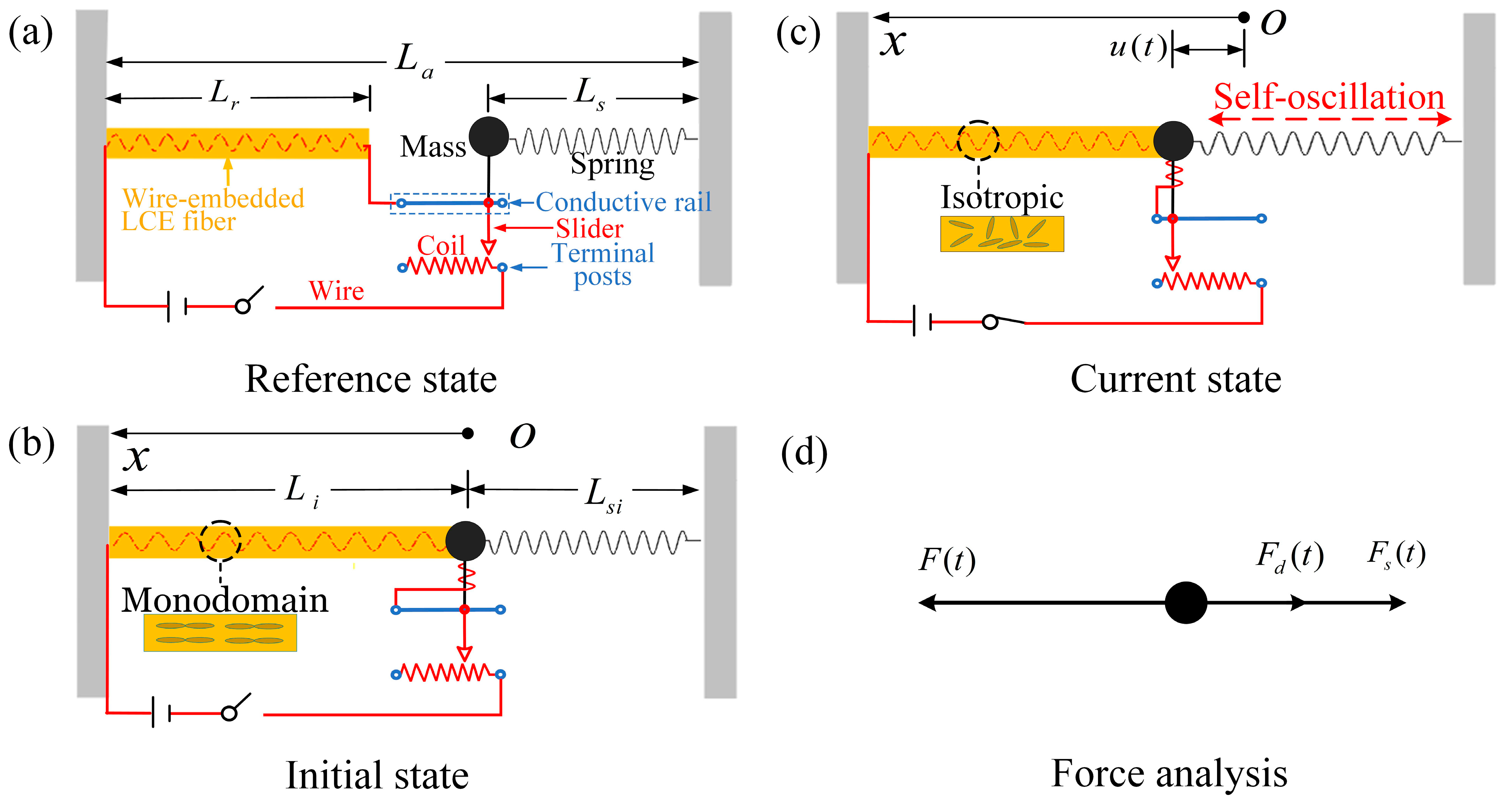
2.1. Dynamic Model of Electrically Driven LCE Self-Oscillator
2.2. Electrothermally Responsive LCE Model
2.3. Nondimensionalization
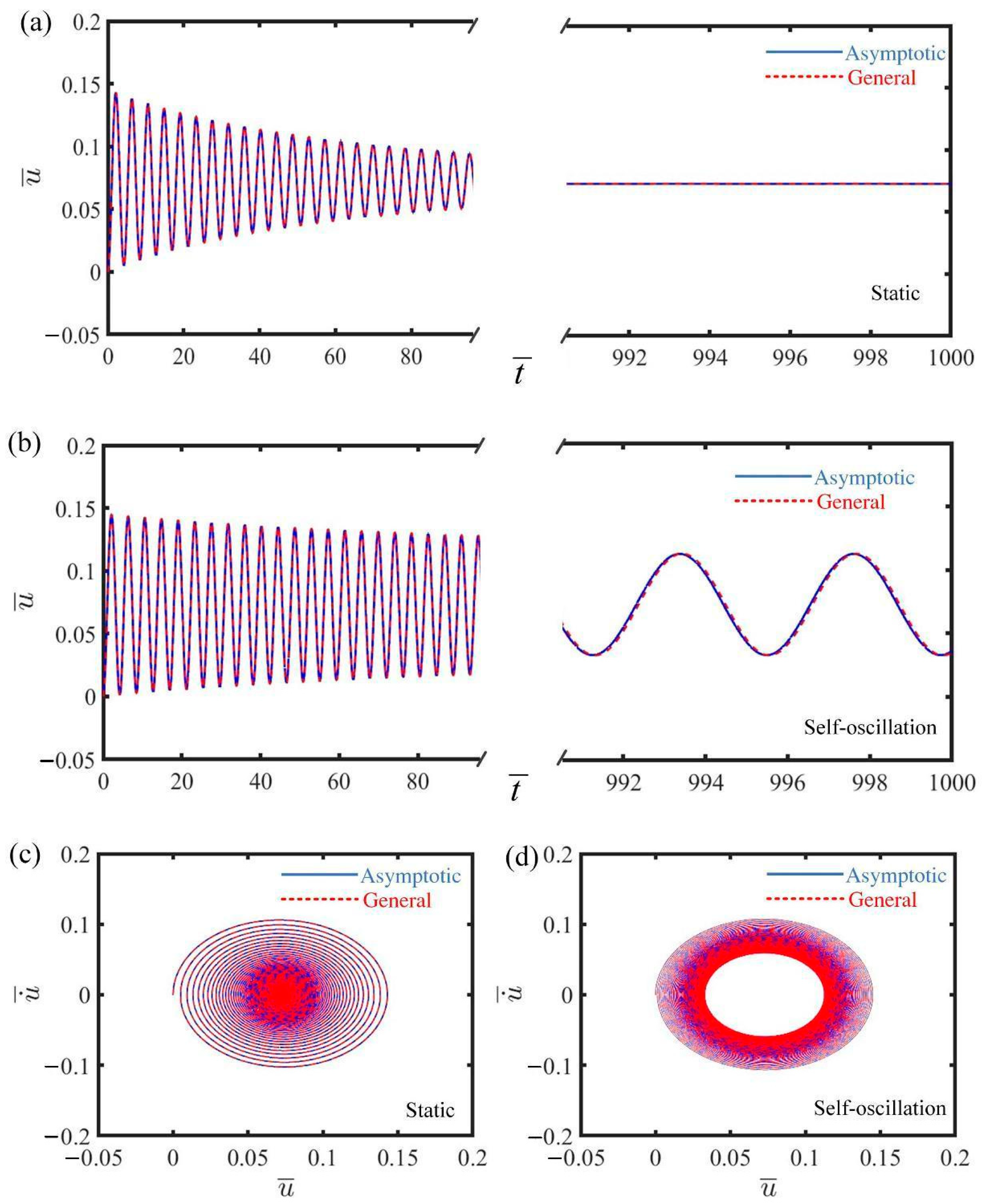
3. Asymptotic Analysis
4. Two Motion Phases and Self-Oscillation Mechanism
4.1. Two Motion Phases
4.2. Self-Oscillation Mechanism
5. Multi-Scale Analysis of Asymptotic Equations
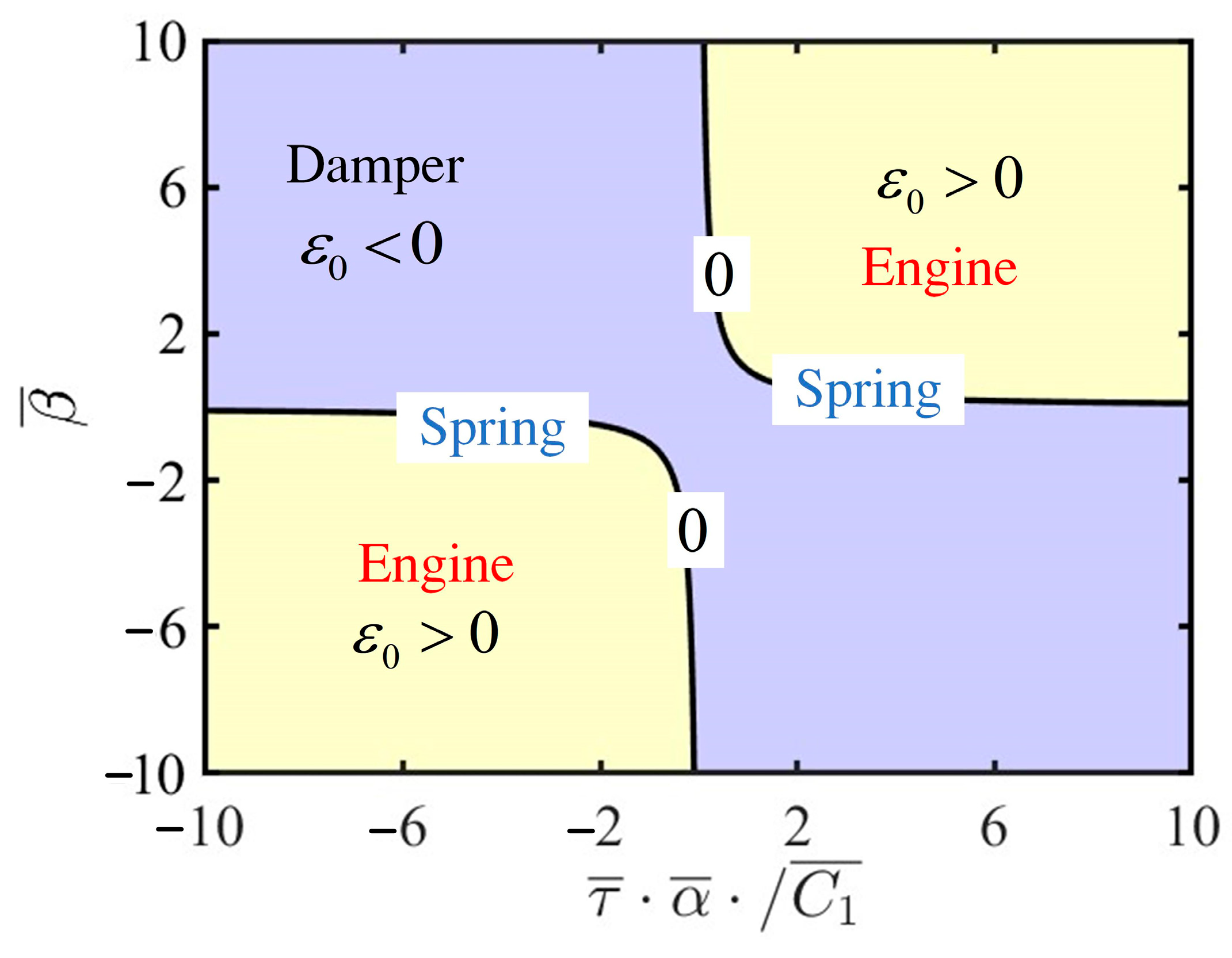
5.1. Hurwitz Criterion
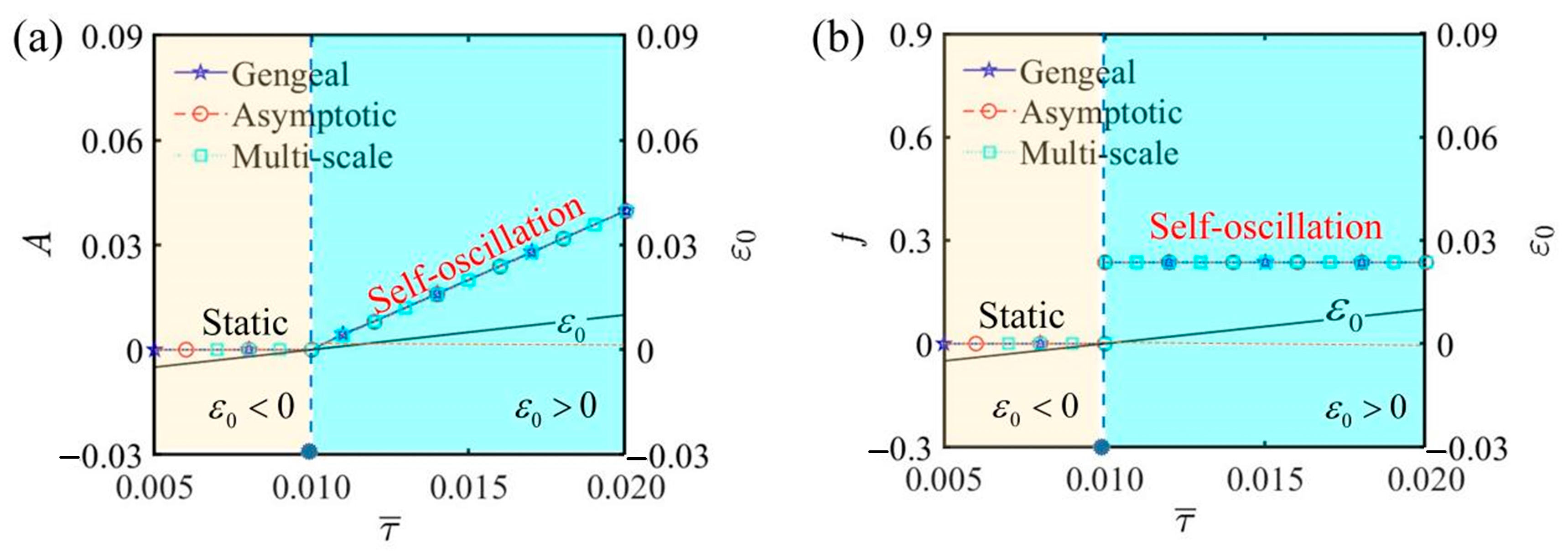
5.2. Amplitude and Frequency
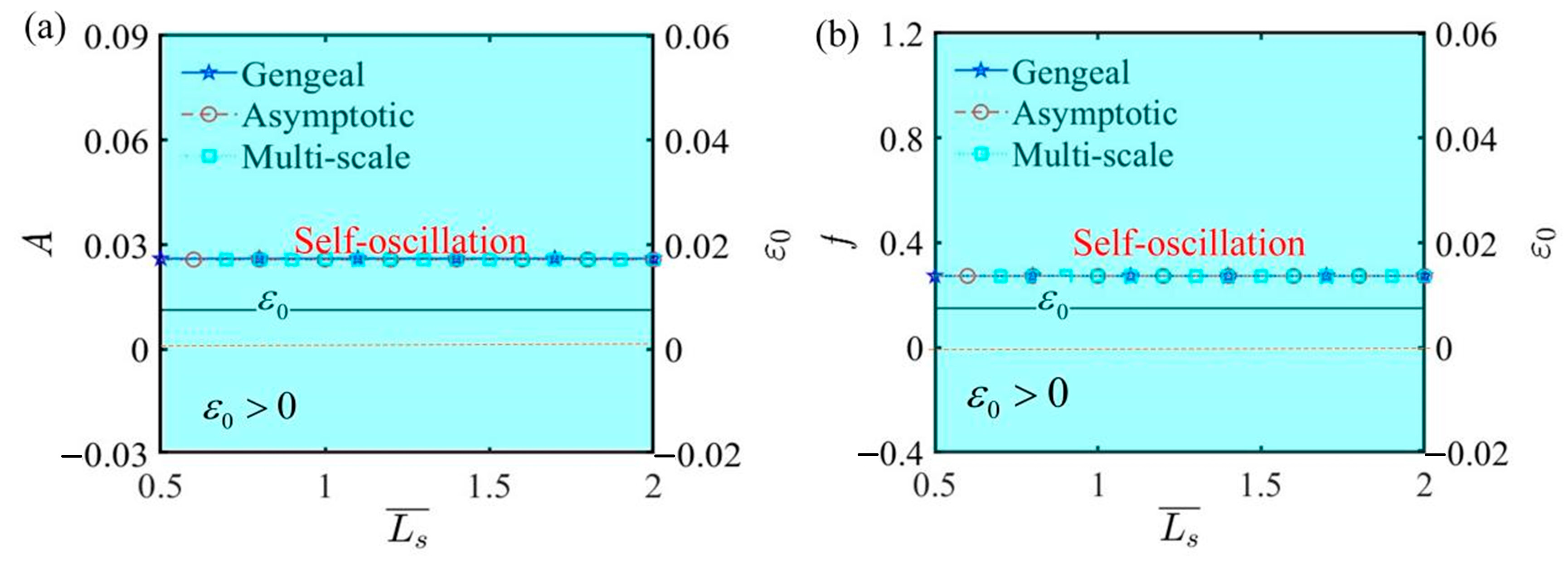
6. Parameter Analysis
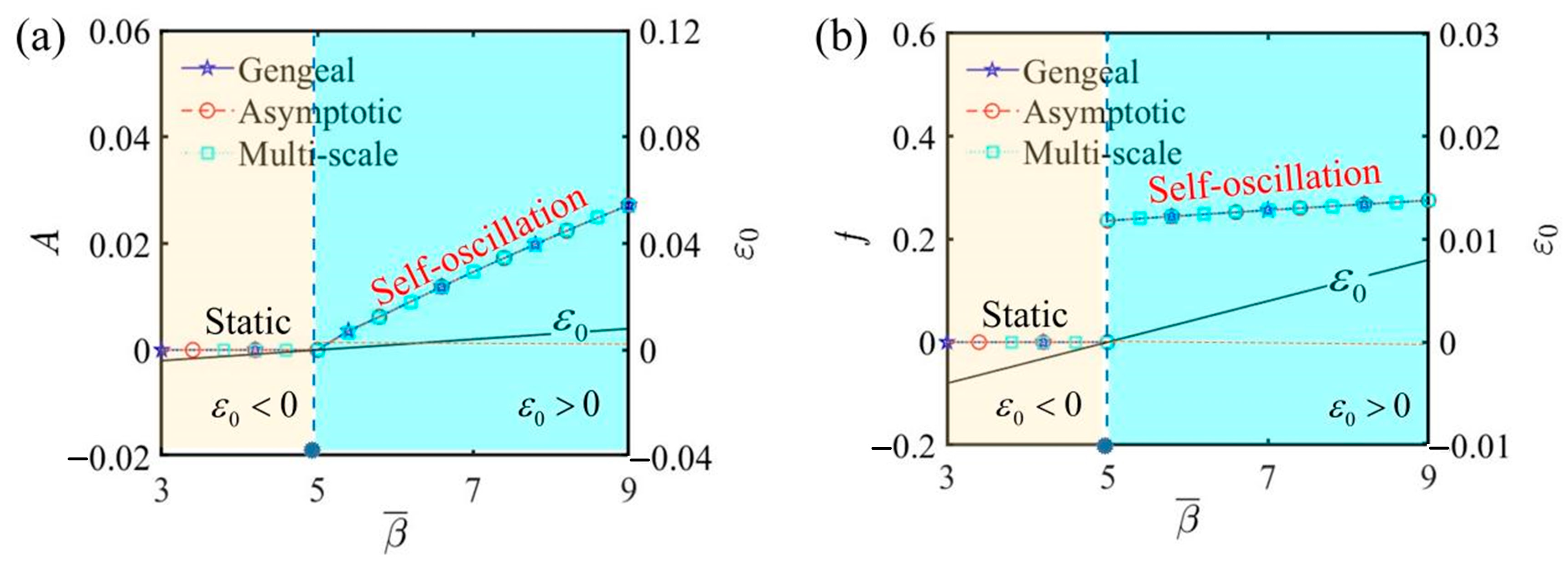
6.1. Effects of Parameters Relevant to Bifurcation Points
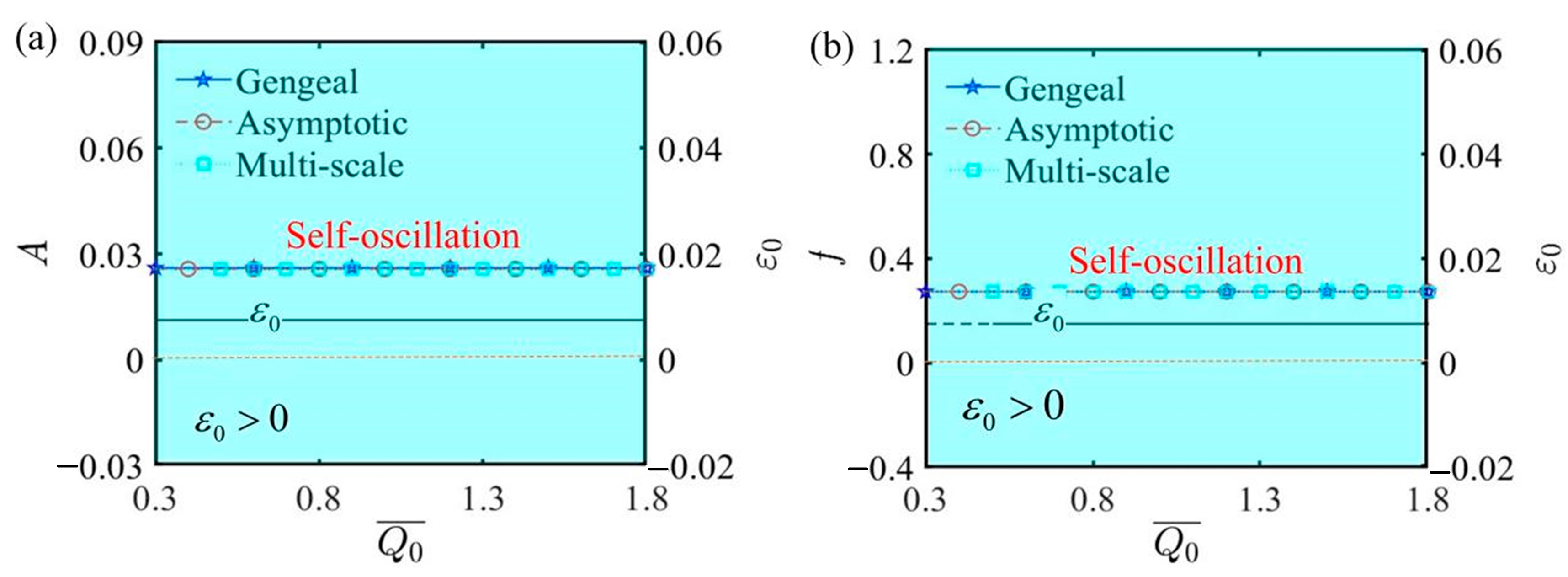
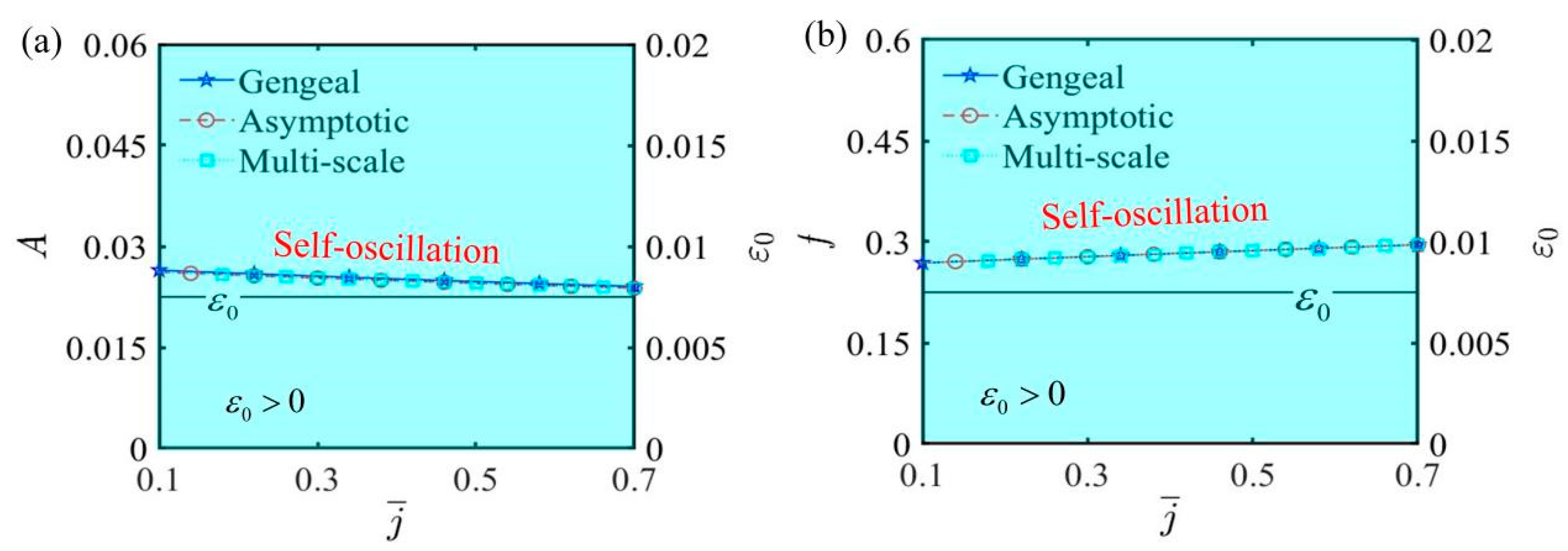
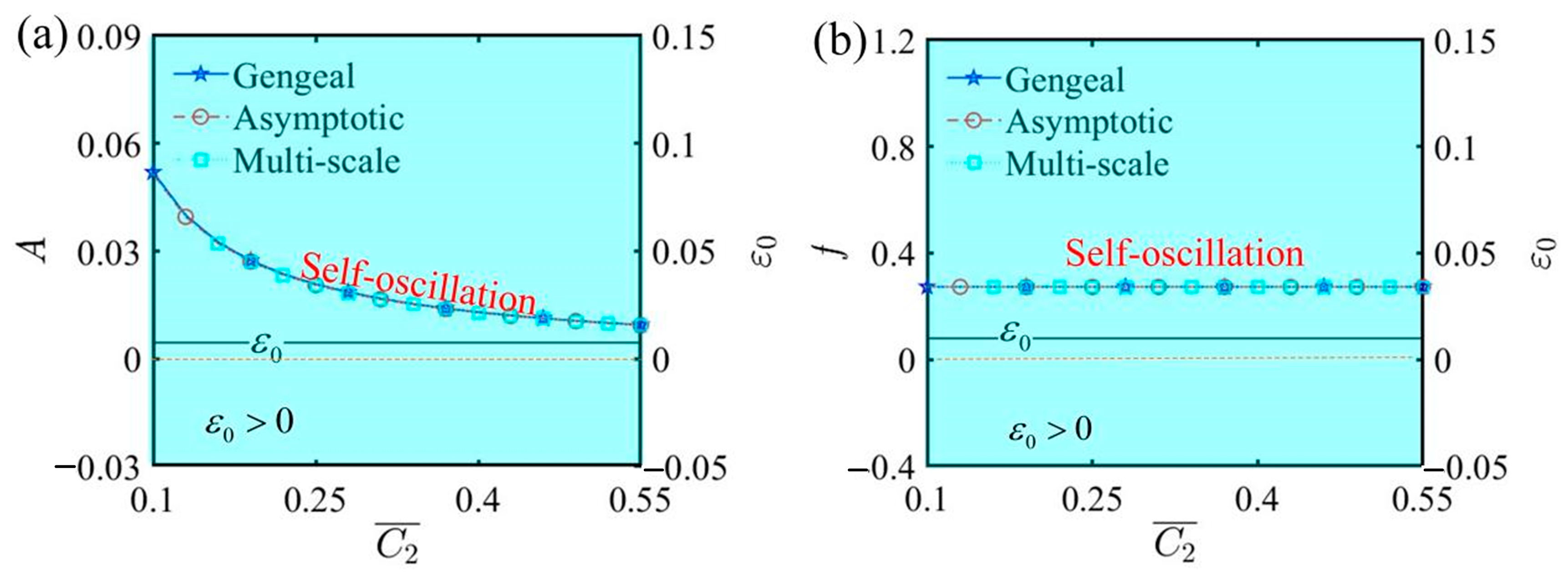
6.2. Effects of Parameters Irrelevant to Bifurcation Points
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, L.; Xu, J.; Xiao, R. Modeling the Stimulus-Responsive Behaviors of Fiber-Reinforced Soft Materials. Int. J. Appl. Mech. 2024, 16, 2450041. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Ji, Q.; Chang, L.; Hu, Y.; Peng, Q.; He, X. A MXene-Based Light-Driven Actuator and Motor with Self-Sustained Oscillation for Versatile Applications. Adv. Funct. Mater. 2024, 34, 2310955. [Google Scholar] [CrossRef]
- Zhao, J.; Dai, C.; Dai, Y.; Wu, J.; Li, K. Self-oscillation of cantilevered silicone oil paper sheet system driven by steam. Thin-Walled Struct. 2024, 203, 112270. [Google Scholar] [CrossRef]
- Tang, K.; Lin, X.; Lei, T.; Jin, T. Study on self-excited oscillation in a thermoacoustic engine with GlansdorffPrigogine stability criterion. J. Non-Equilib. Thermodyn. 2011, 36, 393–404. [Google Scholar]
- Papangelo, A.; Putignano, C.; Hoffmann, N. Self-excited vibrations due to viscoelastic interactions. Mech. Syst. Signal Process 2020, 144, 106894. [Google Scholar] [CrossRef]
- He, Q.; Yin, R.; Hua, Y.; Jiao, W.; Mo, C.; Shu, H.; Raney, J.R. A modular strategy for distributed, embodied control of electronics-free soft robots. Sci. Adv. 2023, 9, eade9247. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Peng, H.; Liu, C.; Ding, C.; Tang, H. Nonlinear characteristic and chip breaking mechanism for an axial low-frequency self-excited vibration drilling robot. Int. J. Mech. Sci. 2022, 230, 107561. [Google Scholar]
- Charroyer, L.; Chiello, O.; Sinou, J. Self-excited vibrations of a non-smooth contact dynamical system with planar friction based on the shooting method. Int. J. Mech. Sci. 2018, 144, 90–101. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Z.; Hu, J.; Swaddiwudhipong, S.; Yang, Z. Inhomogeneous large deformation study of temperature-sensitive hydrogel. Int. J. Solids Struct. 2013, 50, 2610–2619. [Google Scholar] [CrossRef]
- He, X.; Aizenberg, M.; Kuksenok, O.; Zarzar, L.D.; Shastri, A.; Balazs, A.C.; Aizenberg, J. Synthetic homeostatic materials with chemo-mechano-chemical self-regulation. Nature 2012, 487, 214–218. [Google Scholar] [CrossRef]
- Hua, M.; Kim, C.; Du, Y.; Wu, D.; Bai, R.; He, X. Swaying gel: Chemo-mechanical self-oscillation based on dynamic buckling. Matter 2021, 4, 1029–1041. [Google Scholar] [CrossRef]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the Landolt reaction. Phys. Chem. Phys. 2011, 13, 4132–4137. [Google Scholar] [CrossRef]
- Wu, J.; Yao, S.; Zhang, H.; Man, W.; Bai, Z.; Zhang, F.; Wang, X.; Fang, D.; Zhang, Y. Liquid crystal elastomer etamaterials with giant biaxial thermal shrinkage for enhancing skin egeneration. Adv. Mater. 2021, 33, 2170356. [Google Scholar] [CrossRef]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I.K. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending, twisting, and oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2019, 32, 1906233. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Dang, A.; Zhang, Z.; Yin, R.; Gao, Y.; Feng, L.; Yang, S. Repeatable and reprogrammable shape morphing from photoresponsive gold nanorod/liquid crystal elastomers. Adv. Mater. 2020, 32, 2004270. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, R.; Jin, L.; Liu, M.; Gao, Y.; Raney, J.; Yang, S.; Raney, J.; Yang, S. 3D-printed photoresponsive liquid crystal elastomer composites for free-form actuation. Adv. Funct. Mater. 2023, 33, 2210614. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Chen, M.; Wang, Y.; Lang, X.; Zhu, N.; Yang, Z.; Yi, Y. Soft rod-climbing robot inspired by winding locomotion of snake. Soft Robot. 2020, 7, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Lou, J.; Wang, J.; Chuang, K.; Wu, H.; Huang, Z. A self-excited bistable oscillator with a light-powered liquid crystal elastomer. Int. J. Mech. Sci. 2024, 271, 109124. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Choi, G.; Mahadevan, L. Self-excited motions of volatile drops on swellable sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef]
- Wu, H.; Qiu, Y.; Li, K. Modeling of a light-fueled liquid crystal elastomer-steered self-wobbling tumbler. Chaos Solitons Fractals 2025, 191, 115941. [Google Scholar] [CrossRef]
- Liu, J.; Qian, G.; Dai, Y.; Yuan, Z.; Song, W.; Li, K. Nonlinear dynamics modeling of a light-powered liquid crystal elastomer-based perpetual motion machine. Chaos Solitons Fractals 2024, 184, 114957. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z.; Sun, X.; Zuo, W.; Li, K. Multi-modal self-sustained motions of a silicone oil paper disc on a surface driven by hot steam. Chaos Solitons Fractals 2025, 191, 115898. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, X.; Qiu, Y.; Li, K. Stepwise self-oscillation of a photo-oscillator via time delay. Int. J. Mech. Sci. 2025, 288, 110046. [Google Scholar] [CrossRef]
- Zhao, Y.; Chi, Y.; Hong, Y.; Li, Y.; Yang, S.; Yin, J. Twisting for soft intelligent autonomous robot in unstructured environments. Proc. Natl. Acad. Sci. USA 2022, 119, e2200265119. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Ge, D.; Li, K.; Xu, P. Chaotic self-oscillation of liquid crystal elastomer double-line pendulum under a linear temperature field. Chaos Solitons Fractals 2024, 189, 115653. [Google Scholar] [CrossRef]
- Xu, P.; Chen, Y.; Sun, X.; Dai, Y.; Li, K. Light-powered self-sustained chaotic motion of a liquid crystal elastomer-based pendulum. Chaos Solitons Fractals 2024, 184, 115027. [Google Scholar] [CrossRef]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1727. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Berg, J.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Nie, Z.; Wang, M.; Liu, Z.; Huang, S.; Yang, H. Springtail-inspired light-driven soft jumping robots based on liquid crystal elastomers with monolithic three-leaf panel fold structure. Angew. Chem. Int. Ed. 2023, 62, e20230408. [Google Scholar]
- Wu, H.; Ge, D.; Qiu, Y.; Li, K.; Xu, P. Mechanics of light-fueled bidirectional self-rolling in a liquid crystal elastomer rod on a track. Chaos Solitons Fractals 2025, 191, 115901. [Google Scholar] [CrossRef]
- Qiu, Y.; Ge, D.; Wu, H.; Li, K.; Xu, P. Self-rotation of a liquid crystal elastomer rod under constant illumination. Int. J. Mech. Sci. 2024, 284, 109665. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kuli’c, I.M. Dynamics of fiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.; Wang, M.; Yang, H. A3 Priimagi, light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 5057. [Google Scholar] [CrossRef] [PubMed]
- Bai, C.; Kang, J.; Wang, Y. Light-induced motion of three-dimensional pendulum with liquid crystal elastomeric fiber. Int. J. Mech. Sci. 2024, 266, 108911. [Google Scholar] [CrossRef]
- Pilz da Cunha, M.; Peeketi, A.R.; Ramgopal, A.; Annabattula, R.K.; Schenning, A. Light-driven continual oscillatory rocking of a polymer film. ChemistryOpen 2020, 9, 1149–1152. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Bai, H.; Liu, Z.; Zhang, X.; Huang, C.; Wiesner, L.W.; Silberstein, M.; Shepherd, R.F. Digital light processing of liquid crystal elastomers for self-sensing artificial muscles. Sci. Adv. 2021, 7, eabg3677. [Google Scholar] [CrossRef] [PubMed]
- Shen, B.; Kang, S. Designing self-oscillating matter. Matter 2021, 4, 766–769. [Google Scholar] [CrossRef]
- Zhao, T.; Fan, Y.; Lv, J. Photomorphogenesis of diverse Autonomous traveling waves in a monolithic soft artificial muscle. ACS Appl. Mater. Interfaces 2022, 14, 23839–23849. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Li, C. Design of MXene composites withbiomimetic rapid and self-oscillating actuation under ambient circumstances. ACS Appl. Mater. Interfaces 2021, 13, 31978–31985. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Qiu, Y.; Dai, Y.; Yu, Y. Modeling the dynamic response of a light-powered self-rotating liquid crystal elastomer-based system. Int. J. Mech. Sci. 2024, 263, 108794. [Google Scholar] [CrossRef]
- Shin, A.; Ha, J.; Lee, M.; Park, K.; Park, G.H.; Choi, T.H.; Cho, K.J.; Kim, H.Y. Hygrobot: A self-locomotive ratcheted actuator powered by environmental humidity. Sci. Robot. 2018, 3, eaar2629. [Google Scholar] [CrossRef] [PubMed]
- Baumann, A.; S’anchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Houerou, V.L.; Ziebert, F.; Kuli’c, I.M. Motorizing fibers with geometric zero-energy modes. Nat. Mater. 2018, 17, 523. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Li, K.; Zhao, C.; Qiu, Y.; Dai, Y. Light-powered self-rolling of a liquid crystal elastomer-based dicycle. Appl. Math. Mech. 2025, 46, 253–268. [Google Scholar] [CrossRef]
- Vantomme, G.; Elands, L.C.M.; Gelebart, A.H.; Meijer, E.W.; Pogromsky, A.Y.; Nijmeijer, H.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Zhou, K.; Xu, P. Chaotic self-beating of left ventricle modeled by liquid crystal elastomer. Thin-Walled Struct. 2024, 205, 112540. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, M.; Huang, S.; Liu, Z.; Yang, H. Multimodal self-sustainable autonomous locomotions of light-driven seifert ribbon actuators based on liquid crystal elastomers. Angew. Chem. Int. Ed. 2023, 62, e202304081. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhao, C.; Dai, Y.; Li, K. Light-fueled self-fluttering aircraft with a liquid crystal elastomer-based engine. Commun. Nonlinear Sci. Numer. Simul. 2024, 132, 107942. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yang, S. Multi-functional liquid crystal elastomer composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Hauser, A.W.; Sundaram, S.; Hayward, R.C. Photothermocapillary oscillators. Phys. Rev. Lett. 2018, 121, 158001. [Google Scholar] [CrossRef]
- Qiu, Y.; Dai, Y.; Li, K. Self-spinning of liquid crystal elastomer tubes under constant light intensity. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 108296. [Google Scholar] [CrossRef]
- Kim, Y.S.; Tamate, R.; Akimoto, A.M.; Yoshida, R. Recent developments in self-oscillating polymeric systems as smart materials: From polymers to bulk hydrogels. Mater. Horiz. 2017, 4, 38–54. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Vantomme, G.; Meijer, E.W.; Broer, D.J. Mastering the photothermal effect in liquid crystal networks: A general approach for self-sustained mechanical oscillators. Adv. Mater. 2017, 29, 1606712. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Sundaram, S.; Kang, J.H.; Tanjeem, N.; Emrick, T.; Hayward, R.C. Coupled oscillation and spinning of photothermal particles in Marangoni optical traps. Proc. Natl. Acad. Sci. USA 2021, 118, e2024581118. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Liu, W.; Khoruzhenko, O.; Breu, J.; Bai, H.; Hong, W.; Zheng, Q.; Wu, Z. Closed twisted hydrogel ribbons with self-sustained motions under static light irradiation. Adv. Mater. 2024, 36, 2314152. [Google Scholar] [CrossRef]
- Ge, D.; Dai, Y.; Liang, H.; Li, K. Self-rolling and circling of a conical liquid crystal elastomer rod on a hot surface. Int. J. Mech. Sci. 2024, 263, 108780. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, L.; Li, K. Self-oscillation of a liquid crystal elastomer fiber-shading laminate system under line illumination. Chaos Solitons Fractals 2025, 192, 115957. [Google Scholar] [CrossRef]
- Brighenti, R.; McMahan, C.G.; Cosma, M.P.; Kotikian, A.; Lewis, J.A.; Daraio, C. A micromechanical-based model of stimulus responsive liquid crystal elastomers. Int. J. Solids Struct. 2021, 219, 92–105. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, K.; Chen, Y.; Gao, J.; Xu, P. Self-oscillation chaotic motion of a liquid crystal elastomer pendulum under gradient-stabilized illumination. Chaos Solitons Fractals 2025, 193, 116128. [Google Scholar] [CrossRef]
- Herbert, K.M.; Fowler, H.E.; McCracken, J.M.; Schlafmann, K.R.; Koch, J.A.; White, T.J. Synthesis and alignment of liquid crystalline elastomers. Nat. Rev. Mater. 2022, 7, 23–38. [Google Scholar] [CrossRef]
- Dai, L.; Wang, L.; Chen, B.; Xu, Z.; Wang, Z.; Xiao, R. Shape memory behaviors of 3D printed liquid crystal elastomers. Soft Sci. 2023, 3, 4. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Z.W.; Zuo, B.; Chen, X.M.; Huang, S.; Yang, H. Liquid crystal elastomer electric locomotives. ACS Macro Lett. 2020, 9, 860–865. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Y.; Hu, W.; Soon, R.H.; Davidson, Z.S.; Sitti, M. Liquid crystal elastomer-based magnetic composite films for reconfigurable shape-morphing soft miniature machines. Adv. Mater. 2021, 33, 2006191. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Kang, X.; Ji, L.; Zhang, A.; Xia, G. Low frequency vibration energy harvesting of bio-inspired multi-stable piezoelectric vibration system with an adjustable device. Chaos Solitons Fractals 2025, 192, 116026. [Google Scholar] [CrossRef]
- Liao, W.; Yang, Z. The integration of sensing and actuating based on a simple design fiber actuator towards intelligent soft robots. Adv. Mater. Technol. 2022, 7, 2101260. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, C.; Chen, B.; Wang, Z.; Xu, Y.; Xiao, R. Bioinspired design of stimuli-responsive artificial muscles with multiple actuation modes. Smart Mater. Struct. 2023, 32, 085023. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Z.; Xu, Z.; Yu, Q.; Wu, Z.L.; Wang, Z.; Qian, J.; Xiao, R. Shape morphing of 3D printed liquid crystal elastomer structures with precuts. ACS Appl. Polym. Mater. 2023, 5, 7477–7484. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liao, W.; Ultrafast, Y.Z. High-contractile electrothermal-driven liquid crystal elastomer fibers towards artificial muscles. Small 2021, 17, 2103700. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Guo, S.; Tong, X.; Xia, H.; Zhao, Y. Tunable photocontrolled motions using stored strain energy in malleable azobenzene liquid crystalline polymer actuators. Adv. Mater. 2017, 29, 1606467. [Google Scholar] [CrossRef]
- Brighenti, R.; Cosma, M.P. Multiphysics modelling of light-actuated liquid crystal elastomers. Proc. R. Soc. A 2023, 479, 20220417. [Google Scholar] [CrossRef]
- Alyami, A.; Rajapaksha, C.P.H.; Chen, F.; Paudel, P.R.; Paul, A.; Adaka, A.; Dharmarathna, R.; Lüssem, B.; Jákli, A. Ionic liquid crystal elastomers for actuators, sensors, and organic transistors. Liq. Cryst. 2023, 50, 1151–1161. [Google Scholar] [CrossRef]
- Chen, F.; Rajapaksha, C.P.H.; Cedillo, J.M.; Piedrahita, C.; Cao, J.; Kaphle, V.; Lüssem, B.; Kyu, T.; Jákli, A. Electroresponsive ionic liquid crystal elastomers. Macromol. Rapid Commun. 2019, 40, 1900299. [Google Scholar]
- Lehmann, W.; Skupin, H.; Tolksdorf, C.; Gebhard, E.; Zentel, R.; Krüger, P.; Lösche, M.; Kremer, F. Giant lateral electrostriction in ferroelectric liquid-crystalline elastomers. Nature 2001, 410, 447–450. [Google Scholar] [CrossRef] [PubMed]
- Arazoe, H.; Miyajima, D.; Akaike, K.; Araoka, F.; Sato, E.; Hikima, T.; Kawamoto, M.; Aida, T. An autonomous actuator driven by fluctuations in ambient humidity. Nat. Mater. 2016, 15, 1084–1089. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Friedlander, R.S.; Zarzar, L.D.; Aizenberg, J. Chemo-mechanically regulated oscillation of an enzymatic reaction. Chem. Mater. 2013, 25, 521–523. [Google Scholar] [CrossRef][Green Version]
- Kang, X.; Wang, X.; Xia, G. Ultra-low frequency vibration energy harvesting of piezoelectric vibration systems with an adjustable device. Alex. Eng. J. 2024, 100, 92–110. [Google Scholar] [CrossRef]
- Xu, L.; Zhu, C.; Lamont, S.; Zou, X.; Yang, Y.; Chen, S.; Ding, J.; Vernerey, F.J. Programming motion into materials using electricity-driven liquid crystal elastomer actuators. Soft Robot. 2024, 11, 464–472. [Google Scholar] [CrossRef]
- Saeed, M.H.; Choi, M.Y.; Kim, K.; Lee, J.; Kim, K.; Kim, D.; Kim, S.; Kim, H.; Ahn, S.; Lan, R.; et al. Electrostatically powered multimode liquid crystalline elastomer actuators. ACS Appl. Mater. Interfaces 2023, 15, 56285–56292. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, L.; Scalet, G.; Peigney, M.; Azoug, A. Coupling between viscoelasticity and soft elasticity in main-chain nematic liquid crystal elastomers. J. Mech. Phys. Solids 2024, 187, 105612. [Google Scholar] [CrossRef]
- Li, K.; Du, C.; He, Q.; Cai, S. Thermally driven self-oscillation of an elastomer fiber with a hanging weight. Extrem. Mech. Lett. 2022, 50, 101547. [Google Scholar] [CrossRef]
- Braun, L.; Hessberger, T.; Pütz, E.; Müller, C.; Giesselmann, F.; Serra, C.A.; Zentel, R. Actuating thermo-and photo-responsive tubes from liquid crystalline elastomers. J. Mater. Chem. C 2018, 6, 9093–9101. [Google Scholar] [CrossRef]
- Heller, M.D. Hurwitz-based stability criteria for bounded nonlinear time-varying systems. IEEE Int. Conf. Control Autom. 2005, 2, 942–947. [Google Scholar]
- Claeys, M.; Sinou, J.J.; Lambelin, J.P.; Alcoverro, B. Multi-harmonic measurements and numerical simulations of nonlinear vibrations of a beam with non-ideal boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4196–4212. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Ge, W.; Liu, X. Multi-scale methodology for complex systems. Chem. Eng. Sci. 2004, 59, 1687–1700. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Li, Z.; Zhou, L. Electrically Driven Liquid Crystal Elastomer Self-Oscillators via Rheostat Feedback Mechanism. Polymers 2025, 17, 617. https://doi.org/10.3390/polym17050617
Li K, Li Z, Zhou L. Electrically Driven Liquid Crystal Elastomer Self-Oscillators via Rheostat Feedback Mechanism. Polymers. 2025; 17(5):617. https://doi.org/10.3390/polym17050617
Chicago/Turabian StyleLi, Kai, Zuhao Li, and Lin Zhou. 2025. "Electrically Driven Liquid Crystal Elastomer Self-Oscillators via Rheostat Feedback Mechanism" Polymers 17, no. 5: 617. https://doi.org/10.3390/polym17050617
APA StyleLi, K., Li, Z., & Zhou, L. (2025). Electrically Driven Liquid Crystal Elastomer Self-Oscillators via Rheostat Feedback Mechanism. Polymers, 17(5), 617. https://doi.org/10.3390/polym17050617






