Nonlinear Viscoelasticity of and Structural Modulation in Guar Gum-Enhanced Triple-Network Hydrogels
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Hydrogel Preparation
2.3. Characterization
2.3.1. Fourier-Transform Infrared (FTIR) Spectroscopy
2.3.2. Scanning Electron Microscopy (SEM)
2.3.3. X-Ray Diffraction (XRD)
2.3.4. Differential Scanning Calorimetry (DSC)
2.3.5. Tensile Strength
2.3.6. Swelling Properties
2.3.7. Rheological Measurements
3. Results and Discussion
3.1. Hydrogel Formation
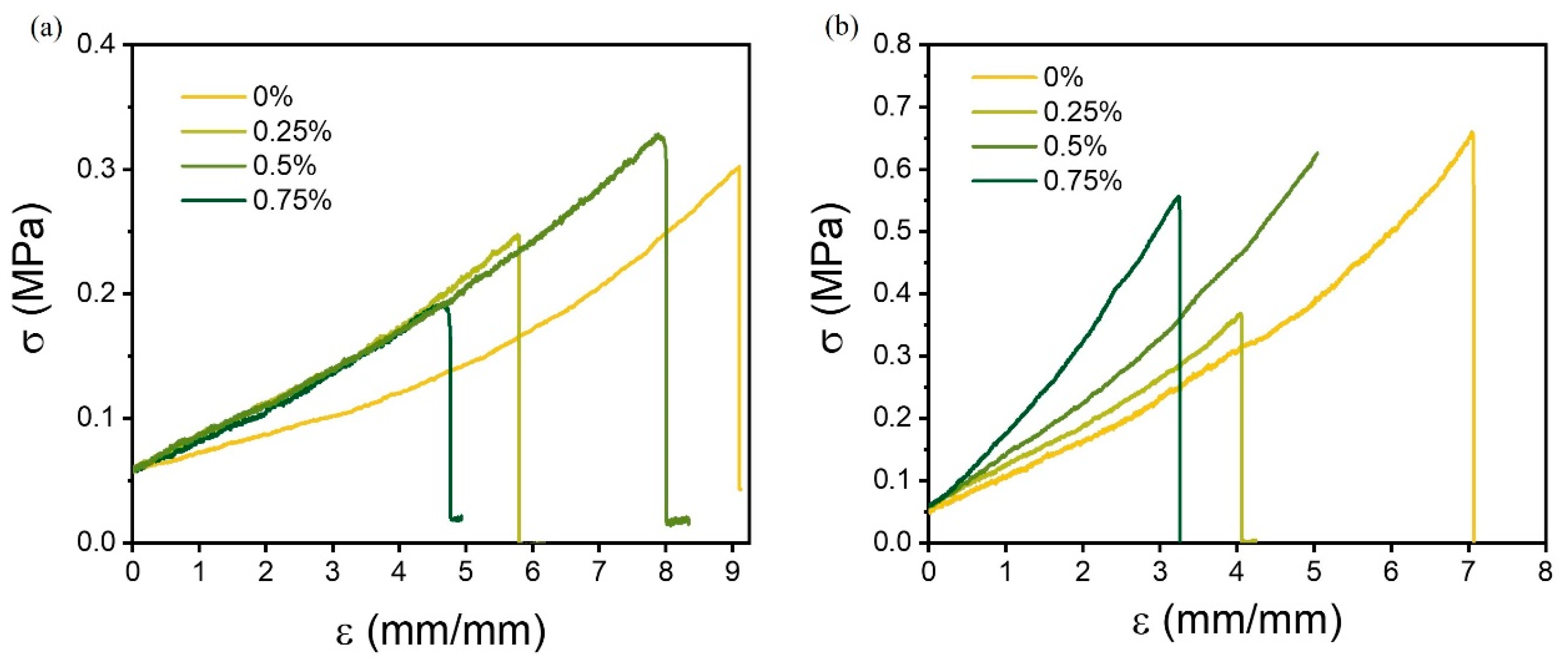
3.2. Mechanical Properties
3.3. Rheological Properties
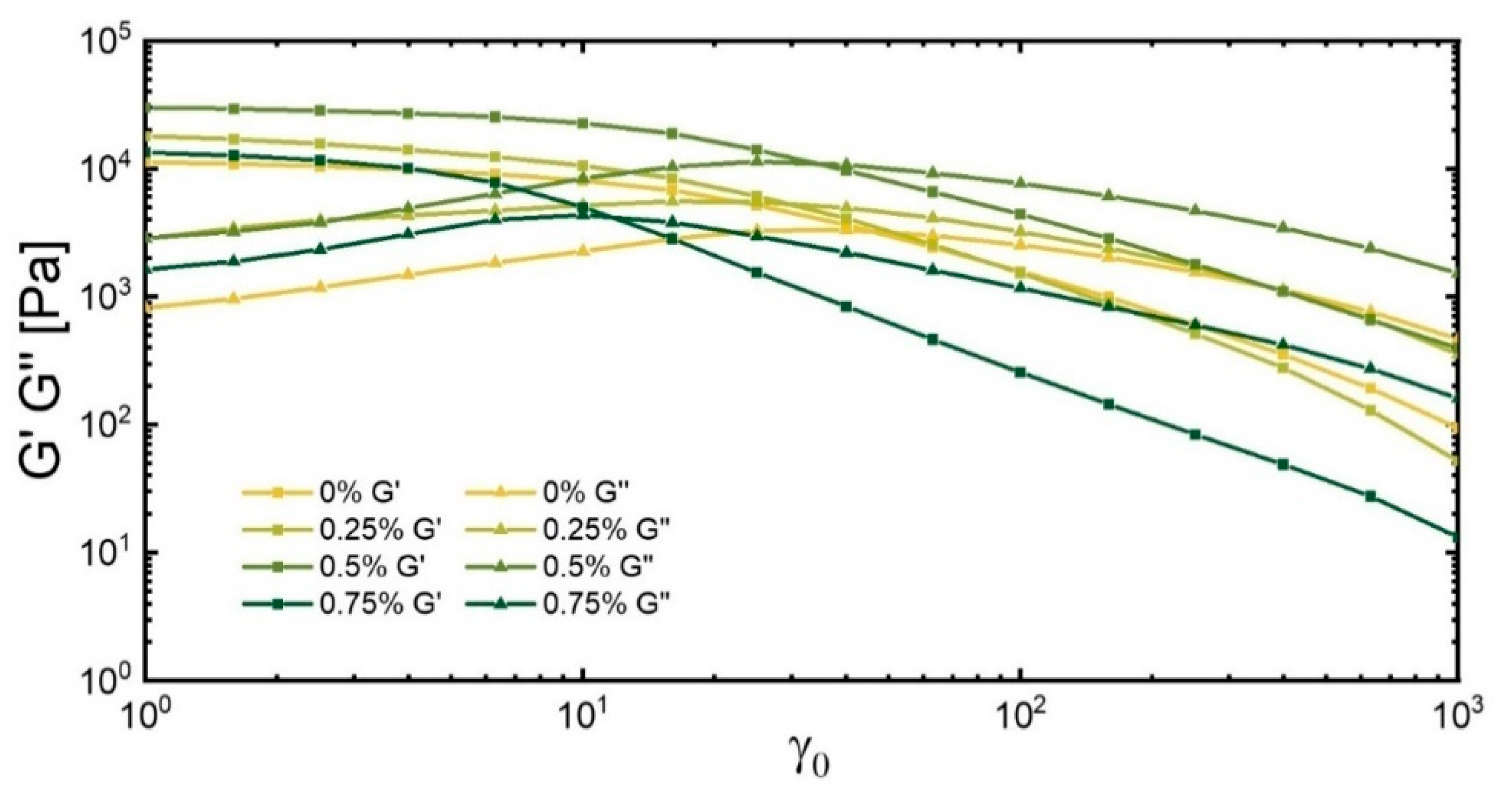
3.3.1. Strain Sweep
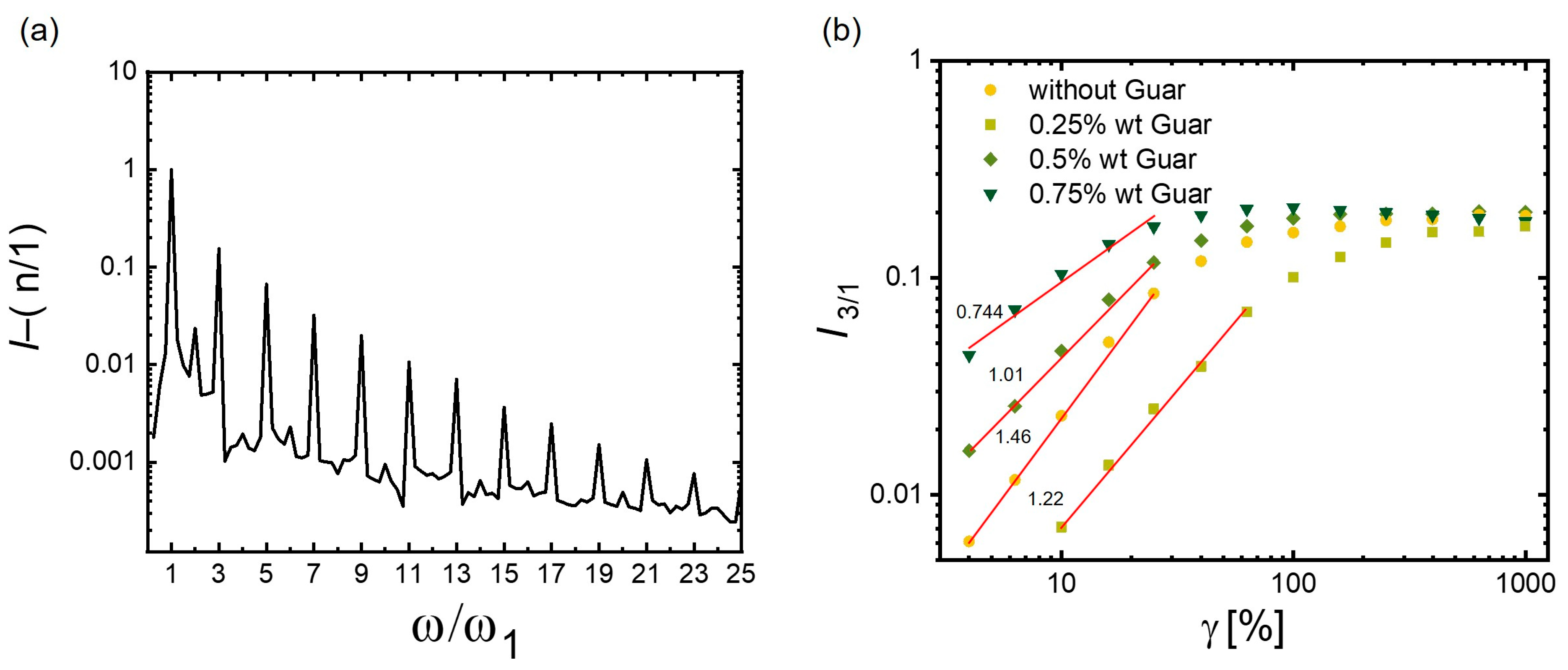
3.3.2. Advanced Structure Analysis by LAOS
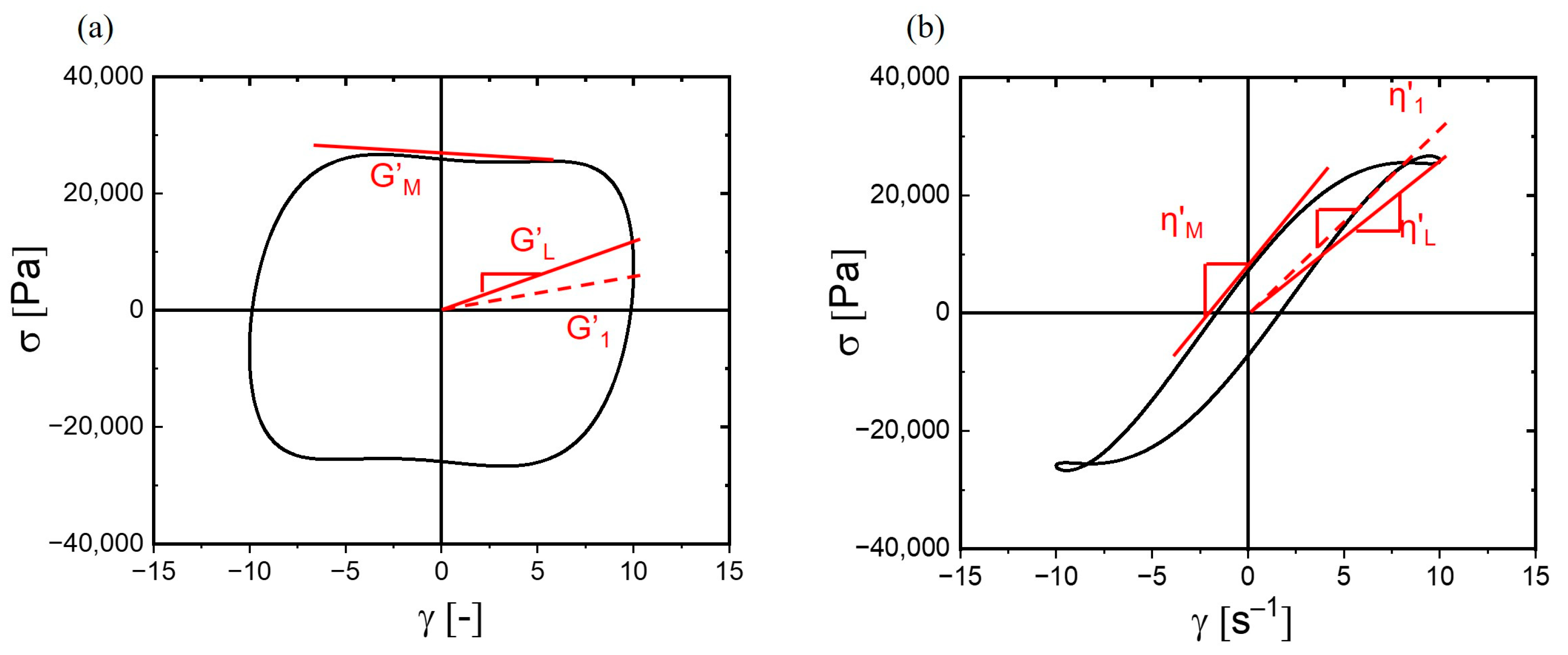
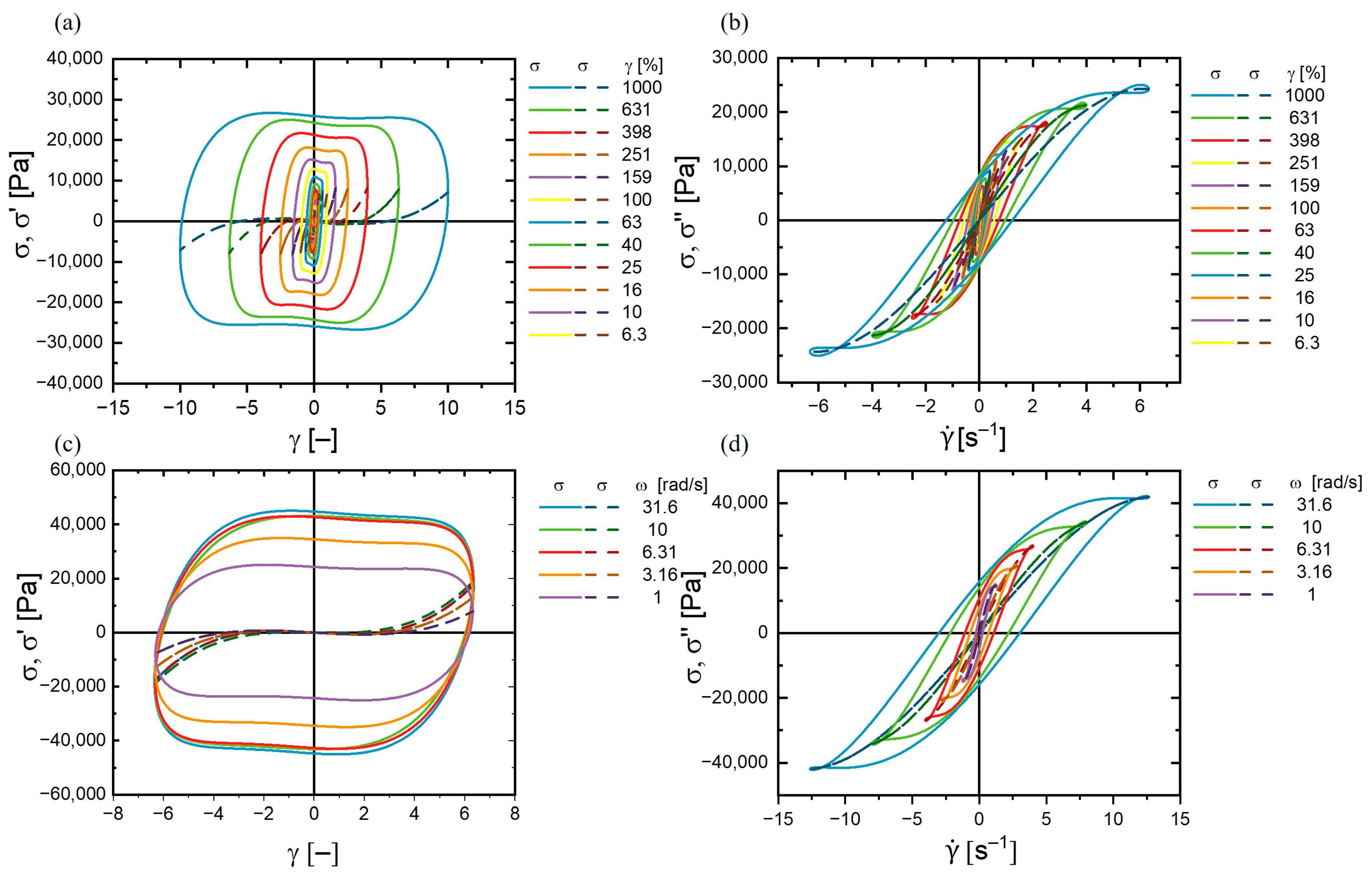
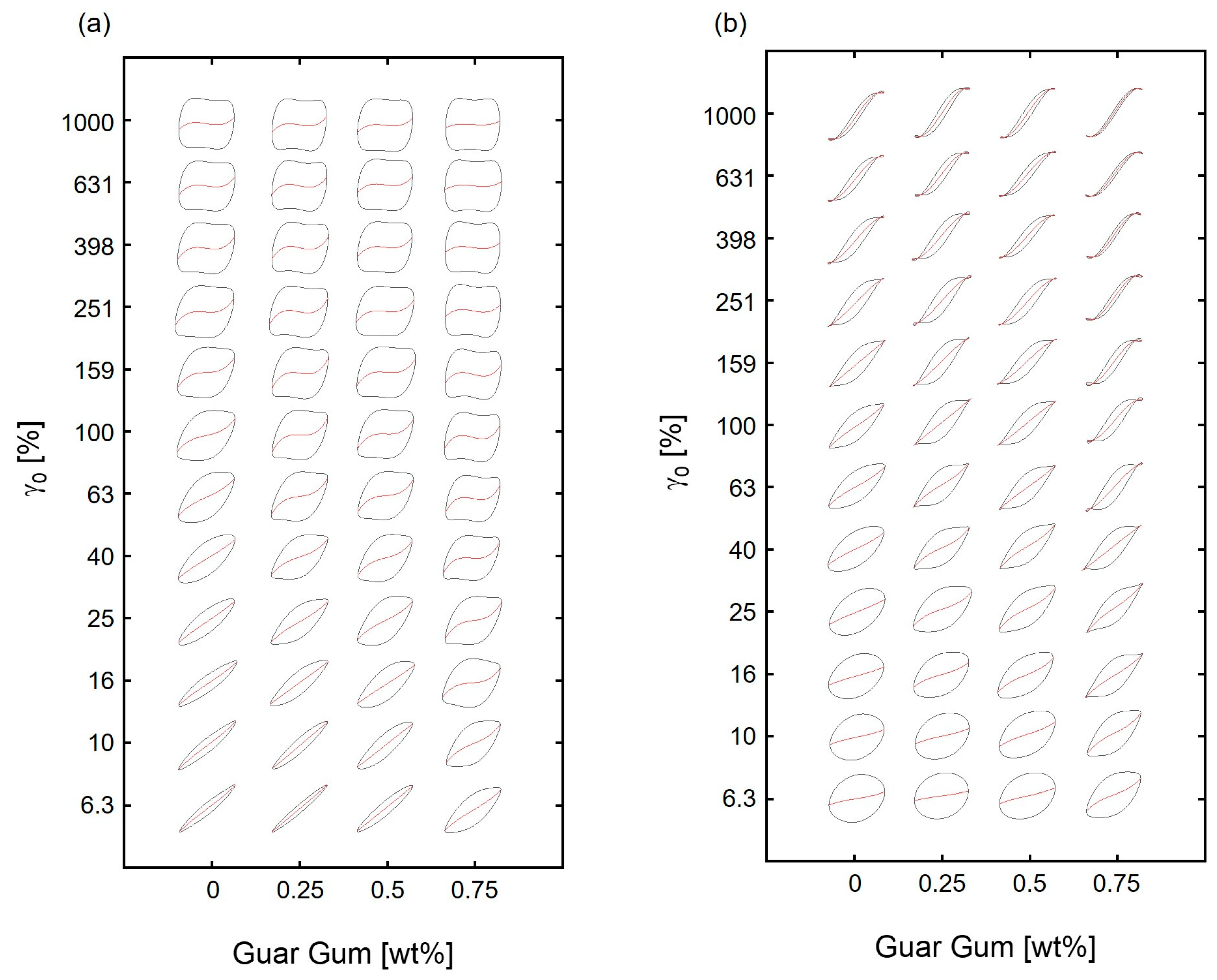
3.3.3. Stress Decomposition and Lissajous–Bowditch Curves
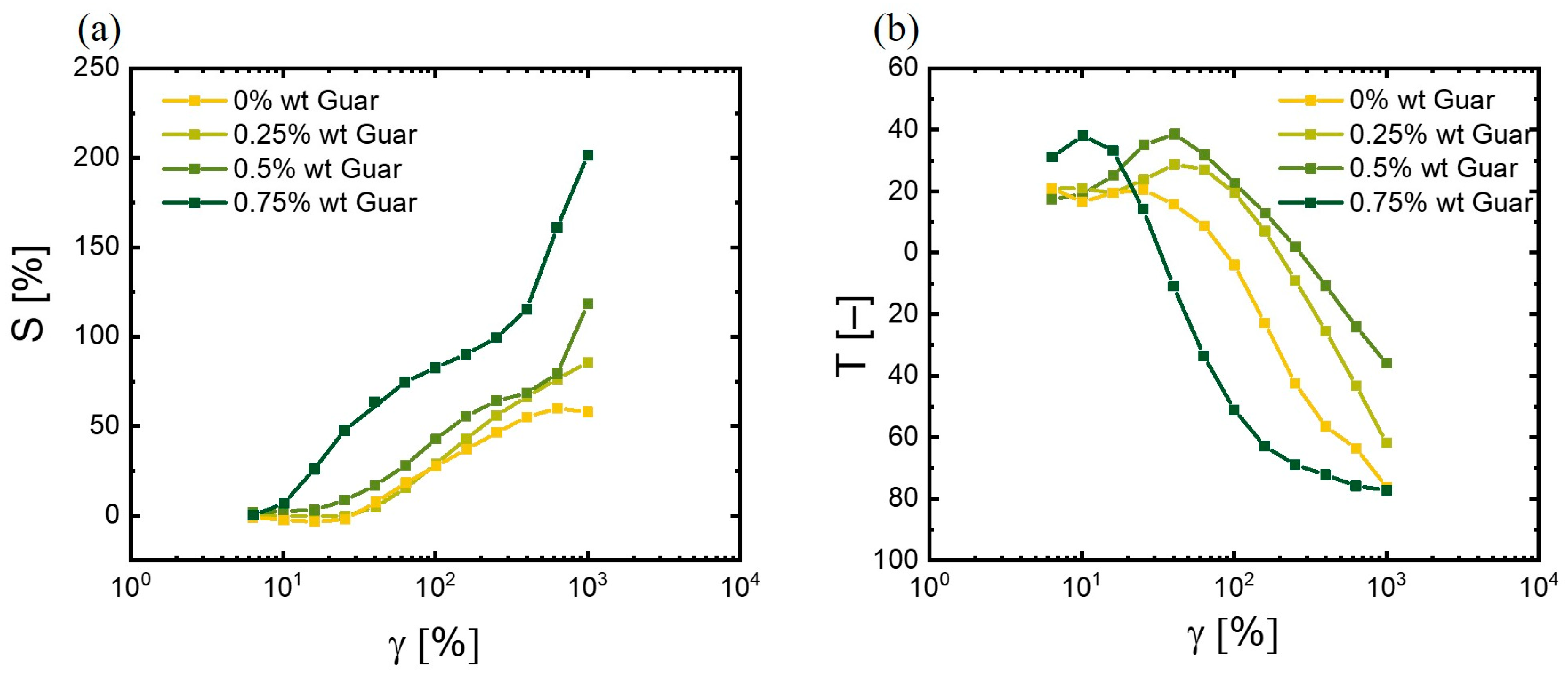
3.3.4. Nonlinear Viscoelastic Parameters of Hydrogels
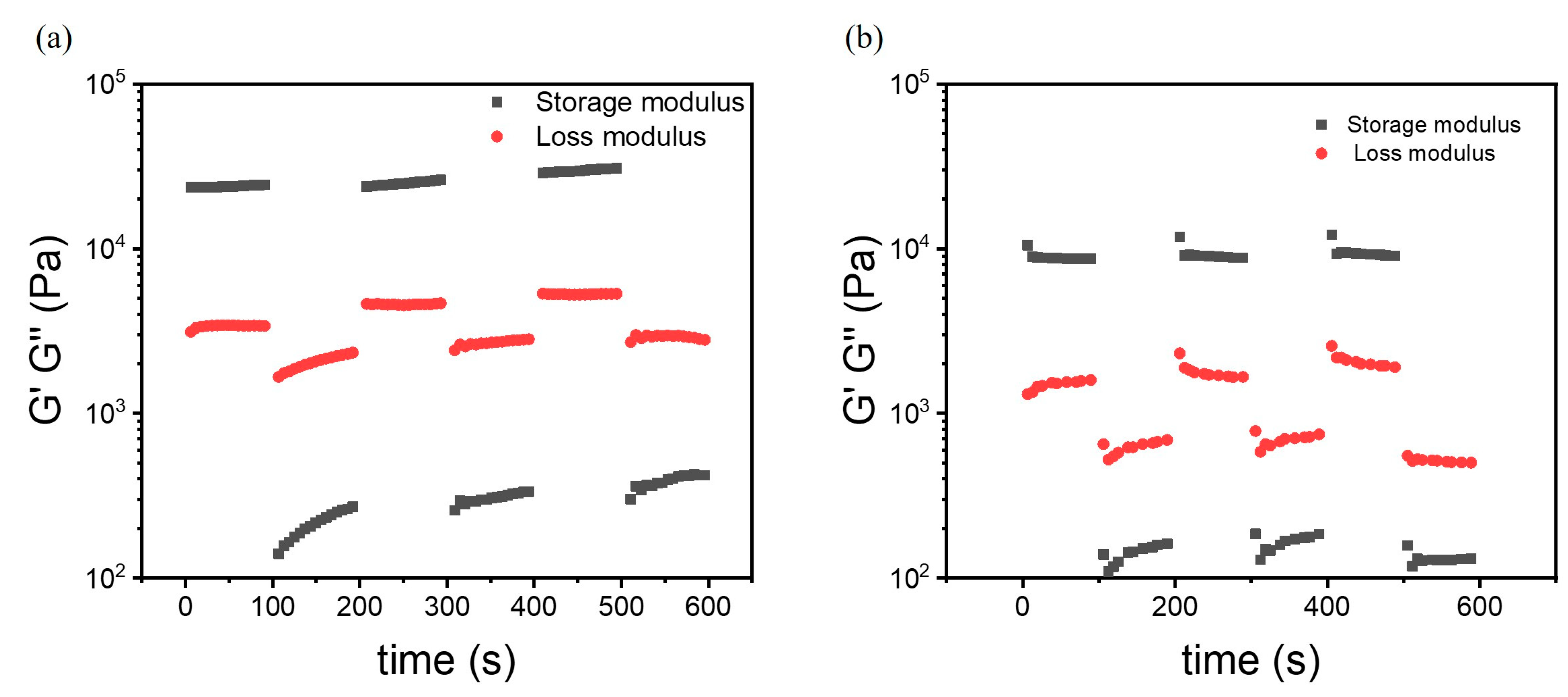
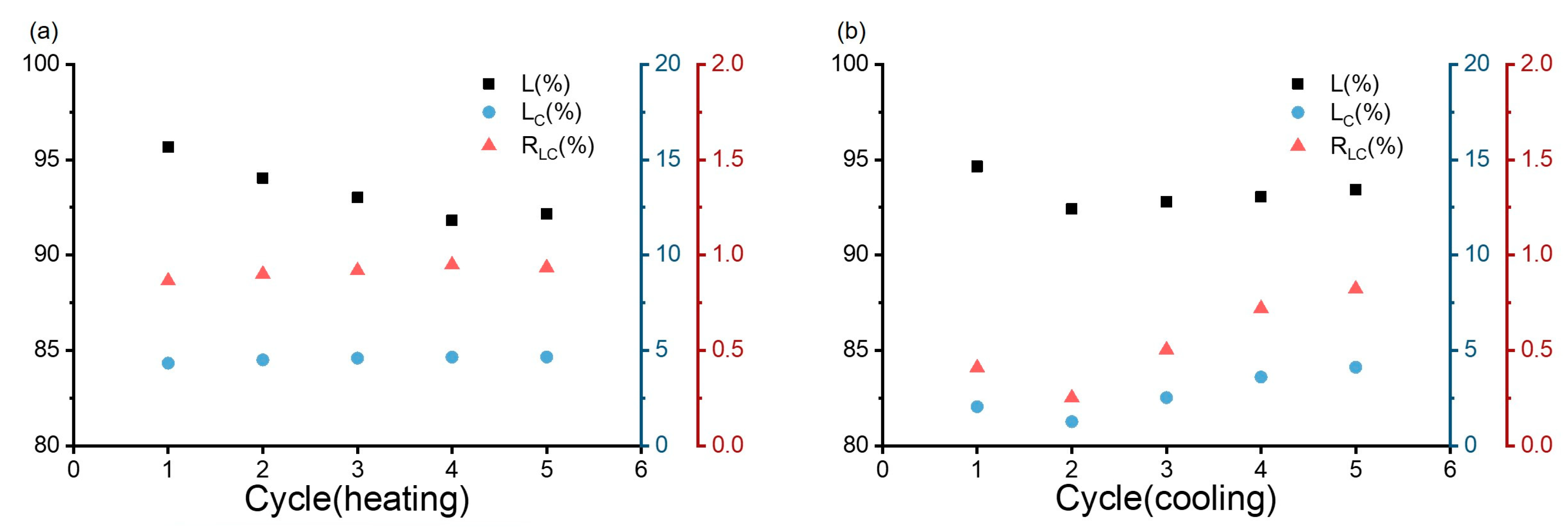
3.3.5. Self-Healing in Dynamic Oscillation Experiments
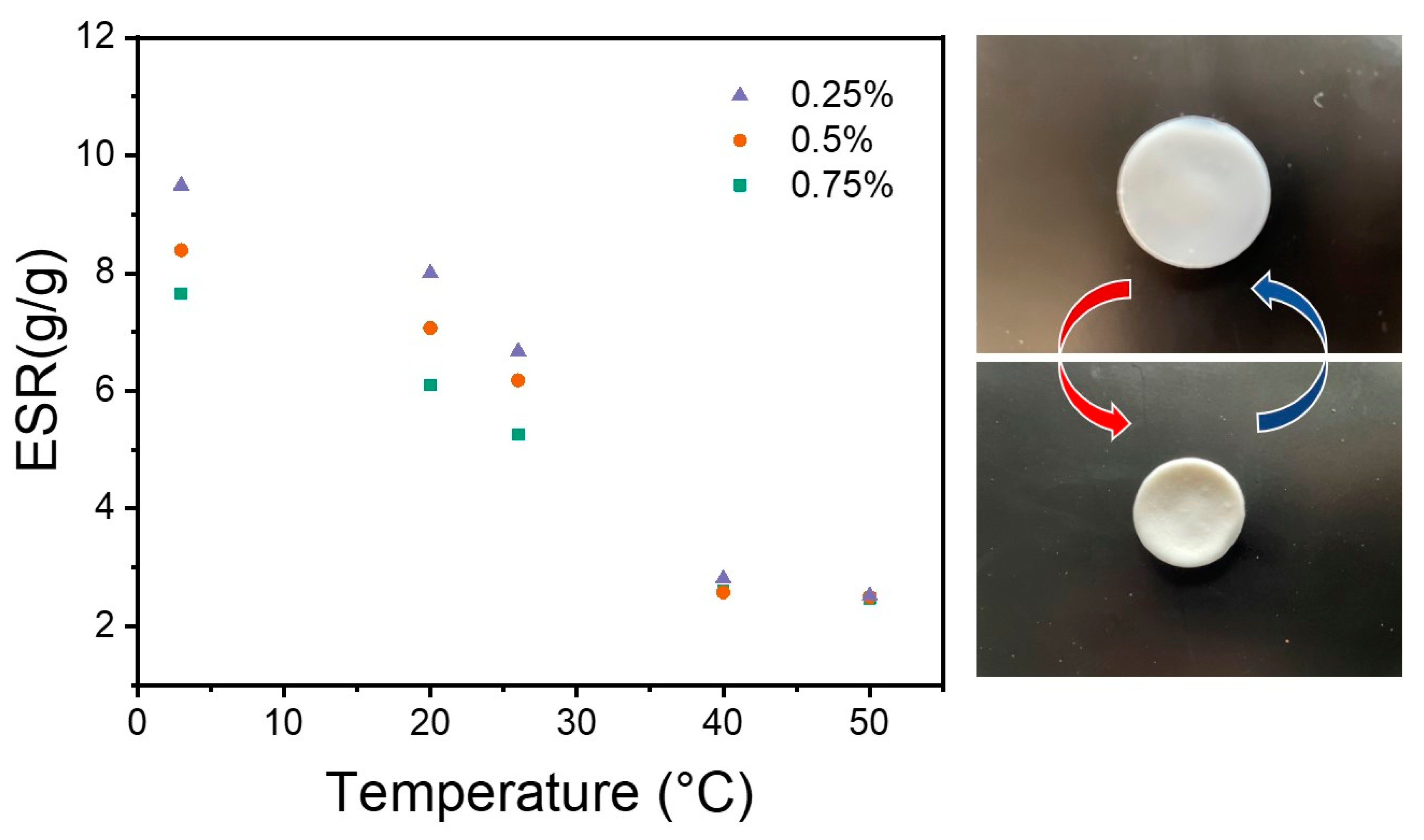
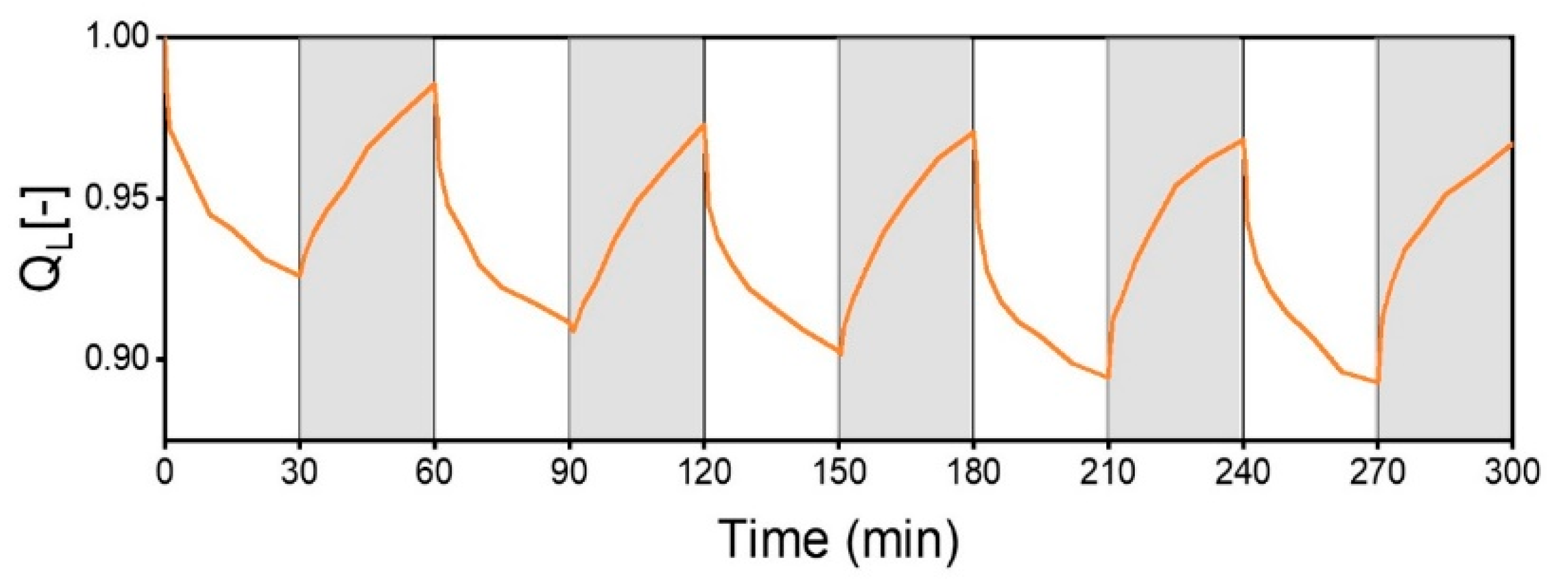
3.4. Thermo-Responsive Behavior
Dynamic Thermo-Responsiveness Properties
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Das, A.; Wadhwa, S.; Srivastava, A.K. Cross-Linked Guar Gum Hydrogel Discs for Colon-Specific Delivery of Ibuprofen: Formulation and In Vitro Evaluation. Drug Deliv. 2006, 13, 139–142. [Google Scholar] [CrossRef]
- Sharma, S.; Afgan, S.; Deepak; Kumar, A.; Kumar, R. l-Alanine induced thermally stable self-healing guar gum hydrogel as potential drug vehicle for sustained release of hydrophilic drug. Mater. Sci. Eng. C 2019, 99, 1384–1391. [Google Scholar] [CrossRef] [PubMed]
- Seeli, D.S.; Prabaharan, M. Guar gum oleate-graft-poly(methacrylic acid) hydrogel as a colon-specific controlled drug delivery carrier. Carbohydr. Polym. 2017, 158, 51–57. [Google Scholar] [CrossRef] [PubMed]
- Krishna, D.V.; Sankar, M.R.; Sarma, P.; Samundeshwari, E.L. Copper nanoparticles loaded gelatin/polyvinyl alcohol/guar gum-based 3D printable multimaterial hydrogel for tissue engineering applications. Int. J. Biol. Macromol. 2024, 276, 133866. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Cheng, C.; Peng, X.; Zhang, K.; Yu, X. A self-healing and injectable oxidized quaternized guar gum/carboxymethyl chitosan hydrogel with efficient hemostatic and antibacterial properties for wound dressing. Colloids Surf. B Biointerfaces 2022, 209, 112207. [Google Scholar] [CrossRef]
- HaqAsif, A.; Karnakar, R.R.; Sreeharsha, N.; Gite, V.V.; Borane, N.; Al-Dhubiab, B.E.; Kaliyadan, F.; Rasool, T.; Nanjappa, S.H.; Meravanige, G. pH and Salt Responsive Hydrogel based on Guar Gum as a Renewable Material for Delivery of Curcumin: A Natural Anti-Cancer Drug. J. Polym. Environ. 2021, 29, 1978–1989. [Google Scholar] [CrossRef]
- Szopinski, D.; Luinstra, G.A. Viscoelastic properties of aqueous guar gum derivative solutions under large amplitude oscillatory shear (LAOS). Carbohydr. Polym. 2016, 153, 312–319. [Google Scholar] [CrossRef] [PubMed]
- Thombare, N.; Jha, U.; Mishra, S.; Siddiqui, M.Z. Guar gum as a promising starting material for diverse applications: A review. Int. J. Biol. Macromol. 2016, 88, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Sharma, G.; Sharma, S.; Kumar, A.; Al-Muhtaseb, A.H.; Naushad, M.; Ghfar, A.A.; Mola, G.T.; Stadler, F.J. Guar gum and its composites as potential materials for diverse applications: A review. Carbohydr. Polym. 2018, 199, 534–545. [Google Scholar] [CrossRef]
- Iqbal, D.N.; Shafiq, S.; Khan, S.M.; Ibrahim, S.M.; Abubshait, S.A.; Nazir, A.; Abbas, M.; Iqbal, M. Novel chitosan/guar gum/PVA hydrogel: Preparation, characterization and antimicrobial activity evaluation. Int. J. Biol. Macromol. 2020, 164, 499–509. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, L.; Wang, B.; Yang, B.; Khan, I.; Khan, A.; Ni, Y. Multifunctional self-assembling hydrogel from guar gum. Chem. Eng. J. 2017, 330, 1044–1051. [Google Scholar] [CrossRef]
- Cunha, P.L.; Castro, R.R.; Rocha, F.A.; de Paula, R.C.; Feitosa, J.P. Low viscosity hydrogel of guar gum: Preparation and physicochemical characterization. Int. J. Biol. Macromol. 2005, 37, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Reis, A.C.; dos Santos, L.V.; Santos, K.R.; Lima-Tenório, M.K.; Paludo, K.S.; Maurício, M.R.; Rubira, A.F.; Viana, A.G.; Tenório-Neto, E.T. Chemically crosslinked guar gum hydrogels: An investigation on the water transport and its relationship with hydrocortisone release. Int. J. Pharm. 2022, 617, 121626. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Guan, S.; Hu, Q.; Gao, G.; Xu, K.; Wang, P. Tough and pH-sensitive hydroxypropyl guar gum/polyacrylamide hybrid double-network hydrogel. Chem. Eng. J. 2016, 306, 953–960. [Google Scholar] [CrossRef]
- Luo, Y.; Pauer, W.; Luinstra, G.A. Tough, Stretchable, and Thermoresponsive Smart Hydrogels. Gels 2023, 9, 695. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Xie, X.; Wang, T.; Cao, C.; Li, J.; Sun, T.; Liu, H.; Geng, S.; Wei, Z.; Li, J.; et al. Wearable Hydrogel-Based Epidermal Sensor with Thermal Compatibility and Long Term Stability for Smart Colorimetric Multi-Signals Monitoring. Adv. Healthc. Mater. 2023, 12, 2201730. [Google Scholar] [CrossRef] [PubMed]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, X.; Zheng, Y.; Liu, J.; Bao, Y.; Shan, G.; Yu, C.; Pan, P. Moisture-responsive ultralow-hysteresis polymer ionogels for adhesion-switchable strain sensing. Mater. Horiz. 2025; advance article. [Google Scholar] [CrossRef] [PubMed]
- Hyun, K.; Kim, S.H.; Ahn, K.H.; Lee, S.J. Large amplitude oscillatory shear as a way to classify the complex fluids. J. Non-Newton. Fluid Mech. 2002, 107, 51–65. [Google Scholar] [CrossRef]
- Krivega, E.S.; Kotova, S.L.; Timashev, P.S.; Efremov, Y.M. Mechanical characterization of soft biomaterials: Which time and spatial scale to choose? bioRxiv 2024, preprint. [Google Scholar] [CrossRef] [PubMed]
- Tarashi, S.; Nazockdast, H.; Bandegi, A.; Shafaghsorkh, S.; Sodeifian, G.; Foudazi, R. Large amplitude oscillatory shear behavior of thermoresponsive hydrogels: Single versus double network. J. Rheol. 2022, 67, 15–33. [Google Scholar] [CrossRef]
- Sun, W.; Huang, L.; Yang, Y.; Liu, X.; Tong, Z. Large amplitude oscillatory shear studies on the strain-stiffening behavior of gelatin gels. Chin. J. Polym. Sci. 2015, 33, 70–83. [Google Scholar] [CrossRef]
- Goudoulas, T.B.; Didonaki, A.; Pan, S.; Fattahi, E.; Becker, T. Comparative Large Amplitude Oscillatory Shear (LAOS) Study of Ionically and Physically Crosslinked Hydrogels. Polymers 2023, 15, 1558. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Bai, Y.; Gu, X.; Kang, S.; Yang, Y.; Wang, K. A Novel Fracturing Fluid Based on Functionally Modified Nano-Silica-Enhanced Hydroxypropyl Guar Gel. Gels 2024, 10, 369. [Google Scholar] [CrossRef]
- Goycoolea, F.M.; Morris, E.R.; Gidley, M.J. Viscosity of galactomannans at alkaline and neutral pH: Evidence of ‘hyperentanglement’ in solution. Carbohydr. Polym. 1995, 27, 69–71. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Hosoi, A.E.; McKinley, G.H. New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J. Rheol. 2008, 52, 1427–1458. [Google Scholar] [CrossRef]
- Luo, Y.; Pauer, W.; Luinstra, G.A. Fabrication of Thermo-Responsive Controllable Shape-Changing Hydrogel. Gels 2022, 8, 531. [Google Scholar] [CrossRef]
- Alang, M.B.; Barminas, J.T.; Aliyu, B.A.; Osemeahon, S.A. Synthesis and optimization of polyacrylamide and gum arabic graft copolymer. Int. J. Biol. Chem. Sci. 2012, 5, 1694–1702. [Google Scholar] [CrossRef][Green Version]
- Kalia, S.; Sabaa, M.W. (Eds.) Polysaccharide Based Graft Copolymers; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-36565-2. [Google Scholar]
- Seguela, R. Critical review of the molecular topology of semicrystalline polymers: The origin and assessment of intercrystalline tie molecules and chain entanglements. J. Polym. Sci. B Polym. Phys. 2005, 43, 1729–1748. [Google Scholar] [CrossRef]
- Manna, S.; Karmakar, S.; Sen, O.; Sinha, P.; Jana, S.; Jana, S. Recent updates on guar gum derivatives in colon specific drug delivery. Carbohydr. Polym. 2024, 334, 122009. [Google Scholar] [CrossRef]
- Hu, X.; Karnetzke, J.; Fassbender, M.; Drücker, S.; Bettermann, S.; Schroeter, B.; Pauer, W.; Moritz, H.-U.; Fiedler, B.; Luinstra, G.; et al. Smart reactors—Combining stimuli-responsive hydrogels and 3D printing. Chem. Eng. J. 2020, 387, 123413. [Google Scholar] [CrossRef]
- Wang, Q.; Mynar, J.L.; Yoshida, M.; Lee, E.; Lee, M.; Okuro, K.; Kinbara, K.; Aida, T. High-water-content mouldable hydrogels by mixing clay and a dendritic molecular binder. Nature 2010, 463, 339–343. [Google Scholar] [CrossRef]
- Szopinski, D.; Handge, U.A.; Kulicke, W.-M.; Abetz, V.; Luinstra, G.A. Extensional flow behavior of aqueous guar gum derivative solutions by capillary breakup elongational rheometry (CaBER). Carbohydr. Polym. 2016, 136, 834–840. [Google Scholar] [CrossRef] [PubMed]
- Al-Taq, A.A.; Aljawad, M.S.; Alade, O.S.; Al-Ajwad, H.; Murtaza, M.; Al-Abdrabalnabi, R.; Alrustum, A.; Mahmoud, M. Investigations of thermochemical fluids as cleanup system for polymer-based fracturing fluids. Geoenergy Sci. Eng. 2024, 242, 213260. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, P.; Zhao, B.; Wang, S.; Zhong, J.; Cao, Z.; Liu, C.; Gong, F.; Matsuyama, H. Swelling Resistance and Mechanical Performance of Physical Crosslink-Based Poly(Vinyl Alcohol) Hydrogel Film with Various Molecular Weight. J. Polym. Sci. B Polym. Phys. 2019, 57, 1673–1683. [Google Scholar] [CrossRef]
- Zhu, R.; Zheng, Z.; Zhu, D.; Wang, X. Hydrogels with high sacrifice efficiency of sacrificial bonds and with high strength and toughness due to dense entanglements of polymer chains. J. Colloid Interface Sci. 2025, 677, 687–696. [Google Scholar] [CrossRef] [PubMed]
- Prabhakaran, P.; Benjamin, C.C. Energy dissipation in pH-sensitive hydrogels subjected to large amplitude oscillatory shear. Mech. Mater. 2020, 140, 103226. [Google Scholar] [CrossRef]
- Giacomin, A.J.; Dealy, J.M. Large-Amplitude Oscillatory Shear. In Techniques in Rheological Measurement; Collyer, A.A., Ed.; Springer: Dordrecht, The Netherlands, 1993; pp. 99–121. ISBN 978-94-011-2114-9. [Google Scholar]
- Hyun, K.; Ahn, K.H.; Lee, S.J.; Sugimoto, M.; Koyama, K. Degree of branching of polypropylene measured from Fourier-transform rheology. Rheol. Acta 2006, 46, 123–129. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 2005, 49, 747–758. [Google Scholar] [CrossRef]



| Guar Content (wt%) | 0 | 0.25 | 0.50 | 0.75 |
|---|---|---|---|---|
| XRD (peak at 19.6°) | ||||
| Integral value | 67,688 | 128,415 | 129,203 | 140,184 |
| Peak | 6049 | 15,057 | 15,907 | 17,406 |
| FWHM * (°) | 15.1 | 8.12 | 7.76 | 7.66 |
| DSC | ||||
| Tm (°C) | 221.8 | 225 | 223.4 | 225.5 |
| Melting range (°C) | 213.7–230.4 | 212.6–229.7 | 214.9–230.3 | |
| ΔHm (J/g) | 20.1 ± 0.1 | 30.1 ± 0.9 | 33.9 ± 0.4 | 41.2 ± 0.5 |
| Crystallinity (%) | 14.6 | 22.0 | 24.2 | 30 |
| Guar Content (wt%) | 0 | 0.25 | 0.5 | 0.75 |
|---|---|---|---|---|
| Initial critical strain(γc) % | 13.7 | 7.2 | 9.6 | 2.8 |
| Subsequent yield strain (γy) % | 46.0 | 29.6 | 34.4 | 11.7 |
| Max of G″ (strain%) | 40 | 25 | 25 | 10 |
| Max of G″ (kPa.s) | 3.3 | 5.5 | 11.4 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Pauer, W.; Luinstra, G.A. Nonlinear Viscoelasticity of and Structural Modulation in Guar Gum-Enhanced Triple-Network Hydrogels. Polymers 2025, 17, 597. https://doi.org/10.3390/polym17050597
Luo Y, Pauer W, Luinstra GA. Nonlinear Viscoelasticity of and Structural Modulation in Guar Gum-Enhanced Triple-Network Hydrogels. Polymers. 2025; 17(5):597. https://doi.org/10.3390/polym17050597
Chicago/Turabian StyleLuo, Yi, Werner Pauer, and Gerrit A. Luinstra. 2025. "Nonlinear Viscoelasticity of and Structural Modulation in Guar Gum-Enhanced Triple-Network Hydrogels" Polymers 17, no. 5: 597. https://doi.org/10.3390/polym17050597
APA StyleLuo, Y., Pauer, W., & Luinstra, G. A. (2025). Nonlinear Viscoelasticity of and Structural Modulation in Guar Gum-Enhanced Triple-Network Hydrogels. Polymers, 17(5), 597. https://doi.org/10.3390/polym17050597






