Heuristic Guidelines for Developing Polymer/Ionic Liquid Blend Membranes
Abstract
1. Introduction
2. Methods
3. Results
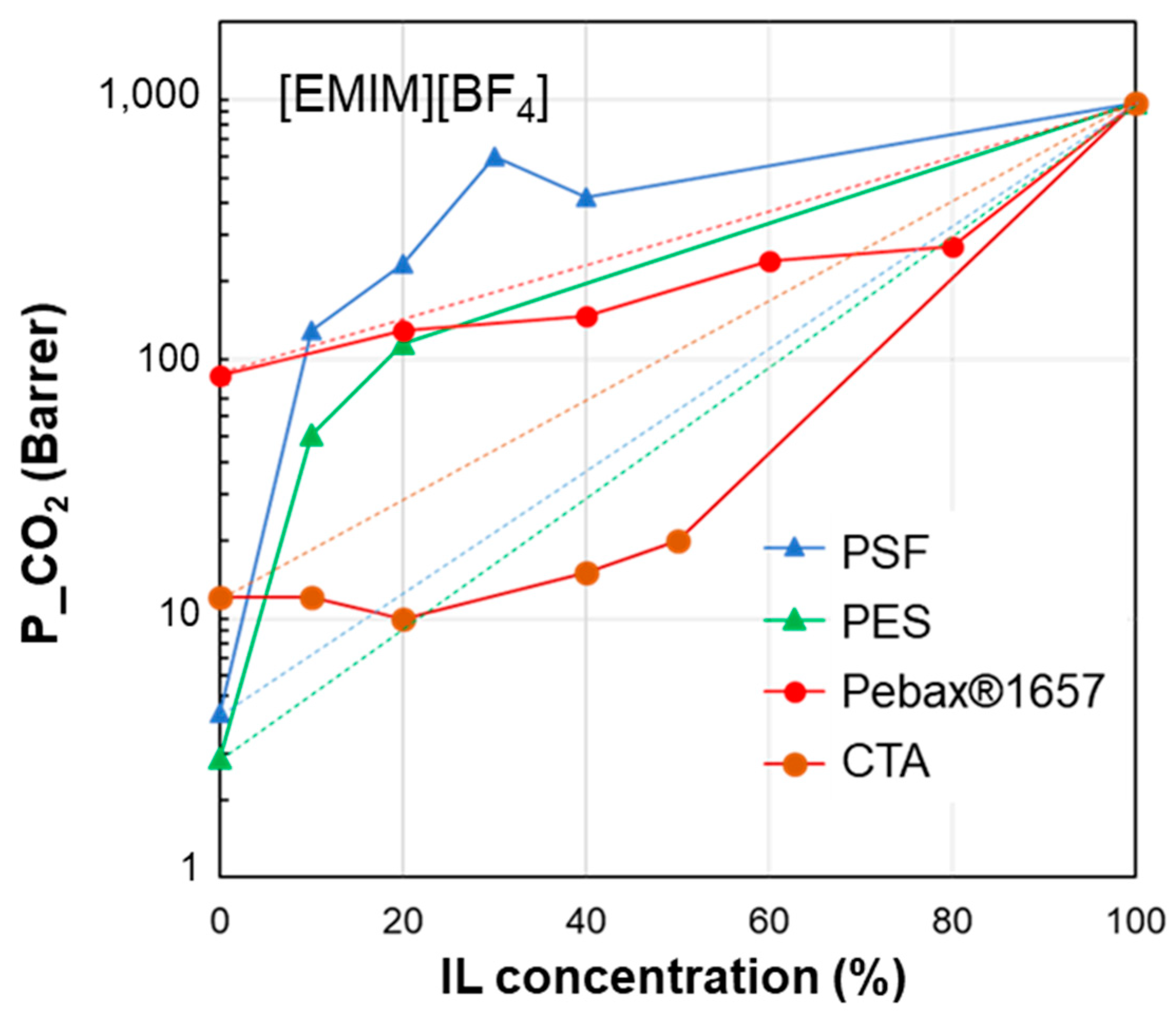
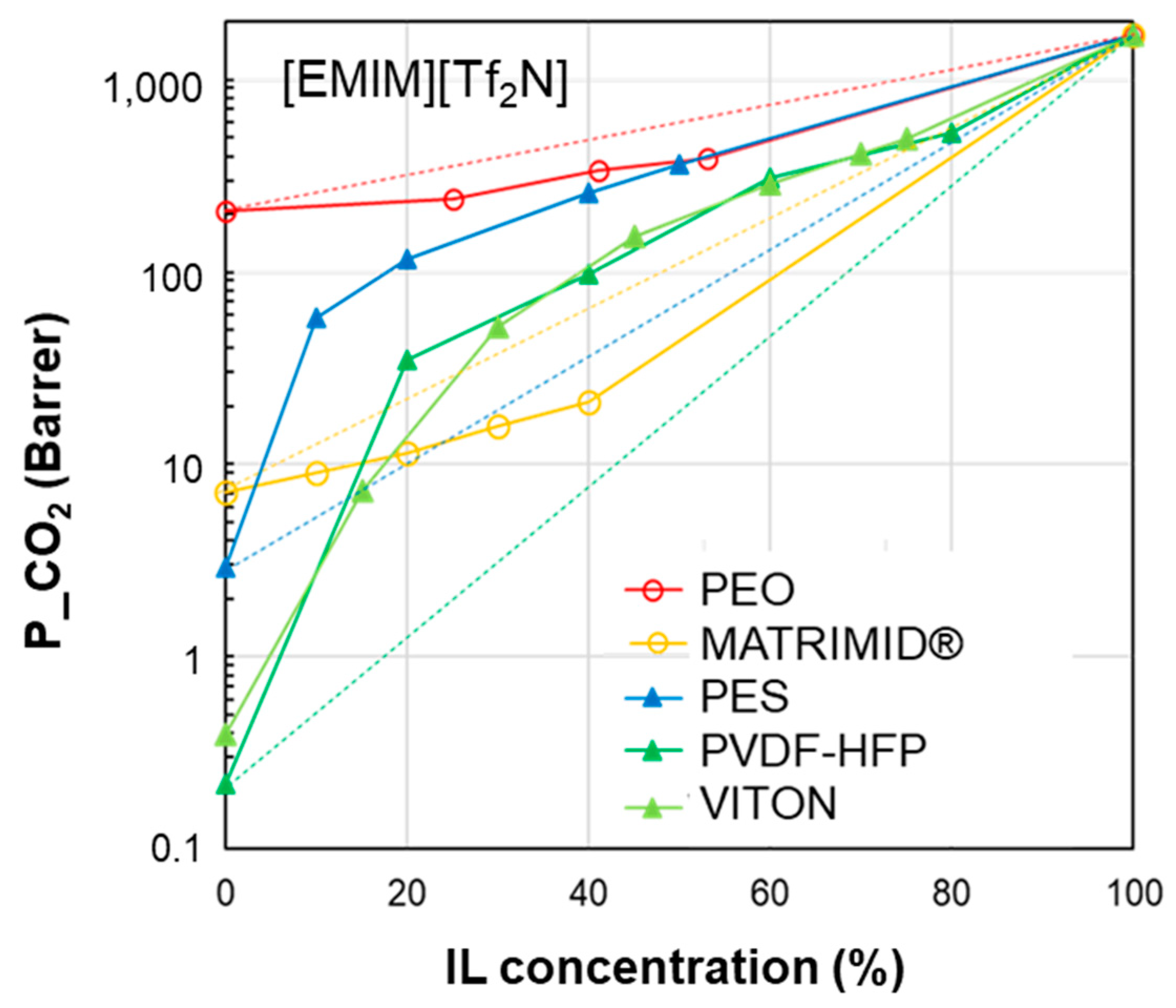
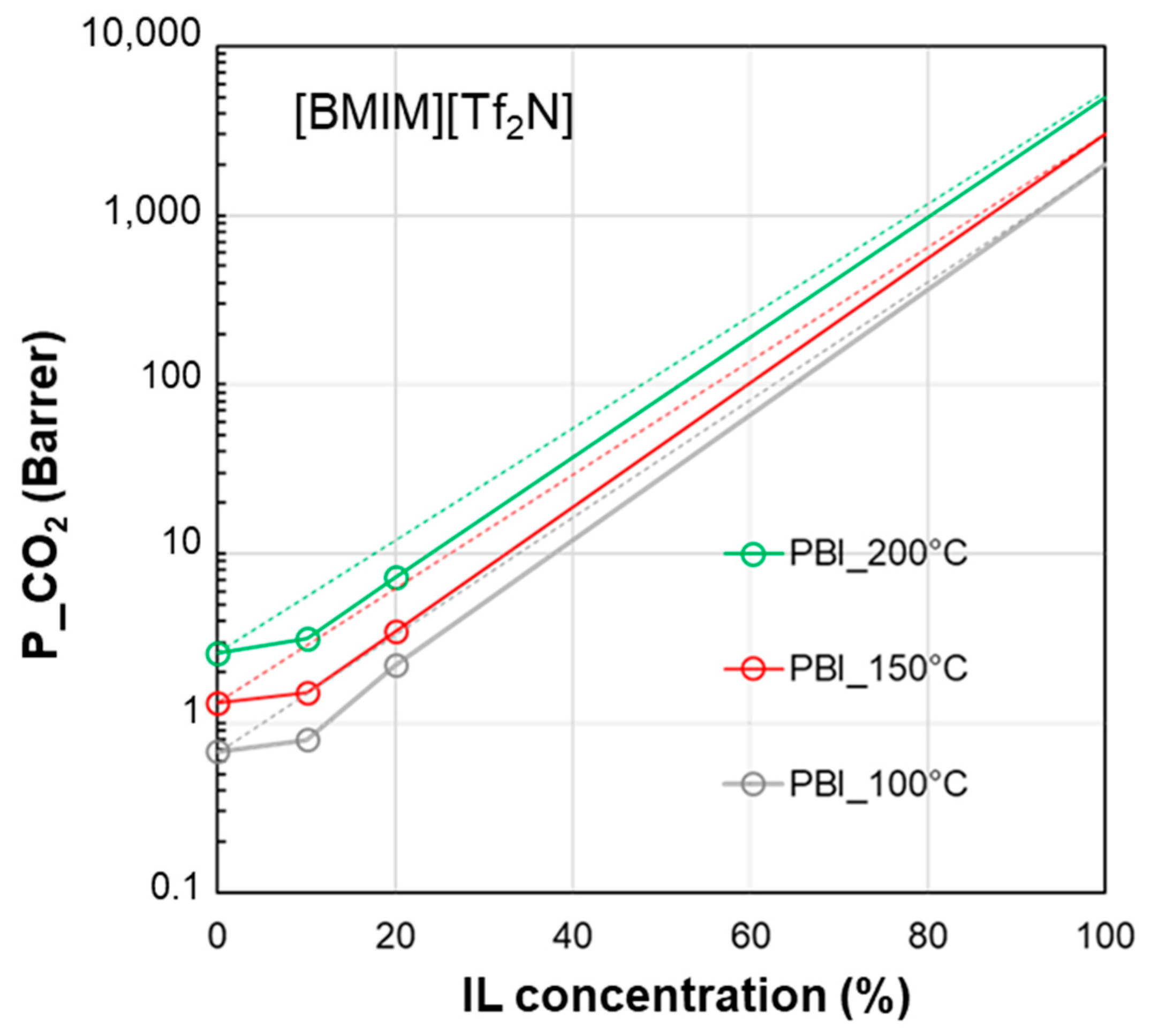
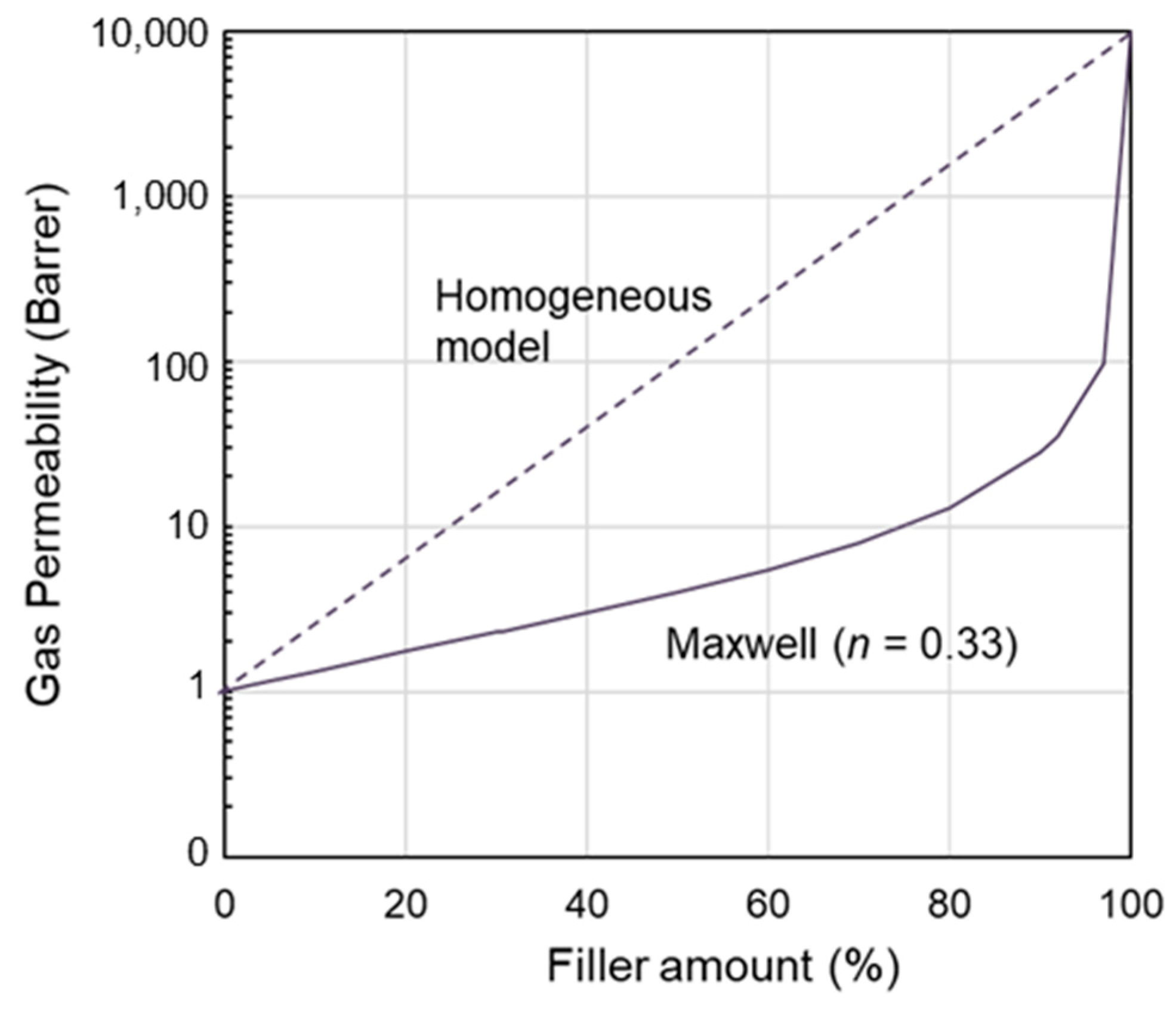
3.1. Permeability vs. IL Loading Profiles
3.2. Polymer State and Interactions Between IL and Polymer Phases
| δD | δP | δH | δTOT | ∆δTOT | ∆δP | ∆δH | |
| [EMIM][BF4] | 17.9 | 14.8 | 12.2 | 26.2 | - | - | - |
| PES | 19.6 | 10.8 | 9.2 | 24.2 | 6.1 | 4.0 | 3.0 |
| PSf | 19.7 | 8.3 | 8.3 | 22.9 | 8.4 | 6.5 | 3.9 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 9.7 | 9.4 | 0.98 |
| CTA | 18.0 | 5.3 | 10.8 | 21.6 | 9.7 | 9.5 | 1.40 |
| δD | δP | δH | δTOT | ∆δTOT | ∆δP | ∆δH | |
| [EMIM][TF2N] | 15.8 | 15.4 | 10.3 | 24.3 | - | - | - |
| VITON | 17.0 | 10.6 | 6.1 | 20.9 | 6.8 | 4.8 | 4.2 |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 8.7 | 2.6 | 1.3 |
| PES | 19.6 | 10.8 | 9.2 | 24.2 | 9.0 | 4.6 | 1.1 |
| MATRIMID | 18.0 | 5.3 | 10.8 | 21.6 | 11.1 | 10.1 | 0.48 |
| PEO | 16.3 | 10.2 | 8.7 | 21.1 | 5.5 | 5.2 | 1.6 |

| δD | δP | δH | δTOT | ∆δTOT | ∆δP | ∆δH | |
| [BMIM][TF2N] | 18.1 | 14.8 | 10.7 | 25.7 | - | - | - |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 4.3 | 2.0 | 0.9 |
| PSf | 19.7 | 8.3 | 8.3 | 22.9 | 7.7 | 6.5 | 2.4 |
| PI | 19.7 | 11.8 | 14.2 | 27.5 | 5.7 | 3.0 | 3.5 |
| PBI | 17.3 | 8.7 | 8.9 | 21.3 | 6.6 | 6.1 | 1.8 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 9.6 | 9.4 | 0.5 |

| δD | δP | δH | δTOT | ∆δTOT | ∆δP | ∆δH | |
| [BMIM][BF4] | 23 | 19 | 10 | 31.5 | - | - | - |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 8.9 | 6.2 | 1.6 |
| NAFION | 17.4 | 12.5 | 9.6 | 23.5 | 13.0 | 6.5 | 0.4 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 16.0 | 13.6 | 1.2 |
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bernardo, P.; Drioli, E.; Golemme, G. Membrane gas separation: A review/state of the art. Ind. Eng. Chem. Res. 2009, 48, 4638–4663. [Google Scholar] [CrossRef]
- Bernardo, P.; Clarizia, G. 30 years of membrane technology for gas separation. Chem. Eng. Trans. 2013, 32, 1999–2004. [Google Scholar]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Blanchard, L.A.; Hancu, D.; Beckman, E.J.; Brennecke, J.F. Green processing using ionic liquids and CO2. Nature 1999, 399, 28–29. [Google Scholar] [CrossRef]
- Welton, T. Ionic Liquids: A Brief History. Biophys. Rev. 2018, 10, 691–706. [Google Scholar] [CrossRef]
- Livi, S.; Duchet-Rumeau, J.; Gérard, J.-F.; Pham, T.N. Polymers and Ionic Liquids: A Successful Wedding. Macromol. Chem. Phys. 2015, 216, 359–368. [Google Scholar] [CrossRef]
- Correia, D.M.; Fernandes, L.C.; Martins, P.M.; García-Astrain, C.; Costa, C.M.; Reguera, J.; Lanceros-Méndez, S. Ionic Liquid–Polymer Composites: A New Platform for Multifunctional Applications. Adv. Funct. Mater. 2020, 30, 1909736. [Google Scholar] [CrossRef]
- Sasikumar, B.; Arthanareeswaran, G.; Ismail, A.F. Recent progress in ionic liquid membranes for gas separation. J. Mol. Liq. 2018, 266, 330–341. [Google Scholar] [CrossRef]
- Dai, Z.; Noble, R.D.; Gin, D.L.; Zhang, X.; Deng, L. Combination of ionic liquids with membrane technology: A new approach for CO2 separation. J. Membr. Sci. 2016, 497, 1–20. [Google Scholar] [CrossRef]
- Elhenawy, S.; Khraisheh, M.; Al Momani, F.; Hassan, M. Key Applications and Potential Limitations of Ionic Liquid Membranes in the Gas Separation Process of CO2, CH4, N2, H2 or Mixtures of These Gases from Various Gas Streams. Molecules 2020, 25, 4274. [Google Scholar] [CrossRef]
- Morgan, D.; Ferguson, L.; Scovazzo, P. Diffusivities of Gases in Room-Temperature Ionic Liquids: Data and Correlations Obtained Using a LagTime Technique. Ind. Eng. Chem. Res. 2005, 44, 4815–4823. [Google Scholar] [CrossRef]
- Friedrich, M.F.; Kokolakis, S.; Lucas, M.; Claus, P. Measuring Diffusion and Solubility of Slightly Soluble Gases in [CnMIM][NTf2] Ionic Liquids. J. Chem. Eng. Data 2016, 61, 1616–1624. [Google Scholar] [CrossRef]
- Hasib-ur-Rahman, M.; Siaj, M.; Larachi, F. Ionic liquids for CO2 capture—Development and progress. Chem. Eng. Process 2010, 49, 313–322. [Google Scholar] [CrossRef]
- Bara, J.E.; Gabriel, C.J.; Carlisle, T.K.; Camper, D.E.; Finotello, A.; Gin, D.L.; Noble, R.D. Gas separations in fluoroalkyl-functionalized room-temperature ionic liquids using supported liquid membranes. Chem. Eng. J. 2009, 147, 43–50. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Soh, L.S.; Hong, S.U.; Liang, C.Z.; Yong, W.F. Green solvent-synthesized polyimide membranes for gas separation: Coupling Hansen solubility parameters and synthesis optimization. Chem. Eng. J. 2023, 478, 147451. [Google Scholar]
- Buckley-Smith, M. The Use of Solubility Parameters to Select Membrane Materials for Pervaporation of Organic Mixtures. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 2006. Available online: https://hdl.handle.net/10289/2625 (accessed on 1 February 2024).
- Saiz, C.A.; Darvishmanesh, S.; Buekenhoudt, A.; Van der Bruggen, B. Shortcut applications of the Hansen Solubility Parameter for Organic Solvent Nanofiltration. J. Membr. Sci. 2018, 546, 120–127. [Google Scholar] [CrossRef]
- Mondal, M.K.; Balsora, H.K.; Varshney, P. Progress and trends in CO2 capture/separation technologies: A review. Energy 2012, 46, 431–441. [Google Scholar] [CrossRef]
- Baker, R.W.; Lokhandwala, K. Natural Gas Processing with Membranes: An Overview. Ind. Eng. Chem. Res. 2008, 47, 2109–2121. [Google Scholar] [CrossRef]
- del Rosario Rodero, M.; Muñoz, R.; González-Sánchez, A.; Ruiz, H.A.; Quijano, G. Membrane materials for biogas purification and upgrading: Fundamentals, recent advances and challenges. J. Environ. Chem. Eng. 2024, 12, 114106. [Google Scholar] [CrossRef]
- Bernardo, P.; Zampino, D.; Clarizia, G. Triggering the gas transport in PVdF-HFP membranes via Imidazolium Ionic Liquids. Sep. Purif. Technol. 2020, 250, 117201. [Google Scholar] [CrossRef]
- Friess, K.; Jansen, J.C.; Bazzarelli, F.; Izák, P.; Jarmarová, V.; Kačírková, M.; Schauer, J.; Clarizia, G.; Bernardo, P. High ionic liquid content polymeric gel membranes: Correlation of membrane structure with gas and vapour transport properties. J. Membr. Sci. 2012, 415–416, 801–809. [Google Scholar] [CrossRef]
- Hong, S.U.; Park, D.; Ko, Y.; Baek, I. Polymer-ionic liquid gels for enhanced gas transport. Chem. Commun. 2009, 7227–7229. [Google Scholar] [CrossRef] [PubMed]
- Uchytil, P.; Schauer, J.; Petrychkovych, R.; Setnickova, K.; Suen, S.Y. Ionic liquid membranes for carbon dioxide–methane separation. J. Membr. Sci. 2011, 383, 262–271. [Google Scholar] [CrossRef]
- Abdollahi, S.; Mortaheb, H.R.; Ghadimi, A.; Esmaeili, M. Improvement in separation performance of Matrimid®5218 with encapsulated [Emim][Tf2N] in a heterogeneous structure: CO2/CH4 separation. J. Membr. Sci. 2018, 557, 38–48. [Google Scholar] [CrossRef]
- Liang, L.; Gan, Q.; Nancarrow, P. Composite ionic liquid and polymer membranes for gas separation at elevated temperatures. J. Membr. Sci. 2014, 450, 407–417. [Google Scholar] [CrossRef]
- Mannan, H.A.; Mohshim, D.F.; Mukhtar, H.; Murugesan, T.; Man, Z.; Bustam, M.A. Synthesis, characterization, and CO2 separation performance of polyether sulfone/[EMIM][Tf2N] ionic liquid-polymeric membranes (ILPMs). J. Ind. Eng. Chem. 2017, 54, 98–106. [Google Scholar] [CrossRef]
- Mustafa, M.Z.; Mukhtar, H.; Nordin, N.A.H.M.; Mannan, H.A. Effect of [emim][BF4] ionic liquid concentration on ionic liquid-polymeric membrane (ILPM) for CO2/CH4 separation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 736, 022028. [Google Scholar] [CrossRef]
- Farrokhara, M.; Dorosti, F. New high permeable polysulfone/ionic liquid membrane for gas separation. Chin. J. Chem. Eng. 2020, 28, 2301–2311. [Google Scholar] [CrossRef]
- Alkhouzaam, A.; Khraisheh, M.; Atilhan, M.; Al-Muhtaseb, S.A.; Qi, L.; Rooney, D. High-pressure CO2/N2 and CO2/CH4 separation using dense polysulfone-supported ionic liquid membranes. J. Nat. Gas Eng. 2016, 36, 472–485. [Google Scholar] [CrossRef]
- Dai, Z.; Ansaloni, L.; Ryan, J.J.; Spontak, R.J.; Deng, L. Nafion/IL hybrid membranes with tuned nanostructure for enhanced CO2 separation: Effects of ionic liquid and water vapor. Green Chem. 2018, 20, 1391–1404. [Google Scholar] [CrossRef]
- Lam, B.; Wei, M.; Zhu, L.; Luo, S.; Guo, R.; Morisato, A.; Alexandridis, P.; Lin, H. Cellulose triacetate doped with ionic liquids for membrane gas separation. Polymer 2016, 89, 1–11. [Google Scholar] [CrossRef]
- Kusuma, V.A.; Macala, M.K.; Liua, J.; Marti, A.M.; Hirsch, R.J.; Hill, L.J.; Hopkinson, D. Ionic liquid compatibility in polyethylene oxide/siloxane ion gel membranes. J. Membr. Sci. 2018, 545, 292–300. [Google Scholar] [CrossRef]
- Rabiee, H.; Ghadimi, A.; Mohammadi, T. Gas transport properties of reverse-selective poly (ether-b-amide6)/[Emim][BF4] gel membranes for CO2/light gases separation. J. Membr. Sci. 2015, 476, 286–302. [Google Scholar] [CrossRef]
- Fam, W.; Mansouri, J.; Li, H.; Chen, V. Improving CO2 separation performance of thin film composite hollow fiber with Pebax®1657/ionic liquid gel membranes. J. Membr. Sci. 2017, 537, 54–68. [Google Scholar] [CrossRef]
- Qiu, Y.; Ren, J.; Zhao, D.; Li, H.; Deng, M. Poly(amide-6-b-ethylene oxide)/[Bmim][Tf2N] blend membranes for carbon dioxide separation. J. Energy Chem. 2016, 25, 122–130. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Zeng, S.; Bai, L.; Gao, H.; Deng, J.; Yang, Q.; Zhang, S. Pebax-based composite membranes with high gas transport properties enhanced by ionic liquids for CO2 separation. RSC Adv. 2017, 7, 6422–6431. [Google Scholar] [CrossRef]
- Camper, D.; Bara, J.; Koval, C.; Noble, R. Bulk-fluid solubility and membrane feasibility of Rmim-based room-temperature ionic liquids. Ind. Eng. Chem. Res. 2006, 45, 6279–6283. [Google Scholar] [CrossRef]
- Muldoon, M.J.; Aki, S.N.V.K.; Anderson, J.L.; Dixon, J.K.; Brennecke, J.F. Improving Carbon Dioxide Solubility in Ionic Liquids. J. Phys. Chem. B 2007, 111, 9001–9009. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, P.; Jansen, J.C.; Bazzarelli, F.; Tasselli, F.; Fuoco, A.; Friess, K.; Izák, P.; Jarmarová, V.; Kačírková, M.; Clarizia, G. Gas transport properties of PEBAX®/Room Temperature Ionic Liquid gel membranes. Sep. Purif. Technol. 2012, 97, 73–82. [Google Scholar] [CrossRef]
- Liu, H.; Dai, S.; Jiang, D. Molecular Dynamics Simulation of Anion Effect on Solubility, Diffusivity, and Permeability of Carbon Dioxide in Ionic Liquids. Ind. Eng. Chem. Res. 2014, 53, 10485–10490. [Google Scholar] [CrossRef]
- Scovazzo, P. Determination of the upper limits, benchmarks, and critical properties for gas separations using stabilized room temperature ionic liquid membranes (SILMs) for the purpose of guiding future research. J. Membr. Sci. 2009, 343, 199–211. [Google Scholar] [CrossRef]
- Krull, F.F.; Fritzmann, C.; Melin, T. Liquid membranes for gas/vapor separations. J. Membr. Sci. 2008, 325, 509–519. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, Y.; Wang, W.; Li, L.; Zhou, Z.; Zhang, Z. Permeability and selectivity of sulfur dioxide and carbon dioxide in supported ionic liquid membranes. Chin. J. Chem. Eng. 2009, 17, 594–601. [Google Scholar] [CrossRef]
- Scovazzo, P.; Havard, D.; McShea, M.; Mixon, S.; Morgan, D. Long-term, continuous mixed-gas dry fed CO2/CH4 and CO2/N2 separation performance and selectivities for room temperature ionic liquid membranes. J. Membr. Sci. 2009, 327, 41–48. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hildebrand, J.H. The Solubility of Non-Electrolytes; Reinhold: New York, NY, USA, 1936. [Google Scholar]
- Batista, M.L.S.; Neves, C.M.S.S.; Carvalho, P.J.; Gani, R.; Coutinho, J.A.P. Chameleonic Behavior of Ionic Liquids and Its Impact on the Estimation of Solubility Parameters. J. Phys. Chem. B 2011, 115, 12879–12888. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Campusano, R.A.; Rojas, R.E. Glass transition temperature of Ionic Liquids using molecular descriptors and artificial neural networks. C. R. Chim. 2017, 20, 573–584. [Google Scholar] [CrossRef]
- Hansen, C.M. The three-dimensional solubility parameter—Key to paint component affinities. Parts II and III. Independent calculation of the parameter components. J. Paint Technol. 1967, 39, 511–514. [Google Scholar]
- Mubashir, M.; Yin, Y.; Kok, F.L.; Thiam, K.C.; Jusoh, L.N. Efficient CO2/N2 and CO2/CH4 separation using NH2-MIL-53(Al)/cellulose acetate (CA) mixed matrix membranes. Sep. Purif. Technol. 2018, 199, 140–151. [Google Scholar] [CrossRef]
- Gong, H.; Lee, S.S.; Bae, T.-H. Mixed-matrix membranes containing inorganically surface-modified 5A zeolite for enhanced CO2/CH4 separation. Microporous Mesoporous Mater. 2017, 237, 82–89. [Google Scholar] [CrossRef]
- Reid, B.D.; Ruiz-Trevino, F.A.; Musselman, I.H.; Balkus, K.J.; Ferraris, J.P. Gas Permeability Properties of Polysulfone Membranes Containing the Mesoporous Molecular Sieve MCM-41. Chem. Mater. 2001, 13, 2366–2373. [Google Scholar] [CrossRef]
- Goh, P.S.; Ismail, A.F.; Sanip, S.M.; Ng, B.C.; Aziz, M. Recent advances of inorganic fillers in mixed matrix membrane for gas separation. Sep. Purif. Technol. 2011, 81, 243–264. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Yan, Y.; Jeong, B.-H. Nanocomposite Membranes and Methods of Making and Using Same. US 2011/0027599 A1, 3 February 2011. [Google Scholar]
- Mahajan, R.; Burns, R.; Schaeffer, M.; Koros, W.J. Challenges in forming successful mixed matrix membranes with rigid polymeric materials. Appl. Polym. J. 2002, 86, 881–890. [Google Scholar] [CrossRef]
- Elamin, K.; Shojaatalhosseini, M.; Danyliv, O.; Martinelli, A.; Swenson, J. Conduction mechanism in polymeric membranes based on PEO or PVdF-HFP and containing a piperidinium ionic liquid. Electrochim. Acta 2019, 299, 979–986. [Google Scholar] [CrossRef]
- Filip, P.; Zelenkova, J.; Peer, P. Electrospinning of a Copolymer PVDF-co-HFP Solved in DMF/Acetone: Explicit Relations among Viscosity, Polymer Concentration, DMF/Acetone Ratio and Mean Nanofiber Diameter. Polymers 2021, 13, 3418. [Google Scholar] [CrossRef]
- Perkins, J.L.; Ridge, M.C.; Holcombe, A.B.; Wang, M.K.; Nonidez, W.E. Skin Protection, Viton, and Solubility Parameters. Am. Ind. Hyg. Assoc. J. 1986, 47, 803–808. [Google Scholar] [CrossRef]
- Kim, Y.S.; Labouriau, A.; Welch, C.; Hjelm, R.; Mack, N. Solvation and Gelation Process of Nafion®. In Proceedings of the 224th ECS Meeting, the Electrochemical Society, San Francisco, CA, USA, 27 October–1 November 2013; Abstract #1390. [Google Scholar] [CrossRef]
- Guillen, G.R.; Pan, Y.; Li, M.; Hoek, E.M.V. Preparation and Characterization of Membranes Formed by Nonsolvent Induced Phase Separation: A Review. Ind. Eng. Chem. Res. 2011, 50, 3798–3817. [Google Scholar] [CrossRef]
- Dibrov, G.; Kagramanov, G.; Sudin, V.; Molchanov, S.; Grushevenko, E.; Yushkin, A.; Volkov, V. Influence of Draw Ratio and Take-Up Velocity on Properties of Ultrafiltration Hollow Fiber Membranes from Polyethersulfone. Fibers 2022, 10, 29. [Google Scholar] [CrossRef]
- Wang, K.Y.; Weber, M.; Chung, T.-S. Polybenzimidazoles (PBIs) and state-of-the-art PBI hollow fiber membranes for water, organic solvent and gas separations: A review. J. Mater. Chem. A 2022, 10, 8687–8718. [Google Scholar] [CrossRef]
- Jazini, F.; Karimi, M.; Azari, S. Tuning the pore features of cellulose acetate/cellulose triacetate membranes via post-casting solvent treatment for forward osmosis. Carbohydr. Polym. 2021, 255, 117348. [Google Scholar] [CrossRef] [PubMed]
- Seoane, B.; Coronas, J.; Gascon, I.; Benavides, M.E.; Karvan, O.; Caro, J.; Kapteijn, F.; Gascon, J. Metal–organic framework based mixed matrix membranes: A solution for highly efficient CO2 capture? Chem. Soc. Rev. 2015, 44, 2421–2454. [Google Scholar] [CrossRef]
- Isanejad, M.; Azizi, N.; Mohammadi, T. Pebax membrane for CO2/CH4 separation: Effects of various solvents on morphology and performance. J. Appl. Polym. Sci. 2017, 134, 44531. [Google Scholar] [CrossRef]
- Heitmann, S.; Krüger, V.; Welz, D.; Lutze, P. Experimental Investigation of Pervaporation Membranes for Biobutanol Separation. J. Membr. Sep. Technol. 2013, 2, 245–262. [Google Scholar] [CrossRef]
- Meaurio, E.; Sanchez-Rexach, E.; Zuza, E.; Lejardi, A.; del Pilar Sanchez-Camargo, A.; Sarasua, J.-R. Predicting miscibility in polymer blends using the Bagley plot: Blends with poly(ethylene oxide). Polymer 2017, 113, 295–309. [Google Scholar] [CrossRef]
- Weerachanchai, P.; Wong, Y.; Lim, K.H.; Tan, T.T.Y.; Lee, J.-M. Determination of Solubility Parameters of Ionic Liquids and Ionic Liquid/Solvent Mixtures from Intrinsic Viscosity. ChemPhysChem 2014, 15, 3580–3591. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Tokishita, S.; Yamamoto, H. Determination of Hansen Solubility Parameters of Ionic Liquids by Using Walden Plots. Ind. Eng. Chem. Res. 2020, 59, 14217–14223. [Google Scholar] [CrossRef]
- Available online: https://pirika.com/ENG/HSP/E-Book/Chap20.html (accessed on 1 February 2024).
- Venkatram, S.; Kim, C.; Chandrasekaran, A.; Ramprasad, R. Critical Assessment of the Hildebrand and Hansen Solubility Parameters for Polymers. J. Chem. Inf. Model. 2019, 59, 4188–4194. [Google Scholar] [CrossRef]
- Greenhalgh, D.J.; Williams, A.C.; Timmins, P.; York, P. Solubility parameters as predictors of miscibility in solid dispersions. J. Pharm. Sci. 1999, 88, 1182–1190. [Google Scholar] [CrossRef]
- Bagley, E.B.; Nelson, T.P.; Scigliano, J.M. Three-dimensional solubility parameters and their relationship to internal pressure measurements in polar and hydrogen bonding solvents. J. Paint Technol. 1971, 43, 35. [Google Scholar]
- Barton, A.F.M. Solubility Parameters. Chem. Rev. 1975, 75, 731–753. [Google Scholar] [CrossRef]
- van Krevelen, D.W. Properties of Polymers; Elsevier Science: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Carlisle, T.K.; Bara, J.E.; Gabriel, C.J.; Noble, R.D.; Gin, D.L. Interpretation of CO2 Solubility and Selectivity in Nitrile-Functionalized Room-Temperature Ionic Liquids Using a Group Contribution Approach. Ind. Eng. Chem. Res. 2008, 47, 7005–7012. [Google Scholar] [CrossRef]
- Agata, Y.; Yamamoto, H. Determination of Hansen Solubility Parameters of Ionic Liquids Using Double-sphere Type of Hansen Solubility Sphere Method. Chem. Phys. 2018, 513, 165–173. [Google Scholar] [CrossRef]
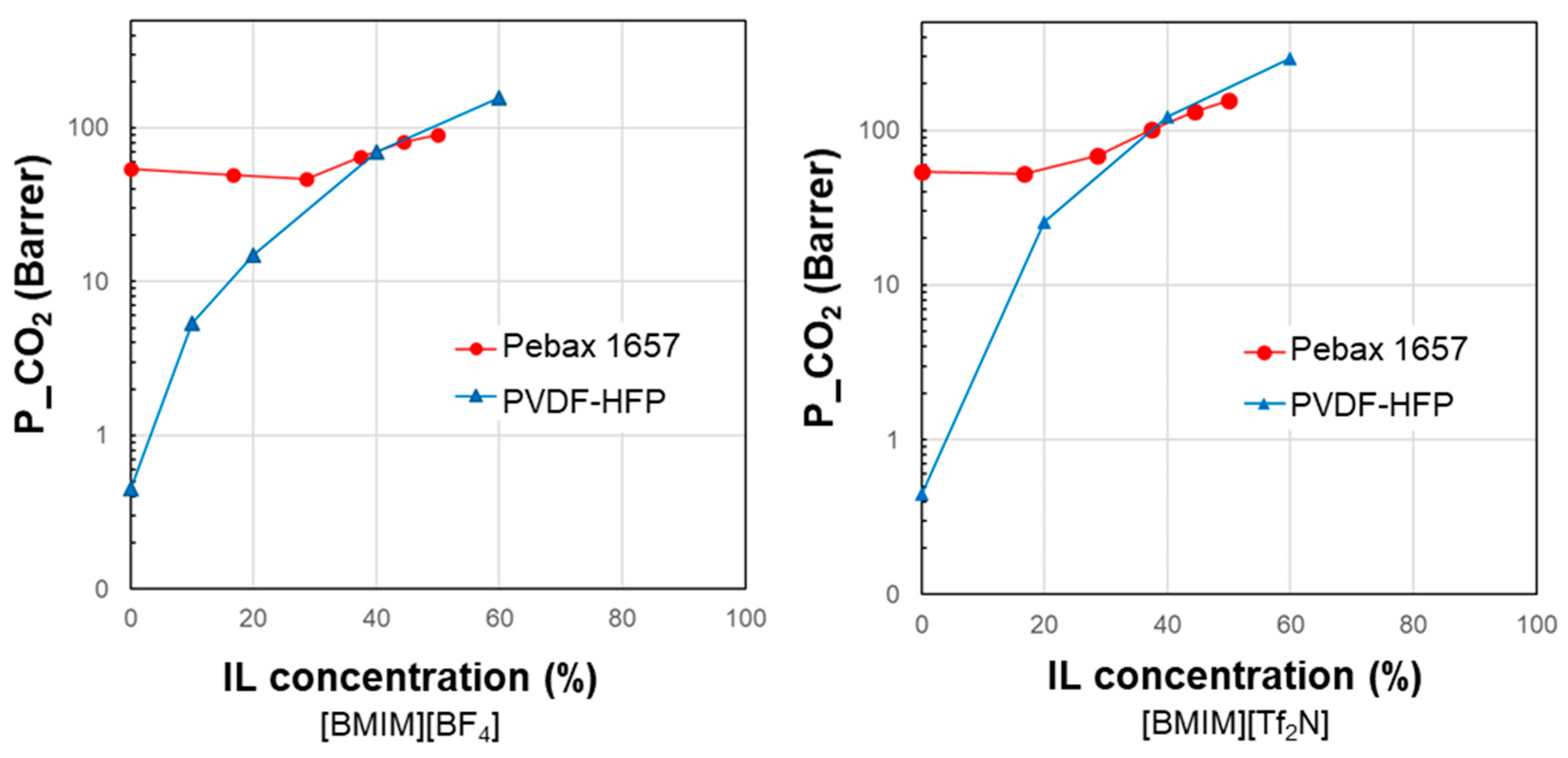

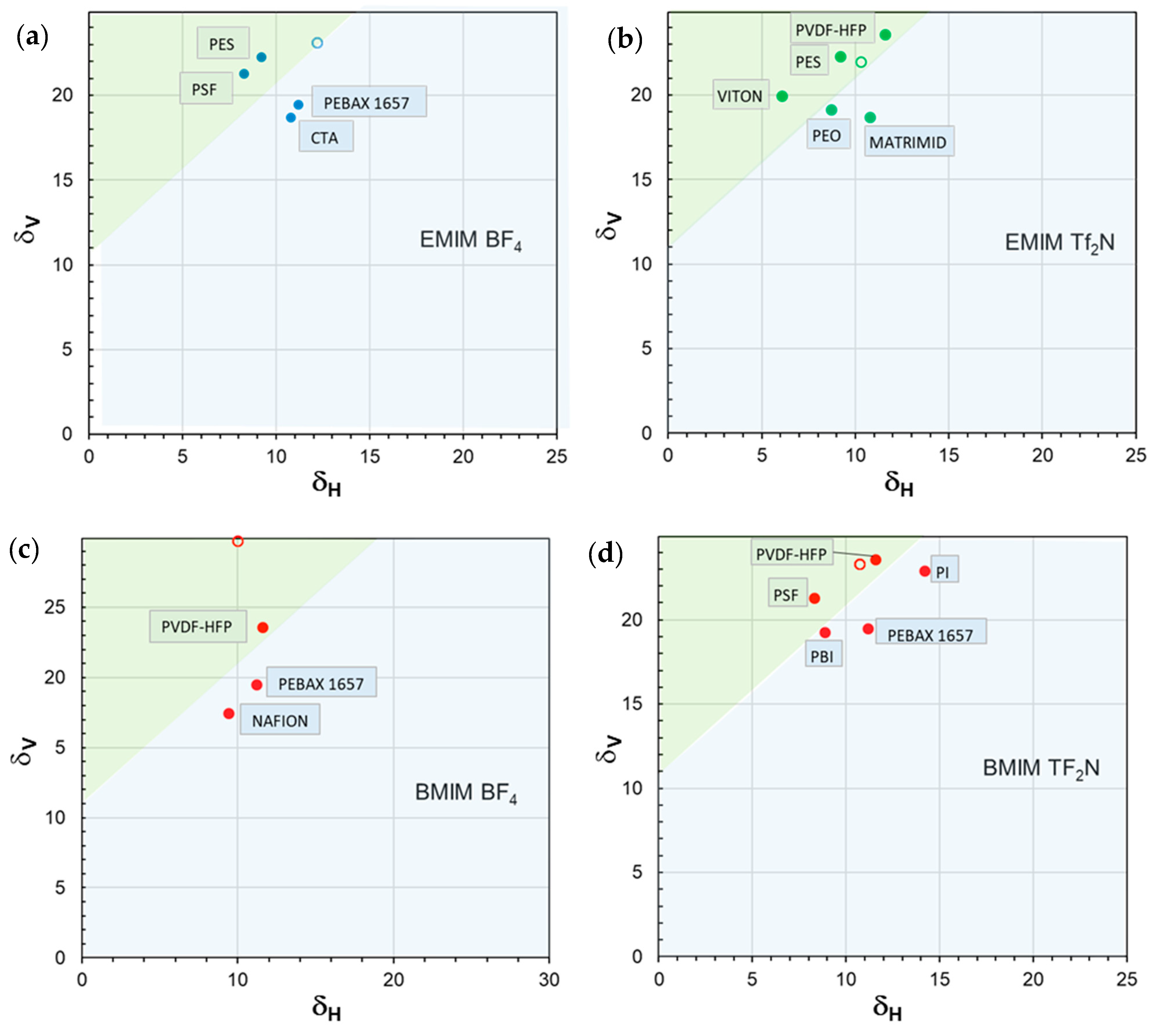
| Polymer | IL Type | IL Conc. (wt%) | Ref. |
|---|---|---|---|
| PVDF-HFP | [Bmim][BF4] | 20–60 | [22] |
| PVDF-HFP | [Bmim][Tf2N] | 20–60 | [22] |
| PVDF-HFP | [Emim][Tf2N] | 20–80 | [23] |
| PVDF-HFP | [Emim][BF4] | 33, 50, 66 | [24] |
| VITON | [Emim][Tf2N] | 15–75 | [25] |
| PI (Matrimid®) | [Emim][Tf2N] | 10–40 | [26] |
| PI (PMDA-ODA) | [Bmim][Tf2N] | 10–40 | [27] |
| PBI | [Bmim][Tf2N] | 10 and 20 | [27] |
| PES | [Emim][Tf2N] | 10–50 | [28] |
| PES | [Emim][BF4] | 10 and 20 | [29] |
| PSf | [Emim][BF4] | 10–40 | [30] |
| PSf | [Bmim][Tf2N] | 0.5–25 | [31] |
| Nafion | [Bmim][BF4] | 10–40 | [32] |
| CTA | [Emim][BF4] | 10–50 | [33] |
| PEO crosslinked | [Emim][Tf2N] | 25–53 vol% | [34] |
| Pebax® 1657 | [Emim][BF4] | 14–33 | [35] |
| Pebax® 1657 | [Emim][BF4] | 20–80 | [36] |
| Pebax® 1657 | [Bmim][Tf2N] | 10–40 | [37] |
| Pebax® 1657 | [Bmim][BF4] | 17–50 | [38] |
| Pebax® 1657 | [Bmim][Tf2N] | 17–50 | [38] |
| Density (g/cm3) | CO2 Permeability (Barrer) | Operating Conditions (T/p) | Ref. | |
|---|---|---|---|---|
| PVDF-HFP | 1.77 | 0.45 | 25 °C | [22] |
| Matrimid | 1.24 | 7.16 | 35 °C/4 atm | [26] |
| PI (PMDA-ODA) | 1.425 | 3.0 | 35 °C | [27] |
| PBI | 1.30 | 0.68 | 100 °C | [27] |
| 1.3 | 150 °C | |||
| 2.6 | 200 °C | |||
| PES | 1.37 | 2.86 | 25 °C/5 bar | [28] |
| 2.9 | 25 °C/4 bar | [29] | ||
| PSf | 1.24 | 4.29 | 25 °C/3 bar | [30] |
| CTA | 1.286 | 12.6 | 35 °C | [33] |
| PEO crosslinked | 208 | 40 °C/1 bar | [34] | |
| Pebax®1657 | 1.14 | 86.4 | 35 °C | [36] |
| 159 | 35 °C | [37] | ||
| 76.2 | 25 °C | [41] | ||
| Pebax®2533 | 1.00 | 257 | 25 °C | [41] |
| [Emim][BF4] | 1.294 | 954 | [42] | |
| 968.5 | 30 °C | [43] | ||
| [Emim][Tf2N] | 1.52 | 1711 | [42] | |
| 1702 | 30 °C | [43] | ||
| 1733 | [34] | |||
| [Bmim][BF4] | 1.203 | 499 | [44] | |
| 470 | [45] | |||
| [Bmim][Tf2N] | 1.44 | 1344 | 30 °C | [43] |
| Material | Solubility Parameter (MPa0.5) | Ref. | |||
|---|---|---|---|---|---|
| δD | δP | δH | δTOT | ||
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | [59] |
| VITON | 17.0 | 10.6 | 6.1 | 20.9 | [60] |
| NAFION | 17.4 | 12.5 | 9.6 | 23.5 | [61] |
| PSF | 19.7 | 8.3 | 8.3 | 22.9 | [62] |
| PES | 19.6 | 10.8 | 9.2 | 24.2 | [63] |
| PBI | 17.3 | 8.7 | 8.9 | 21.3 | [64] |
| CTA | 18.0 | 5.27 | 10.8 | 21.65 | [65] |
| Matrimid® | 18.7 | 9.6 | 6.7 | 22.1 | [66] |
| PI | 19.7 | 11.8 | 14.2 | 27.5 | [17] |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | [67] |
| Pebax®2533 | 17.6 | 7.6 | 6.8 | 20.3 | [68] |
| PEO | 16.3 | 10.2 | 8.7 | 21.1 | [69] |
| [Emim][BF4] | 17.9 | 14.8 | 12.2 | 26.2 | [70] |
| [Emim][Tf2N] | 15.8 | 15.4 | 10.3 | 24.3 | [71] |
| [Bmim][BF4] | 23.0 | 19.0 | 10.0 | 31.5 | [72] |
| [Bmim][Tf2N] | 18.1 | 14.8 | 10.70 | 25.7 | [70] |
| Material | δD | δP | δH | δTOT | δv (P D) | ∆δv |
|---|---|---|---|---|---|---|
| [MPa0.5] | ||||||
| [EMIM][BF4] | 17.9 | 14.8 | 12.2 | 26.2 | 23.2 | - |
| PES | 19.6 | 10.8 | 9.2 | 24.2 | 22.4 | 14.2 |
| PSf | 19.7 | 8.3 | 8.3 | 22.9 | 21.4 | 11.7 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 19.6 | 12.4 |
| CTA | 18.0 | 5.27 | 10.8 | 21.6 | 18.8 | 12.0 |
| [EMIM][TF2N] | 15.8 | 15.4 | 10.3 | 24.3 | 22.1 | - |
| PES | 19.6 | 10.8 | 9.2 | 24.2 | 23.3 | 0.3 |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 23.7 | 1.6 |
| VITON | 17 | 10.6 | 6.1 | 20.9 | 20.0 | 2.0 |
| PEO | 16.3 | 10.2 | 8.7 | 21.1 | 19.2 | 2.8 |
| MATRIMID | 18.0 | 5.27 | 10.8 | 21.6 | 18.8 | 3.3 |
| [BMIM][TF2N] | 18.1 | 14.8 | 10.7 | 25.7 | 23.4 | - |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 23.7 | 0.3 |
| PSf | 19.7 | 8.3 | 8.3 | 22.9 | 21.4 | 2.0 |
| PI | 19.7 | 11.8 | 14.2 | 27.5 | 23.0 | 0.4 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 19.6 | 3.8 |
| PBI | 17.3 | 8.7 | 8.9 | 21.3 | 19.4 | 4.0 |
| [BMIM][BF4] | 23 | 19 | 10 | 31.5 | 29.8 | - |
| PVDF-HFP | 19.9 | 12.8 | 11.6 | 26.4 | 23.7 | 6.2 |
| NAFION | 17.4 | 12.5 | 9.6 | 23.5 | 21.4 | 8.4 |
| Pebax®1657 | 18.8 | 5.4 | 11.2 | 22.5 | 19.6 | 10.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardo, P.; Clarizia, G. Heuristic Guidelines for Developing Polymer/Ionic Liquid Blend Membranes. Polymers 2025, 17, 439. https://doi.org/10.3390/polym17040439
Bernardo P, Clarizia G. Heuristic Guidelines for Developing Polymer/Ionic Liquid Blend Membranes. Polymers. 2025; 17(4):439. https://doi.org/10.3390/polym17040439
Chicago/Turabian StyleBernardo, Paola, and Gabriele Clarizia. 2025. "Heuristic Guidelines for Developing Polymer/Ionic Liquid Blend Membranes" Polymers 17, no. 4: 439. https://doi.org/10.3390/polym17040439
APA StyleBernardo, P., & Clarizia, G. (2025). Heuristic Guidelines for Developing Polymer/Ionic Liquid Blend Membranes. Polymers, 17(4), 439. https://doi.org/10.3390/polym17040439








