A Numerical Study on the Drug Release Process of Biodegradable Polymer Drug-Loaded Vascular Stents
Abstract
1. Introduction
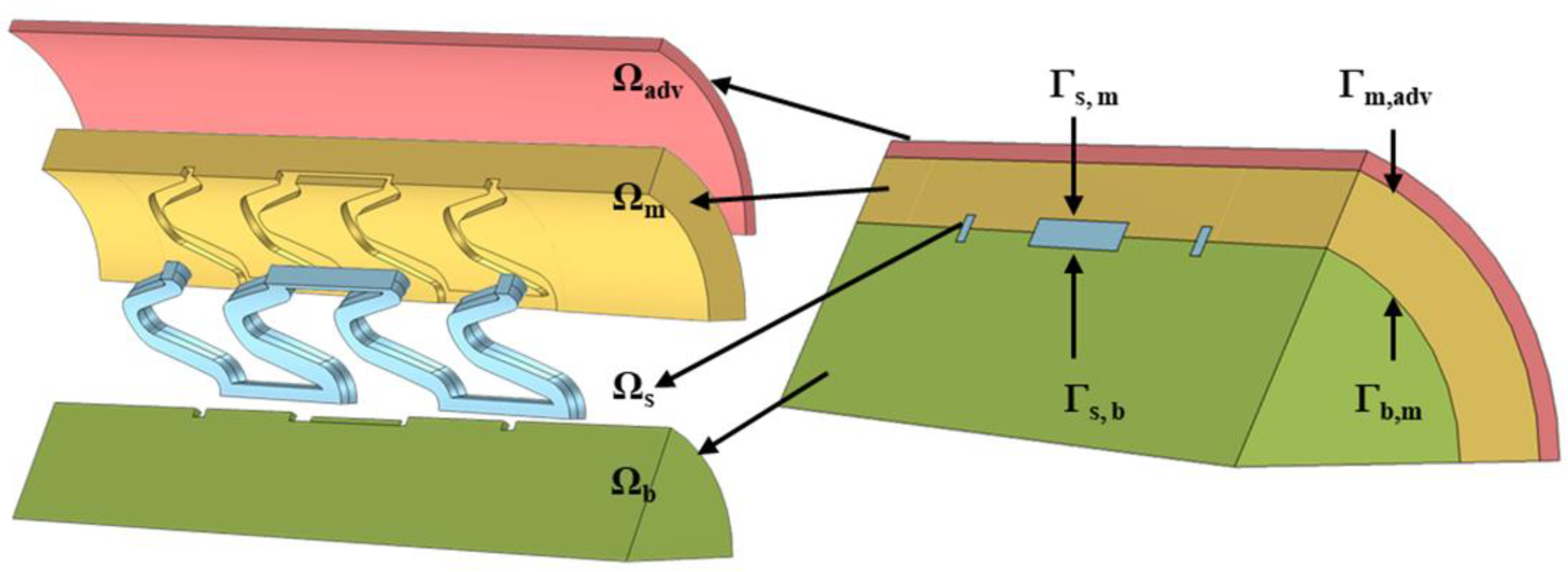
2. Method
3. Numerical Results
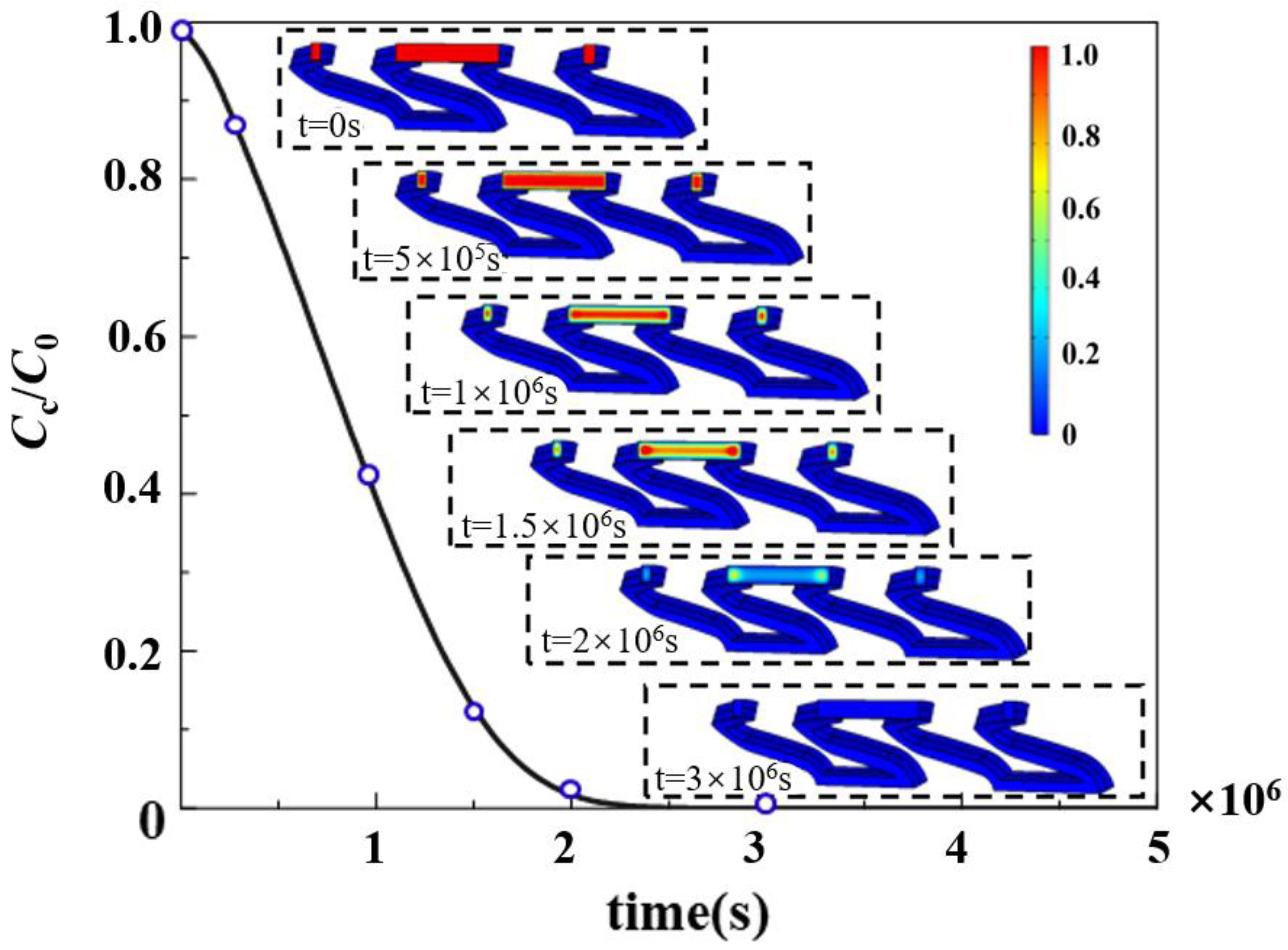
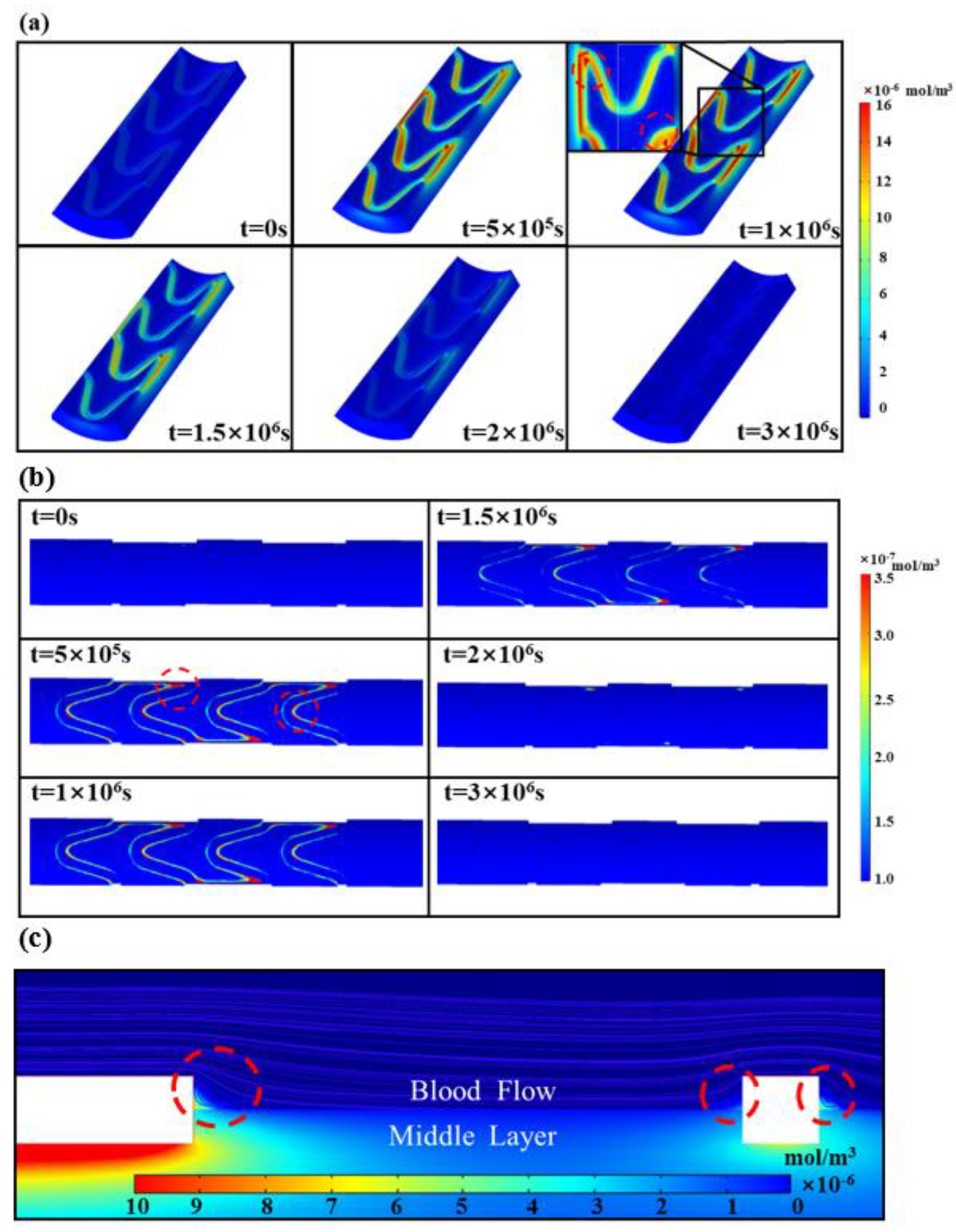
3.1. Drug Release in Biodegradable Polymeric Drug-Loaded Stents
3.2. Intravascular Pharmacokinetics
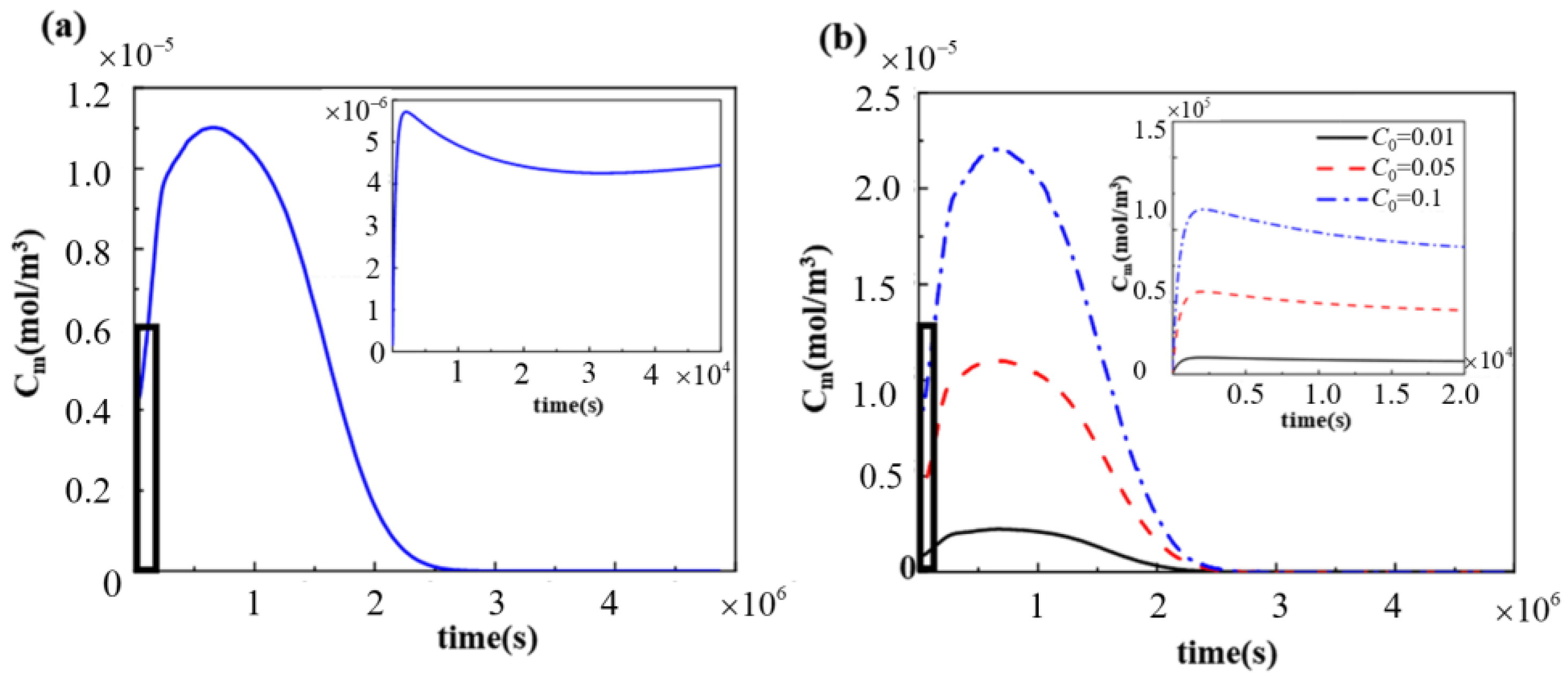
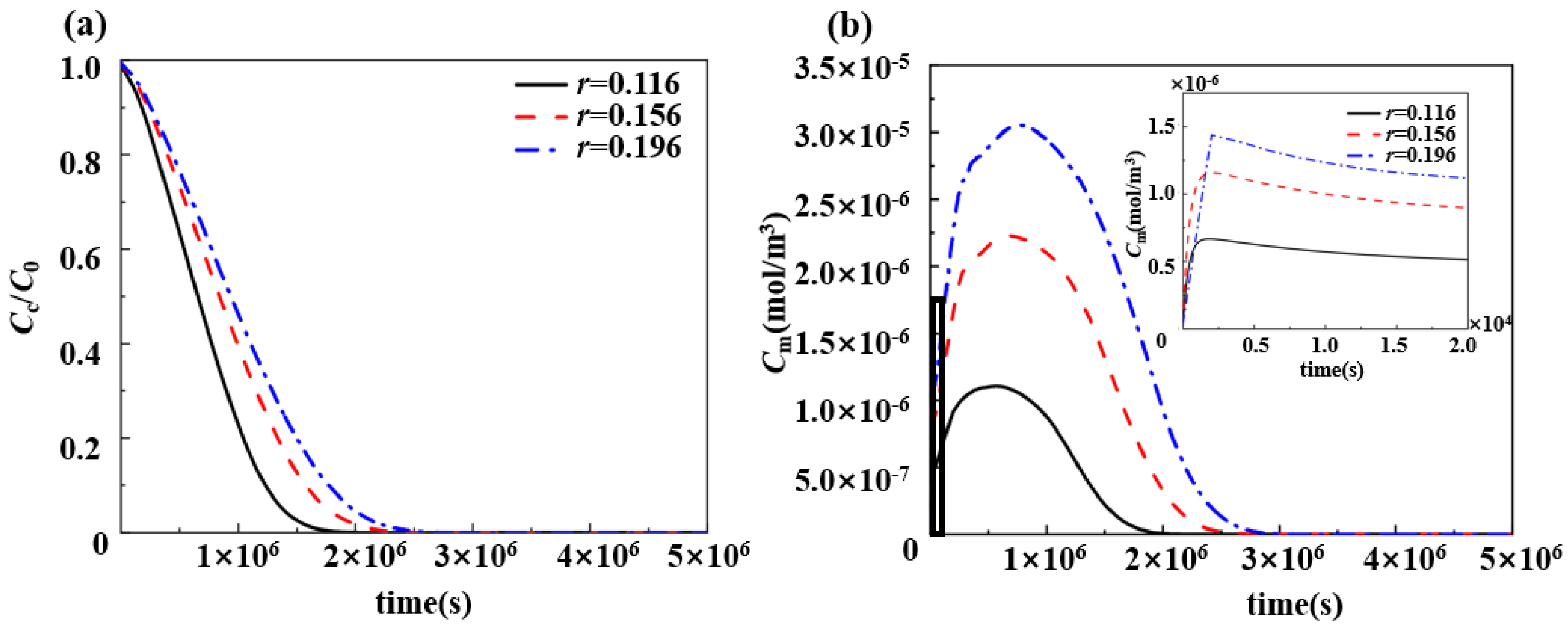
3.3. Effect of Drug Loading of Drug-Loaded Stent on Pharmacokinetics
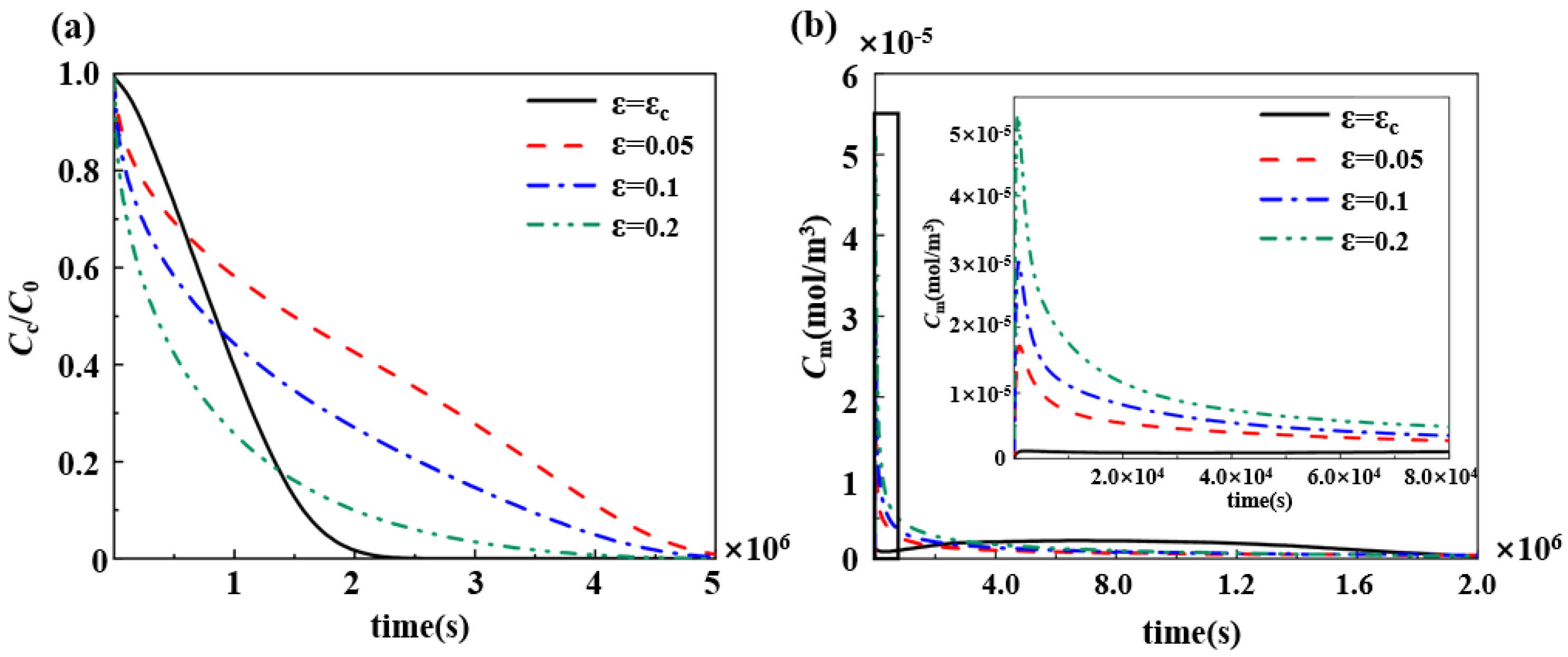
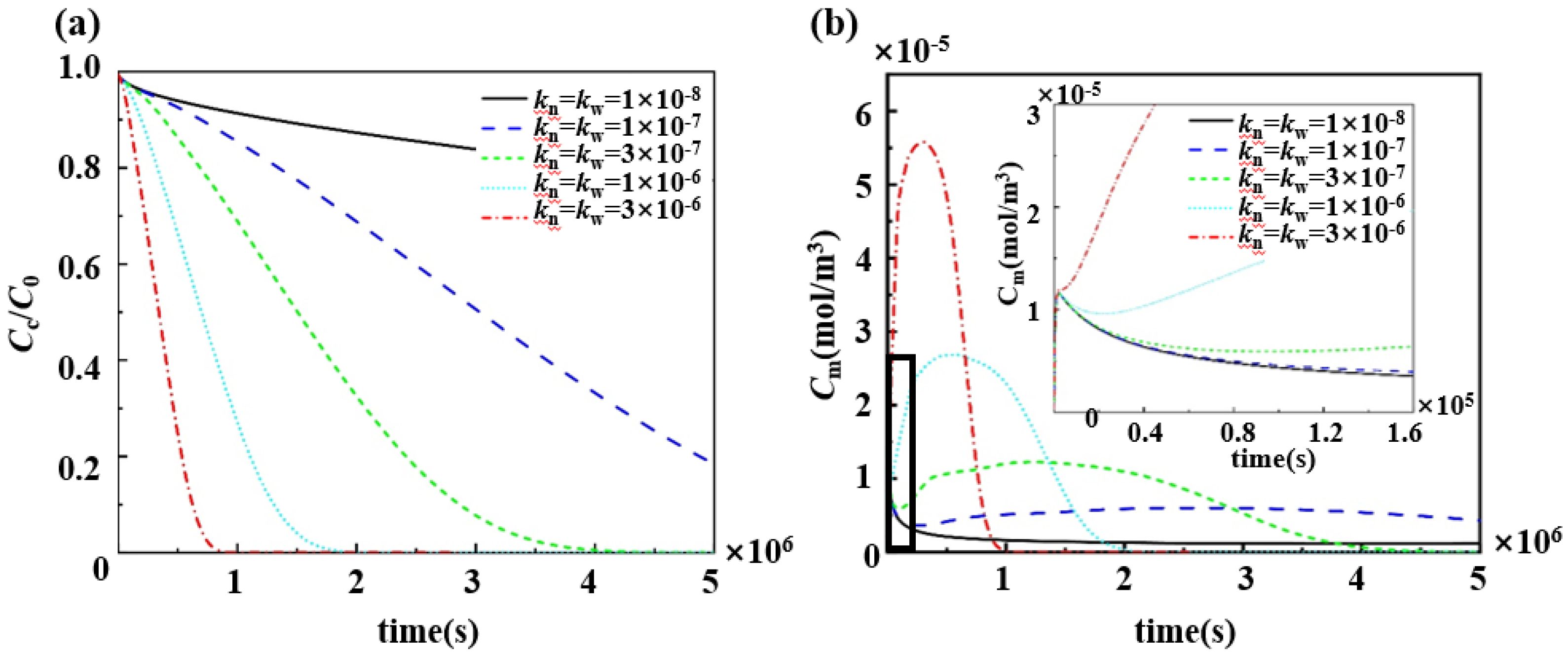
3.4. Effect of Porosity and Degradation Rate Coefficients of Polymers on the Pharmacokinetics
4. Discussion
4.1. Effect of Varying Drug Loading on the Slow-Release Process of Drugs
4.2. Adjustment of the Drug Slow-Release Process by Changing the Physical and Chemical Properties of the Polymer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Control Equations and Boundary Conditions
| Model Domain | Parameters | Reference Value |
| The blood basin | Vascular wall radius, R (mm) Blood viscosity, (g/cm·s) Density, Maximum flow rate at the entrance, Paclitaxel diffusion coefficient, (m2/s) | 1.5 3.5 × 10−2 1.057 0.14 10−10 |
| Blood vessel wall | Thickness of the middle layer, rm (mm) Thickness of the outer layer, radv (mm) Plasma viscosity, (g/cm·s) | 0.4 0.1 0.72 × 10−2 |
| Drug-loaded stents | Diffusion coefficient of paclitaxel in biodegradable polymer drug-loaded stent,
The paclitaxel liquid phase diffusion coefficient, Drug partition coefficient, Correlation of diffusion coefficient to polymer molecular weight, α | 10−17 5 × 10−11 10−4 1.714 |
| Middle layer | (s−1) | 0.61 2 × 10−18 2.6 × 10−12 2.6 × 10−11 20 1 10−4 |
| Outer film layer | 2 Outer boundary permeability, P0 (m/s) | 0.85 2 × 10−18 4 × 10−12 4 × 10−11 20 1 10−6 |
References
- Schakenraad, J.M.; Oosterbaan, J.A.; Nieuwenhuis, P.; Molenaar, I.; Olijslager, J.; Potman, W.; Eenink, M.J.D.; Feijen, J. Biodegradable hollow fibres for the controlled release of drugs. Biomaterials 1988, 9, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Holmes, D.R.; Leon, M.B.; Moses, J.W.; Popma, J.J.; Cutlip, D.; Fitzgerald, P.J.; Brown, C.; Fischell, T.; Wong, S.C.; Midei, M.; et al. Analysis of 1-Year Clinical Outcomes in the Sirius Trial—A Randomized Trial of a Sirolimus-Eluting Stent Versus a Standard Stent in Patients at High Risk for Coronary Restenosis. Circulation 2004, 109, 634–640. [Google Scholar] [CrossRef] [PubMed]
- McGinty, S.; Mckee, S.; Wadsworth, R.M.; McCormick, C. Modelling Drug-Eluting Stents. Math. Med. Biol. 2011, 28, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, D.V.; Kalachev, L.V.; Rijken, D.C. Numerical Simulation of Local Pharmacokinetics of a Drug after Intravascular Delivery with an Eluting Stent. J. Drug Target. 2002, 10, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Sarika, A.J.; Ankur, J.R.; Arpit, B.J.; Chhaya, B.E.; Jaynish, T.; Vandana, B.P. In vitro drug release profiling of Sirolimus polymeric microparticles coatedlong-acting stents. Int. J. Pharm. 2024, 664, 124572. [Google Scholar]
- Jian, Y.; Zhu, Y. Drug Release Property of Poly 3-Hydroxybutyrate 4-Hydroxybutyrate (P34HB) as Drug-Eluting Coatings on Metal Coronary Stents. Polymers 2022, 14, 3018. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Fu, Y.; Zhang, Y.; Guo, S. Lesion-Adaptative Bionic Tracheal Stent with Local Paclitaxel Release for Enhanced Therapy of Tracheal Tumor and Stenosis. ACS Biomater. Sci. Eng. 2024, 10, 6677–6689. [Google Scholar] [CrossRef]
- Dae, S.P.; Mi, H.N.; Myung, H.J.; Doo, S.S.; Yu, J.J.; Hae, J.K.; Mun, K.K.; Jeong, H.K.; Young, J.H.; Kyung, H.C.; et al. Efficacy and Safety Evaluation of Tacrolimus-Eluting Stent in a Porcine Coronary Artery Model. Tissue Eng. Regen. Med. 2024, 21, 723–735. [Google Scholar]
- Tang, H.; Li, S.; Zhao, Y.; Liu, C.; Gu, X.; Fan, Y. A surface-eroding poly(1,3-trimethylene carbonate) coating for magnesium based cardiovascular stents with stable drug release and improved corrosion resistance. Bioact. Mater. 2022, 7, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Mohamad, A.J.; Pascale, C.; Diego, M.; Syafiqah, S. Everolimus immobilisation using polydopamine intermediate layer on poly (l-lactic acid)/poly(d-lactic acid) scaffold for sustainable anti-proliferative drug release. Mater. Today Commun. 2022, 31, 103720. [Google Scholar]
- Abbasnezhad, N.; Shirinbayan, M.; Champmartin, S.; Bakir, F. Analyzing the impact of pulsatile flow on drug release from a single strut of a drug-eluting stent. J. Biomech. 2023, 146, 111425. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Qin, J.; Zeng, C.; Du, R.; Pan, T.; Ji, J.; Lu, L.; Chen, L.; Liu, D.; Yang, J.; et al. Biodegradable PTX-PLGA-coated magnesium stent for benign esophageal stricture: An experimental study. Acta Biomater. 2022, 146, 495–505. [Google Scholar] [CrossRef]
- Wang, H.J.; Hao, M.F.; Wang, G.; Peng, H.; Wahid, F.; Yang, Y.; Liang, L.; Liu, S.Q.; Li, R.L.; Feng, S.Y. Zein nanospheres assisting inorganic and organic drug combination to overcome stent implantation-induced thrombosis and infection. Sci. Total Environ. 2023, 873, 162438. [Google Scholar] [CrossRef] [PubMed]
- Naghipoor, J.; Ferreira, J.A.; de Oliveira, P.; Rabczuk, T. Tuning Polymeric and Drug Properties in a Drug Eluting Stent: A Numerical Study. Appl. Math. Model. 2016, 40, 8067–8086. [Google Scholar] [CrossRef]
- Wu, H.; Jiang, W.T.; Yan, F. Numerical study on the effect of drug release profiles of two types of drug-eluting stents on drug concentration in the vessel wall. Biomed. Eng. Res. 2013, 32, 206–211. [Google Scholar]
- Vijayaratnam, P.R.S.; Reizes, J.A.; Barber, T.J. The Impact of Strut Profile Geometry and Malapposition on the Haemodynamics and Drug-Transport Behaviour of Arteries Treated with Drug-Eluting Stents. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 3881–3907. [Google Scholar] [CrossRef]
- Vairo, G.; Cioffi, M.; Cottone, R.; Dubini, G.; Migliavacca, F. Drug Release from Coronary Eluting Stents: A Multidomain Approach. J. Biomech. 2010, 43, 1580–1589. [Google Scholar] [CrossRef]
- Zhu, X.; Braatz, R. Modeling and Analysis of Drug-Eluting Stents with Biodegradable Plga Coating: Consequences on Intravascular Drug Delivery. J. Biomech. Eng.-T ASME 2014, 136, 1110041–11100410. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Chen, S.L.; Zhang, Y.; Yang, Y.J.; Song, H.F.; Zhang, Y.P.; Du, T.M.; Qiao, A.K. A quantitative study of the effects of a dual layer coating drug-eluting stent on safety and efficacy. J. Biomech. 2024, 176, 112304. [Google Scholar] [CrossRef] [PubMed]
- Anna, C.; Alistair, M.Q.; Francesco, M.; Claudio, C.; Sean, M.G. Investigating the effect of drug release on in-stent restenosis: A hybrid continuum—Agent-based modelling approach. Comput. Meth Prog. Bio 2023, 241, 107739. [Google Scholar]
- Versypt, A.N.F.; Pack, D.W.; Braatz, R.D. Mathematical Modeling of Drug Delivery from Autocatalytically Degradable Plga Microspheres—A Review. J. Control Release 2013, 165, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Perez-Puyana, V.M.; Capezza, A.J.; Newson, W.R.; Bengoechea, C.; Johansson, E.; Guerrero, A.; Hendeqvist, M.S. Functionalization Routes for Keratin from Poultry Industry Side-Streams—Towards Bio-Based Absorbent Polymers. Polymers 2023, 15, 351. [Google Scholar] [CrossRef] [PubMed]
- Muñana-González, S.; Veloso-Fernández, A.; Ruiz-Rubio, L.; Pérez-Álvarez, L.; Vilas-Vilela, J.L. Covalent Cross-Linking as a Strategy to Prepare Water-Dispersible Chitosan Nanogels. Polymers 2023, 15, 434. [Google Scholar] [CrossRef] [PubMed]
- Steele, T.W.J.; Huang, C.L.; Widjaja, E.; Boey, F.Y.C.; Loo, J.S.C.; Venkatraman, S.S. The Effect of Polyethylene Glycol Structure on Paclitaxel Drug Release and Mechanical Properties of Plga Thin Films. Acta Biomater. 2011, 7, 1973–1983. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Hanif, M.; Li, J.; Shah, A.H.; Hussain, W.; Zhang, G. Fused Deposition Modeling and Characterization of Heat Shape Memory Poly(lactic) Acid-Based Porous Vascular Scaffold. Polymers 2023, 15, 390. [Google Scholar] [CrossRef]
- KyoungWon, K.; Bogyu, C.; Eun, Y.K.; SangWoo, S.; SeunWoon, B.; Dong, K.H. The antagonistic effect of magnesium hydroxide particles on vascular endothelial activation induced by acidic PLGA degradation products. Biomater. Sci. 2021, 9, 892–907. [Google Scholar]
- Yamawaki, T.; Shimokawa, H.; Kozai, T.; Higo, T.; Tanaka, T.; Egashira, K.; Shiraishi, T.; Tamai, H.; Igaki, K.; Takeshita, A. Intramural delivery of a specific tyrosine kinase inhibitor with biodegradable stent suppresses the restenotic changes of the coronary artery in pigs in vivo. J. Am. Coll. Cardiol. 1998, 32, 780–786. [Google Scholar] [CrossRef]
- McGinty, S.; King, D.; Pontrelli, G. Mathematical Modelling of Variable Porosity Coatings for Controlled Drug Release. Med. Eng. Phys. 2017, 45, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Naghipoor, J.; Rabczuk, T. A Mechanistic Model for Drug Release from Plga-Based Drug Eluting Stent: A Computational Study. Comput. Biol. Med. 2017, 90, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Denny, W.J.; Walsh, M.T. Numerical Modelling of the Physical Factors That Affect Mass Transport in the Vasculature at Early Time Periods. Med. Eng. Phys. 2014, 36, 308–317. [Google Scholar] [CrossRef] [PubMed]
- Pontrelli, G.; Di Mascio, A.; De Monte, F. Local Mass Non-Equilibrium Dynamics in Multi-Layered Porous Media: Application to the Drug-Eluting Stent. Int. J. Heat Mass Transf. 2013, 66, 844–854. [Google Scholar] [CrossRef]
- Bourantas, C.V.; Onuma, Y.; Farooq, V.; Zhang, Y.J.; Garcia-Garcia, H.M.; Serruys, P.W. Bioresorbable Scaffolds: Current Knowledge, Potentialities and Limitations Experienced During Their First Clinical Applications. Int. J. Cardiol. 2013, 167, 11–21. [Google Scholar] [CrossRef]
- Mongrain, R.; Faik, I.; Leask, R.L.; Rodés-Cabau, J.; Larose, E.; Bertrand, O.F. Effects of Diffusion Coefficients and Struts Apposition Using Numerical Simulations for Drug Eluting Coronary Stents. J. Biomech. Eng-T ASME 2007, 129, 733–742. [Google Scholar] [CrossRef]
- Pontrelli, G.; de Monte, F. Mass Diffusion through Two-Layer Porous Media: An Application to the Drug-Eluting Stent. Int. J. Heat Mass Transf. 2007, 50, 3658–3669. [Google Scholar] [CrossRef]
- Lao, L.L.; Venkatraman, S.S. Adjustable Paclitaxel Release Kinetics and Its Efficacy to Inhibit Smooth Muscle Cells Proliferation. J. Control Release 2008, 130, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Tesfamariam, B. Drug Release Kinetics from Stent Device-Based Delivery Systems. J. Cardiovasc. Pharm. 2008, 51, 118–125. [Google Scholar] [CrossRef] [PubMed]
- Waugh, J.; Wagstaff, A.J. The Paclitaxel (Taxus)-Eluting Stent: A Review of Its Use in the Management of De Novo Coronary Artery Lesions. Am. J. Cardiovasc. Drugs 2004, 4, 257–268. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Luo, W.; Zhuang, H.; Ren, C.; Pan, X.; Xu, Y.; Wang, H.; Li, X.; Yuan, Y.; Zhu, R.; et al. Dual-layer drug release system based on ureteral stents inhibits the formation of ureteral stricture. Chem. Eng. J. 2023, 471, 144596. [Google Scholar] [CrossRef]
- Zhuo, Z.; Ouyang, Y.; Zheng, X.; Chen, X.; Lin, Z.; Zhu, R.; Lan, L.; Qian, D.; Li, R.; Zhu, J.; et al. Design, fabrication, and in vitro studies of sustained paclitaxel release from 3D-printed TPU/P407 airway stents for treating airway stenosis. Mater. Des. 2024, 245, 113252. [Google Scholar] [CrossRef]
- Serruys, P.W.; Sianos, G.; Abizaid, A.; Aoki, J.; den Heijer, P.; Bonnier, H.; Smits, P.; McClean, D.; Verheye, S.; Belardi, J.; et al. The Effect of Variable Dose and Release Kinetics on Neointimal Hyperplasia Using a Novel Paclitaxel-Eluting Stent Platform: The Paclitaxel in-Stent Controlled Elution Study (Pisces). J. Am. Coll. Cardiol. 2005, 46, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Ali, M.N.; Ghafoor, B. Evolutionary Perspective of Drug Eluting Stents: From Thick Polymer to Polymer Free Approach. J. Cardiothorac. Surg. 2022, 17, 65. [Google Scholar] [CrossRef]
- Pan, C.J.; Tang, J.J.; Weng, Y.J.; Wang, J.; Huang, N. Preparation and in Vitro Release Profiles of Drug-Eluting Controlled Biodegradable Polymer Coating Stents. Colloids Surf. B Biointerfaces 2009, 73, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Lei, L.; Hou, J.W.; Tang, M.F.; Guo, S.R.; Wang, Z.M.; Chen, K.M. Evaluation of Two Polymeric Blends (Eva/Pla and Eva/Peg) as Coating Film Materials for Paclitaxel-Eluting Stent Application. J. Mater. Sci.-Mater. Med. 2011, 22, 327–337. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Braatz, R.D. A Mechanistic Model for Drug Release in Plga Biodegradable Stent Coatings Coupled with Polymer Degradation and Erosion. J. Biomed. Mater. Res. A 2015, 103, 2269–2279. [Google Scholar] [CrossRef]
- Batycky, R.P.; Hanes, J.; Langer, R.; Edwards, D.A. A Theoretical Model of Erosion and Macromolecular Drug Release from Biodegrading Microspheres. J. Pharm. Sci. 1997, 86, 1464–1477. [Google Scholar] [CrossRef] [PubMed]
- Xi, T.; Gao, R.; Xu, B.; Chen, L.; Luo, T.; Liu, J.; Wei, Y.; Zhong, S. In Vitro and in Vivo Changes to Plga/Sirolimus Coating on Drug Eluting Stents. Biomaterials 2010, 31, 5151–5158. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.W.; Edelman, E.R. Arterial Ultrastructure Influences Transport of Locally Delivered Drugs. Circ. Res. 2002, 90, 826–832. [Google Scholar] [CrossRef]
- Hwang, C.W.; Wu, D.; Edelman, E.R. Physiological Transport Forces Govern Drug Distribution for Stent-Based Delivery. Circulation 2001, 104, 600–605. [Google Scholar] [CrossRef]
- Baines, D.K.; Wright, K.; Douglas, T.E.L. Preliminary In Vitro Assessment of Whey Protein Isolate Hydrogel with Cannabidiol as a Potential Hydrophobic Oral Drug Delivery System for Colorectal Cancer Therapy. Polymers 2024, 16, 3273. [Google Scholar] [CrossRef] [PubMed]
- Mourad, G.; Ribstein, J.; Argiles, A.; Mion, C.; Mimran, A. Hypertension and Stenosis of the Graft Artery: Effects of Conversion Enzyme Inhibition. Arch. Mal. Coeur Vaiss. 1986, 79, 892–895. [Google Scholar] [PubMed]
- Pontrelli, G.; de Monte, F. A Multi-Layer Porous Wall Model for Coronary Drug-Eluting Stents. Int. J. Heat Mass Transf. 2010, 53, 3629–3637. [Google Scholar] [CrossRef]
- Pant, S.; Bressloff, N.W.; Limbert, G. Geometry Parameterization and Multidisciplinary Constrained Optimization of Coronary Stents. Biomech. Model. Mechanobiol. 2012, 11, 61–82. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Guo, J.; Li, Y.; Yang, W.; Ni, W.; Jia, Y.; Yu, M.; Zhang, J. Improve Solubility and Develop Personalized Itraconazole Dosages via Forming Amorphous Solid Dispersions with Hydrophilic Polymers Utilizing HME and 3D Printing Technologies. Polymers 2024, 16, 3302. [Google Scholar] [CrossRef] [PubMed]
- Yamdech, R.; Terahsongkran, V.; Terahsongkran, V.; Cherdchom, S.; Aramwit, P. Development of Antioxidant-Active Sericin–Curcumin-Loaded Sodium Alginate/Polyvinyl Alcohol Films Crosslinked with Calcium Chloride as a Promising Wound Dressing Application. Polymers 2024, 16, 3197. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wei, Y.; Li, H. A Numerical Study on the Drug Release Process of Biodegradable Polymer Drug-Loaded Vascular Stents. Polymers 2025, 17, 420. https://doi.org/10.3390/polym17030420
Li S, Wei Y, Li H. A Numerical Study on the Drug Release Process of Biodegradable Polymer Drug-Loaded Vascular Stents. Polymers. 2025; 17(3):420. https://doi.org/10.3390/polym17030420
Chicago/Turabian StyleLi, Shiyong, Yunbo Wei, and Hongxia Li. 2025. "A Numerical Study on the Drug Release Process of Biodegradable Polymer Drug-Loaded Vascular Stents" Polymers 17, no. 3: 420. https://doi.org/10.3390/polym17030420
APA StyleLi, S., Wei, Y., & Li, H. (2025). A Numerical Study on the Drug Release Process of Biodegradable Polymer Drug-Loaded Vascular Stents. Polymers, 17(3), 420. https://doi.org/10.3390/polym17030420






