Dipolar Brush Polymers: A Numerical Study of the Force Exerted onto a Penetrating Colloidal Particle Under an External Field
Abstract
1. Introduction
2. Numerical Method
2.1. Brush Setup and Initial Equilibration Protocol
2.2. Brush–Particle Force Measuring Protocol
2.3. Correspondence Between the Numerical Model and Experimental Dipolar Brushes
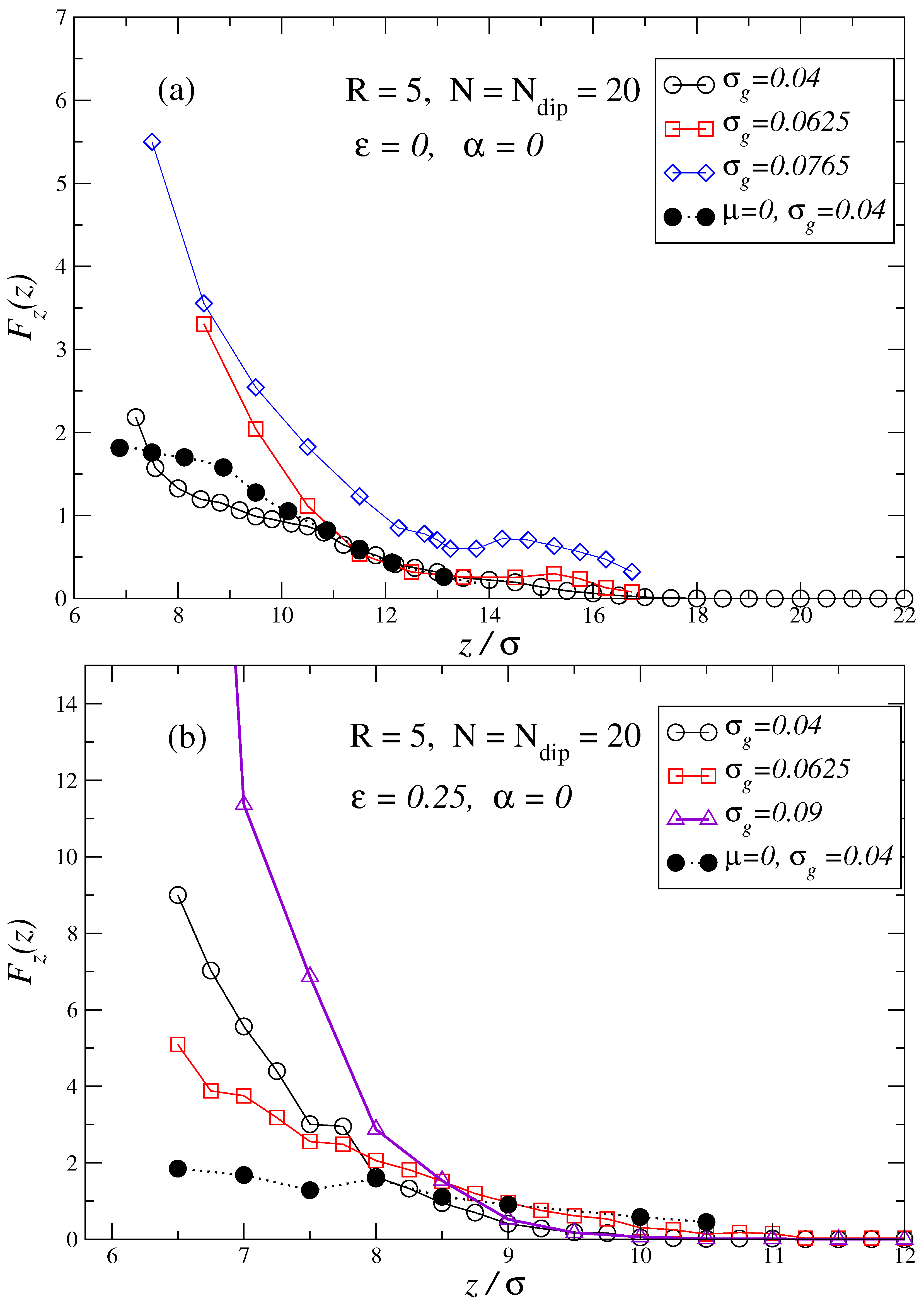
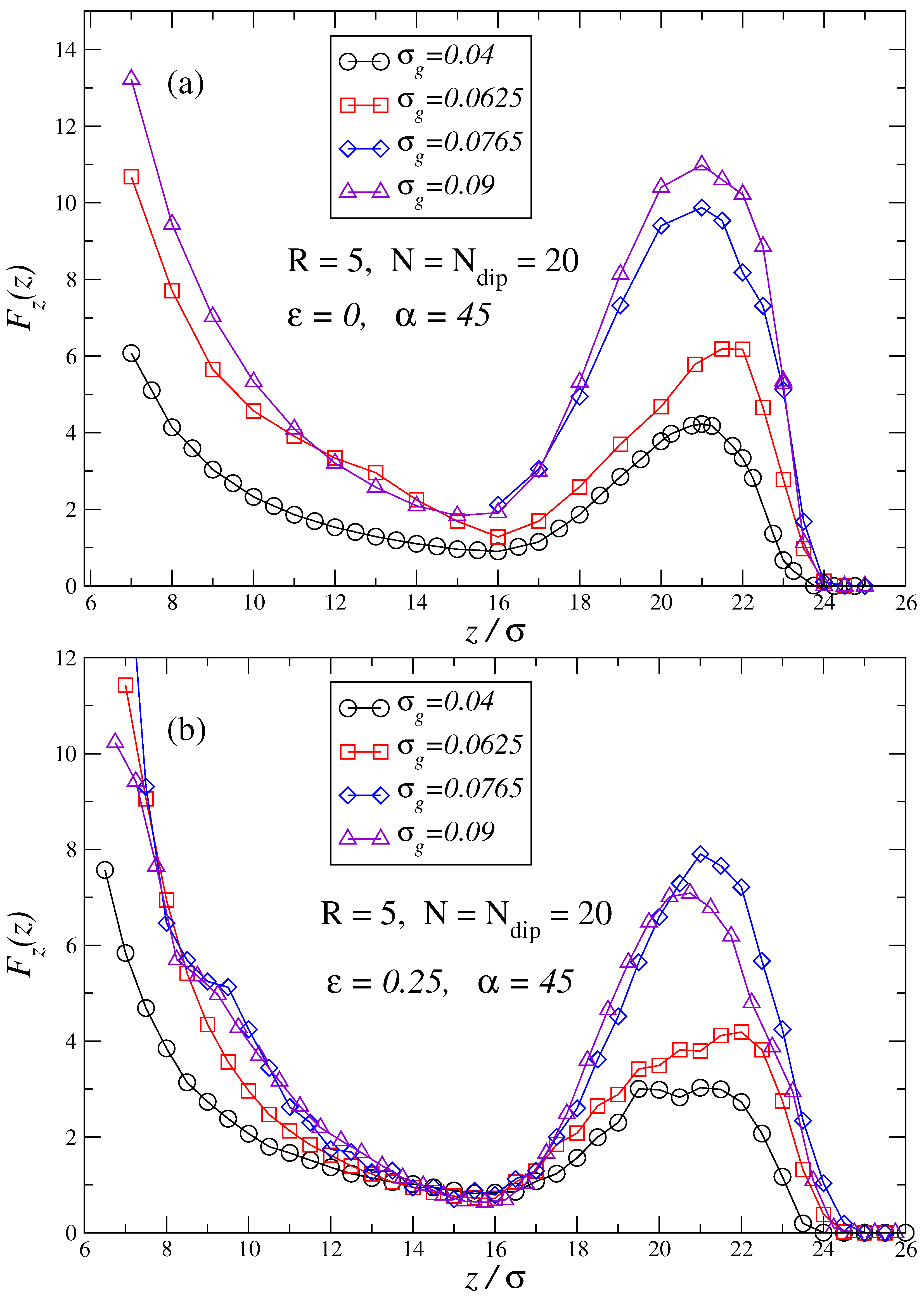
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Li, M.; Li, B.; Sheng, W. Surface Functionalization with Polymer Brushes via Surface-Initiated Atom Transfer Radical Polymerization: Synthesis, Applications, and Current Challenges. Langmuir 2024, 40, 5571–5589. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, H. Polymer Brushes and Surface Nanostructures: Molecular Design, Precise Synthesis, and Self-Assembly. Langmuir 2024, 40, 2439–2464. [Google Scholar] [CrossRef]
- Feng, Y.; Wei, C.; Zhao, T. Molecular brushes based on poly(amino acid)s: Synthesis, structures, and applications. J. Polym. Sci. 2024, 62, 480–491. [Google Scholar] [CrossRef]
- Wang, R.; Wei, Q.; Sheng, W.; Yu, B.; Zhou, F.; Li, B. Driving Polymer Brushes from Synthesis to Functioning. Angew. Chem. Int. Ed. 2023, 62, e202219312. [Google Scholar] [CrossRef]
- Metze, F.K.; Klok, H.A. Supramolecular Polymer Brushes. ACS Polym. AU 2023, 3, 228–238. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.Q.; Zhu, W.; Guo, W.J.; Li, Q.; Ma, S.; Bucher, C.; Liu, B.; Ji, X.; Huang, F.; Sessler, J.L. Supramolecular polymers: Recent advances based on the types of underlying interactions. Prog. Polym. Sci. 2023, 137, 101635. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, H. Polymer brush-based nanostructures: From surface self-assembly to surface co-assembly. Soft Matter 2022, 18, 5138–5152. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Liu, L.; Zhang, N. Brush-like polymers: Design, synthesis and applications. Chem. Commun. 2021, 57, 10484–10499. [Google Scholar] [CrossRef]
- Yang, R.; Wang, X.; Yan, S.; Dong, A.; Luan, S.; Yin, J. Advances in design and biomedical application of hierarchical polymer brushes. Prog. Polym. Sci. 2021, 118, 101409. [Google Scholar] [CrossRef]
- Reese, C.J.; Boyes, S.G. New methods in polymer brush synthesis: Non-vinyl-based semiflexible and rigid-rod polymer brushes. Prog. Polym. Sci. 2021, 114, 101361. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Yu, B.; Zhou, F. Brushing up functional materials. NPG Asia Mater. 2019, 11, 24. [Google Scholar] [CrossRef]
- Conrad, J.C.; Robertson, M.L. Towards mimicking biological function with responsive surface-grafted polymer brushes. Curr. Opin. Solid State Mater. Sci. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Xu, X.; Billing, M.; Ruths, M.; Klok, H.A.; Yu, J. Structure and Functionality of Polyelectrolyte Brushes: A Surface Force Perspective. Chem. Asian J. 2018, 13, 3411–3436. [Google Scholar] [CrossRef]
- Welch, M.E.; Ober, C.K. Responsive and patterned polymer brushes. J. Polym. Sci. Part B Polim. Phys. 2013, 51, 1457–1472. [Google Scholar] [CrossRef]
- Lokesh, M.G.; Tiwari, A.K. A concise review on polymer brushes and its interaction with surfactants: An approach towards smart materials. J. Mol. Liq. 2024, 407, 125168. [Google Scholar] [CrossRef]
- Conrad, J.C.; Robertson, M.L. Shaping the Structure and Response of Surface-Grafted Polymer Brushes via the Molecular Weight Distribution. JACS AU 2023, 3, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wu, Y.; Zhou, F. Shear-Stable Polymer Brush Surfaces. Langmuir 2023, 39, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, R.; Duval, J.F.L.; Werner, C.; Sterling, J.D. Quantitative insights into electrostatics and structure of polymer brushes from microslit electrokinetic experiments and advanced modelling of interfacial electrohydrodynamics. Curr. Opin. Colloid Interface Sci. 2022, 59, 101590. [Google Scholar] [CrossRef]
- Geoghegan, M. Weak polyelectrolyte brushes. Soft Matter 2022, 18, 2500–2511. [Google Scholar] [CrossRef]
- Wang, S.; Jing, B.; Zhu, Y. Molecule Motion at Polymer Brush Interfaces from Single-Molecule Experimental Perspectives. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 85–103. [Google Scholar] [CrossRef]
- Reznik, C.; Landes, C.F. Transport in Supported Polyelectrolyte Brushes. Accounts Chem. Res. 2012, 45, 1927–1935. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ballauff, M. Spherical polyelectrolyte brushes. Prog. Polym. Sci. 2007, 32, 1135–1151. [Google Scholar] [CrossRef]
- Ballauff, M.; Borisov, O. Polyelectrolyte brushes. Curr. Opin. Colloid Interface Sci. 2006, 11, 316–323. [Google Scholar] [CrossRef]
- Das, S.; Banik, M.; Chen, G.; Sinha, S.; Mukherjee, R. Polyelectrolyte brushes: Theory, modelling, synthesis and applications. Soft Matter 2015, 11, 8550–8583. [Google Scholar] [CrossRef] [PubMed]
- Mikhailov, V.I.; Darinskii, A.A.; Birshtein, T.M. Bending Rigidity of Branched Polymer Brushes with Finite Membrane Thickness. Polym. Sci. Ser. C 2022, 64, 110–122. [Google Scholar] [CrossRef]
- Niu, Y.; Bu, X.; Zhang, X. Single Chain Mean-Field Theory Study on Responsive Behavior of Semiflexible Polymer Brush. Materials 2021, 14, 778. [Google Scholar] [CrossRef] [PubMed]
- Klushin, L.I.; Skvortsov, A.M.; Qi, S.; Schmid, F. Polydisperse Brush with the Linear Density Profile. Polym. Sci. Ser. C 2018, 60, 84–94. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Dendritic polyelectrolyte brushes. Polym. Sci. Ser. C 2017, 59, 106–118. [Google Scholar] [CrossRef]
- Wang, Z.; Li, B.H. Self-assembly of block copolymers grafted onto a flat substrate: Recent progress in theory and simulations. Chin. Phys. B 2016, 25, 016402. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B Polim. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Tagliazucchi, M.; Szleifer, I. Stimuli-responsive polymers grafted to nanopores and other nano-curved surfaces: Structure, chemical equilibrium and transport. Soft Matter 2012, 8, 7292–7305. [Google Scholar] [CrossRef]
- Xu, X.; Cao, D.; Wu, J. Density functional theory for predicting polymeric forces against surface fouling. Soft Matter 2010, 6, 4631–4646. [Google Scholar] [CrossRef]
- Naji, A.; Seidel, C.; Netz, R.R. Theoretical approaches to neutral and charged polymer brushes. In Surface—Initiated Polymerization II. Advances in Polymer Science; Jordan, R., Ed.; Springer: Heidelberger/Berlin, Germany, 2006; Volume 198, pp. 149–183. [Google Scholar] [CrossRef]
- Rühe, J.; Ballauff, M.; Biesalski, M.; Dziezok, P.; Gröhn, F.; Johannsmann, D.; Houbenov, N.; Hugenberg, N.; Konradi, R.; Minko, S.; et al. Polyelectrolyte brushes. In Polyelectrolytes with Defined Molecular Architecture I. Advances in Polymer Science; Schmidt, M., Ed.; Springer: Heidelberger/Berlin, Germany, 2004; Volume 165, pp. 79–150. [Google Scholar] [CrossRef]
- Vorsmann, C.F.; Del Galdo, S.; Capone, B.; Locatelli, E. Colloidal adsorption in planar polymeric brushes. Nanoscale Adv. 2024, 6, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Dimitrov, D.; Milchev, A.; Binder, K. Polymer brushes on flat and curved substrates: Scaling concepts and computer simulations. Macromol. Symp. 2007, 252, 47–57. [Google Scholar] [CrossRef]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479–3501. [Google Scholar] [CrossRef]
- Larin, D.E.; Govorun, E.N. Surfactant-Induced Patterns in Polymer Brushes. Langmuir 2017, 33, 8545–8552. [Google Scholar] [CrossRef] [PubMed]
- Ishraaq, R.; Das, S. All-atom molecular dynamics simulations of polymer and polyelectrolyte brushes. Chem. Commun. 2024, 60, 6093–6129. [Google Scholar] [CrossRef]
- Abdelbar, M.A.A.; Ewen, J.P.P.; Dini, D.; Angioletti-Uberti, S. Polymer brushes for friction control: Contributions of molecular simulations. Biointerphases 2023, 18, 010801. [Google Scholar] [CrossRef]
- Binder, K.; Kreer, T.; Milchev, A. Polymer brushes under flow and in other out-of-equilibrium conditions. Soft Matter 2011, 7, 7159–7172. [Google Scholar] [CrossRef]
- Descas, R.; Sommer, J.U.; Blumen, A. Grafted Polymer Chains Interacting with Substrates: Computer Simulations and scaling. Macromol. Theory Simulations 2008, 17, 429–453. [Google Scholar] [CrossRef]
- Viduna, D.; Limpouchová, Z.; Procházka, K. Monte Carlo simulation of polymer brushes in narrow pores. J. Chem. Phys. 2001, 115, 7309–7318. [Google Scholar] [CrossRef]
- Grest, G. Normal and shear forces between polymer brushes. In Polymers in Confined Environments, Advances in Polymer Science; Granick, S., Ed.; Springer: Heidelberger/Berlin, Germany, 1999; Volume 138, pp. 149–183. [Google Scholar]
- Grest, G. Computer simulations of shear and friction between polymer brushes. Curr. Opin. Colloid Interface Sci. 1997, 2, 271–277. [Google Scholar] [CrossRef]
- Mikhailov, I.V.; Amoskov, V.M.; Darinskii, A.A.; Birshtein, T.M. The Structure of Dipolar Polymer Brushes and Their Interaction in the Melt. Impact of Chain Stiffness. Polymers 2020, 12, 2887. [Google Scholar] [CrossRef]
- Birshtein, T.; Polotsky, A.; Glova, A.; Amoskov, V.; Mercurieva, A.; Nazarychev, V.; Lyulin, S. How to fold back grafted chains in dipolar brushes. Polymer 2018, 147, 213–224. [Google Scholar] [CrossRef]
- Okrugin, B.M.; Richter, R.P.; Leermakers, F.A.M.; Neelov, I.M.; Zhulina, E.B.; Borisov, O.V. Electroresponsive Polyelectrolyte Brushes Studied by Self-Consistent Field Theory. Polymers 2020, 12, 898. [Google Scholar] [CrossRef]
- Lukiev, I.V.; Mogelnitskaya, Y.A.; Mikhailov, I.V.; Darinskii, A.A. Chains Stiffness Effect on the Vertical Segregation of Mixed Polymer Brushes in Selective Solvent. Polymers 2023, 15, 644. [Google Scholar] [CrossRef]
- Kielbasa, A.; Kowalczyk, K.; Chajec-Gierczak, K.; Bala, J.; Zapotoczny, S. Applications of surface-grafted polymer brushes with various architectures. Polym. Adv. Technol. 2024, 35, e6397. [Google Scholar] [CrossRef]
- Chen, W.L.; Cordero, R.; Tran, H.; Ober, C.K. 50th Anniversary Perspective: Polymer Brushes: Novel Surfaces for Future Materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Su, N. Advances and Prospects in the Study of Spherical Polyelectrolyte Brushes as a Dopant for Conducting Polymers. Molecules 2024, 29, 1315. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, S.; Diekmann, J.; Greve, D.; Thiele, U. Drops on Polymer Brushes: Advances in Thin-Film Modeling of Adaptive Substrates. Langmuir 2024, 40, 4001–4021. [Google Scholar] [CrossRef] [PubMed]
- Atif, M.; Balasini, A. Mixed polymer brushes for controlled protein adsorption: State of the art and future prospective. Mater. Adv. 2024, 5, 1420–1439. [Google Scholar] [CrossRef]
- Liu, J.; Tang, K.; Wang, M.; Shen, C.; Deng, R. Recent Progress in Janus Nano-Objects with Asymmetric Polymer Brushes. Chem. Asian J. 2024, 19, e202301023. [Google Scholar] [CrossRef] [PubMed]
- Bhayo, A.M.; Yang, Y.; He, X. Polymer brushes: Synthesis, characterization, properties and applications. Prog. Mater. Sci. 2022, 130, 101000. [Google Scholar] [CrossRef]
- Poisson, J.; Hudson, Z.M. Luminescent Surface-Tethered Polymer Brush Materials. Chem. A Eur. J. 2022, 28, e202200552. [Google Scholar] [CrossRef]
- Pradhan, S.S.; Saha, S. Advances in design and applications of polymer brush modified anisotropic particles. Adv. Colloid Interface Sci. 2022, 300, 102580. [Google Scholar] [CrossRef] [PubMed]
- van Eck, G.C.R.; Chiappisi, L.; de Beer, S. Fundamentals and Applications of Polymer Brushes in Air. ACS Appl. Polym. Mater. 2022, 4, 3062–3087. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Luo, H.N.; Zhang, W.; Liu, Y. Research progress in self-oscillating polymer brushes. RSC Adv. 2022, 12, 1366–1374. [Google Scholar] [CrossRef]
- Nakamura, S.; Mitomo, H.; Ijiro, K. Assembly and Active Control of Nanoparticles using Polymer Brushes as a Scaffold. Chem. Lett. 2021, 50, 361–370. [Google Scholar] [CrossRef]
- Li, D.; Xu, L.; Wang, J.; Gautrot, J.E. Responsive Polymer Brush Design and Emerging Applications for Nanotheranostics. Adv. Healthc. Mater. 2021, 10, e202000953. [Google Scholar] [CrossRef]
- Li, M.; Pester, C.W. Mixed Polymer Brushes for “Smart” Surfaces. Polymers 2020, 12, 1553. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, Z.; Li, J.; Li, L.; Hu, W. Surface-grafting polymers: From chemistry to organic electronics. Mater. Chem. Front. 2020, 4, 692–714. [Google Scholar] [CrossRef]
- Heggestad, J.T.; Fontes, C.M.; Joh, D.Y.; Hucknall, A.M.; Chilkoti, A. In Pursuit of Zero 2.0: Recent Developments in Nonfouling Polymer Brushes for Immunoassays. Adv. Mater. 2020, 32, e201903285. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Ren, B.; Huang, L.; Shen, M.; Zhang, Y.; Zhong, M.; Yang, J.; Zheng, J. Salt-responsive zwitterionic polymer brushes with anti-polyelectrolyte property. Curr. Opin. Chem. Eng. 2018, 19, 86–93. [Google Scholar] [CrossRef]
- Keating, J.J.; Imbrogno, J.; Belfort, G. Polymer Brushes for Membrane Separations: A Review. ACS Appl. Mater. Interfaces 2016, 8, 28383–28399. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Ista, L.K.; Gu, R.; Zauscher, S.; Lopez, G.P. Nanopatterned polymer brushes: Conformation, fabrication and applications. Nanoscale 2016, 8, 680–700. [Google Scholar] [CrossRef] [PubMed]
- Azzaroni, O. Polymer brushes here, there, and everywhere: Recent advances in their practical applications and emerging opportunities in multiple research fields. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 3225–3258. [Google Scholar] [CrossRef]
- Mocny, P.; Klok, H.A. Tribology of surface-grafted polymer brushes. Mol. Syst. Des. Eng. 2016, 1, 141–154. [Google Scholar] [CrossRef]
- Kim, J.U.; Matsen, M.W. Repulsion Exerted on a Spherical Particle by a Polymer Brush. Macromolecules 2008, 41, 246–252. [Google Scholar] [CrossRef]
- Egorov, S.A. Insertion of nanoparticles into polymer brush under variable solvent conditions. J. Chem. Phys. 2012, 137, 134905. [Google Scholar] [CrossRef] [PubMed]
- Lian, Z.; Qi, S.; Zhou, J.; Schmid, F. Solvent Determines Nature of Effective Interactions between Nanoparticles in Polymer Brushes. J. Phys. Chem. B 2015, 119, 4099–4108. [Google Scholar] [CrossRef] [PubMed]
- Spencer, R.K.W.; Ha, B.Y. How a Polymer Brush Interacts with Inclusions and Alters Their Interaction. Macromolecules 2021, 54, 1304–1313. [Google Scholar] [CrossRef]
- Laktionov, M.Y.; Shavykin, O.V.; Leermakers, F.A.M.; Zhulina, E.B.; Borisov, O.V. Colloidal particles interacting with a polymer brush: A self-consistent field theory. Phys. Chem. Chem. Phys. 2022, 24, 8463–8476. [Google Scholar] [CrossRef]
- Santo, K.P.; Vishnyakov, A.; Brun, Y.; Neimark, A.V. Adhesion and Separation of Nanoparticles on Polymer-Grafted Porous Substrates. Langmuir 2018, 34, 1481–1496. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A.; Dimitrov, D.; Binder, K. Excess free energy of nanoparticles in a polymer brush. Polymer 2008, 49, 3611–3618. [Google Scholar] [CrossRef]
- Ermilov, V.; Lazutin, A.; Halperin, A. Colloids in Brushes: The Insertion Free Energy via Monte Carlo Simulation with Umbrella Sampling. Macromolecules 2010, 43, 3511–3520. [Google Scholar] [CrossRef]
- Merlitz, H.; Wu, C.X.; Sommer, J.U. Inclusion Free Energy of Nanoparticles in Polymer Brushes. Macromolecules 2012, 45, 8494–8501. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiang, X. Adsorption of a spherical nanoparticle in polymer brushes: Brownian dynamics investigation. Phys. A Stat. Mech. Appl. 2013, 392, 3857–3862. [Google Scholar] [CrossRef]
- Milchev, A.; Dimitrov, D.I.; Binder, K. Polymer brushes with nanoinclusions under shear: A molecular dynamics investigation. Biomicrofluidics 2010, 4, 032202. [Google Scholar] [CrossRef] [PubMed]
- de Beer, S.; Mensink, L.I.S.; Kieviet, B.D. Geometry-Dependent Insertion Forces on Particles in Swollen Polymer Brushes. Macromolecules 2016, 49, 1070–1078. [Google Scholar] [CrossRef]
- Gao, H.M.; Li, B.; Zhang, R.; Sun, Z.Y.; Lu, Z.Y. Free energy for inclusion of nanoparticles in solvated polymer brushes from molecular dynamics simulations. J. Chem. Phys. 2020, 152, 094905. [Google Scholar] [CrossRef]
- Offner, A.; Ramon, G.Z. The interaction of a particle and a polymer brush coating a permeable surface. J. Fluid Mech. 2021, 913, R3. [Google Scholar] [CrossRef]
- Laktionov, M.Y.; Zhulina, E.B.; Klushin, L.; Richter, R.P.; Borisov, O.V. Selective Colloid Transport across Planar Polymer Brushes. Macromol. Rapid Commun. 2023, 44, 2200980. [Google Scholar] [CrossRef]
- Tom, A.M.; Kim, W.K.; Hyeon, C. Polymer brush-induced depletion interactions and clustering of membrane proteins. J. Chem. Phys. 2021, 154, 214901. [Google Scholar] [CrossRef]
- Nourbakhsh, S.; Yu, L.; Ha, B.Y. Modeling the Protective Role of Bacterial Lipopolysaccharides against Membrane-Rupturing Peptides. J. Phys. Chem. B 2021, 125, 8839–8854. [Google Scholar] [CrossRef] [PubMed]
- Astier, S.; Johnson, E.C.; Norvilaite, O.; Varlas, S.; Brotherton, E.E.; Sanderson, G.; Leggett, G.J.; Armes, S.P. Controlling Adsorption of Diblock Copolymer Nanoparticles onto an Aldehyde-Functionalized Hydrophilic Polymer Brush via pH Modulation. Langmuir 2024, 40, 3667–3676. [Google Scholar] [CrossRef] [PubMed]
- Popova, T.O.; Borisov, O.V.; Zhulina, E.B. Polyelectrolyte Brushes with Protein-Like Nanocolloids. Langmuir 2024, 40, 1232–1246. [Google Scholar] [CrossRef] [PubMed]
- Stockmayer, W.H. Dielectric dispersion in solutions of flexible polymers. Pure Appl. Chem. 1967, 15, 539–554. [Google Scholar] [CrossRef]
- Mahalik, J.P.; Sumpter, B.G.; Kumar, R. Understanding the effects of symmetric salt on the structure of a planar dipolar polymer brush. J. Chem. Phys. 2018, 149, 163334. [Google Scholar] [CrossRef]
- Mahalik, J.P.; Sumpter, B.G.; Kumar, R. Vertical Phase Segregation Induced by Dipolar Interactions in Planar Polymer Brushes. Macromolecules 2016, 49, 7096–7107. [Google Scholar] [CrossRef]
- Kamachi, M. Magnetic polymers. J. Macromol. Sci. Pol. R 2002, C42, 541–561. [Google Scholar] [CrossRef]
- Blundell, S.J.; Pratt, F.L. Organic and molecular magnets. J. Phys. Condens. Matter 2004, 16, R771–R828. [Google Scholar] [CrossRef]
- Gorka, W.; Kuciel, T.; Nalepa, P.; Lachowicz, D.; Zapotoczny, S.; Szuwarzynski, M. Homogeneous Embedding of Magnetic Nanoparticles into Polymer Brushes during Simultaneous Surface-Initiated Polymerization. Nanomaterials 2019, 9, 456. [Google Scholar] [CrossRef] [PubMed]
- San Choi, W.; Young Koo, H.; Young Kim, J.; Huck, W.T.S. Collective Behavior of Magnetic Nanoparticles in Polyelectrolyte Brushes. Adv. Mater. 2008, 20, 4504–4508. [Google Scholar] [CrossRef]
- Evans, B.A.; Shields, A.R.; Carroll, R.L.; Washburn, S.; Falvo, M.R.; Superfine, R. Magnetically Actuated Nanorod Arrays as Biomimetic Cilia. Nano Lett. 2007, 7, 1428–1434. [Google Scholar] [CrossRef] [PubMed]
- Benkoski, J.J.; Deacon, R.M.; Land, H.B.; Baird, L.M.; Breidenich, J.L.; Srinivasan, R.; Clatterbaugh, G.V.; Keng, P.Y.; Pyun, J. Dipolar assembly of ferromagnetic nanoparticles into magnetically driven artificial cilia. Soft Matter 2010, 6, 602–609. [Google Scholar] [CrossRef]
- Haddour, N.; Chevolot, Y.; Trévisan, M.; Souteyrand, E.; Cloarec, J.P. Use of magnetic field for addressing, grafting onto support and actuating permanent magnetic filaments applied to enhanced biodetection. J. Mater. Chem. 2010, 20, 8266–8271. [Google Scholar] [CrossRef]
- Vilfan, M.; Potočnik, A.; Kavčič, B.; Osterman, N.; Poberaj, I.; Vilfan, A.; Babič, D. Self-assembled artificial cilia. Proc. Natl. Acad. Sci. USA 2010, 107, 1844–1847. [Google Scholar] [CrossRef]
- Trévisan, M.; Duval, A.; Moreau, J.; Bartelian, B.; Canva, M.; Monnier, V.; Chevolot, Y.; Cloarec, J.; Souteyrand, E. Assembling, locating, grafting and actuating permanent filaments for validation of Polarimetric Surface Plasmon Resonance Imaging system. Procedia Eng. 2011, 25, 872–875, EurosensorsXXV. [Google Scholar] [CrossRef]
- Trévisan, M.; Chevolot, Y.; Monnier, V.; Cloarec, J.P.; Souteyrand, E.; Duval, A.; Moreau, J.; Canva, M. Elaboration and grafting of magnetic bead-chains for detection of anisotropy with polarimetric surface plasmon resonance imaging system. Int. J. Nanosci. 2012, 11, 1240012. [Google Scholar] [CrossRef]
- Breidenich, J.L.; Wei, M.C.; Clatterbaugh, G.V.; Benkoski, J.J.; Keng, P.Y.; Pyun, J. Controlling length and areal density of artificial cilia through the dipolar assembly of ferromagnetic nanoparticles. Soft Matter 2012, 8, 5334–5341. [Google Scholar] [CrossRef]
- Tokarev, A.; Gu, Y.; Zakharchenko, A.; Trotsenko, O.; Luzinov, I.; Kornev, K.G.; Minko, S. Reconfigurable Anisotropic Coatings via Magnetic Field-Directed Assembly and Translocation of Locking Magnetic Chains. Adv. Funct. Mater. 2014, 24, 4738–4745. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Y. Bio-inspired artificial cilia with magnetic dynamic properties. Front. Mater. Sci. 2015, 9, 178. [Google Scholar] [CrossRef]
- Hanasoge, S.; Hesketh, P.J.; Alexeev, A. Microfluidic pumping using artificial magnetic cilia. Microsystems Nanoeng. 2018, 4, 11. [Google Scholar] [CrossRef]
- Vu, A.; Freeman, E.; Qian, X.; Ulbricht, M.; Ranil Wickramasinghe, S. Tailoring and remotely switching performance of ultrafiltration membranes by magneticaly responsive polymer chains. Membranes 2020, 10, 219. [Google Scholar] [CrossRef]
- Akkilic, N.; Leermakers, F.A.M.; de Vos, W.M. Responsive polymer brushes for controlled nanoparticle exposure. Nanoscale 2015, 7, 17871–17878. [Google Scholar] [CrossRef]
- Fahrni, F.; Prins, M.W.J.; van IJzendoorn, L.J. Micro-fluidic actuation using magnetic artificial cilia. Lab. Chip 2009, 9, 3413–3421. [Google Scholar] [CrossRef]
- Babataheri, A.; Roper, M.; Fermigier, M.; Roure, O.D. Tethered fleximags as artificial cilia. J. Fluid Mech. 2011, 678, 5–13. [Google Scholar] [CrossRef]
- Ben, S.; Zhou, T.; Ma, H.; Yao, J.; Ning, Y.; Tian, D.; Liu, K.; Jiang, L. Multifunctional Magnetocontrollable Superwettable-Microcilia Surface for Directional Droplet Manipulation. Adv. Sci. 2019, 6, 1900834. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Song, F.J.; Dobnikar, J. Assembly of Superparamagnetic Filaments in External Field. Langmuir ACS J. Surfaces Colloids 2016, 32–36, 9321–9328. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Pyanzina, E.S.; Novak, E.V.; Cerdà, J.J.; Sintes, T.; Kantorovich, S.S. Magnetic filament brushes: Tuning the properties of a magnetoresponsive supracolloidal coating. Faraday Discuss. 2016, 186, 241–263. [Google Scholar] [CrossRef] [PubMed]
- Pyanzina, E.S.; Sánchez, P.A.; Cerdà, J.J.; Sintes, T.; Kantorovich, S.S. Scattering properties and internal structure of magnetic filament brushes. Soft Matter 2017, 13, 2590–2602. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Pyanzina, E.S.; Novak, E.V.; Cerdà, J.J.; Sintes, T.; Kantorovich, S.S. Supramolecular Magnetic Brushes: The Impact of Dipolar Interactions on the Equilibrium Structure. Macromolecules 2015, 48, 7658–7669. [Google Scholar] [CrossRef] [PubMed]
- Rozhkov, D.A.; Pyanzina, E.S.; Novak, E.V.; Cerdà, J.J.; Sintes, T.; Ronti, M.; Sánchez, P.A.; Kantorovich, S.S. Self-assembly of polymer-like structures of magnetic colloids: Langevin dynamics study of basic topologies. Mol. Simul. 2018, 44, 507–515. [Google Scholar] [CrossRef]
- Cerdà, J.J.; Bona-Casas, C.; Cerrato, A.; Novak, E.V.; Pyanzina, E.S.; Sánchez, P.A.; Kantorovich, S.; Sintes, T. Magnetic responsive brushes under flow in strongly confined slits: External field control of brush structure and flowing particle mixture separation. Soft Matter 2019, 15, 8982–8991. [Google Scholar] [CrossRef] [PubMed]
- Cerdà, J.J.; Bona-Casas, C.; Cerrato, A.; Sintes, T.; Massó, J. Colloidal magnetic brushes: Influence of the magnetic content and presence of short-range attractive forces in the micro-structure and field response. Soft Matter 2021, 17, 5780–5791. [Google Scholar] [CrossRef] [PubMed]
- Zaben, A.; Kitenbergs, G.; Cebers, A. Deformation of flexible ferromagnetic filaments under a rotating magnetic field. J. Magn. Magn. Mater. 2020, 499, 166233. [Google Scholar] [CrossRef]
- Belovs, M.; Cēbers, A. Ferromagnetic microswimmer. Phys. Rev. E 2009, 79, 051503. [Google Scholar] [CrossRef]
- Hoang, N.; Zhang, N.; Du, H. A dynamic absorber with a soft magnetorheological elastomer for powertrain vibration suppression. Smart Mater. Struct. 2009, 18, 074009. [Google Scholar] [CrossRef]
- Goubault, C.; Jop, P.; Fermigier, M.; Baudry, J.; Bertrand, E.; Bibette, J. Flexible Magnetic Filaments as Micromechanical Sensors. Phys. Rev. Lett. 2003, 91, 260802. [Google Scholar] [CrossRef]
- Liu, J.; Mao, Y.; Ge, J. The magnetic assembly of polymer colloids in a ferrofluid and its display applications. Nanoscale 2012, 4, 1598–1605. [Google Scholar] [CrossRef]
- Huang, Y.W.; Hu, S.T.; Yang, S.Y.; Horng, H.E.; Hung, J.C.; Hong, C.Y.; Yang, H.C.; Chao, C.H.; Lin, C.F. Tunable diffraction of magnetic fluid films and its potential application in coarse wavelength-division multiplexing. Opt. Lett. 2004, 29, 1867–1869. [Google Scholar] [CrossRef]
- Pirmoradi, F.N.; Jackson, J.K.; Burt, H.M.; Chiao, M. A magnetically controlled MEMS device for drug delivery: Design, fabrication, and testing. Lab. Chip 2011, 11, 3072–3080. [Google Scholar] [CrossRef]
- Corr, S.A.; Byrne, S.J.; Tekoriute, R.; Meledandri, C.J.; Brougham, D.F.; Lynch, M.; Kerskens, C.; O’Dwyer, L.; Gun’ko, Y.K. Linear Assemblies of Magnetic Nanoparticles as MRI Contrast Agents. J. Am. Chem. Soc. 2008, 130, 4214–4215. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yu, Y.; Sun, Y.; Chen, Q. Magnetic Nanochains: A review. Nano 2011, 6, 1–17. [Google Scholar] [CrossRef]
- Warner, H.R., Jr. Kinetic Theory and Rheology of Dilute Suspensions of Finitely Extendible Dumbbells. Ind. Eng. Chem. Fundam. 1972, 11, 379–387. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Cerdà, J.J.; Ballenegger, V.; Lenz, O.; Holm, C. P3M algorithm for dipolar interactions. J. Chem. Phys. 2008, 129, 234104. [Google Scholar] [CrossRef] [PubMed]
- Arnold, A.; de Joannis, J.; Holm, C.J. Electrostatics in periodic slab geometries I. J. Chem. 2002, 117, 2496. [Google Scholar] [CrossRef]
- Wang, Z.; Holm, C. Estimate of the cutoff errors in the Ewald summation for dipolar systems. J. Chem. 2001, 115, 6351. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 1st ed.; Oxford Science Publications, Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Limbach, H.J.; Arnold, A.; Mann, B.A.; Holm, C. ESPResSo—An Extensible Simulation Package for Research on Soft Matter Systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Malassagne-Bulgarelli, N. Emulsion Microstructure and Dynamics. Ph.D. Thesis, Te Herenga Waka-Victoria University of Wellington, Wellington, New Zealand, 2010. [Google Scholar] [CrossRef]
- Huke, B.; Lücke, M. Magnetic properties of colloidal suspensions of interacting magnetic particles. Rep. Prog. Phys. 2004, 67, 1731. [Google Scholar] [CrossRef]
- Katubi, K.M.; Shah, S.S.A.; Naeem, S.; Najam, T.; Alrowaili, Z.; Al-Buriahi, M. A systematic approach to generate polymer library: A search for polymers with high dipole moment. Chem. Phys. Lett. 2024, 850, 141450. [Google Scholar] [CrossRef]
- Soundaram jeevarathinam, A.; Murthy, K.; Somanathan, N.; Mandal, A. Computational studies of functional polythiophenes: Overlap with device characteristics. J. Polym. Mater. 2011, 28, 395–419. [Google Scholar]
- Aaron, M.W.; Grant, E.H. Dielectric relaxation of glycine in water. Trans. Faraday Soc. 1963, 59, 85–89. [Google Scholar] [CrossRef]
- Sato, T.; Buchner, R.; Fernandez, Š.; Chiba, A.; Kunz, W. Dielectric relaxation spectroscopy of aqueous amino acid solutions: Dynamics and interactions in aqueous glycine. J. Mol. Liq. 2005, 117, 93–98. [Google Scholar] [CrossRef]
- Ren, F.; Liu, F. Impacts of polarizable continuum models on the SCF convergence and DFT delocalization error of large molecules. J. Chem. Phys. 2022, 157, 184106. [Google Scholar] [CrossRef]
- Mei, W.; Colby, R.H.; Hickey, R.J. Enhancing the dielectric constant of zwitterionic liquids via dipole moment and anion chemistry. J. Chem. Phys. 2024, 161, 014506. [Google Scholar] [CrossRef]
- Margossian, K.O.; Brown, M.U.; Emrick, T.; Muthukumar, M. Coacervation in polyzwitterion-polyelectrolyte systems and their potential applications for gastrointestinal drug delivery platforms. Nat. Commun. 2022, 13, 2250. [Google Scholar] [CrossRef] [PubMed]
- Suwa, M.; Tsukahara, S.; Watarai, H. Applications of magnetic and electromagnetic forces in micro-analytical systems. Lab. Chip 2023, 23, 1097–1127. [Google Scholar] [CrossRef] [PubMed]
- Skjeltorp, A.T. One- and Two-Dimensional Crystallization of Magnetic Holes. Phys. Rev. Lett. 1983, 51, 2306–2309. [Google Scholar] [CrossRef]
- Ramos, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R.; de Vicente, J. Steady shear magnetorheology of inverse ferrofluids. J. Rheol. 2011, 55, 127–152. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuster-Aparisi, A.; Cerrato, A.; Batle, J.; Cerdà, J.J. Dipolar Brush Polymers: A Numerical Study of the Force Exerted onto a Penetrating Colloidal Particle Under an External Field. Polymers 2025, 17, 366. https://doi.org/10.3390/polym17030366
Fuster-Aparisi A, Cerrato A, Batle J, Cerdà JJ. Dipolar Brush Polymers: A Numerical Study of the Force Exerted onto a Penetrating Colloidal Particle Under an External Field. Polymers. 2025; 17(3):366. https://doi.org/10.3390/polym17030366
Chicago/Turabian StyleFuster-Aparisi, A., Antonio Cerrato, Josep Batle, and Joan Josep Cerdà. 2025. "Dipolar Brush Polymers: A Numerical Study of the Force Exerted onto a Penetrating Colloidal Particle Under an External Field" Polymers 17, no. 3: 366. https://doi.org/10.3390/polym17030366
APA StyleFuster-Aparisi, A., Cerrato, A., Batle, J., & Cerdà, J. J. (2025). Dipolar Brush Polymers: A Numerical Study of the Force Exerted onto a Penetrating Colloidal Particle Under an External Field. Polymers, 17(3), 366. https://doi.org/10.3390/polym17030366






