Analysis of the Hertz Contact Model for Evaluating Mechanical Properties of Polymers Using the Finite Element Method
Abstract
1. Introduction
2. Materials and Methods
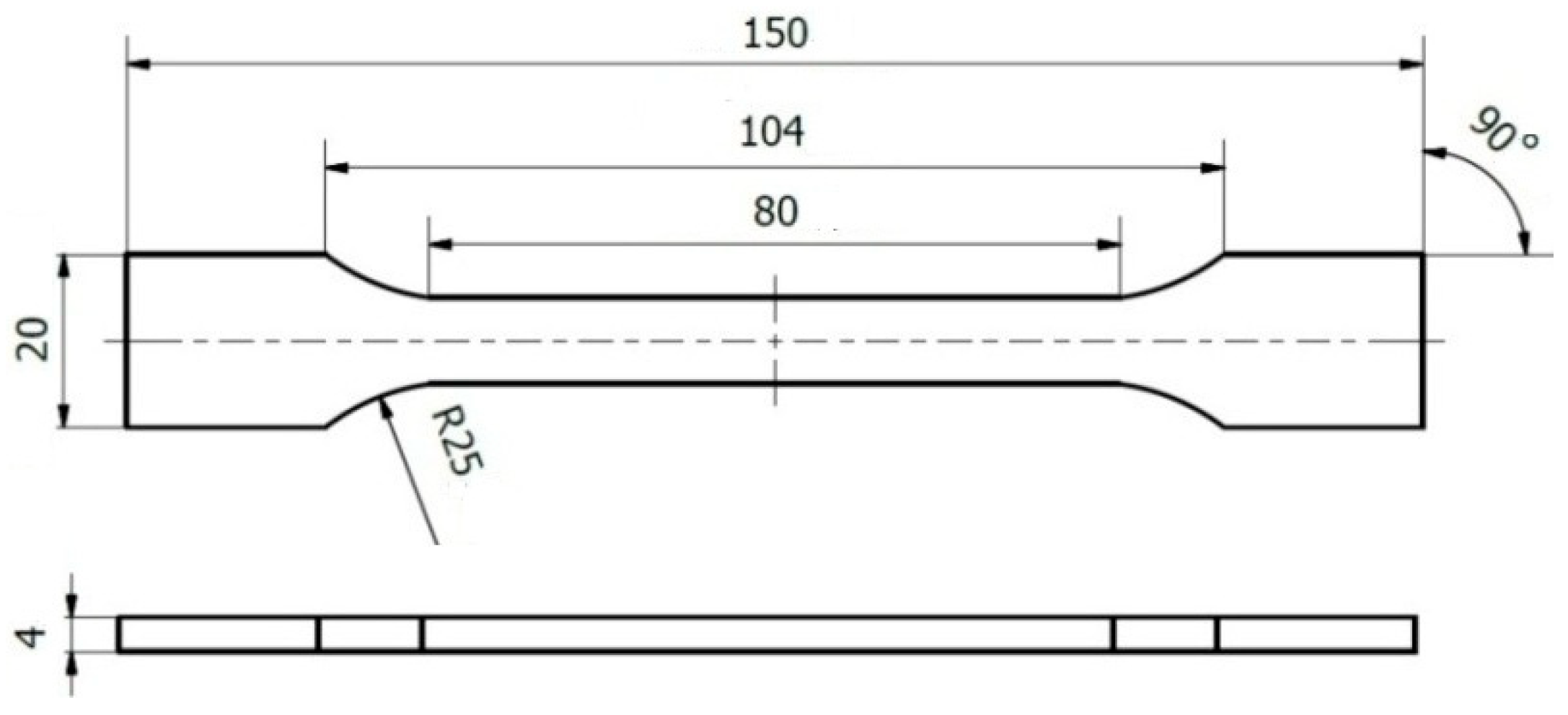
2.1. Materials and Equipment
2.2. Determination of Young’s Modulus and Contact Radius
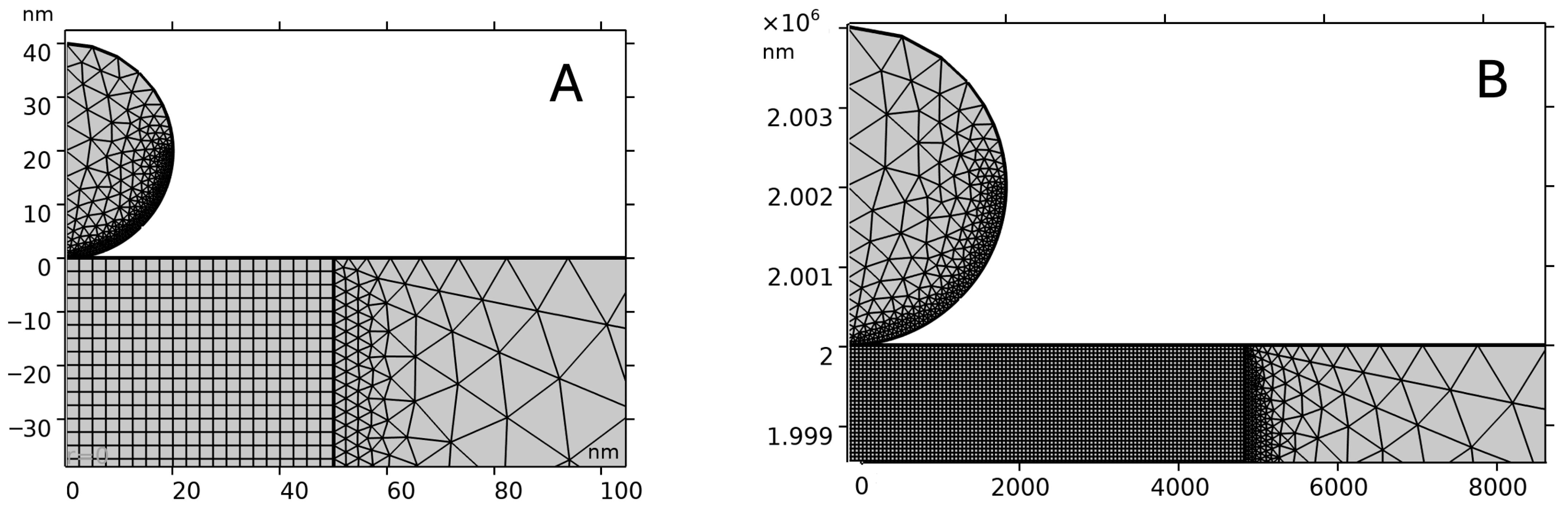
2.3. Modeling and Simulation
3. Results
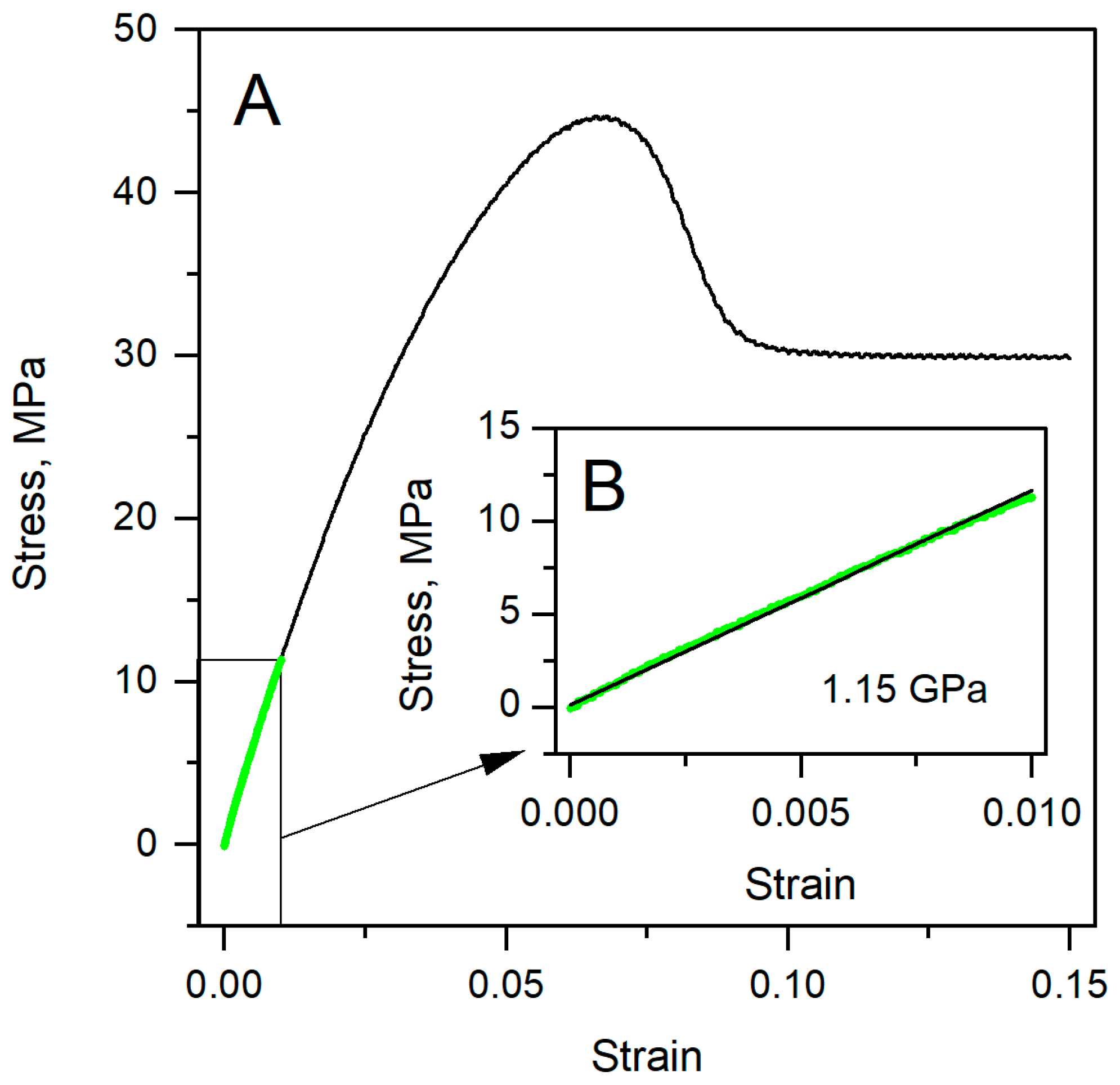
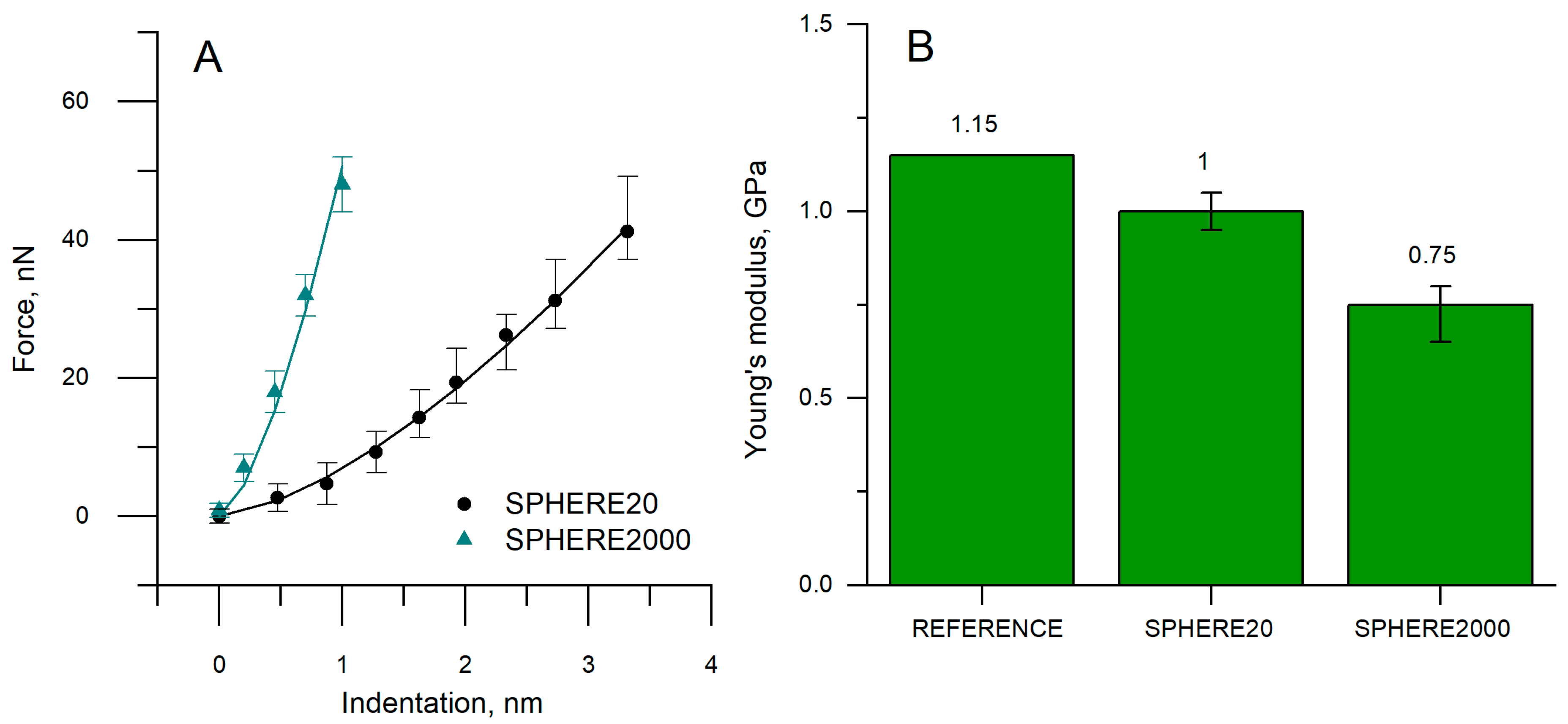
3.1. Specimens’ Young’s Modulus Determination by the Standard Method
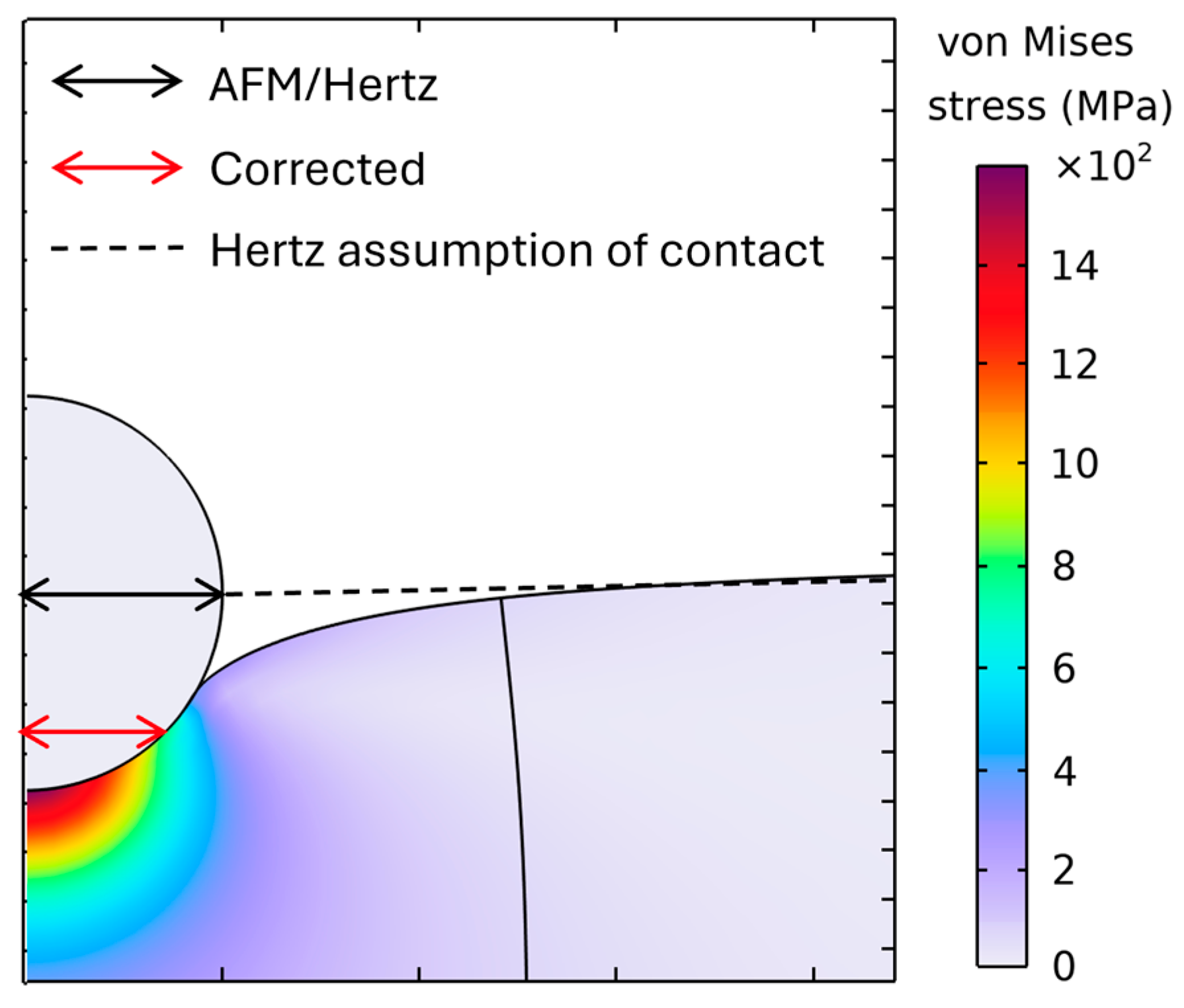
3.2. Validation of the Finite-Element Model
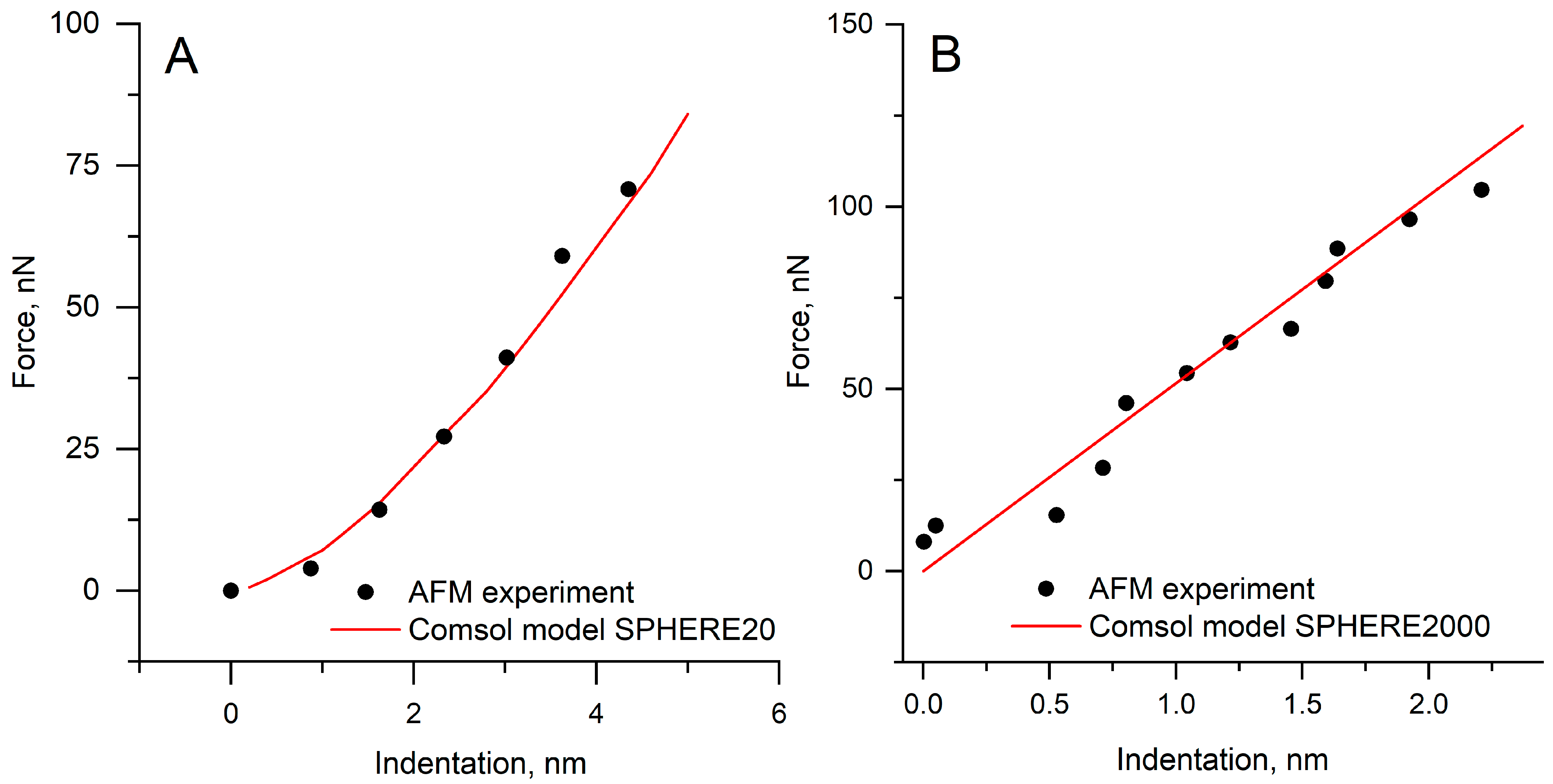
3.3. Specimens Determination of Young’s Modulus by the Hertz Model
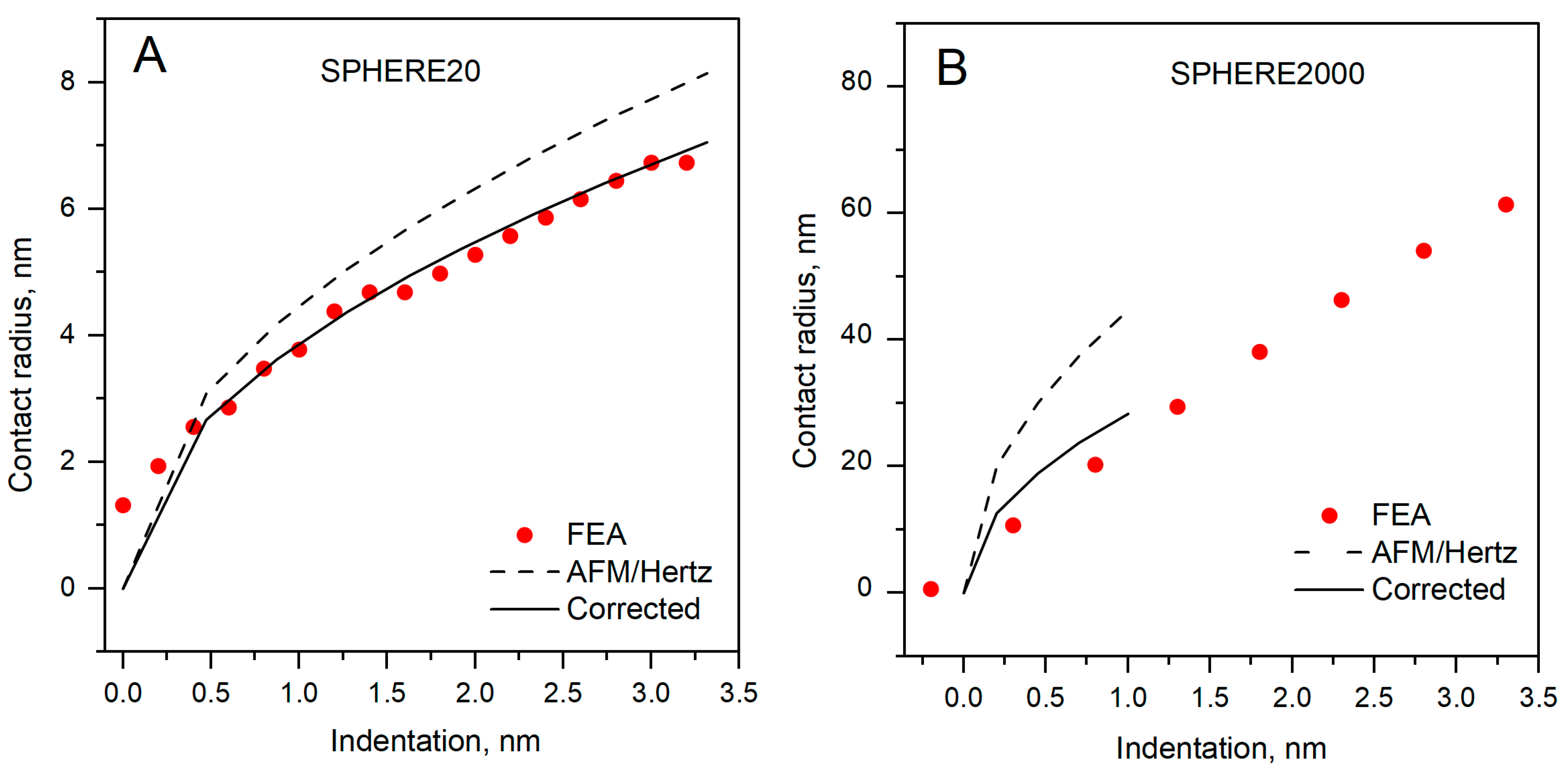
3.4. Contact Radius Determined by Hertz Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Norman, M.D.A.; Ferreira, S.A.; Jowett, G.M.; Bozec, L.; Gentleman, E. Measuring the Elastic Modulus of Soft Culture Surfaces and Three-Dimensional Hydrogels Using Atomic Force Microscopy. Nat. Protoc. 2021, 16, 2418–2449. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.; Lee, M.; An, S.; Cho, S.J. Quantitative Visualization of the Nanomechanical Young’s Modulus of Soft Materials by Atomic Force Microscopy. Nanomaterials 2021, 11, 1593. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Shi, X.; Yao, G.; Pharr, G.M.; Wu, J.Y. Surface Characterization of an Ultra-Soft Contact Lens Material Using an Atomic Force Microscopy Nanoindentation Method. Sci. Rep. 2022, 12, 20013. [Google Scholar] [CrossRef] [PubMed]
- JPK Instruments AG Determining the Elastic Modulus of Biological Samples Using the Atomic Force Microscope. Available online: https://www.bruker.com/en/products-and-solutions/microscopes/bioafm/resource-library/determining-the-elastic-modulus-of-biological-samples-using-the-atomic-force-microscope.html (accessed on 2 November 2025).
- Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. A New Elementary Method for Determining the Tip Radius and Young’s Modulus in AFM Spherical Indentations. Micromachines 2023, 14, 1716. [Google Scholar] [CrossRef] [PubMed]
- Kontomaris, S.V.; Stylianou, A.; Malamou, A. Is It Possible to Directly Determine the Radius of a Spherical Indenter Using Force Indentation Data on Soft Samples? Scanning 2022, 2022, 6463063. [Google Scholar] [CrossRef]
- Fabbro, L.D.; Holuigue, H.; Chighizola, M.; Podestà, A. Validation of Contact Mechanics Models for Atomic Force Microscopy via Finite Elements Analysis and Nanoindentation Experiments. arXiv 2025, arXiv:2406.17157. [Google Scholar]
- Cortelli, G.; Patruno, L.; Cramer, T.; Murgia, M.; Fraboni, B.; De Miranda, S. Atomic Force Microscopy Nanomechanics of Hard Nanometer-Thick Films on Soft Substrates: Insights into Stretchable Conductors. ACS Appl. Nano Mater. 2021, 4, 8376–8382. [Google Scholar] [CrossRef]
- Holuigue, H.; Lorenc, E.; Chighizola, M.; Schulte, C.; Varinelli, L.; Deraco, M.; Guaglio, M.; Gariboldi, M.; Podestà, A. Force Sensing on Cells and Tissues by Atomic Force Microscopy. Sensors 2022, 22, 2197. [Google Scholar] [CrossRef]
- Plichta, T.; Zahradnicek, R.; Cech, V. Surface Topography Affects the Nanoindentation Data. Thin Solid Films 2022, 745, 139105. [Google Scholar] [CrossRef]
- Saringer, C.; Tkadletz, M.; Kratzer, M.; Cordill, M.J. Direct Determination of the Area Function for Nanoindentation Experiments. J. Mater. Res. 2021, 36, 2154–2165. [Google Scholar] [CrossRef]
- Huang, F.Y.; Liu, Y.W.; Kuo, J.C. Uncertainties in the Representative Indentation Stress and Strain Using Spherical Nanoindentation. Appl. Nanosci. 2021, 11, 895–909. [Google Scholar] [CrossRef]
- Kulkarni, S.G.; Pérez-Domínguez, S.; Radmacher, M. Influence of Cantilever Tip Geometry and Contact Model on AFM Elasticity Measurement of Cells. J. Mol. Recognit. 2023, 36, e3018. [Google Scholar] [CrossRef]
- Owen, D.S. Toward a Better Modulus at Shallow Indentations—Enhanced Tip and Sample Characterization for Quantitative Atomic Force Microscopy. Microsc. Res. Tech. 2023, 86, 84–96. [Google Scholar] [CrossRef]
- Albayda, A.; Bartier, O.; Hernot, X.; Mauvoisin, G. A Novel Gradient Method for Extracting Elastoplastic Properties of Metals from Spherical Indentation Force-Contact Radius Data. Acta Mech. 2024, 236, 915–935. [Google Scholar] [CrossRef]
- Managuli, V.; Bothra, Y.S.; Kumar, S.S.; Gaur, P.; Chandracharya, P.L. Overview of Mechanical Characterization of Bone Using Nanoindentation Technique and Its Applications. Eng. Sci. 2023, 22, 820. [Google Scholar] [CrossRef]
- Savin, N.; Erofeev, A.; Gorelkin, P. Analytical Models for Measuring the Mechanical Properties of Yeast. Cells 2023, 12, 1946. [Google Scholar] [CrossRef]
- Mishra, R.; Minc, N.; Peter, M. Cells under Pressure: How Yeast Cells Respond to Mechanical Forces. Trends Microbiol. 2022, 30, 495–510. [Google Scholar] [CrossRef] [PubMed]
- Waeytens, J.; Doneux, T.; Napolitano, S. Evaluating Mechanical Properties of Polymers at the Nanoscale Level via Atomic Force Microscopy-Infrared Spectroscopy. ACS Appl. Polym. Mater. 2019, 1, 3–7. [Google Scholar] [CrossRef]
- Nguyen-Tri, P.; Ghassemi, P.; Carriere, P.; Nanda, S.; Assadi, A.A.; Nguyen, D.D. Recent Applications of Advanced Atomic Force Microscopy in Polymer Science: A Review. Polymers 2020, 12, 1142. [Google Scholar] [CrossRef] [PubMed]
- ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. ISO: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/527-1 (accessed on 7 November 2025).
- Striška, L.; Vaičiulis, D.; Tolvaišienė, S.; Udris, D.; Kozulinas, N.; Astrauskas, R.; Ramanavičius, A.; Morkvėnaitė, I. 3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones. Coatings 2025, 15, 963. [Google Scholar] [CrossRef]
- Bruker Corporation Determine Cantilever Spring Constant by Thermal Tune. Available online: https://www.nanophys.kth.se/nanolab/afm/icon/bruker-help/Content/Probe%20and%20Sample%20Guide/ThermalTune/ThermalTune.htm? (accessed on 19 September 2025).
- Bruker. NanoScope Analysis 1.50 User Manual; Bruker: Singapore, 2020. [Google Scholar]
- Butt, H.-J.; Cappella, B.; Kappl, M. Force Measurements with the Atomic Force Microscope: Technique, Interpretation and Applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]
- Ahmine, A.N.; Bdiri, M.; Féréol, S.; Fodil, R. A Comprehensive Study of AFM Stiffness Measurements on Inclined Surfaces: Theoretical, Numerical, and Experimental Evaluation Using a Hertz Approach. Sci. Rep. 2024, 14, 25869. [Google Scholar] [CrossRef]
- Huang, S.; Tian, Y.; Wang, T. Experimental Investigation of Tip Wear of AFM Monocrystalline Silicon Probes. Sensors 2023, 23, 4084. [Google Scholar] [CrossRef]
- Lekka, M. Applicability of Atomic Force Microscopy to Determine Cancer-Related Changes in Cells. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210346. [Google Scholar] [CrossRef] [PubMed]
- Saito, I.; Sheridan, R.J.; Zauscher, S.; Brinson, L.C. Pushing AFM to the Boundaries: Interphase Mechanical Property Measurements near a Rigid Body. Macromolecules 2024, 58, 980–988. [Google Scholar] [CrossRef]
- Mendová, K.; Otáhal, M.; Drab, M.; Daniel, M. Size Matters: Rethinking Hertz Model Interpretation for Cell Mechanics Using AFM. Int. J. Mol. Sci. 2024, 25, 7186. [Google Scholar] [CrossRef] [PubMed]
- Makarova, N.; Sokolov, I. Cell Mechanics Can Be Robustly Derived from AFM Indentation Data Using the Brush Model: Error Analysis. Nanoscale 2022, 14, 4334–4347. [Google Scholar] [CrossRef]

 | SPHERE20: HDCT (biosphere B20-NCH). Geometry: Spherical. Dimensions: T = 4 µm, L = 125 µm, W = 30 µm, f0 = 330 kHz. Spring constant: 40 N/m. Measured: 52.5 N/m. Tip radius: 20 nm ± 5 nm. Nominal tip radius: 20 nm. Nanotools (Munchen, Germany). |
 | SPHERE2000: CP-FM-SiO-A-5. Geometry: Spherical. Dimensions: T = 3 ± 1 µm, L = 225 ± 10 µm, W = 28 ± 7.5 µm. Spring constant: 0.5–9.5 N/m. Measured: 4.18 N/m. f0 = 45–115 kHz. Tip radius: 2 µm ± 5%. Nominal tip radius: 2 µm. sQube (Sofia, Bulgaria). |
| Tip | Reference ISO [GPa] | AFM/Hertz [GPa] | Δ (GPa) | Δ (%) | With Corrected Contact Radius (GPa) | Δ with Corrected Contact Radius (GPa) |
|---|---|---|---|---|---|---|
| SPHERE20 | PVC (1.15) | 1.00 | −0.15 | −13.00 | 1.15 | 0.00 |
| SPHERE2000 | 0.75 | −0.40 | −35.00 | 1.15 | 0.00 |
| Tip | Corrected, nm | AFM/Hertz, nm | Δa | a Overestimation [%] |
|---|---|---|---|---|
| SPHERE20 | 7.05 | 8.14 | 1.09 | 15.46 |
| SPHERE2000 | 28.3 | 44.7 | 16.4 | 57.9 |
| Polymer Material | Probe Used | Analyzed Property | Model Used | Findings and Deviation | Ref. |
|---|---|---|---|---|---|
| Various polymers | AFM and FEA combined | Viscoelastic modulus | Hertz + time-dependent model | Time-dependent modulus variations up to 40%; relaxation significant | [20] |
| PMMA, PS | AFM spherical probe (100–500 nm) | Young’s modulus | Hertz + FEA correction | Demonstrated tip–radius dependence of modulus up to 20%; smaller probes yield higher apparent stiffness. | [19] |
| Epoxy and PET blends | PeakForce QNM | Modulus mapping | DMT and Hertz | Reported nanoscale modulus variation depending on probe curvature and phase heterogeneity. | [2] |
| Soft polyurethane | AFM colloidal (2 µm) | Viscoelastic modulus | Hertz + time-dependent correction | Introduced rate-dependent model; large probes underestimated modulus due to creep. | [5] |
| Poly(lactic acid) composites | AFM tip (50–200 nm) | Elastic modulus | Hertz model | Observed probe–size dependence: smaller tips gave up to 30% higher modulus values. | [7] |
| PMMA thin films | AFM spherical tip (500 nm) | Contact radius and modulus | Hertz + FEA validation | Finite element correction reduced Hertz overestimation of contact radius by ~25%. | [29] |
| Soft biological-like polymers | Spherical tip (2–10 µm) | Elastic modulus | Hertz vs. Hyperelastic model | Showed breakdown of Hertz assumptions under large deformations; hyperelastic model improved fit. | [30] |
| PVC | Spherical AFM tips, with radius 20 nm and 2000 nm | Hertz contact radius vs. real (corrected) | Hertz and FEA | Contact radius was overestimated by 15.5% and 57.9% | Present work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Striska, L.; Astrauskas, R.; Kozulinas, N.; Udris, D.; Tolvaisiene, S.; Macerauskas, E.; Morkvenaite, I.; Ramanavicius, A. Analysis of the Hertz Contact Model for Evaluating Mechanical Properties of Polymers Using the Finite Element Method. Polymers 2025, 17, 3018. https://doi.org/10.3390/polym17223018
Striska L, Astrauskas R, Kozulinas N, Udris D, Tolvaisiene S, Macerauskas E, Morkvenaite I, Ramanavicius A. Analysis of the Hertz Contact Model for Evaluating Mechanical Properties of Polymers Using the Finite Element Method. Polymers. 2025; 17(22):3018. https://doi.org/10.3390/polym17223018
Chicago/Turabian StyleStriska, Laisvidas, Rokas Astrauskas, Nikolajus Kozulinas, Dainius Udris, Sonata Tolvaisiene, Eugenijus Macerauskas, Inga Morkvenaite, and Arunas Ramanavicius. 2025. "Analysis of the Hertz Contact Model for Evaluating Mechanical Properties of Polymers Using the Finite Element Method" Polymers 17, no. 22: 3018. https://doi.org/10.3390/polym17223018
APA StyleStriska, L., Astrauskas, R., Kozulinas, N., Udris, D., Tolvaisiene, S., Macerauskas, E., Morkvenaite, I., & Ramanavicius, A. (2025). Analysis of the Hertz Contact Model for Evaluating Mechanical Properties of Polymers Using the Finite Element Method. Polymers, 17(22), 3018. https://doi.org/10.3390/polym17223018









