Rheology for Wood Plastic Composite Extrusion—Part 1: Laboratory vs. On-Line Rheometry
Abstract
1. Introduction
2. WPCs Characteristics
3. Rheological Modeling
3.1. Laboratory Rheometry
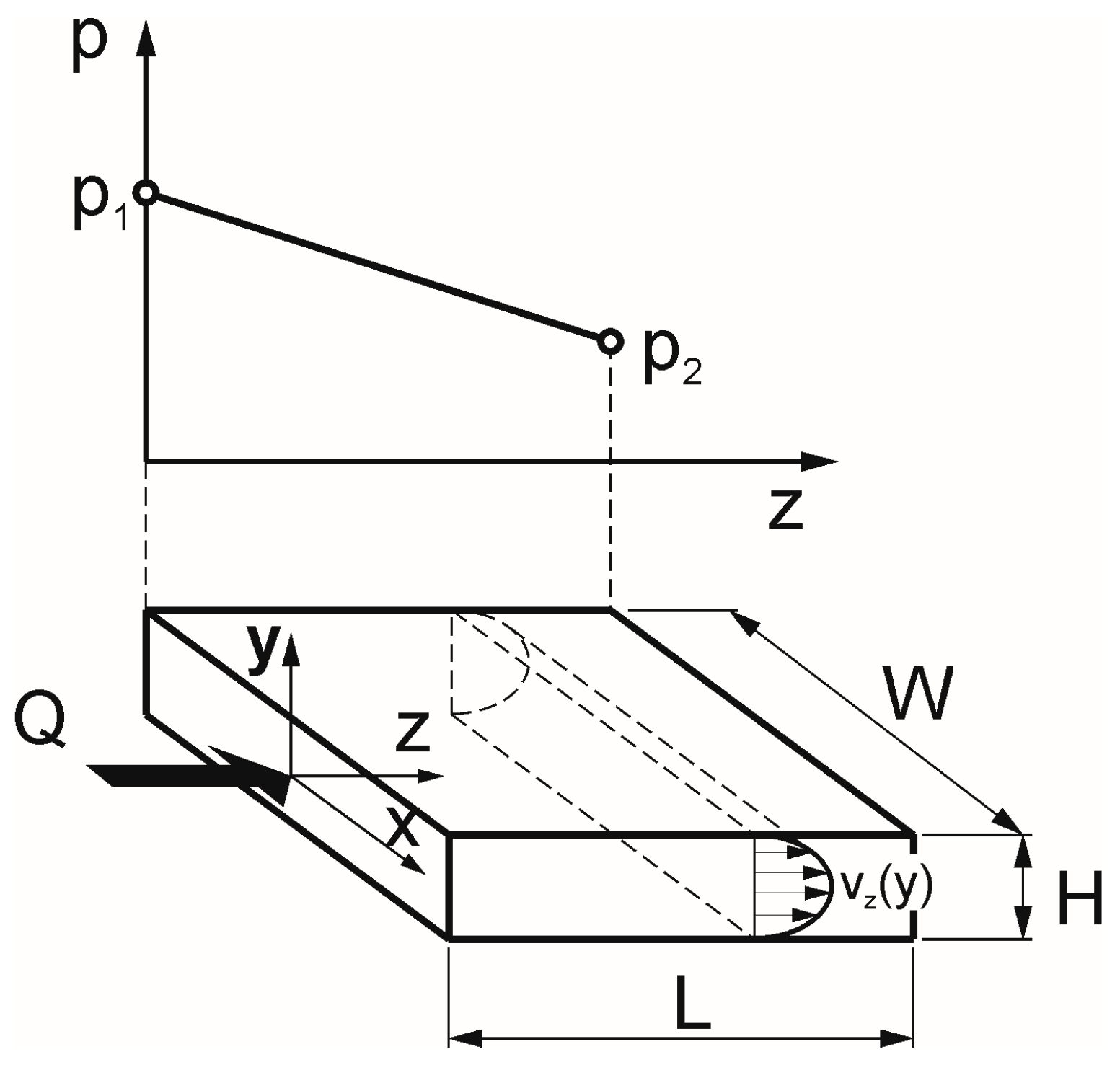
3.1.1. High-Pressure Capillary Rheometry (HPCR)
- -
- Rabinowitsch–Mooney Correction
- -
- Bagley Correction
- -
- Mooney Correction
- -
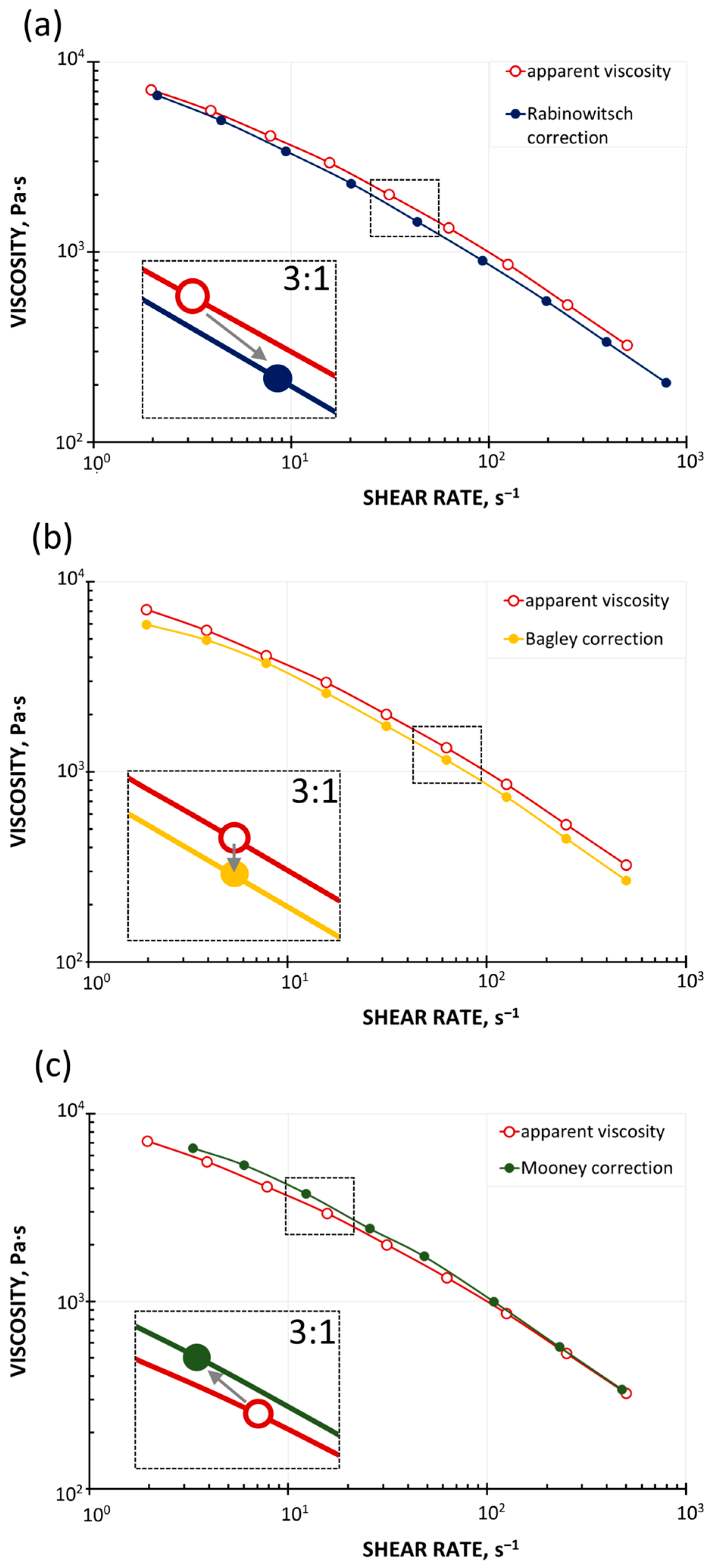
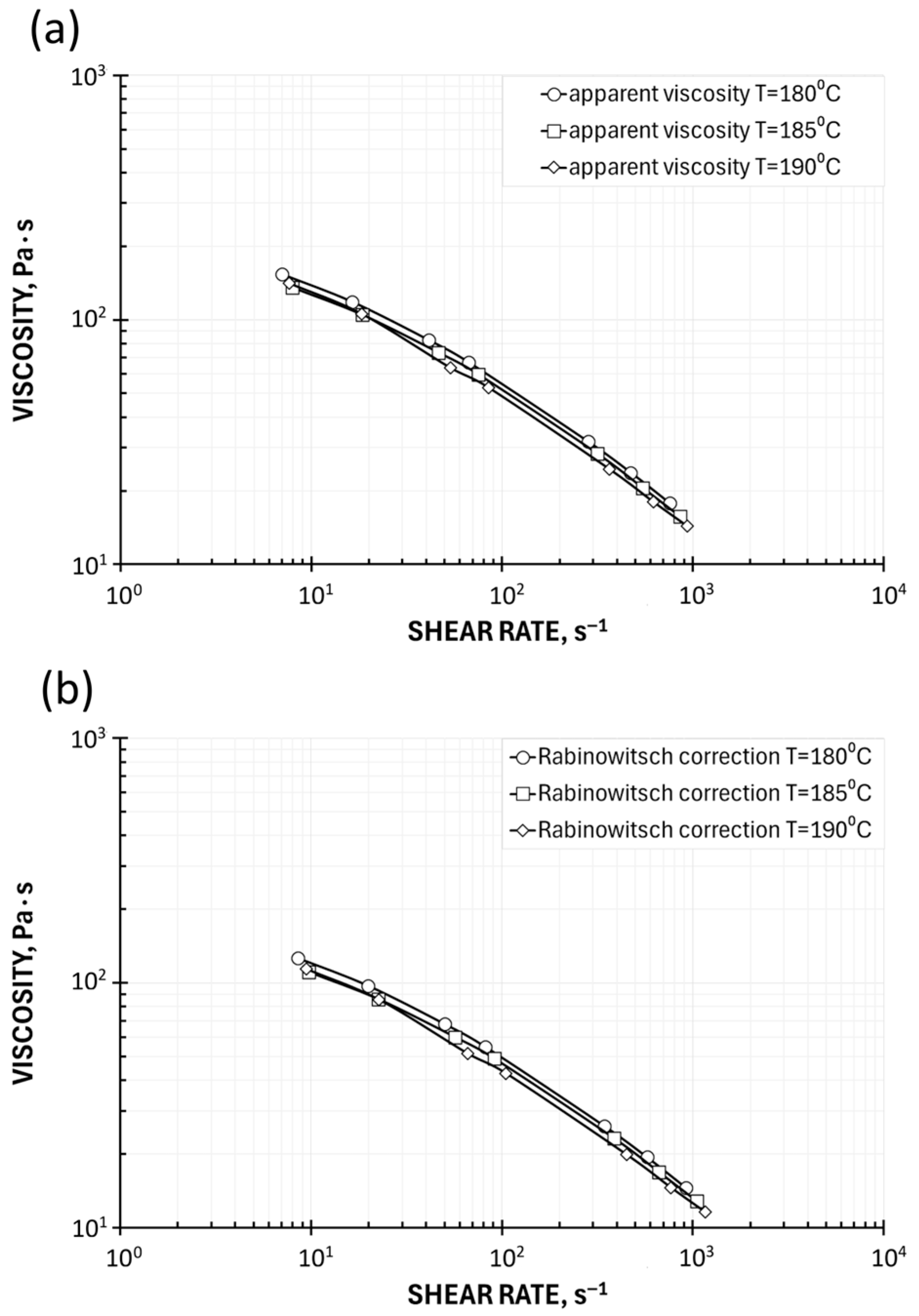
- Analysis of Rheological Corrections
3.1.2. MFI (Melt Flow Index) Rheometry
- One-Point Method of Determining the Viscosity Curve—Vinogradov–Malkin Model
- Two-Point Method of Determining the Viscosity Curve—Ostwald–de Waele Model
- Three-Point Method of Determining the Viscosity Curve—Klein Model
3.2. On-Line Rheometry
4. Material
5. Experimental
5.1. Laboratory Measurements
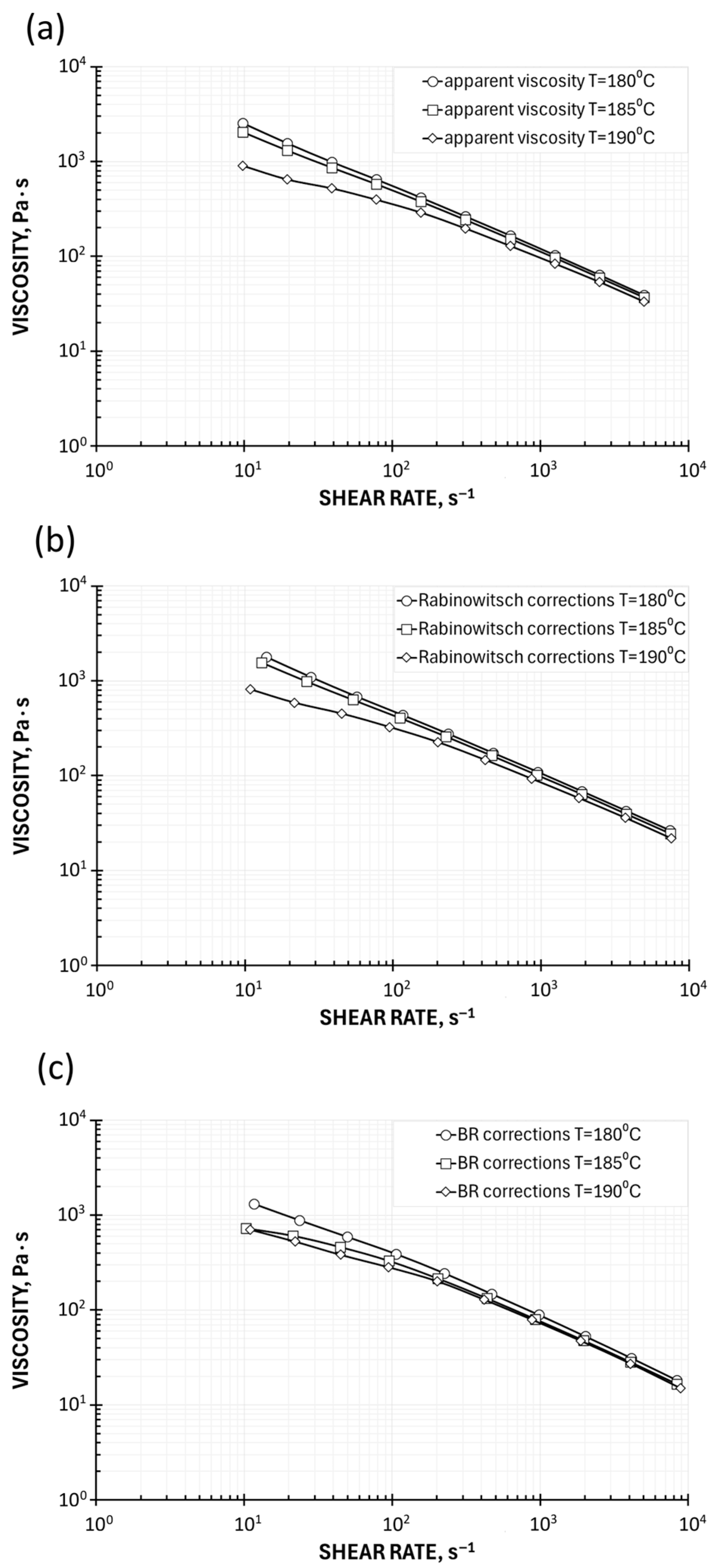
5.1.1. Determination of Viscosity Based on High-Pressure Capillary Rheometry (HPCR)
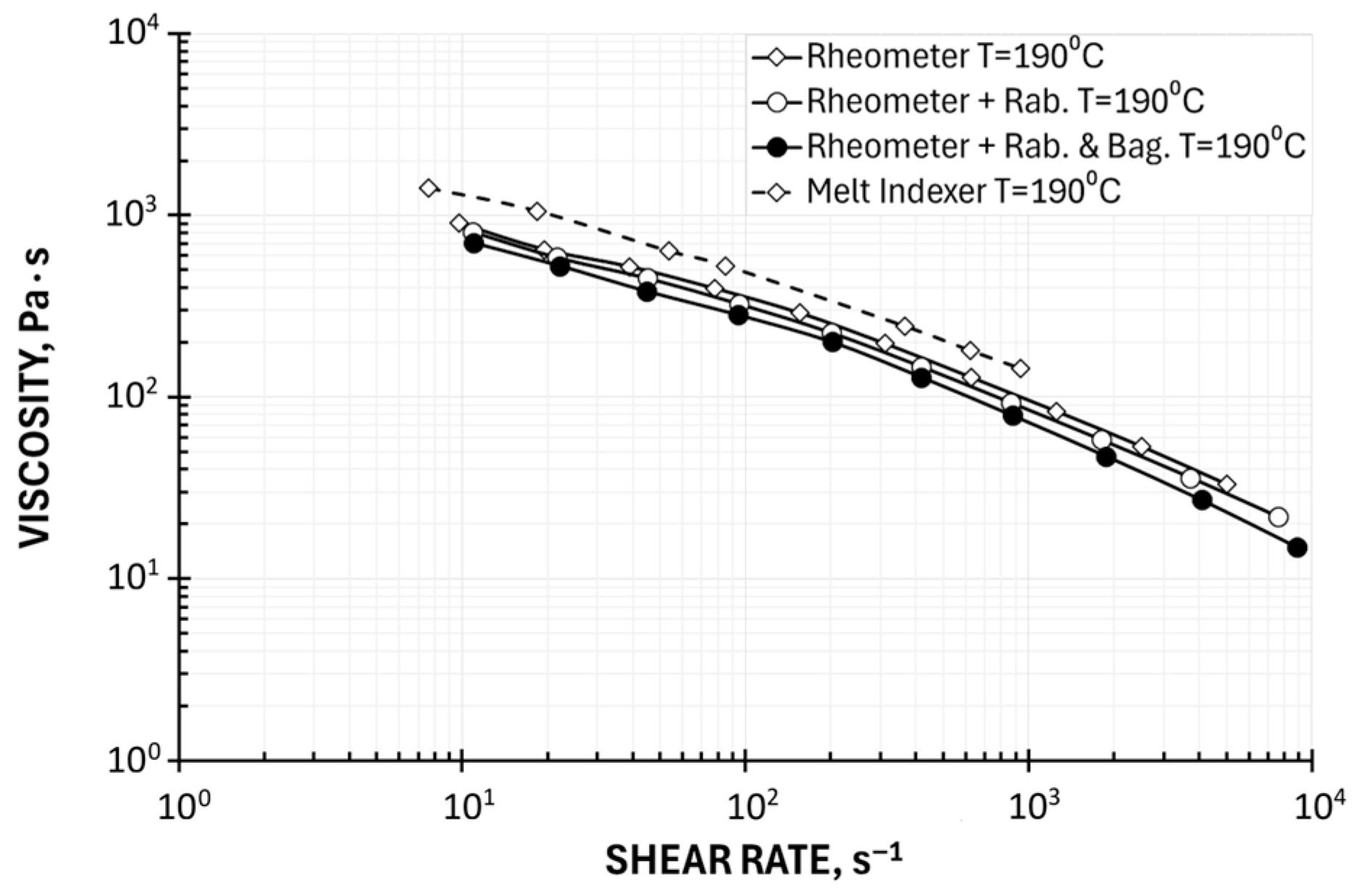
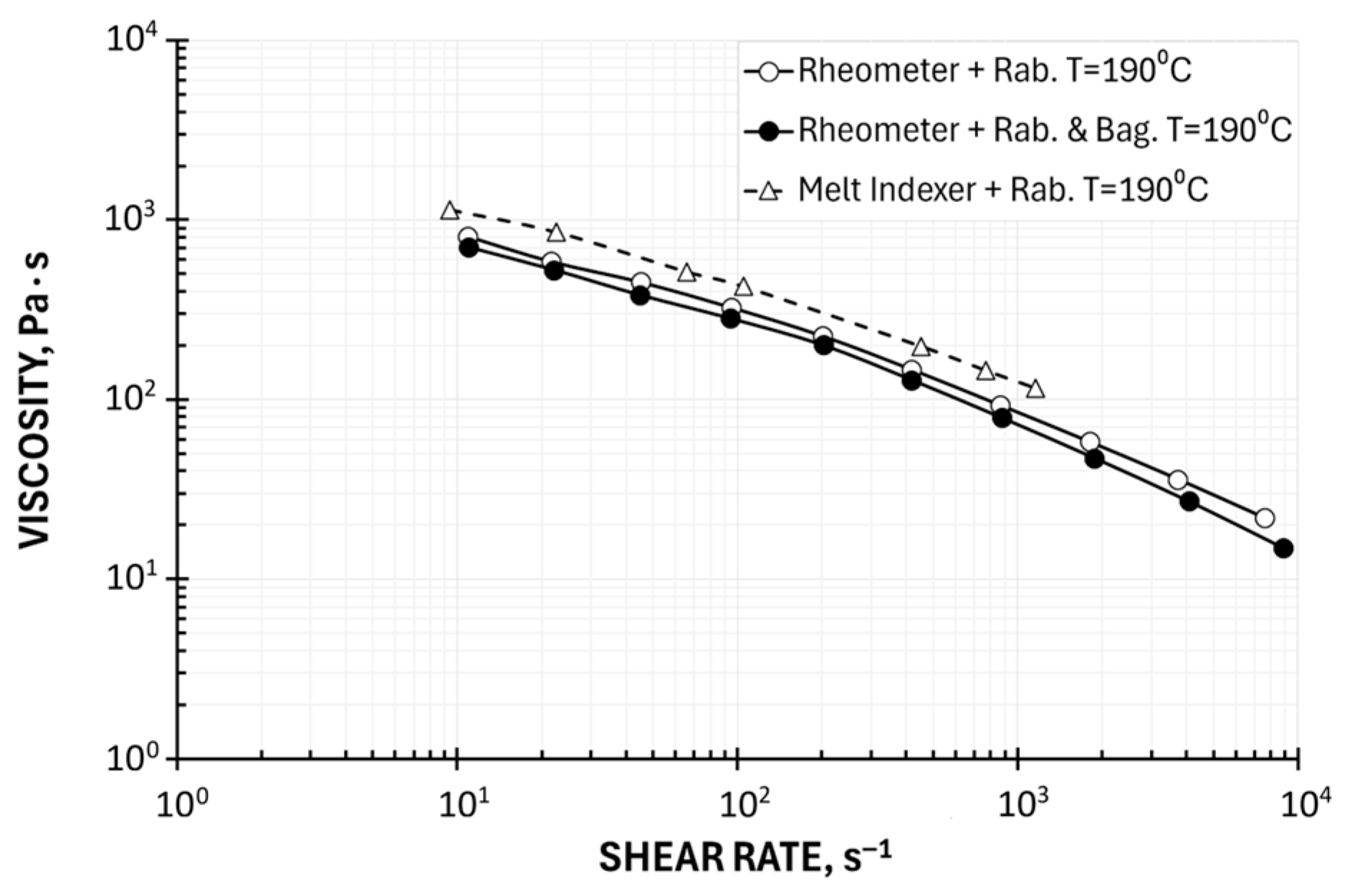
5.1.2. Determination of Viscosity Based on Melt Flow Index (MFI)
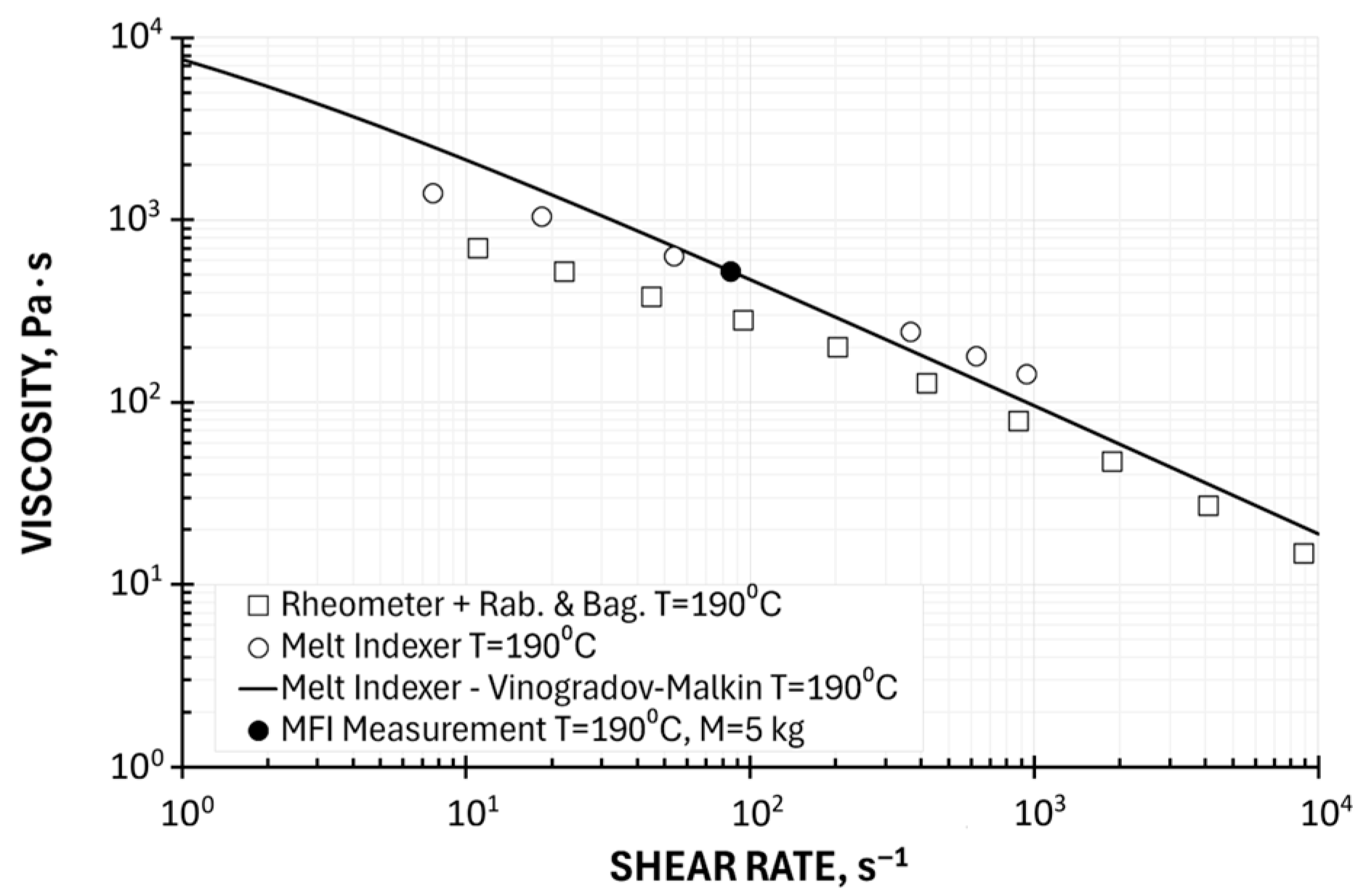
- One Point Method of Determining the Viscosity Curve—Vinogradov–Malkin Model
- Two Point Method of Determining the Viscosity Curve—Ostwald–de Waele Model
- Three Point Method of Determining the Viscosity Curve—the reduced Klein Model
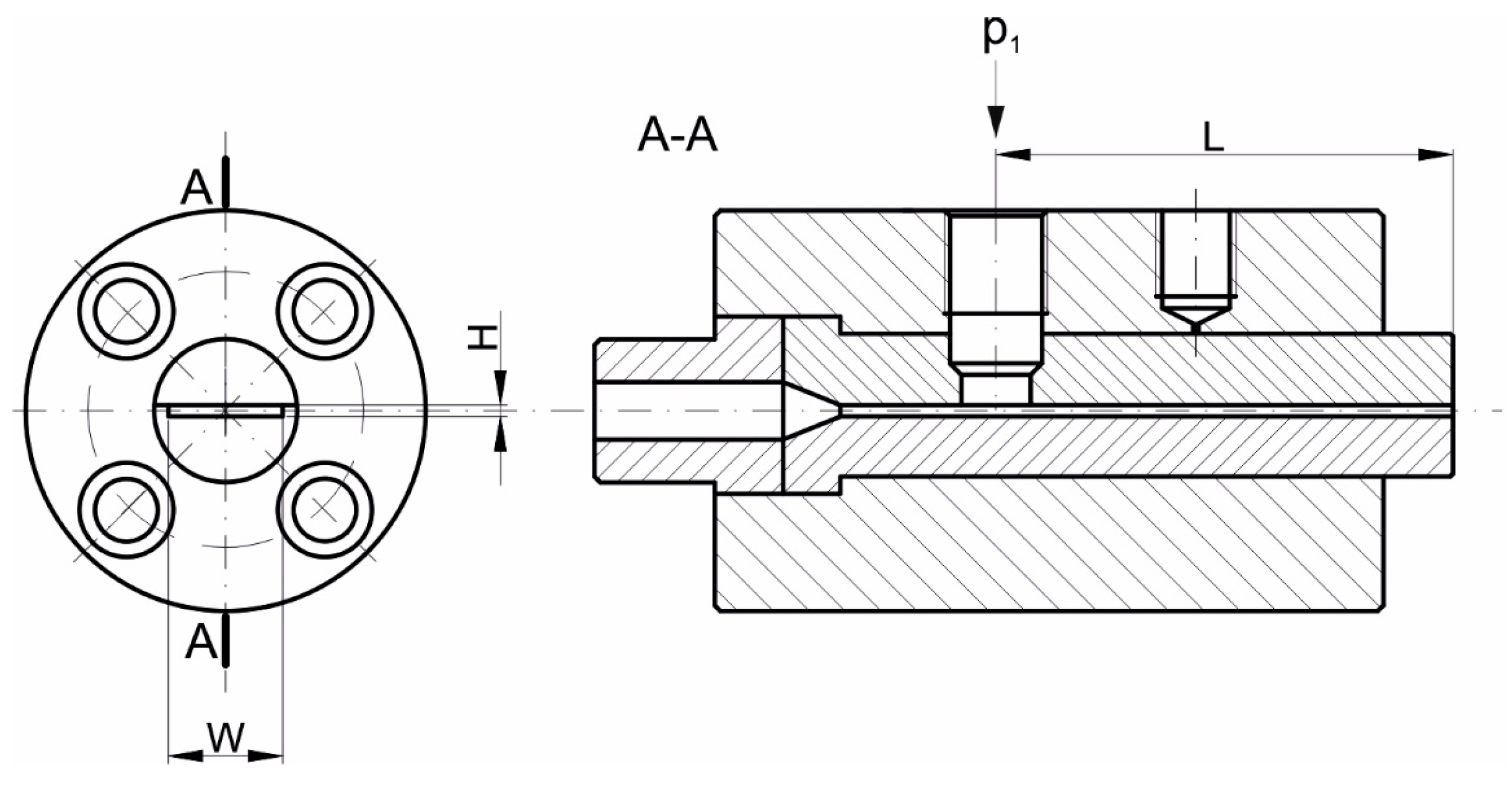
5.2. On-Line Measurements
6. Conclusions and Future Trends
- -
- A complete rheological analysis of the flow of wood plastic composites requires consideration of possible slippage on the flow channel walls and the yield stress. Slippage and yield stress can lead to plug flow, requiring a fundamental change in the calculation procedures used.
- -
- These issues must also be taken into account when modeling polymer processing, e.g., extrusion or injection molding. Two aspects of slip effects should be considered: rheological and process flow modeling. The effect of slipping can be removed from viscosity measurements by using the Mooney correction, which results in an increase in viscosity since the shear rate decreases as the shear stress remains unchanged. This may have substantial effects on process modeling. On the other hand, considering the slip effects in process modeling results in an increase in the flow rate and pressure decrease. These issues were discussed in [74,75], and, e.g., in [76,77,78,79,80].
- -
- The rheological characteristics of wood plastic composites are generally not available in the material databases. There is no data at all that take into account slip and yield stress, and these data should be obtained in-house, preferably in on-line production conditions.
- -
- The (WPC) material characteristics are highly dependent on the material structure and the size of the fiber or flour. The smaller the size of the filler, the easier and more reliable the measurement. Proper preparation of the material is very important. The results are generally difficult to reproduce. When the material is more homogeneous, the results are more reproducible.
- -
- There is generally no valid thermal data for wood plastic composites, e.g., melting or softening point, heat of fusion, etc. The temperature flow range is narrow, and it is difficult to determine the melting point. Therefore, the concept of no-flow temperature can be used to determine the onset of the flow.
- -
- Due to the lack of rheological data of wood plastic composites in available databases, we propose in-house research methods based on the two-point viscosity curve determination in plastometric (MFI) tests and tests under production conditions, that is, on-line. The two-point method, based on the power law, is quick and easy to implement and allows for solving many polymer processing issues analytically. Of course, the power law model does not describe the low-shear Newtonian plateau, but this is beyond the scope of polymer processing. Production tests, despite limited accuracy, have the significant advantage of being conducted under the actual flow conditions of the tested material, rather than under laboratory conditions, as is the case with rheometric and plastometric tests, which do not take into account the processing history of the tested material.
- -
- A systematic error in plastometric measurements (MFI) was observed, resulting from the use of a short capillary and failure to apply the Bagley correction in the calculations. It seems reasonable to seek a calculation method that takes this systematic error into account.
- -
- A novel concept for on-line testing is proposed, employing a dual-channel measuring die (with different channel lengths) and independent pressure measurement in these channels. This design will eliminate the effect of inlet losses in the measurements and will allow for introducing the Bagley correction into the calculations.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich, Germany, 2014; ISBN 978-1-56-990-516-6. [Google Scholar]
- Vlachopoulos, J. Polymer Rheology and Extrusion; Polydynamics Inc.: Dundas, ON, Canada, 2011. [Google Scholar]
- Vlachopoulos, J.; Polychronopoulos, N.D. Understanding Rheology and Technology of Polymer Extrusion; Polydynamics Inc.: Dundas, ON, Canada, 2019; ISBN 978-0-9952407-2-8. [Google Scholar]
- Wilczyński, K. Rheology in Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2021; ISBN 978-1-56990-660-6. [Google Scholar]
- Shaw, M.T. Introduction to Polymer Rheology; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-38844-0. [Google Scholar]
- Osswald, T.; Rudolph, N. Polymer Rheology. Fundamentals and Applications; Carl Hanser Verlag: Munich, Germany, 2015; ISBN 978-1-56990-517-3. [Google Scholar]
- CAMPUS–Material Information System for Plastics Industry. Available online: https://www.campusplastics.com (accessed on 7 September 2025).
- MOLDFLOW–Plastic Injection and Compression Mold Simulation. Available online: https://www.autodesk.com/products/moldflow (accessed on 7 September 2025).
- Moldex3D–Plastic Injection Molding Simulation Software. Available online: https://www.moldex3d.com (accessed on 7 September 2025).
- CADMOULD–Plastic Injection Molding Simulation. Available online: https://www.simcon.com (accessed on 7 September 2025).
- Ansys Polyflow–Polymer Processing Simulation Software. Available online: https://www.ansys.com (accessed on 7 September 2025).
- Malkin, A.Y.; Isayev, A.I. Rheology. Concepts, Methods, and Applications; ChemTec Publishing: Toronto, Canada, 2012; ISBN 978-1-895198-49-2. [Google Scholar]
- Mohanty, A.K.; Misra, M.; Drzal, L.T. Natural Fibers, Biopolymers, and Biocomposites; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 978-084-931-741-5. [Google Scholar]
- Klyosov, A.A. Wood-Plastic Composites; John Wiley & Sons: New Jersey, NJ, USA, 2007; ISBN 978-047-014-891-4. [Google Scholar]
- Oksman Niska, K.; Sain, M. Wood-Polymer Composites; Woodhead Publishing Ltd.: Cambridge, UK, 2008; ISBN 978-184-569-272-8. [Google Scholar]
- Ariffin, A.; Ahmad, M.S.B. Review: Single Screw Extruder in Particulate Filler Composite. Polym.-Plast. Technol. Eng. 2011, 50, 395–403. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Multipurpose Computer Model for Screw Processing of Plastics. Polym.-Plast. Techn. Eng. 2012, 51, 626–633. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Fundamentals of Global Modeling for Polymer Extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef]
- Hyvärinen, M.; Jabeen, R.; Kärki, T. The Modelling of Extrusion Processes for Polymers—A Review. Polymers 2020, 12, 1306. [Google Scholar] [CrossRef]
- Wilczyński, K.; Tyszkiewicz, A.; Szymaniak, Z. Modeling for Morphology Development during Single-Screw Extrusion of LDPE/PS Blend. J. Mater. Process. Technol. 2001, 109, 320–323. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental Study of Melting of LDPE/PS Polyblend in an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 2012, 52, 449–458. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A. Modeling of Starve-Fed Single-Screw Extrusion of Thermoplastic Polyblends/Modelowanie procesu wytłaczania jednoślimakowego z dozowanym zasilaniem mieszanin tworzyw termoplastycznych. Polimery 2015, 60, 199–208. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A. Modeling for Starve Fed Single-Screw Extrusion of Polyblends Using Mixing Screws/Modelowanie procesu wytłaczania jednoślimakowego mieszanin polimerów z zastosowaniem ślimaków mieszających i dozowanego zasilania wytłaczarki. Polimery 2016, 61, 279–285. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A. Modeling of Starve Fed Single-Screw Extrusion of Polyblends Using Non-Conventional Screws/Modelowanie procesu wytłaczania jednoślimakowego mieszanin polimerów z zastosowaniem ślimaków niekonwencjonalnych i dozowanego zasilania wytłaczarki. Polimery 2016, 61, 357–3362. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Wilczyński, K. Experimental Study of Melting of Polymer Blends in a Starve Fed Single Screw Extruder. Polym. Eng. Sci. 2016, 56, 1349–1356. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Computer Model for Starve-Fed Single-Screw Extrusion of Polymer Blends. Adv. Polym. Technol. 2018, 37, 2142–2151. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization for Starve Fed/Flood Fed Single Screw Extrusion of Polymeric Materials. Polymers 2020, 12, 295. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Experimental Study for Extrusion of Polypropylene/Wood Flour Composites. Intern. Polym. Proc. 2015, 30, 113–120. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Bartnik, M. Study on the Flow of Wood-Plastic Composites in the Single-Screw Extrusion Process/Badanie przeplywu kompozytow polimerowo-drzewnych w procesie wytlaczania jednoślimakowego. Polimery 2016, 61, 195–201. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Buziak, K. Study on the Flow of Wood Plastic Composites in the Starve Fed Single Screw Extrusion/Badanie przepływu polimerowych kompozytów drzewnych w procesie wytłaczania jednoślimakowego z dozowanym zasilaniem. Polimery 2017, 62, 680–685. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Wilczyński, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites. Polymers 2018, 10, 295. [Google Scholar] [CrossRef] [PubMed]
- Wilczyński, K.J.; Nastaj, A.; Buziak, K. Modeling of Starve-Fed Single Screw Extrusion of Wood-Polymer Composites/Modelowanie procesu wytłaczania jednoślimakowego z dozowanym zasilaniem polimerowych kompozytów drzewnych. Polimery 2018, 63, 542–548. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Buziak, K. A Computer Model of Starve Fed Single Screw Extrusion of Wood Plastic Composites. Polymers 2021, 13, 1252. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Lewandowski, A.; Nastaj, A.; Wilczyński, K.J. Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites. Polymers 2021, 13, 622. [Google Scholar] [CrossRef]
- Wilczyński, K.; Narowski, P. Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds. Polymers 2019, 11, 638. [Google Scholar] [CrossRef]
- Wilczyński, K.; Narowski, P. A Strategy for Problem Solving of Filling Imbalance in Geometrically Balanced Injection Molds. Polymers 2020, 12, 638. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry; HAAKE: Karlsruhe, Germany, 1994. [Google Scholar]
- GOETTFERT–High Quality Materials Testing Instruments. Available online: https://www.goettfert.com (accessed on 7 September 2025).
- Lewandowski, K.; Piszczek, K.; Zajchowski, S.; Mirowski, J. Rheological Properties of Wood Polymer Composites at High Shear Rates. Polym. Test. 2016, 51, 58–62. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Reihmane, S.; Gassan, J. Thermoplastics Reinforced with Wood Fillers: A Literature Review. Polym.-Plast. Technol. Eng. 1998, 37, 451–468. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J. Composites Reinforced with Cellulose Based Fibres. Prog. Polym. Sci. 1999, 24, 221–273. [Google Scholar] [CrossRef]
- Zajchowski, S.; Ryszkowska, J. Kompozyty polimerowo-drzewne-charakterystyka ogólna oraz ich otrzymywanie z materiałów odpadowych. Polimery 2009, 10, 674–682. [Google Scholar] [CrossRef][Green Version]
- Wilczyński, K.; Buziak, K.; Wilczyński, A. Wood-Plastic Composites: Manufacturing, Rheology and Processing and Process Modeling. Materials 2025, 18, 4042. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt. Part 1. Capillary Rheometry of HDPE Filled with Maple. Polym. Eng. Sci. 2005, 45, 549–559. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt, Part 2: Effects of Lubricating Systems in HDPE/Maple Composites. Polym. Eng. Sci. 2006, 46, 464–473. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt, Part 3: NonLinear Nature of the Flow. Polym. Eng. Sci. 2006, 46, 114–121. [Google Scholar] [CrossRef]
- Xiao, K.; Tzoganakis, C. Rheological Properties and Their Influence on Extrusion Characteristics of HDPE-Wood Composite Resins. SPE ANTEC 2002, 39, 252–257. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusion Characteristic of HDPE-Wood Composites. SPE ANTEC 2003, 39, 197–201. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Rheological Properties of HDPE-Wood Composites. SPE ANTEC 2003, 39, 975–979. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusion of HDPE-Wood Blends. SPE ANTEC 2004, 40, 448–453. [Google Scholar]
- Hristov, V.; Takács, E.; Vlachopoulos, J. Surface Tearing and Wall Slip Phenomena in Extrusion of Highly Filled HDPE/Wood Flour Composites. Polym. Eng. Sci. 2006, 46, 1204–1214. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Hristov, V. Rheology of Wood Polymer Composites. In Proceedings of the Regional PPS Meeting, Pretoria, South Africa, 9–13 October 2006. [Google Scholar]
- Santi, C.R.; Hage, E.; Vlachopoulos, J.; Correa, C.A. Rheology and Processing of HDPE/Wood Flour Composites. Int. Polym. Process. 2009, 24, 346–353. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.P.; Sain, M. Biocomposites Reinforced with Natural Fibers: 2000–2010. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Chan, C.M.; Vandi, L.J.; Pratt, S.; Halley, P.; Richardson, D.; Werker, A.; Laycock, B. Composites. of wood and biodegradable thermoplastics: A review. Polym. Rev. 2018, 58, 444–494. [Google Scholar] [CrossRef]
- Khan, M.Z.; Srivastava, S.K.; Gupta, M.K. A state-of-the-art review on particulate wood polymer composites: Processing, properties and applications. Polym. Test. 2020, 89, 106721. [Google Scholar] [CrossRef]
- Yadav, S.M.; Lubis, M.A.R.; Sihag, K. A Comprehensive Review on Process and Technological Aspects of Wood-Plastic Composites. J. Sylva Lestari 2021, 9, 329–356. [Google Scholar] [CrossRef]
- Ramesh, M.; Rajeshkumar, L.; Sasikala, G.; Balaji, D.; Saravanakumar, A.; Bhuvaneswari, V.; Bhoopathi, R. A Critical Review on Wood-Based Polymer Composites: Processing, Properties, and Prospects. Polymers 2022, 14, 589. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Panchal, H.; Shanmugan, S.; Muthuramalingam, T.; El-Kassas, A.M.; Ramesh, B. Recent progresses in wood-plastic composites: Pre-processing treatments, manufacturing techniques, recyclability and eco-friendly assessment. Clean Eng. Technol. 2022, 8, 100450. [Google Scholar] [CrossRef]
- Sun, Z.; Duan, Y.; An, H.; Wang, X.; Liang, S.; Li, N. Research Progress and Application of Natural Fiber Composites. J. Nat. Fibers 2023, 20, 2206591. [Google Scholar] [CrossRef]
- Mital’ová, Z.; Mital’, D.; Berladir, K. A Concise Review of the Components and Properties of Wood–Plastic Composites. Polymers 2024, 16, 1556. [Google Scholar] [CrossRef]
- Mooney, M. Explicit Formulas for Slip and Fluidity. J. Rheol. 1931, 2, 210–222. [Google Scholar] [CrossRef]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing. Principles and Modelling, 2nd ed.; Carl Hanser Verlag: Munich, Germany, 2017; ISBN 978-1-56990-605-7. [Google Scholar]
- Vinogradov, G.V.; Malkin, A.Y.J. Temperature-independent viscosity characteristics of polymer systems. Polym. Sci. Part. A 1964, 2, 2357. [Google Scholar] [CrossRef]
- Vinogradov, G.V.; Malkin, A.Y.J. Rheological properties of polymer melts. Polym. Sci. Part. B 1966, 4, 135. [Google Scholar] [CrossRef]
- Shenoy, A.V. Rheology of Filled Polymer Systems; Springer Publisher: Dordrecht, The Netherlands, 1999; ISBN 978-0-412-83100-3. [Google Scholar] [CrossRef]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970; ISBN 978-044-215-635-0. [Google Scholar]
- Winter, H.H. Wärmeübertragung und Dissipation in Scherströmungen von Polymerschmelzen. Adv. Heat Transf. 1977, 13, 205. [Google Scholar]
- Hopmann, C.h.; Michaeli, W. Extrusion Dies for Plastics and Rubber, 4th ed.; Carl Hanser Verlag: Munich, Germany, 2016; ISBN 978-1-56990-624-8. [Google Scholar]
- Moigne, N.; Van den Oever, M.; Budtova, T. Dynamic and Capillary Shear Rheology of Natural Fiber-Reinforced Composites. Polym. Eng. Sci. 2013, 53, 2582–2593. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Charlton, Z.; Suwanda, D.; Vlachopoulos, J. Measurements and Comparison to Predictions of Viscosity of Heavily Filled HDPE with Natural Fibers. Adv. Polym. Techn. 2016, 37, 1161–1167. [Google Scholar] [CrossRef]
- Rao, N.S.; Scott, N.R. Understanding Plastics Engineering Calculations; Carl Hanser Verlag: Munich, Germany, 2012; ISBN 978-1-56990-509-1. [Google Scholar]
- Wilczyński, K. Reologia w Przetwórstwie Tworzyw sztucznych/Rheology in Polymer Processing; Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 2001; ISBN 83-204-2561-1. [Google Scholar]
- Lewandowski, A.; Wilczyński, K. Global Modeling of Single Screw Extrusion with Slip Effects. Int. Polym. Process. 2019, 34, 81–90. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Global Modeling for Single Screw Extrusion of Viscoplastics. Int. Polym. Process. 2020, 35, 26–36. [Google Scholar] [CrossRef]
- Potente, H.; Kurte–Jardin, M.; Klus, S.; Timmermann, K. Two Dimensional Description of Pressure-Throughput Behaviour of Newtonian Materials Considering Wall Slippage Effects. Int. Polym. Process. 2005, 20, 312–321. [Google Scholar] [CrossRef]
- Potente, H.; Timmermann, K.; Kurte-Jardin, M. Description of the Pressure/Throughput Behavior of a Single-Screw Plasticating Unit in Consideration of Wall Slippage Effects for Non-Newtonian Material and 1-D Flow. Int. Polym. Process. 2006, 21, 272–282. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G.; Mitsoulis, E. Slip Effects in Tapered Dies. Polym. Eng. Sci. 2009, 49, 1960–1969. [Google Scholar] [CrossRef]
- Mitsoulis, E. Flows of Viscoplastic Materials: Models and Computations. In Rheology Reviews 2007; Binding, D.M., Hudson, N.E., Keunings, R., Eds.; The British Society of Rheology: London, UK, 2007; pp. 135–178. [Google Scholar]
- Duretek, I.; Schuschnigg, S.; Gooneie, A.; Langecker, G.R.; Holzer, C. Rheological Properties of Wood Polymer Composites and Their Role in Extrusion. J. Phys. Conf. Ser. 2015, 602, 012014. [Google Scholar] [CrossRef]
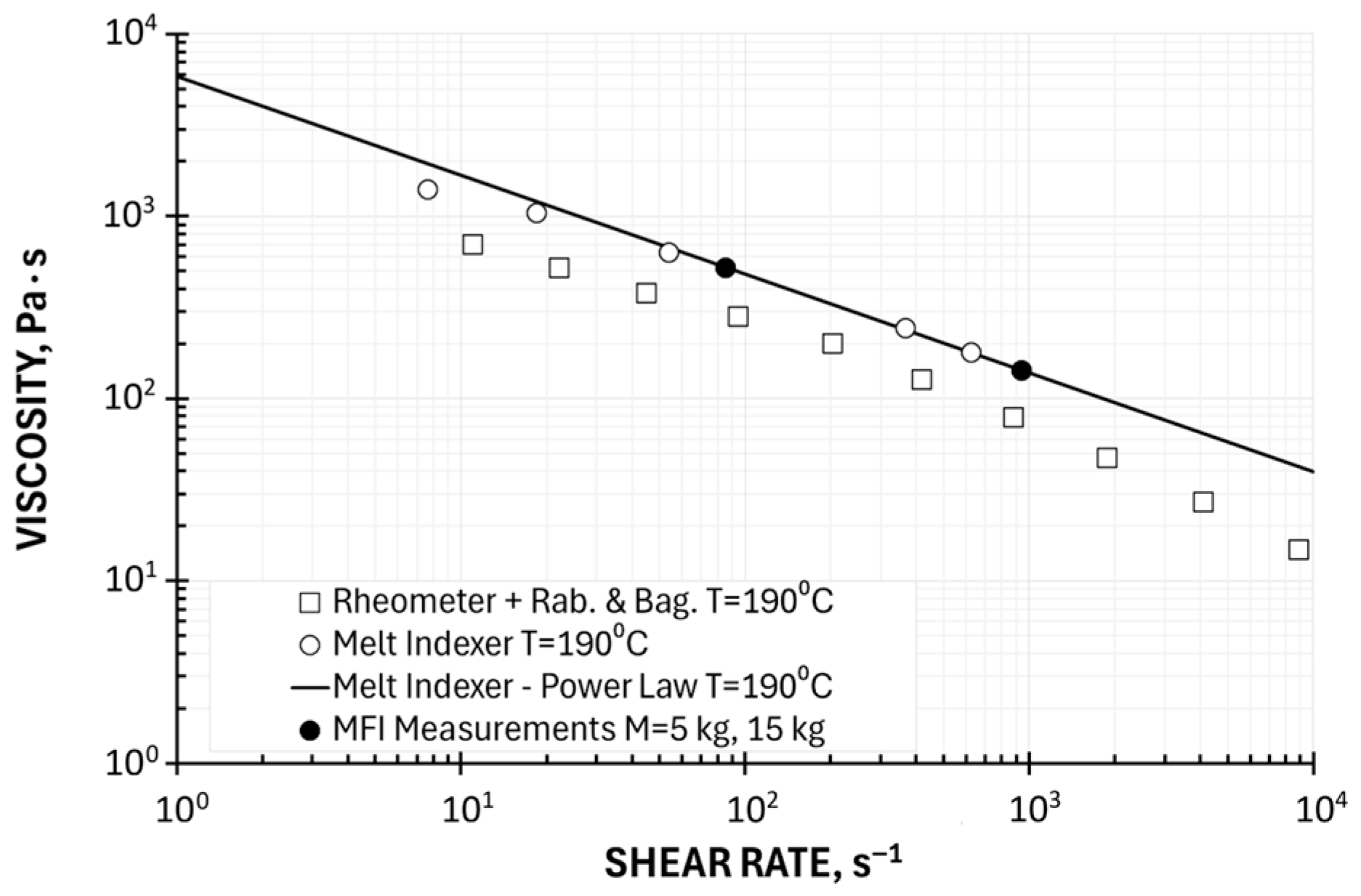
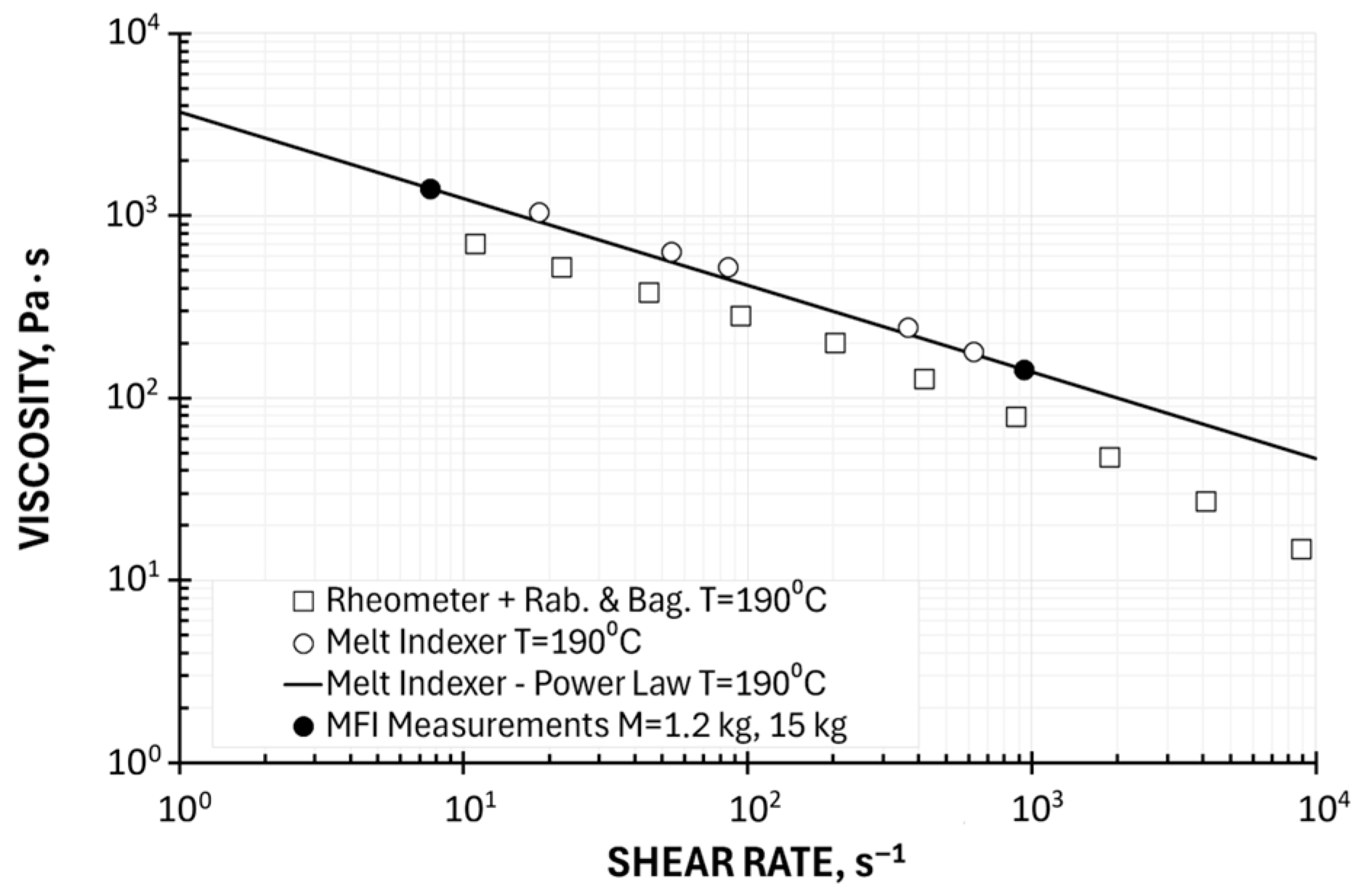
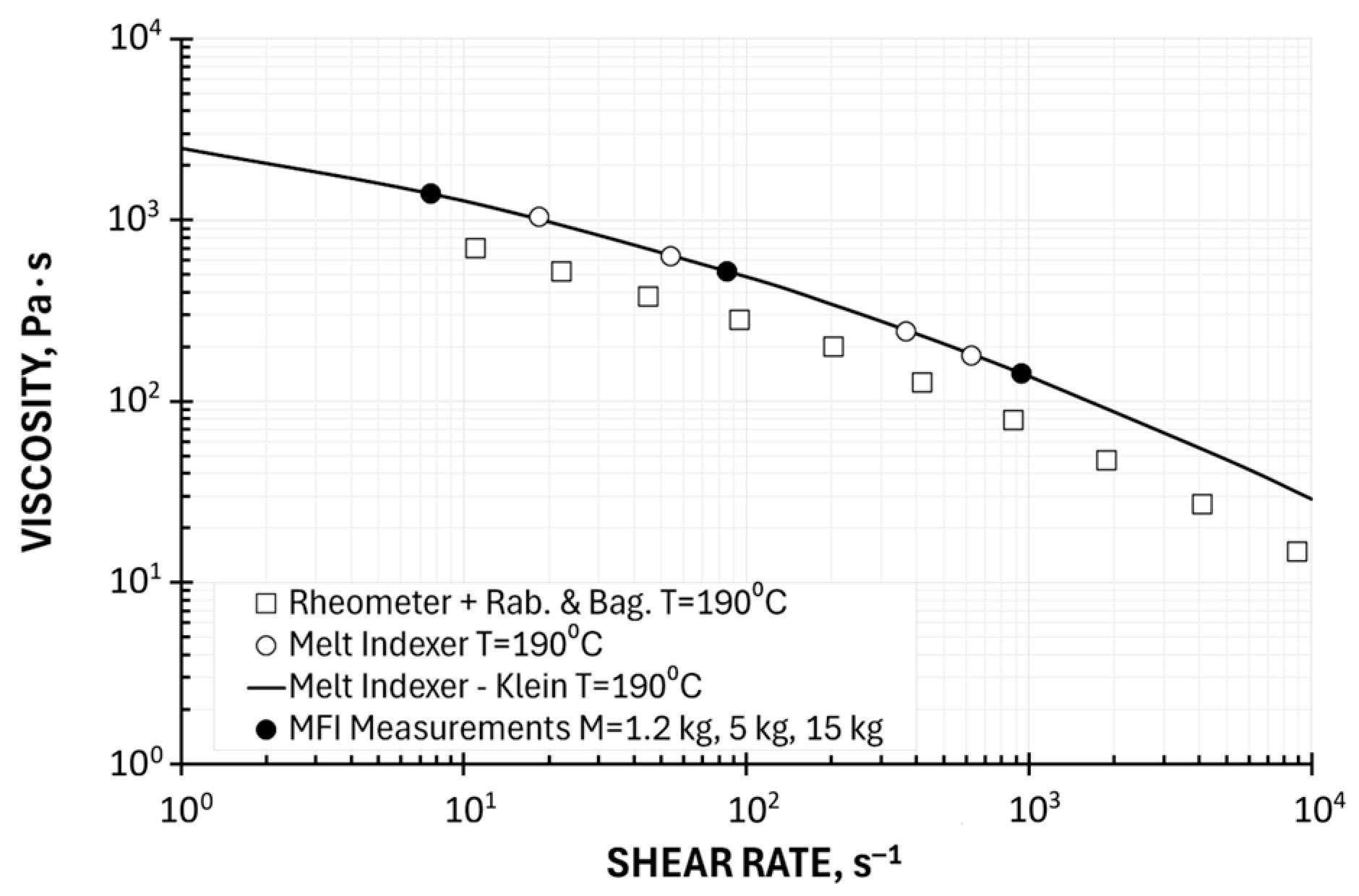
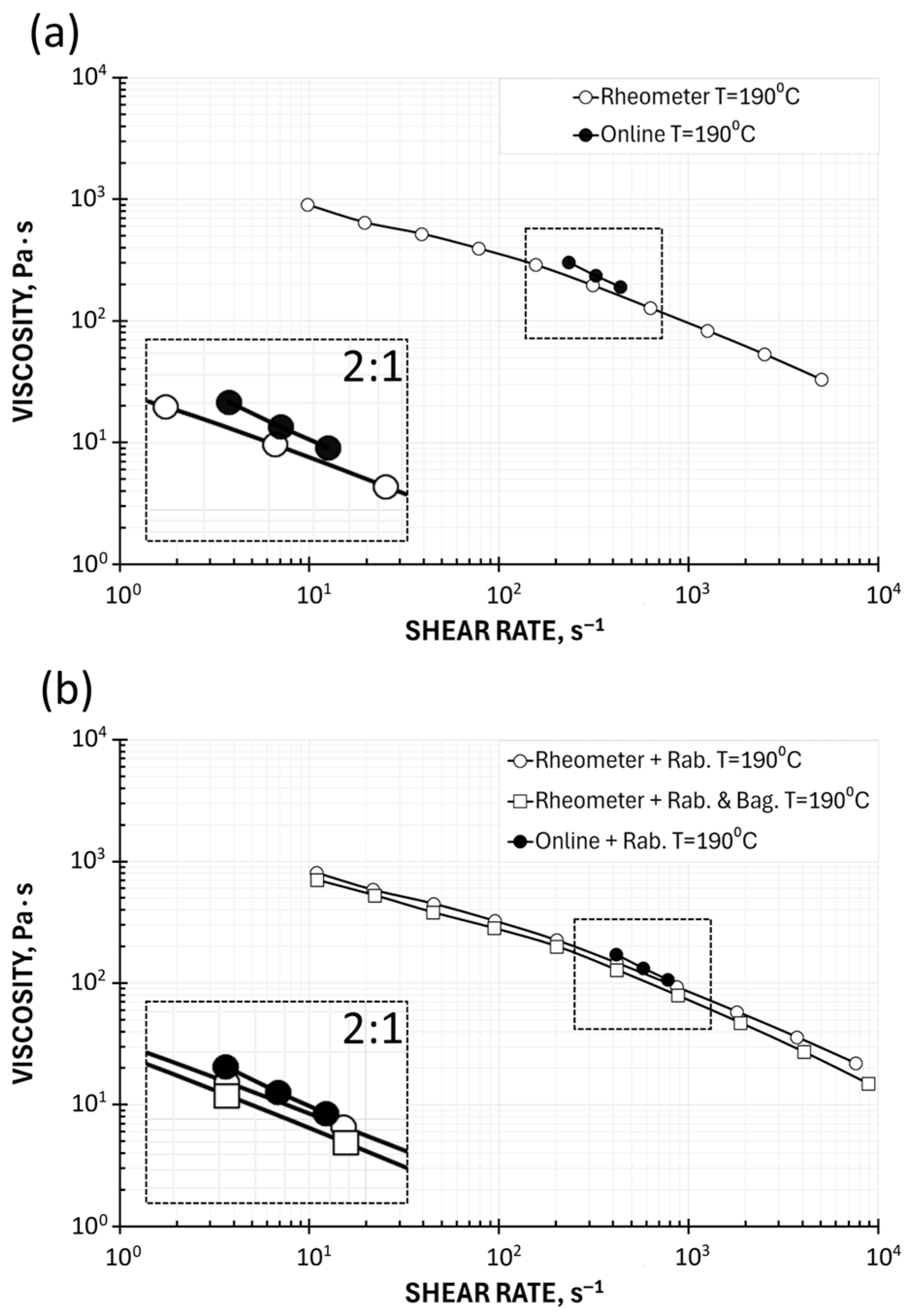
| Screw Speed | Throughput | Die Pressure | Shear Stress | Shear Rate Apparent | Shear Rate | Viscosity Apparent | Viscosity |
|---|---|---|---|---|---|---|---|
| N, rpm | G, kg/h | pD, MPa | τw, Pa | , s−1 | , s−1 | ηa, Pa∙s | η, Pa∙s |
| 30 | 9.4 | 5.4 | 71052.6 | 232.4 | 414.1 | 305.7 | 171.6 |
| 50 | 13.0 | 5.8 | 76315.8 | 323.2 | 575.8 | 236.2 | 132.5 |
| 70 | 17.6 | 6.3 | 82894.7 | 436.3 | 777.3 | 190.0 | 106.6 |
| Screw Speed | Shear Rate | On-line Viscosity | HPCR Viscosity | Error | HPCR Apparent Viscosity | Error |
|---|---|---|---|---|---|---|
| N, rpm | ηon-line, Pa∙s | ηrheo, Pa∙s | δ1, % | ηa_rheo, Pa∙s | δ2, % | |
| 30 | 414.1 | 171.6 | 129.1 | 24.8 | 147.3 | 14.2 |
| 50 | 575.8 | 132.5 | 107.7 | 18.8 | 123.9 | 6.6 |
| 70 | 777.3 | 106.6 | 91.3 | 14.4 | 105.8 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczyński, K.J.; Buziak, K.; Lewandowski, A.; Wilczyński, K. Rheology for Wood Plastic Composite Extrusion—Part 1: Laboratory vs. On-Line Rheometry. Polymers 2025, 17, 2782. https://doi.org/10.3390/polym17202782
Wilczyński KJ, Buziak K, Lewandowski A, Wilczyński K. Rheology for Wood Plastic Composite Extrusion—Part 1: Laboratory vs. On-Line Rheometry. Polymers. 2025; 17(20):2782. https://doi.org/10.3390/polym17202782
Chicago/Turabian StyleWilczyński, Krzysztof J., Kamila Buziak, Adrian Lewandowski, and Krzysztof Wilczyński. 2025. "Rheology for Wood Plastic Composite Extrusion—Part 1: Laboratory vs. On-Line Rheometry" Polymers 17, no. 20: 2782. https://doi.org/10.3390/polym17202782
APA StyleWilczyński, K. J., Buziak, K., Lewandowski, A., & Wilczyński, K. (2025). Rheology for Wood Plastic Composite Extrusion—Part 1: Laboratory vs. On-Line Rheometry. Polymers, 17(20), 2782. https://doi.org/10.3390/polym17202782









