Effects of Stress Level and Elevated Temperature on Transverse Compression Stress Relaxation Behavior and Post-Relaxation Mechanical Performance of UD-CFRP
Abstract
1. Introduction
2. Experimental Program
2.1. Materials
2.2. Experimental Set-Up
2.3. Specimens
3. Test Results and Discussions
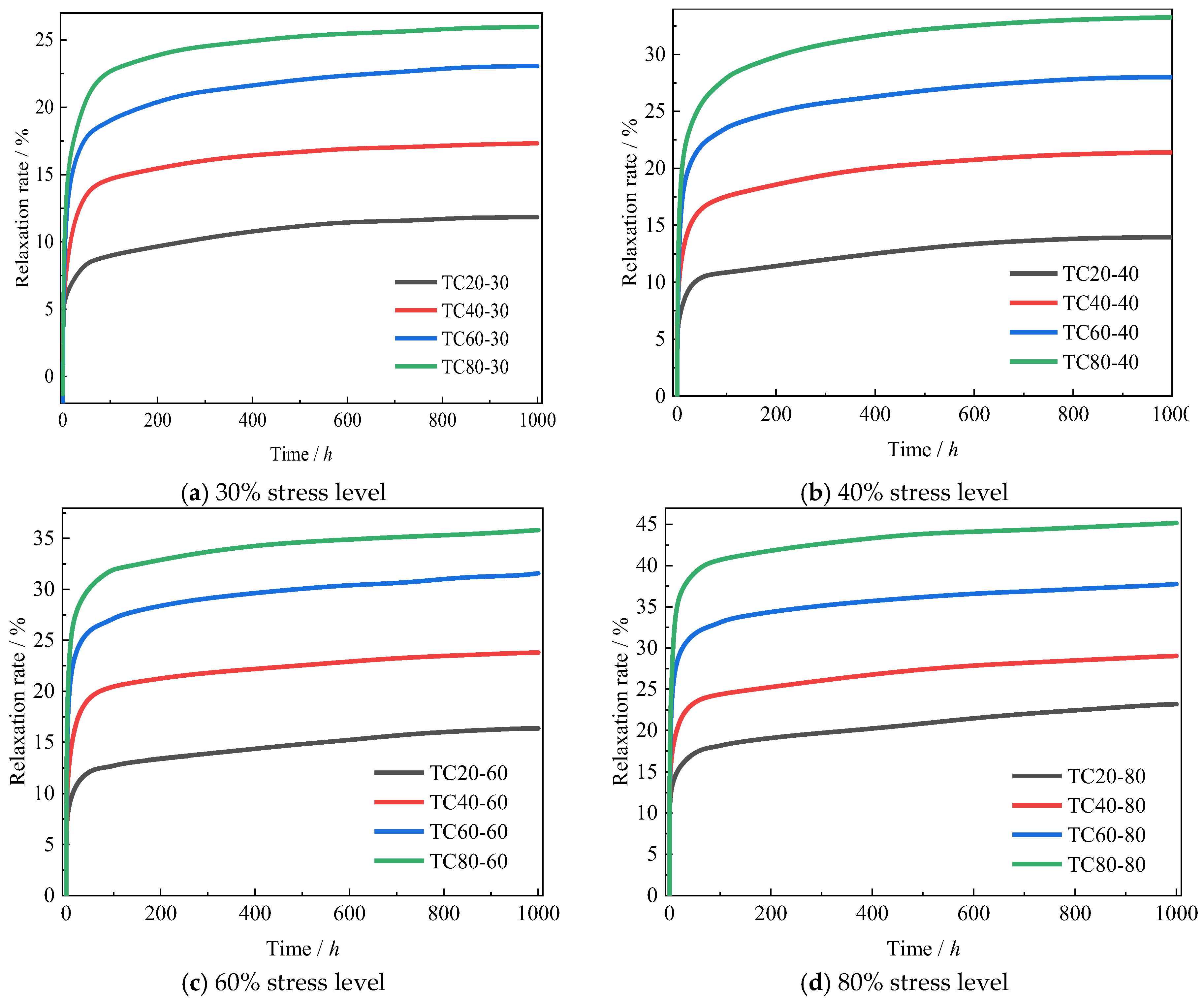
3.1. Relaxation Process
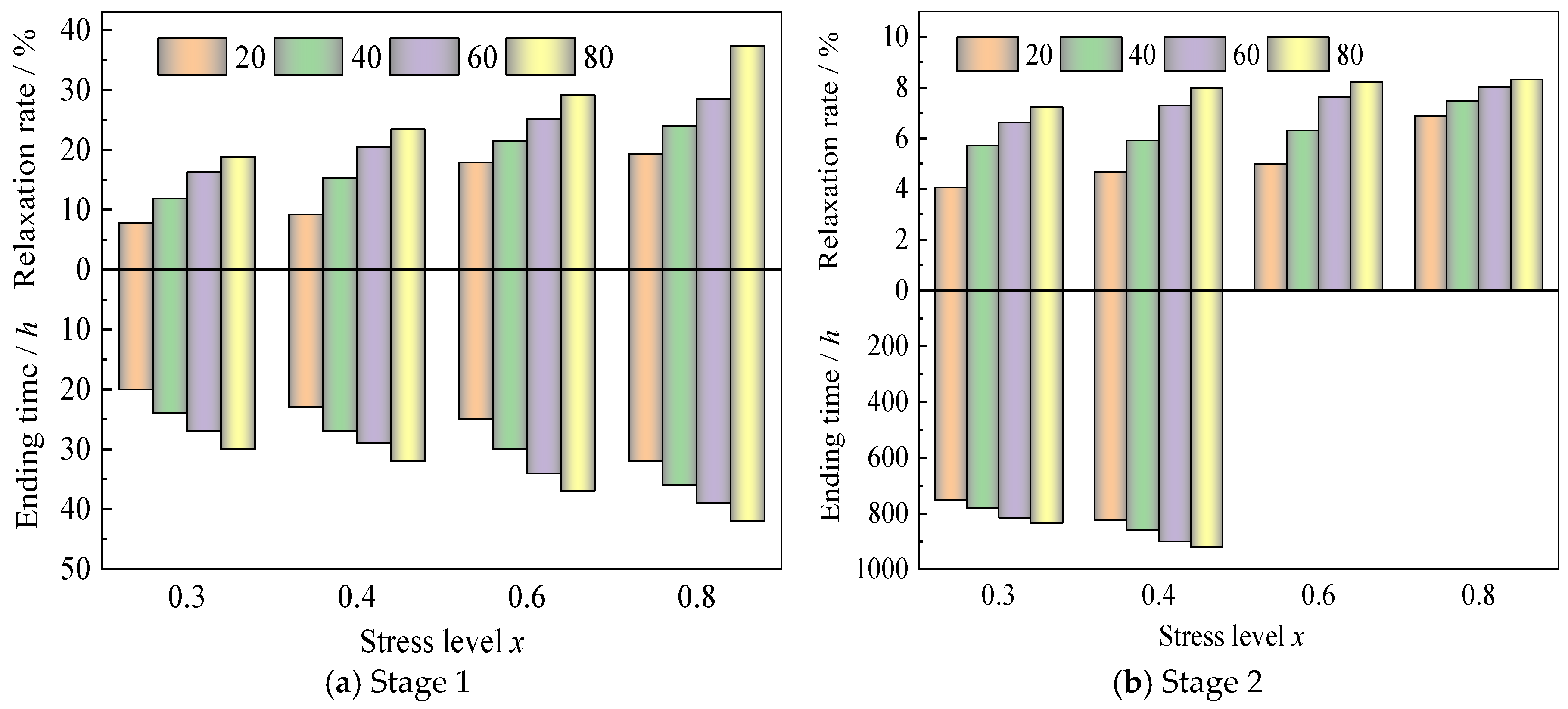
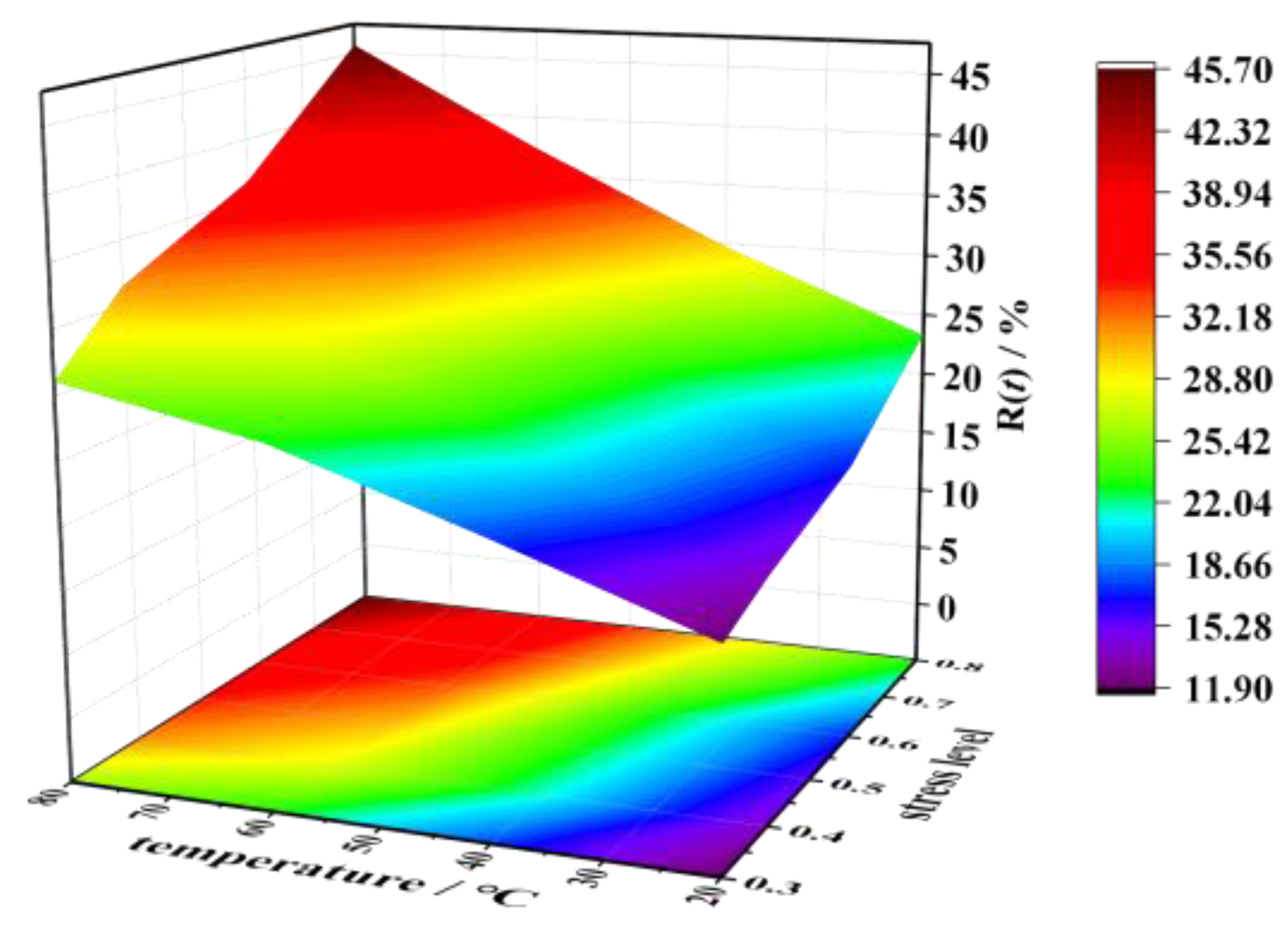
3.2. Relaxation Rate
3.3. Post-Relaxation Strength and Modulus
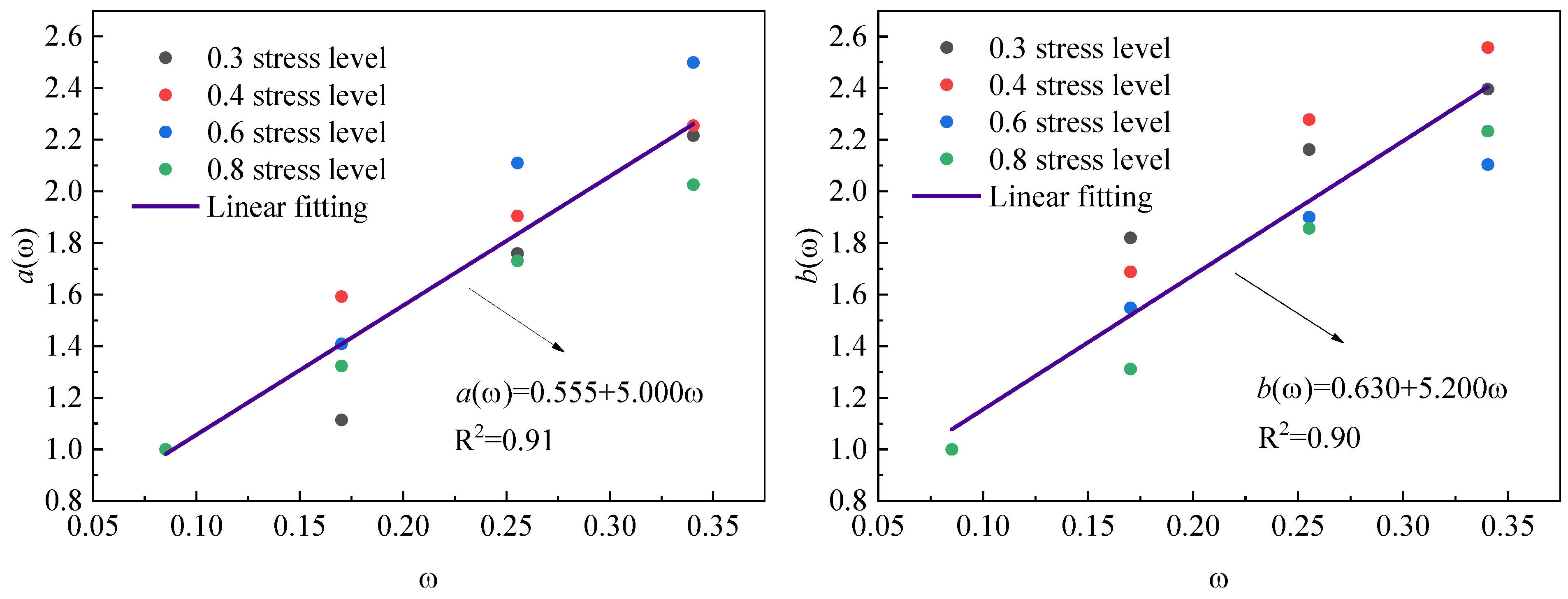
4. Stress Relaxation Prediction
5. Conclusions
- (1)
- The stress relaxation behavior of UD-CFRP specimens under varying temperatures and stress levels demonstrates distinct two-stage evolution characteristics. The initial phase shows accelerated relaxation attributed to surface roughness compaction and resin matrix pore compaction. The subsequent phase manifests decelerated relaxation kinetics governed by time-dependent viscoelastic responses at the polymer matrix, especially around the fiber-resin interface, achieving quasi-equilibrium at reduced stress levels (30–40%). Notably, specimens under elevated stress conditions (60–80%) maintain progressive relaxation patterns throughout the 1000 h test duration.
- (2)
- Elevated stress levels and temperature conditions significantly enhance both the temporal duration and magnitude of first-stage relaxation. Specifically, temperature intensification prolongs secondary relaxation completion in lower stress regimes (30–40%) while amplifying relaxation extents across all loading levels. The relaxation demonstrates marked temperature sensitivity, with thermal activation mechanisms governing the relaxation rate more profoundly than mechanical stress parameters, especially for million-hour conditions.
- (3)
- The stress relaxation process exhibits minimal alteration of static transverse compressive strength while inducing modulus enhancement through pressure-induced porosity reduction in the resin matrix. Particularly under elevated temperatures, modulus retention demonstrates pronounced improvement (3–5% increase compared to ambient conditions) driven by thermally accelerated porosity reduction.
- (4)
- The developed stress relaxation model demonstrates high-fidelity predictive capability across 30–80% stress levels and 20–80 °C conditions.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Mei, K.; Wu, J. Long-term mechanical properties of FRP tendon–anchor systems—A review. Constr. Build. Mater. 2020, 230, 117017. [Google Scholar] [CrossRef]
- Tahsiri, H.; Belarbi, A. Evaluation of prestress relaxation loss and harping characteristics of prestressing CFRP systems. Constr. Build. Mater. 2022, 331, 127339. [Google Scholar] [CrossRef]
- Wu, J.Y.; Xian, G.J.; Li, H. A novel anchorage system for CFRP cable: Experimental and numerical investigation. Compos. Struct. 2018, 194, 555–563. [Google Scholar] [CrossRef]
- Duo, Y.; Qi, L.; Huang, S.; Yue, Q.; Liu, X. Planar clamping anchorage for CFRP plate: Experimental research, friction-adhesion synergistic mechanism and theoretical model. Constr. Build. Mater. 2024, 441, 137540. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Progressive damage and residual strength of open-hole thin-ply CFRP laminates under tensile fatigue loading. Compos. Struct. 2023, 314, 116973. [Google Scholar] [CrossRef]
- Xia, L.; Feng, L.; Xin, W.; Zhou, J.; Liang, M.; Zhang, L.; Huang, H.; Wu, Z. Fatigue damage propagation of FRP under coupling effect of cyclic load and corrosion. Polym. Compos. 2024, 45, 933–945. [Google Scholar] [CrossRef]
- Tanks, J.; Sharp, S.; Harris, D.; Ozyildirim, C. Durability of CFRP cables exposed to simulated concrete environments. Adv. Compos. Mater. 2017, 26, 245–258. [Google Scholar] [CrossRef]
- Su, C.; Wang, X.; Ding, L.; Liu, S.; Chen, Z.; Wu, Z. Prediction of long-term durability of unidirectional/multidirectional basalt fiber- and hybrid fiber-reinforced polymer profiles under concrete environment. Constr. Build. Mater. 2023, 384, 131248. [Google Scholar] [CrossRef]
- Fang, Y.; Xiang, Y.; Fang, Z. Impact behaviour of carbon fibre-reinforced polymer (cfrp) cables with protective sheaths. Constr. Build. Mater. 2024, 450, 138599. [Google Scholar] [CrossRef]
- Wang, Z.; Xian, G. Impact performances of fiber reinforced polymer composites and cables: A review. Compos. Struct. 2023, 319, 117128. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Xu, J.; Han, Q. Anchorage systems of CFRP cables in cable structures-A review. Constr. Build. Mater. 2018, 160, 82–99. [Google Scholar] [CrossRef]
- Yang, Y.; Fahmy, M.F.; Guan, S.; Pan, Z.; Zhan, Y.; Zhao, T. Properties and applications of FRP cable on long-span cable-supported bridges: A review. Compos. Part B Eng. 2020, 190, 107934. [Google Scholar] [CrossRef]
- Ascione, F.; Berardi, V.; Feo, L.; Giordano, A. An experimental study on the long-term behavior of CFRP pultruded laminates suitable to concrete structures rehabilitation. Compos. Part B Eng. 2008, 39, 1147–1150. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, J.; Song, S.; Zhou, F.; Wang, C. Experimental investigation on the creep property of carbon fiber reinforced polymer tendons under high stress levels. Materials 2018, 11, 2273. [Google Scholar] [CrossRef]
- Ding, G.; Feng, P.; Wang, Y.; Ai, P.; Wang, Q. Long-term bolt preload relaxation and contact pressure distribution in clamping anchorages for CFRP plates. Compos. Struct. 2024, 329, 117780. [Google Scholar] [CrossRef]
- Pei, R.; Xiao, Y.; Chen, H.; Xue, Y. Temperature-time dependent behavior for preload relaxation in bolted composite joints. Acta Mater. Compos. Sin. 2016, 33, 768–778. (In Chinese) [Google Scholar]
- Wang, X.; Shi, J.; Liu, J.; Yang, L.; Wu, Z. Creep behavior of basalt fiber reinforced polymer tendons for prestressing application. Mater. Des. 2014, 59, 558–564. [Google Scholar] [CrossRef]
- Zou, P.X.W. Long-term properties and transfer length of fiber-reinforced polymers. J. Compos. Constr. 2003, 7, 10–19. [Google Scholar] [CrossRef]
- Chandra, V. Individual and Interactive Influence of Temperature, Stress, Physical Aging and Moisture on Creep, Creep Rupture and Fracture of Epoxy Resin and Its Composite. Ph.D. Thesis, The University of Manitoba, Winnipeg, MB, Canada, 2001. [Google Scholar]
- Batra, S. Creep Rupture and Life Prediction of Polymer Composites. Ph.D. Thesis, College of Engineering and Mineral Resources at West Virginia University, Morgantown, WV, USA, 2009. [Google Scholar]
- Li, J.; Wang, M.; Yue, Q.; Liu, X. Transverse compressive properties, long-term stress relaxation, and post-relaxation properties of unidirectional CFRP composites. J. Build. Eng. 2025, 105, 112526. [Google Scholar] [CrossRef]
- Scattina, A.; Roncato, D.; Belingardi, G.; Martino, G. Investigation of creep phenomenon on composite material for bolt connections. Compos. Struct. 2015, 134, 378–383. [Google Scholar] [CrossRef]
- Xin, H.; Gao, Q.; Feng, P.; Liu, Y. Creep behavior of E-GFRP unidirectional lamina for bridge engineering using two-scale numerical homogenization evaluation method. Eng. Mech. 2024, 8, 93–106. [Google Scholar]
- Perrella, M.; Berardi, V.P.; Cricrì, G.; Esposito, R. Experimental evaluation of the long-term creep deformations of epoxy resin. Procedia Struct. Integr. 2019, 24, 601–611. [Google Scholar] [CrossRef]
- Jiang, Z.; Fang, Z.; Fang, C.; Li, Q.; Wang, Z. Experimental investigation on high-temperature creep behavior of carbon fiber reinforced polymer cable. Compos. Struct. 2022, 291, 115533. [Google Scholar] [CrossRef]
- Jiang, Z.; Lv, R.; Fang, Z.; Li, Q.; Fang, C.; Wang, Z. Experimental study on high-temperature relaxation behavior of carbon fiber reinforced polymer cable. Constr. Build. Mater. 2022, 330, 127207. [Google Scholar] [CrossRef]
- BS ISO 20975-1:2023; Fiber-Reinforced Plastics Composites-Determination of Laminate pf Though-Thickness Properties. BSI Standards Limited 2023: Switzerland, Germany, 2023.
- ACI 440.3R-04; Guide Test Methods for Fiber-Reinforced Polymers (FRPs) for Reinforcing or Strengthening Concrete Structures. American Concrete Institute Committee 440: Farmington Hills, MI, USA, 2004.
- JSCE-E 534-1995; Test Method for Creep Failure of Continuous Fiber Reinforcing Materials. Japan Society of Civil Engineers: Tokyo, Japan, 1995.
- ASTM D-2990; Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics. In Annual Book of Standards, vol. 08.01; ASTM International: West Conshohocken, PA, USA, 2003.
- Liu, Q.; Shi, Z.; Liu, X. Transverse compressive properties of unidirectional GFRP composites: Size effect, elevated temperature, and cyclic freezing-hydrothermal aging. Constr. Build. Mater. 2025, 460, 139860. [Google Scholar] [CrossRef]
- GB51160-2016; Standardization Administration of the People’s Republic of China. Technical Code for Fibre Reinforced Plastics Equipment and Piping Engineering. China Standards Press: Beijing, China, 2016. (In Chinese)


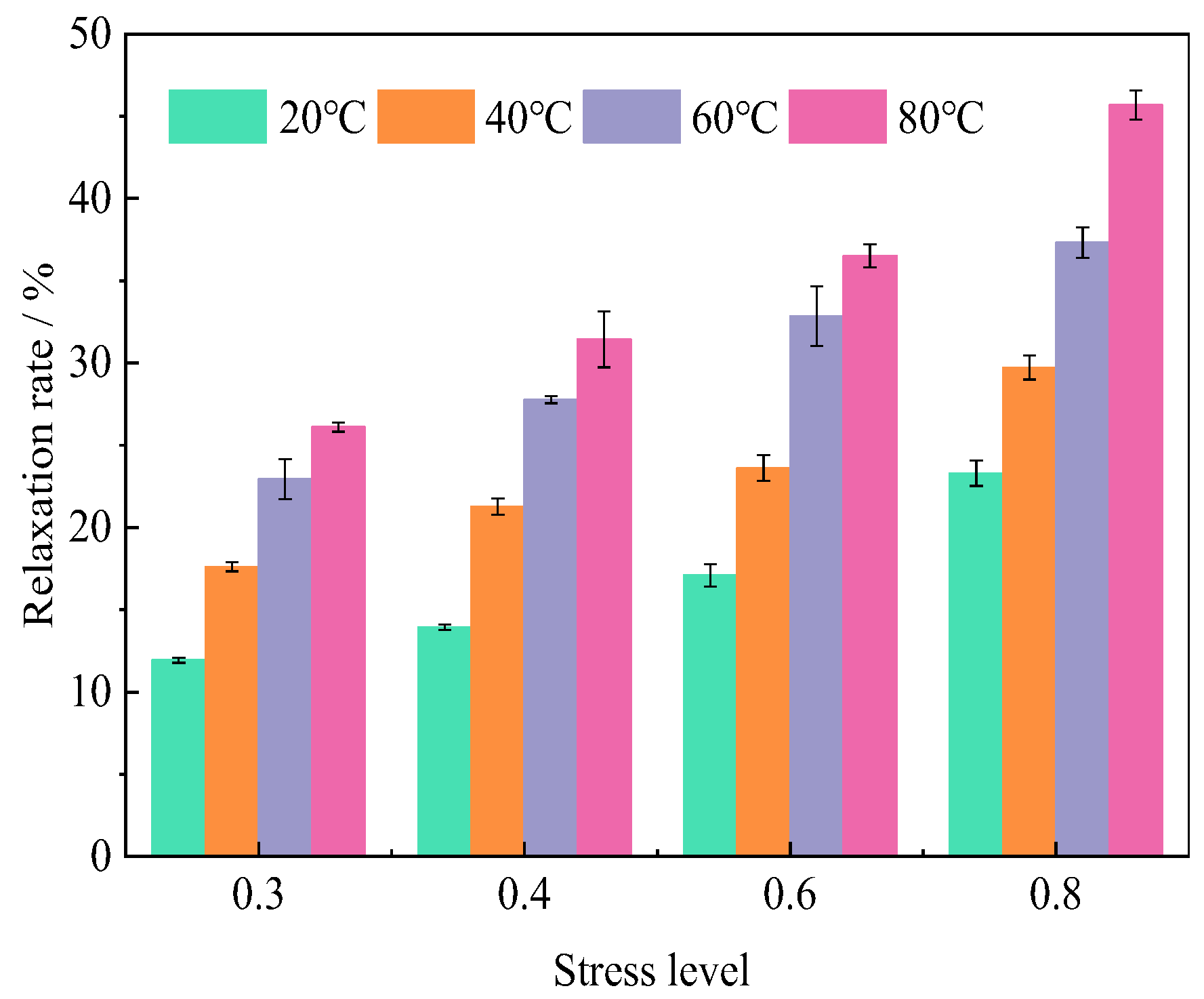

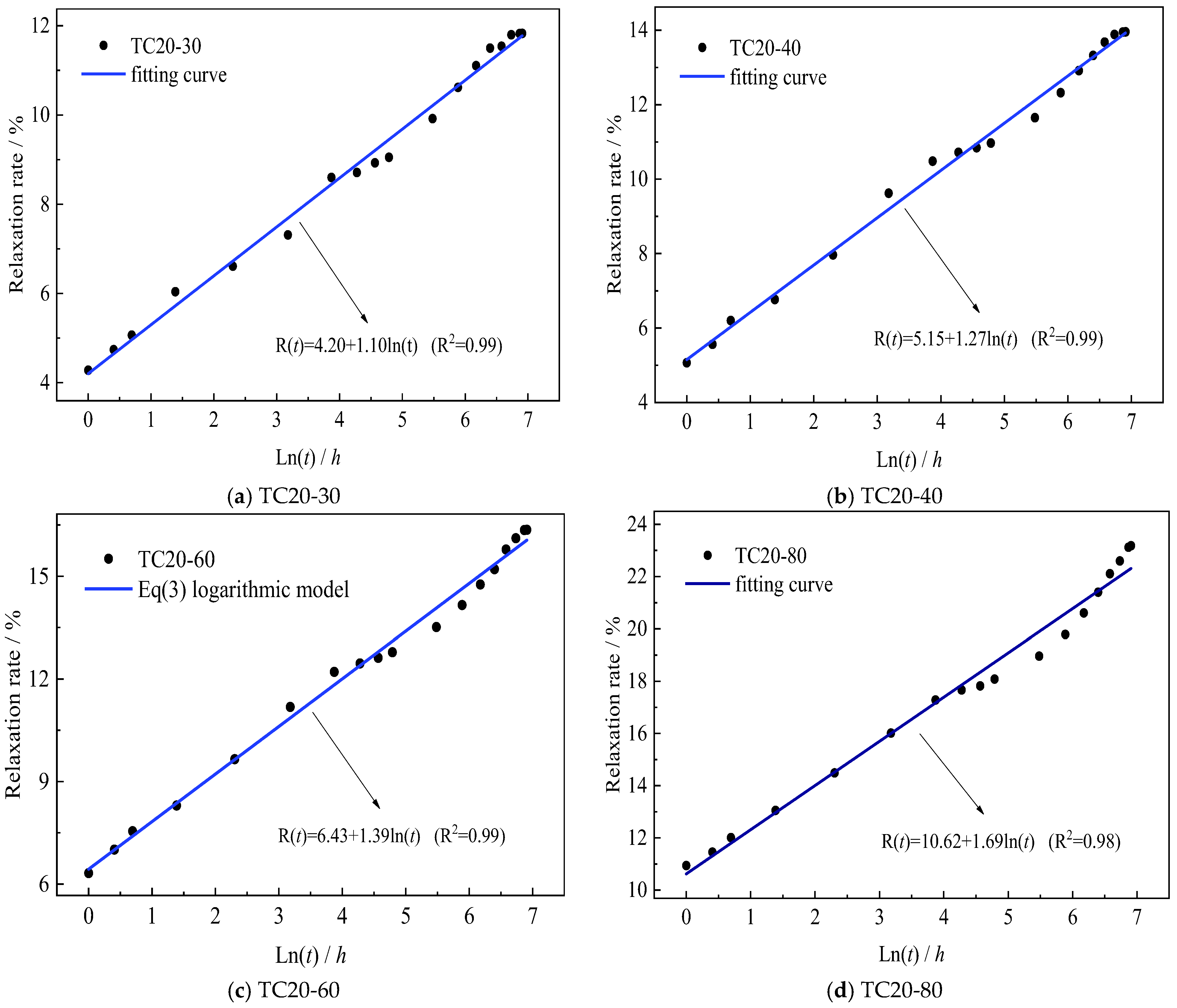
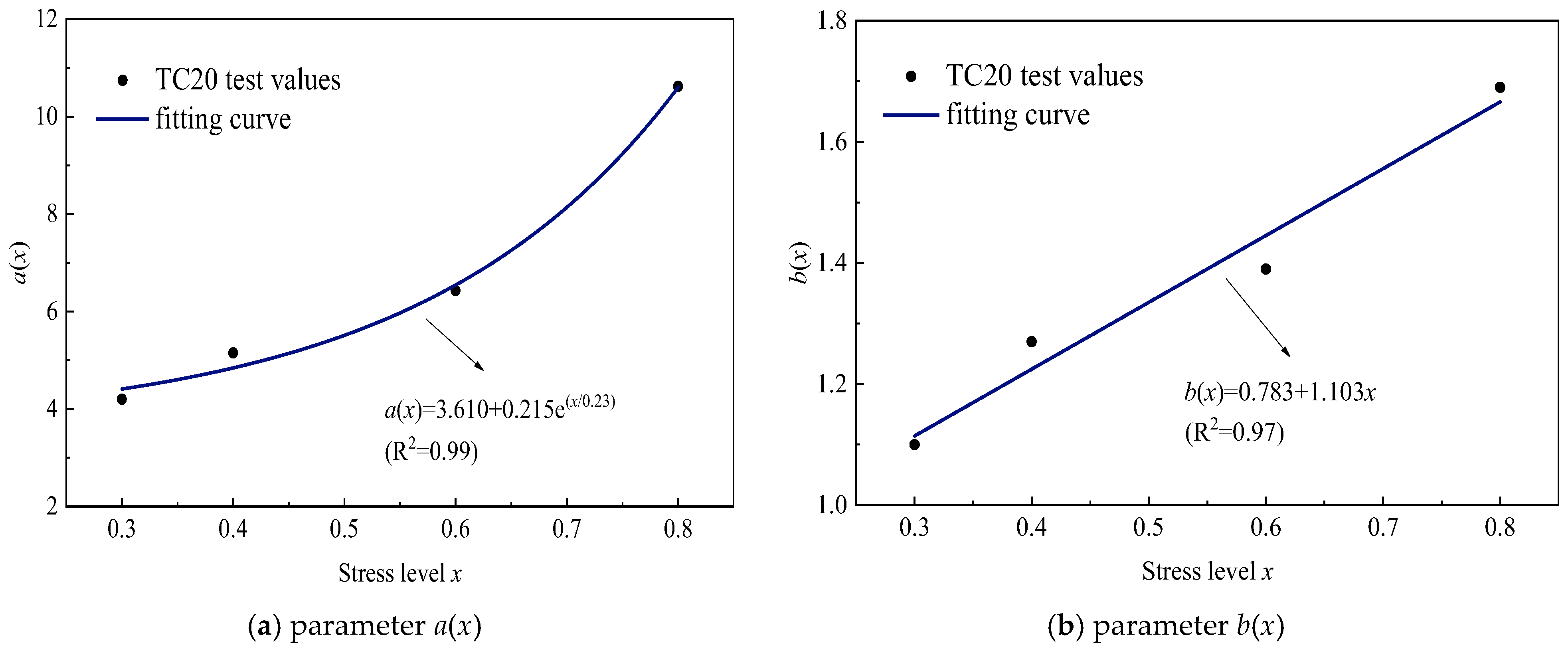

| Material | Type | Tensile Strength/MPa | Elastic Modulus/GPa | Compressive Strength/MPa | Tg/°C |
|---|---|---|---|---|---|
| fiber | T700 (SYT49S) | 4900 | 240 | - | - |
| resin | Trascite GL6831A/B | 77.62 | 2.81 | - | 235 |
| Specimen ID | T/°C | Stress Level/% | Specimen ID | T/°C | Stress Level/% |
|---|---|---|---|---|---|
| TC20-30 | 20 | 30 | TC60-30 | 60 | 30 |
| TC20-40 | 40 | TC60-40 | 40 | ||
| TC20-60 | 60 | TC60-60 | 60 | ||
| TC20-80 | 80 | TC60-80 | 80 | ||
| TC40-30 | 40 | 30 | TC80-30 | 80 | 30 |
| TC40-40 | 40 | TC80-40 | 40 | ||
| TC40-60 | 60 | TC80-60 | 60 | ||
| TC40-80 | 80 | TC80-80 | 80 |
| T | Stage | Stress Level | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 30% | 40% | 60% | 80% | ||||||
| Ending Time | Relaxation Rate | Ending Time | Relaxation Rate | Ending Time | Relaxation Rate | Ending Time | Relaxation Rate | ||
| 20 °C | 1st | 20 h | 7.85% | 23 h | 9.22% | 25 h | 17.94% | 32 h | 19.24% |
| 2nd | 750 h | 4.07% | 825 h | 4.68% | / | 4.99% | / | 6.87% | |
| 40 °C | 1st | 24 h | 11.86% | 27 h | 15.30% | 30 h | 21.46% | 36 h | 23.96% |
| 2nd | 780 h | 5.71% | 860 h | 5.92% | / | 6.30% | / | 7.47% | |
| 60 °C | 1st | 27 h | 16.27% | 29 h | 20.43% | 34 h | 25.21% | 39 h | 28.48% |
| 2nd | 815 h | 6.62% | 900 h | 7.30% | / | 7.64% | / | 8.03% | |
| 80 °C | 1st | 30 h | 18.84% | 32 h | 23.41% | 37 h | 29.11% | 42 h | 37.36% |
| 2nd | 835 h | 7.22% | 920 h | 7.99% | / | 8.21% | / | 8.32% | |
| Stress Level | Relaxation Rate | Temperature/°C | |||
|---|---|---|---|---|---|
| 20 | 40 | 60 | 80 | ||
| 0.3 | Average/% | 11.93 | 17.61 | 22.93 | 26.11 |
| SD/% | 0.16 | 0.27 | 1.21 | 0.28 | |
| CoV (%) | 1.34 | 1.53 | 5.28 | 1.08 | |
| 0.4 | Average/% | 13.94 | 21.27 | 27.76 | 31.43 |
| SD/% | 0.17 | 0.50 | 0.21 | 1.70 | |
| CoV (%) | 1.22 | 2.35 | 0.77 | 5.41 | |
| 0.6 | Average/% | 17.09 | 23.62 | 32.85 | 36.51 |
| SD/% | 0.69 | 0.79 | 1.81 | 0.7 | |
| CoV (%) | 4.04 | 3.34 | 5.51 | 1.92 | |
| 0.8 | Average/% | 23.30 | 29.73 | 37.32 | 45.68 |
| SD/% | 0.77 | 0.73 | 0.92 | 0.88 | |
| CoV (%) | 3.30 | 2.44 | 2.47 | 1.93 | |
| Stress Level | Strength & Modulus | 20 °C | 40 °C | 60 °C | 80 °C | ||||
|---|---|---|---|---|---|---|---|---|---|
| Strength | Modulus | Strength | Modulus | Strength | Modulus | Strength | Modulus | ||
| 30% | Average/Mpa | 154.08 | 9.68 | 153.95 | 9.89 | 157.48 | 9.84 | 157.85 | 9.80 |
| SD | 4.40 | 0.29 | 3.45 | 0.54 | 4.36 | 0.42 | 10.80 | 0.56 | |
| CoV/% | 2.86 | 3.00 | 2.24 | 5.48 | 2.77 | 4.24 | 6.84 | 5.72 | |
| η | / | 1.08 | / | 1.11 | / | 1.10 | / | 1.10 | |
| 40% | Average/% | 144.10 | 9.92 | 149.80 | 10.20 | 161.42 | 10.14 | 152.68 | 10.33 |
| SD | 9.09 | 0.49 | 3.04 | 0.69 | 3.47 | 0.15 | 8.14 | 0.80 | |
| CoV/% | 6.31 | 4.94 | 2.03 | 6.74 | 2.15 | 1.47 | 5.33 | 7.71 | |
| η | / | 1.11 | / | 1.14 | / | 1.14 | / | 1.16 | |
| 60% | Average/% | 151.36 | 9.81 | 147.70 | 10.27 | 155.76 | 10.07 | 164.94 | 10.41 |
| SD | 9.78 | 0.75 | 3.00 | 0.78 | 9.39 | 0.47 | 9.00 | 0.77 | |
| CoV/% | 6.46 | 7.65 | 2.03 | 7.56 | 6.03 | 4.66 | 5.46 | 7.44 | |
| η | / | 1.10 | / | 1.15 | / | 1.13 | / | 1.17 | |
| 80% | Average/% | 158.13 | 9.79 | 146.88 | 10.04 | 150.94 | 10.05 | 156.90 | 10.30 |
| SD | 4.58 | 0.36 | 4.07 | 0.51 | 9.51 | 0.40 | 19.85 | 1.02 | |
| CoV/% | 2.90 | 3.68 | 2.77 | 5.03 | 6.30 | 3.99 | 12.65 | 9.90 | |
| η | / | 1.10 | / | 1.13 | / | 1.13 | / | 1.15 | |
| Stress Level | a(x) | b(x) | R2 |
|---|---|---|---|
| 30% | 4.20 | 1.10 | 0.99 |
| 40% | 5.15 | 1.27 | 0.99 |
| 60% | 6.43 | 1.39 | 0.99 |
| 80% | 10.62 | 1.69 | 0.98 |
| Temperature/°C | ω | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stress Level | |||||||||
| 0.3 | 0.4 | 0.6 | 0.8 | 0.3 | 0.4 | 0.6 | 0.8 | ||
| 20 | 0.085 | 4.40 | 4.83 | 6.53 | 10.58 | 1.11 | 1.22 | 1.44 | 1.67 |
| 40 | 0.170 | 4.90 | 7.69 | 9.20 | 14.00 | 2.02 | 2.06 | 2.23 | 2.19 |
| 60 | 0.255 | 7.74 | 9.20 | 13.78 | 18.32 | 2.40 | 2.78 | 2.70 | 3.10 |
| 80 | 0.340 | 9.75 | 10.89 | 16.32 | 21.43 | 2.66 | 3.12 | 3.03 | 3.73 |
| Temperature/°C | ω | a(ω) | b(ω) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stress Level | |||||||||
| 0.3 | 0.4 | 0.6 | 0.8 | 0.3 | 0.4 | 0.6 | 0.8 | ||
| 20 | 0.085 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 40 | 0.170 | 1.11 | 1.59 | 1.41 | 1.32 | 1.82 | 1.69 | 1.55 | 1.31 |
| 60 | 0.255 | 1.76 | 1.90 | 2.11 | 1.73 | 2.16 | 2.28 | 1.88 | 1.86 |
| 80 | 0.340 | 2.22 | 2.25 | 2.50 | 2.03 | 2.40 | 2.56 | 2.10 | 2.23 |
| Temperature/°C | Values | Stress Level | |||
|---|---|---|---|---|---|
| 30% | 40% | 60% | 80% | ||
| 20 | test | 11.93 | 13.94 | 17.09 | 23.30 |
| prediction | 12.57 | 13.81 | 17.11 | 22.71 | |
| 40 | test | 17.61 | 21.27 | 23.62 | 29.73 |
| prediction | 17.85 | 19.61 | 24.30 | 32.04 | |
| 60 | test | 22.93 | 27.76 | 32.85 | 37.32 |
| prediction | 23.13 | 25.63 | 31.50 | 41.70 | |
| 80 | test | 26.11 | 31.43 | 36.51 | 45.68 |
| prediction | 28.40 | 31.21 | 38.69 | 50.75 | |
| Temperature/°C | Stress Level | |||
|---|---|---|---|---|
| 30% | 40% | 60% | 80% | |
| 20 | 20.82 | 22.88 | 27.81 | 35.05 |
| 40 | 29.51 | 32.42 | 39.42 | 49.73 |
| 60 | 38.19 | 41.96 | 51.04 | 64.41 |
| 80 | 46.87 | 51.51 | 62.65 | 79.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, M.; Hu, L.; Liu, X. Effects of Stress Level and Elevated Temperature on Transverse Compression Stress Relaxation Behavior and Post-Relaxation Mechanical Performance of UD-CFRP. Polymers 2025, 17, 2718. https://doi.org/10.3390/polym17202718
Li J, Wang M, Hu L, Liu X. Effects of Stress Level and Elevated Temperature on Transverse Compression Stress Relaxation Behavior and Post-Relaxation Mechanical Performance of UD-CFRP. Polymers. 2025; 17(20):2718. https://doi.org/10.3390/polym17202718
Chicago/Turabian StyleLi, Jianwen, Maoqiang Wang, Lili Hu, and Xiaogang Liu. 2025. "Effects of Stress Level and Elevated Temperature on Transverse Compression Stress Relaxation Behavior and Post-Relaxation Mechanical Performance of UD-CFRP" Polymers 17, no. 20: 2718. https://doi.org/10.3390/polym17202718
APA StyleLi, J., Wang, M., Hu, L., & Liu, X. (2025). Effects of Stress Level and Elevated Temperature on Transverse Compression Stress Relaxation Behavior and Post-Relaxation Mechanical Performance of UD-CFRP. Polymers, 17(20), 2718. https://doi.org/10.3390/polym17202718







