Considering a Non-Constant Anisotropicity Parameter in the Giesekus Model
Abstract
1. Introduction
2. Constitutive Model
Asymptotic Behavior of the Model for Steady-State and Start-Up Shear Flow
3. Results and Discussion
3.1. Model Predictions in Steady-State Shear Flow
3.2. Model Predictions in Steady-State Uniaxial Elongational Flow
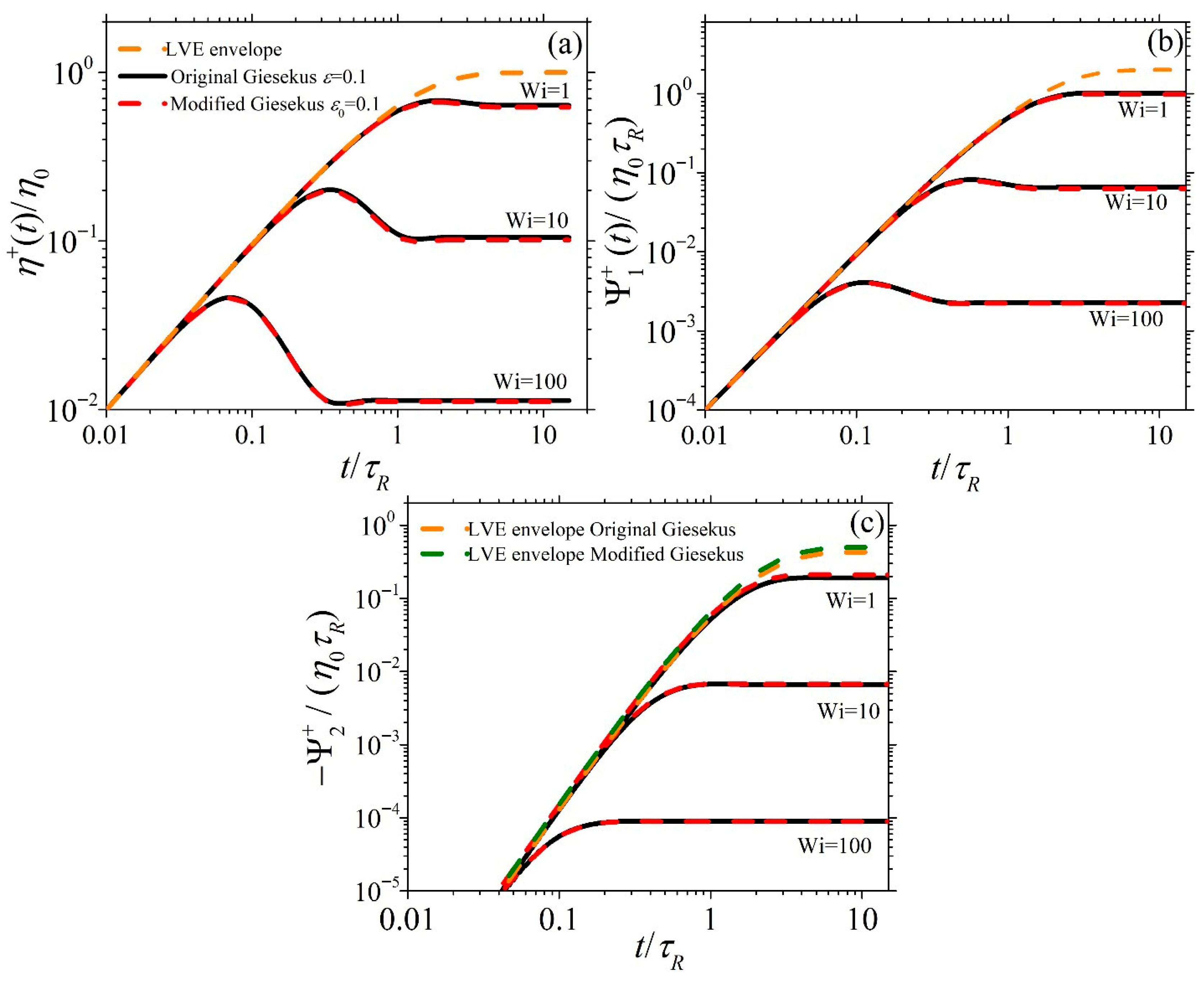
3.3. Model Predictions in Start-Up Shear Flow
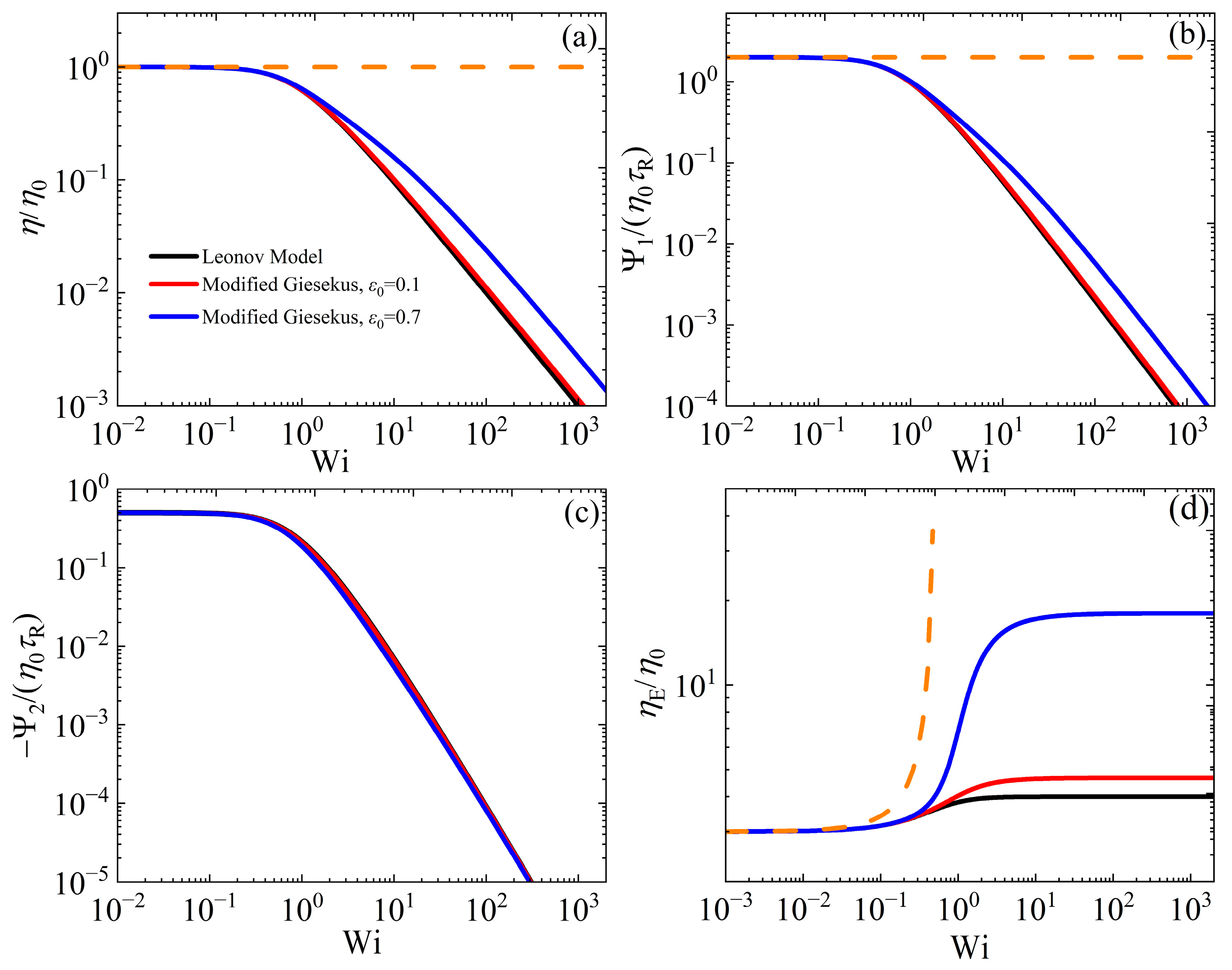
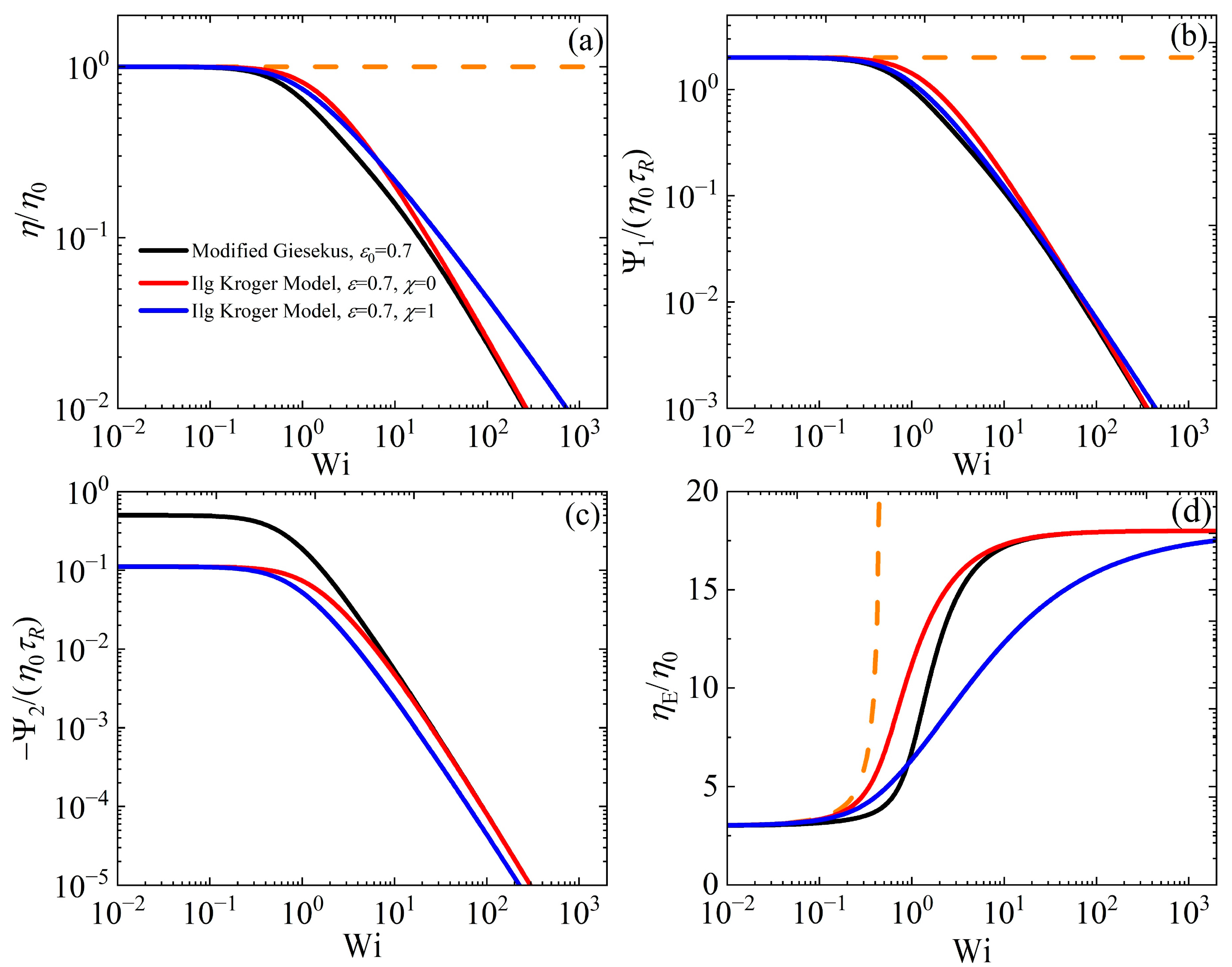
3.4. Comparison Against the Leonov and IK Models
3.5. Comparison with Experimental Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graham, M.D. The Sharkskin Instability of Polymer Melt Flows. Chaos 1999, 9, 154–163. [Google Scholar] [CrossRef]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; ISBN 978-0-471-38770-1. [Google Scholar]
- Maklad, O.; Poole, R.J. A Review of the Second Normal-Stress Difference; Its Importance in Various Flows, Measurement Techniques, Results for Various Complex Fluids and Theoretical Predictions. J. Non-Newton. Fluid Mech. 2021, 292, 104522. [Google Scholar] [CrossRef]
- Germann, N. Preface to Special Topic: One Hundred Years of Giesekus. Phys. Fluids 2024, 36, 050401. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999; ISBN 9780195121971. [Google Scholar]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions, 1st ed.; Butterworth-Heinemann: Oxford, UK, 1988; ISBN 978-0-409-90119-1. [Google Scholar]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Volume 1. Fluid Mechanics, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 1987; ISBN 047107375X. [Google Scholar]
- Tanner, R.I. Engineering Rheology, 2nd ed.; Oxford Engineering Science Series; Oxford University Press: Oxford, UK, 2002; ISBN 9780198564737. [Google Scholar]
- Kudish, I.I.; Volkov, S.S. A General Case of a Line Contact Lubricated by a Non-Newtonian Giesekus Fluid. Mathematics 2023, 11, 4679. [Google Scholar] [CrossRef]
- Hasani, M.A.; Norouzi, M.; Larimi, M.M.; Rooki, R. Computational Study on Drilling Mud Flow through Wellbore Annulus by Giesekus Viscoelastic Model. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 66–79. [Google Scholar] [CrossRef]
- Kadyirov, A.; Zaripov, R.; Makarushkin, D. Some Experimental Results for Converging Flow of Dilute Polymer Solution. Phys. Fluids 2024, 36, 033110. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, H. Finite Element Analysis as a Promising Approach for Texture Development of Plant-Based Meat Analogs. Phys. Fluids 2025, 37, 031302. [Google Scholar] [CrossRef]
- Giesekus, H. Stressing Behaviour in Simple Shear Flow as Predicted by a New Constitutive Model for Polymer Fluids. J. Non-Newton. Fluid Mech. 1983, 12, 367–374. [Google Scholar] [CrossRef]
- Giesekus, H. On Configuration-Dependent Generalized Oldroyd Derivatives. J. Non-Newton. Fluid Mech. 1984, 14, 47–65. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, F.C.; Amstrong, C.R.; Ole, H. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 1987; ISBN 978-0-471-80244-0. [Google Scholar]
- Curtiss, C.F.; Bird, R.B. A Kinetic Theory for Polymer Melts. I. The Equation for the Single-Link Orientational Distribution Function. J. Chem. Phys. 1980, 74, 2016–2025. [Google Scholar] [CrossRef]
- Curtiss, C.F.; Bird, R.B. A Kinetic Theory for Polymer Melts. II. The Stress Tensor and the Rheological Equation of State. J. Chem. Phys. 1980, 74, 2026–2033. [Google Scholar] [CrossRef]
- Giesekus, H. A Simple Constitutive Equation for Polymer Fluids Based on the Concept of Deformation-Dependent Tensorial Mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Schweizer, T.; Kröger, M. Communication: Appearance of Undershoots in Start-up Shear: Experimental Findings Captured by Tumbling-Snake Dynamics. J. Chem. Phys. 2017, 146, 161101. [Google Scholar] [CrossRef] [PubMed]
- Stephanou, P.S.; Kröger, M. Non-Constant Link Tension Coefficient in the Tumbling-Snake Model Subjected to Simple Shear. J. Chem. Phys. 2017, 147, 174903. [Google Scholar] [CrossRef]
- Ilg, P.; Kröger, M. Molecularly Derived Constitutive Equation for Low-Molecular Polymer Melts from Thermodynamically Guided Simulation. J. Rheol. 2011, 55, 69–93. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Mavrantzas, V.G. A Generalized Differential Constitutive Equation for Polymer Melts Based on Principles of Nonequilibrium Thermodynamics. J. Rheol. 2009, 53, 309–337. [Google Scholar] [CrossRef]
- Kröger, M. Models for Polymeric and Anisotropic Liquids; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-26210-7. [Google Scholar]
- Ehrentraut, H.; Hess, S. Viscosity Coefficients of Partially Aligned Nematic and Nematic Discotic Liquid Crystals. Phys. Rev. E 1995, 51, 2203. [Google Scholar] [CrossRef]
- Kröger, M.; Ammar, A.; Chinesta, F. Consistent Closure Schemes for Statistical Models of Anisotropic Fluids. J. Non-Newton. Fluid Mech. 2008, 149, 40–55. [Google Scholar] [CrossRef]
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems: With Internal Microstructure; Oxford University Press: New York, NY, USA, 1994; ISBN 019507694X. [Google Scholar]
- Nikiforidis, V.-M.; Tsalikis, D.G.; Stephanou, P.S. On The Use of a Non-Constant Non-Affine or Slip Parameter in Polymer Rheology Constitutive Modeling. Dynamics 2022, 2, 380–398. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Tsimouri, I.C.; Mavrantzas, V.G. Simple, Accurate and User-Friendly Differential Constitutive Model for the Rheology of Entangled Polymer Melts and Solutions from Nonequilibrium Thermodynamics. Materials 2020, 13, 2867. [Google Scholar] [CrossRef] [PubMed]
- Costanzo, S.; Huang, Q.; Ianniruberto, G.; Marrucci, G.; Hassager, O.; Vlassopoulos, D. Shear and Extensional Rheology of Polystyrene Melts and Solutions with the Same Number of Entanglements. Macromolecules 2016, 49, 3925–3935. [Google Scholar] [CrossRef]
- Kim, J.M.; Baig, C. Precise Analysis of Polymer Rotational Dynamics. Sci. Rep. 2016, 6, 19127. [Google Scholar] [CrossRef] [PubMed]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Individual Chain Dynamics of a Polyethylene Melt Undergoing Steady Shear Flow. J. Rheol. 2015, 59, 119–153. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, F.; Stephanou, P.S. Considering a Non-Constant Anisotropicity Parameter in the Giesekus Model. Polymers 2025, 17, 2510. https://doi.org/10.3390/polym17182510
Karami F, Stephanou PS. Considering a Non-Constant Anisotropicity Parameter in the Giesekus Model. Polymers. 2025; 17(18):2510. https://doi.org/10.3390/polym17182510
Chicago/Turabian StyleKarami, Fatemeh, and Pavlos S. Stephanou. 2025. "Considering a Non-Constant Anisotropicity Parameter in the Giesekus Model" Polymers 17, no. 18: 2510. https://doi.org/10.3390/polym17182510
APA StyleKarami, F., & Stephanou, P. S. (2025). Considering a Non-Constant Anisotropicity Parameter in the Giesekus Model. Polymers, 17(18), 2510. https://doi.org/10.3390/polym17182510





