Finite Element Analysis and Experimental Investigation on the Machinability of PMMA/CNT Composites via Nanosectioning
Abstract
1. Introduction
2. Preparation of Nanocomposites
2.1. Materials and Preparation
2.2. Carbon Nanotube Distribution
3. Experimental Sectioning
4. Modeling of Sectioning of PMMA/CNT
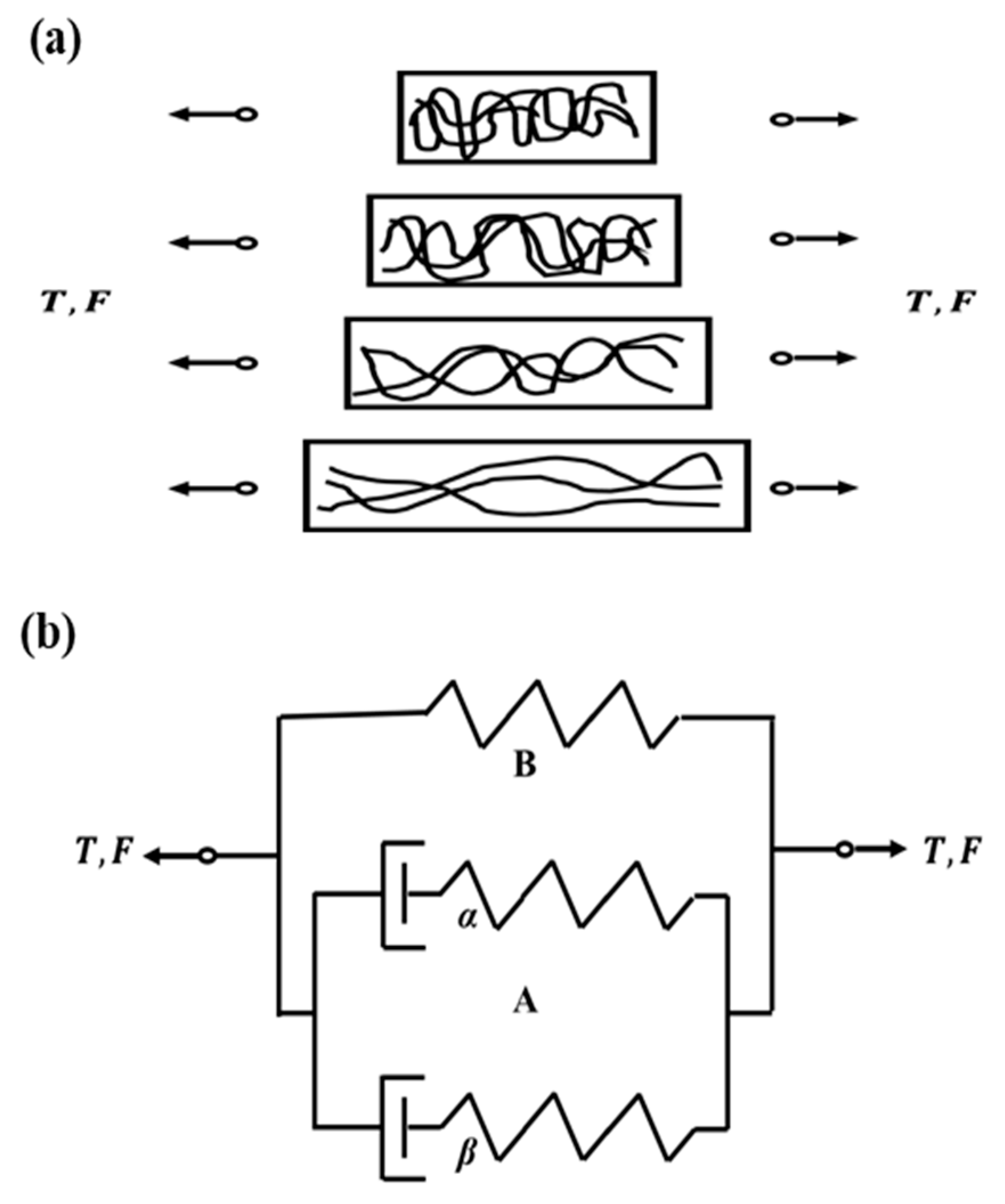
4.1. Mulliken–Boyce Model
4.2. Kinematics
4.3. Material Description and Constitutive Relations
4.4. Parameters for PMMA
4.5. Sectioning Model
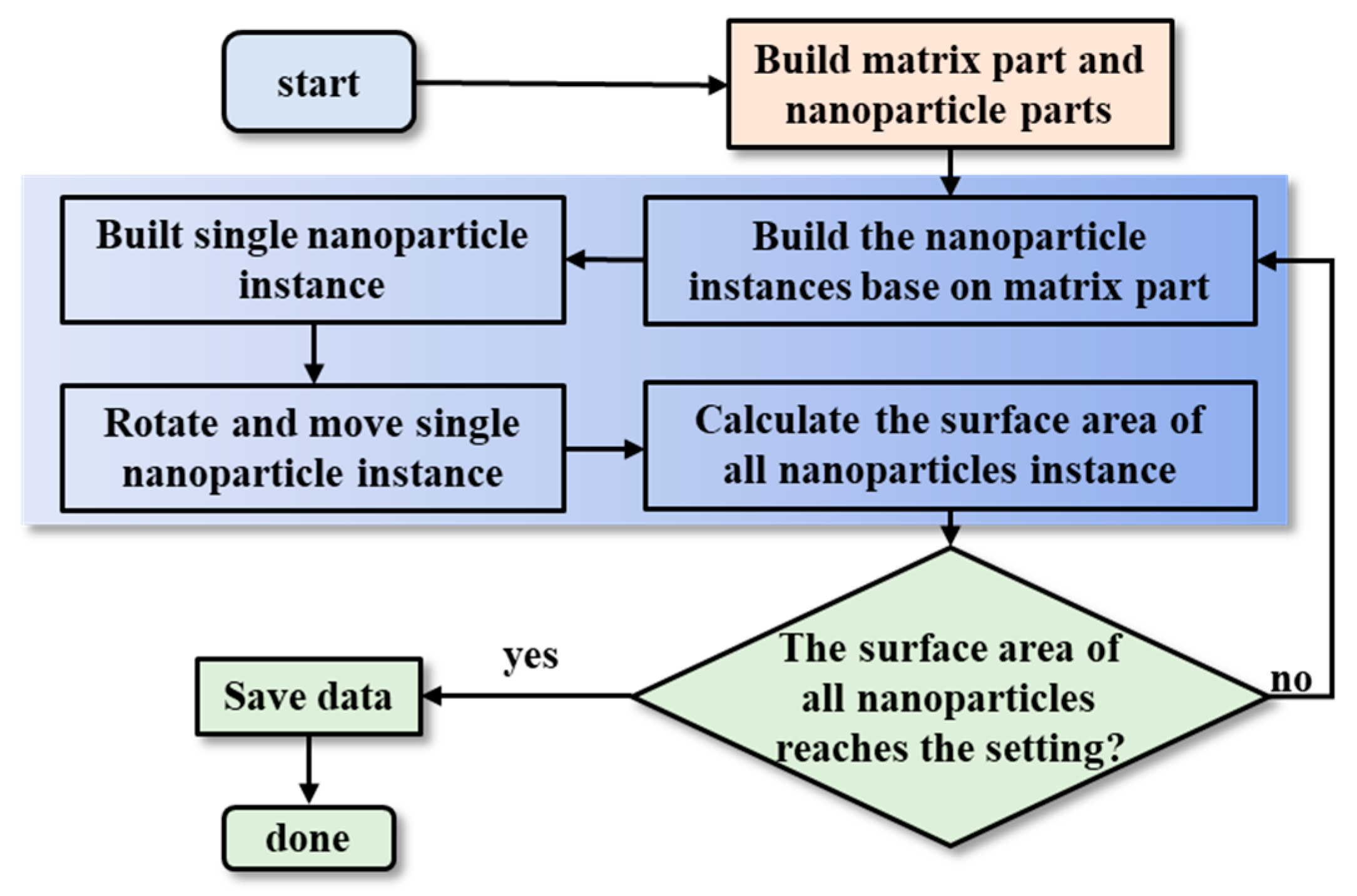
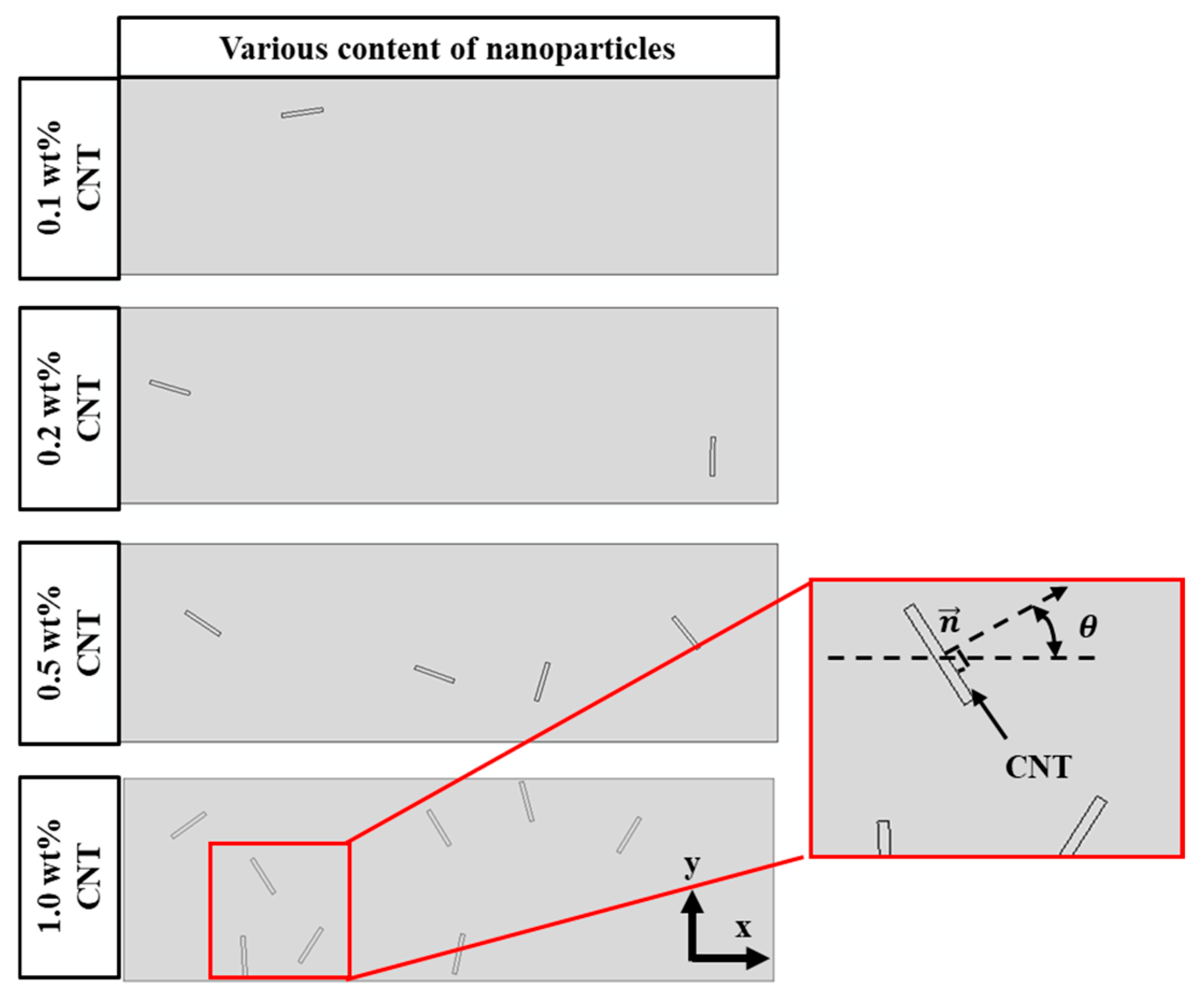
4.6. Distribution of CNTs
5. Results and Discussion
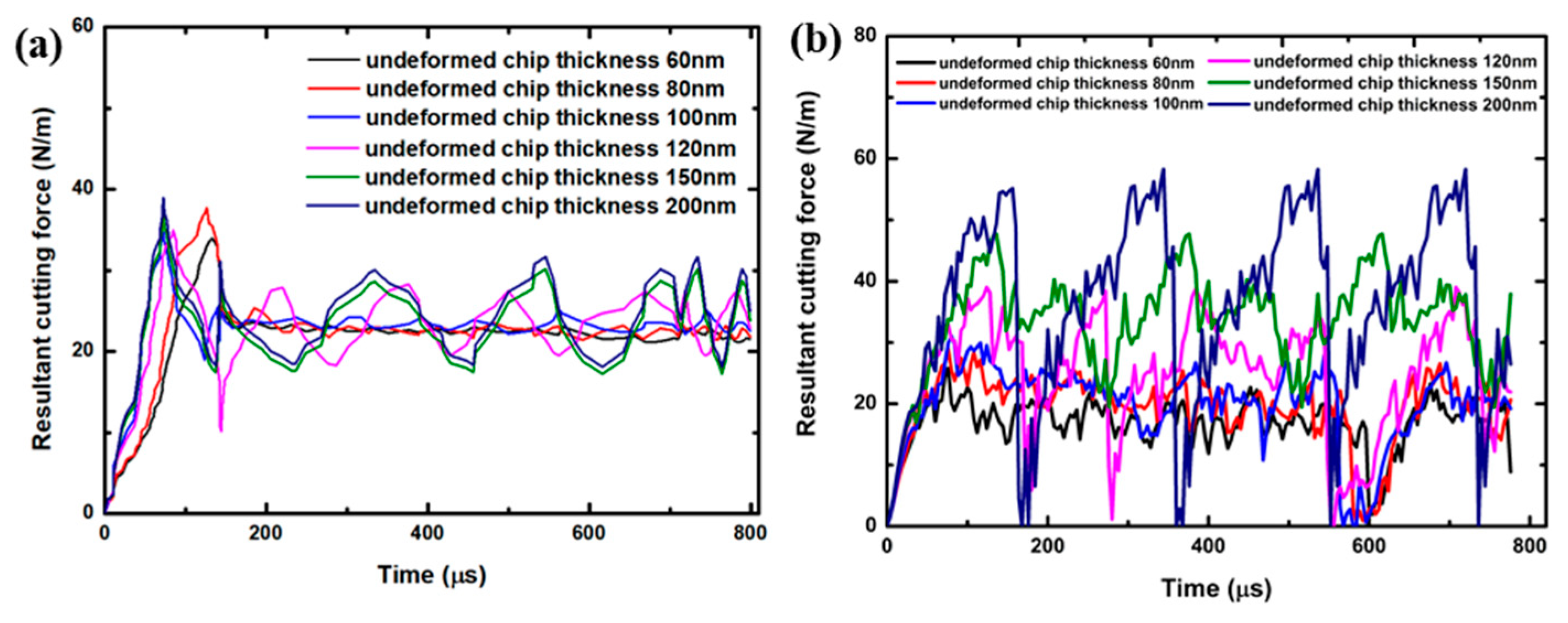
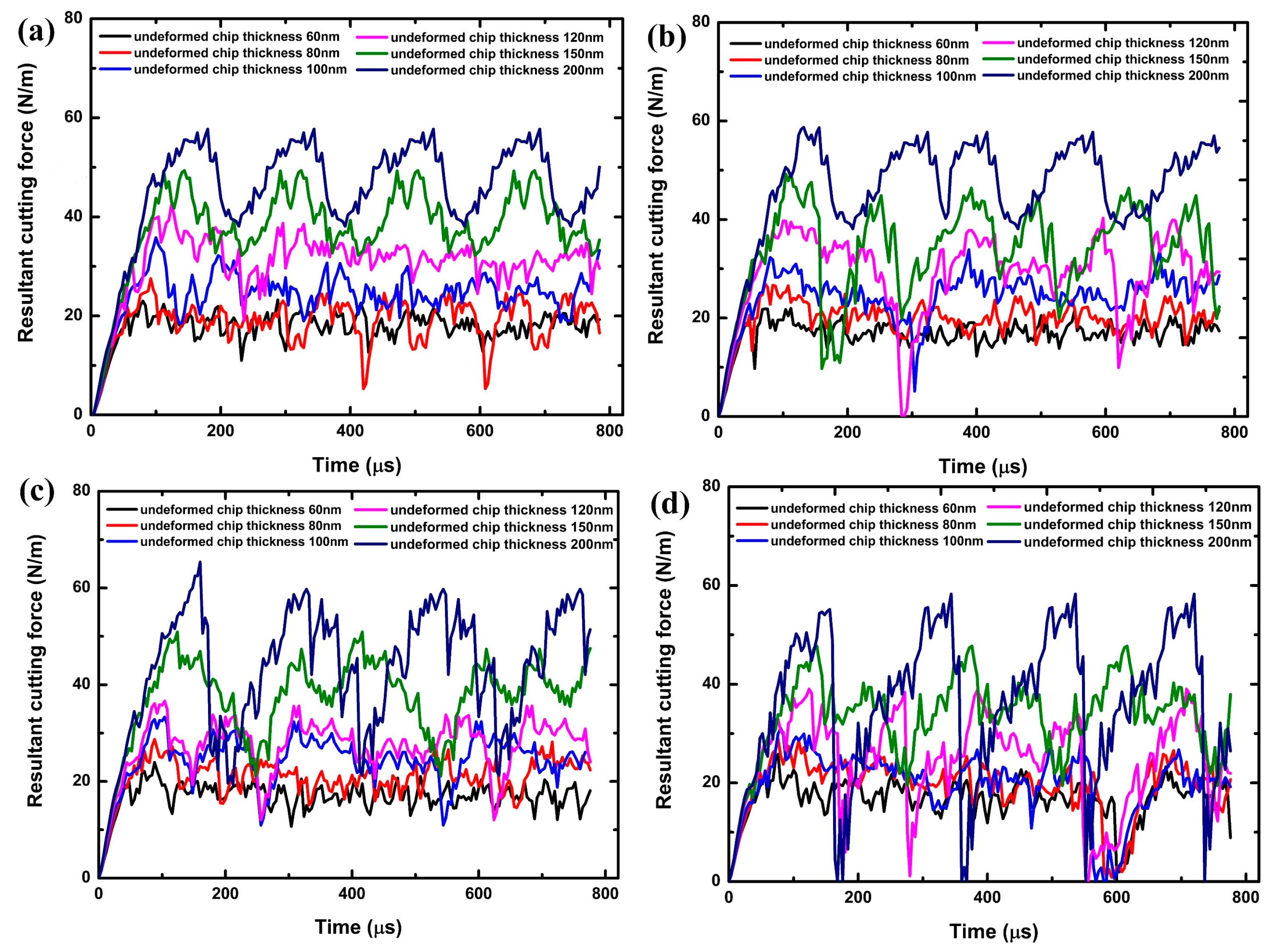
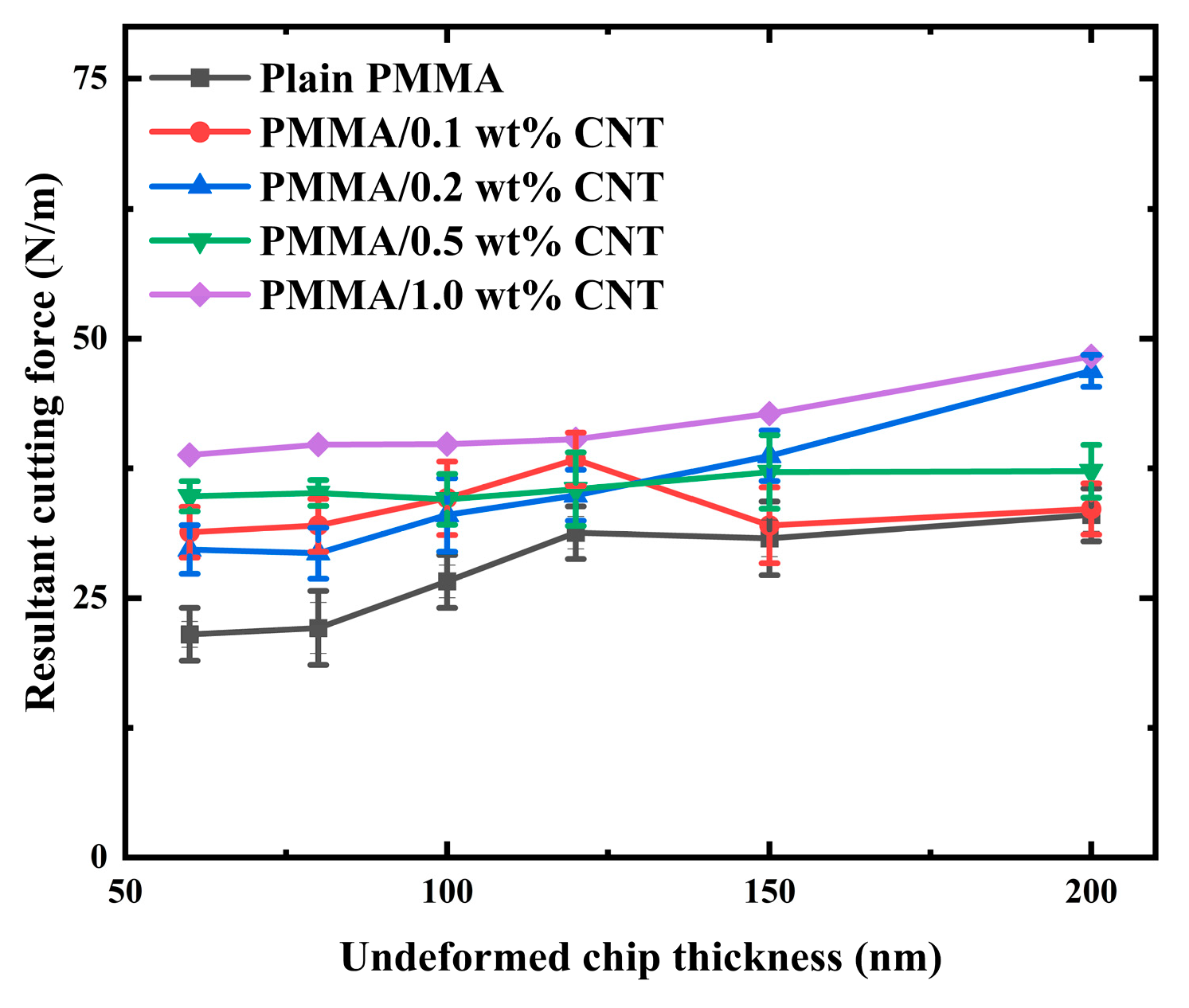
5.1. Cutting Force
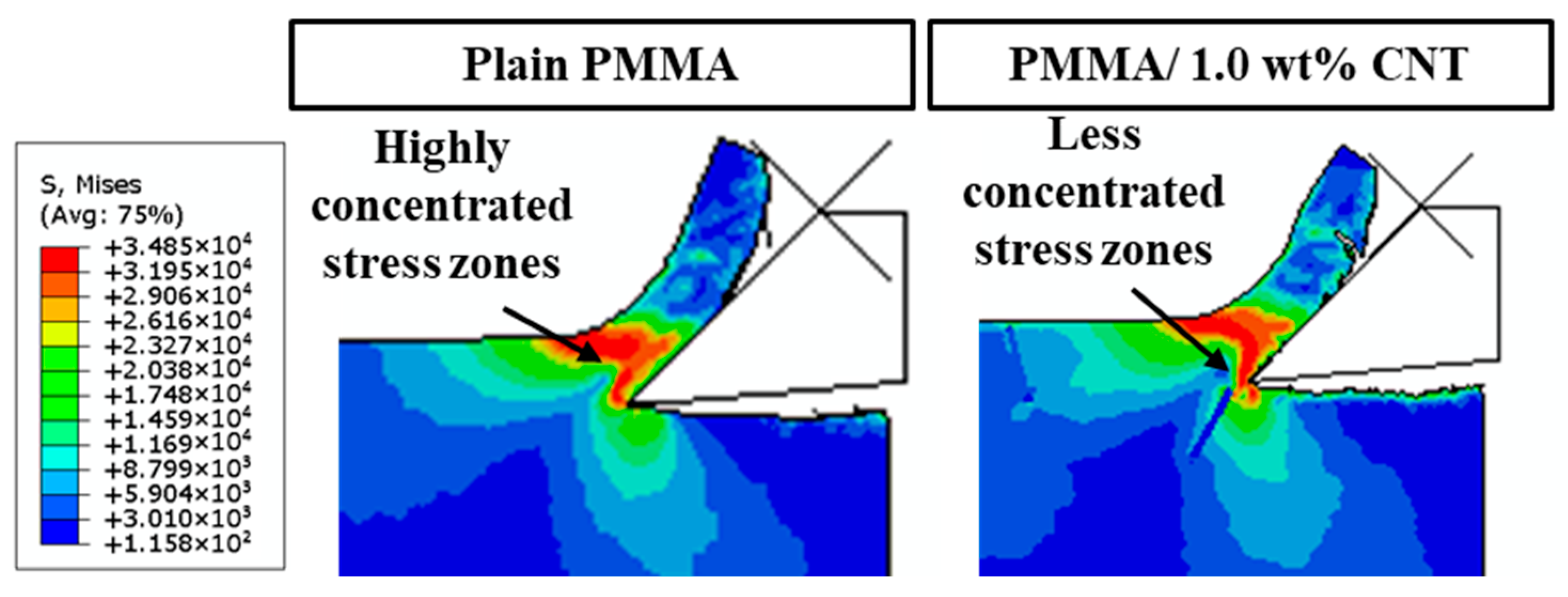
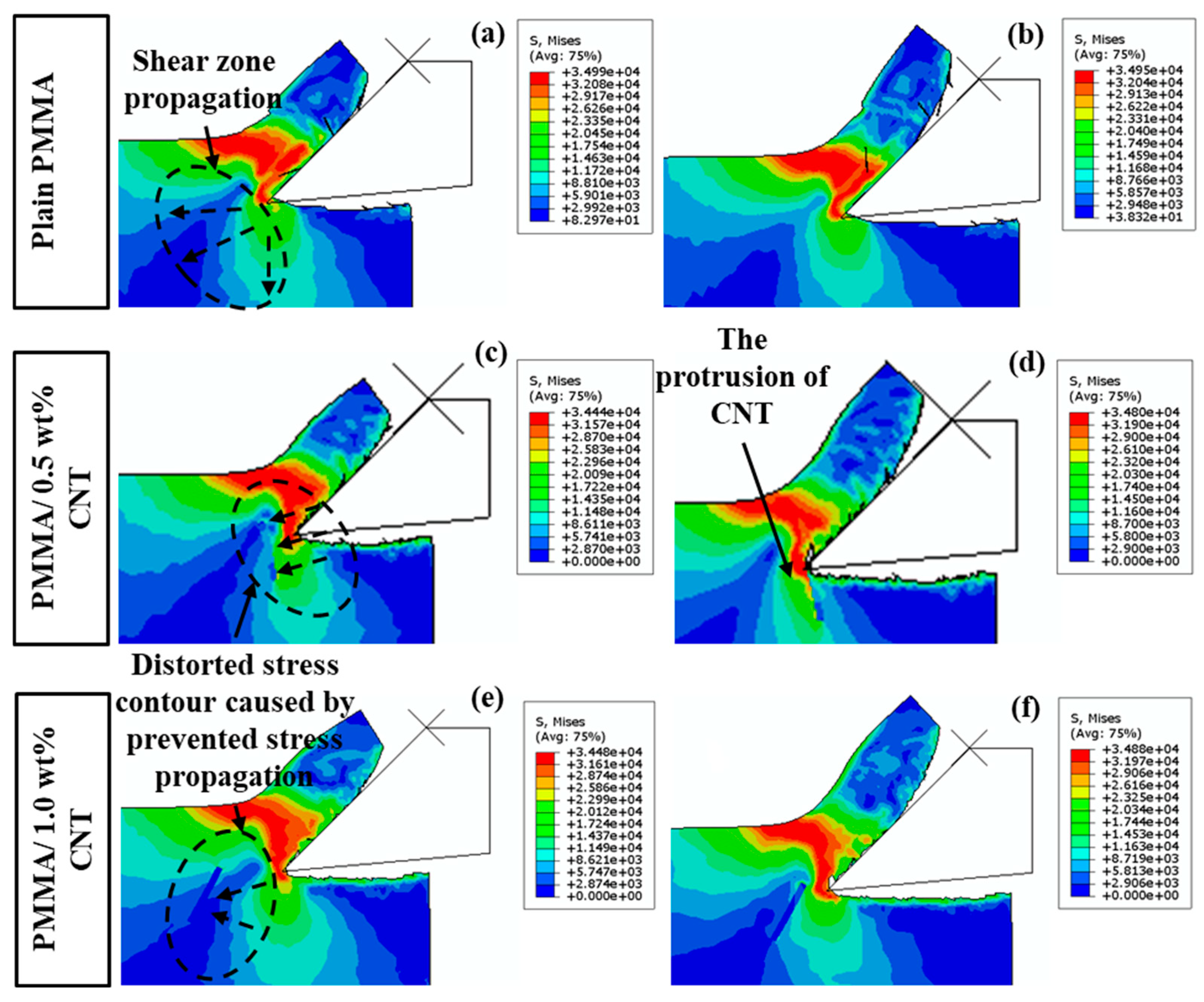
5.2. Stress Distribution
5.3. Validity and Limitations of the Geometric Approximation
5.4. Experimental Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fenta, E.W.; Mebratie, B.A. Advancements in carbon nanotube–polymer composites: Enhancing properties and applications through advanced manufacturing techniques. Heliyon 2024, 10, e36490. [Google Scholar] [CrossRef] [PubMed]
- Teymouri, A.; Al-Mahaidi, R.; Kazemi-Kamyab, H. A review on carbon nanofiber production and application in cementitious mixtures. J. Build. Eng. 2024, 84, 108519. [Google Scholar] [CrossRef]
- Yuan, J.; Yu, S.; Wang, Y.; Chen, X.; Zhou, S.; Zhong, J.; Lu, D. Nanocarbon-enhanced cement composites for self-sensing and monitoring in transport infrastructure. Case Stud. Constr. Mater. 2024, 21, e04082. [Google Scholar] [CrossRef]
- Yu, K.; Tay, Y.W.D.; Ting, S.J.; Yang, E.-H. Bacterially Derived Cellulose/Reduced Graphene Oxide Composite Films: Mechanical, Electrical, and Thermal Properties. ACS Appl. Nano Mater. 2020, 3, 12055–12063. [Google Scholar] [CrossRef]
- Ge, J.; Catalanotti, G.; Falzon, B.G.; Higgins, C.; McClory, C.; Thiebot, J.A.; Zhang, L.; He, M.; Jin, Y.; Sun, D. Process characteristics, damage mechanisms and challenges in machining of fibre-reinforced thermoplastic polymer (FRTP) composites: A review. Compos. Part B Eng. 2024, 273, 111247. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, W.; Luo, M.; Catalanotti, G.; Falzon, B.G.; Higgins, C.; Zhang, D.; Jin, Y.; Sun, D. Multi-objective optimization of thermoplastic CF/PEKK drilling through a hybrid method: An approach towards sustainable manufacturing. Compos. Part A Appl. Sci. Manuf. 2023, 167, 107418. [Google Scholar] [CrossRef]
- Smoleń, P.; Czujko, T.; Komorek, Z.; Grochala, D.; Rutkowska, A.; Osiewicz-Powęzka, M. Mechanical and Electrical Properties of Epoxy Composites Modified by Functionalized Multiwalled Carbon Nanotubes. Materials 2021, 14, 3325. [Google Scholar] [CrossRef]
- Wang, H.; Shin, H. A multiscale model to predict fatigue crack growth behavior of carbon nanofiber/epoxy nanocomposites. Int. J. Fatigue 2023, 168, 107467. [Google Scholar] [CrossRef]
- Yazdanparast, R.; Rafiee, R.; Kalhori, H.; Li, B. Dynamic mechanical behavior of CNT-reinforced epoxy under medium-strain rate: A comparative study. Compos. Struct. 2024, 344, 118343. [Google Scholar] [CrossRef]
- Ge, J.; Fu, G.; Almeida Jr, J.H.S.; Jin, Y.; Sun, D. Thermal effect in CFRP machining: Temperature field characteristics, heat generation mechanism and thermal damage management. Compos. Struct. 2025, 356, 118845. [Google Scholar] [CrossRef]
- Uyor, U.O.; Popoola, P.A.; Popoola, O.M.; Aigbodion, V.S. A Review of Recent Advances on the Properties of Polypropylene–Carbon Nanotubes Composites. J. Thermoplast. Compos. Mater. 2023, 36, 3737–3770. [Google Scholar] [CrossRef]
- Mousavi, S.R.; Estaji, S.; Kiaei, H.; Mansourian-Tabaei, M.; Nouranian, S.; Jafari, S.H.; Ruckdäschel, H.; Arjmand, M.; Khonakdar, H.A. A Review of Electrical and Thermal Conductivities of Epoxy Resin Systems Reinforced with Carbon Nanotubes and Graphene-Based Nanoparticles. Polym. Test. 2022, 112, 107645. [Google Scholar] [CrossRef]
- Sarode, V.B.; Patil, R.D.; Chaudhari, G.E. Characterization of functionalized multi-walled carbon nanotubes. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Le, B.D.Q.; Vu, N.V.; Ngoi, B.K.A.; Nguyen, N.-T. Micro-end-milling of carbon nanotube-reinforced epoxy nanocomposites manufactured using three-roll mill technique. J. Manuf. Process. 2021, 70, 307–320. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Mostofa, M.G.; Jun, M.; Park, S.S. Characterization and micromilling of flow induced aligned carbon nanotube nanocomposites. J. Micro. NanoManuf. 2013, 1, 011005. [Google Scholar] [CrossRef]
- Samuel, J.; Dikshit, A.; DeVor, R.E.; Kapoor, S.G.; Hsia, K.J. Effect of carbon nanotube (CNT) loading on the thermomechanical properties and the machinability of CNT-reinforced polymer composites. J. Manuf. Sci. Eng. 2009, 131, 031008. [Google Scholar] [CrossRef]
- Gong, Y.; Baik, Y.J.; Li, C.P.; Byon, C.; Park, J.M.; Ko, T.J. Experimental and modeling investigation on machined surfaces of HDPE-MWCNT polymer nanocomposite. Int. J. Adv. Manuf. Technol. 2017, 91, 3527. [Google Scholar] [CrossRef]
- Weule, H.; Hüntrup, V.; Tritschle, H. Micro-cutting of steel to meet new requirements in miniaturization. CIRP Ann. 2001, 50, 61–64. [Google Scholar] [CrossRef]
- Liu, X.; DeVor, R.E.; Kapoor, S.G. An analytical model for the prediction of minimum chip thickness in micromachining. J. Manuf. Sci. Eng. 2006, 128, 474–481. [Google Scholar] [CrossRef]
- Ge, J.; Luo, M.; Zhang, D.; Catalanotti, G.; Falzon, B.G.; McClelland, J.; Higgins, C.; Jin, Y.; Sun, D. Temperature field evolution and thermal-mechanical interaction induced damage in drilling of thermoplastic CF/PEKK—A comparative study with thermoset CF/epoxy. J. Manuf. Process. 2023, 88, 167–183. [Google Scholar] [CrossRef]
- Kim, J.D.; Kim, D.S. Theoretical analysis of micro-cutting characteristics in ultraprecision machining. J. Mater. Process. Tech. 1995, 49, 387–398. [Google Scholar] [CrossRef]
- Saito, K. Fracture phenomena of high polymers in cutting. J. Macromol. Sci. Part B 1981, 19, 459–485. [Google Scholar] [CrossRef]
- Liu, X.; DeVor, R.E.; Kapoor, S.G.; Ehmann, K.F. The mechanics of machining at the microscale: Assessment of the current state of the science. J. Manuf. Sci. Eng. 2004, 126, 666–678. [Google Scholar] [CrossRef]
- Park, S.S.; Malekian, M. Mechanistic modeling and accurate measurement of micro end milling forces. CIRP Ann. 2009, 58, 49–52. [Google Scholar] [CrossRef]
- Ge, J.; Catalanotti, G.; Falzon, B.G.; McClelland, J.; Higgins, C.; Jin, Y.; Sun, D. Towards understanding the hole making performance and chip formation mechanism of thermoplastic carbon fibre/polyetherketoneketone composite. Compos. Part B Eng. 2022, 234, 109752. [Google Scholar] [CrossRef]
- Vogler, M.P.; DeVor, R.E.; Kapoor, S.G. On the modeling and analysis of machining performance in micro-endmilling, Part I: Surface generation. J. Manuf. Sci. Eng. 2005, 126, 685–694. [Google Scholar] [CrossRef]
- Aramcharoen, A.; Mativenga, P.T. Size effect and tool geometry in micromilling of tool steel. Precis. Eng. 2009, 33, 402–407. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Ge, J.; Tan, W.; Ahmad, S.; Falzon, B.G.; Catalanotti, G.; Higgins, C.; Jin, Y.; Sun, D. Temperature-dependent cutting physics in orthogonal cutting of carbon fibre reinforced thermoplastic (CFRTP) composite. Compos. Part A Appl. Sci. Manuf. 2024, 176, 107820. [Google Scholar] [CrossRef]
- Ge, J.; Yao, Z.; Wu, M.; Almeida Jr, J.H.S.; Jin, Y.; Sun, D. Tackling data scarcity in machine learning-based CFRP drilling performance prediction through a broad learning system with virtual sample generation (BLS-VSG). Compos. Part B Eng. 2025, 305, 112701. [Google Scholar] [CrossRef]
- Mulliken, A.D.; Boyce, M.C. Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Rennhofer, H.; Zanghellini, B. Dispersion State and Damage of Carbon Nanotubes and Carbon Nanofibers by Ultrasonic Dispersion: A Review. Nanomaterials 2021, 11, 1469. [Google Scholar] [CrossRef]
- Ma, P.C.; Siddiqui, N.A.; Marom, G.; Kim, J.-K. Dispersion and Functionalization of Carbon Nanotubes for Polymer-Based Nanocomposites: A Review. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1345–1367. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Terentjev, E.M. Dispersion of Carbon Nanotubes: Mixing, Sonication, Stabilization, and Composite Properties. Polymers 2012, 4, 275–295. [Google Scholar] [CrossRef]
- Zheng, X.L.; Wang, H.; Yan, J.H. Notch strength and notch sensitivity of polymethyl methacrylate glasses. Mater. Sci. Eng. A 2003, 349, 80–88. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Stern, T.; Marom, G. Fracture mechanisms and toughness in polymer nanocomposites: A brief review. J. Compos. Sci. 2024, 8, 395. [Google Scholar] [CrossRef]
- Böhm, H.J.; Eckschlager, A.; Han, W. Multi-inclusion unit cell models for metal matrix composites with randomly oriented discontinuous reinforcements. Comput. Mater. Sci. 2002, 25, 42–53. [Google Scholar] [CrossRef]
- Kari, S.; Berger, H.; Gabbert, U. Numerical evaluation of effective material properties of randomly distributed short cylindrical fibre composites. Comput. Mater. Sci. 2007, 39, 198–204. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Blum Enthal, W.R.; Lowe, T.C. The tensile strength of short fibre-reinforced composites. J. Mater. Sci. 1997, 32, 2037–2043. [Google Scholar] [CrossRef]
- Gearing, B.P.; Anand, L. On modeling the deformation and fracture response of glassy polymers due to shear-yielding and crazing. Int. J. Solids Struct. 2004, 41, 3125–3150. [Google Scholar] [CrossRef]
- Fu, G.; Sun, F.; Sun, F.; Huo, D.; Shyha, I.; Fang, C.; Gao, Q. Finite element and experimental studies on the machining process of polymer/graphene nanoplatelet nanocomposites. Compos. Part B Eng. 2022, 230, 109545. [Google Scholar] [CrossRef]
- Dikshit, A.; Samuel, J.; DeVor, R.E.; Kapoor, S.G. Microstructure-level machining simulation of carbon nanotube reinforced polymer composites—Part II: Model interpretation and application. J. Manuf. Sci. Eng. 2008, 130, 031115. [Google Scholar] [CrossRef]
- Sun, F.; Gamstedt, E.K. Experimental and numerical investigation on shear banding during nanomachining of an amorphous glassy polymer. Int. J. Mech. Sci. 2019, 151, 13–21. [Google Scholar] [CrossRef]
- Dikshit, A.; Samuel, J.; DeVor, R.E.; Kapoor, S.G. Microstructure-level machining simulation of carbon nanotube reinforced polymer composites-Part I: Model development and validation. J. Manuf. Sci. Eng. 2008, 130, 031114. [Google Scholar] [CrossRef]
- Petrone, L.; Cieśla, M. Random sequential adsorption of oriented rectangles with random aspect ratio. Phys. Rev. E 2021, 104, 034903. [Google Scholar] [CrossRef] [PubMed]
- Estakhrianhaghighi, E.; Mirabolghasemi, A.; Shi, J.; Lessard, L.; Akbarzadeh, A. Architected cellular fiber-reinforced composite. Compos. Part B Eng. 2022, 238, 109894. [Google Scholar] [CrossRef]
- Kloza, P.A.; Elliott, J.A. Inverse projection of axisymmetric orientation distributions. arXiv 2023, arXiv:2305.06433. [Google Scholar] [CrossRef]
- He, Y.; Luo, M.; Wu, B.; Yao, C.; Wang, D. Study on the cutting force responses in machining multiscale carbon nanotube/carbon fiber reinforced polymer composites. J. Manuf. Process. 2023, 95, 160–170. [Google Scholar] [CrossRef]
- Wacker, I.; Curticean, R.; Ryklin, D.; Hutzler, A.; Grill, W. Deconstructing 3D structured materials by modern ultramicrotomy for multimodal imaging and volume analysis across length scales. Adv. Funct. Mater. 2023, 33, 2302025. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Shao, L.-H.; Wang, J.; Li, Y. Micromechanics-based modeling of temperature-dependent effective moduli of fiber-reinforced polymer composites with interfacial debonding. Compos. Part A Appl. Sci. Manuf. 2024, 180, 108049. [Google Scholar] [CrossRef]
- Yazdanparast, R.; Rafiee, R. A rate-dependent cohesive zone model for dynamic crack growth in carbon nanotube reinforced polymers. Int. J. Solids Struct. 2024, 300, 112932. [Google Scholar] [CrossRef]
- Mirkhalaf, S.M.; van Beurden, T.J.H.; Ekh, M.; Larsson, F.; Fagerström, M. An FE-based orientation averaging model for elasto-plastic behavior of short fiber composites. Int. J. Mech. Sci. 2022, 219, 107097. [Google Scholar] [CrossRef]
- Hessman, P.A.; Riedel, T.; Welschinger, F.; Hornberger, K.; Böhlke, T. Microstructural analysis of short glass fiber reinforced thermoplastics based on X-ray micro-computed tomography. Compos. Sci. Technol. 2019, 183, 107752. [Google Scholar] [CrossRef]
- Aliotta, L.; Lazzeri, A. A proposal to modify the Kelly–Tyson equation to calculate the interfacial shear strength (IFSS) of composites with low aspect ratio fibers. Compos. Sci. Technol. 2020, 186, 107920. [Google Scholar] [CrossRef]
- Razavi, M.; Cheng, S.; Huang, D.; Zhang, S.; Wang, S.-Q. Crazing and yielding in glassy polymers of high molecular weight. Polymer 2020, 197, 122445. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, F.; Song, D.; Liu, J.; Xu, Q.; Zhou, Q.; Wang, H. A study on the effect of cutting temperature on CFRP hole wall damage in continuous drilling process. Machines 2024, 12, 809. [Google Scholar] [CrossRef]
- Palacios, G. Random sequential adsorption with correlated defects. Phys. Rev. E 2024, 109, 064154. [Google Scholar] [CrossRef] [PubMed]
- Mentges, N.; Çelik, H.; Hopmann, C.; Fagerström, M.; Mirkhalaf, S.M. Micromechanical modelling of short fibre composites considering fibre length distributions. Compos. Part B Eng. 2023, 264, 110868. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J.; Zheng, Z.; Li, X.; Zhang, C. Repetitive ultramicrotome trimming and SEM imaging for large-volume polymer microstructures. Sci. Rep. 2024, 14, 9221. [Google Scholar] [CrossRef] [PubMed]
- Nabergoj, M.; Urevc, J.; Halilovič, M. Function-based reconstruction of the fiber orientation distribution function of short-fiber-reinforced polymers. J. Rheol. 2022, 66, 147–160. [Google Scholar] [CrossRef]
- Rashid, M.K.; Kahraman, R.; Boyaci, B.; Yildiz, M.; Canyurt, O.E.; Ertugrul, O. Nanotechnology-enhanced fibre-reinforced polymer composites: A comprehensive review. Heliyon 2024, 10, e33126. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Fisher, T.; Kazanci, Z.; Jin, Y.; Sun, D. Drilling-induced defects and mechanical performance of open-hole structures in thermoplastic and thermoset polymer composites. Compos. Commun. 2025, 53, 102223. [Google Scholar] [CrossRef]
- Yi, Q.; Tian, G.Y.; Malekmohammadi, H.; Laureti, S.; Ricci, M.; Gao, S. Inverse reconstruction of fibre orientation in multilayer CFRP using forward FEM and eddy current pulsed thermography. NDTE Int. 2021, 122, 102474. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, J.; Xu, M.; Wu, M.; Yao, Z.; Fu, G.; Zhang, W.; Falzon, B.G.; Catalanotti, G.; Xu, J.; et al. Data-driven CFRP machining performance prediction and optimization: Advances, challenges and future prospects. Thin-Walled Struct. 2025, 216, 113721. [Google Scholar] [CrossRef]
- Atkins, A.G. Toughness and cutting: A new way of simultaneously determining ductile fracture toughness and strength. Eng. Fract. Mech. 2005, 72, 849–860. [Google Scholar] [CrossRef]
- Patel, Y.; Blackman, B.R.K.; Williams, J.G. Determining fracture toughness from cutting tests on polymers. Eng. Fract. Mech. 2009, 76, 2711–2730. [Google Scholar] [CrossRef]
- Satapathy, B.; Weidisch, R.; Pötschke, P.; Janke, A. Tough-to-brittle transition in multiwalled carbon nanotube (MWNT)/polycarbonate nanocomposites. Compos. Sci. Technol. 2007, 67, 867–879. [Google Scholar] [CrossRef]
- Sun, F.; Wiklund, U.; Avilés, F.; Gamstedt, E.K. Assessing local yield stress and fracture toughness of carbon nanotube poly (methyl methacrylate) composite by nanosectioning. Compos. Sci. Technol. 2017, 153, 95–102. [Google Scholar] [CrossRef]




| Symbol | Unit | Value |
|---|---|---|
| 6.95 | ||
| 1.77 | ||
| 5.528 | ||
| 6.036 | ||
| 0.26 | ||
| 0.26 | ||
| MPa | 200 | |
| MPa | 500 | |
| MPa | 14 | |
| N | 2.1 |
| Parameter | Value |
|---|---|
| Cutting speed | 1.0 mm/s |
| Cutting thickness | 60, 80, 100, 120, 150, 200 nm |
| Tool rake angle | 45.0° |
| Tool clearance angle | 5.0° |
| Content of nanoparticles | 0.1 wt%, 0.2 wt%, 0.5 wt%, 1.0 wt% |
| Surface area fraction of nanoparticles | 0.05%, 0.1%, 0.25%, 0.5% |
| Length of nanoparticle | 100 nm |
| Width of nanoparticle | 10 nm |
| Length of model | 1.6 µm |
| Height of model | 0.5 µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, G.; Ge, J.; Li, H.; Sun, F.; Wu, W. Finite Element Analysis and Experimental Investigation on the Machinability of PMMA/CNT Composites via Nanosectioning. Polymers 2025, 17, 2441. https://doi.org/10.3390/polym17182441
Fu G, Ge J, Li H, Sun F, Wu W. Finite Element Analysis and Experimental Investigation on the Machinability of PMMA/CNT Composites via Nanosectioning. Polymers. 2025; 17(18):2441. https://doi.org/10.3390/polym17182441
Chicago/Turabian StyleFu, Guoyu, Jia Ge, Hao Li, Fengzhen Sun, and Weizhou Wu. 2025. "Finite Element Analysis and Experimental Investigation on the Machinability of PMMA/CNT Composites via Nanosectioning" Polymers 17, no. 18: 2441. https://doi.org/10.3390/polym17182441
APA StyleFu, G., Ge, J., Li, H., Sun, F., & Wu, W. (2025). Finite Element Analysis and Experimental Investigation on the Machinability of PMMA/CNT Composites via Nanosectioning. Polymers, 17(18), 2441. https://doi.org/10.3390/polym17182441






